Suspended Sediment Source and Transport Mechanisms in a Himalayan River
Abstract
1. Introduction
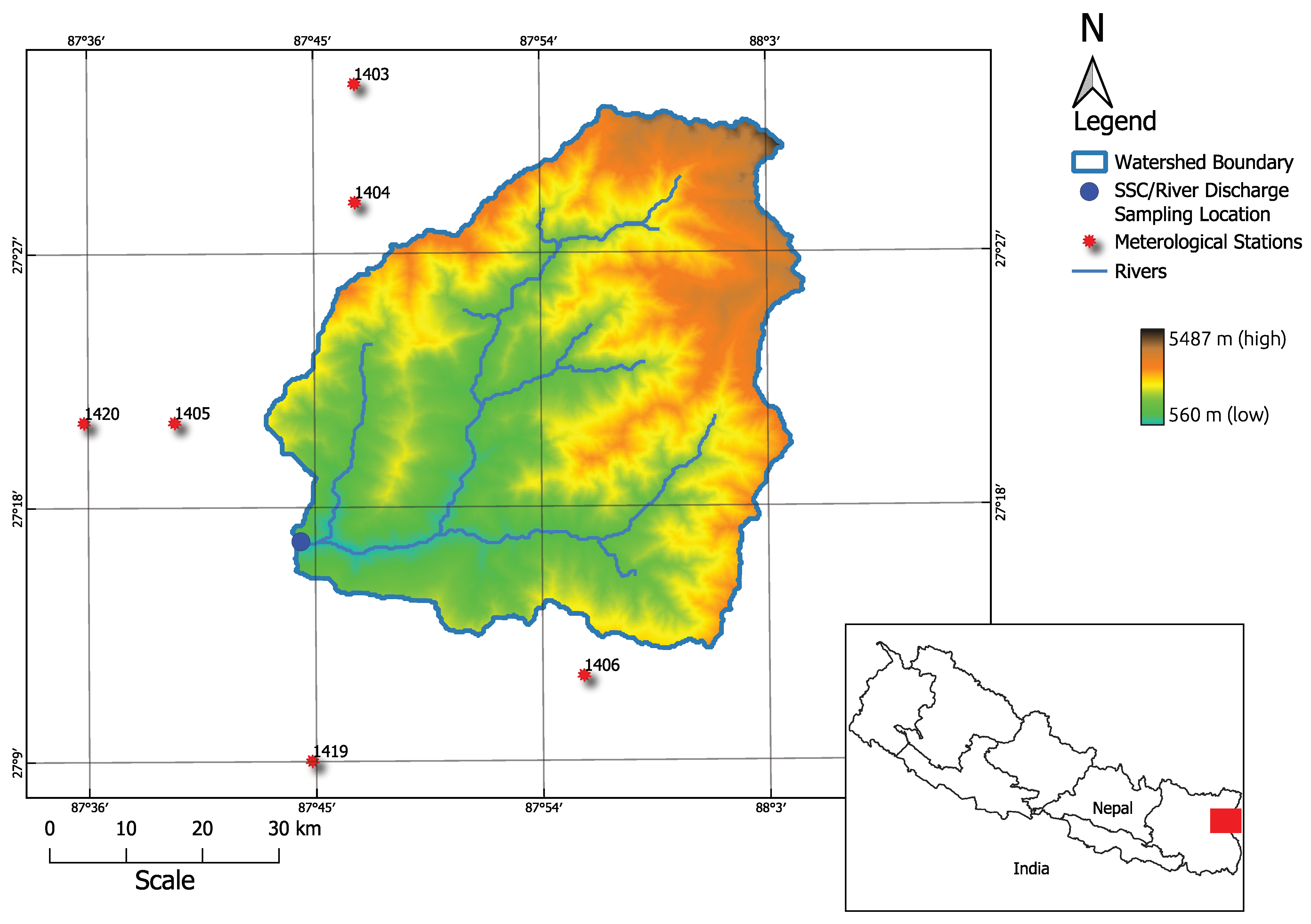
2. Study Area
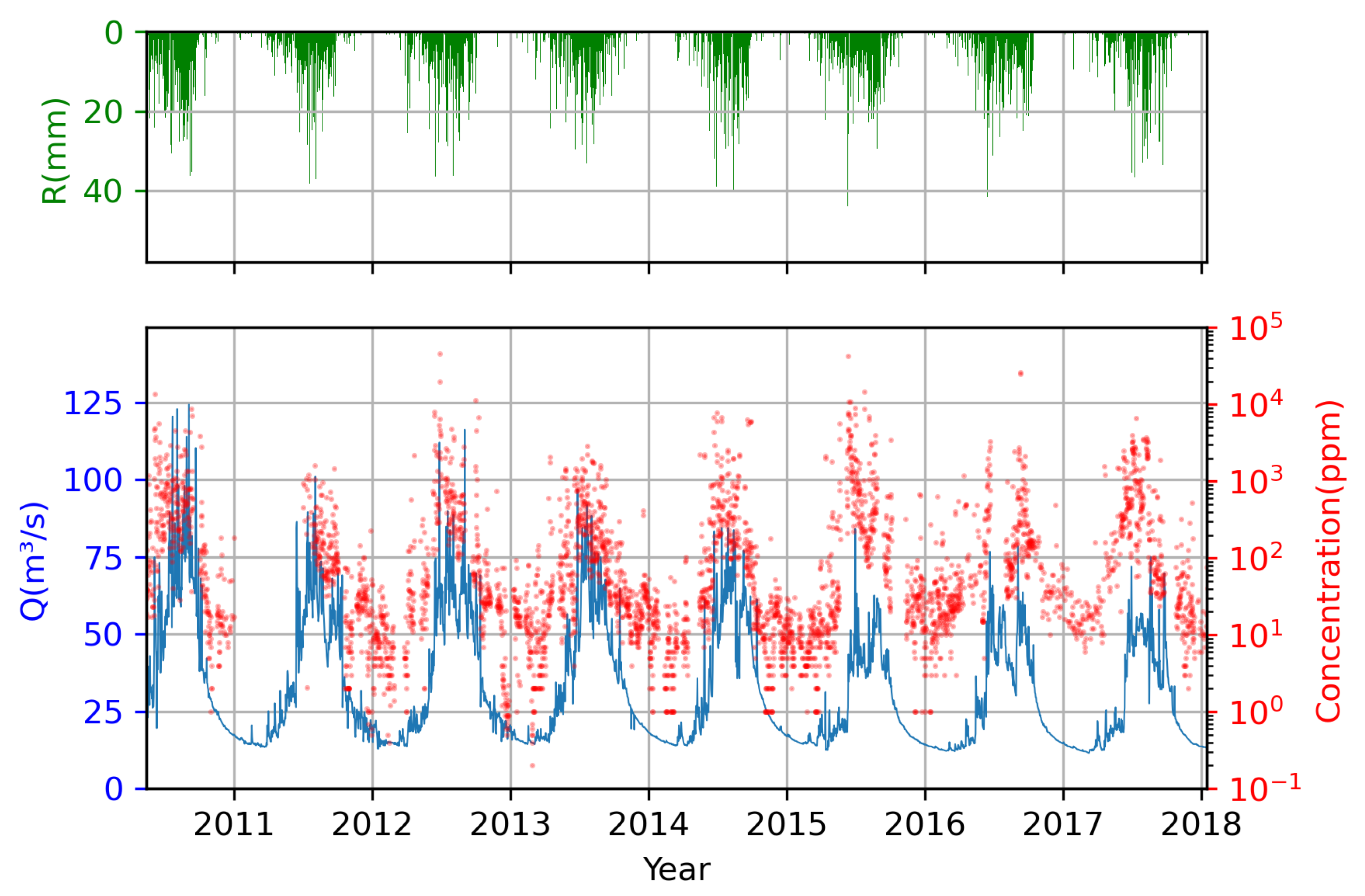
3. Data
4. Research Methodology
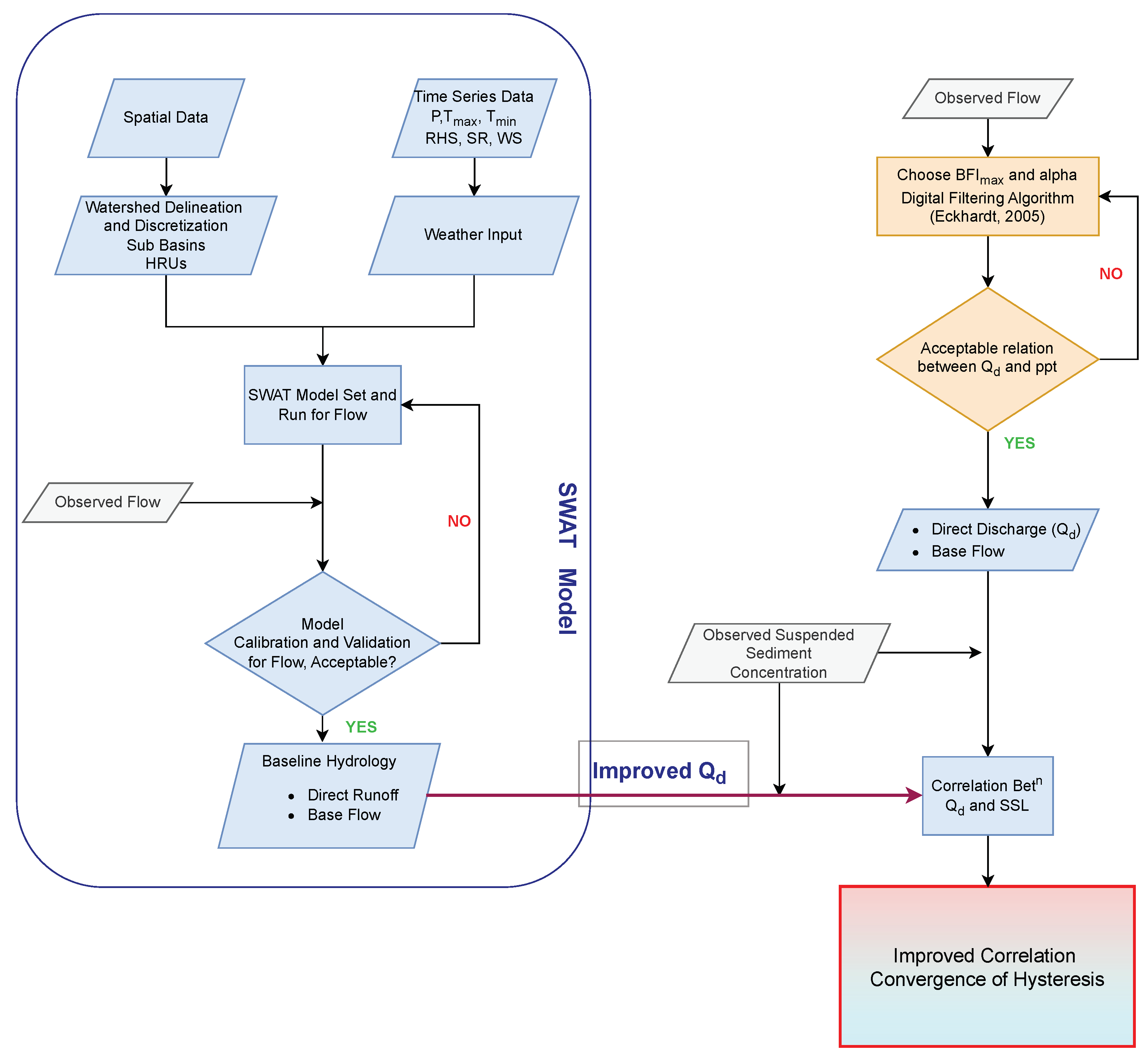
4.1. Flow Separation Using Digital Filtering Method
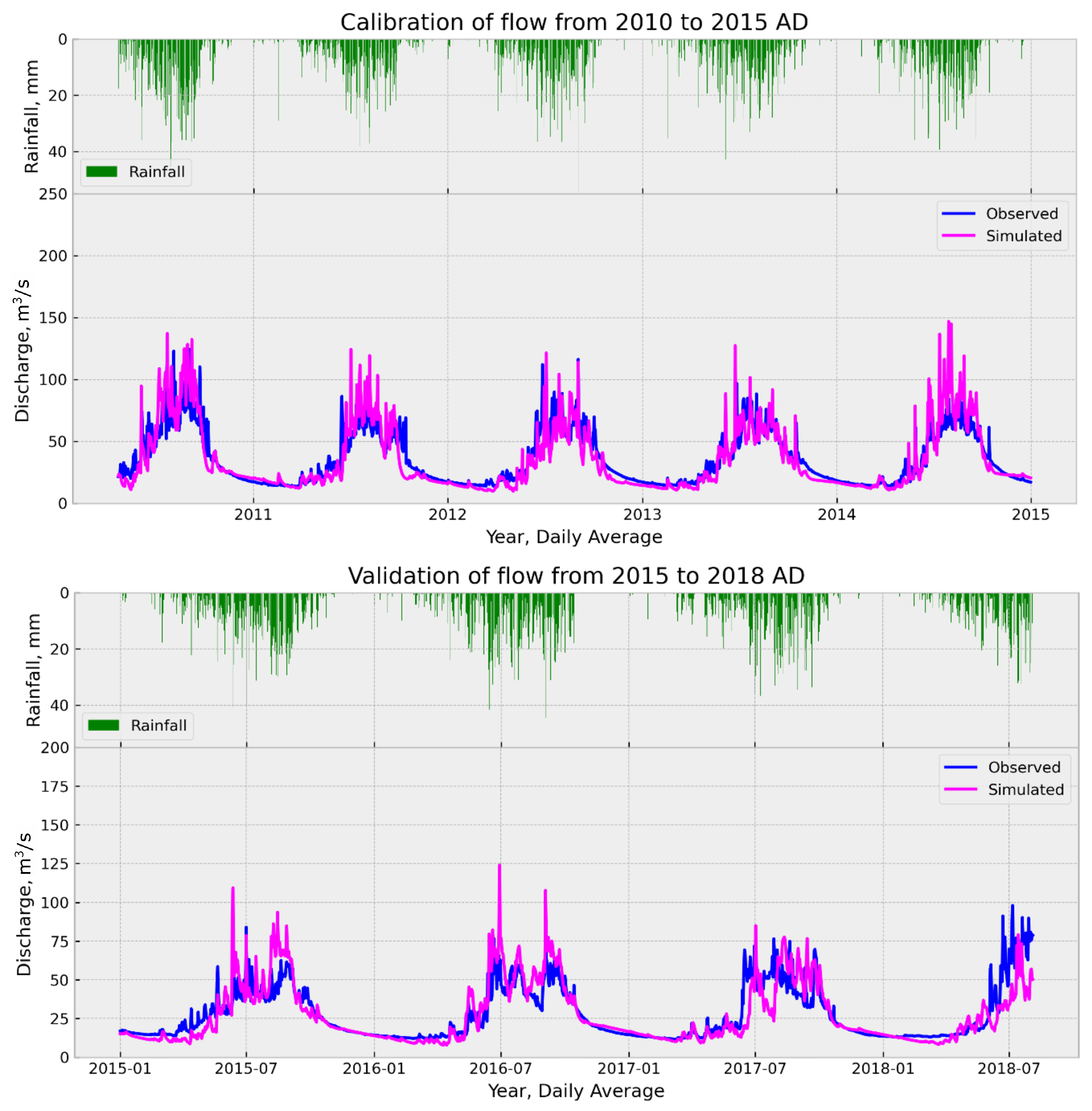
4.2. Flow Separation Using the SWAT Model
5. Results and Discussion
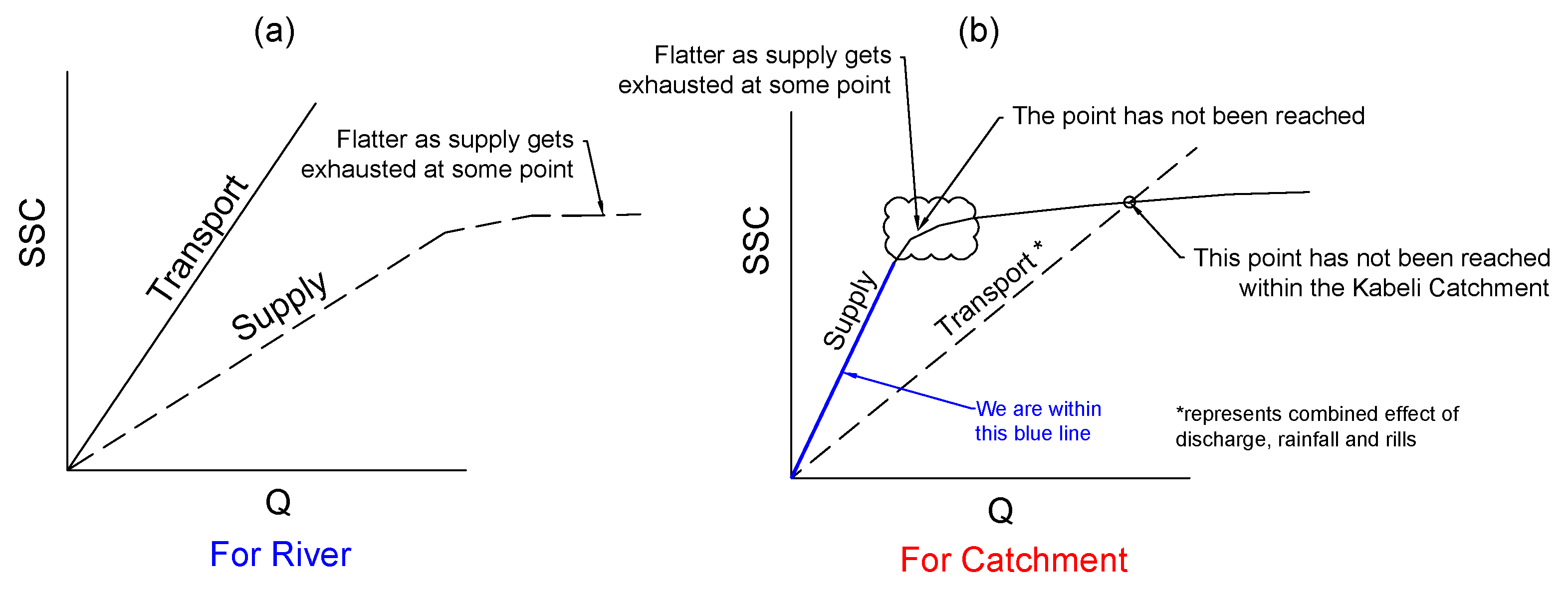
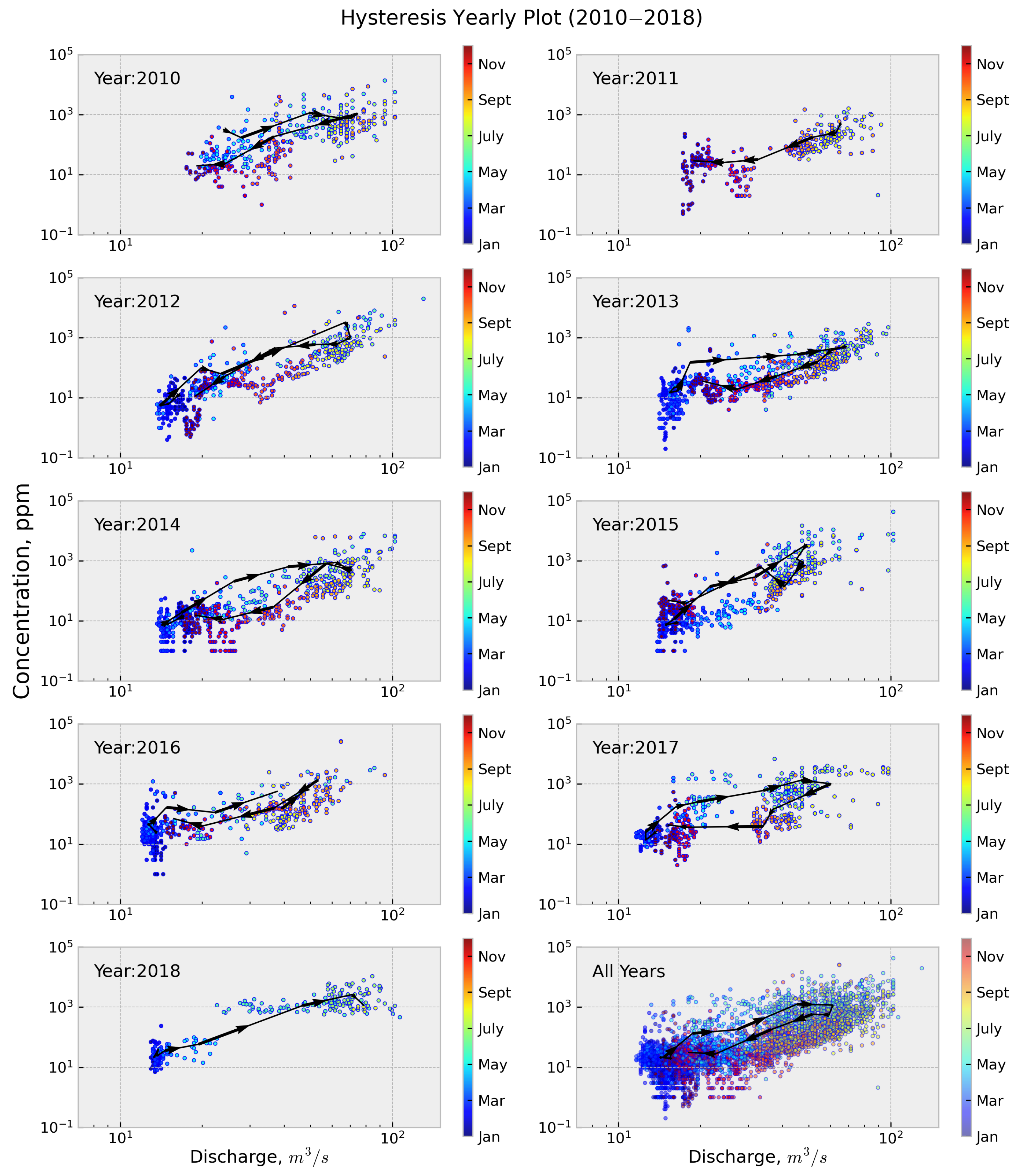
5.1. Hysteresis Loop
5.2. Base Flow from SWAT
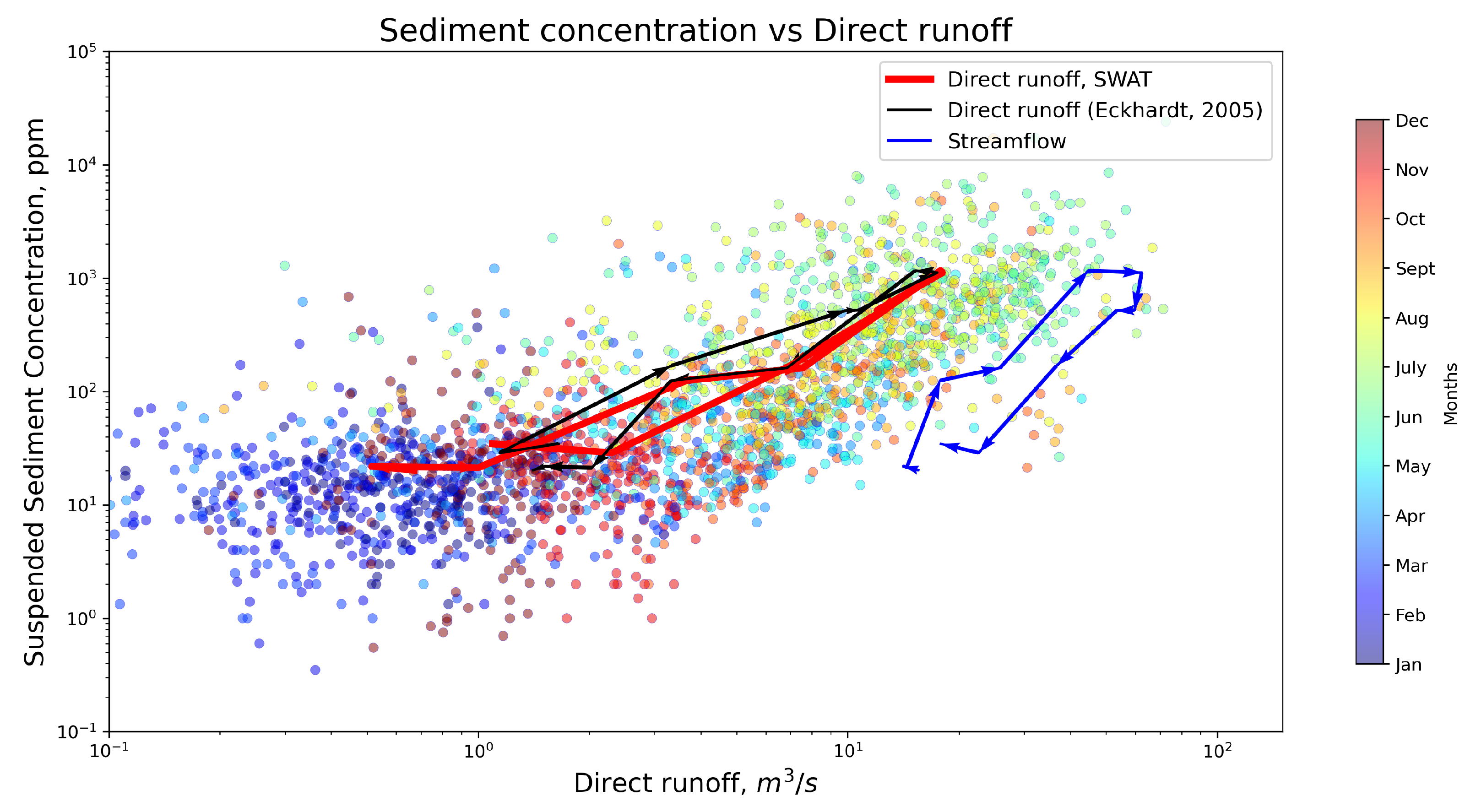
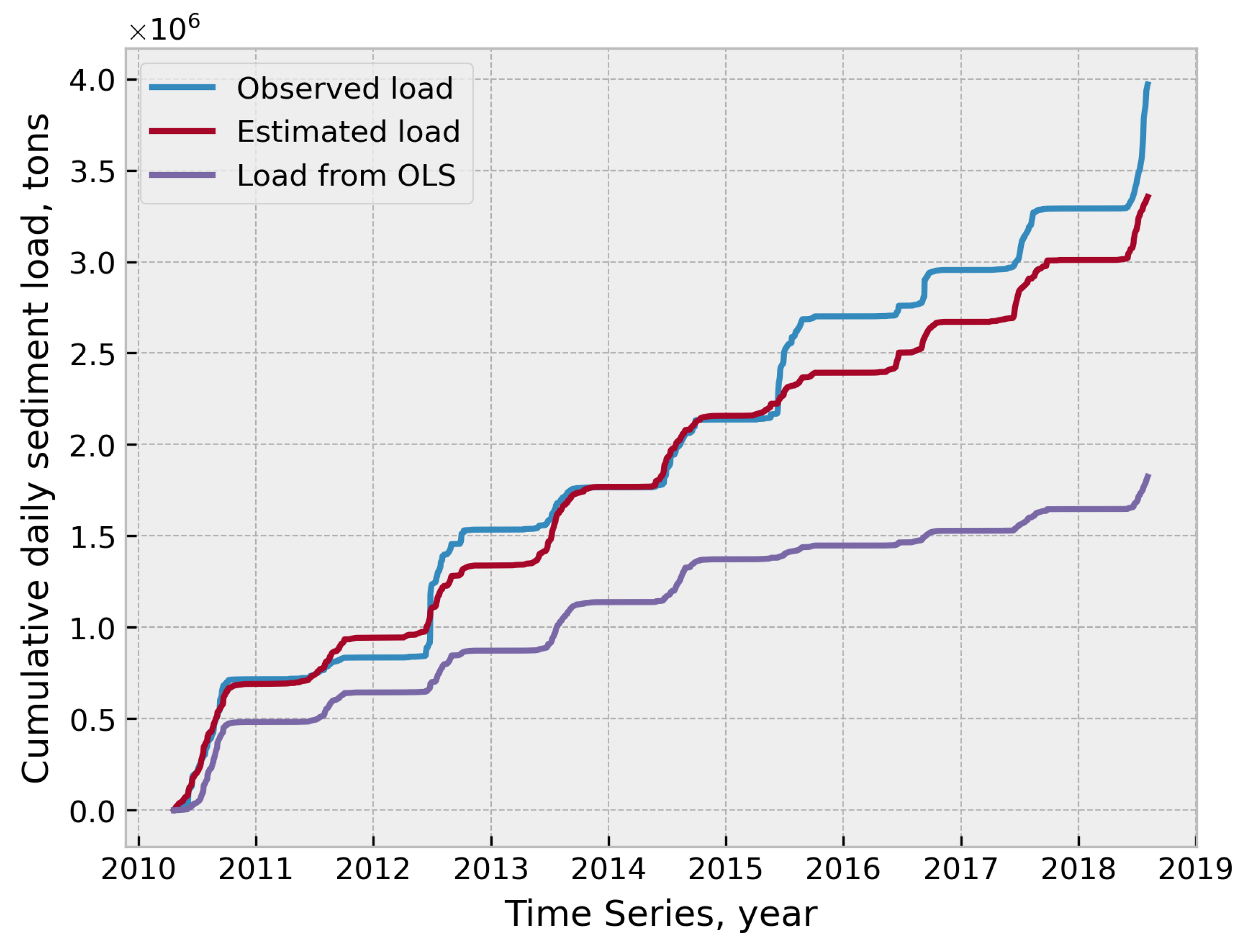
5.3. Mechanism of Sediment Yield
5.4. Rating Curves from Direct Runoff
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| APHRODITE | Asian Precipitation Highly Resolved Observational Data Integration towards Evaluation of Water Resources |
| ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer |
| DEM | Digital Elevation Model |
| DHM | Department of Hydrology and Meteorology |
| ICIMOD | International Centre for Integrated Mountain Development |
| ISRIC | International Soil Reference and Information Center |
| KS | Kolmogorov–Smirnov |
| LRMP | Land Resource Mapping Project |
| masl | Meters Above Sea Level |
| MCM | Million Cubic Meters |
| NSE | Nash–Sutcliffe Efficiency |
| OLS | Ordinary Least Square |
| PBIAS | Percentage Bias |
| SOTER | Soils and Terrain Digital Databases |
| SSC | Suspended Sediment Concentration |
| SSL | Suspended Sediment Load |
| SWAT | Soil and Water Assessment Tool |
| Table of Notations | |
| base flow recession parameter | |
| maximum base flow index | |
| Q | total stream runoff |
| base flow | |
| direct runoff | |
| suspended sediment load when > 0 | |
| mean daily direct suspended sediment load | |
| suspended sediment load when > 0, normalized by | |
| R | precipitation |
References
- Milliman, J. River Inputs. In Encyclopedia of Ocean Sciences; Elsevier: Amsterdam, The Netherlands, 2001; pp. 2419–2427. [Google Scholar] [CrossRef]
- Milliman, J.D.; Meade, R.H. World-wide delivery of sediment to the oceans. J. Geol. 1983, 91, 1. [Google Scholar] [CrossRef]
- Roback, K.; Clark, M.K.; West, A.J.; Zekkos, D.; Li, G.; Gallen, S.F.; Chamlagain, D.; Godt, J.W. The size, distribution, and mobility of landslides caused by the 2015 Mw7.8 Gorkha earthquake, Nepal. Geomorphology 2018, 301, 121–138. [Google Scholar] [CrossRef]
- Mahmood, K. Reservoir Sedimentation: Impact, Extent, and Mitigation. World Bank Tech. Pap. Number 1988, 69, 850. [Google Scholar]
- Ghimire, S.; Singh, U.; Bhattarai, P.K. Generation of a Suspended Sediment Rating Curve of a Himalayan River based on a Long-term Data: A case study of Kabeli River. Proc. 10th Ioe Grad. Conf. 2021, 8914, 1110–1118. [Google Scholar]
- Duru, U. Modeling Sediment Yield and Deposition Using the Swat Model. Doctoral Thesis, Colorado State University, Fort Collins, FL, USA, 2015. [Google Scholar]
- Efthimiou, N.; Lykoudi, E.; Karavitis, C. Comparative analysis of sediment yield estimations using different empirical soil erosion models. Hydrol. Sci. J. 2017, 62, 2674–2694. [Google Scholar] [CrossRef]
- Hajigholizadeh, M.; Melesse, A.M.; Fuentes, H.R. Erosion and Sediment Transport Modelling in Shallow Waters: A Review on Approaches, Models and Applications. Int. J. Environ. Res. Public Health 2018, 15, 518. [Google Scholar] [CrossRef] [PubMed]
- Merritt, W.S.; Letcher, R.A.; Jakeman, A.J. A review of erosion and sediment transport models. Environ. Model. Softw. 2003, 18, 761–799. [Google Scholar] [CrossRef]
- Dadson, S.J.; Hovius, N.; Chen, H.; Dade, W.B.; Hsieh, M.L.; Willett, S.D.; Hu, J.C.; Horng, M.J.; Chen, M.C.; Stark, C.P.; et al. Links between erosion, runoff variability and seismicity in the Taiwan orogen. Nature 2003, 426, 648–651. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, R.I. River Loads Underestimated by Rating Curves. Water Resour. Res. 1986, 22, 74–76. [Google Scholar] [CrossRef]
- Duan, N. Smearing estimate: A nonparametric retransformation method. J. Am. Stat. Assoc. 1983, 78, 605–610. [Google Scholar] [CrossRef]
- Annandale, G.; Morris, G.; Karki, P. Extending the Life of Reservoirs: Sustainable Sediment Management for Dams and Run-of-River Hydropower; World Bank Group: Washington, DC, USA, 2016. [Google Scholar]
- Fuller, C.W.; Willett, S.D.; Hovius, N.; Slingerland, R. Erosion rates for Taiwan mountain basins: New determinations from suspended sediment records and a stochastic model of their temporal variation. J. Geol. 2003, 111, 71–87. [Google Scholar] [CrossRef]
- Ponce, V.M. Ultimate Sediment Concentration. In Proceedings of the National Conference on Hydraulic Engineering, Colorado Springs, CO, USA, 8–12 August 1988; pp. 311–315. [Google Scholar]
- Holmes, R.R. Measurement of Bedload Transport in Sand-Bed Rivers: A Look at Two Indirect Sampling Methods. In U.S. Geological Survey Scientific Investigations Report; USGS: Wriston, VA, USA, 2010. [Google Scholar]
- Morin, G.; Lavé, J.; France-Lanord, C.; Rigaudier, T.; Gajurel, A.P.; Sinha, R. Annual Sediment Transport Dynamics in the Narayani Basin, Central Nepal: Assessing the Impacts of Erosion Processes in the Annual Sediment Budget. J. Geophys. Res. Earth Surf. 2018, 123, 2341–2376. [Google Scholar] [CrossRef]
- Lane, E.W.; Borland, W.M. Estimating bed load. Eos, Trans. Am. Geophys. Union 1951, 32, 121–123. [Google Scholar] [CrossRef]
- Pratt-Sitaula, B.; Garde, M.; Burbank, D.W.; Oskin, M.; Heimsath, A.; Gabet, E. Bedload-to-suspended load ratio and rapid bedrock incision from Himalayan landslide-dam lake record. Quat. Res. 2007, 68, 111–120. [Google Scholar] [CrossRef]
- Attal, M.; Lavé, J. Changes of bedload characteristics along the Marsyandi River (central Nepal): Implications for understanding hillslope sediment supply, sediment load evolution along fluvial networks, and denudation in active orogenic belts. In Special Paper of the Geological Society of America Special Papers; Geological Society of America: Boulder, CO, USA, 2006; Volume 398, pp. 143–171. [Google Scholar] [CrossRef]
- Andermann, C.; Crave, A.; Gloaguen, R.; Davy, P.; Bonnet, S. Connecting source and transport: Suspended sediments in the Nepal Himalayas. Earth Planet. Sci. Lett. 2012, 351-352, 158–170. [Google Scholar] [CrossRef]
- Lloyd, C.E.; Freer, J.E.; Johnes, P.J.; Collins, A.L. Using hysteresis analysis of high-resolution water quality monitoring data, including uncertainty, to infer controls on nutrient and sediment transfer in catchments. Sci. Total. Environ. 2016, 543, 388–404. [Google Scholar] [CrossRef] [PubMed]
- Malutta, S.; Kobiyama, M.; Chaffe, P.L.B.; Bonumá, N.B. Hysteresis analysis to quantify and qualify the sediment dynamics: State of the art. Water Sci. Technol. 2020, 81, 2471–2487. [Google Scholar] [CrossRef] [PubMed]
- Asselman, N.E. Suspended sediment dynamics in a large drainage basin: The River Rhine. Hydrol. Process. 1999, 13, 1437–1450. [Google Scholar] [CrossRef]
- Misset, C.; Recking, A.; Legout, C.; Poirel, A.; Cazilhac, M. Geomorphological factors influencing hysteresis patterns between suspended load and flow rate in Alpine rivers. E3s Web Conf. 2018, 40, 1–8. [Google Scholar] [CrossRef]
- Chhetri, A.; Kayastha, R.B.; Shrestha, A. Assessment of Sediment Load of Langtang River in Rasuwa District, Nepal. J. Water Resour. Prot. 2016, 08, 84–92. [Google Scholar] [CrossRef][Green Version]
- Gabet, E.J.; Burbank, D.W.; Pratt-Sitaula, B.; Putkonen, J.; Bookhagen, B. Modern erosion rates in the High Himalayas of Nepal. Earth Planet. Sci. Lett. 2008, 267, 482–494. [Google Scholar] [CrossRef]
- Hasnain, S.I.; Thayyen, R.J. Discharge and suspended-sediment concentration of meltwaters, draining from the Dokriani glacier, Garhwal Himalaya, India. J. Hydrol. 1999, 218, 191–198. [Google Scholar] [CrossRef]
- LRMP. Land Resource Mapping Project: Summary Report; Survey Department, HMGN and Kenting Earth Sciences: Kathmandu, Nepal, 1986. [Google Scholar]
- Andermann, C.; Bonnet, S.; Gloaguen, R. Evaluation of precipitation data sets along the Himalayan front. Geochem. Geophys. Geosystems 2011, 12, 1–16. [Google Scholar] [CrossRef]
- Andermann, C.; Longuevergne, L.; Bonnet, S.; Crave, A.; Davy, P.; Gloaguen, R. Impact of transient groundwater storage on the discharge of Himalayan rivers. Nat. Geosci. 2012, 5, 127–132. [Google Scholar] [CrossRef]
- Ponce, V. Engineering Hydrology: Principles and Practices; Prentice Hall: Saddle River, NY, USA, 1989. [Google Scholar]
- Eckhardt, K. How to construct recursive digital filters for baseflow separation. Hydrol. Process. 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Furey, P.R.; Gupta, V.K. A physically based filter for separating base flow from streamflow time series. Water Resour. Res. 2001, 37, 2709–2722. [Google Scholar] [CrossRef]
- Lim, K.J.; Engel, B.A.; Tang, Z.; Choi, J. Automated Web GIS Based Hydrograph Analysis Tool, WHAT. J. Am. Water Resour. Assoc. 2006, 1397, 1407–1416. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, R.; Xie, J.; Zhao, Y.; Yan, D.; Yang, S. Soil and Water Assessment Tool (SWAT) Model: A Systemic Review. J. Coast. Res. 2019, 93, 22–30. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Jang, W.; Lim, K.; Engel, B. Assessment of Baseflow Estimates Considering Recession Characteristics in SWAT. Water 2018, 10, 371. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines For Systematic Quantification Of Accuracy In Watershed Simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Am. Soc. Agric. Biol. Eng. 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Tucker, G.E.; Slingerland, R. Drainage basin responses to climate change. Water Resour. Res. 1997, 33, 2031–2047. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S. Representative rainfall thresholds for landslides in the Nepal Himalaya. Geomorphology 2008, 100, 429–443. [Google Scholar] [CrossRef]
- Shrestha, H.S. Sedimentation and Sediment Handling in Himalayan Reservoirs. Doctoral Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2012. [Google Scholar]
- Alstott, J.; Bullmore, E.; Plenz, D. Powerlaw: A python package for analysis of heavy-tailed distributions. PLoS ONE 2014, 9, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, C.S. Fitting heavy tailed distributions: The powerlaw package. J. Stat. Softw. 2015, 64, 1–16. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. Siam Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Goldstein, M.L.; Morris, S.A.; Yen, G.G. Problems with fitting to the power-law distribution. Eur. Phys. J. 2004, 41, 255–258. [Google Scholar] [CrossRef]
- Hovius, N.; Stark, C.P.; Hao-Tsu, C.; Jiun-Chuan, L. Supply and removal of sediment in a landslide-dominated mountain belt: Central Range, Taiwan. J. Geol. 2000, 108, 73–89. [Google Scholar] [CrossRef] [PubMed]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45, 1–34. [Google Scholar] [CrossRef]




| Statistical Measures | SSC (ppm) | Gauge Height (m) | Discharge (m3/s) |
|---|---|---|---|
| Mean | 404.12 | 0.85 | 34.75 |
| Standard Deviation | 1468.69 | 0.46 | 20.75 |
| Minimum | 0 | 0.21 | 11.63 |
| 25% | 15 | 0.43 | 16.98 |
| 50% | 45 | 0.77 | 27.96 |
| 75% | 262 | 1.23 | 48.85 |
| Maximum | 46137 | 2.60 | 162.69 |
| Data | Source | Spatial Resolution | Temporal Resolution |
|---|---|---|---|
| Topography | ASTER GDEM 30 m DEM | 30 m × 30 m | - |
| Observed Meteorological Data | Department of Hydrology and Meteorology (DHM) | Point Dataset | Daily |
| Sediment Concentration | Kabeli Energy Limited | Point Dataset | Twice Daily |
| Daily Discharge | Kabeli Energy Limited | Point Dataset | Twice Daily |
| Land Cover Map | ICIMOD Land Cover Map 2010 | - | - |
| Soil Map | Soil and Terrain (SOTER) Database Programme, ISRIC | 1:1,000,000 | - |
| Precipitation | APHRODITE Dataset APHRO_MA_V110_1EXR1 | ∼30 km × 30 km | Daily |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghimire, S.; Singh, U.; Panthi, K.K.; Bhattarai, P.K. Suspended Sediment Source and Transport Mechanisms in a Himalayan River. Water 2024, 16, 1063. https://doi.org/10.3390/w16071063
Ghimire S, Singh U, Panthi KK, Bhattarai PK. Suspended Sediment Source and Transport Mechanisms in a Himalayan River. Water. 2024; 16(7):1063. https://doi.org/10.3390/w16071063
Chicago/Turabian StyleGhimire, Sanyam, Umesh Singh, Krishna Kanta Panthi, and Pawan Kumar Bhattarai. 2024. "Suspended Sediment Source and Transport Mechanisms in a Himalayan River" Water 16, no. 7: 1063. https://doi.org/10.3390/w16071063
APA StyleGhimire, S., Singh, U., Panthi, K. K., & Bhattarai, P. K. (2024). Suspended Sediment Source and Transport Mechanisms in a Himalayan River. Water, 16(7), 1063. https://doi.org/10.3390/w16071063








