Abstract
Landslides represent a significant global natural hazard, threatening human settlements and the natural environment. The primary objective of the study was to develop a landslide susceptibility modeling approach that enhances prediction accuracy and informs land-use planning decisions. The study utilized a hybrid ensemble-based methodology to improve prediction accuracy and effectively capture the complexity of landslide susceptibility patterns. This approach harnessed the power of ensemble models, employing a bagging algorithm with base learners, including the reduced error pruning decision tree (REPTree) and functional tree (FT) models. Ensemble models are particularly valuable because they combine the strengths of multiple models, enhancing the overall performance and robustness of the landslide susceptibility prediction. The study focused on Yanchuan County, situated within the hilly and gully region of China’s Loess Plateau, known for its susceptibility to landslides, using sixteen critical landslide conditioning factors, encompassing topographic, environmental, and geospatial variables, namely elevation, slope, aspect, proximity to rivers and roads, rainfall, the normalized difference vegetation index, soil composition, land use, and more. Model performances were evaluated and verified using a range of metrics, including receiver operating characteristic (ROC) curves, trade-off statistical metrics, and chi-square analysis. The results demonstrated the superiority of the integrated models, particularly the bagging FT (BFT) model, in accurately predicting landslide susceptibility, as evidenced by its high area under the curve area (AUC) value (0.895), compared to the other models. The model excelled in both positive predictive rate (0.847) and negative predictive rate (0.886), indicating its efficacy in identifying landslide and non-landslide areas and also in the F-score metric with a value of 0.869. The study contributes to the field of landslide risk assessment, offering a significant investigation tool for managing and mitigating landslide hazards in Yanchuan County and similar regions worldwide.
1. Introduction
Landslides represent a significant natural disaster phenomenon triggered by various mechanisms within diverse geomorphic contexts, such as heavy rainfall and seismic activity, often with complex and poorly understood causes. The consequences of landslides pose substantial threats to human civilization, resulting in immeasurable damage and impacting economic development. In many countries, landslides are a leading cause of injuries and economic losses [1]. China faces annual geological disasters related to landslides that cannot be underestimated, leading to risks to human life and property and the depletion of natural resources [2,3,4]. Therefore, it is evident that effective monitoring and prediction of landslides are imperative to minimize losses and mitigate the aftermath of these disasters. Various methods exist for predicting and preventing landslides, with landslide susceptibility mapping emerging as a valuable strategy to mitigate landslide-related damage. Landslide susceptibility refers to the assessment of the likelihood or probability of landslides occurring in a particular area based on geological, seismo–tectonic, and environmental factors. While our models incorporate multiple variables to predict landslide susceptibility accurately, the spatial predictions are subject to uncertainties due to potential data quality variations and the dynamic nature of the environmental factors. Acknowledging these uncertainties is vital for carefully interpreting the models’ outputs, especially when applied to land-use planning and risk management decisions. Future research should focus on improving data quality, exploring more sophisticated modeling techniques, and incorporating uncertainty analysis methods, such as Monte Carlo simulations, to quantify and reduce these uncertainties, thereby enhancing the reliability of spatial predictions [5,6,7].
In recent years, there has been a growing focus among experts on landslide susceptibility analysis [8,9,10,11]. Geographic information systems (GIS), recognized as an essential tool for landslide susceptibility mapping, have gained widespread popularity in spatial modeling for landslides [12]. With the advancements in GIS and remote sensing (RS) technologies, a significant amount of data has become available, while the development of sophisticated algorithms and the increased computational power have opened up numerous opportunities for research and applications in various fields [8,13]. Machine learning techniques for predicting landslide susceptibility have been steadily replacing traditional statistical methods, a trend that has gained significant attention from experts and scholars alike [6,14,15]. When assessing landslide susceptibility, quantitative analysis has emerged as a more practical, objective, and favored approach [16,17]. Machine learning algorithms have proven invaluable by mitigating the limitations of subjective assumptions, offering enhanced accuracy and effectiveness compared to expert-based theoretical models and statistical analyses [18,19]. Machine learning methodologies provide a reliable means of interpreting and processing large datasets in a manner analogous to engineering methods [6,20]. These techniques enable the exploration of intricate relationships between landslide occurrences and various conditioning factors within extensive datasets [21,22]. A multitude of machine learning methods, including decision trees (DT) [19,23,24], function trees (FT) [25,26,27], logistic regression (LR) [12,28,29,30], support vector machines (SVM) [31,32,33], frequency ratios [30,34,35], multiple regression [36,37,38], evidential belief functions [13,39,40,41], weight of evidence [42,43,44,45], artificial neural networks (ANN) [46,47,48,49], Naïve Bayes trees (NBT) [50,51,52], kernel logistic regression [53,54,55], boosted regression trees [56,57], classification and regression trees (CART) [23,56,58], and random forest (RF) [59,60,61], have been successfully employed in landslide susceptibility analysis and zoning.
Despite the successful implementation of the above methods, recent research concerning the accuracy and reliability of models has highlighted the limitations of relying solely on single machine learning algorithms when confronted with the superior performance of hybrid machine learning methods, underscoring the growing significance of ensemble models [62]. Integration technology has emerged as a pivotal advancement in this domain [4,19,63,64,65]. The primary advantage of integrated models lies in their heightened recognition capabilities and their ability to deliver more accurate and robust predictions compared to individual models [64,66]. Notably, the rotation forest-functional trees (RFFT) aggregate model surpasses the performance of standalone SVM and FT models, showcasing superior prediction abilities [67]. Similarly, the fusion of ANN, SVM, and maximum entropy (MaxEnt) models introduces a novel hybrid integration method for spatial landslide susceptibility prediction in the Wanyuan area, as reported by Chen et al. [64]. This is also the case for Pham et al. [58], who presented a hybrid machine learning model based on random subspace classification and regression trees, which have been compared and evaluated against SVM, CART, NBT, and LR models for landslide susceptibility prediction, consistently demonstrating excellent performance. Furthermore, the recurrent error pruning tree (REPTree) model, in conjunction with various integration technologies such as bagging, multi-boss, rotation forest, and random subspace, has yielded a novel integrated model with improved performance [68]. The advance of ensemble and hybrid models has been highlighted by Hong et al. [69]. The authors conducted a study in the Guangchang district of Jiangxi province, China, with the research aimed to assess and compare the performance of various ensemble techniques, including AdaBoost, bagging, and rotation forest, alongside the base classifier of the J48 decision tree (JDT), for landslide susceptibility prediction. The results revealed that all models exhibited high predictive capabilities (AUC > 0.8), with JDT combined with rotation forest demonstrating the highest accuracy (AUC = 0.855).
In this context, our research aimed to develop a landslide susceptibility model for Yanchuan County, situated in the hilly and gully region of the Loess Plateau in northern Shaanxi, China. This area is prone to landslides, which pose substantial threats to human life and the environment. To address this challenge, we introduced a hybrid ensemble-based methodology combining machine learning models, including REPTree and FT, with the bagging algorithm. Our comprehensive approach to modeling landslide susceptibility and evaluating the proposed models sets our study apart. While previous studies have examined the performance of FT, REPT, and bagging models individually, our research combines these models in a novel ensemble approach, leading to more accurate landslide susceptibility predictions. The evaluation approach includes the use of various metrics such as receiver operating characteristic (ROC) curves, trade-off statistical metrics (positive predictive rate (PPR), negative predictive rate (NPR), sensitivity, specificity, etc.), and chi-square analysis for an overall evaluation. This comprehensive approach enhances prediction accuracy and provides valuable insights into landslide susceptibility, supporting more informed land-use and planning decisions. By offering a more comprehensive assessment of model performance and verification using a range of metrics, our research provides a powerful tool for assessing landslide risks in the study area and other regions with similar geological and environmental characteristics.
2. Study Area
Yanchuan County is situated in the northeastern part of the Yan’an region, within the northern reaches of Shaanxi Province, China. Its geographical coordinates range from 109°36′20” to 110°26′44” east longitude and from 36°37′15” to 37°5′55” north latitude, encompassing a total land area of approximately 1985 km2 (Figure 1). The topography of this region exhibits significant variations in altitude, with elevations ranging from 492 m to 1392 m. The terrain presents a distinct pattern, with higher elevations prevailing in the northwest and gradually decreasing towards the southeast. The terrain predominantly slopes from the northwest to the southeast. Notably, the steepest slopes in this area exhibit angles reaching up to 68.30°, while a substantial portion, approximately 58.19% of the total area, comprises slopes with angles less than 20°. Areas characterized by slope angles between 20° and 60° encompass roughly 41.80% of the study area.
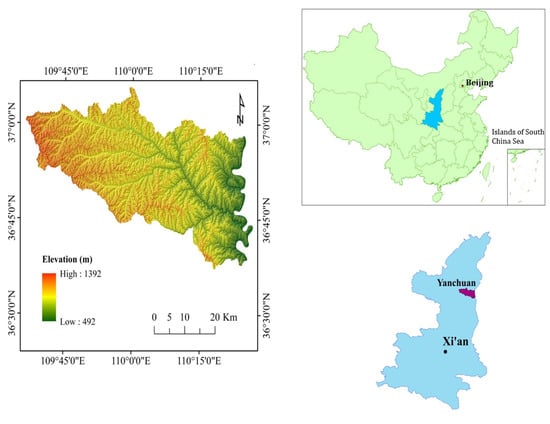
Figure 1.
Study area.
The study area, situated in the hilly and gully region of the Loess Plateau in northern Shaanxi, experiences a temperate continental monsoon climate characterized by higher elevations in the northwest and lower altitudes in the southeast. Several geological and environmental factors contribute to the development of unstable slopes in Yanchuan County, primarily owing to substantial loess accumulation, loose soil structure, severe soil erosion, intricate gully networks, rugged terrain, and significant human engineering activities. Consequently, landslides in this region predominantly manifest as loess and soil landslides characterized by traction movements. These unstable slopes tend to concentrate along larger riverbanks, convex and linear slopes, and the northern loess beam area. In high and steep slopes, cracks resulting from differential weathering often precipitate landslide disasters. Landslides occur in all directions but show a pronounced concentration on northwest-facing shady slopes (45–90°, 135–180°, and 225–300°), contributing to the asymmetric distribution of landslides on both sides of valleys. Concerning the geometric characteristics of landslides, the main length varies between 40 and 160 m, the width varies between 60 and 200 m, and the thickness is mainly concentrated in 2 to 25 m.
3. Materials and Methods
In this study, we adopted a comprehensive modeling approach to assess and compare landslide susceptibility in the Yanchuan area of China, using single tree-based models and hybrid-bagging-based models. Specifically, REPTree and FT were the two single tree-based models, whereas using the bagging method models and having as base learns the REPTree and FT models, including their combined forms, bagging REPTree (BREPTree) and bagging FT (BFT). These models were evaluated using a range of assessment metrics, including ROC curves and trade-off statistical metrics.
DTs are predictive models that segment data into subsets based on feature value differences, constructing a tree for decision-making. The result is a tree with decision nodes and leaf nodes, where each node represents a feature in the instance to be classified, and each branch represents a decision rule, ultimately leading to a leaf node that indicates the outcome. The REPTree model refines this by pruning less accurate branches to enhance prediction. The model uses a regression tree that prunes using reduced error pruning and is capable of learning from both nominal and numerical data. FT enhances the decision-making process by constructing a DT that classifies samples using the gain ratio as the split criterion. This allows for the integration of logistic regression functions at the leaves or nodes of the tree, combining the interpretability of the DT with the predictive power of logistic regression. Bagging, short for bootstrap aggregating, is an ensemble machine learning technique that improves the stability and accuracy of machine learning algorithms. It works by creating multiple versions of a predictor model (such as a DT) and then combining them to form an aggregated model with better performance. Bagging involves training each model on a random distribution of the dataset and then combining the models by averaging the output (for regression) or voting (for classification). Our modeling approach involved considering the strengths and weaknesses of each model to select the most suitable one for landslide susceptibility assessment. Further explanation concerning models will follow in the following paragraphs.
The proposed methodology follows a five-step analysis, which involves: (i) constructing the landslide and non-landslide inventory, (ii) data selection and classification, (iii) correlation attribute evaluation process, certainty factor analysis and normalization (iv), applying the tree-based and hybrid models to produce the four landslide susceptibility models and estimating the learning and predictive performance of the four models (v), generate the susceptibility maps and calculate the relative landslide density. A detailed description of our modeling methods is provided below, complemented by Figure 2, which illustrates the flowchart of our hybrid-ensemble model approach.
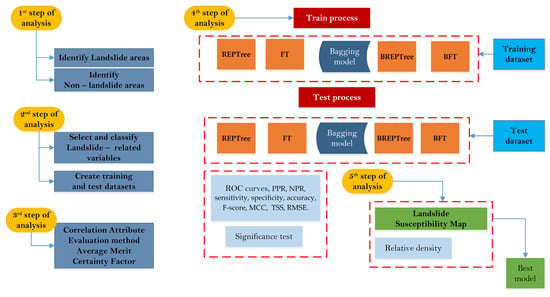
Figure 2.
Flowchart of the proposed methodology.
3.1. First Step of Analysis
The accuracy and reliability of a landslide susceptibility model are greatly influenced by the quality of the landslide inventory map, which is essential for recording vital information about various aspects of landslides, including their types, occurrence timing, and precise locations [70,71,72,73]. A fundamental assumption underlying landslide susceptibility modeling is that future landslides will exhibit patterns similar to those observed in the past [74,75]. Consequently, the composition of the landslide inventory map primarily draws from historical records, field surveys, and the interpretation of remote sensing imagery, resulting in a comprehensive dataset comprising a total of 311 distinct landslide areas. It is important to note that these areas have been represented as single points, referencing the centroid of each respective landslide region. To develop the landslide susceptibility model, we employed random sampling techniques, selecting 218 landslide disaster points, which account for 70% of the dataset, using the Subset Features in the Geostatistical Analyst toolbox of the ArcGIS suite. The remaining 93 points, constituting 30% of the dataset, were set aside for model verification purposes. Non-landslide areas were identified through a combination of methods. These methods included random point selection within the study area, ensuring that these points did not coincide with known landslide locations. Additionally, satellite imagery analysis of Landsat 8 images, obtained from the International Scientific and Technical Data Mirror Site of the Computer Network Information Center, Chinese Academy of Sciences, available at http://www.gscloud.cn (accessed on 22 August 2023), was employed to pinpoint regions characterized by stable vegetation cover, flat terrain, or solid bedrock—criteria that, in theory, denote areas less susceptible to landslides and thus suitable for classification as non-landslide areas. The spatial distribution of the landslide and non-landslide datasets is illustrated in Figure 3.
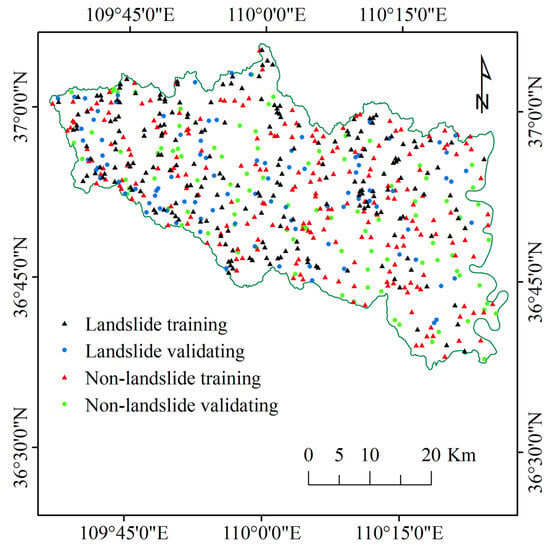
Figure 3.
Landslide and non-landslide spatial distribution.
3.2. Second Step of Analysis
Selection and Classification of Landslide—Related Variables
The occurrence of landslide disasters in Yanchuan County is linked to a combination of local geological, topographic, and environmental factors [71,76]. The selection of appropriate conditioning factors for landslide susceptibility modeling is a critical step, as these factors may exhibit interdependencies that could impact predictive accuracy [77,78,79]. Consequently, this study carefully selected 16 landslide conditioning factors to create thematic maps for landslide susceptibility modeling (Figure 2), which include slope, aspect, elevation, plan curvature, profile curvature, slope length, the topographic position index (TPI), terrain ruggedness index (TRI), convergence index (CI), distance to rivers, distance to roads, rainfall, the normalized difference vegetation index (NDVI), soil type, lithology, and land use. The main data sources for the 16 landslide—related factors included digital elevation model (DEM) data, Landsat 8 Operational Land Imager imagery with a 30 m by 30 m resolution, a 1:200,000 geological map, 1:100,000 land use/land cover map, and 1:1,000,000 soil type map. Utilizing geospatial transformation functions available in the ArcGIS suite, we categorized the 16 landslide conditioning factors into thematic layers, distinguishing between continuous and discontinuous data.
In more detail, from the DEM file (resolution 30 × 30 m) obtained by the International Scientific and Technical Data Mirror Site of the Computer Network Information Center, Chinese Academy of Sciences, available at http://www.gscloud.cn, slope, aspect, plan and profile curvature, slope length, TPI, TRI, and CI were constructed using the ArcGIS suite and the Spatial Analyst Tools toolbox. For these continuous raster files, the slope length, TPI, TRI, and CI were reclassified into five classes using the natural break classification method having the same resolution (30 × 30) as the DEM file. For slope, aspect, elevation, plan and profile curvature, distance from the river, distance from roads, and rainfall, we applied a manual classification scheme, and the files were reclassified in the same resolution (30 × 30) as the DEM file. The slope was classified into seven classes, aspect and elevation into nine classes, plan and profile curvature into three classes, distance from the river and distance from roads into five classes, and rainfall into six classes. Soil type, lithology, and land use were digitized from the available maps and transformed into a 30 × 30 resolution raster format to match the rest of the files. The NDVI and land use maps were generated by processing Landsat 8 satellite images using ENVI 5.1 software. The Landsat 8 images, which had a spatial resolution of 30 × 30 m, were also sourced from the same website as the ASTER Global DEM data, accessed on 22 August 2023. The NDVI was classified into five classes according to the natural break classification scheme, whereas land use was classified into six classes. Finally, the rainfall map was created using comprehensive rainfall data that covered the study area and reclassified into six classes. These data were collected and compiled in collaboration with the Meteorological Bureau of the region. Each of the raster format files was weighted according to the certainty factor values, as discussed in Section 3.3.2 (Figure 4).
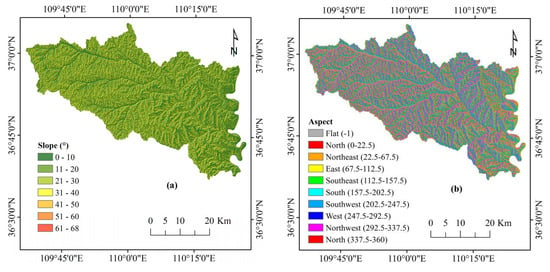
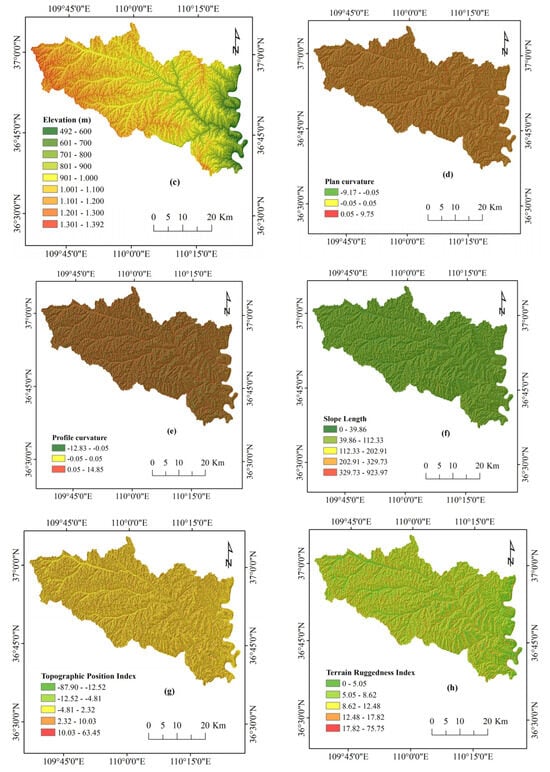
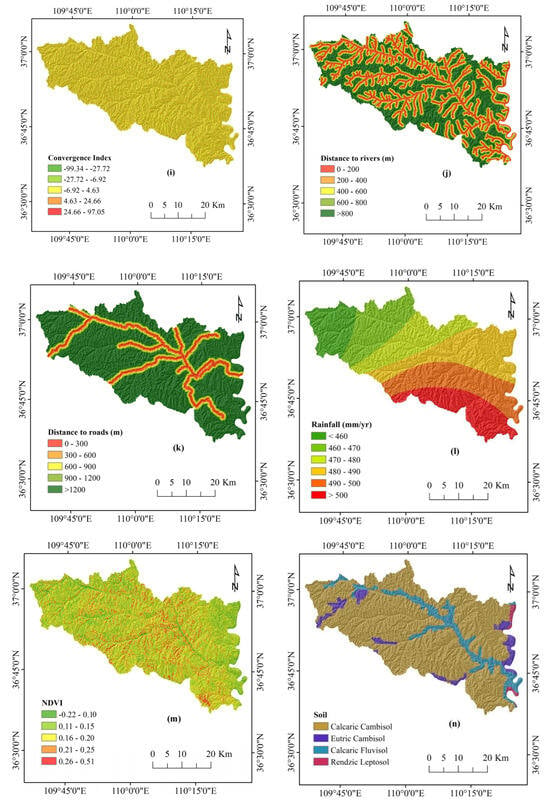
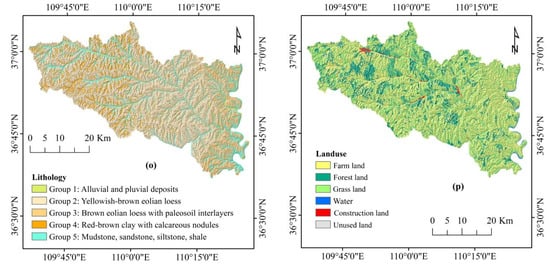
Figure 4.
Thematic maps: (a) slope, (b) aspect, (c) elevation, (d) plan curvature, (e) profile curvature, (f) slope length, (g) topographic position Index, (h) terrain ruggedness Index, (i) convergence index, (j) distance to rivers, (k) distance to roads, (l) rainfall, (m) NDVI, (n) soil, (o) lithology, and (p) land use.
3.3. Third Step of Analysis
3.3.1. Correlation Attribute Evaluation—Importance Analysis
In landslide susceptibility modeling, the selection of landslide conditioning factors significantly influences landslide susceptibility. Therefore, selecting the landslide conditioning factors and evaluating the prediction ability to optimize the spatial analysis of landslide susceptibility is necessary. The influence of landslide conditioning factors on the landslide susceptibility model is not certain. If there are factors that are not conducive to modeling, they must be eliminated to ensure the good quality of the model. In this research, 16 factors were selected, and their prediction ability was evaluated using the CorrelationAttributeEval (correlation attribute evaluation) (CAE) method. A compatible ranking technique was used to rank the overall attributes of each factor evaluation. Afterward, Spearman’s rank correlation coefficient was used to quantify the correlation between the factors, indicating the correlation between each factor [65]. To ascertain the reliability of the selected landslide susceptibility factors, this study adopts the 10-fold cross-validation attribute selection models to assess the importance of each factor.
3.3.2. Certainty Factor Analysis
The certainty coefficient (CF) method employed in this study serves as a robust tool for assessing the correlation between various conditioning factors and landslide occurrences [71,80,81,82]. Despite its simplicity, this method is known for its high accuracy in evaluating landslide susceptibility. Its accuracy stems from the assumption that geological disasters that have occurred and those that may occur in the future will manifest under the same geological conditions. The CF calculation formula is as follows [71] (Equation (1)):
where PPa represents the conditional probability of landslides in a specific impact factor classification “a”. It is calculated as the ratio of landslide points within classification “a” to the total area covered by that classification. On the other hand, PPs signifies the probability of historical landslides across the entire study area. It is calculated as the ratio of historical landslide points to the total area of the study. The CF values fall within the range of −1 to 1. When CF values are between zero and 1, it indicates that landslides are more likely to occur in the geological environment corresponding to the specific classification. The closer the CF value is to 1, the higher the sensitivity of that unit to landslides. Conversely, when CF values are between −1 and zero, it suggests that landslides are less likely to occur in the corresponding geological environment.
3.4. Fourth Step of Analysis
The fourth step of analysis involved the implementation of the single-based tree models, the REPTree and FT, and the hybrid bagging-based REPTree and FT models. The hybrid bagging-based models are used as base learners for the two single-based tree models. The purpose of this step is to compare the performance of the four models in terms of (ROC curves, accuracy, sensitivity, specificity, the F-score, Matthews correlation coefficient (MCC), true skill statistic (TSS), and root-mean-square error (RMSE).
3.4.1. Reduced Error Pruning Decision Tree
The REPTree model serves as a crucial element within our modeling approach, effectively merging the foundational principles of the DT with error pruning reduction (REP). At the heart of the REPTree algorithm lies the concept of information gain, aimed at simplifying the often-intricate DT model structure to attain objectives of minimizing variance and enhancing prediction accuracy [83,84].
The maximum information gain ratio is calculated as follows [24] (Equation (2)):
where in our case, attribute x representing various landslide conditioning factors is sourced from the training subset Ai (i = 1, 2, …, n) within the landslide training dataset A. These factors include slope, aspect, elevation, plan curvature, profile curvature, slope length, topography position index, terrain ruggedness index, convergence index, distance to rivers, distance to roads, rainfall, NDVI, soil, lithology, and land use.
Error reduction pruning (REP) is based on the principles of empirical risk minimization, as established by empirical observations and analyses [85,86]. By combining with the DT framework, REP effectively minimizes errors, ensuring the highest level of accuracy possible [87]. To mitigate the risk of excessive complexities during the learning process, REP employs a post-pruning technique that strategically removes branches and leaves that make only marginal contributions to the model. This process is essential for reducing the overall size of the DT model, optimizing its efficiency, and maintaining robust predictive accuracy [82].
3.4.2. Function Trees
The FT, an algorithm derived from the DT, represents a fusion of discriminant functions and a multivariate DT, initially proposed by Gama [27]. The FT model has found extensive application in landslide modeling across various studies [52,60,88]. FT’s primary objective is to construct a DT capable of distinguishing samples (x, y) within the training dataset A, where “y” denotes the output value, either 0 or 1, signifying the presence or absence of landslides.
In the FT model, each sample navigates from the root node to a leaf node, and functions are constructed at each node to expand the attribute set at decision nodes. The decision-making tests performed at each node determine the sample’s path, ultimately leading to classification into functions or constants at the leaves [27].
The FT employs the gain ratio as the split criterion to select input attributes for splitting. To prevent overfitting, it utilizes the standard C4.5 pruning technique [88]. FT employs logistic regression functions for calculations to handle internal node fission (oblique cracking) and predict outcomes at leaf nodes [89]. In this context, Wi represents the coefficient of the i-th component in the input vector Ai (i = 1, 2, …, n), and P(x) signifies the probability prediction value. The posterior probability of a leaf node, P(x), is computed as follows [90] (Equations (3) and (4)):
3.4.3. Bagging
The bagging model represents an intelligent integrated machine learning technique pioneered by Breiman, grounded in the principles of clustering and bootstrapping [69,91]. As one of the most widely adopted combinatorial construction methods, the bagging algorithm plays a pivotal role in acquiring more precise and robust models [69,91]. Its primary function revolves around enhancing classification accuracy by diminishing the variance associated with classification errors [69,91]. The bagging model possesses a keen aptitude for detecting and analyzing fluctuations within training data, rendering it exceptionally effective in the realm of landslide susceptibility modeling. This capability significantly elevates the model’s predictive prowess [68,92].
The bagging algorithm is an ensemble machine learning technique that combines the predictions from multiple base models to improve overall predictive performance. The theoretical expression of the bagging estimator can be described as follows:
Let us assume a dataset D containing N samples (D = {x1, x2, …, xN}) and their corresponding labels (target values) Y = {y1, y2, …, yN}. There is also a base model (e.g., decision tree and neural network) denoted as M, and the purpose is to train B different instances of this base model to create an ensemble.
For each of the B base models, a new dataset (Di) is generated by randomly sampling N samples with replacement from the original dataset D. This process creates multiple bootstrapped datasets. The next step is to train each B base model independently on these bootstrapped datasets. Each model Mi (i = 1 to B) is trained on a different dataset Di. To make predictions, you apply each of the B models to a new input sample x (where x is not necessarily part of the training data). Each model Mi produces its prediction, denoted as ŷi. Finally, you aggregate the predictions from all B models to obtain the final prediction. Common aggregation methods include taking the majority vote for classification tasks (e.g., counting the most frequent class among the predictions) or averaging the predictions for regression tasks. Mathematically, for a classification problem with binary outcomes (0 or 1), you can express the bagging estimator as follows:
Given B base models Mi, i = 1 to B, each trained on bootstrapped datasets Di, you can calculate the final prediction as (Equation (5)):
where ŷ is the final prediction, ŷi is the prediction from the i-th base model, and B is the total number of base models in the ensemble.
The bagging algorithm effectively reduces overfitting, improves model stability, and enhances predictive performance by combining the diversity of individual models trained on different data subsets.
3.4.4. Receiver Operating Characteristic (ROC) Curves
The area under the ROC curve (AUC) serves as a crucial metric obtained through the integration of the ROC curve. It plays a pivotal role in assessing the overall performance of the model and facilitating comparisons among various models [93,94]. The ROC curve is widely embraced as a tool to assess the quality of probability prediction systems [71,95]. It presents a graphical representation where the horizontal axis (X-axis) portrays 1-Specificity (the false positive rate), while the vertical axis (Y-axis) represents Sensitivity (the true positive rate) [71,95]. The ROC curve and its corresponding AUC value are instrumental in quantifying the likelihood of event occurrence and are pivotal in diagnosing and evaluating landslide susceptibility. The ROC curve takes shape by establishing the relationship between the true and false positive rates within a binary classification system. Notably, ROC curves exhibit a unique appeal as they do not heavily rely on the class ratio, making them impervious to discrepancies between the training and validation datasets [65]. AUC values provide a definitive measure of ROC curve analysis, offering a specific numeric representation of the model’s quality on the training dataset and its predictive capabilities on the validation dataset. AUC values range from 0 to 1, with a curve closer to the upper left corner indicating superior model performance [71]. Larger AUC values denote a more accurate model with enhanced performance. An AUC value of 1 signifies the highest level of model accuracy, an ideal achievement. Generally, AUC values are categorized into distinct ranges: excellent (0.9 to 1), very good (0.8 to 0.9), good (0.7 to 0.8), average (0.6 to 0.7), and poor (0.5 to 0.6) [96]. When the AUC value falls between 0 and 0.5, it implies that the classification needs to be inverted [97].
3.4.5. Trade-Off Statistical Metrics
A confusion matrix for in-depth analysis was constructed to achieve a more precise evaluation of the four models. Within this matrix, several fundamental statistical indicators are utilized: TP (true positive), indicating the number of pixels correctly classified as landslide occurrences; TN (true negative), representing the number of pixels accurately classified as non-landslide areas; FP (false positive), denoting the number of pixels incorrectly identified as landslides when they are not; and FN (false negative), indicating the number of pixels wrongly classified as non-landslide areas when they are indeed landslides. Furthermore, within the evaluation step, a range of trade-off statistical metrics from the confusion matrix, including the positive predictive rate (PPR), negative predictive rate (NPR), sensitivity, specificity, accuracy, F-score, Matthews correlation coefficient (MCC), true skill statistics (TSS), and root-mean-square error (RMSE) were calculated. Trade-off statistical metrics refer to a set of metrics used to assess the balance between different aspects of model performance, particularly in binary classification problems like landslide susceptibility mapping. These metrics help evaluate how well a model performs in terms of making trade-offs between different types of errors (e.g., false positives and false negatives) and various aspects of classification, such as sensitivity, specificity, positive predictive rate (PPR), negative predictive rate (NPR), accuracy, and more. These metrics provide a more nuanced understanding of a model’s performance by considering both its ability to correctly identify positive cases (landslides) and negative cases (non-landslides) and the potential trade-offs between them, providing a more robust assessment of model performance beyond the ROC curve and AUC values as being reported in previous research [65,98,99,100]. The following Equations (6)–(15) provide the mathematical expression of the above comprehensive evaluation metrics.
where m is a value that corresponds to the sum of the total number of non-landslides and the number of landslides. In the model, is the observed value of the landslide and is the predicted value of the landslide.
3.4.6. Pairwise Comparison Based on Chi-Square Test (χ2 Test)
In the present study, the Chi-Square test (χ2 test) was used to perform pairwise comparisons of the four models (BREPTree, REPTree, FT, and BFT) to determine whether there are significant differences in their performance based on a categorical outcome. The first action is to set up the hypotheses. Specifically, the null hypothesis (H0) assumes that there is no significant difference in the performance between the two models being compared, whereas the alternative hypothesis (H1) assumes that there is a significant difference in performance between the two models being compared.
The comparison was based on the performance of each model’s correct and incorrect predictions, with degrees of freedom set to 1 and significance level α = 0.05, thus χ2_critical value set to 3.841. The chi-square statistic, χ2, is calculated as (Equations (15) and (16)):
where O is the observed frequency and E is the expected frequency under the null hypothesis.
If χ2 > χ2_critical, the null hypothesis is rejected, which means that there is a significant difference in performance between the two models; otherwise, the null hypothesis is not rejected, which means that there is no significant difference in performance between the two models.
3.4.7. Landslide Susceptibility Mapping
The final step in our proposed methodology involves the creation of landslide susceptibility maps, a crucial component of our analysis. In more detail, within this final step, the landslide susceptibility index (LSI) is calculated for every pixel, utilizing the powerful capabilities of ArcGIS 10.5 software. ArcGIS offers several techniques for map classification, including Jenks natural breaks, geometric intervals, equal intervals, standard deviation, quantile, and manual methods [101,102]. Our study employed the Jenks natural breaks classification method to reclassify the results obtained from the four different landslide susceptibility models. The natural breaks method was particularly useful for continuous data to identify meaningful classes based on natural groupings inherent in the data. This classification process assigns each model’s output to one of five distinct susceptibility levels, encompassing very low, low, medium, high, and very high categories. This final susceptibility map visually represents landslide susceptibility across the study area, offering valuable insights for effective landslide risk assessment and management.
4. Results
Importance of Landslide Conditioning Factors
The initial output of the proposed methodology focuses on assessing the predictive capability and significance of each landslide-related factor. The average merit (AM) assigned to each factor serves as an indicator of its importance in the context of landslide occurrences. Notably, there is a standard deviation (Std.) associated with each average merit (AM), reflecting the degree of variability in their importance assessments. The results underscore a positive correlation among the 16 conditioning factors, collectively contributing to the enhancement of landslide susceptibility modeling. These factors, characterized by positive correlations, remain pivotal for further analysis (Table 1). Among the 16 landslide conditioning factors, the analysis reveals that the slope (AM = 0.612, Std. = ±0.012) and terrain ruggedness index (AM = 0.456, Std. = ±0.015) exhibit the highest predictive capabilities. Following closely are the distance to rivers (AM = 0.262, Std. = ±0.019), convergence index (AM = 0.187, Std. = ±0.012), aspect (AM = 0.182, Std. = ±0.011), rainfall (AM = 0.176, Std. = ±0.012), Land Use (AM = 0.172, Std. = ±0.011), Plan Curvature (AM = 0.159, Std. = ±0.009), profile curvature (AM = 0.157, Std. = ±0.007), slope length (AM = 0.140, Std. = ±0.011), distance to roads (AM = 0.116, Std. = ±0.014), elevation (AM = 0.115, Std. = ±0.116), NDVI (AM = 0.088, Std. = ±0.010), lithology (AM = 0.071, Std. = ±0.017), soil (AM = 0.029, Std. = ±0.014), and topography position index (AM = 0.029, Std. = ±0.014). These findings provide valuable insights into the significance and relative contributions of these factors to landslide susceptibility modeling.

Table 1.
Predictive ability and importance of landslide-related factors—average merit values.
Concerning the analysis of the CF value and the three landslide factors with the most predictive ability, the “21–30” and “31–40” slope classes exhibit the highest percentages of landslide occurrences, followed by the “41–50” class. Conversely, the “51–60” and “61–68.30” slope classes show no landslides, and their negative certainty factors suggest lower confidence in landslide occurrences in these ranges. Ranging from 0 to 75.75, each interval provides details on the number and percentage of landslides within the specified TRI range, the total number of pixels in the domain, the percentage of the domain covered, and the associated certainty factor. Notably, the TRI intervals demonstrate varying degrees of terrain complexity, with higher TRI values indicating increased ruggedness. The CF analysis reveals a strong trend between terrain ruggedness and landslides, with higher certainty factors in intervals such as 8.62–12.48, 12.48–17.82, and 17.82–75.75, suggesting a positive correlation between rugged terrain and landslide susceptibility. Concerning proximity to rivers, a positive correlation between the proximity to rivers and landslide susceptibility, with higher certainty factors in intervals such as 0–200 m and 200–400 m, suggests an increased likelihood of landslides in closer proximity to rivers. Conversely, as the distance from rivers increases in the 400–600 m, 600–800 m, and > 800 m intervals, the certainty factors become negative, indicating a perceived decrease in landslide susceptibility with greater distances from rivers. The rest of the CF values for each class and each factor are documented in Table 2.

Table 2.
Certainty factor values.
Passing to the implementation of the models, the first action was to set the optimal parameters for each model. Table 3 provides the values of the structural parameters that were applied to the predictive models using a trial-and-error procedure using accuracy as the evaluation metric. Specifically, the bagging model performed 10 iterations, using only one execution slot for constructing the ensemble, indicating a sequential processing approach. For the REPTree model, the tree construction process used 3-fold cross-validation to evaluate splits and a minimum proportion of variance for considering a split set at 0.001, allowing for fine-grained splits. The maximum tree depth was unrestricted (−1), enabling the tree to grow as needed, while the minimum total weight (sum of instances’ weights) in a leaf was set to 2, preventing overly small leaves. The FT model was configured for 15 iterations of LogitBoost, considering splitting nodes if they contain at least 15 instances, focusing on significant data partitions, and avoiding overfitting on small data subsets.

Table 3.
Optimal values of structural parameters.
The results of the ROC curve analysis for both the training and validation datasets revealed important insights into model performance (Figure 5 and Table 4 and Table 5). In the success rate curve (Figure 5a), the BREPTree model demonstrated the highest AUC value of 0.853, closely followed by the BFT model with an AUC of 0.851. The REPTree model achieved an AUC of 0.798, and the FT model recorded an AUC of 0.795. Furthermore, the BREPTree model exhibited the smallest standard error (0.018), underscoring the precision and reliability of its AUC estimate. The narrow 95% confidence interval (0.816 to 0.889) and the highly significant p-value (“<0.0001”) further supported the robustness of the BREPTree model. In the prediction rate curve (Figure 5b), the BFT model outperformed all others with the largest AUC value of 0.895, followed by the BREPTree model with an AUC of 0.886. The FT model exhibited an AUC of 0.856, while the REPTree model achieved an AUC of 0.842. Importantly, the BFT and BREPTree models exhibited the same and minimal standard error (0.025), suggesting a high confidence level in their AUC estimates. The significance levels of these parameters, as indicated by the low p-values, underscore the robustness of the models. These findings collectively demonstrate that all models in the study perform reasonably well, with the hybrid BFT model consistently exhibiting the highest AUC values, indicating its superior predictive accuracy.
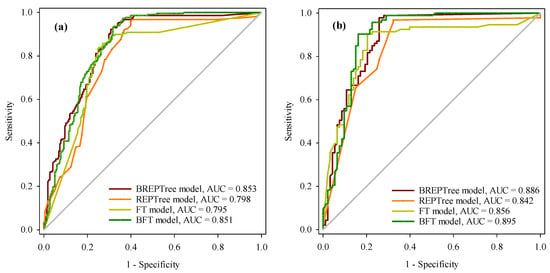
Figure 5.
ROC curves: (a) the training dataset; (b) the validation dataset.

Table 4.
Parameters of ROC curves using the training data.

Table 5.
Parameters of ROC curves using the validation data.
The significance of model verification in the context of landslide susceptibility assessment cannot be overstated, as it serves as the crucial step in ensuring the reliability and accuracy of the predictive models. In this study, the verification process employed a comprehensive set of trade-off statistical metrics, effectively quantifying the performance of the four models. The results (Table 6) highlight the strengths and capabilities of each model in predicting landslides and non-landslide areas, ultimately guiding decision-making processes related to landslide risk management. The positive predictive rate (PPR) assesses the models’ ability to correctly identify areas prone to landslides, with the BFT model achieving the highest PPR (0.847), followed by the FT model (PPR = 0.815). Furthermore, the BFT model excels in the negative predictive rate (NPR) in correctly identifying non-landslide areas, with an NPR value of 0.886. Regarding landslide classification, sensitivity measures the models’ capacity to accurately detect actual landslide occurrences, and once again, the BFT model achieves the highest value of 0.892, followed by the REPTree model (0.871). The BFT model has the highest value in specificity (0.839), a metric that evaluates the models’ effectiveness in correctly classifying non-landslide areas, followed by the FT model (0.817). Accuracy, as a holistic measure of correctness, underlines the BFT model’s dominance, achieving the highest accuracy score of 0.866, followed by the BREPTree model (0.812), the FT model (0.812), and the REPTree model (0.790). Concerning the F-score, which balances precision and recall, the BFT model’s performance is the highest (F-score = 0.869), whereas BFT demonstrates the highest MCC (0.732), a vital metric for binary classifications. The TSS, a metric that emphasizes sensitivity and specificity, corroborates the BFT model’s robustness, with a TSS score of 0.731, followed by the BREPTree model (0.624). Lastly, the RMSE, quantifying prediction errors, showcases the BREPTree model as the most accurate in terms of landslide susceptibility prediction, with the lowest RMSE value of 0.245, followed by the REPTree model (0.274).

Table 6.
Validation of results using cutoff-dependent metrics.
Table 7 compares the four models, BREPTree, REPTree, FT, and BFT, using the chi-square test. This statistical analysis is crucial for determining whether there are significant differences in the performance of these models, which can provide valuable insights into their relative strengths and weaknesses. The chi-square values in the table quantify the degree of dissimilarity between each pair of models. When comparing BREPTree to REPTree, the chi-square value is 11.205, indicating a significant difference in their performance (p-value = 0.001). Similarly, when comparing the BREPTree to the FT, the chi-square value is 9.264, signifying a substantial performance difference (p-value = 0.002). However, when comparing BREPTree to BFT, the chi-square value is only 0.0230, with a high p-value of 0.879, suggesting no significant difference in performance. Comparing REPTree to FT yields a chi-square value of 0.0214 and a p-value of 0.884, indicating no significant difference in performance between these two models. Conversely, when comparing REPTree to BFT, the chi-square value is 8.436, with a p-value of 0.004, signifying a significant performance difference. Finally, when comparing the FT to the BFT, the chi-square value is 9.547, also indicating a significant difference in their performance (p-value = 0.002).

Table 7.
Pairwise comparison of models using chi-square.
The resulting susceptibility maps illustrate the spatial distribution of landslide susceptibility across the study area (Figure 6a–d). For the REPTree model, the majority of the area falls under the very low susceptibility category (58.74%), followed by low (7.92%), medium (6.08%), high (26.46%), and very high (0.81%) susceptibility. Similarly, the BREPTree model designates the largest portion of the area as very low susceptibility (58.99%), with the rest classified as low (6.20%), medium (9.81%), high (12.13%), and very high (12.87%) susceptibility. In the case of the FT model, the susceptibility classes consist of very low (56.40%), low (7.08%), medium (9.18%), high (11.31%), and very high (16.03%). Finally, the BFT model categorizes the study area into very low susceptibility (45.52%), low (11.11%), medium (13.47%), high (15.99%), and very high susceptibility (13.91%) (Figure 7, Table 8). Each of the four landslide susceptibility maps reveals that while the very low susceptibility class dominates the landscape, there are variations in the overall distribution of susceptibility levels among the models. Notably, the bagging algorithm employed in the integrated models (BREPTree and BFT) demonstrates its effectiveness by improving the predictive accuracy and fine-tuning the susceptibility classification.
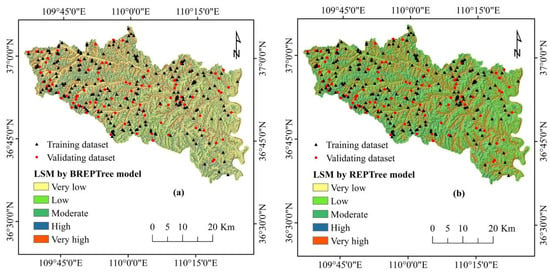
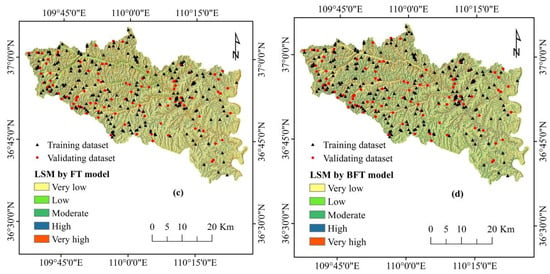
Figure 6.
Landslide susceptibility maps: (a) BREPTree model, (b) REPTree model, (c) FT model, and (d) BFT model.
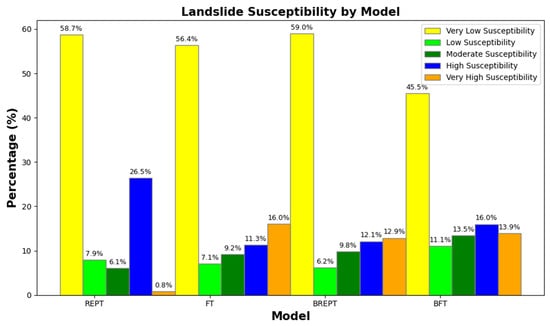
Figure 7.
Percentages of landslide susceptibility classes.

Table 8.
Landslide susceptibility zoning.
5. Discussion
Landslides represent a worldwide natural disaster, a significant threat to human life, the man-made and natural environment. These characteristics command the accurate spatial prediction of their occurrence and evolution, a process that is the initial crucial step in landslide disaster risk assessment, essential for informed land-use and planning decisions [103]. As already discussed, identifying landslide-prone areas is not an easy task. Traditional statistical approaches are gradually giving way to machine learning techniques for landslide susceptibility prediction since machine learning algorithms have proven invaluable in mitigating the limitations of subjective assumptions, offering enhanced accuracy and effectiveness compared to expert-based models and traditional statistical analyses. However, recent research highlights the limitations of relying solely on single machine learning algorithms, emphasizing the growing significance of ensemble models. As widely acknowledged, integrated models tend to outperform individual models in general [104,105]. In this context, the current study introduces a five-step methodology approach with the main objective of delivering two hybrid bagging-based models, BDT and BREPTree, which had a REPTree and FT model as base learners, respectively. These hybrid models were evaluated and compared to estimate the most accurate and reliable model. In more detail, the methodology commences with the construction of both landslide and non-landslide inventories, selects and classifies the various landslide-related factors, and incorporates the crucial aspects of correlation attribute evaluation, certainty factor analysis, and normalization, which collectively aid in identifying and quantifying the influences of these factors on landslide susceptibility. It deploys the tree-based and hybrid models to create the four distinct landslide susceptibility models and evaluates their learning and predictive performance with varying statistical metrics and chi-square tests [106,107]. The certainty factor method was applied to identify the trends, patterns, and potential association between landslide factors and landslide manifestation, providing a means to highlight their contribution to landslide susceptibility [108].
Based on the correlation attribute evaluation (CAE) method and the average merit information (AM) values, it has been affirmed that all 16 landslide conditioning factors exert a positive and varying influence on landslide susceptibility, underscoring their individual contributions. Slope, TRI, and the distance to rivers have been identified as having the highest predictive capabilities. These factors are well-known as significant factors in landslide susceptibility modeling due to their direct physical and hydrological connections with landslide occurrence. They are all physical characteristics of the terrain that are directly related to hydrological patterns and landslide susceptibility. Steeper slopes generally pose a higher risk of landslides, rugged terrain can increase landslide potential, and proximity to rivers can affect soil moisture levels and slope stability [7,22,76]. The above factors, along with CI, aspect, and rainfall, are significant factors related to water-related issues. Specifically, in most cases, rivers with high-volume water flow are associated with areas of higher landslide susceptibility [109]. These interconnections highlight how accurately predicting landslide-prone areas is vital for managing and mitigating potential disruptions to water systems. Landslide occurrences can lead to significant consequences such as blockage of rivers and streams, contamination of water supplies from soil and debris, and alterations in hydrological patterns, affecting water availability. By addressing these factors in landslide susceptibility models, we can provide crucial insights for effective water resource management, particularly in mitigating the impacts of landslides on water flow and quality.
Concerning the low AM values of lithology and soil type covers, the study area is characterized by a high degree of geological uniformity; the diversity and influence of lithology and soil types on landslide susceptibility might be less pronounced than they would be in areas with more geological diversity. In regions where geological features are relatively homogenous, other factors, such as topography or hydrological conditions, may play a more pivotal role in triggering landslides.
Among the factors influencing landslide susceptibility, certain classes within each variable exhibit notably higher certainty factor values. Notably, the class ranging from 40 to 50 degrees for slope holds the highest certainty factor at 0.656, suggesting a strong positive correlation with landslide susceptibility. Similarly, in terms of aspect, the “North” class stands out with a certainty factor of 0.340, indicating an inclination towards increased susceptibility. Elevation-wise, areas higher than 1300 m demonstrate the highest certainty factor of 0.349. Other influential factors include the terrain ruggedness index, where the class ranging from 17.82 to 75.75 exhibits a substantial certainty factor of 0.574. Additionally, classes within distance to rivers (0–200 m) and distance to roads (300–600 m) also show heightened certainty factors of 0.446 and 0.392, respectively, emphasizing their significance in landslide susceptibility assessment. Red-brown clay with calcareous nodules and construction land show the highest certainty factor values of 0.544.
The main idea behind using bagging with base learners is to reduce overfitting and variance, thus improving the overall model’s generalization performance. It can lead to better predictive accuracy and stability, especially when individual base learners might have different strengths and weaknesses. The bagging approach builds multiple classifiers through random sampling with replacement in parallel, meaning that each model is constructed independently of the others. Our study’s hybrid approach leverages the strengths of both base learners and the bagging method to create a more powerful predictive model. In general, bagging approaches are more effective when base models appear unstable or prone to overfitting. The evaluation of the hybrid models using both training and validation datasets yielded valuable insights into their respective strengths and reliability. The high AUC values, minimal standard errors, narrow confidence intervals, and significant p-values collectively indicated the models’ effectiveness in predicting landslide susceptibility. The robustness and reliability of the BFT model stem from the combined benefits of bagging’s variance reduction and error compensation, along with the functional trees’ ability to capture complex data patterns. This synergy makes BFT models particularly effective for tasks like landslide susceptibility prediction, where the complexity and variability of the data require sophisticated modeling techniques. Comparing the concept of FBT models with RF, which are known for their robustness and ability to handle diverse datasets, BFT extends the bagging concept by incorporating FT, which can capture complex nonlinear relationships within the data (Table 9). Similar to our findings, Zhao and Chen [71] report that the BFT model was the best optimization ensemble model in their study among the FT, Dagging-FT, and Rotation Forest-FT models, and it could be used as an advantageous and promising method for landslide susceptibility modeling. Also, Peng et al. [110] implemented an advanced random subspace (RS) and FT-coupled model and compared its performance with BFT, CART, and NBT models. Their findings agreed with ours in terms of higher accuracy achieved from hybrid models; however, they found that the RS-FT model was more accurate compared to BFT.

Table 9.
Description of the four models: REPT, FT, BREPT, and BFT.
In conclusion, while other bagging-based tree models, like RF, appear as promising methods and are widely applicable, BFT may outperform them when there are complex, nonlinear relationships to uncover. However, as in any classification problem addressed through machine learning techniques, it is advisable to employ multiple methods with either similar or preferably diverse learning mechanisms. This approach allows for a comprehensive examination of the problem and facilitates a relative comparison between the performance metrics of each model to identify the optimal model.
In more detail, the analysis of various metrics reveals that the BFT model emerges as the top performer in landslide susceptibility assessment. BFT exhibits the highest values across key metrics such as accuracy, sensitivity, specificity, and the F-score, providing evidence of its ability to make reliable predictions and maintain a balanced approach in identifying both positive and negative landslide cases. Notably, BFT excels in reducing false positives and false negatives, a critical aspect in landslide susceptibility modeling where erroneous predictions can have significant consequences. Additionally, the BFT model’s high MCC and TSS scores underscore its robustness and discriminatory power in handling complex datasets. Moreover, it achieves the lowest RMSE, indicating minimal prediction errors. Considering these findings, the BFT model is highly recommended for landslide susceptibility assessment in the study area, as it consistently demonstrates superior performance and reliability, promising more accurate and effective risk assessment and management strategies.
The observation that none of the models exceeded a 90% F-score, along with similar trends in other metrics, can be attributed to several factors intrinsic to modeling complex natural phenomena such as landslides. These factors encompass potential data-related limitations, including the dataset’s resolution, coverage, or completeness, as well as the inherent challenges posed by accurately modeling environmental risks. This situation underscores the inherent difficulty in attaining extremely high accuracy levels in the prediction of natural events. It also highlights the ongoing necessity to enhance both the modeling methodologies and the data quality used for such analyses.
Even if our study provides significant insights, it is important to acknowledge its limitations. The reliance on specific data sets and environmental factors may limit the generalizability of our findings. Future studies should aim to address these limitations by incorporating a broader range of data and testing the models in varied geographical contexts. Also, while our study has concentrated on surface geomorphological features as primary indicators for landslide susceptibility in China’s Loess Plateau, we recognize that human activities can significantly influence the activation of landslides. It is well-documented that land use and land cover alterations, such as deforestation, construction, and agricultural practices, can destabilize slopes and precipitate landslide events. In our analysis, land use and land cover data and distance from road networks were utilized; however, more detailed aspects of human activity, including urban development, infrastructure expansion, and intensive agriculture, were not explicitly included. We acknowledge that this is an important dimension of landslide susceptibility and that the exclusion of detailed human activity-related factors could be seen as a limitation of the current study. Future research should aim to integrate these factors to provide a more holistic understanding of the conditions leading to landslide occurrences. Incorporating detailed data on human activities will enhance the accuracy of predictive models and contribute to more effective risk management and mitigation strategies in regions similar to Yanchuan County. Furthermore, while our models incorporate multiple variables to predict landslide susceptibility accurately, the spatial predictions are subject to uncertainties due to potential data quality variations and the dynamic nature of the environmental factors. Acknowledging these uncertainties is vital for carefully interpreting the models’ outputs, especially when applied to land-use planning and risk management decisions. Future research should focus on improving data quality, exploring more sophisticated modeling techniques, and incorporating uncertainty analysis methods, such as Monte Carlo simulations, to quantify and reduce these uncertainties, thereby enhancing the reliability of spatial predictions. Future work may include a comprehensive project aimed at integrating an uncertainty analysis into the landslide susceptibility modeling, which will focus on quantifying the confidence levels associated with the susceptibility predictions by implementing advanced statistical techniques such as bootstrapping and Bayesian inference. This will allow us to identify zones where model predictions are less certain, thereby guiding targeted data collection to refine model inputs and improve predictive accuracy.
The potential to extend our methodology into a spatio-temporal model offers an exciting avenue for advancing landslide susceptibility assessment. By incorporating multi-date landslide inventories and analyzing changes over time, a spatio-temporal model could capture the dynamics of landslide susceptibility, reflecting how it evolves in response to changes in environmental conditions and human activities. This approach would enable the identification of trends and patterns in landslide occurrences, providing insights into areas that are becoming more susceptible over time. Such a model would be particularly useful for monitoring the effectiveness of mitigation measures, planning future land use, and adapting to climate change impacts. Incorporating temporal data requires robust methodologies to handle the added complexity, including time-series analysis and dynamic modeling techniques, which could significantly enhance our understanding of landslide risks and inform more proactive management strategies.
In conclusion, the landslide susceptibility maps generated by the four models using the natural breaks method effectively depict susceptibility zoning across the entire county, offering valuable insights. The diversity in susceptibility distributions among the four models underscores the significance of considering different modeling approaches. The successful application of the bagging algorithm, particularly in the integrated models, demonstrates its potential to enhance the accuracy and reliability of landslide susceptibility assessments, ultimately contributing to informed decision-making and the reduction of landslide risks in the study area. The results underscore the suitability of the selected models for the study area and suggest that, from a probabilistic standpoint, most regions in Yanchuan County are relatively safe in terms of landslide hazards.
6. Conclusions
The present study addresses the critical need for accurate landslide prediction, a vital step in disaster risk assessment and land-use planning. Focusing on the landslide-prone Yanchuan County, the research integrates advanced techniques and comprehensive analyses to develop landslide susceptibility models. Our research introduced a hybrid ensemble-based methodology, developing four distinct landslide susceptibility tree-based models: REPTree, BREPTree, FT, and BFT. These models were rigorously evaluated and compared to identify the most accurate and reliable model for landslide susceptibility assessment. Yanchuan County’s unique geographical and environmental characteristics, characterized by loess accumulation, soil erosion, gully networks, rugged terrain, and human activities, contribute to unstable slopes and landslide occurrences. The selection and evaluation of 16 landslide conditioning factors affirmed their positive influence on landslide susceptibility, underscoring their individual significance. The study’s findings underscore the significance of various conditioning factors, including slope, terrain ruggedness, distance to rivers, rainfall, and land uses, in influencing regional landslide occurrences. Current research highlights the power of integrating methodologies by utilizing ensemble models, particularly the bagging-enhanced REPTree and FT models (BREPTree and BFT). These hybrid models outperform their individual counterparts, emphasizing the value of ensemble techniques in improving prediction accuracy and model reliability. The evaluation metrics, including ROC curves, AUC values, and trade-off statistical metrics, confirm the superiority of the BFT model in accurately predicting landslide susceptibility. The study’s detailed analyses contribute to the specific understanding of landslides in Yanchuan County and shed light on the broader application of ensemble models in landslide susceptibility mapping. Adopting integrated ensemble models, particularly the combination of bagging with the REPTree and FT models to create the BREPTree and BFT models, proved advantageous. This approach effectively reduced data dimensionality and enhanced sensitivity to data variations, resulting in more optimized models. The chi-square analysis conducted on the various model pairs has provided valuable insights into their relative performance in predicting landslide susceptibility. The results highlight significant differences in performance between certain model pairs, notably BREPTree vs. REPTree, BREPTree vs. FT, and REPTree vs. BFT. These findings underscore the importance of selecting the most suitable model based on statistical evidence when tackling landslide susceptibility assessments. Interestingly, no statistically significant differences were observed when comparing BREPTree to BFT and REPTree to FT, indicating that these model pairs exhibit similar predictive capabilities. Each of the four landslide susceptibility maps generated in this study highlights the prevalence of areas classified as having very low susceptibility to landslides. This finding indicates that a significant portion of Yanchuan County is at a relatively low risk of experiencing landslides. However, it is crucial to recognize that there are noteworthy distinctions in the distribution of susceptibility levels across the landscape when comparing the four models. However, the need for further investigation is worth noting, especially in understanding the differences in model performance. This ongoing pursuit of optimization reflects the dynamic nature of predictive modeling and opens avenues for future research in landslide susceptibility assessment in Yanchuan County and similar regions globally. In summary, our research highlights the significance of ensemble models and the potential of the BFT model in improving landslide susceptibility prediction. It also underscores the continuing need for research in this field to enhance our understanding and preparedness for landslide-related disasters.
Author Contributions
Conceptualization, Q.Z. and Z.N.; methodology, Q.Z., Z.N. and J.W.; software, Z.W. and Y.W.; validation, W.C., Z.W. and Y.W.; formal analysis, Z.N. and X.D.; investigation, Q.Z. and W.C.; writing—original draft preparation, Q.Z., P.T. and I.I.; writing—review and editing, W.C., P.T. and I.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors wish to express their sincere thanks to Ruixin Zhao’s technical support.
Conflicts of Interest
Qi Zhang and Yukun Wang were employed by Shenmu Ningtiaota Coal Mining Co., Ltd., Shaanxi Coal and Chemical Industry Group Co., Ltd. Zixin Ning and Junfeng Wu were employed by No. 7 Oil Production Plant, Changqing Oilfield Company, PetroChina. Xiaohu Ding was employed by Changqing Oilfield Company, PetroChina. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Akgun, A.; Türk, N. Landslide susceptibility mapping for Ayvalik (Western Turkey) and its vicinity by multicriteria decision analysis. Environ. Earth Sci. 2010, 61, 595–611. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Landslide susceptibility mapping using a modified decision tree classifier in the Xanthi perfection, Greece. Landslides 2016, 13, 305–320. [Google Scholar] [CrossRef]
- Dagdelenler, G.; Nefeslioglu, H.A.; Gokceoglu, C. Modification of seed cell sampling strategy for landslide susceptibility mapping: An application from the eastern part of the Gallipoli Peninsula (Canakkale, Turkey). Bull. Eng. Geol. Environ. 2016, 75, 575–590. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Varzandeh, M.H.M. A new hybrid model using step-wise weight assessment ratio analysis (Swara) technique and adaptive neuro-fuzzy inference system (Anfis) for regional landslide hazard assessment in Iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A.-X. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. Catena 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Yuan, C.; Moayedi, H. Evaluation and comparison of the advanced metaheuristic and conventional machine learning methods for the prediction of landslide occurrence. Eng. Comput. 2020, 36, 1801–1811. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Pourghasemi, H.R.; Indra, P.; Dholakia, M. Landslide susceptibility assesssment in the uttarakhand area (India) using gis: A comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2017, 128, 255–273. [Google Scholar] [CrossRef]
- Dou, J.; Paudel, U.; Oguchi, T.; Uchiyama, S.; Hayakavva, Y.S. Shallow and deep-seated landslide differentiation using support vector machines: A case study of the Chuetsu area, Japan. Terr. Atmos. Ocean. Sci. 2015, 26, 227. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Bui, D.T. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Selecting optimal conditioning factors in shallow translational landslide susceptibility mapping using genetic algorithm. Eng. Geol. 2015, 192, 101–112. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of gis-based logistic regression for landslide susceptibility mapping in the Kakuda-yahiko mountains, central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. Application of an evidential belief function model in landslide susceptibility mapping. Comput. Geosci. 2012, 44, 120–135. [Google Scholar] [CrossRef]
- Su, G.; Zhang, Y.; Chen, G.; Yan, L. Fast estimation of slope stability based on gaussian process machine learning. Disaster Adv. 2013, 6, 81–91. [Google Scholar]
- Rodrigues, É.O.; Pinheiro, V.; Liatsis, P.; Conci, A. Machine learning in the prediction of cardiac epicardial and mediastinal fat volumes. Comput. Biol. Med. 2017, 89, 520–529. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I. In A novel hybrid intelligent approach of random subspace ensemble and reduced error pruning trees for landslide susceptibility modeling: A case study at Mu Cang Chai district, Yen Bai province, Viet Nam. In International Conference on Geo-Spatial Technologies and Earth Resources; Springer: Berlin/Heidelberg, Germany, 2017; pp. 255–269. [Google Scholar]
- Mathew, J.; Jha, V.; Rawat, G. Landslide susceptibility zonation mapping and its validation in part of garhwal lesser himalaya, India, using binary logistic regression analysis and receiver operating characteristic curve method. Landslides 2009, 6, 17–26. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I. Bagging based support vector machines for spatial prediction of landslides. Environ. Earth Sci. 2018, 77, 146. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using gis. Comput. Geosci. 2012, 51, 350–365. [Google Scholar] [CrossRef]
- Lu, P.; Rosenbaum, M. Artificial neural networks and grey systems for the prediction of slope stability. Nat. Hazards 2003, 30, 383–398. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L.; Li, S.; Ren, F.; Du, Q. A hybrid model considering spatial heterogeneity for landslide susceptibility mapping in Zhejiang province, China. CATENA 2020, 188, 104425. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Miao, Y.; Wang, R.; Zhu, T.; Deng, Y.; Liu, J.; Yang, L.; Qin, C.-Z.; Hong, H. A comparative study of an expert knowledge-based model and two data-driven models for landslide susceptibility mapping. Catena 2018, 166, 317–327. [Google Scholar] [CrossRef]
- Alkhasawneh, M.S.; Ngah, U.K.; Tay, L.T.; Isa, N.A.M.; Al-Batah, M.S. Modeling and testing landslide hazard using decision tree. J. Appl. Math. 2014, 2014, 929768. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide susceptibility assessment in vietnam using support vector machines, decision tree, and naive bayes models. Math. Probl. Eng. 2012, 2012, 974638. [Google Scholar]
- Easdale, T.A.; Healey, J.R.; Grau, H.R.; Malizia, A. Tree life histories in a montane subtropical forest: Species differ independently by shade-tolerance, turnover rate and substrate preference. J. Ecol. 2007, 95, 1234–1249. [Google Scholar] [CrossRef]
- Gama, J. Functional trees for classification. In Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, USA, 29 November–2 December 2001. [Google Scholar]
- Gama, J. Functional Trees. Mach. Learn. 2004, 55, 219–250. [Google Scholar] [CrossRef]
- Bai, S.B.; Wang, J.; Lü, G.-N.; Zhou, P.-G.; Hou, S.-S.; Xu, S.-N. Gis-based logistic regression for landslide susceptibility mapping of the Zhongxian segment in the three Gorges area, China. Geomorphology 2010, 115, 23–31. [Google Scholar] [CrossRef]
- Lee, S. Application of likelihood ratio and logistic regression models to landslide susceptibility mapping using gis. Environ. Manag. 2004, 34, 223–232. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Choi, C.; Kim, B.; Kim, J. Landslide susceptibility mapping using frequency ratio, analytic hierarchy process, logistic regression, and artificial neural network methods at the Inje area, Korea. Environ. Earth Sci. 2013, 68, 1443–1464. [Google Scholar] [CrossRef]
- Chen, W.; Chai, H.; Zhao, Z.; Wang, Q.; Hong, H. Landslide susceptibility mapping based on gis and support vector machine models for the Qianyang county, China. Environ. Earth Sci. 2016, 75, 474. [Google Scholar] [CrossRef]
- Kumar, D.; Thakur, M.; Dubey, C.S.; Shukla, D.P. Landslide susceptibility mapping & prediction using support vector machine for Mandakini River Basin, Garhwal Himalaya, India. Geomorphology 2017, 295, 115–125. [Google Scholar]
- Yang, D.; Li, J. Study on application of support vector machine in slope realibility analtsis. Ground Water 2010, 32, 141–142+145. [Google Scholar]
- Poudyal, C.P.; Chang, C.; Oh, H.-J.; Lee, S. Landslide susceptibility maps comparing frequency ratio and artificial neural networks: A case study from the Nepal Himalaya. Environ. Earth Sci. 2010, 61, 1049–1064. [Google Scholar] [CrossRef]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at central zab basin, iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]
- Dai, F.; Lee, C. Landslide characteristics and slope instability modeling using gis, Lantau Island, Hong Kong. Geomorphology 2002, 42, 213–228. [Google Scholar] [CrossRef]
- Pan, X.D.; Nakamura, H.; Tamotsu, N.; Nan, Z.T. A gis-based landslide hazard assessment by multiple regression analysis—Art. No. 67541m. In Geoinformatics 2007: Geospatial Information Technology and Applications; SPIE: Bellingham, WA, USA, 2007. [Google Scholar]
- Yong, J.W.; Tao, J.P.; Zhong, Z.C. Factors influencing the distribution and growth of dwarf Bamboo, Fargesia Nitida, in a subalpine forest in wolong nature reserve, Southwest China. Ecol. Res. 2009, 24, 1013–1021. [Google Scholar]
- Ibrahim, A.L.B.; Jaw, S.W.; Abdullah, M.A.B.; Reba, M.N.M.; Tam, T.H.; Tan, M.L. Landslide susceptibility mapping using evidential belief function model. Geocarto Int. 2015, 34, 348–367. [Google Scholar]
- Moon, W.M. Integration of geophysical and geological data using evidential belief function. IEEE Trans. Geosci. Remote Sens. 1990, 28, 711–720. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Yang, F.; Chen, H.; Wu, Y.; Li, T.; Li, W.; Wang, Q.; Liu, P. Gis-based landslide susceptibility analysis using frequency ratio and evidential belief function models. Environ. Earth Sci. 2016, 75, 948. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S.; Nonomura, A.; Yamanaka, M.; Masuda, T.; Nishino, K. Gis-based weights-of-evidence modelling of rainfall-induced landslides in small catchments for landslide susceptibility mapping. Environ. Geol. 2008, 54, 311–324. [Google Scholar] [CrossRef]
- Hong, H. Rainfall induced landslide susceptibility mapping using weight-of-evidence, linear and quadratic discriminant and logistic model tree method. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
- Lee, S.; Choi, J.; Chwae, U.; Chang, B. Landslide susceptibility analysis using weight of evidence. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002. [Google Scholar]
- Zhu, C.; Wang, X. Landslide Susceptibility Mapping: A Comparison of Information and Weights-of-Evidence Methods in Three Gorges Area. In Proceedings of the 2009 International Conference on Environmental Science and Information Application Technology, Wuhan, China, 4–5 July 2009; Volume III; pp. 342–346. [Google Scholar] [CrossRef]
- Choi, J.; Oh, H.-J.; Won, J.-S.; Lee, S. Validation of an artificial neural network model for landslide susceptibility mapping. Environ. Earth Sci. 2010, 60, 473–483. [Google Scholar] [CrossRef]
- Mansor, S. Landslide susceptibility analysis using an artificial neural network model. In Remote Sensing for Environmental Monitoring, GIS Applications, and Geology VII; SPIE: Bellingham, WA, USA, 2007; Volume 6749, p. 67490J. [Google Scholar]
- Pradhan, B.; Lee, S. Landslide risk analysis using artificial neural network model focusing on different training sites. Int. J. Phys. Sci. 2009, 4, 1–15. [Google Scholar]
- Lee, S.; Ryu, J.H.; Won, J.S.; Park, H.J. Determination and application of the weights for landslide susceptibility mapping using an artificial neural network. Eng. Geol. 2004, 71, 289–302. [Google Scholar] [CrossRef]
- Ma, S.C.; Shi, H.B. Tree-augmented naive bayes ensembles. In Proceedings of the 2004 International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004. [Google Scholar]
- Wang, S.; Jiang, L.; Li, C. Adapting naive bayes tree for text classification. Knowl. Inf. Syst. 2015, 44, 77–89. [Google Scholar] [CrossRef]
- Chen, W.; Yan, X.; Zhou, Z.; Hong, H.; Pradhan, B. Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression, naive bayes and rbfnetwork models for the Long County area (China). Bull. Eng. Geol. Environ. 2019, 78, 247–266. [Google Scholar] [CrossRef]
- Cawley, G.; Talbot, N. Efficient model selection for kernel logistic regression. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 26 August 2004. [Google Scholar]
- Cawley, G.C.; Talbot, N.L.C. Efficient approximate leave-one-out cross-validation for kernel logistic regression. Mach. Learn. 2008, 71, 243–264. [Google Scholar] [CrossRef]
- Keerthi, S.S.; Duan, K.; Shevade, S.K.; Poo, A.N. A fast dual algorithm for kernel logistic regression. Mach. Learn. 2002, 61, 151–165. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856, Erratum in Landslides 2016, 13, 1315–1318. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Sohrabi, M.; Kalantari, Z. Gis-based landslide susceptibility mapping using numerical risk factor bivariate model and its ensemble with linear multivariate regression and boosted regression tree algorithms. J. Mt. Sci. 2019, 16, 595–618. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Bui, D.T. Spatial prediction of landslides using a hybrid machine learning approach based on random subspace and classification and regression trees. Geomorphology 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Breiman, L. Random forrest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Provost, F.; Hibert, C.; Malet, J.-P. Automatic classification of endogenous landslide seismicity using the random forest supervised classifier. Geophys. Res. Lett. 2017, 44, 113–120. [Google Scholar] [CrossRef]
- Tien Bui, D.; Nguyen, Q.P.; Hoang, N.-D.; Klempe, H. A novel fuzzy k-nearest neighbor inference model with differential evolution for spatial prediction of rainfall-induced shallow landslides in a tropical hilly area using gis. Landslides 2017, 14, 1–17. [Google Scholar] [CrossRef]
- Aghdam, I.N.; Pradhan, B.; Panahi, M. Landslide susceptibility assessment using a novel hybrid model of statistical bivariate methods (fr and woe) and adaptive neuro-fuzzy inference system (anfis) at southern zagros mountains in Iran. Environ. Earth Sci. 2017, 76, 237. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ann, maxent, and svm machine learning techniques. Geofis. Int. 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Tien Bui, D.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. Gis-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with adaboost, bagging, and multiboost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. A novel integrated model for assessing landslide susceptibility mapping using chaid and ahp pair-wise comparison. Int. J. Remote Sens. 2016, 37, 1190–1209. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, V.-T.; Ngo, V.-L.; Trinh, P.T.; Ngo, H.T.T.; Bui, D.T. A novel hybrid model of rotation forest based functional trees for landslide susceptibility mapping: A case study at Kon Tum province, Vietnam. In International Conference on Geo-Spatial Technologies and Earth Resources; Springer: Berlin/Heidelberg, Germany, 2017; pp. 186–201. [Google Scholar]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide susceptibility modeling using reduced error pruning trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using j48 decision tree with adaboost, bagging and rotation forest ensembles in the Guangchang area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.T.; Zhang, T.; Zhang, L.; Chai, H. Landslide susceptibility modeling based on gis and novel bagging-based kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. Gis-based evaluation of landslide susceptibility models using certainty factors and functional trees-based ensemble techniques. Appl. Sci. 2020, 10, 16. [Google Scholar] [CrossRef]
- Pradhan, A.; Kim, Y. Evaluation of a combined spatial multi-criteria evaluation model and deterministic model for landslide susceptibility mapping. Catena 2016, 140, 125–139. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the three Gorges Reservoir area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef]
- Hu, Q.; Zhou, Y.; Wang, S.; Wang, F. Machine learning and fractal theory models for landslide susceptibility mapping: Case study from the Jinsha River Basin. Geomorphology 2020, 351, 106975. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Süzen, M.L.; Kaya, B.Ş. Evaluation of environmental parameters in logistic regression models for landslide susceptibility mapping. Int. J. Digit. Earth 2012, 5, 338–355. [Google Scholar] [CrossRef]
- Dou, J.; Bui, D.T.; Yunus, A.P.; Jia, K.; Song, X.; Revhaug, I.; Xia, H.; Zhu, Z. Optimization of causative factors for landslide susceptibility evaluation using remote sensing and gis data in parts of Niigata, Japan. PLoS ONE 2015, 10, e0133262. [Google Scholar] [CrossRef] [PubMed]
- Dou, J.; Oguchi, T.; Hayakawa, Y.S.; Uchiyama, S.; Saito, H.; Paudel, U. Gis-based landslide susceptibility mapping using a certainty factor model and its validation in the Chuetsu area, central Japan. In Landslide Science for a Safer Geoenvironment; Springer: Berlin/Heidelberg, Germany, 2014; pp. 419–424. [Google Scholar]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C.; Mohammadi, M.; Moradi, H.R. Application of weights-of-evidence and certainty factor models and their comparison in landslide susceptibility mapping at Haraz Watershed, Iran. Arab. J. Geosci. 2013, 6, 2351–2365. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. Gis-based landslide susceptibility modelling: A comparative assessment of kernel logistic regression, naïve-bayes tree, and alternating decision tree models. Geomat. Nat. Hazards Risk 2017, 8, 950–973. [Google Scholar] [CrossRef]
- Galathiya, A.; Ganatra, A.; Bhensdadia, C. Improved decision tree induction algorithm with feature selection, cross validation, model complexity and reduced error pruning. Int. J. Comput. Sci. Inf. Technol. 2012, 3, 3427–3431. [Google Scholar]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz Watershed, Northern iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef] [PubMed]
- Kääriäinen, M.; Malinen, T.; Elomaa, T. Selective rademacher penalization and reduced error pruning of decision trees. J. Mach. Learn. Res. 2004, 5, 1107–1126. [Google Scholar]
- Quinlan, J.R. Simplifying decision trees. Int. J. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Polo, J.-L.; Berzal, F.; Cubero, J.-C. Class-oriented reduction of decision tree complexity. In International Symposium on Methodologies for Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 48–57. [Google Scholar]
- WANG, D. A three-dimensional two-level gradient smoothing meshfree method for rainfall induced landslide simulations. Front. Struct. Civ. Eng. 2019, 13, 337–352. [Google Scholar] [CrossRef]
- Quinlan, J.R. Improved use of continuous attributes in c4.5. J. Artif. Intell. Res. 1996, 4, 77–90. [Google Scholar] [CrossRef]
- Doetsch, P.; Buck, C.; Golik, P.; Kramp, M.; Laudenberg, J.; Oberdörfer, C.; Steingrube, P.; Forster, J.; Mauser, A.; Dror, G. Logistic model trees with auc split criterion for the kdd cup 2009 small challenge. In KDD-Cup 2009 Competition; PMLR: Lille, France, 2009. [Google Scholar]
- Landwehr, N.; Hall, M.; Frank, E. Logistic model trees. Mach. Learn. 2005, 59, 161–205. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Revhaug, I.; Tran, C.T. A comparative assessment between the application of fuzzy unordered rules induction algorithm and j48 decision tree models in spatial prediction of shallow landslides at lang son city, vietnam. In Remote Sensing Applications in Environmental Research; Springer: Berlin/Heidelberg, Germany, 2014; pp. 87–111. [Google Scholar]
- Youssef, A.M.; Pradhan, B.; Jebur, M.N.; El-Harbi, H.M. Landslide susceptibility mapping using ensemble bivariate and multivariate statistical models in Fayfa Area, Saudi Arabia. Environ. Earth Sci. 2015, 73, 3745–3761. [Google Scholar] [CrossRef]
- Chen, W.; Tsangaratos, P.; Ilia, I.; Duan, Z.; Chen, X. Groundwater spring potential mapping using population-based evolutionary algorithms and data mining methods. Sci. Total Environ. 2019, 684, 31–49. [Google Scholar] [CrossRef] [PubMed]
- Akgun, A. A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at İzmir, Turkey. Landslides 2012, 9, 93–106. [Google Scholar] [CrossRef]
- Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of alternating decision tree with adaboost and bagging ensembles for landslide susceptibility mapping. Catena 2020, 187, 104396. [Google Scholar] [CrossRef]
- Arabameri, A.; Chen, W.; Lombardo, L.; Blaschke, T.; Tien Bui, D. Hybrid computational intelligence models for improvement gully erosion assessment. Remote Sens. 2020, 12, 140. [Google Scholar] [CrossRef]
- Rahmati, O.; Kornejady, A.; Samadi, M.; Deo, R.C.; Conoscenti, C.; Lombardo, L.; Dayal, K.; Taghizadeh-Mehrjardi, R.; Pourghasemi, H.R.; Kumar, S. Pmt: New analytical framework for automated evaluation of geo-environmental modelling approaches. Sci. Total Environ. 2019, 664, 296–311. [Google Scholar] [CrossRef] [PubMed]
- Thiery, Y.; Malet, J.P.; Sterlacchini, S.; Puissant, A.; Maquaire, O. Landslide susceptibility assessment by bivariate methods at large scales: Application to a complex mountainous environment. Geomorphology 2007, 92, 38–59. [Google Scholar] [CrossRef]
- Chung, C.-J.F.; Fabbri, A.G. Validation of spatial prediction models for landslide hazard mapping. Nat. Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.-X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 4397–4419. [Google Scholar] [CrossRef]
- Bui, D.T.; Panahi, M.; Shahabi, H.; Singh, V.P.; Shirzadi, A.; Chapi, K.; Khosravi, K.; Chen, W.; Panahi, S.; Li, S. Novel hybrid evolutionary algorithms for spatial prediction of floods. Sci. Rep. 2018, 8, 15364. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Lee, M.J.; Choi, J.-W.; Oh, H.-J.; Won, J.-S.; Park, I.; Lee, S. Ensemble-based landslide susceptibility maps in Jinbu area, Korea. Environ. Earth Sci. 2012, 67, 23–37. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhao, D.; Ding, Y.; Liu, Y.; Xu, Q.; Qiu, Y.; Liu, C.; Liu, Z.; Zha, Z.; Li, R. Performance evaluation for four gis-based models purposed to predict and map landslide susceptibility: A case study at a world heritage site in Southwest China. CATENA 2019, 183, 104221. [Google Scholar] [CrossRef]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Ilia, I.; Koumantakis, I.; Rozos, D.; Koukis, G.; Tsangaratos, P. A geographical information system (GIS) based probabilistic certainty factor approach in assessing landslide susceptibility: The case study of Kimi, Euboea, Greece. In Engineering Geology for Society and Territory—Volume 2: Landslide Processes; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1199–1204. [Google Scholar]
- Tsangaratos, P.; Ilia, I.; Rozos, D. Case event system for landslide susceptibility analysis. In Landslide Science and Practice: Landslide Inventory and Susceptibility and Hazard Zoning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 1, pp. 585–593. [Google Scholar]
- Peng, T.; Chen, Y.; Chen, W. Landslide Susceptibility Modeling Using Remote Sensing Data and Random SubSpace-Based Functional Tree Classifier. Remote Sens. 2022, 14, 4803. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).