Numerical Simulation and Application of Radial Steel Gate Structure Based on Building Information Modeling under Different Opening Degrees

Abstract

The safe and stable operation of the radial gate is highly essential for hydropower stations. As the dynamic load of gate, water flow generally causes the irregular distribution of strength, stiffness, and the stability of the gate structure. Traditional simulation technology is usually used to investigate the impact of water flow on gate structure; however, there is a lack of integration and interaction of building information modeling (BIM) and numerical simulation technology to study this issue. Therefore, this paper proposed a computational framework combing BIM and numerical simulation to calculate and analyze the large complex hydraulic radial steel structure. Firstly, the 3D model of the radial gate was established by MicroStation2020, then, the finite element model was output by using it. Secondly, the change laws of strength, stiffness, and stability of the radial gate were analyzed by Ansys-Workbench2020R2 under different opening degrees. The numerical simulation results show that the maximum equivalent stress value was 142.19 MPa, which occurred at the joint between the lower longitudinal beam and the door blade. The maximum deformation was 3.446 mm, which occurred at two longitudinal beams’ middle in the lower part of the panel. When the opening degree is 0.0 m–9.0 m, the natural vibration frequency increases irregularly with the increase in the opening of the gate. Three main vibration modes of the gate vibration were obtained. It proves that it is feasible to analyze the structural performance of radial gates by using BIM and numerical simulation. Finally, the BIM and numerical simulation information management process was established to make the simulation results more valuable. This study expands the application value of BIM and provides a new research idea for large complex hydraulic steel structural analysis. The information management process described in this research can serve as a guide for gate operation and maintenance management.

1. Introduction

A hydraulic steel gate is the core component of large-scale water conservancy projects, and its safety and stability are the basic guarantee for the operation of water conservancy projects [1]. A radial gate is a typical space frame structure; it is widely used in various hydraulic projects because it has the advantages of light weight, small opening and closing force, no gate groove at the bottom edge, and easy operation [2]. In addition, radial gates play a key role in flood control, regulation of upstream and downstream water levels, ecological recharge, and energy transformation [3]. However, under the different opening and closing operations of the spillway surface orifice radial gate, the flow pattern is complex and the mixed phenomenon is serious, which leads to complex and variable fluid-induced vibrations [4]. Simultaneously, because of the uncertainty of the fluid–structure coupling effect and the instability of water flow, it is difficult to obtain the distribution law of the load acting on the radial gate [5]. At present, scholars have adopted field prototype observation, hydraulic model tests [6], and numerical simulation [7] to solve this problem [8]. Field prototype observation requires image velocimetry equipment, high-precision digital pressure sensors, and a multi-channel vibrating data acquisition system, and it is obviously affected by the environment, sensors are expensive, and there is a complex sensor layout, which makes the field prototype observation of radial gates difficult and it cannot predict the dynamic changes of the gate [9]. Hydraulic model tests are difficult and expensive to design and perform; they are limited by the similarity of the scaled physical models made with related materials, structures, geometry, physics, and mechanics; and their analysis cannot meet the accuracy requirements. The numerical simulation method has a low calculation cost and strong operability [10], which can reduce the number of tests [11], cycles, and costs [12]. Moreover, compared with the field prototype observation and model tests, numerical simulation provides a more specific and insightful understanding of fluid motion processes [13], which can not only obtain simulation results that are similar to the field prototype observation data but can also understand detailed motion trajectories [14]. Therefore, numerical simulation has been widely used and promoted in the water conservancy industry [15].

Scholars have achieved satisfactory results with respect to the structural calculation response of gates by using numerical simulation. Zhang C et al. [16] conducted finite element simulations and field measurement and monitoring and obtained the stress and deformation of the open-top radial gate with different opening degrees at a water depth of 0–6.5 m. Jafari A et al. [17] used Ansys-CFX2020 to simulate the coupling of the horizontal and vertical flow-induced vibration of sluice gates; they obtained the optimal dip angle of the sluice bottom edge under the condition of the minimum flow-induced vibration of the sluice gate; and they concluded that the horizontal and vertical synchronous vibration of the sluice gate can be achieved by changing the lifting height of the sluice gate. Through finite element analysis, Oh LS et al. [18] found that the vertical acceleration and vibration strength of the gate can be increased by 70% and 57%, respectively, when the auxiliary plate is installed behind the radial gate. Ng CF et al. [19] studied the effect of radial gate elevation on the loading of the gate wall under the action of water flow, and they obtained numerical results similar to the experimental results by using the numerical simulation and experimental comparison of the three-dimensional model of the shrinkage dam. Shen C et al. [20] carried out numerical simulation and field prototype observation on a plane gate and found that the numerical simulation’s results were not much different from the prototype observation results. In summary, many researchers have studied the structural calculation of the gate, mainly using the combination of model tests and numerical simulation. These methods require long test cycles and are limited by issues such as model size. Therefore, numerical simulation is used in the present study as the method for the structure analysis of radial gates. However, traditional pre-processing functions for numerical simulations are weak, especially for some complex and large assembly components, pre-processing is not convenient, and the operability is poor [21].

Building information modeling (BIM) technology is the carrier of building three-dimensional spatial information, which has the characteristics of more detailed and convenient modeling information [22]. BIM technology is characterized by its physical properties and intuition [23], and it has been rapidly applied and developed in the bridge and road industries [24]. Moreover, with the construction of the digital twin project, more and more industries are using BIM technology as a digital base for digital and intelligent transformation and upgrading [25], and the water industry is also actively transforming and upgrading to the digital base [26]. Simultaneously, different from the plane gate, there are many different complexity components inside the radial gate, and the force transfer and distribution are more complicated and the regularity is poor. Therefore, it is particularly important to explore a BIM-based numerical simulation analysis method for the structural calculation of a radial gate’s structure to analyze the strength, stiffness, and stability of a radial gate with different opening degrees. This can not only improve the modeling efficiency but also contribute to the digital development of the water industry.

At present, some scholars have investigated the combined application of BIM and numerical simulation technology. Moreover, model transformation is the core of the combination of BIM and numerical simulation technology. In terms of the conversion of a BIM model to a finite element model, Jing J et al. [27] proposed a technical route and software framework for converting an APDL statement BIM model into a finite element model based on JAVA and C #. Relying on Revit2018 and the Midas/Civil2018 software platform, He X P et al. [28] proposed an automatic conversion method from a BIM model to a finite element model under the VS development environment of Revit API and the c# language, and they realized the conversion program from the Revit model to the Midas/Civil model, which improved the efficiency of manual modeling. Zhang X Y et al. [29] extracted BIM geometric parameter information of a continuous beam with corrugated steel webs based on Dynamo programming, and they completed the transformation from a BIM model to a finite element model through the secondary development of Python programming, which improved the accuracy of the finite element simulation. At the same time, the combination of BIM technology and numerical simulation is more and more frequently applied in various fields, such as the construction of bridges and roads. Muhammad F et al. [30] used the visual programming language script to generate the BIM-based finite element model, completed the automatic conversion of the bridge BIM model to the finite element model, deployed the Structure Health Monitoring (SHM) device into the bridge BIM model, and then used the BIM model to monitor and manage the SHM system. Tang F et al. [31] constructed a three-dimensional visualization model of asphalt pavement in Revit2018, converted it into .inp format files through format conversion software, and then imported it into Abaqus2018 for structural calculation and analysis, which significantly enhanced the computing power of BIM in road structures.

However, the existing research has hardly applied the combination of BIM and numerical simulation to the structural calculation analysis of hydraulic radial steel gates, and there is a lack of a complete analysis process based on BIM and simulation technology. Therefore, this paper attempts to use BIM and numerical simulation methods to study the structural calculation of hydraulic radial steel gates. The main research questions in this paper are as follows: (1) How can we conduct numerical simulation based on a BIM model? (2) How can we judge the safety and stability of a radial gate structure by the BIM and numerical simulation method? (3) How can we obtain an effective data set of gate information through the established BIM and numerical simulation analysis method? In this paper, BIM technology was used to establish the 3D model of a radial gate, and the data conversion from a BIM model to a finite element model was completed. The finite element analysis of the flow-induced vibrations of the open-top radial gate was performed by combining the VOF method and the fluid–structure coupling method. The results were obtained separately from the flow rate, water pressure, stress, deformation, and frequency of the radial gate under different opening degrees. Overall, the structure of the paper is organized as follows: Section 2 gives a brief introduction to the relevant basic theory. Section 3 describes the process of constructing the simulation model by combining BIM and Ansys. In Section 4, a case study of the simulation of a radial gate is provided and the results are highlighted through discussion. Section 5 establishes an information management process to expand the application of the simulation results. Section 6 summarizes the present study and outlines the future work preliminaries.

2. Methodology

2.1. VOF Two-Phase Flow

The Volume of Fluid (VOF) method is suitable for water–gas two-phase flow with a large discharge and a complex mixing shear phenomenon [32]. In order to better track the water vapor interface in real time, the Channel Flow module was selected in Fluent2020R2 [33]. The standard Re-Normalization Group (RNG) k-ε turbulence model is adopted to deal with unsteady incompressible water–gas two-phase flow [34]. The volume fraction ${\alpha }_q$ is introduced into the two-phase flow, which represents the relative ratio of the volume of a certain liquid in the computational fluid unit to the volume of the computational fluid unit [35]. There are three cases of ${\alpha }_q$: ${\alpha }_q$= 1 indicates that the computing fluid unit is full of water; $0<{\alpha }_q<1$ indicates the presence of a water–gas two-phase flow interface in the computational fluid cell; and ${\alpha }_q=0$ indicates that no water body exists in the computed fluid unit.

2.2. Governing Equation of Fluid–Structure Coupling

(1)

Fluid dynamic pressure

Assuming that the water body is incompressible [36], the flow velocity and pressure at any point in the flow field obey the three-dimensional wave equation [37], according to the dynamic pressure equilibrium condition and acceleration coordination condition at the node. The basic equation of the whole fluid domain can be obtained by Equation (1) as follows:

$$\begin{array}{c}\left[H\right]\\ N_P\times N_P\end{array}\begin{array}{c}\left\{Q\right\}\\ N_P\times 1\end{array}=\begin{array}{c}{\left\{F\right\}}_e\\ N_P\times 1\end{array}=-\begin{array}{c}\left[B\right]\\ N_P\times g\end{array}\begin{array}{c}\ddot{\left\{D_s\right\}}\\ g\times 1\end{array}$$

(1)

where [H] is the node force vector of the fluid domain; {Q} is the fluid domain node dynamic pressure; {F} is the equivalent node load; $\ddot{\left\{D_s\right\}}$ is the normal acceleration of the node; [B] is the interpolation function on the coupling surface; $N_P$ represents the discrete nodes throughout the fluid domain; and $g$ is all nodes on the coupling surface.

(2)

Contact dynamic pressure

Considering the coupling effect between the fluid domain and the structure, the dynamic pressure equation between the fluid domain and the structure contact surface is established to ensure the dynamic pressure transfer to the structure contact surface, as shown in Formula (2):

$$\begin{array}{c}\left\{Q\right\}\\ N_P\times 1\end{array}=\left[\begin{array}{c}{\left\{Q_P\right\}}^{\mathrm{T}}\\ f\times 1\end{array}\begin{array}{c}{\left\{Q_n\right\}}^{\mathrm{T}}\\ g\times 1\end{array}\begin{array}{c}{\left\{Q_u\right\}}^{\mathrm{T}}\\ h\times 1\end{array}\right]$$

(2)

where $\left\{Q_P\right\}$ is the node dynamic pressure on the boundary $S_P$; $\left\{Q_n\right\}$ is the node dynamic pressure on the contact surface $S_n$; $\left\{Q_u\right\}$ is the dynamic pressure of the other nodes; $N_P$ is the number of rows in the node matrix; $f, g , \mathrm{and} h$ are the corresponding matrix rows, respectively; and 1 represents the dynamic pressure of the first column’s matrix nodes. The basic equation of the node dynamic pressure on the $S_n$ contact surface is derived, as shown in Formula (3):

$$\begin{array}{c}{Q}_n\\ h\times 1\end{array}=\begin{array}{c}{\left[H_{uu}\right]}^{-1}\\ h\times h\end{array}\left(\begin{array}{c}\left\{F_u\right\}\\ h\times 1\end{array}-\begin{array}{c}\left[H_{uu}\right]\\ h\times g\end{array}\begin{array}{c}\left\{Q_n\right\}\\ g\times 1\end{array}\right)$$

(3)

(3)

Equivalent node stress

With introducing the sequence matrix ${\left[A\right]}_{\left(k\right)}$, the dynamic pressure at S nodes on $S_{nk}$ on the contact surface of unit $k$ is decomposed from $\left\{Q_n\right\}$, as shown in Formula (4):

$$\begin{array}{c}{\left\{q\right\}}_{\left(k\right)}\\ g\times 1\end{array}=\begin{array}{c}{\left[A\right]}_{\left(k\right)}\\ S\times g\end{array}\begin{array}{c}\left\{Q_n\right\}\\ g\times 1\end{array}, k=1,2,\dots ,S_E$$

(4)

where $S_E$ is the number of fluid units in contact with the structure on the coupling surface.

(4)

Coupling surface finite element equation

The finite element equation of a coupled system between a fluid domain and structure is as follows (5):

$$\left[\begin{array}{cc}{A}_{ff}& A_{fs}\\ A_{sf}& A_{ss}\end{array}\right]\left[\begin{array}{c}\Delta X_{f,s}\\ \Delta X_{s,f}\end{array}\right]=\left[\begin{array}{c}{D}_f\\ D_s\end{array}\right]$$

(5)

where $A_{ff}$ represents the fluid region system matrix; $A_{ss}$ represents the solid region system matrix; $A_{sf}$ and $A_{fs}$ are the fluid–structure coupling system matrix; $D_f$ represents the external force matrix of the fluid region; $D_s$ represents the external force matrix in the solid region; and $\Delta X_{f,s}$ and $\Delta X_{s,f}$ are the change in the $k$ iterative step of the solution vector on the coupling node of the water region and the solid region.

2.3. Dynamic Balance Equation of the Gate

As the main water-retaining structure, the gate is directly affected by the high-speed impact of the water body, and the high-speed water flow impacts the gate [38], resulting in the fluid-induced vibration response of the gate [39]. The coupled vibrational equations are established for the coupled action of the water body and the gate. The coupled oscillator equation can be written as follows.

$$\left[M\right]\left\{x^{″}\right\}+\left[C\right]\left\{x^{\prime }\right\}+\left[K\right]\left\{x\right\}=\left\{F\left(t\right)\right\}$$

(6)

where $\left[M\right]$ is the mass matrix; $\left[C\right]$ is the damping matrix; $\left[K\right]$ is the stiffness matrix; $\left\{x\right\}$ is the displacement vector; $\left\{x^{\prime }\right\}$ is the velocity vector; $\left\{x^{″}\right\}$ is the acceleration vector; and $\left\{F\left(t\right)\right\}$ is the power vector, where $\left[M\right]$ consists of two parts, namely, the $\left[M_s\right]$ structure mass matrix and $\left[M_p\right]$ additional water mass matrix.

In actual sluice engineering, the internal damping of the sluice gates has a negligible effect on the natural vibrational frequencies and modes of the structure. Therefore, Equation (6) is simplified to obtain the undamped vibration equation:

$$\left[M\right]\left\{x^{″}\right\}+\left[K\right]\left\{x\right\}=\left\{F\left(t\right)\right\}$$

(7)

When the water flow reaches a stable state, the gate makes a simple harmonic motion. Assuming $\left\{F\left(t\right)\right\}$ = 0, we solve $x$ for the conventional solution, $x=\{\varnothing \}\sin (\omega t+\phi )$, and bring it into Equation (7) to obtain the vibration equation:

$$\left(\left[K\right]-{\omega }^2\left[M\right]\right)\{\varnothing \}=0$$

(8)

where $\{\varnothing \}$ represents the node amplitude and $\omega$ represents the angular frequency of simple harmonic vibration. The amplitude of the node must not be 0, so the natural vibration frequency equation of the gate structure is obtained:

$$\left|\left[K\right]-{\omega }^2\left[M\right]\right|=0$$

(9)

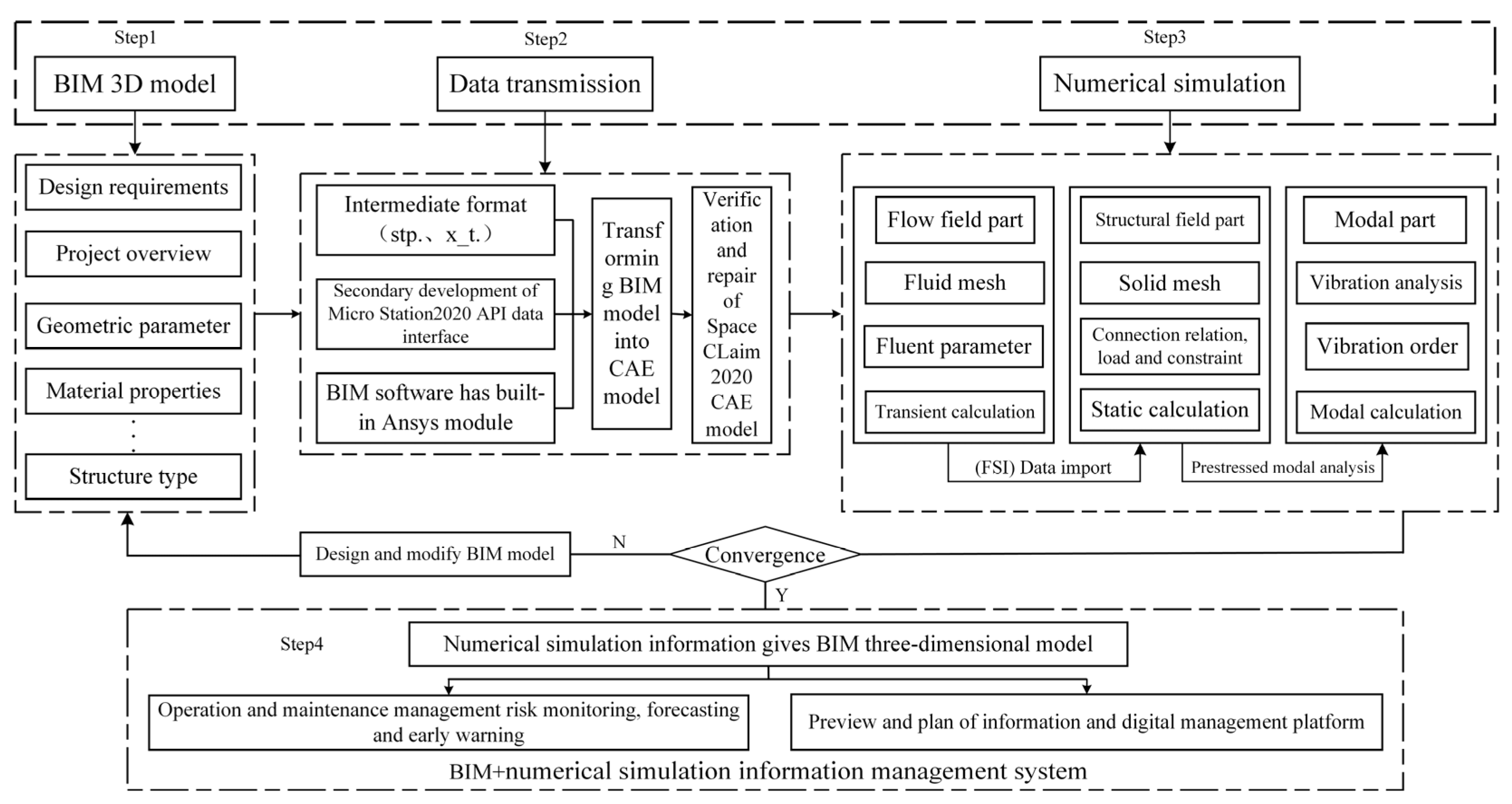
2.4. The Numerical Simulation Framework Based on BIM

The numerical simulation framework based on BIM of the structural calculation of radial gate structures under different opening degrees is shown in Figure 1, which is mainly divided into four steps:

Step 1: Establish the 1:1 BIM model by MicroStation2020 of the radial gate according to design requirements and project overview.

Step 2: Convert the BIM solid model to stp.; after export, the model is imported into the Workbench Ansys platform and verified in Ansys Space Claim2020 software.

Step 3: The simulation calculations are divided into three processes, which are flow field calculation, structural field statics calculation, and the vibration mode calculation.

Step 4: The numerical simulation results are graphically processed by CFD-Post, Tecplot, Origin, and other software.

3. Numerical Simulation of a Radial Gate Based on BIM

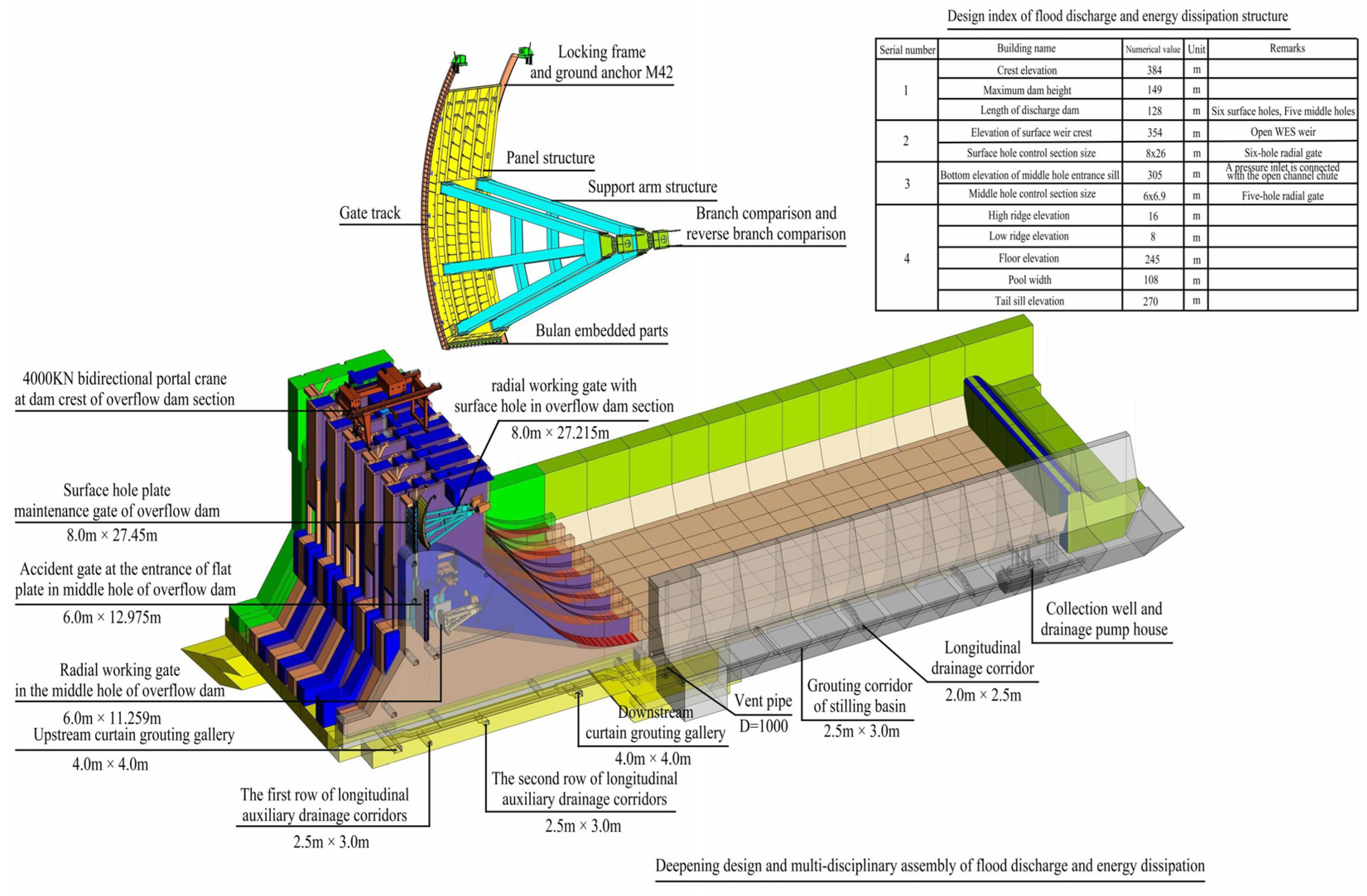
3.1. Project Overview

In this paper, the open-top large and complex radial gate of the spillway of a hydropower station was taken as the research object. The normal water level of the reservoir of the hydropower station is 380.000 m, the checked flood level is 381.860 m, the net width of the radial gate is 8.0 m, the radius is 30.0 m and the net height along the radius is 28.247 m. The central elevation of the hinge of the radial gate is 367.000 m and the top elevation of the surface hole is 354.000 m. The overflow weir is of the WES weir type. The type of the crest curve of the surface hole is $y=0.031x^{1.85}$. The intermediate surface is the inclined straight section. The downstream section is connected with the reverse radial section, the equation of the head of the inlet of the overflow dam section is $x^2/{6.4}^2+{\left(y-3.7\right)}^2/{3.7}^2$ = 1, the material is Q345 structural steel with a density of 7850 kg/m³, Young’s modulus of 2.06 × 10⁵ MPa, Poisson’s ratio of 0.3, and the linear elasticity values of the structure are all identical. A 1:1 three-dimensional solid structure model of the whole spillway was established by using BIM technology. The 3D BIM model of the overflow dam and radial gate is shown in Figure 2.

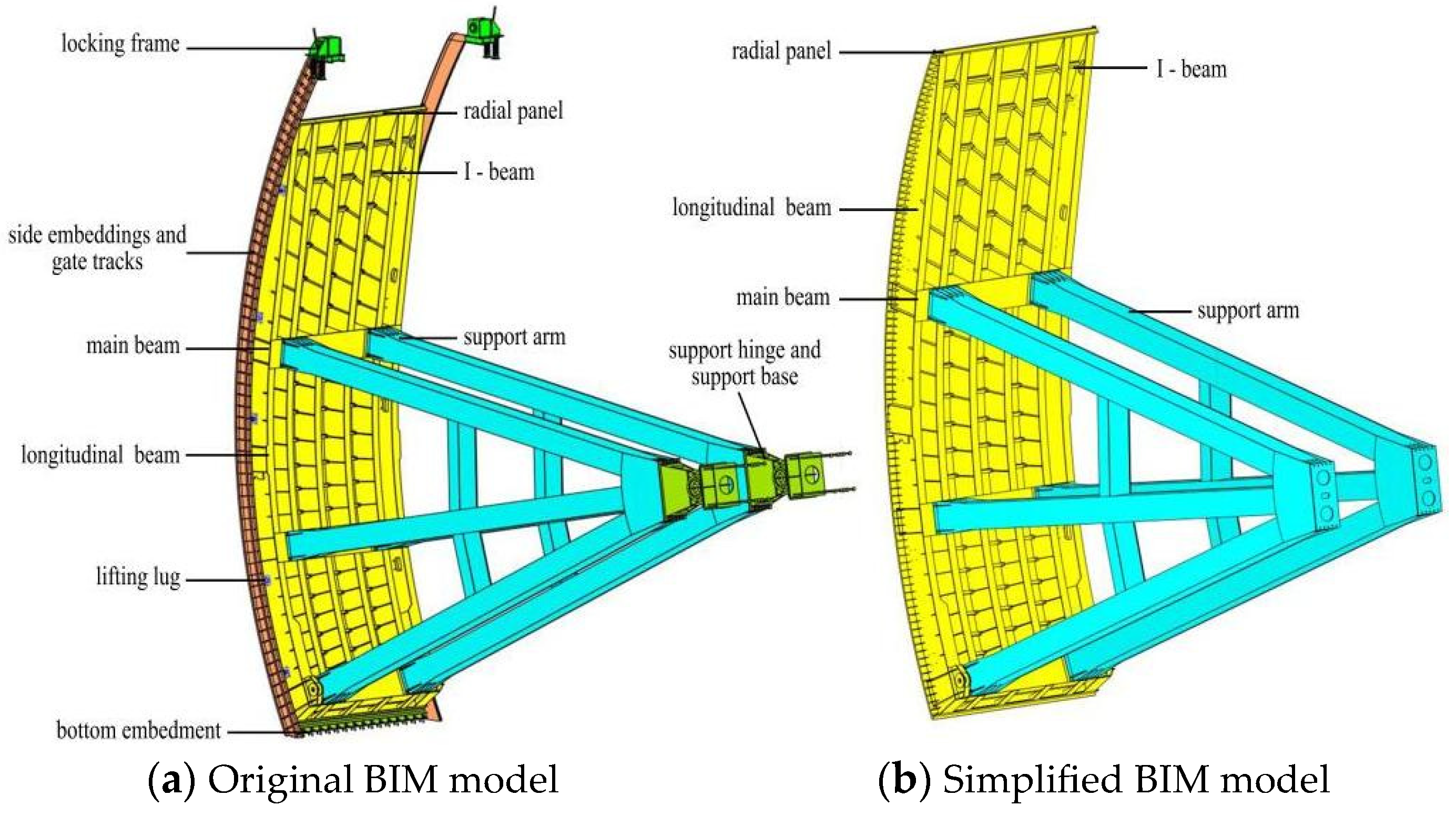
3.2. BIM Model of the Gate

In MicroStation, each sub-component of the radial gate was built by creating points, lines, and surfaces, and the assembly of each sub-component was completed. Collision detection was carried out during assembly. If there was a collision point, the adjustment and modification of each component was conducted in time, and the BIM model of the radial gate was gradually improved. The structure of the gate consists mainly of a radial panel, main beam, longitudinal beam, I-beam, supporting arm structure, bottom embedment, side embeddings and gate tracks, support hinge and support base, lifting lug, and locking frame. The gate was simplified without affecting the force distribution and transmission form of the main components, in order to save numerical simulation analysis and computational time. The main components of the simplified gate include the radial panel, main beam, longitudinal beam, supporting arm, and the I-beam. The BIM model of the original radial gate and the simplified radial gate model were obtained by MicroStation2020, as shown in Figure 3.

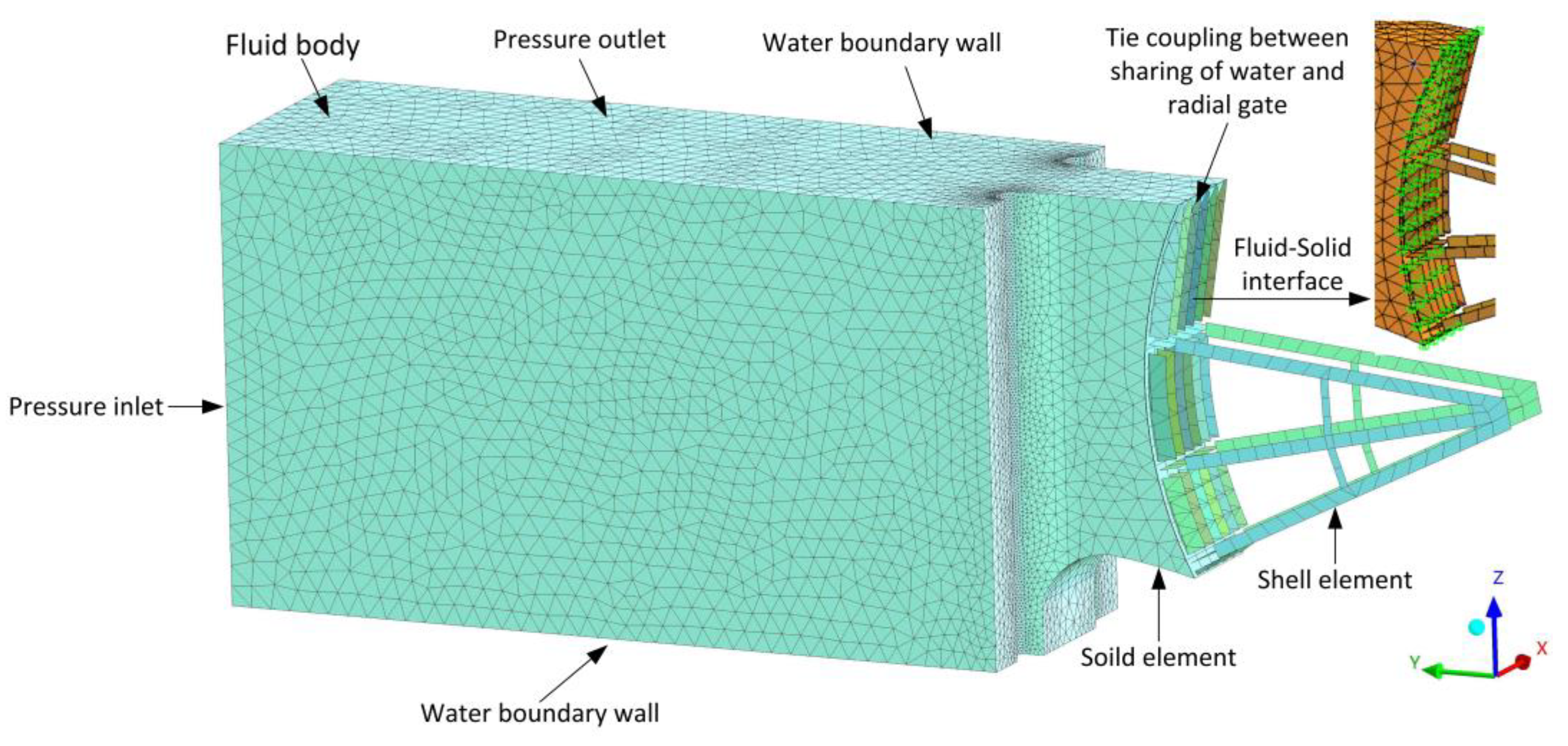
3.3. Finite Element Model of the Radial Gate

The simplified BIM model of the radial gate was converted into an intermediate format, and then the BIM model was checked by using Ansys SpaceClaim 2020R2 software; no model defects or deviations were found. In addition, the model was pre-processed to extract the middle-shell surface from the longitudinal beam, the main beam and the supporting arm structure, and the beam elements from the I-beam. In order to share the coupling with the fluid part, the panel structure uses solid units. The unit structure has 10 higher-order 3D nodes, each with three translational degrees of freedom in the 3D coordinate system, which is suitable for simulating thin plate members of irregular radial gate spaces. The vertical flow direction was set to the X-axis, the flow direction was set to the Y-axis, and the vertical and horizontal upward direction was set to the Z-axis.

3.4. Finite Element Model Meshing

The computational domain consists of a fluid part and a structural part. The upper surface elevation of the fluid part was 381.860 m. The lower surface elevation was one-quarter of the difference between the surface hole and the middle hole. The fluid domain width was 20 m of the center line on both sides of the pier. The fluid domain length was 60 m. The accuracy and time of the numerical simulation was determined by the unit mass and number of units in the mesh partition. The numerical simulation’s accuracy can be improved by reasonable unit quality. A large amount of numerical simulation experimental data show that when the mesh quality is above 0.8, the numerical simulation results are similar to the theoretical calculation results. Taking the fully closed state of the radial gate as an example, the mesh type in this paper took the form of a tetrahedral mesh, which was convenient for coordinating the segmentation algorithm. The mesh unit size of the fluid domain was set to 300 mm and the mesh unit size of the radial gate was set to 70 mm. The number of mesh elements generated in the fluid domain was 322,444 and the number of nodes was 590,556. The number of mesh elements generated by the radial gate was 128,161, and the number of nodes was 414,620. The expansion ratio of the mesh was 0.272. The expansion growth rate was 1.2. The expansion layer was 5, and the average unit mass was 0.844 and 0.820. When the mesh mass reaches 0.8 or more, the units’ mesh splitting is determined to satisfy the requirements of the finite element simulation analysis [40]. The fluid domain and radial gate structure mesh effect is shown in Figure 4.

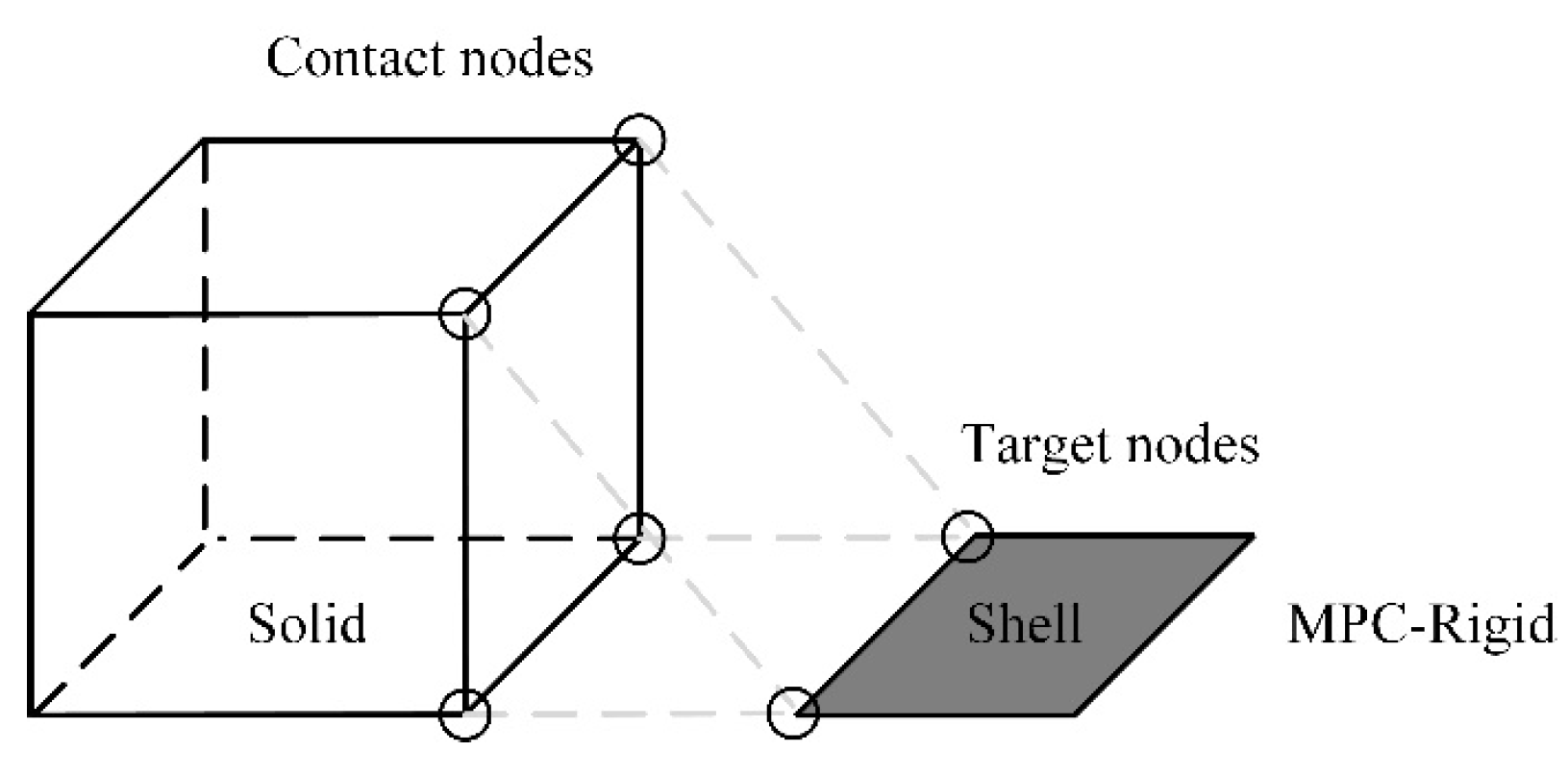
3.5. Connection Relation

The setting of the connection relationships between different element types determines whether the solution can proceed normally. Due to the different degrees of freedom of the solid, shell, and beam elements, it is difficult to implement force transfer between different elements [41]. The shell unit and beam unit adopt a shared topology to implement data transfer, while the solid unit and shell unit adopt a binding contact type and the multi-point constraint algorithm (MPC) [42]. The MPC algorithm is a coupling relationship of node degrees of freedom, that some degrees of freedom of one node are taken as the standard value, and then some degrees of freedom of other specified nodes are established with this standard value [43]. The contact geometry is defined as the solid element, the target geometry is defined as the shell element, and the tolerance search radius was set to 10 mm, thus, completing the transmission of the coupling between the solid and the shell element. The MPC contact method is shown in Figure 5.

3.6. Constraints and Solution Parameters

There were two kinds of settings of radial gate constraint conditions: One was the closed radial gate condition. When the radial gate was fully closed, the upright displacement constraint was set at the bottom water stop and the vertical flow direction displacement constraint was set at the side water stop. The second was the opening of the gate. When the gate was open under instantaneous conditions and under different opening degrees, the water stop at the bottom was considered free and the position of the hinge base was fixed and constrained. Moreover, all nodes of the other members of the gate were kept in the default setting to preserve the freedom of the intrinsic nodes of the structure.

Water flow simulation includes steady-state simulation and transient simulation, where the variations in dynamical performance parameters are studied. The spillway discharge has typical fluid dynamics. In order to obtain the dynamic water pressure at the coupled surface, transient simulation was used [44]. The direction of gravitational acceleration was set to be the negative direction of the Z-axis, with a magnitude of 9.81 m/s². The inlet of the fluid domain was set with a pressure inlet. The outlet was set with a pressure outlet. The other surfaces were provided with non-slip walls, and the FSI coupled surfaces were set at the contact points between the fluid and the structure. The VOF two-phase flow method was used to trace the free surface of the open-top surface gate. The VOF method is suitable for tracking free surfaces with complex deformations. The first flow was air, and the second was water. The surface orifice spillway discharge is prone to eddy currents, which affects the turbulence. Therefore, in order to improve the accuracy of the vortex and water flow in the drainage process, the RNG k-ε turbulence model was used for fluid calculation. The solution methods include PISO, SIMPLER, and SIMPLEC. The PISO method is a “non-iterative” pressure speed coupling solution calculation method, which can better solve the unsteady state problem. This paper studies the incompressible spillway discharge transient deformation flow [45]; therefore, it is more suitable to use the PISO algorithm. The exit flow monitor was set during the solution. When the outflow was a bit different from the theoretically calculated value and fluctuated around a certain value, the convergence stability calculation was said to be over.

4. Results and Discussion

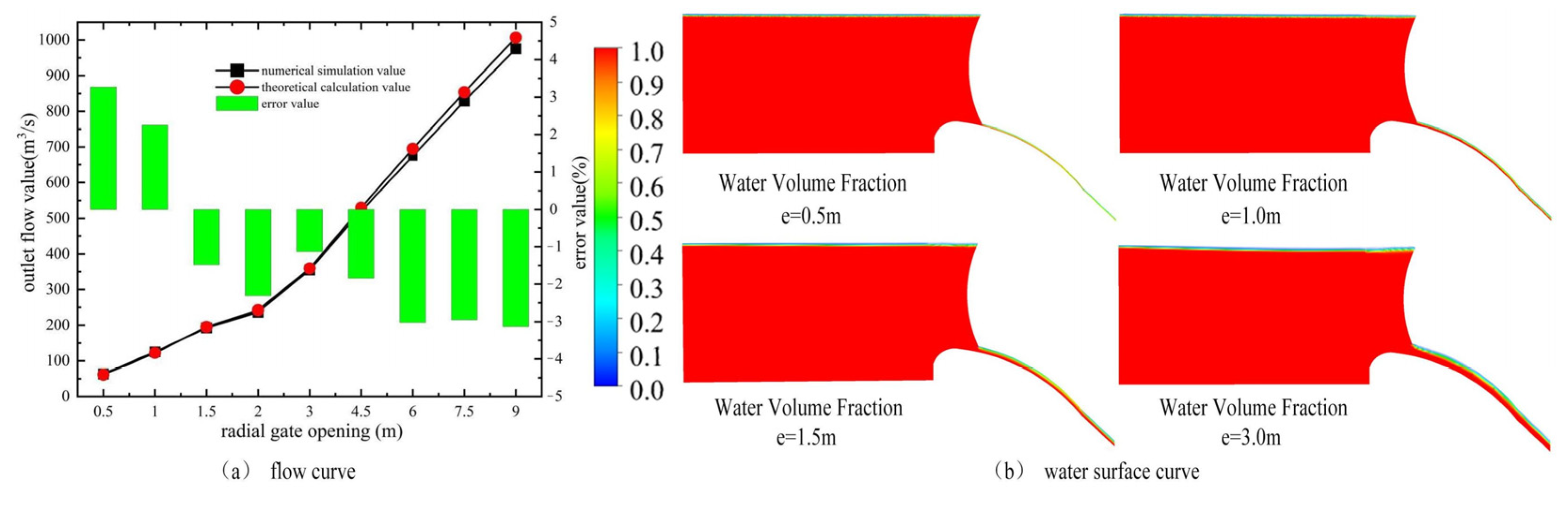
4.1. Flow Value and Surface Curve Analysis

The discharge rate of the radial gate depends on the upstream gate head, gate width, gate opening, flow coefficient, and gravitational acceleration. The radial gate has single hole free flow. The upstream flow rate head has little influence on the outlet flow rate, and the traveling flow rate head can be ignored [46]. Therefore, the velocity head is not considered in this paper. The theoretical formulation is as follows:

$$Q=\mu be\sqrt{2g{H}_0}$$

(10)

where $Q$ is the flow rate through the gate hole; $H_0$ is the total head of water in front of the gate; $\mu$ is the flow coefficient of the gate on the radial sill; $e$ is the opening of the gate; $b$ is the net width of the individual holes; and $g$ is the gravitational acceleration.

Figure 6 indicates that the difference in the opening between the spillway outlet flow value and the theoretical calculation value is less than 4%. The water surface curves under four different openings were extracted, and the volume fraction was set to 0.5. When the volume fraction was 0.5, the water vapor interface level was clear. In addition, through the observation of the water surface curve, it was found that the water flow in the spillway was stable under four different opening degrees. By comparing the outlet flow value and water surface curve, it was proved that the BIM model and fluid simulation parameters were reasonable and correct. The numerical simulation results were true and effective, which can reflect the real water flow situation.

4.2. Water Pressure Result Analysis

The water pressure results of three representative radial gate opening degrees were extracted, as shown in Figure 7. The upstream water level was taken from the normal storage level of 380.000 m, without considering the influence of the downstream water level (the spillway flood discharge type was free flow). When water flows through the bottom edge of the spillway, the upstream water body exerts a huge instantaneous impact force on the overall structure of the radial gate under the action of its own gravity impulse. With the increase in the flood discharge time, the pressure influence of the impact force on the gate leaf tends to be stable. When the opening of the radial gate was kept at a constant height, the flow pressure gradually decreased from bottom to top. In the fully closed state, the maximum pressure appeared at the lower one-third of the gate blade, and the minimum pressure appeared at the top of the gate. At the same time, it was also found that with the increase in the opening of the radial gate, the pressure value also shows a decreasing trend.

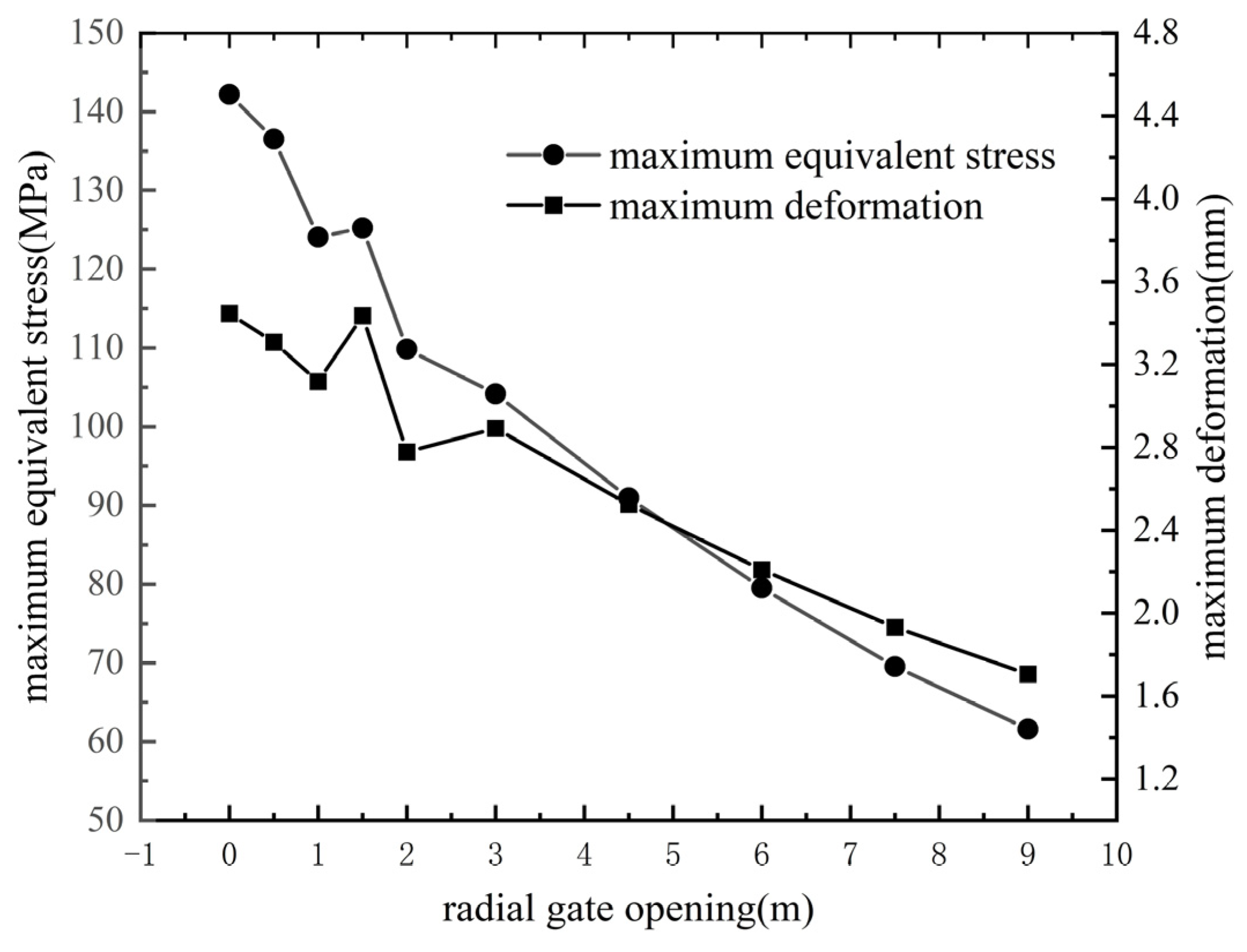
4.3. Analysis of the Stress Results of the Radial Gate

Considering the structural properties of the bent gate, including the radial gate panel, the beam lattice, and the junction system, the bent gate is in the multi-directional stress regime [47]. Using the fourth strength theory, the equivalent Von-Mises stress ${\sigma }_{\epsilon }$ is used to determine whether the gate meets the strength requirements [48], as shown in the following formula:

$${\sigma }_{\epsilon }=\sqrt{\frac{1}{2}\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2\right]}\le \left[{\sigma }_0\right]$$

(11)

where ${\sigma }_{\epsilon }$ is the equivalent stress and ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ are the first, second, and third principal stresses, respectively. When ${\sigma }_{\epsilon }\le \left[{\sigma }_0\right]$ ($\left[{\sigma }_0\right]$ is the allowable stress), the material strength meets the design requirements. Considering that the panel structure is directly subjected to water pressure, the bending of the structure itself is also affected by the bending deformation of the main beam, longitudinal beam, and other structures, so the equivalent stress ${\sigma }_{\epsilon }$ is adjusted for the panel, and the adjusted formula is as follows:

$${\sigma }_{\epsilon }\le 1.1\alpha {\left[\sigma \right]}_t$$

(12)

where $\alpha$ is the elastic-plastic adjustment coefficient, and ${\left[\sigma \right]}_t$ is the allowable stress after adjustment. The specification specifies that when $b/\alpha >3$, $\alpha$ is 1.4; when $b/\alpha \le 3$, $\alpha$ is 1.5; and $\alpha$ and $b$ are the lengths of the short and long sides of the panel simulation calculation area (a single area surrounded by longitudinal beams and beams on the panel), respectively.

According to the size of the geometric model of the radial gate [49], $b/\alpha \le 3$, so $\alpha$ was 1.5, and ${\left[\sigma \right]}_t$ = 371.250 MPa was obtained. Numerical simulation calculations were performed to obtain the equivalent stress value of a completely closed radial gate, as shown in Figure 8. After processing the simulation results, the equivalent stress values of the main beam, longitudinal beam, and support arm of the radial gate structure were obtained. The maximum stress region of the radial gate was located at the binding joint between the bottom of the radial gate panel and the longitudinal beam. The value of the stress in the connecting part of the transverse longitudinal beam was larger than the stress in the surrounding region. The distribution law of the equivalent stress value was that the gate gradually decreases from the bottom to the top. We found that the maximum equivalent stress value of the radial gate was 142.19 MPa when the radial gate was completely closed, and the stress values of the main beam, longitudinal beam, and support arm of other members meet the allowable values of the design code.

4.4. Analysis of the Deformation Results of the Radial Gate

In the design code for hydraulic steel gates (SL 74-2019) [47], it is stipulated that for spillway open-top working gates, the ratio of the maximum deflection of the main beam to the calculated span does not exceed 1/600. The ratio of the maximum deflection of the secondary beam to the calculated span should not exceed 1/250.

Through calculation and analysis, it was found that the deformation was the largest when the radial gate was closed; therefore, this paper selects the whole structure deformation when the radial gate was closed, as shown in Figure 9. The main form of deformation of the radial gate was bent deformation along the flow direction. The overall deformation of the radial gate was mainly the horizontal deformation in the vertical flow direction, and the deformation response was dominated by the pulsed water pressure upstream. The maximum deformation value was 3.446 mm, and the overall deformation of the lower part was larger than that of the upper part. The deformation of the radial gate panel gradually decreases from the bottom to the top. The deformation of the left and right support arms and connecting parts of the radial gate also gradually decreased from the bottom to the top. The longitudinal beam deformation was dominated by the inward bending deformation, which has a maximum deformation value of 3.342 mm. The largest deformation location occurred in the lower part of the middle longitudinal beam. The deformation forms of the main beam and auxiliary beam were also mainly inward bending, with a maximum deformation value of 3.288 mm. The largest deformations were located in the middle and lower sections. The maximum relative deformation value of the whole structure of the radial gate was 3.446 mm when completely closed. The maximum deformation value was 3.446 mm < 800/600 = 13.33 mm in the allowed deformation range, meeting the design requirements.

Figure 10 shows the change rule of the maximum equivalent stress value and the maximum deformation value of the overall structure of the radial gate. The maximum equivalent stress value of the overall structure decreases with increasing radial gate opening height at this water level. Preliminary analysis shows that when the radial gate was closed, the contact area between the water body and the radial gate was large, and the water body exerts the maximum pressure on the radial gate. With the gradual opening of the radial gate, the contact area between the water flow and the radial gate decreases, so the equivalent stress value decreases accordingly. When the opening of the radial gate increases from 1.5 m to 2.0 m, the equivalent stress increases. At this degree of opening, the water flow was unstable and easily caused an impact force on the radial gate panel, and a reverse upward trend was observed in the value of the stress acting on the radial gate. The overall deformation value of the radial gate decreases and gradually increases then decreases with the opening of the radial gate gradually increasing. The change rule of the deformation value was found to be largest when the gate opening degree was between 1.5 m and 2.0 m. Combined with the change curve of the equivalent stress value, the preliminary analysis was made on the complicated flow pattern of the water under this opening degree, and the water surface fluctuation and rolling phenomenon were serious. The flow-induced vibration of the radial gate occurred easily in the high-speed water flow. Therefore, the operation time of the radial gate at this opening degree should be reduced to avoid vibration damage accidents.

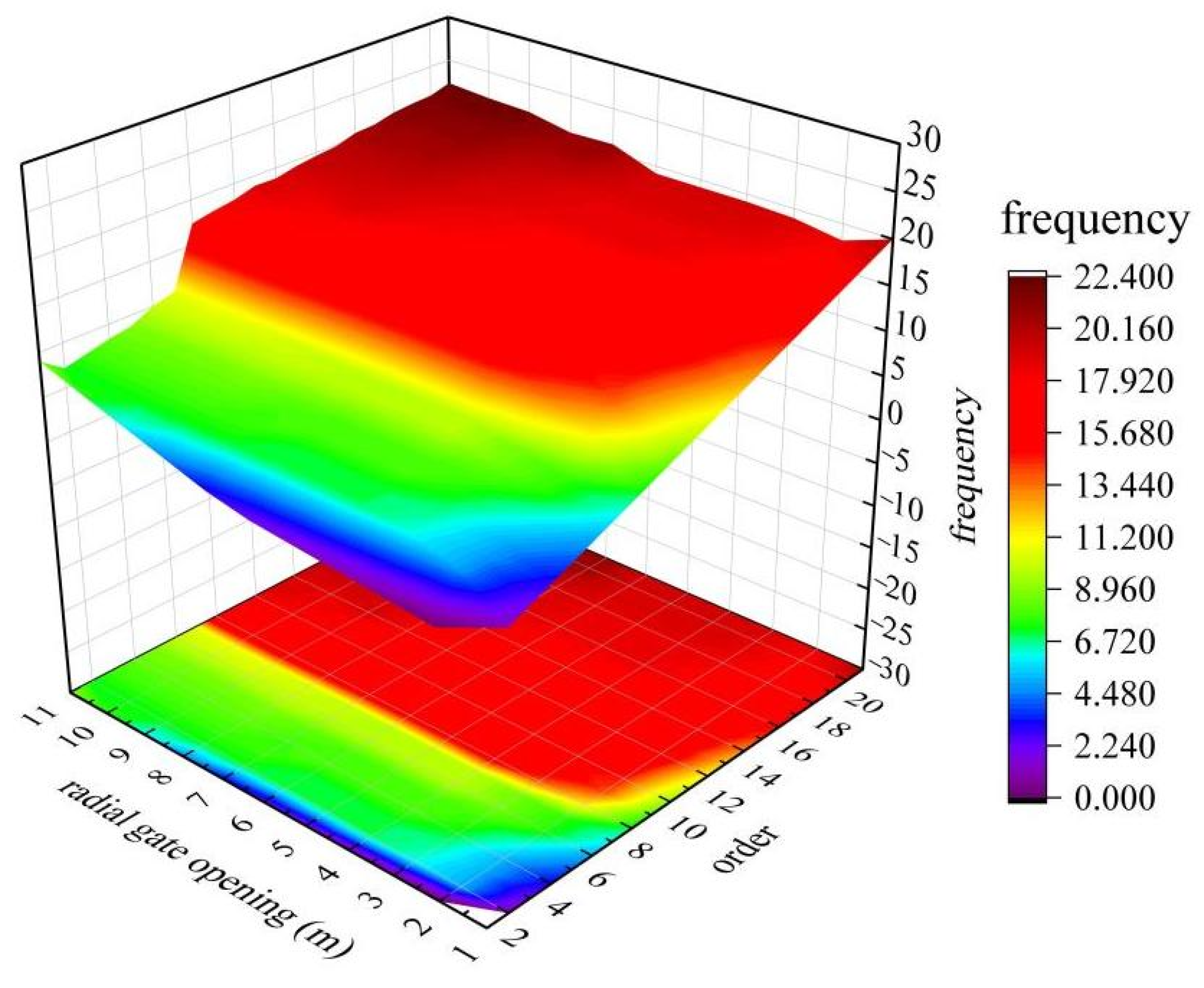
4.5. Analysis of the Natural Vibration Frequency Results of the Radial Gate

The free-mode analysis of the entire radial gate structure can be performed to obtain the vibrational strength and the weak back-off region of each part of the structure. The results of the numerical simulation of the distribution of the vibrational properties and the vibration frequency values of the radial gate under different opening degrees are presented in Figure 11. Through the analysis of the results of the numerical simulation for different values of the opening frequency, it was found that when the opening of the radial gate was between 0.0 m and 9.0 m, with the increase in the opening, the natural vibration frequency of the radial gate generally increases, which is infinitely close to the dry mode vibration frequency of the gate. This is because the cross-section of the flow through the bottom edge of the radial gate increases, the radial gate was reduced by water coupling action, and the coupling effect of the radial gate decreases. When the gate was partially opened, the natural vibration frequency of the partially opened gate was close to 10 Hz, which was close to the water pulsation value. This is the most dangerous state of radial gate operation, and long-term operation may lead to radial gate resonance and even radial gate vibration instability. It is suggested that special attention should be paid to the natural vibration frequency of 10 Hz in radial gate design, radial gate manufacture, and later operation and maintenance management.

As shown in Figure 12, the vibration frequency was maximum when the radial gate was closed. Therefore, representative vibrational modes of different orders of the radial gate under the fully closed condition were selected separately. The vibration of the radial gate was mainly the vibration of the panel and the support arm. The vibration deformation of the first six orders of the radial gate was mainly concentrated on the left and right support arms of the radial gate, and the vibration patterns of the radial gate were different in different orders. The second-order vibration mode change was the tangential swing vibration of the left and right support arms in the same direction as the Z-axis. The fourth-order vibration mode change was the tangential swing vibration of the left and right support arms in the opposite direction of the Z-axis. The sixth-order vibration mode change was the lateral swing vibration of a single support arm. The seventh-order vibration mode change was the horizontal bending vibration of the upper part of the panel and the I-beam. The ninth-order variation mode change was the bending vibration of the whole structure of the radial gate in different directions. The tenth-order variation mode was the transverse oscillatory vibration of the longitudinal beam in the middle of the panel in opposite directions. Through the analysis of the vibration modes of radial gates, it is concluded that the vibration modes of a radial gate can be divided into three types: second-, fourth-, and sixth-order vibration mode forms were the swing resonance of the support arm; seventh- and ninth-order vibration mode forms were bending resonance of the gate blade; and tenth-order vibration mode forms were the swing resonance of the longitudinal beam.

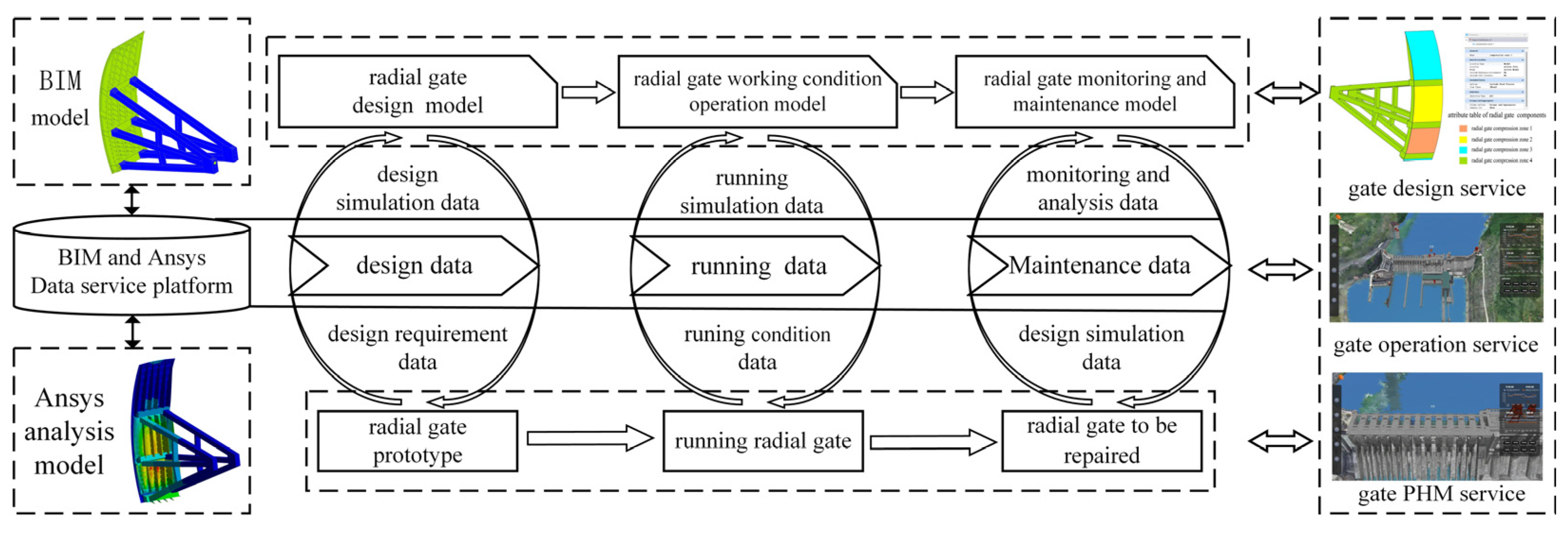
5. Information Management Process Based on BIM and Numerical Simulation Results

5.1. Establishment of Information Management Process

The change rules of stress, deformation, and frequency of the radial gate were obtained through the numerical simulation, and the obtained information was assigned to the BIM model by adding the properties form. The process of radial gate information management based on BIM and numerical simulation was established, as shown in Figure 13. The BIM and simulation information management process can mainly address two core issues: one is the integration and fusion of BIM model data of the radial gate, and the other is the iteration and inversion of BIM model data and Ansys finite element model data of the radial gate.

In terms of data integration and fusion, it is manifested in the collaboration and sharing of real-time, multidimensional, and heterogeneous model data, as well as the sharing of real-time perception data, numerical simulation data, and Prognostics Health Management service display information data of multi-element 3D entities and environments. Data integration and fusion are fundamental to drive the establishment and application of a radial gate to the entire information process. In data interaction, iteration, and reverse applications, the most unfavorable data subset under different opening degrees of the radial gate was sorted out through the association and integration of real-time physical model data and simulation data. Then, the mapping and interaction between BIM and the finite element of the radial gate model are formed.

5.2. Application of Information Management Process

The application of the radial gate information management process of BIM and numerical simulation includes three aspects. In the design of radial gates, the BIM and numerical simulation method can improve the design accuracy and speed up the design speed. In the operation of the radial gate, on the one hand, data sets of radial gate operations can be collected to monitor and preview the radial gate operation status under different opening degrees and feed back to the operator in real time. On the other hand, each radial gate can be adjusted and scheduled to better accomplish the spillway discharge task. In addition, BIM combined with numerical simulation can complete radial gate fault warning, prediction, and health monitoring; quickly and accurately capture the radial gate fault location; evaluate the health status of various mechanical equipment; and carry out the fault maintenance of radial gate equipment.

6. Conclusions

The radial steel gate is an important adjustment mechanism for water conservancy projects, and its hydraulic performance is very important for the safety of water conservancy projects. According to the characteristics of BIM technology and finite element simulation, the numerical simulation model of radial gate based on BIM is proposed in this paper, and the mechanical properties of a radial gate with different opening degrees were simulated by use of an engineering example. In terms of strength, the maximum equivalent stress value of the gate occurs at the connection between the lower part of the gate panel and the longitudinal beam when the gate is closed. The maximum equivalent stress value is 142.19 MPa. The maximum equivalent stress value of the other components is less than the allowable stress value. In terms of stiffness, the maximum value of the deformation of the gate is 3.46 mm. The maximum deformation value was less than the allowable deformation value, and the stiffness shift rate is largest when the gate is open from 1.5 to 2.0 m. In terms of stability, the value of the natural vibrational frequency gradually increases with the gate opening. At a partial opening, the value of the natural vibrational frequency is close to 10 Hz. In this situation, the gate is prone to vibration damage. The main radial gate vibration types include swing resonances of the support arms, bending resonances of the gate blades, and swing resonances of the longitudinal beam. The numerical simulation results show that the ratio between the simulated value and the theoretical value of the outflow value is no more than 4 percent, which proves that the numerical simulation model based on BIM is feasible. Finally, the information management process is constructed, which served as a guide for the safety assessment and project management study of the radial steel gate.

Regarding the applicability of the developed framework, the proposed framework can be replicated and applied to other hydraulic gate types. The combined use of BIM and numerical simulation has a wide range of applications and can exert its value in optimizing the design, operation, and maintenance management of gates. This method can improve the efficiency of traditional finite element numerical simulation and analysis and help decision makers in the whole process of gate management.

Significant as it is, this study still has limitations that should not be overlooked. The numerical simulation results are not compared with the field observation data. Therefore, it is recommended that future studies should be combined with the field observation methods to evaluate the validity of the model in this study. In future research, it is planned to expand the number of numerical simulation experiments to improve the reliability of numerical simulation experiments and to collect better cases to further validate the conclusions. In the meantime, realizing the automatic synchronous coupling between the numerical simulation results and the BIM model is also a meaningful research direction in the future.