Extensive Study of Electrocoagulation-Based Adsorption Process of Real Groundwater Treatment: Isotherm Modeling, Adsorption Kinetics, and Thermodynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals and Analytical Analysis
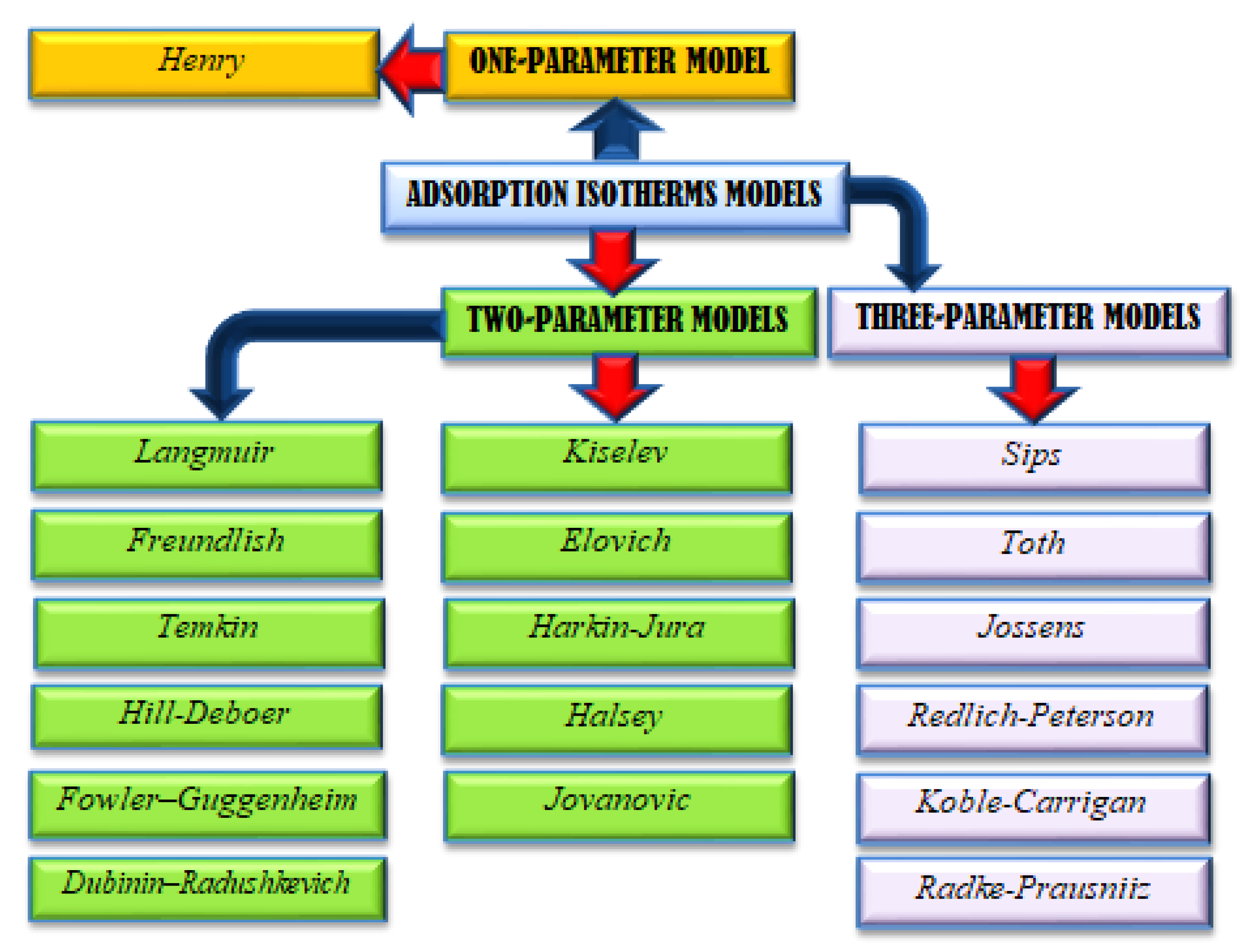
2.2. Adsorption Models
2.2.1. Henry Adsorption Model
2.2.2. Langmuir Adsorption Model
2.2.3. Freundlich Adsorption Model
2.2.4. Temkin Adsorption Model
2.2.5. Dubinin–Radushkevich Adsorption Model
2.2.6. Kiselev Adsorption Model
2.2.7. Fowler–Guggenheim Adsorption Model
2.2.8. Hill–Deboer Adsorption Model
2.2.9. Elovich Adsorption Model
2.2.10. Jovanovic Adsorption Model
2.2.11. Harkins–Jura Adsorption Model
2.2.12. Halsey Adsorption Model
2.2.13. Sips Adsorption Model
2.2.14. Toth Adsorption Model
2.2.15. Jossens Adsorption Model
2.2.16. Radke–Prausnitz Adsorption Model
2.2.17. Koble–Carrigan Adsorption Model
2.2.18. Redlich–Peterson Adsorption Model
2.3. Thermodynamic Investigation
2.4. Kinetic Investigation
2.5. Models of Mass Transfer via Adsorption
2.5.1. Weber and Morris Model
2.5.2. Liquid-Film Diffusion Model
2.5.3. Bangham and Burt Model
3. Results and Discussion
3.1. Experimental Outcomes and Calculations
3.2. Outcomes of Adsorption Models
3.2.1. Henry Adsorption Model
3.2.2. Langmuir Adsorption Model
3.2.3. Freundlich Adsorption Model
3.2.4. Temkin Adsorption Model
3.2.5. Dubinin–Radushkevich Adsorption Model
3.2.6. Kiselev Adsorption Model
3.2.7. Fowler–Guggenheim Adsorption Model
3.2.8. Hill–Deboer Adsorption Model
3.2.9. Elovich Adsorption Model
3.2.10. Jovanovic Adsorption Model
3.2.11. Harkins–Jura Adsorption Model
3.2.12. Halsey Adsorption Model
3.2.13. Sips Adsorption Model
3.2.14. Toth Adsorption Model
3.2.15. Jossens Adsorption Model
3.2.16. Radke–Prausnitz Adsorption Model
3.2.17. Koble–Carrigan Adsorption Model
3.2.18. Redlich–Peterson Adsorption Model
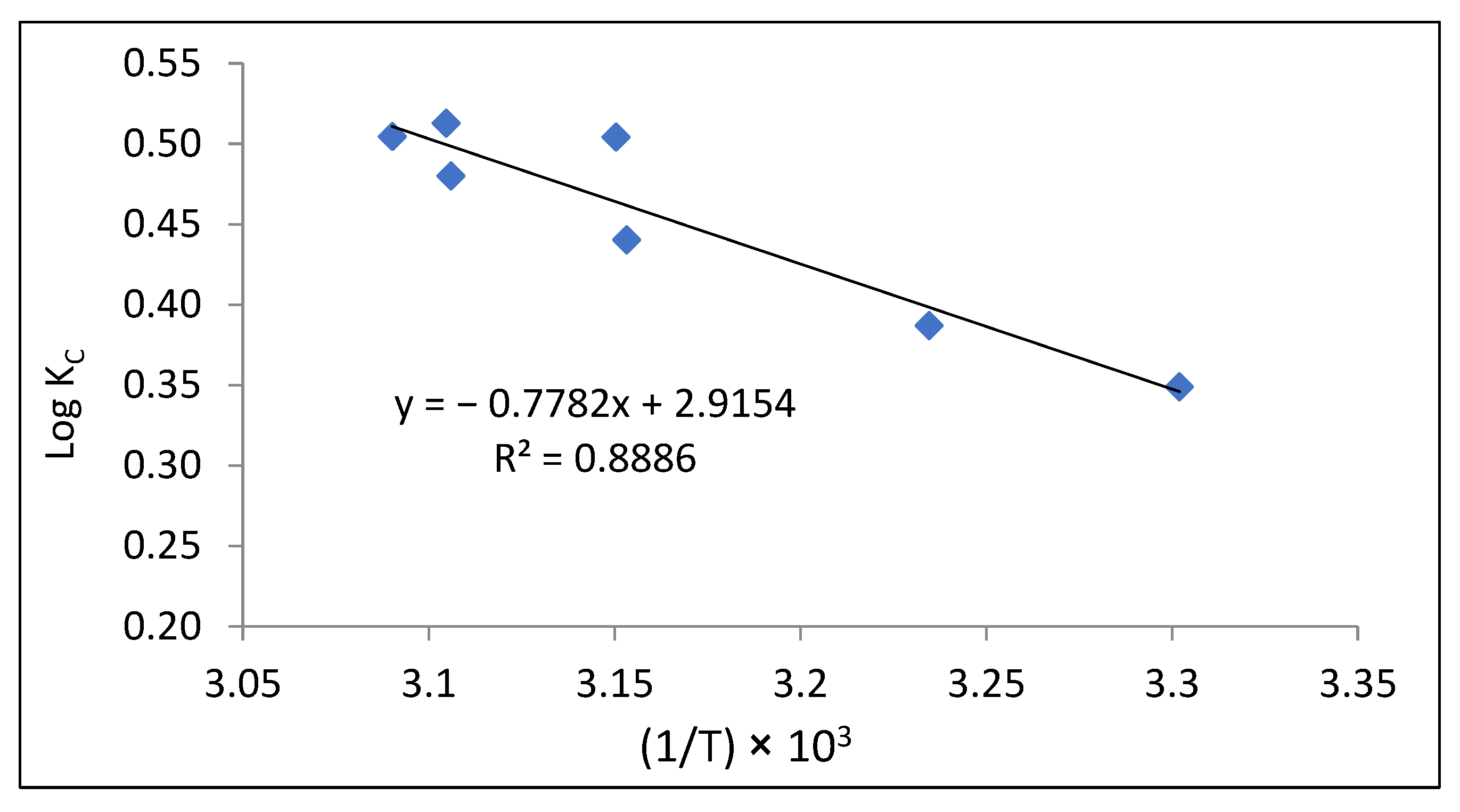
3.3. Thermodynamic Investigation Outcomes
3.4. Kinetics Investigation Outcomes
3.5. Investigation Outcomes of Mass Transfer Models
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jasim, M.A.; AlJaberi, F.Y. Treatment of oily wastewater by electrocoagulation technology: A general review (2018–2022): Review paper. J. Electrochem. Sci. Eng. 2022, 13, 361–372. [Google Scholar] [CrossRef]
- Devlin, T.R.; Kowalski, M.S.; Pagaduan, E.; Zhang, X.; Oleszkiewicz, J.A. Electrocoagulation of wastewater using aluminum, iron, and magnesium electrodes. J. Hazard. Mater. 2019, 368, 862–868. [Google Scholar] [CrossRef]
- Omwene, P.I.; Kobya, M.; Can, O.T. Phosphorus removal from domestic wastewater in electrocoagulation reactor using aluminium and iron plate hybrid anodes. Ecol. Eng. 2018, 123, 65–73. [Google Scholar] [CrossRef]
- AlJaberi, F.Y. Removal of TOC from oily wastewater by electrocoagulation technology. IOP Conf. Ser. Mater. Sci. Eng. 2020, 928, 22024. [Google Scholar] [CrossRef]
- Si, Y.; Li, G.; Wu, Y.; Zhang, H.; Zhang, F. Tradeoff between groundwater arsenite removal efficiency and current production in the self-powered air cathode electrocoagulation with different oxygen reduction pathways. J. Hazard. Mater. 2018, 357, 38–145. [Google Scholar] [CrossRef]
- Schaep, J.; Bruggen, B.V.; Uytterhoeven, S.; Croux, R.; Vandecasteele, C.; Wilms, D.; Houtte, E.V.; Vanlerbergheb, F. Removal of hardness from groundwater by nanofiltration. Desalination 1998, 119, 295–301. [Google Scholar] [CrossRef]
- Nariyan, E.; Wolkersdorfer, C.; Sillanpää, M. Sulfate removal from acid mine water from the deepest active European mine by precipitation and various electrocoagulation configurations. J. Environ. Manag. 2018, 227, 162–171. [Google Scholar] [CrossRef]
- Prasanth, S.V.; Magesh, N.S.; Jitheshlal, K.V.; Chandrasekar, N.; Gangadhar, K. Evaluation of groundwater quality and its suitability for drinking and agricultural use in the coastal stretch of Alappuzha District, Kerala, India. Appl. Water Sci. 2012, 2, 165–175. [Google Scholar] [CrossRef]
- Rosales, M.; Coreño, O.; Nava, J.L. Removal of hydrated silica, fluoride and arsenic from groundwater by electrocoagulation using a continuous reactor with a twelve-cell stack. Chemosphere 2018, 211, 149–155. [Google Scholar] [CrossRef]
- Mohora, E.; Rončević, S.; Agbaba, J.; Zrnić, K.; Dalmacija, B. Arsenic removal from groundwater by horizontal-flow continuous electrocoagulation (EC) as a standalone process. J. Environ. Chem. Eng. 2018, 6, 512–519. [Google Scholar] [CrossRef]
- Goren, A.Y.; Kobya, M.; Oncel, M.S. Arsenite removal from groundwater by aerated electrocoagulation reactor with Al ball electrodes: Human health risk assessment. Chemosphere 2020, 251, 126363. [Google Scholar] [CrossRef]
- AlJaberi, F.Y.; Ahmed, S.A.; Makki, H.F. Electrocoagulation treatment of high saline oily wastewater: Evaluation and optimization. Heliyon 2020, 6, e03988. [Google Scholar] [CrossRef]
- Highly cost-efficient sorption and desorption of mercury ions onto regenerable poly(m-phenylenediamine) microspheres with many active groups. Chem. Eng. J. 2020, 391, 123515. [CrossRef]
- Synthesis of poly(1,5-diaminonaphthalene) microparticles with abundant amino and imino groups as strong adsorbers for heavy metal ions. Microchim. Acta 2019, 186, 208. [CrossRef]
- Tan, J.Z.; Nursam, N.M.; Xia, F.; Sani, M.A.; Li, W.; Wang, X.; Caruso, R.A. High-Performance Coral Reef-like Carbon Nitrides: Synthesis and Application in Photocatalysis and Heavy Metal Ion Adsorption. ACS Appl. Mater. Interfaces 2017, 9, 4540–4547. [Google Scholar] [CrossRef]
- Benekos, A.K.; Tziora, F.E.; Tekerlekopoulou, A.G.; Pavlou, S.; Qun, Y.; Katsaounis, A.; Vayenas, D.V. Nitrate removal from groundwater using a batch and continuous flow hybrid Fe-electrocoagulation and electrooxidation system. J. Environ. Manag. 2019, 368, 113387. [Google Scholar] [CrossRef]
- Shrestha, S.; Kafle, R.; Pandey, V.P. Evaluation of index-overlay methods for groundwater vulnerability and risk assessment in Kathmandu Valley, Nepal. Sci. Total Environ. 2017, 575, 779–790. [Google Scholar] [CrossRef]
- Acharya, S.; Sharma, S.K.; Khandegar, V. Nitrate Removal from Groundwater by Electrocoagulation: Process Optimization through Response Surface Method. J. Hazard. Toxic Radioact. Waste 2021, 25, 04021014. [Google Scholar] [CrossRef]
- Morales, M.M.; Sáez, C.; Cañizares, P.; Rodrigo, M.A. Improvement of electrochemical oxidation efficiency through combination with adsorption processes. J. Environ. Manag. 2020, 262, 110364. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, Z. Recovery of lithium from spent lithium-ion batteries using precipitation and electrodialysis techniques. Sep. Purif. Technol. 2018, 206, 335–342. [Google Scholar] [CrossRef]
- Chang, H.; Hu, R.; Zou, Y.; Quan, X.; Zhong, N.; Zhao, S.; Sun, Y. Highly efficient reverse osmosis concentrate remediation by microalgae for biolipid production assisted with electrooxidation. Water Res. 2020, 174, 115642. [Google Scholar] [CrossRef]
- Xu, P.; Xu, H.; Zheng, D. The efficiency and mechanism in a novel electro-Fenton process assisted by anodic photocatalysis on advanced treatment of coal gasification wastewater. Chem. Eng. J. 2019, 361, 968–974. [Google Scholar] [CrossRef]
- Martins, V.L.; Ogden, M.D.; Jones, M.R.; Trowsdale, S.A.; Hall, P.J.; Jensen, H.S. Opportunities for coupled electrochemical and ion-exchange technologies to remove recalcitrant micropollutants in water. Sep. Purif. Technol. 2020, 239, 116522. [Google Scholar] [CrossRef]
- Cuprys, A.; Thomson, P.; Ouarda, Y.; Suresh, G.; Rouissi, T.; Brar, S.K.; Drogui, P.; Surampalli, R.Y. Ciprofloxacin removal via sequential electro-oxidation and enzymatic oxidation. J. Hazard. Mater. 2020, 389, 121890. [Google Scholar] [CrossRef]
- Zhao, K.; Quan, X.; Chen, S.; Yu, H.; Zhang, Y.; Zhao, H. Enhanced electro-Fenton performance by fluorine-doped porous carbon for removal of organic pollutants in wastewater. Chem. Eng. J. 2018, 354, 606–615. [Google Scholar] [CrossRef]
- Mohtashami, R.; Shang, J.Q. Treatment of automotive paint wastewater in continuous-flow electroflotation reactor. J. Clean. Prod. 2019, 218, 335–346. [Google Scholar] [CrossRef]
- Rotta, E.H.; Bitencourt, C.S.; Marder, L.; Bernardes, A.M. Phosphorus recovery from low phosphate-containing solution by electrodialysis. J. Membr. Sci. 2019, 573, 293–300. [Google Scholar] [CrossRef]
- AlJaberi, F.Y. Investigation of electrocoagulation reactor design effect on the value of total dissolved solids via the treatment of simulated wastewater. Desalination Water Treat. 2018, 120, 141–149. [Google Scholar] [CrossRef]
- AlJaberi, F.Y. Studies of autocatalytic electrocoagulation reactor for lead removal from simulated wastewater. J. Environ. Chem. Eng. 2018, 6, 6069–6078. [Google Scholar] [CrossRef]
- Adamović, S.; Prica, M.; Dalmacija, B.; Isakovski, M.K.; Adamović, D. Measurement of copper deposition by electrocoagulation/flotation from waste printing developer. Measurement 2019, 131, 288–299. [Google Scholar] [CrossRef]
- Kong, F.X.; Lin, X.F.; Sun, D.; Chen, J.F.; Xie, Y.F. Enhanced organic removal for shale gas fracturing flowback water by electrocoagulation and simultaneous electro-peroxone process. Chemosphere 2019, 218, 252–258. [Google Scholar] [CrossRef]
- Changmai, M.; Pasawan, M.K.; Purkait, M.K. Treatment of oily wastewater from drilling site using electrocoagulation followed by microfiltration. Sep. Purif. Technol. 2019, 210, 463–472. [Google Scholar] [CrossRef]
- Kumar, A.; Nidheesh, P.V.; Kumar, M.S. Composite wastewater treatment by aerated electrocoagulation and modified peroxi-coagulation processes. Chemosphere 2018, 205, 587–593. [Google Scholar] [CrossRef]
- Nidheesh, P.V.; Kumar, A.; Babu, D.S.; Scaria, J.; Kumar, M.S. Treatment of mixed industrial wastewater by electrocoagulation and indirect electrochemical oxidation. Chemosphere 2020, 251, 126437. [Google Scholar] [CrossRef]
- AlJaberi, F.Y. Desalination of groundwater by electrocoagulation using a novel design of electrodes. Chem. Eng. Process.-Process Intensif. 2022, 174, 108864. [Google Scholar] [CrossRef]
- Abbas, A.H.; Aljaberi, F.Y. Utilization of Agricultural Waste as Low-Cost Adsorbents in Dye Wastewater Treatment: Kinetic and Thermodynamic Study. IOP Conf. Ser. Earth Environ. Sci. 2023, 1215, 012055. [Google Scholar] [CrossRef]
- Hamdaoui, O.; Naffrechoux, E. Modeling of adsorption isotherms of phenol and chlorophenols onto granular activated carbon: Part I. Two-parameter models and equations allowing determination of thermodynamic parameters. J. Hazard. Mater. 2007, 147, 381–394. [Google Scholar] [CrossRef]
- Hamdaoui, O.; Naffrechoux, E. Modeling of adsorption isotherms of phenol and chlorophenols onto granular activated carbon: Part II. Models with more than two parameters. J. Hazard. Mater. 2007, 147, 401–411. [Google Scholar] [CrossRef]
- Lucas, S.; Cocero, J.; Zetzl, C.; Brunner, G. Adsorption isotherms for ethylacetate and furfural on activated carbon from supercritical carbon dioxide. Fluid Phase Equilibria 2004, 219, 171–179. [Google Scholar] [CrossRef]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem. 2017, 2017, 3039817. [Google Scholar] [CrossRef]
- Kumar, V. Adsorption kinetics and isotherms for the removal of rhodamine B dye and Pb+2 ions from aqueous solutions by a hybrid ion-exchanger. Arab. J. Chem. 2019, 12, 316–329. [Google Scholar] [CrossRef]
- Largitte, L.; Pasquier, R. A review of the kinetics adsorption models and their application to the adsorption of lead by an activated carbon. Chem. Eng. Res. Des. 2016, 109, 495–504. [Google Scholar] [CrossRef]
- Ituen, E.; Akaranta, O.; James, A. Evaluation of Performance of Corrosion Inhibitors Using Adsorption Isotherm Models: An Overview. Chem. Sci. Int. J. 2017, 18, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Bayuo, J.; Pelig-Ba, K.B.; Abukari, M.A. Isotherm Modeling of Lead (II) Adsorption from Aqueous Solution Using Groundnut Shell as a Low-Cost Adsorbent. J. Appl. Chem. 2018, 11, 18–23. [Google Scholar]
- Prajapati, A.K.; Mondal, M.K. Comprehensive kinetic and mass transfer modeling for methylene blue dye adsorption onto CuO nanoparticles loaded on nanoporous activated carbon prepared from waste coconut shell. J. Mol. Liq. 2020, 307, 112949. [Google Scholar] [CrossRef]
- Ramadoss, R.; Subramaniam, D. Removal of divalent nickel from aqueous solution using blue-green marine algae: Adsorption modeling and applicability of various isotherm models. Sep. Sci. Technol. 2019, 54, 943–961. [Google Scholar] [CrossRef]
- Tran, H.N.; You, S.-J.; Hosseini-Bandegharaei, A.; Chao, H.-P. Mistakes and inconsistencies regarding adsorption of contaminants from aqueous solutions: A critical review. Water Res. 2017, 120, 88–116. [Google Scholar] [CrossRef]

| Parameters | TDS (mg/L) | TSS (mg/L) | Total Hardness (mg/L) | Turbidity (mg/L) | pH | Conductivity (µS/cm) |
|---|---|---|---|---|---|---|
| Values | 1514 | 58 | 3053 | 49.34 | 8.1 | 2020 |
| Adsorption Model | Best-Fit Parameters | Determination Parameters |
|---|---|---|
| Henry adsorption model | KHE = 1.282 L/g | R2 = 1.000 Adj-R2 = 1.000 |
| Langmuir adsorption model | qmax = 28.986 mg/g Ke = 0.197 L/mg RL = 0.1 (favorable) | R2 = 0.9991 Adj-R2 = 0.9982 |
| Freundlich adsorption model | KF = 157.779 mg/g n = 2.118 (it is a physical process) | R2 = 0.9979 Adj-R2 = 0.9958 |
| Temkin adsorption model | KT = 0.008 L/gm b = 129.758 kJ/mol | R2 = 0.9990 Adj-R2 = 0.9980 |
| Kiselev adsorption model | KK = 22.955 L/mg Kn = 1.136 | R2 = 0.8029 Adj-R2 = 0.6058 |
| Harkins–Jura adsorption model | AH = 0.0084 g2/L BH = 0.738 mg/L | R2 = 0.9943 Adj-R2 = 0.9886 |
| Halsey adsorption model | KH = 45.126 g/L nH = 4.876 | R2 = 0.9979 Adj-R2 = 0.9958 |
| Elovich adsorption model | qmax = 13.755 mg/g KE = 0.009 L/mg | R2 = 0.9997 Adj-R2 = 0.9994 |
| Jovanovic adsorption model | qmax = 68.910 mg/g KJ = 0.0299 L/g | R2 = 0.9998 Adj-R2 = 0.9996 |
| Hill–Deboer adsorption model | K1 = 2.26 × 10−15 L/mg (insignificant) K2 = 1049.3 kJ/mol | R2 = 0.8346 Adj-R2 = 0.6692 |
| Fowler–Guggenheim adsorption model | W = −35.337 kJ/mol KFG = 3.337 × 10−12 L/mg | R2 = 0.8834 Adj-R2 = 0.7668 |
| Dubinin–Radushkevich adsorption model | qmax = 3.559 mg/g KDR = 8.00 × 10−6 E = 0.25 kJ/mol | R2 = 0.9907 Adj-R2 = 0.9814 |
|
Sips adsorption model | qmax = 43 mg/g KS = 0.03 (m3/kg)1/ms ms = 3.1 | R2 = 0.9834 Adj-R2 = 0.9668 |
| Toth adsorption model | qmax = 48.5 mg/g n = 1.1 (heterogeneous systems) KS = 0.35 mg/g | R2 = 0.9966 Adj-R2 = 0.9932 |
| Jossens adsorption model | KJ = 3.4 L/g J = 0.02 n = 1.04 (heterogeneous systems) | R2 = 0.9998 Adj-R2 = 0.9996 |
| Redlich–Peterson adsorption model | KR-P = 4.15 L/g A = 0.051 n = 0.85 (heterogeneous systems) | R2 = 0.9991 Adj-R2 = 0.9982 |
| Koble–Carrigan adsorption model | KK-C = 3.7 (L/g)−n AK-C = 0.05 n = 1.2 (heterogeneous systems) | R2 = 0.9929 Adj-R2 = 0.9858 |
| Radke–Prausnitz adsorption model | qmax = 50.3 mg/g ARP = 0.42 n = 1.01 (heterogeneous systems) | R2 = 0.9965 Adj-R2 = 0.9930 |
| Adsorption Kinetic Model | Best-Fit Parameters |
|---|---|
| First-order model | k1 = 0.0919 (1/min) R2 = 0.8824 |
| Second-order model | k2 = 0.0801 (g/mg.min) R2 = 0.8537 |
| Mass Transfer Model | Best-Fit Parameters |
|---|---|
| Weber and Morris model | Kwmd = 1.3387 (mg/(g.min0.5)) R2 = 0.9380 |
| Liquid-film diffusion model | Klf = 0.1652 (1/min) R2 = 0.9556 |
| Bangham and Burt model | Klf = 0.5759 (L/mg) R2 = 0.9735 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlJaberi, F.Y. Extensive Study of Electrocoagulation-Based Adsorption Process of Real Groundwater Treatment: Isotherm Modeling, Adsorption Kinetics, and Thermodynamics. Water 2024, 16, 619. https://doi.org/10.3390/w16040619
AlJaberi FY. Extensive Study of Electrocoagulation-Based Adsorption Process of Real Groundwater Treatment: Isotherm Modeling, Adsorption Kinetics, and Thermodynamics. Water. 2024; 16(4):619. https://doi.org/10.3390/w16040619
Chicago/Turabian StyleAlJaberi, Forat Yasir. 2024. "Extensive Study of Electrocoagulation-Based Adsorption Process of Real Groundwater Treatment: Isotherm Modeling, Adsorption Kinetics, and Thermodynamics" Water 16, no. 4: 619. https://doi.org/10.3390/w16040619
APA StyleAlJaberi, F. Y. (2024). Extensive Study of Electrocoagulation-Based Adsorption Process of Real Groundwater Treatment: Isotherm Modeling, Adsorption Kinetics, and Thermodynamics. Water, 16(4), 619. https://doi.org/10.3390/w16040619






