Quantifying Uncertainty in Runoff Simulation According to Multiple Evaluation Metrics and Varying Calibration Data Length
Abstract
1. Introduction
2. Methodology
2.1. Study Procedure
2.2. Geospatial Data
2.3. Soil and Water Assessment Tool (SWAT) Model
2.4. Hydrological Model Parameter Calibration
2.5. Uncertainty Assessment
3. Results
3.1. Model Performance over the Calibration Period
3.2. Evaluation of Performance over Validation Period
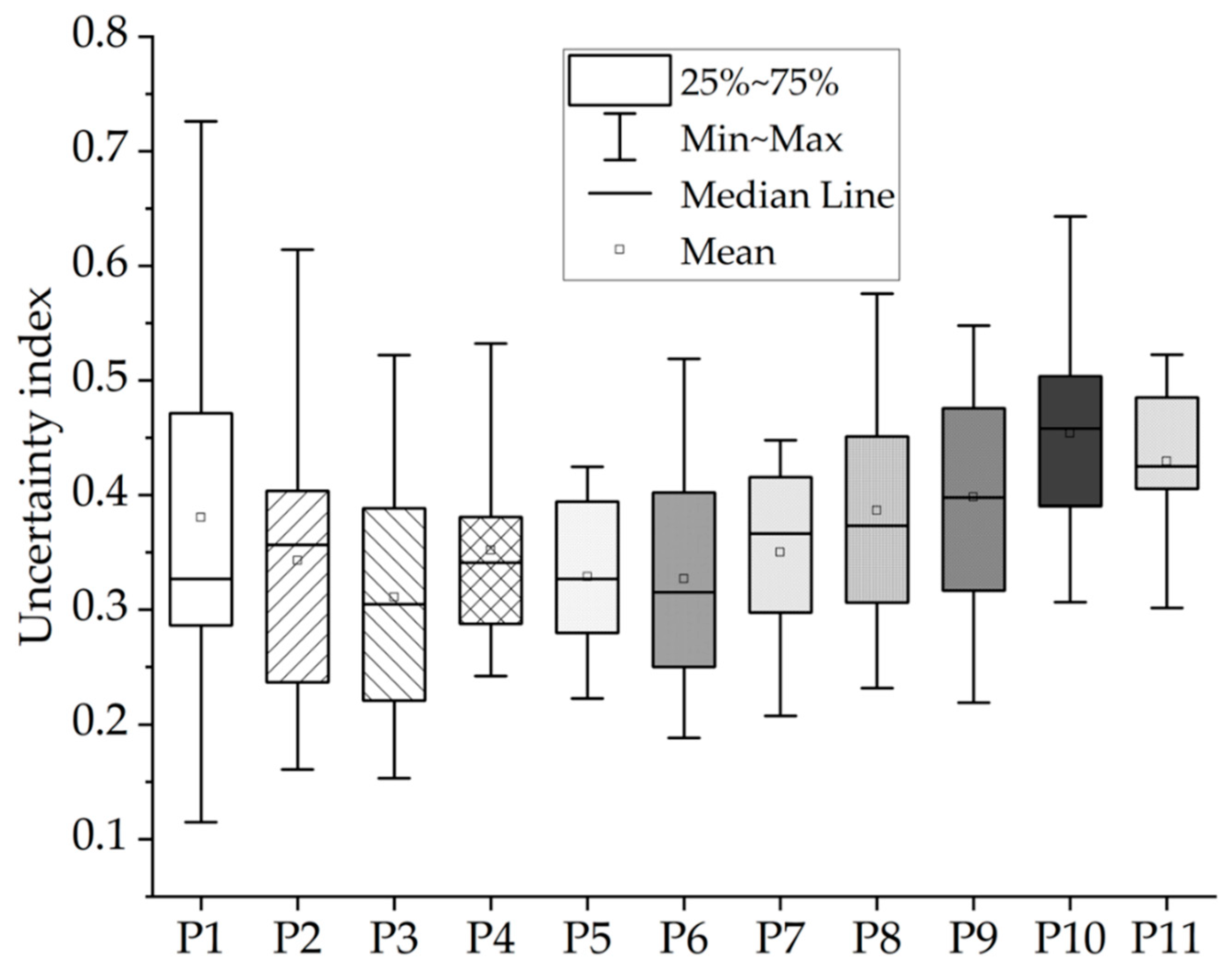
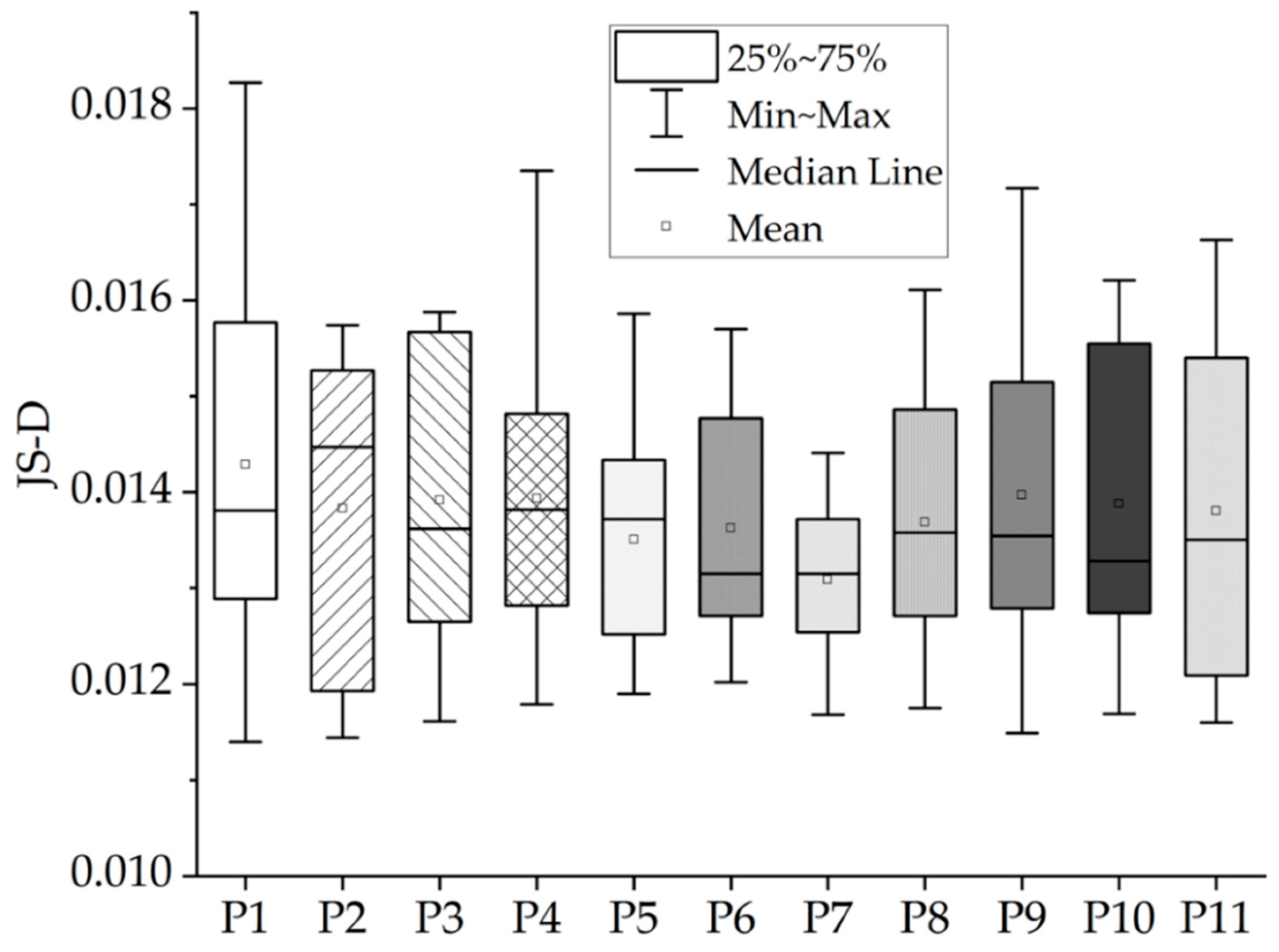
3.3. Uncertainty Index
3.4. Evaluation of the Extreme Runoff
3.5. Overall Uncertainty Assessment
4. Discussion
5. Conclusions
- Different evaluation metrics all showed different levels of uncertainty, which means it is necessary to consider multiple evaluation metrics rather than relying on any one single metric;
- Runoff simulations using a hydrological model had the least uncertainty owing to the calibration data length when using a parameter set of seven years, and the uncertainty increased for calibration data lengths longer than seven years;
- Parameter sets with the same calibration length showed period-dependent uncertainty, which led to uncertainty differences within the same length;
- For extreme runoff simulations, employing long calibration data lengths (of more than seven years) achieved lower uncertainty than shorter calibration data lengths.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beven, K. Linking parameters across scales: Subgrid parameterizations and scale dependent hydrological models. Hydrol. Process 1995, 9, 507–525. [Google Scholar] [CrossRef]
- Harmel, R.D.; Smith, P.K. Consideration of measurement uncertainty in the evaluation of goodness-of-fit in hydrologic and water quality modeling. J. Hydrol. 2007, 337, 326–336. [Google Scholar] [CrossRef]
- He, Y.; Bárdossy, A.; Zehe, E. A review of regionalisation for continuous streamflow simulation. Hydrol. Earth Syst. Sci. 2011, 15, 3539–3553. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Larsen, L.; Yassin, F. Review: Sources of hydrological model uncertainties and advances in their analysis. Water 2020, 13, 28. [Google Scholar] [CrossRef]
- Wang, X.; Yang, T.; Wortmann, M.; Shi, P.; Hattermann, F.; Lobanova, A.; Aich, V. Analysis of multi-dimensional hydrological alterations under climate change for four major river basins in different climate zones. Clim. Change 2017, 141, 483–498. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F.; Martel, J.L. The hazards of split-sample validation in hydrological model calibration. J. Hydrol. 2018, 566, 346–362. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Martel, J.L.; Brissette, F. Uncertainty of hydrological model components in climate change studies over two Nordic Quebec catchments. J. Hydrometeorol. 2018, 19, 27–46. [Google Scholar] [CrossRef]
- Gong, W.; Gupta, H.V.; Yang, D.; Sricharan, K.; Hero III, A.O. Estimating epistemic and aleatory uncertainties during hydrologic modeling: An information theoretic approach. Water Resour. Res. 2013, 49, 2253–2273. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.S.; Shahid, S. Differences in extremes and uncertainties in future runoff simulations using SWAT and LSTM for SSP scenarios. Sci. Total Environ. 2022, 838, 156162. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Zhou, Q.; McKeand, A.; Xie, T.; Choi, S.K. A model validation framework based on parameter calibration under aleatory and epistemic uncertainty. Struct. Multidiscipl. Optim. 2021, 63, 645–660. [Google Scholar] [CrossRef]
- Clark, M.P.; Nijssen, B.; Lundquist, J.D.; Kavetski, D.; Rupp, D.E.; Woods, R.A.; Freer, J.E.; Gutmann, E.D.; Wood, A.W.; Gochis, D.J.; et al. A unified approach for process-based hydrologic modeling: Part 1. Modeling concept. Water Resour. Res. 2015, 51, 2498–2514. [Google Scholar] [CrossRef]
- Van der Spek, J.E.; Bakker, M. The influence of the length of the calibration period and observation frequency on predictive uncertainty in time series modeling of groundwater dynamics. Water Resour. Res. 2017, 53, 2294–2311. [Google Scholar] [CrossRef]
- Myers, D.T.; Ficklin, D.L.; Robeson, S.M.; Neupane, R.P.; Botero-Acosta, A.; Avellaneda, P.M. Choosing an arbitrary calibration period for hydrologic models: How much does it influence water balance simulations? Hydrol. Process 2021, 35, e14045. [Google Scholar] [CrossRef]
- Razavi, S.; Tolson, B.A. An efficient framework for hydrologic model calibration on long data periods. Water Resour. Res. 2013, 49, 8418–8431. [Google Scholar] [CrossRef]
- Perrin, C.; Oudin, L.; Andreassian, V.; Rojas-Serna, C.; Michel, C.; Mathevet, T. Impact of limited streamflow data on the efficiency and the parameters of rainfall—Runoff models. Hydrol. Sci. J. 2007, 52, 131–151. [Google Scholar] [CrossRef]
- Motavita, D.F.; Chow, R.; Guthke, A.; Nowak, W. The comprehensive differential split-sample test: A stress-test for hydrological model robustness under climate variability. J. Hydrol. 2019, 573, 501–515. [Google Scholar] [CrossRef]
- Sorooshian, S.; Gupta, V.K.; Fulton, J.L. Evaluation of maximum likelihood parameter estimation techniques for conceptual rainfall-runoff models: Influence of calibration data variability and length on model credibility. Water Resour. Res. 1983, 19, 251–259. [Google Scholar] [CrossRef]
- Harlin, J. Development of a process oriented calibration scheme for the HBV hydrological model. Hydrol. Res. 1991, 22, 15–36. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Knudsen, J. Operational validation and intercomparison of different types of hydrological models. Water Resour. Res. 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Automatic calibration of conceptual rainfall-runoff models: Sensitivity to calibration data. J. Hydrol. 1996, 181, 23–48. [Google Scholar] [CrossRef]
- Anctil, F.; Perrin, C.; Andréassian, V. Impact of the length of observed records on the performance of ANN and of conceptual parsimonious rainfall-runoff forecasting models. Environ. Model. Softw. 2004, 19, 357–368. [Google Scholar] [CrossRef]
- Vaze, J.; Post, D.A.; Chiew, F.H.S.; Perraud, J.M.; Viney, N.R.; Teng, J. Climate non-stationarity–validity of calibrated rainfall–runoff models for use in climate change studies. J. Hydrol. 2010, 394, 447–457. [Google Scholar] [CrossRef]
- Kim, H.S.; Croke, B.F.; Jakeman, A.J.; Chiew, F.H. An assessment of modelling capacity to identify the impacts of climate variability on catchment hydrology. Math. Comput. Simul. 2011, 81, 1419–1429. [Google Scholar] [CrossRef]
- Jin, J.; Zhang, Y.; Hao, Z.; Xia, R.; Yang, W.; Yin, H.; Zhang, X. Benchmarking data-driven rainfall-runoff modeling across 54 catchments in the Yellow River Basin: Overfitting, calibration length, dry frequency. J. Hydrol. Reg. Stud. 2022, 42, 101119. [Google Scholar] [CrossRef]
- Shin, M.J.; Jung, Y. Using a global sensitivity analysis to estimate the appropriate length of calibration period in the presence of high hydrological model uncertainty. J. Hydrol. 2022, 607, 127546. [Google Scholar] [CrossRef]
- Noor, M.; Ismail, T.B.; Shahid, S.; Ahmed, K.; Chung, E.S.; Nawaz, N. Selection of CMIP5 multi-model ensemble for the projection of spatial and temporal variability of rainfall in peninsular Malaysia. Theor. Appl. Climatol. 2019, 138, 999–1012. [Google Scholar] [CrossRef]
- Raju, K.S.; Kumar, D.N. Review of approaches for selection and ensembling of GCMs. J. Water Clim. Change 2020, 11, 577–599. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Kim, J.H.; Sung, J.H.; Shahid, S.; Chung, E.S. Future hydrological drought analysis considering agricultural water withdrawal under SSP scenarios. Water Resour. Manag. 2022, 36, 2913–2930. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Dietrich, J.; Dang, T.D.; Tran, D.A.; Van Doan, B.; Sarrazin, F.J.; Abbaspour, K.; Srinivasan, R. An interactive graphical interface tool for parameter calibration, sensitivity analysis, uncertainty analysis, and visualization for the Soil and Water Assessment Tool. Environ. Model. Softw. 2022, 156, 105497. [Google Scholar] [CrossRef]
- Ahmed, N.; Wang, G.; Booij, M.J.; Xiangyang, S.; Hussain, F.; Nabi, G. Separation of the impact of landuse/landcover change and climate change on runoff in the upstream area of the Yangtze River, China. Water Resour. Manag. 2022, 36, 181–201. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C. Calibration and uncertainty issues of a hydrological model (SWAT) applied to West Africa. Adv. Geosci. 2006, 9, 137–143. [Google Scholar] [CrossRef]
- Kim, J.H.; Sung, J.H.; Chung, E.S.; Kim, S.U.; Son, M.; Shiru, M.S. Comparison of Projection in Meteorological and Hydrological Droughts in the Cheongmicheon Watershed for RCP4. 5 and SSP2-4.5. Sustainability 2021, 13, 2066. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Nicótina, L.; Alessi Celegon, E.; Rinaldo, A.; Marani, M. On the impact of rainfall patterns on the hydrologic response. Water Resour. Res. 2008, 44, W12401. [Google Scholar] [CrossRef]
- Majtey, A.; Lamberti, P.W.; Martin, M.T.; Plastino, A. Wootters’ distance revisited: A new distinguishability criterium. Eur. Phys. J. D At. Mol. Opt. Phys. 2005, 32, 413–419. [Google Scholar] [CrossRef]
- Bosshard, T.; Carambia, M.; Goergen, K.; Kotlarski, S.; Krahe, P.; Zappa, M.; Schär, C. Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections. Water Resour. Res. 2013, 49, 1523–1536. [Google Scholar] [CrossRef]
- Mockler, E.M.; Chun, K.P.; Sapriza-Azuri, G.; Bruen, M.; Wheater, H.S. Assessing the relative importance of parameter and forcing uncertainty and their interactions in conceptual hydrological model simulations. Adv. Water Resour. 2016, 97, 299–313. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Y.; Li, Z.; Chang, J.; Guo, A. Quantifying the uncertainty interaction between the model input and structure on hydrological processes. Water Resour. Manag. 2021, 35, 3915–3935. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Fowler, K.; Peel, M.; Western, A.; Zhang, L. Improved rainfall-runoff calibration for drying climate: Choice of objective function. Water Resour. Res. 2018, 54, 3392–3408. [Google Scholar] [CrossRef]







| Calibration | Criteria | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before | 25% | 0.649 | 0.630 | 0.631 | 0.630 | 0.640 | 0.638 | 0.640 | 0.653 | 0.650 | 0.650 | 0.660 | 0.643 |
| 75% | 0.771 | 0.743 | 0.742 | 0.736 | 0.730 | 0.730 | 0.730 | 0.723 | 0.700 | 0.708 | 0.690 | 0.727 | |
| IQR | 0.122 | 0.113 | 0.110 | 0.107 | 0.090 | 0.093 | 0.090 | 0.070 | 0.050 | 0.058 | 0.030 | 0.085 | |
| After | 25% | 0.719 | 0.714 | 0.722 | 0.705 | 0.697 | 0.693 | 0.690 | 0.690 | 0.704 | 0.701 | 0.702 | 0.703 |
| 75% | 0.819 | 0.806 | 0.791 | 0.794 | 0.784 | 0.777 | 0.761 | 0.754 | 0.744 | 0.734 | 0.726 | 0.772 | |
| IQR | 0.100 | 0.092 | 0.069 | 0.089 | 0.087 | 0.084 | 0.072 | 0.064 | 0.040 | 0.033 | 0.024 | 0.069 |
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | 0.385 | 0.343 | 0.311 | 0.352 | 0.329 | 0.327 | 0.350 | 0.387 | 0.398 | 0.454 | 0.430 |
| Median | 0.340 | 0.357 | 0.305 | 0.341 | 0.327 | 0.316 | 0.366 | 0.373 | 0.398 | 0.458 | 0.425 |
| 25% | 0.287 | 0.237 | 0.217 | 0.277 | 0.277 | 0.250 | 0.287 | 0.284 | 0.312 | 0.390 | 0.385 |
| 75% | 0.469 | 0.404 | 0.390 | 0.384 | 0.401 | 0.402 | 0.419 | 0.465 | 0.476 | 0.504 | 0.491 |
| IQR | 0.181 | 0.167 | 0.173 | 0.107 | 0.124 | 0.152 | 0.132 | 0.181 | 0.163 | 0.114 | 0.105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziarh, G.F.; Kim, J.H.; Song, J.Y.; Chung, E.-S. Quantifying Uncertainty in Runoff Simulation According to Multiple Evaluation Metrics and Varying Calibration Data Length. Water 2024, 16, 517. https://doi.org/10.3390/w16040517
Ziarh GF, Kim JH, Song JY, Chung E-S. Quantifying Uncertainty in Runoff Simulation According to Multiple Evaluation Metrics and Varying Calibration Data Length. Water. 2024; 16(4):517. https://doi.org/10.3390/w16040517
Chicago/Turabian StyleZiarh, Ghaith Falah, Jin Hyuck Kim, Jae Yeol Song, and Eun-Sung Chung. 2024. "Quantifying Uncertainty in Runoff Simulation According to Multiple Evaluation Metrics and Varying Calibration Data Length" Water 16, no. 4: 517. https://doi.org/10.3390/w16040517
APA StyleZiarh, G. F., Kim, J. H., Song, J. Y., & Chung, E.-S. (2024). Quantifying Uncertainty in Runoff Simulation According to Multiple Evaluation Metrics and Varying Calibration Data Length. Water, 16(4), 517. https://doi.org/10.3390/w16040517








