Abstract
The floodplain transverse slope is a significant parameter reflecting the degree of development of a secondary suspended river, as well as a crucial index of the flood risk in the river channel. Clarifying the factors that influence the evolution of the floodplain transverse slope has always been a hot and difficult topic for researchers working on the Yellow River management. We took the severe section of the secondary suspended river from Dongbatou to Gaocun in the lower Yellow River as the research object, selecting the annual runoff, annual sediment load, annual sediment coefficient, and the intensity of flood-season flow scouring at the Huayuankou station in the downstream as the water–sediment indexes. The correlation between different water–sediment indexes and the floodplain transverse slope under three modes: interannual, flood season, and flood-season overbank was studied through methods such as cross-wavelet transform and wavelet coherence analysis. The results showed that under the three modes, the annual sediment load and annual sediment coefficient had a high correlation with the evolution cycle of the transverse slope, followed by the intensity of flood-season flow scouring, and the annual runoff had the lowest correlation. Meanwhile, the change in the transverse slope had a good correlation with the flood-season overbank mode, indicating there was a high similarity between the water–sediment characteristics of floodplain flooding and the evolution cycle of the transverse slope; that is, the change in the transverse slope is greatly influenced by floodplain flooding events.
1. Introduction
The Yellow River has a problem of scarce water but abundant sediment, resulting in an imbalanced water–sediment relationship. Since the completion and operation of the Sanmenxia Reservoir in 1960, sediment deposition in the lower reaches of the Yellow River has been severe, leading to the formation of a secondary suspended river. Since 1986, the Yellow River has entered a relatively dry period, with a decrease in downstream runoff and an increase in water consumption for various projects along the river. The probability of major floods has decreased, while the number of small flow processes has increased. Under the long-term influence of small and medium floods, the main channel of the lower Yellow River has severely silted up and shrunk. In 2002, the bankfull discharge in the lower Yellow River dropped to 1800 m3/s (Shuangheli section), indicating an extremely severe situation for the secondary suspended river and flood control. The completion and operation of the Xiaolangdi Reservoir has alleviated sediment deposition in the downstream river channel somewhat, but the situation of the secondary suspended river has not improved, and the threat it poses to flood control has not been effectively controlled. In the event of a major flood, there is a possibility of cross-river, oblique-river, or even rolling-river conditions, posing a serious threat to the safety of the Yellow River embankment and even the lives of 1.89 million people in the floodplain areas.
For a long time, researchers working on the Yellow River management have conducted extensive studies on the formation and development of the secondary suspended river, believing that its occurrence and development are closely related to the incoming water and sediment of the river [1]. Hu Yisan [2] and Wang Kairong et al. [3] outlined the formation process of the secondary suspended river in different sections of the lower Yellow River based on measured data. Zhang Chuhan [4] believed that residents in the beach area of the lower Yellow River have built a large number of production embankments for a long time in order to prevent frequent flooding of small and medium-sized floods, which exacerbated the formation of the secondary suspended river. Jing Laihong et al. [5] believed that due to the decrease in flood in the middle reaches and the construction of production levees in the lower reaches, the proportion of sediment deposition in the main channel of the lower reaches increased, and the secondary suspended river gradually developed in the lower reaches. Zhang Ren [6] pointed out that the secondary suspended river is mainly caused by the construction of production dikes, including some river channel control projects, which prevent the exchange of water and sediment between the floodplain and the main channel. Pang Jiazhen [7] believed that excessive diversion of the water from the Yellow River has caused the total amount of diverted water to exceed the carrying capacity of the Yellow River, and the long-term large-scale occupation of water for production and social use has squeezed out the water used for sediment flushing, which is the main reason for the formation of the secondary suspended river. Jiang Enhui et al. [8] believe that during the period of flood detention and sediment discharge operation of the Sanmenxia Reservoir and the long-term period of low water and sediment, the elevation of the beach lip increased significantly, while the elevation of the tender beach edge changed little, resulting in an increase in the transverse slope of the beach, which accelerated the development of the secondary suspended river. In other words, the imbalanced sediment transport in the cross-section of the river channel gradually led to the formation of the secondary suspended river.
The aforementioned studies have focused on the causes of the secondary suspended river. Due to the influence of human activities, the amount of water and sediment flowing downstream has decreased [9], especially the reduction in flood peak flow and flood frequency, significantly reducing the occurrence of overbank floods that “deposit sediment on the floodplain and scour the channel”. At the same time, persistent low water flows have caused siltation and shrinkage of the riverbed, accelerating the development of the secondary suspended river [10,11,12]. However, current studies have mainly used qualitative descriptions to introduce the process and causes of the development of the secondary suspended river, and there is little research on how various indexes in the water–sediment conditions affect it. This study selects the severely affected section of the secondary suspended river in the lower Yellow River, Dongbatou–Gaocun, as the research object. Using wavelet transformation and wavelet coherence analysis methods, it analyzes the water–sediment indexes such as annual runoff, annual sediment load, annual sediment coefficient, and flood-season water scouring intensity that affect the development of the secondary suspended river, aiming to quantitatively explore the impacts of different water–sediment indexes on the secondary suspended river.
2. Materials and Methods
2.1. Study Area
The Dongbatou–Taochengpu section (Figure 1) of the lower Yellow River, which is the most severely affected section by the secondary suspended river in the lower Yellow River, spans a total length of 220 km [12]. Among this, the Dongbatou–Gaocun section is a wandering river channel with a length of approximately 66 km. The distance between the embankments on both sides of the Yellow River is approximately 5 to 10 km, with the widest point exceeding 20 km. The longitudinal gradient of the river channel ranges from 1.720/000 to 2.650/000. The Gaocun–Taochengpu section belongs to a transitional river channel transforming from wandering to curved, spanning a length of about 154 km. The distance between the embankments on both sides of the Yellow River ranges from 1.4 to 8.5 km, with most sections being over 5 km. The average longitudinal gradient of the river channel is 1.150/000. In the late 1990s, the bankfull discharge of this river section once dropped to around 2000 m3/s, indicating severe siltation, and the situation of the secondary suspended river was exceptionally critical. Historically, wandering river channels have always been the focus of flood prevention, so this study selects the Dongbatou–Gaocun section, located in the wandering river section, as the key research area.
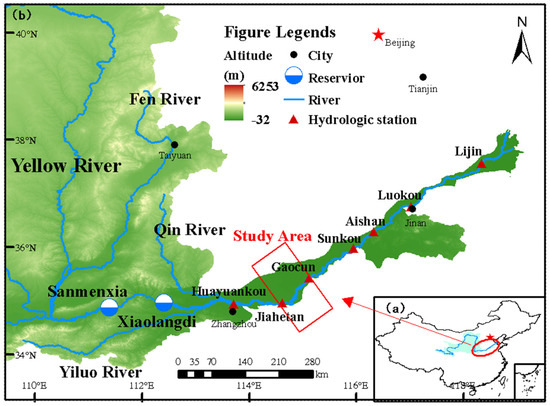
Figure 1.
Study area location: (a) location of the lower Yellow River in China; (b) magnified lower Yellow River and location of the study area [13].
2.2. Study Methods
2.2.1. Data Sources
The research period of this paper is from 1960 to 2022, and the basic data involved mainly include the large cross-section topographic data of the Dongbatou–Gaocun river section, as well as the measured water and sediment data such as annual water volume, annual sediment volume, maximum peak flow, and bankfull flow at the downstream Huayuankou station. The large cross-section data were uniformly measured by the professional departments of the Yellow River Water Conservancy Commission, and the water and sediment data of the series years come from the Sediment Bulletin of the Yellow River Water Conservancy Commission and the hydrological data of the Yellow River Basin. All data are official and highly authoritative.
2.2.2. Data Processing Methods
- (1)
- Water–sediment conditions
The average flow scour intensity can reflect the sediment content and flow into the downstream channel and its combination process to some extent, which is expressed as [14]:
where is the average flow rate, m3/s; is the average sediment content, kg/m3.
The sediment coefficient is an indicator to measure the water and sediment conditions, and its expression is:
where Q is the flow rate, m3/s; S is the sediment content, kg/m3.
- (2)
- Floodplain transverse slope [13]
The floodplain transverse slope is one of the main characteristic parameters indicating the development degree of the secondary suspended river. Its calculation formula is:
where i represents the floodplain transverse slope, expressed in ‱; H1 and H2 refer to the elevation of the floodplain lip and the elevation of the floodplain near the embankment, both in meters; d1 and d2 represent the distance from the starting point of the floodplain lip and the distance from the starting point of the floodplain near the embankment, both in meters; (H1 − H2) represents the height difference in meters; (d1 − d2) represents the width of the floodplain in meters. Due to the change in the position of the main channel along the river, the width of the floodplain on the left and right banks varies greatly, resulting in significant differences in the transverse slope between the two banks of the same cross-section. To better represent the floodplain transverse slope, the average value of the left and right banks is taken. When there is no floodplain on one bank, the cross-slope of the other bank is taken as the average floodplain transverse slope of the cross-section.
- (3)
- Cross-wavelet transform (XWT)
Continuous wavelet transform is often used for analyzing information such as the periodic strength of a single time series. However, the cross-wavelet transform, based on the continuous wavelet transform, analyzes the interrelationship between two time series, such as water–sediment conditions and lateral slope changes, across multiple time scales, revealing their common power and relative phase in the time–frequency space. The cross-wavelet spectrum of two time series X and Y is defined as [15].
where WX(a) represents the cross-wavelet transform of time series X, while WY(a) represents the cross-wavelet transform of time series Y. The power spectrum of the cross-wavelet is denoted as |WXY (a)|, and a higher value indicates a stronger correlation between time series X and Y.
Since wavelets are not fully localized in the time domain, continuous wavelet transforms have the issue of edge artifacts. To address this problem, the Cone of Influence (COI) is introduced. In this paper, the Cone of Influence is defined as the region where the discontinuous wavelet power near the edge decreases to the edge value of e2.
Since many geophysical time series exhibit red noise characteristics (i.e., the variance decreases with the decrease in scale or increase in frequency), red noise is often used as the background spectrum to validate the cross-wavelet power spectrum. Assuming that the expected spectra of time series X and Y under the red noise background are and , the distribution equation for the cross-wavelet power spectrum is given as [16]:
where represents the standard deviation of time series X, and represents the standard deviation of time series Y. In the Morlet wavelet transform, v = 2 indicates the degree of freedom, and represents the confidence level associated with the probability P. First, the upper limit of the 95% confidence interval for the red noise power spectrum is calculated. When the left-hand side of Equation (5) exceeds the confidence level boundary, it is considered to have passed the red noise standard spectrum test at a significance level of α = 0.05, indicating a significant correlation between the two series [17]. Cross-wavelet transform is suitable for highlighting regions where the coupling between the two time series is relatively significant. For regions where the consistency of the cross-wavelet power spectrum between the two series is low, the wavelet coherence spectrum can be utilized to characterize the degree of consistency in the changes between the two series.
- (4)
- Wavelet coherence analysis (WTC)
For the time series of water–sediment conditions and transverse slope changes, continuous wavelet transform and cross-wavelet transform can reveal their common high-energy regions and phase relationships. The wavelet coherence spectrum is used to measure the degree of local correlation between two time series in the time–frequency space. Even for regions with low energy in the cross-wavelet power spectrum, the correlation between the two in the wavelet coherence spectrum may still be significant. The wavelet coherence spectrum of time series X and Y is defined as [18]:
where S is the smoothing operator, and the scale at which S is smoothed in time and frequency defines the scale of the variance of the wavelet coherence spectrum measurement.
The smoothing operator S can be written as:
where Sscale and Stime represent wavelet scale axis smoothing and temporal smoothing, respectively, with the following expressions:
where c1 and c2 are normalization constants, ∏ is the rectangular function, and 0.6 is the empirically determined scale-decorrelation length factor for Morlet wavelets.
The cross wavelet transform and the wavelet coherence spectrum can obtain the phase information between two time series. However, the cross-wavelet transform mainly shows the region where the periodic strength of the two series is consistent in the time–frequency domain, which can intuitively understand the strength of the common cycle between the two sequences. In contrast, the wavelet coherence spectrum focuses on showing the consistency of the periodic trend of the two sequences. It does not directly show the strength of the cycle of the change relationship.
- (5)
- Wavelet phase angle
The local relative phase relationship between the time series X and Y can be expressed by the complex angle of . Based on the relationship between the phase angle and the period, the length of time after or before the phase of the bit can be calculated. For regions that are statistically significantly correlated but outside the cone of influence, the circular mean of the phases can be used to quantify the phase relationship. By estimating the mean of the phase difference and its confidence interval, the phase difference of the encounter points between each scale component of the two time series can be calculated, thus achieving a quantitative representation of the phase relationship between X and Y. Which is represented by using the circular mean locus angle in the region of greater than 95% confidence level. There are i angles qi (i = 1, 2,…, n), and the sample mean of angle qi is denoted as q, which is calculated as [19]:
The direction of the wavelet phase angle arrow determines the phase relationship between the two time series at the corresponding time scale. When the cross-wavelet correlation coefficient values of the two time series are high, the degree of overshooting (lagging) of the two series can be estimated by the direction of the arrow of the wavelet phase angle and the angle of the time axis. → indicates that the two are congruent, a positive correlation; ← indicates that the two are antipodal, a negative correlation; ↙ indicates that Y is ahead of X and is positively and negatively correlated, respectively; ↘, indicates that Y is lagging behind X and is positively and negatively correlated, respectively.
Figure 2 shows the structure flowchart of the study structure.
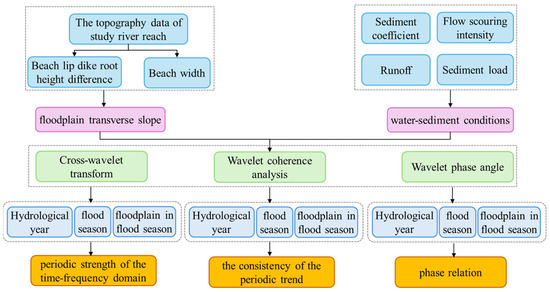
Figure 2.
The flowchart of the study structure.
3. Results
3.1. Evolution Characteristics of Transverse Slope in Dongbatou–Gaocun River Section
The formation of the secondary suspended river is mainly due to changes in the conditions of incoming water and sediment. The floodplain transverse slope is an important parameter reflecting the degree of development of the secondary suspended river, and also an important index reflecting the risk of flood disasters in the river channel.
Figure 3a depicts the evolution of the floodplain transverse slope on both banks of the Dongbatou–Gaocun river section from 1960 to 2022. Overall, the floodplain transverse slope in this river section showed an upward trend, particularly before 2000, where the transverse slope experienced a significant increase. After 2000, the transverse slope showed a relatively stable fluctuation. Figure 3b presents a box plot showing the evolution of the transverse slope of the floodplains on both banks of the Dongbatou–Gaocun river section from 1960 to 2022. It can be observed that the various characteristic values of the variation in the height difference of the floodplains in this river section include a maximum transverse slope of 6.870/000 (right bank) and a minimum transverse slope of 2.340/000 (right bank). The average transverse slopes of the left and right banks are 4.520/000 and 4.200/000 respectively.
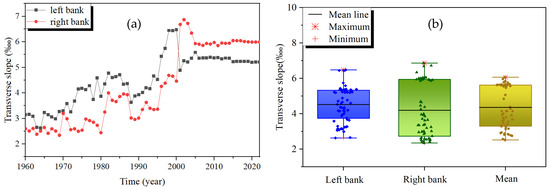
Figure 3.
Evolution of floodplain transverse slope in Dongbatou–Gaocun river section: (a) Evolution Process of the left and right banks; (b) Box plot of evolution of the left and right banks.
3.2. Correlation Analysis of Different Water and Sediment Indexes and Transverse Slope
Based on the topographic data of large cross-sections in the Dongbatou–Gaocun river section from 1960 to 2022, the floodplain transverse slope for each year was calculated. By calculating the difference between the transverse slope in the nth year and the transverse slope in the (n − 1)th year of the time series, an interannual variation time series of the transverse slope was obtained. The periodic similarity between the conditions of incoming water and sediment and the changes in the transverse slope of the secondary suspended river was studied using the methods of cross-wavelet transform and wavelet coherence analysis.
The data of runoff, sediment load, maximum flood peak flow, and bankfull discharge from the Huayuankou station in the lower Yellow River from 1960 to 2022 were selected, to calculate the sediment coefficient and flow scouring intensity during flood season. The runoff, sediment load, sediment coefficient, and flow scouring intensity during flood season were chosen as the water and sediment conditions. Three modes were set such as interannual (hydrological year), flood season (July to October), and floodplain overflow during the flood season (floodplain coefficient × flood-season runoff). The wavelet cross-spectrum and wavelet coherence spectrum between different water and sediment conditions and the transverse slope were calculated separately to analyze the correlation between various water and sediment factors and the variation series of the transverse slope. In the wavelet cross-spectrum, warm colors indicate regions where the two time series have the same higher power. In the wavelet coherence spectrum, warm colors indicate regions where the two time series have a strong correlation. The arrows represent the lag (or lead) relationship between the two time series. The thin black lines represent the cone of influence from the wavelet boundary effect, while the areas enclosed by the thick solid lines indicate the regions determined by the red noise test at the 95% confidence level.
3.2.1. Correlation between Runoff and Changes in Transverse Slope
Figure 4 shows the wavelet cross-spectrum and coherence spectrum between runoff and transverse slope under three different indexes. The runoff wavelet cross-spectra exist in the same high-power region on the period of 0~3a, 3~6a, 6~12a, and 12~24a, among which the high-power regions of 0~3a, 3~6a, and 6~12a are mainly distributed in the period before the year 2000, and there are dispersed regions of significance. The 12~24a high power region is almost spread throughout the period, but no region passes the significance test. Analyzing the locational relationship by the arrow direction, the two time series are positively correlated in the regions of 0~3a, 6~12a, and 12~24a and negatively correlated in the region of 3~6a. The change in transverse slope lags behind the change in runoff volume. The wavelet coherence spectrum shows that the two sequences correlate highly on cycles 0~4a, 4~6a, and 6~16a. The region of high correlation from 0 to 4a is distributed at intervals throughout the period, in which flood-season runoff is significantly correlated with transverse slope change in 1979–1982, and the region of high correlation from 6 to 16a is distributed in 1970–1996 under interannual and flood-season indexes and flood-season flooding indexes. The time domain was expanded to 1964–2010 and significantly correlated with 1972–1978. The site–phase relationship is positively correlated, with changes in transverse slope lagging behind changes in runoff volume.
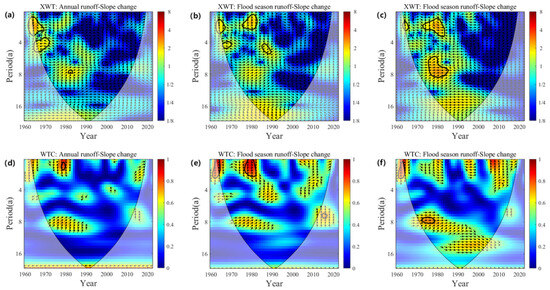
Figure 4.
Wavelet cross-spectrum (a–c) and wavelet coherence spectrum (d–f) of interannual variability of runoff and transverse slope: (a,d): interannual; (b,e): interannual; (c,f): flood-season overbank.
3.2.2. Correlation between Sediment Load and Changes in Transverse Slope
Figure 5 shows the wavelet cross-spectrum and wavelet coherence spectrum between sediment load and transverse slope under three different indexes. There is a significant common high-power region on the 0~4a cycle for sediment delivery and transverse slope variations, with time distributions in 1968–1972 and 1980–1988. The wavelet coherence spectrum shows a significant correlation region between the two time series for 12~24a. The critical correlation region gradually expands with the index change, and the time distributions are 1990–2008, 1982–2012, and 1960–2022. The site–phase relationship is positively correlated, with changes in transverse slope lagging behind changes in sediment delivery.
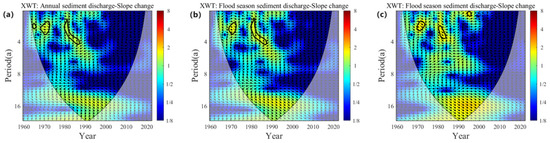

Figure 5.
Wavelet cross-spectrum (a–c) and wavelet coherence spectrum (d–f) of interannual variation of sediment transport and transverse slope: (a,d): interannual; (b,e) interannual; (c,f): flood-season overbank.
3.2.3. Correlation between Sediment Coefficient and Changes in Transverse Slope
Figure 6 shows the wavelet cross-spectrum and wavelet coherence spectrum between the sediment coefficient and the changes in the transverse slope. The wavelet cross-spectra of the incoming sediment coefficient and transverse slope variation shows a significant high-power region at the periods of 0~2a, 2~4a, 5~7a, and 14~24a, with the highest region at the period of 14~24a, and the distribution of the period is from 1980 to 2004. The wavelet coherence spectra showed a significant correlation region between 4~7a and 12~24a cycles. The critical correlation region on 4~7a cycles has the most considerable area at the time of the flood index, which is distributed in 1990–2008, and the rest of the indexes are distributed in 1992–2004, whereas the significant correlation region on 12~24a cycles has the smallest area at the time of the flood index, which is distributed in 1982–2010. The rest of the indexes are distributed in 1970–2020. The phase relationship shows a positive correlation between the incoming sediment coefficient and the change in transverse slope, except that the change in transverse slope exceeds the change in incoming sediment coefficient in the cycle of 4~7a, and the change in transverse slope lags behind the change in incoming sediment coefficient in the rest of the significant correlation areas.
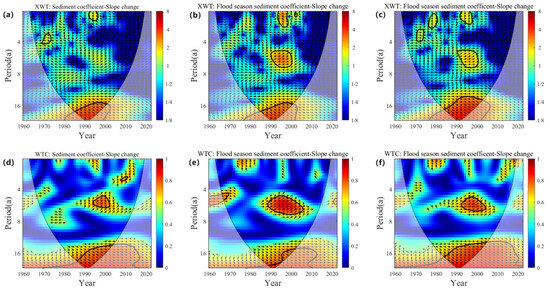
Figure 6.
Wavelet cross-spectrum (a–c) and wavelet coherence spectrum (d–f) of interannual variation in incoming sediment coefficient and transverse slope: (a,d): interannual; (b,e): interannual; (c,f): flood-season overbank.
3.2.4. Correlation between Flow Scouring Intensity and Changes in Transverse Slope
Figure 7 shows the wavelet cross-spectrum and wavelet coherence spectrum between flow scouring intensity during flood season and changes in transverse slope. The wavelet cross-spectrum of scour intensity has no significant common high-power region under both interannual and flood-season indexes, and there are significant common high-power regions on the cycles of 1~3a, 6~8a, and 16~24a under flood-season indexes, 6~8a cycles in 1978–1985, and 16~24a cycles in 1978–1992. The significant correlation period of the wavelet coherence spectrum is 0~2a, 3~5a, and 6~10a, the significant correlation area on the 0~2a period appeared in the flood-season index and flood-season diffuse beach index in 1974–1980, the significant correlation area on the 3~5a period appeared in the flood-season index in 1984–1988, the significant correlation area on the 6~10a period appeared in all the three indexes, and the distribution range gradually increased as the time distribution range of the index changes gradually increased, 1978–1984, 1974–1990, and 1970–1990, respectively. The bitemporal relationship shows a positive correlation, and the transverse slope change lags behind the scour intensity change.
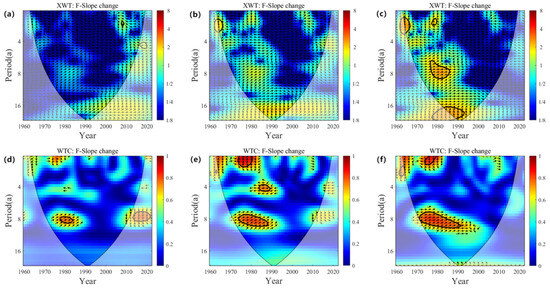
Figure 7.
Wavelet cross-spectrum (a–c) and wavelet coherence spectrum (d–f) of inter-annual variation in scour intensity and transverse slope: (a,d): interannual; (b,e): interannual; (c,f): flood-season overbank.
4. Discussion
Studies have shown that [20,21,22] the annual runoff and sediment load of the Yellow River are important factors affecting the transverse slope of the river. When the runoff is large, the water flow has a strong scouring ability, which may cause the river channel to cut down and lateral erosion. Sediment transport will affect the scouring and silting of the river channel. Large amounts of sediment transport and deposition will raise the riverbed. The sediment coefficient is an important indicator to measure the sediment transport capacity of a river. When the sediment coefficient is large, it may cause river siltation. When the sediment coefficient is small, the river channel may be scoured.
In particular, the intensity of water flow during flood season directly affects the scouring and siltation process of the river channel. The strong scouring force of water flow during the flood season can significantly change the shape and transverse slope of the river channel [23].
The transverse slope of the beach in the lower Yellow River is an important parameter reflecting the development degree of the secondary suspended river, and the incoming water and sediment conditions directly affect the transverse slope. This study shows that the annual sediment load, annual sediment coefficient, flood-season flow scouring intensity, annual runoff, and other water and sediment indicators are related to the evolution cycle of the transverse slope. In addition, the similarity between the flood and sediment characteristics of the floodplain and the evolution cycle of the transverse slope is high.
In addition, the transverse slope is also affected by many factors. Future research can further explore other factors that may affect the evolution of the transverse slope, such as human activities, climate change, etc., providing a more comprehensive scientific basis for the management of secondary suspended river and flood risk.
5. Conclusions
- (1)
- From 1960 to 2022, the floodplain transverse slope in the Dongbatou–Gaocun section of the lower Yellow River generally showed an upward trend, particularly before 2000, the increase in the transverse slope was more significant. After 2000, the floodplain transverse slope exhibited relatively stable fluctuations. The amplitude of changes in the transverse slope varied in different periods.
- (2)
- Through the analysis of wavelet cross-transform and wavelet coherence spectrum of the time series of changes in transverse slope and the conditions of incoming water and sediment, both annual sediment load and annual sediment coefficient have a high correlation with the evolution cycle of the transverse slope, followed by the flow scouring intensity during the flood season. However, the correlation between annual runoff and the evolution cycle of the transverse slope is relatively small, indicating that compared to water flow conditions, the change in sediment load has a greater impact on the secondary suspended river. Through phase correlation analysis, it can be observed that there is a positive correlation between changes in transverse slope and water–sediment conditions, and the change in transverse slope lags behind the variation in incoming water and sediment conditions, which is consistent with the hysteresis of riverbed evolution.
- (3)
- Through a comparative analysis of the evolution of transverse slope under different modes, the change in transverse slope has a good correlation with the floodplain overflow mode during the flood season, indicating that the water–sediment characteristics of floodplain floods have a high similarity with the evolution cycle of the transverse slope; that is, the change in transverse slope is significantly influenced by individual floodplain floods.
Author Contributions
Conceptualization, L.X., H.X. and J.Y.; methodology, L.X. and H.X.; software, H.X.; formal analysis, H.X. and L.X.; investigation, H.X., Z.K. and X.G.; data curation, H.X. and L.X.; writing—original draft preparation, L.X. and H.X.; writing—review and editing, J.Y., J.L. and L.X.; visualization, H.X.; supervision, L.X. and J.Y.; project administration, J.L. and L.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the National Natural Science Foundation of China (No. U2243222, U2243219), the Major Science and Technology Project of Henan Province (No. 231100320100), the Excellent Youth Foundation of Henan Scientific Committee (No. 222300420013), the Significant Science and Technology Project of the Ministry of Water Resources (No. SKS-2022011), the Excellent Young Talents Project of the Yellow River Conservancy Commission (No. HQK-202309), Henan Province Natural Science Foundation Project (No. 242300420039).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, J.; Liu, J.; Lu, J.; Luo, Q. Theories and practices of sediment engineering control in the Yellow River. J. Sediment Res. 2023, 48, 1–8. [Google Scholar] [CrossRef]
- Hu, Y. Perched River Discussion. J. North China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2001, 3, 12–18. [Google Scholar] [CrossRef]
- Wang, K.; Wang, C.; Du, X.; Wang, G.; Zhang, J. Practice and evaluation of sediment control in the Yellow River Estuary. J. Sediment Res. 2024, 22, 12–18. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, G. Thoughts on Ecological Protection and High-Quality Development in the Yellow River Basin. Yellow River 2024, 46, 271–277. [Google Scholar]
- Jing, L.; Wan, Z.; Chen, C. Significance of extending the service life of Xiaolangdi reservoir insediment retention for Yellow River flood control and security. Yellow River 2024, 46, 1–4+24. [Google Scholar] [CrossRef]
- Zhang, R. Suggestions on a General Plan for Lower Yellow River Management. Yellow River 2004, 26, 1–4. [Google Scholar] [CrossRef]
- Pang, J. Pondering over Issues of a General Plan of the Lower Yellow River Harnessing. Yellow River 2005, 27, 3–4. [Google Scholar] [CrossRef]
- Jiang, E.; Han, Q.; Li, J.; Cao, Y. Outline of Typical Phenomena of Bed Development of the Yellow River and Its Related Study. Yellow River 2010, 8, 5–7. [Google Scholar]
- Liu, X. The Water and Sediment Situation and Countermeasure. Yellow River 2020, 42, 34–40. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, M.; Yao, W.; Li, Y.; Ma, D. Mainstream swing rule and its driving mechanism in the Sanguanmiao to Weitan reach of the lower Yellow River. J. Basic Sci. Eng. Mech. 2023, 31, 1110–1124. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Q.; Liu, Y.; Liu, G.; Jiang, E. Morphological effects of the operation of Xiaolangdi Reservoir on the Lower Yellow River in recent years. J. Hydraul. Eng. 2024, 55, 505–515. [Google Scholar] [CrossRef]
- Jiang, E.; Cao, Y.; Zhang, L. Study on the Evolution Law and Mechanism of River Regime in the Wandering Reach of the Lower Yellow River; China Water & Power Press: Beijing, China, 2006. [Google Scholar]
- Xu, L.; Li, J.; Xu, H.; Zhang, X.; Lai, R.; Zhang, X.; Gao, X. Evolution and drivers of secondary suspended rivers in typical wandering sections of the lower Yellow River from 1960–2021. Front. Ecol. Evol. 2023, 11, 1330749. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, J.; Zhou, M.; Li, J. Characteristics of main channel migration in the braided reach of the Lower Yellow River after the Xiaolangdi Reservoir operation. Adv. Water Sci. 2019, 2, 198–209. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Y. Evolution characteristics of runoff and sediment fluxes of Yellow River, Yangtze River and Pearl River into sea during 1960-2020. Bull. Soil Water Conserv. 2024, 44, 147–157. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Z. Trend and multi-time scale cross-wavelet analysis on precipitation and temperature in Tianjin area. J. Tianjin Norm. Univ. (Nat. Sci. Ed.) 2016, 1, 32–39. [Google Scholar]
- Thompson, D.; Wallace, J. The Arctic oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. 1998, 25, 1297–1300. [Google Scholar] [CrossRef]
- Firouzi, S.; Wang, X. A comparative study of exchange rates and order flow based on wavelet transform coherence and cross wavelet transform. Econ. Model. 2019, 82, 42–56. [Google Scholar] [CrossRef]
- Yellow River Conservancy Commission. Causes and Control Measures of the “Secondary Suspended River” in the Lower Yellow River; The Yellow River Water Conservancy Press: Zhengzhou, China, 2003. [Google Scholar]
- Xie, F.; Zhao, X.; Mu, X.; Gao, P.; Sun, W. The change of water-sediment relationship in the main stream of the Yellow River in the past 70 years. Sci. Soil Water Conserv. 2021, 19, 1–9. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, Y.; Ma, J.; Guo, J.; Chen, P. Variation of Observed and Natural Runoff of Yellow River from 1969 to 2018. Bull. Soil Water Conserv. 2020, 40, 1–7. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, J.; Liu, C. Data on Annual and Interannual Changes in Runoff in the Yellow River Basin from 2015 to 2019; National Cryosphere Desert Data Center: Lanzhou, China, 2021; Available online: http://www.ncdc.ac.cn (accessed on 16 June 2024). [CrossRef]
- Hu, C.; Zhang, X.; Zhao, Y. Cause analysis of the centennial trend and recent fluctuation of the Yellow River sediment load. Adv. Water Sci. 2020, 31, 725–733. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).