Comprehensive Evaluation of Crack Safety of Hydraulic Concrete Based on Improved Combination Weighted-Extension Cloud Theory
Abstract
1. Introduction
2. Improved Combination Weighting Method Based on EAHP-CRITIC
2.1. Subjective Weighting Analysis
- (1)
- Creation of the matrix of comparisons
- (2)
- Determined the eigenvector and eigenvalue maxima.
- (3)
- Verification of rationality
2.2. Objective Weighting Analysis
- (1)
- Construction of the initial indicator data matrix X = (xij)n×n.
- (2)
- Standardization of raw data.
- (3)
- The index comparison intensity was determined.
- (4)
- The conflict correlation coefficient was determined.where cov (Dk, Dj) was the covariance of the evaluation data between the kth and jth indicators, k ≠ j; Sk and Sj were the comparative strengths of the kth and jth indicators, respectively.
- (5)
- The amount of information synthesized between indicators was determined.
- (6)
- Determination of weighting factors for indicators was as follows.
2.3. Improved Combinatorial Weighting Analysis
- (1)
- The weight vector ωi (i = 1, 2, …, n) was obtained by using N weighting methods, respectively, thus forming the initial weight vector set Wn = {ω1, ω2, …, ωn}, i = 1, 2, …, n. Given a set of combination coefficients (α1, α2, …, αn), the comprehensive weight of every component could be expressed as:
- (2)
- To define the objective function, a Matlab 2023a calculation (α1, α2, …, αN) was used to find the value that minimized the deficiencies of the combination coefficients. This would yield the weight W at its optimal value.
- (3)
- The optimal linear equations that are equal to Equation (8) could be found as follows, based on the differential properties of the matrix:
- (4)
- After the computation was finished and the αi was normalized to αi*, the comprehensive weight W based on the improved combinational game theory may be ultimately determined as follows:
3. Extension Cloud Theory Method
3.1. Basic Concepts of Extension Cloud
3.2. Evaluation Steps of Extension Cloud Theory
- (1)
- Determine the object-element and evaluation criteria cloud of the sample.
- (2)
- The correlation degree between the things to be evaluated and each evaluation grade index was determined.
- Matlab was used to generate a normal random number En′ with En as the mean, and He as the standard deviation.
- Let the deterministic value of the thing to be evaluated be xi. Then, the calculation formula of cloud correlation degree μi was as follows:
- c.
- In order to evaluate the reliability of evaluation results more intuitively, the confidence factor θ was introduced [28]. Its value was inversely proportional to confidence, and the formula was as follows:
- d.
- When the value of the confidence factor was reasonable, the cloud affiliation obtained from Equation (16) can be utilized to form the extension cloud matrix Q. It represented the cloud affiliation between each metric in the sample and the standard cloud of the first to mth level.
- (3)
- The combined weight was calculated.
- (4)
- A comprehensive certainty matrix was established.By combining the results (2) and (3), the matrix K of sample certainty was obtained.
- (5)
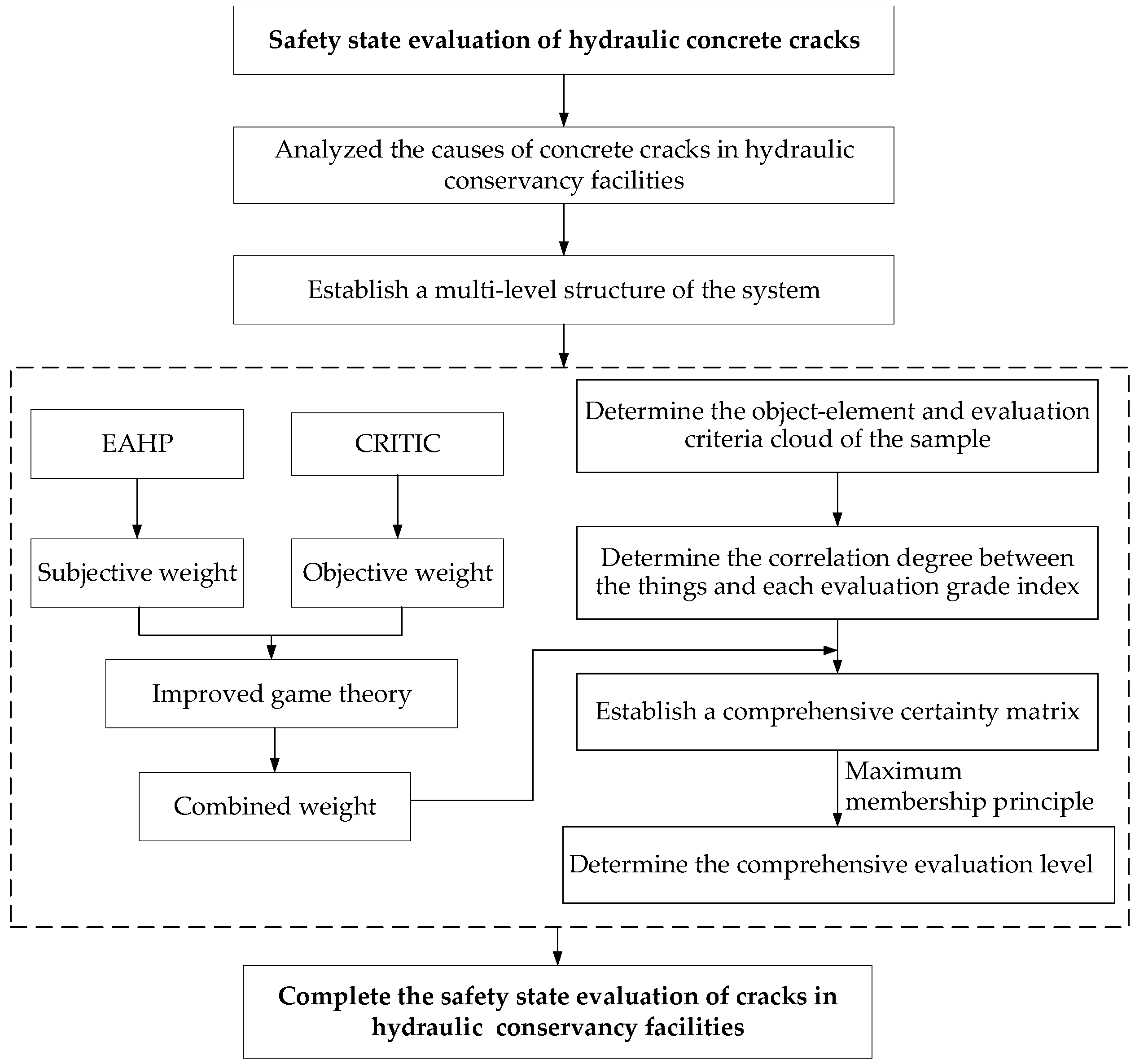
- Each of the corresponding levels had a corresponding degree of certainty, and the same level of certainty was added, according to the principle of maximum membership; the comprehensive evaluation level could be determined [29]. That was, kj = maxkj (p), p belongs to grade j.In summary, Figure 1 displayed the technology roadmap for this paper.
4. Examples of Engineering Applications
4.1. Establishment of a Hierarchy
4.2. Determination of Standard Cloud Parameters
4.3. Determination of Comprehensive Weight
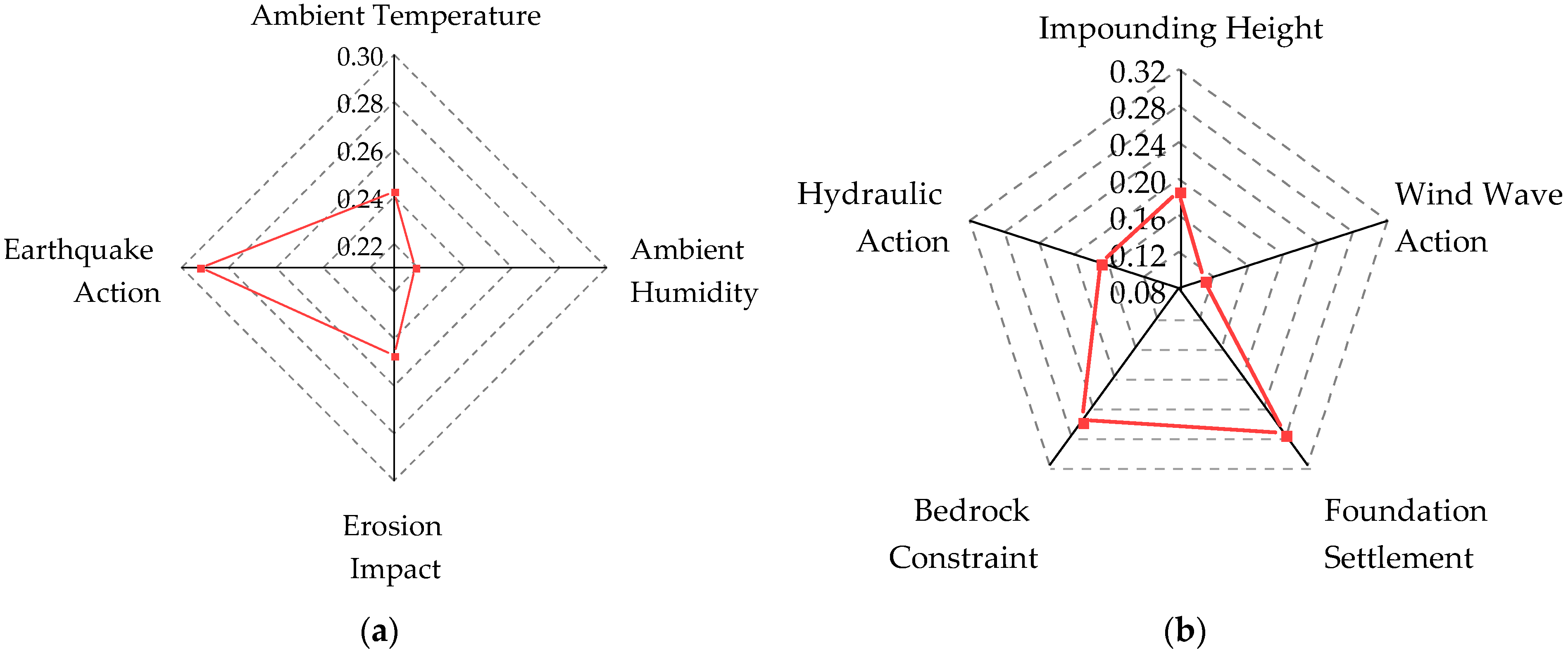
4.3.1. Comprehensive Weight of Dimension Layer
4.3.2. Comprehensive Weight of Presentation Layer
4.4. Evaluation Results and Validation
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Russel, N.S.; Selvaraj, A. MultiScaleCrackNet: A parallel multiscale deep CNN architecture for concrete crack classification. Expert Syst. Appl. 2024, 249, 123658. [Google Scholar] [CrossRef]
- Gavzan, M.R.; Ahmadi, M.T. Numerical investigation of static failure scenario of concrete gravity dams considering water–crack interaction. Int. J. Civ. Eng. 2023, 21, 391–408. [Google Scholar] [CrossRef]
- Zainal, S.M.I.S.; Hejazi, F.; Abd Aziz, F.N.A.; Jaafar, M.S. The synergistic effects of different types of hybridized synthetic fibers on concrete post-crack residual strength. KSCE J. Civ. Eng. 2022, 26, 131–142. [Google Scholar] [CrossRef]
- Sohaib, M.; Hasan, M.J.; Shah, M.A.; Zheng, Z. A robust self-supervised approach for fine-grained crack detection in concrete structures. Sci. Rep. 2024, 14, 12646. [Google Scholar] [CrossRef] [PubMed]
- Kapadia, H.K.; Patel, P.V.; Patel, J.B. Monitoring and analysis of crack developments in concrete using machine vision. J. Struct. Eng. 2022, 49, 204–222. [Google Scholar]
- Wang, Y.; Zhang, S.; Niu, D.; Fu, Q. Quantitative evaluation of the characteristics of air voids and their relationship with the permeability and salt freeze–thaw resistance of hybrid steel-polypropylene fiber–reinforced concrete composites. Cem. Concr. Compos. 2022, 125, 104292. [Google Scholar] [CrossRef]
- Tan, Y.; Al-Huqail, A.A.; Chen, Q.S.; Majdi, H.S.; Algethami, J.; Ali, H.E. Analysis of groundwater pollution in a petroleum refinery energy contributed in rock mechanics through ANFIS-AHP. Int. J. Energy Res. 2022, 46, 20928–20938. [Google Scholar] [CrossRef]
- Liu, H.; Wang, S.; Qiao, L. Cloud model membership degree of rock slope stability evaluation: Method and a case study. Pol. J. Environ. Stud. 2022, 31, 3181–3193. [Google Scholar] [CrossRef] [PubMed]
- Yuvaraj, R.M.; Ambrisha, S.; Muthunagai, S. Integrated AHP-TOPSIS models to evaluate suitability and sustainable development of beach tourism: A case in Chennai City, Tamil Nadu, India. J. Coast. Conserv. 2024, 28, 32. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Senani, A.G.; Fadaei, A.; Simaee, M.; Moltames, R. A framework for GIS-based site selection and technical potential evaluation of PV solar farm using fuzzy-boolean logic and AHP multi-criteria decision-making approach. Renew. Energy 2022, 186, 89–104. [Google Scholar] [CrossRef]
- Lukose, N.; Sunilkumar, N. Risk assessment and categorization of flood risk zones using geospatial data and multi-criteria decision model in a low-lying deltaic region, Kuttanad, India. J. Indian Soc. Remote Sens. 2024, 52, 985–1002. [Google Scholar] [CrossRef]
- Cimino, A.; Gnoni, M.G.; Longo, F.; Nicoletti, L. A risk assessment framework based on ergonomic methods and AHP for prioritizing interventions to prevent container terminal operators musculoskeletal disorders. Saf. Sci. 2023, 159, 106017. [Google Scholar] [CrossRef]
- Zhou, X.; Xiang, X.; Zhou, L.J. Study on evaluation method for the rural solid waste fixed bed gasification using the AHP-FCE based on exergy analysis. Int. J. Exergy 2023, 40, 365–391. [Google Scholar] [CrossRef]
- Lu, N.; Li, Y.; Xu, B. Evaluation of the suitability of smart health products for aging based on the IIVAHP-CRITIC model: A case study of smart health kiosk. Sustainability 2022, 14, 9212. [Google Scholar] [CrossRef]
- Zhong, S.; Chen, Y.; Miao, Y. Using improved CRITIC method to evaluate thermal coal suppliers. Sci. Rep. 2023, 13, 195. [Google Scholar] [CrossRef]
- Akram, M.; Ramzan, N.; Deveci, M. Linguistic pythagorean fuzzy CRITIC-EDAS method for multiple-attribute group decision analysis. Eng. Appl. Artif. Intell. 2023, 119, 105777. [Google Scholar] [CrossRef]
- Zhao, Y.; Tan, Z.; Bao, B.; Tu, Z. Centralized SUB-CRITIC based hierarchical-structured reinforcement learning for temporal sentence grounding. Multimed. Syst. 2023, 29, 21811–22191. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, H.; Li, H.; Zhong, B.; Fung, I.; Raymond, L.Y.Y. Exploring the adoption of blockchain in modular integrated construction projects: A game theory-based analysis. J. Clean. Prod. 2023, 408, 137115. [Google Scholar] [CrossRef]
- Ereiz, S.; Jiménez-Alonso, J.F.; Duvnjak, I.; Pavi, A. Game theory-based maximum likelihood method for finite-element-model updating of civil engineering structures. Eng. Struct. 2023, 277, 115458. [Google Scholar] [CrossRef]
- Houda, Z.A.E.; Brik, B.; Ksentini, A.; Khoukhi, L.; Guizani, M. When federated learning meets game theory: A cooperative framework to secure IIoT applications on edge computing. IEEE Trans. Ind. Inform. 2022, 18, 7988–7997. [Google Scholar] [CrossRef]
- Leng, M.; Zhou, G.; Li, H.; Xu, G.; Blaabjerg, F.; Dragievi, T. Impedance-based stability evaluation for multibus dc microgrid without constraints on subsystems. IEEE Trans. Power Electron. 2022, 37, 932–943. [Google Scholar] [CrossRef]
- Zareen, S.; Anwar, S.M. BPMN extension evaluation for security requirements engineering framework. Requir. Eng. 2024, 29, 261–278. [Google Scholar] [CrossRef]
- Wei, X.; Huang, J.; Deng, Z.; Ding, Z. Modified extension evaluation of foundation pit engineering combined with orthogonal experiments and multiple linear regression. Arab. J. Geosci. 2022, 15, 724. [Google Scholar] [CrossRef]
- Wang, Y. A novel evaluation model based on connection cloud model and game theory under multiple uncertainties. Soft Comput. 2023, 27, 645–656. [Google Scholar] [CrossRef]
- Al-Iessa, S.M.; Sheibani, R.; Veisi, G. A resource allocation and scheduling model for hierarchical distributed services in cloud environment using game theory. Int. J. Commun. Syst. 2022, 35, 5075. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Li, S.; Guo, Y.; Liu, Q.; Wang, G. Cloud-cluster: An uncertainty clustering algorithm based on cloud model. Knowl.-Based Syst. 2023, 263, 110261. [Google Scholar] [CrossRef]
- Zhan, Z.; Xu, W.; Xu, L.; Qi, X.; Song, W.; Wang, C.; Huang, Z. BIM-based green hospital building performance pre-evaluation: A case study. Sustainability 2022, 14, 2066. [Google Scholar] [CrossRef]
- Wang, Z.; Han, F.; Li, C.; Shen, W.; Yang, Z.; Li, K.; Yao, Q. Analysis of vertical differentiation of vegetation in taishan world heritage site based on cloud model. Sci. Rep. 2024, 14, 10948. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, P.; Gupta, A.; Malhotra, T. A novel cloud model based on multiplicative unbalanced linguistic term set. Extremes 2023, 26, 16378–16408. [Google Scholar] [CrossRef]
- Kim, H.; Sim, S.H.; Spencer, B.F. Automated concrete crack evaluation using stereo vision with two different focal lengths. Autom. Constr. 2022, 135, 104136. [Google Scholar] [CrossRef]
- Cheng, W.; Fan, Z.; Tan, K.H. Characterisation of corrosion-induced crack in concrete using ultrasonic diffuse coda wave. Ultrasonics 2023, 128, 106883. [Google Scholar] [CrossRef]
- Singh, P.; Ojha, P.N.; Singh, S.A. Crack detection and crack segmentation in concrete beams undergoing mode I fracture using computer vision and convolutional neural network. Can. J. Civ. Eng. 2023, 50, 432–443. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, H.; Eastwood, J.; Qi, X.; Jia, J.; Cao, Y. Concrete crack detection using lightweight attention feature fusion single shot multibox detector. Knowl.-Based Syst. 2023, 261, 110216. [Google Scholar] [CrossRef]
- SL677-2014; Specifications for Hydraulic Concrete Construction. Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2014.
- GB 55008-2021; General Code for Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2021.
- Yang, D. Treatment technology and practice of cracks on slab concrete of soft rock face rockfill dam. Yunnan Water Power 2022, 38, 185–191. [Google Scholar]




| Element Values | Judging Standard |
|---|---|
| e0/5 | Xi is as equally important as Xj |
| e2/5 | Xi is slightly more important than Xj |
| e4/5 | Xi is significantly more important than Xj |
| e6/5 | Xi is strongly more important than Xj |
| e8/5 | Xi is absolutely more important than Xj |
| e1/5, e3/5, e5/5, e7/5 | Between the above two neighboring judgments |
| multiplicative inverse | Importance of Xj compared to Xi |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 1.49 |
| Evaluation Level | Score | Significance | Ex | En | He |
|---|---|---|---|---|---|
| Safe (I) | 95~100 | Essentially harmless | 97.5 | 2.12 | 0.21 |
| Relatively Safe (II) | 80~95 | Slightly affects structural performance | 87.5 | 6.37 | 0.64 |
| Moderate (III) | 60~80 | Significantly affects structural performance | 70.0 | 8.49 | 0.85 |
| Relatively Hazardous (IV) | 30~60 | Seriously affects structural performance | 47.5 | 10.62 | 1.06 |
| Hazardous (V) | 0~30 | Fatally affects structural performance | 15.0 | 12.74 | 1.27 |
| Dimension Level | Weight | Presentation Layer | Weight | ||||
|---|---|---|---|---|---|---|---|
| Subjective | Objective | Combined | Subjective | Objective | Combined | ||
| A | 0.261 | 0.279 | 0.273 | A1 | 0.266 | 0.234 | 0.253 |
| A2 | 0.195 | 0.201 | 0.197 | ||||
| A3 | 0.102 | 0.163 | 0.127 | ||||
| A4 | 0.279 | 0.193 | 0.244 | ||||
| A5 | 0.158 | 0.209 | 0.179 | ||||
| B | 0.258 | 0.267 | 0.264 | B1 | 0.277 | 0.213 | 0.251 |
| B2 | 0.235 | 0.215 | 0.227 | ||||
| B3 | 0.176 | 0.236 | 0.201 | ||||
| B4 | 0.122 | 0.139 | 0.129 | ||||
| B5 | 0.103 | 0.104 | 0.103 | ||||
| B6 | 0.087 | 0.093 | 0.089 | ||||
| C | 0.248 | 0.228 | 0.225 | C1 | 0.232 | 0.257 | 0.242 |
| C2 | 0.208 | 0.235 | 0.219 | ||||
| C3 | 0.258 | 0.231 | 0.247 | ||||
| C4 | 0.302 | 0.277 | 0.292 | ||||
| D | 0.233 | 0.226 | 0.238 | D1 | 0.248 | 0.096 | 0.186 |
| D2 | 0.078 | 0.154 | 0.109 | ||||
| D3 | 0.282 | 0.268 | 0.276 | ||||
| D4 | 0.261 | 0.257 | 0.259 | ||||
| D5 | 0.131 | 0.226 | 0.170 | ||||
| Factors | I | II | III | IV | V | Results | θ |
|---|---|---|---|---|---|---|---|
| B1 | 0.235 | 0.344 | 0.126 | 0.189 | 0.106 | II | 0.0063 |
| B2 | 0.212 | 0.266 | 0.287 | 0.114 | 0.121 | III | 0.0055 |
| B3 | 0.295 | 0.337 | 0.178 | 0.136 | 0.054 | II | 0.0032 |
| B4 | 0.206 | 0.243 | 0.241 | 0.124 | 0.186 | II | 0.0028 |
| B5 | 0.204 | 0.172 | 0.268 | 0.253 | 0.103 | III | 0.0069 |
| B6 | 0.251 | 0.205 | 0.183 | 0.218 | 0.143 | I | 0.0074 |
| A | 0.256 | 0.279 | 0.247 | 0.102 | 0.116 | II | 0.0066 |
| B | 0.236 | 0.282 | 0.208 | 0.162 | 0.112 | II | 0.0059 |
| C | 0.114 | 0.253 | 0.333 | 0.172 | 0.128 | III | 0.0042 |
| D | 0.006 | 0.264 | 0.287 | 0.242 | 0.201 | III | 0.0061 |
| W | 0.151 | 0.270 | 0.274 | 0.167 | 0.138 | III | 0.0054 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Liu, L.; Zheng, M.; Wan, H.; Dong, Y.; Lu, G.; Xu, C. Comprehensive Evaluation of Crack Safety of Hydraulic Concrete Based on Improved Combination Weighted-Extension Cloud Theory. Water 2024, 16, 2031. https://doi.org/10.3390/w16142031
Cheng Y, Liu L, Zheng M, Wan H, Dong Y, Lu G, Xu C. Comprehensive Evaluation of Crack Safety of Hydraulic Concrete Based on Improved Combination Weighted-Extension Cloud Theory. Water. 2024; 16(14):2031. https://doi.org/10.3390/w16142031
Chicago/Turabian StyleCheng, Yu, Lizhen Liu, Maohai Zheng, Hai Wan, Yanpeng Dong, Guangxu Lu, and Cundong Xu. 2024. "Comprehensive Evaluation of Crack Safety of Hydraulic Concrete Based on Improved Combination Weighted-Extension Cloud Theory" Water 16, no. 14: 2031. https://doi.org/10.3390/w16142031
APA StyleCheng, Y., Liu, L., Zheng, M., Wan, H., Dong, Y., Lu, G., & Xu, C. (2024). Comprehensive Evaluation of Crack Safety of Hydraulic Concrete Based on Improved Combination Weighted-Extension Cloud Theory. Water, 16(14), 2031. https://doi.org/10.3390/w16142031





