Overflow Simulation and Optimization of a Drainage System in an Urban Area in the Northern Anhui Plain
Abstract
1. Introduction
2. Study Area and Methods
2.1. Overview of the Study Area
2.2. Data Collection
2.2.1. Rainfall Data
2.2.2. Drainage Network Data
2.2.3. Sub-Catchment Data
2.3. Model Construction
2.3.1. Hydrological and Hydraulic Model Parameter Setting
- (1)
- Manning Coefficient
- (2)
- Parameters of Infiltration Model
- (3)
- Depression Storage Capacity
- (4)
- Comprehensive Runoff Coefficient
2.3.2. Parameter Sensitivity Analyses
- (1)
- Rainfall Data Selection
- (2)
- Selection of Model Parameters and Change Steps
- (3)
- Evaluation Index Selection
- (1)
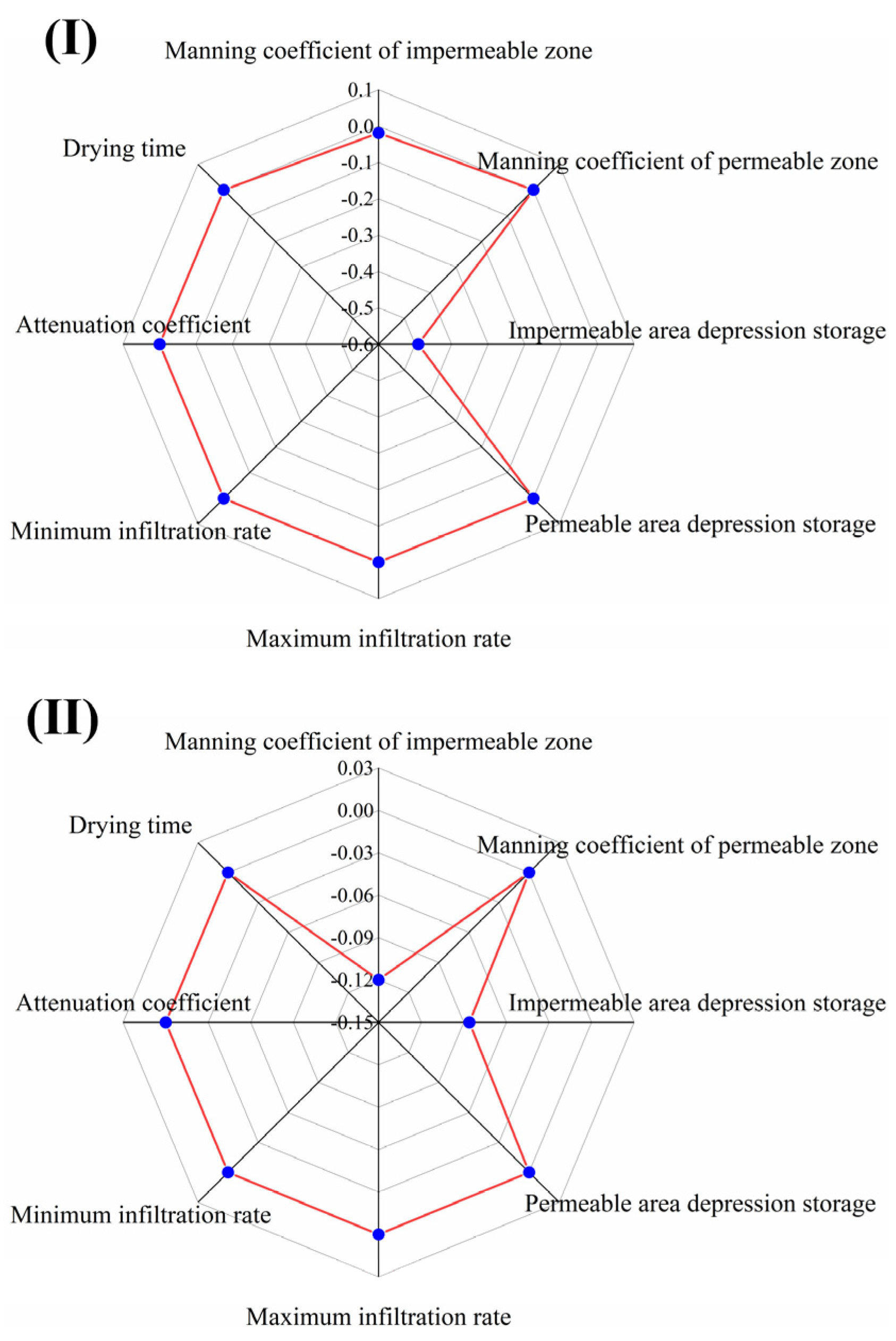
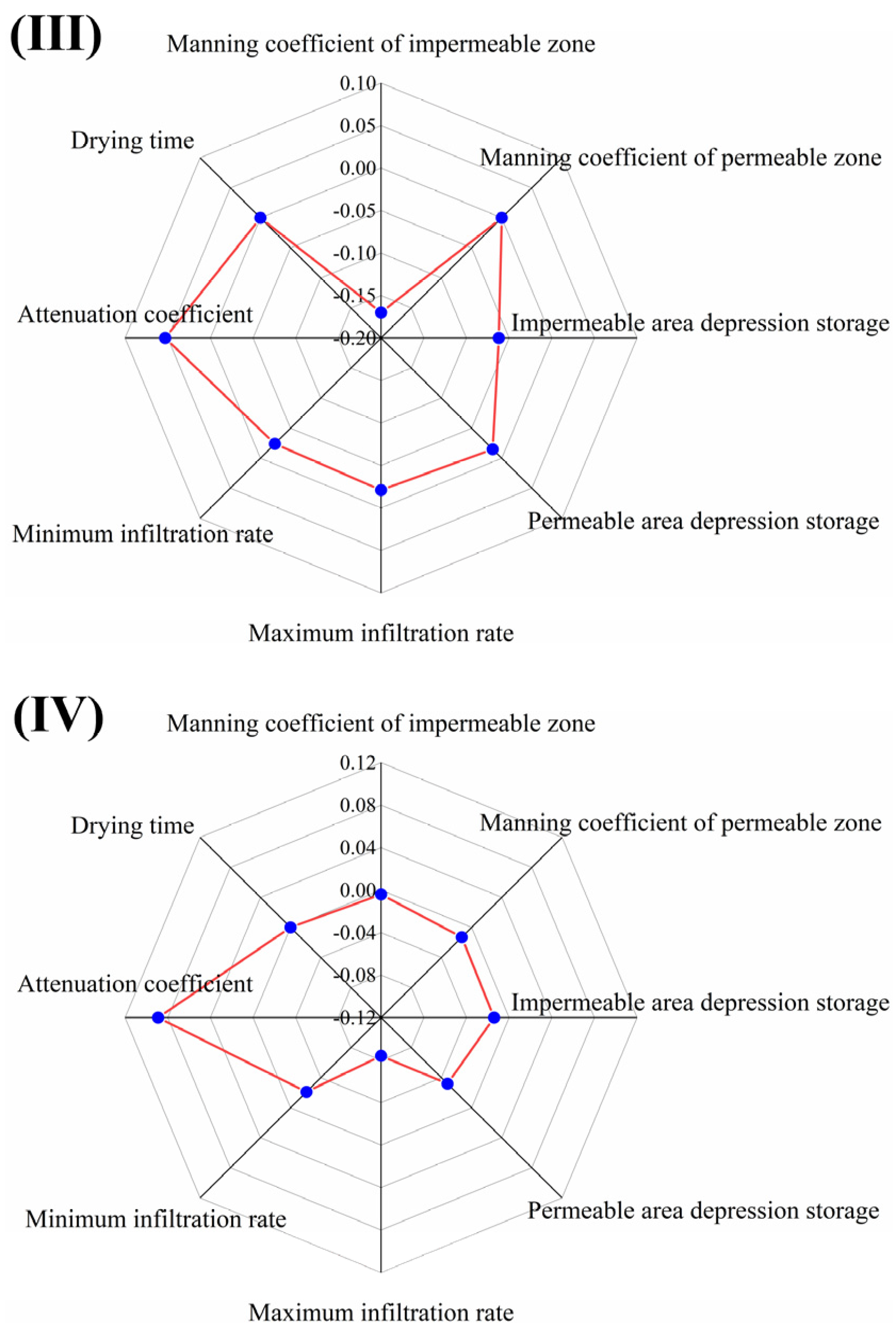
- Sensitivity Analysis of Each Parameter to the Total Runoff under Different Rainfall Conditions
- (2)
- Sensitivity Analysis of Each Parameter for Peak Runoff under Different Rainfall Conditions
2.3.3. Modelling Rates
3. Results and Discussion
3.1. Surface Runoff Simulation Analysis
3.2. Pipeline Operation Simulation Analysis
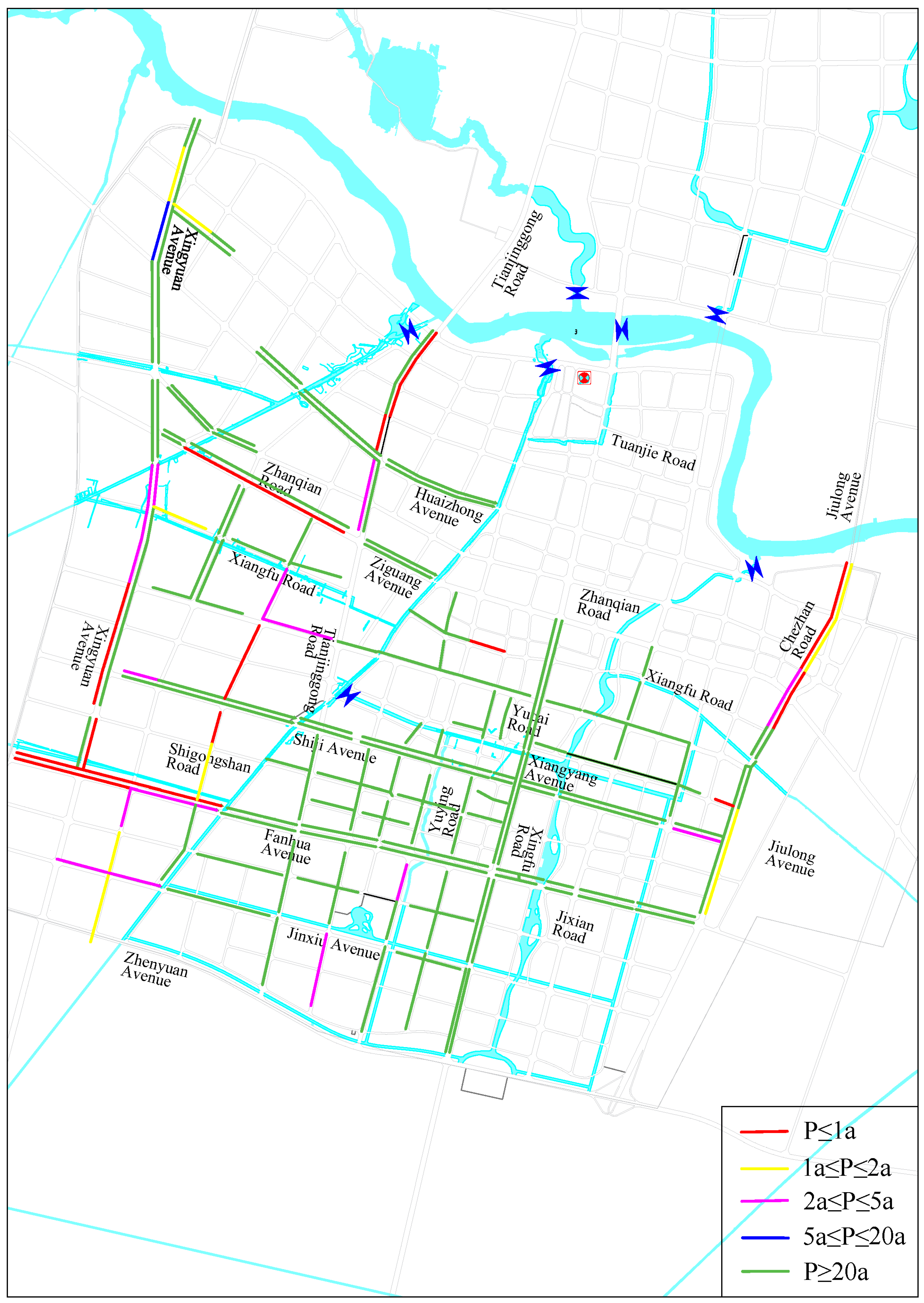
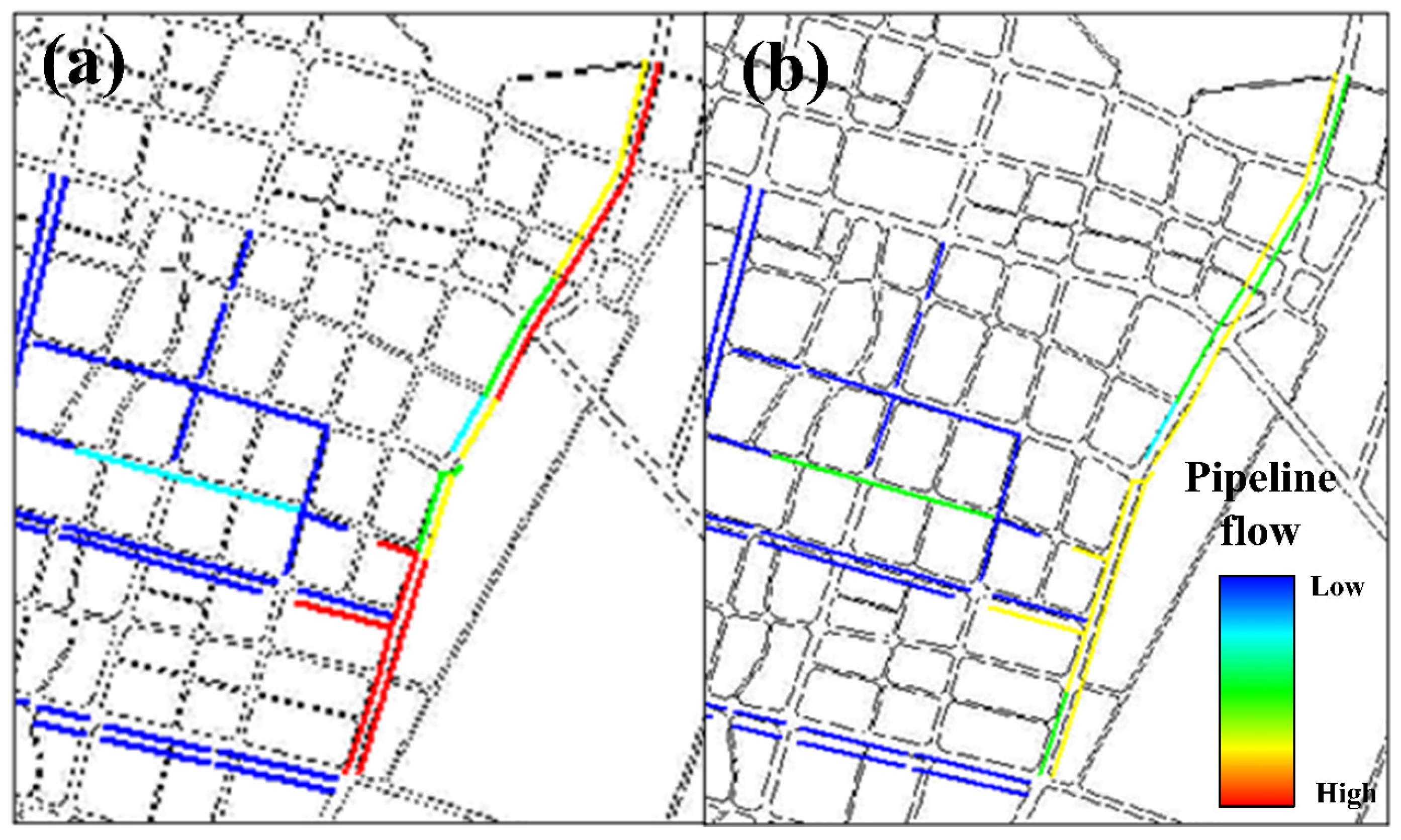
3.2.1. Analysis of Overloading of Pipe Sections
3.2.2. Location Analysis of Overloaded Pipe Sections
3.2.3. Analysis of Pipe Section Operation Dynamics
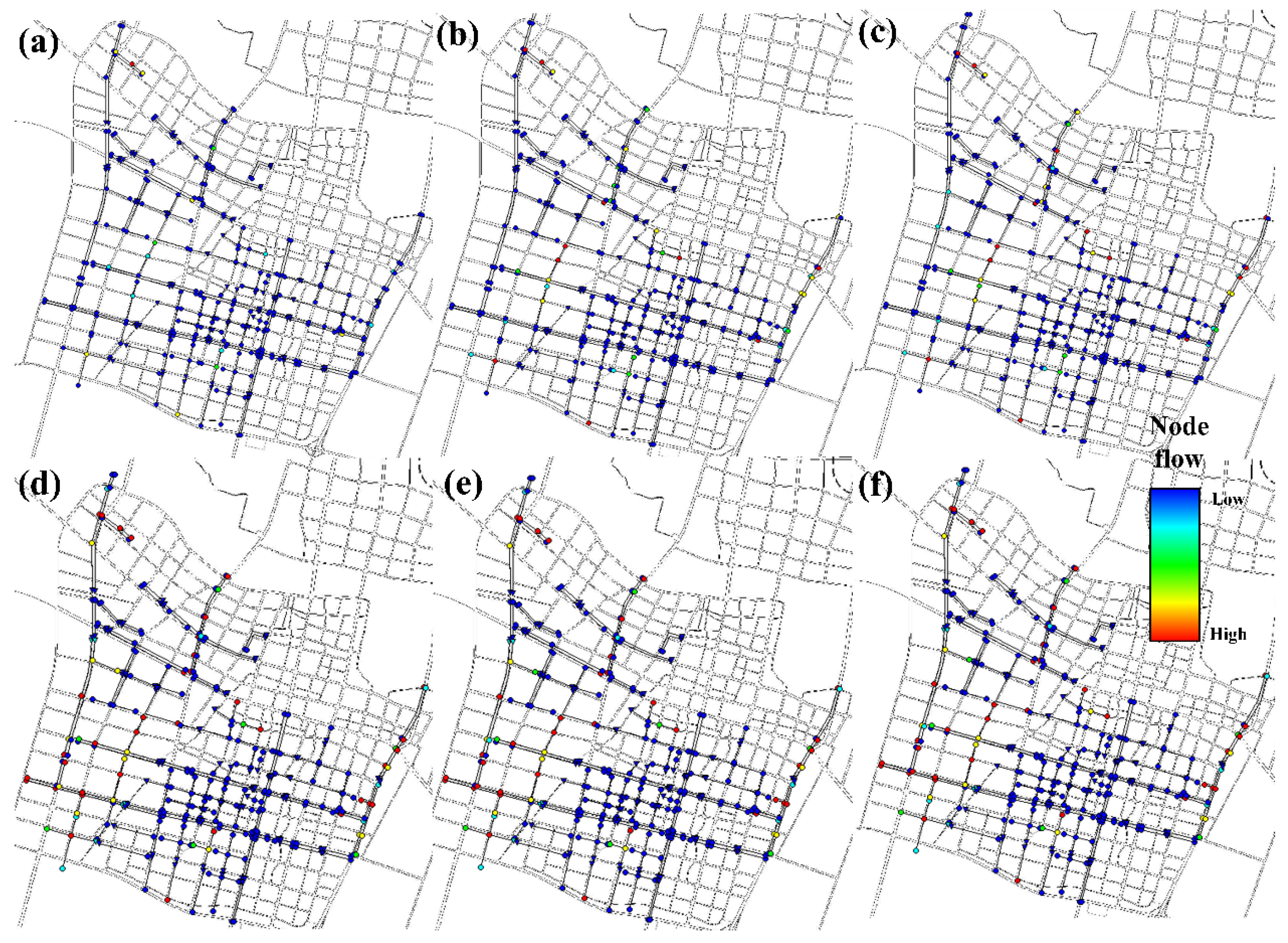
3.3. Node Overload Analysis
3.3.1. Analysis of Node Overloading and Overflow
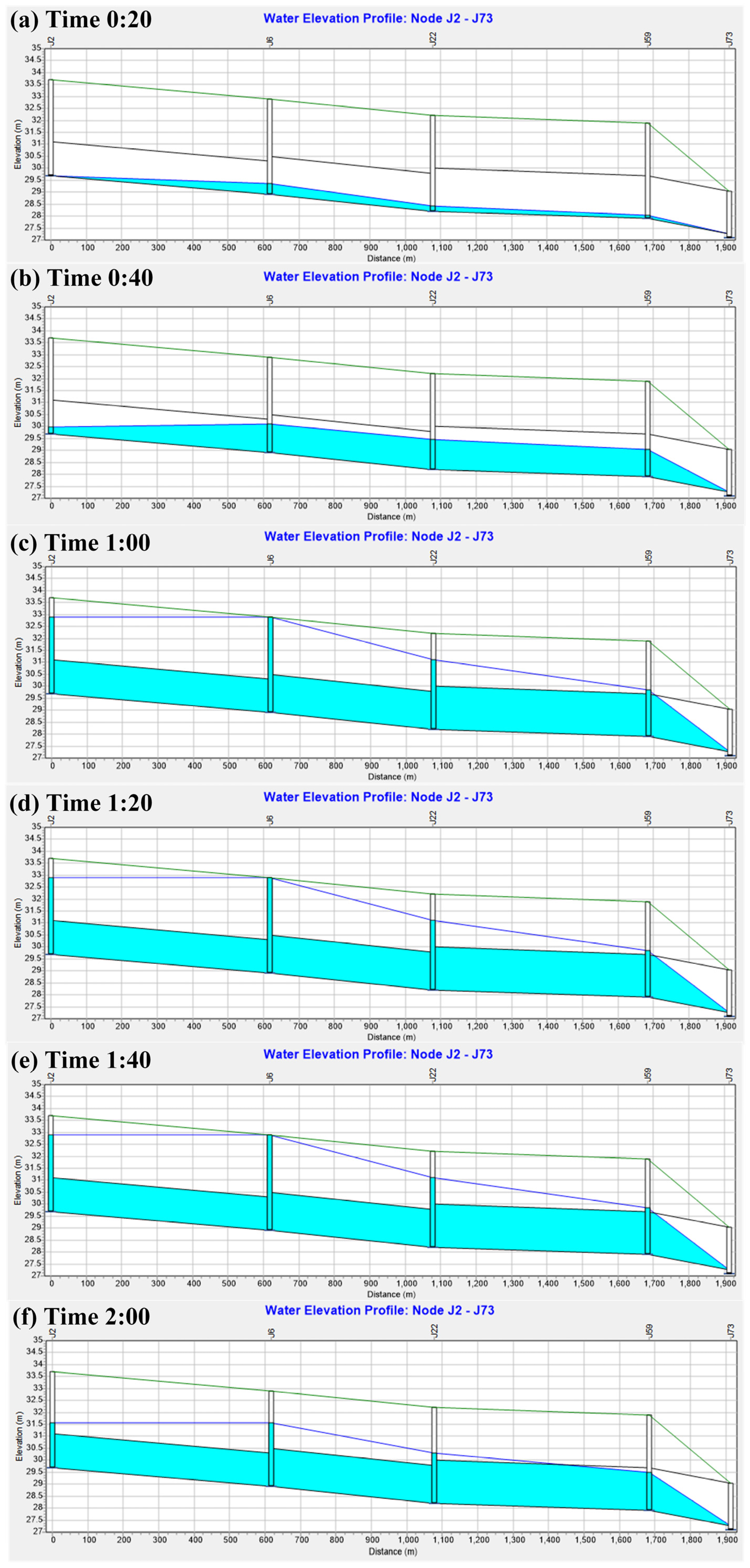
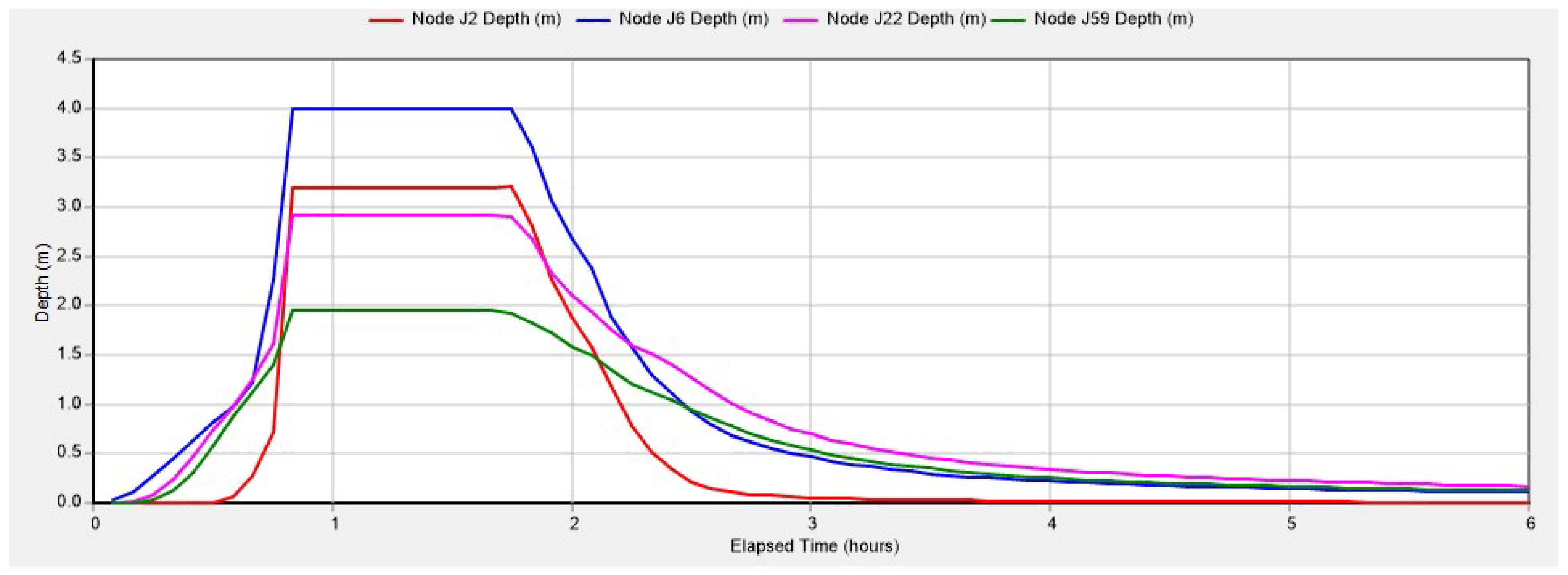
3.3.2. Dynamic Analysis of Water Level at Typical Nodes
3.4. Pipe Network System Optimization
3.4.1. Nodal Overflow Control
3.4.2. Pipeline Optimization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hou, J.; Mao, H.; Li, J.; Sun, S. Spatial simulation of the ecological processes of stormwater for sponge cities. J. Environ. Manag. 2019, 232, 574–583. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Mei, C.; Wang, H.; Lu, J. A multi-objective optimization model for synergistic effect analysis of integrated green-gray-blue drainage system in urban inundation control. J. Hydrol. 2022, 609, 127725. [Google Scholar] [CrossRef]
- Dhakal, K.P.; Chevalier, L.R. Urban stormwater governance: The need for a paradigm shift. Environ. Manag. 2016, 57, 1112–1124. [Google Scholar] [CrossRef]
- Arya, S.; Kumar, A. Evaluation of stormwater management approaches and challenges in urban flood control. Urban Clim. 2023, 51, 101643. [Google Scholar] [CrossRef]
- Dong, B.; Xia, J.; Li, Q.; Zhou, M. Risk assessment for people and vehicles in an extreme urban flood: Case study of the “7.20” flood event in Zhengzhou, China. Int. J. Disaster Risk Reduct. 2022, 80, 103205. [Google Scholar] [CrossRef]
- Liu, W.; Chen, W.; Feng, Q.; Peng, C.; Kang, P. Cost-benefit analysis of green infrastructures on community stormwater reduction and utilization: A case of Beijing, China. Environ. Manag. 2016, 58, 1015–1026. [Google Scholar] [CrossRef]
- Saadatpour, M.; Delkhosh, F.; Afshar, A.; Solis, S.S. Developing a simulation-optimization approach to allocate low impact development practices for managing hydrological alterations in urban watershed. Sustain. Cities Soc. 2020, 61, 102334. [Google Scholar] [CrossRef]
- Taji, S.G.; Regulwar, D.G. LID coupled design of drainage model using GIS and SWMM. ISH J. Hydraul. Eng. 2021, 27 (Suppl. 1), 376–389. [Google Scholar] [CrossRef]
- Habibi, H.; Seo, D.J. Simple and modular integrated modeling of storm drain network with gridded distributed hydrologic model via grid-rendering of storm drains for large urban areas. J. Hydrol. 2018, 567, 637–653. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.; Kim, J.; Jun, S.M.; Hwang, S.; Song, J.H.; Kang, M.S. Analysis of the effects of low impact development practices on hydrological components using HSPF. J. Hydro-Environ. Res. 2023, 46, 72–85. [Google Scholar] [CrossRef]
- Sidek, L.M.; Jaafar, A.S.; Majid WHA, W.A.; Basri, H.; Marufuzzaman, M.; Fared, M.M.; Moon, W.C. High-resolution hydrological-hydraulic modeling of urban floods using InfoWorks ICM. Sustainability 2021, 13, 10259. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Xu, J.; Pan, G.; Zhao, Y.; Liu, Y.; Liu, J. Accumulated impacts of imperviousness on surface and subsurface hydrology—Continuous modelling at urban street block scale. J. Hydrol. 2022, 608, 127621. [Google Scholar] [CrossRef]
- Barclay, N.; Klotz, L. Role of community participation for green stormwater infrastructure development. J. Environ. Manag. 2019, 251, 109620. [Google Scholar] [CrossRef] [PubMed]
- Azari, B.; Tabesh, M. Urban storm water drainage system optimization using a sustainability index and LID/BMPs. Sustain. Cities Soc. 2022, 76, 103500. [Google Scholar] [CrossRef]
- Feng, W.; Wang, C.; Lei, X.; Wang, H. A simplified modeling approach for optimization of urban river systems. J. Hydrol. 2023, 623, 129689. [Google Scholar] [CrossRef]
- Buisan, Z.A.; Milano, A.E.; Suson, P.D.; Mostrales, D.S.; Taclendo, C.S.; Blasco, J.G. The impact of sound land use management to reduce runoff. Glob. J. Environ. Sci. Manag. 2019, 5, 399–414. [Google Scholar]
- Lin, J.; He, P.; Yang, L.; He, X.; Lu, S.; Liu, D. Predicting future urban waterlogging-prone areas by coupling the maximum entropy and FLUS model. Sustain. Cities Soc. 2022, 80, 103812. [Google Scholar] [CrossRef]
- Kapoor, A.; Pathiraja, S.; Marshall, L.; Chandra, R. DeepGR4J: A deep learning hybridization approach for conceptual rainfall-runoff modelling. Environ. Model. Softw. 2023, 169, 105831. [Google Scholar] [CrossRef]
- Niyazi, B.A.; Masoud, M.H.; Ahmed, M.; Basahi, J.M.; Rashed, M.A. Runoff assessment and modeling in arid regions by integration of watershed and hydrologic models with GIS techniques. J. Afr. Earth Sci. 2020, 172, 103966. [Google Scholar] [CrossRef]
- Babaei, S.; Ghazavi, R.; Erfanian, M. Urban flood simulation and prioritization of critical urban sub-catchments using SWMM model and PROMETHEE II approach. Phys. Chem. Earth Parts A/B/C 2018, 105, 3–11. [Google Scholar] [CrossRef]
- Paleari, L.; Movedi, E.; Zoli, M.; Burato, A.; Cecconi, I.; Errahouly, J.; Confalonieri, R. Sensitivity analysis using Morris: Just screening or an effective ranking method? Ecol. Model. 2021, 455, 109648. [Google Scholar] [CrossRef]
- Sang, G.Q.; Cao, S.L.; Wei, Z.B. Research and Application of the Combined of SWMM and Tank Model. Appl. Mech. Mater. 2012, 166, 593–599. [Google Scholar] [CrossRef]
- Tang, S.; Yan, X.; Jiang, J.; Zheng, Y.; Yang, Y.; Xu, P.; Shang, F. Catchment-scale life cycle impacts of green infrastructures and sensitivity to runoff coefficient with stormwater modelling. Sci. Total Environ. 2023, 904, 166736. [Google Scholar] [CrossRef] [PubMed]
- Akdoğan, Z.; Güven, B. Assessing the sensitivity of SWMM to variations in hydrological and hydraulic parameters: A case study for the city of Istanbul. Glob. Nest J. 2016, 18, 831–841. [Google Scholar] [CrossRef]
- Wu, X.; Huang, X. Screening of urban environmental vulnerability indicators based on coefficient of variation and anti-image correlation matrix method. Ecol. Indic. 2023, 150, 110196. [Google Scholar] [CrossRef]
- Peng, Z.; Lin, X.; Simon, M.; Niu, N. Unit and regression tests of scientific software: A study on SWMM. J. Comput. Sci. 2021, 53, 101347. [Google Scholar] [CrossRef] [PubMed]
- Hsu, M.H.; Chen, S.H.; Chang, T.J. Inundation simulation for urban drainage basin with storm sewer system. J. Hydrol. 2000, 234, 21–37. [Google Scholar] [CrossRef]
- Ju, X.; Li, W.; Li, J.; He, L.; Mao, J.; Han, L. Future climate change and urban growth together affect surface runoff in a large-scale urban agglomeration. Sustain. Cities Soc. 2023, 99, 104970. [Google Scholar] [CrossRef]
- Wang, R.; Wu, H.; Chiles, R. Ecosystem benefits provision of green stormwater infrastructure in Chinese sponge cities. Environ. Manag. 2022, 69, 558–575. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Ma, B.; Wu, Z.; Hu, C.; Wang, H.; Xu, H.; Yan, D. Process-oriented SWMM real-time correction and urban flood dynamic simulation. J. Hydrol. 2022, 605, 127269. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Y.; Wang, C. A SWMM-Based Screening Model for Estimating Wastewater Treatment Burden of Pesticides on the Urban Scale. Environ. Manag. 2023, 71, 785–794. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Li, Q.; He, P.; Du, Y.; Zou, Z.; Xu, S.; Zeng, T. Impacts of rainstorm characteristics on flood inundation mitigation performance of LID measures throughout an urban catchment. J. Hydrol. 2023, 624, 129841. [Google Scholar] [CrossRef]
- Gao, Y.; Church, S.P.; Peel, S.; Prokopy, L.S. Public perception towards river and water conservation practices: Opportunities for implementing urban stormwater management practices. J. Environ. Manag. 2018, 223, 478–488. [Google Scholar] [CrossRef] [PubMed]
- Chan, F.K.S.; Griffiths, J.A.; Higgitt, D.; Xu, S.; Zhu, F.; Tang, Y.T.; Thorne, C.R. “Sponge City” in China—A breakthrough of planning and flood risk management in the urban context. Land Use Policy 2018, 76, 772–778. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, Z.; Chen, X.; He, P. Approach for evaluating inundation risks in urban drainage systems. Sci. Total Environ. 2016, 553, 1–12. [Google Scholar] [CrossRef]





| Rainfall Time | Rainfall (mm) | Maximum Rainfall Intensity (mm/h) | Average Rainfall Intensity (mm/h) | Rainfall Type |
|---|---|---|---|---|
| 13 June 2022 | 18.2 | 5.9 | 1.82 | Moderate rain |
| 23 June 2022 | 31.6 | 16.8 | 3.16 | Heavy rain |
| 20 July 2022 | 63.2 | 32.7 | 5.74 | Rainstorm |
| 27 August 2022 | 7.3 | 2.7 | 0.52 | Light rain |
| Recurrence Period/a | 120 min Total Cumulative Rainfall (mm) | 120 min Average Rainfall Intensity (mm/min) |
|---|---|---|
| P = 0.5 | 41.6299 | 0.344 |
| P = 1 | 53.5406 | 0.4425 |
| P = 2 | 65.4513 | 0.5409 |
| P = 5 | 81.1965 | 0.671 |
| P = 10 | 93.1072 | 0.7695 |
| P = 20 | 105.0179 | 0.8679 |
| Manning Coefficient | ||
|---|---|---|
| Manning coefficient of permeable zone | Manning coefficient of impermeable zone | Manning coefficient of pipes |
| 0.24 | 0.012 | 0.013 |
| Parameter | Value Range | Preliminary Value |
|---|---|---|
| Maximum infiltration rate (mm/h) | 20–120 | 79 |
| Minimum infiltration rate (mm/h) | 0–20 | 2.5 |
| Attenuation factor (h−1) | 1–7 | 2 |
| Drainage time (d) | 2–14 | 6 |
| Lower Cushion Surface | Area/km2 | Total Area/km2 | Proportion of Total Area | Runoff Coefficient | Comprehensive Runoff Coefficient |
|---|---|---|---|---|---|
| Greenbelt | 17.56 | 46.69 | 37.60% | 0.1 | 0.599 |
| Roofing | 22.73 | 48.68% | 0.9 | ||
| Pavement | 6.4 | 13.71% | 0.9 |
| Parameter Name | Initialization Value | Parameter Debugging Value | |||||
|---|---|---|---|---|---|---|---|
| −30% | −20% | −10% | 10% | 20% | 30% | ||
| Manning coefficient of permeable zone | 0.24 | 0.168 | 0.192 | 0.216 | 0.264 | 0.288 | 0.312 |
| Manning coefficient of impermeable zone | 0.012 | 0.0084 | 0.0096 | 0.0108 | 0.0132 | 0.0144 | 0.0156 |
| Maximum infiltration rate (mm/h) | 78 | 54.6 | 62.4 | 70.2 | 85.8 | 93.6 | 101.4 |
| Minimum infiltration rate (mm/h) | 3 | 2.1 | 2.4 | 2.7 | 3.3 | 3.6 | 3.9 |
| Attenuation coefficient (h−1) | 4 | 2.8 | 3.2 | 3.6 | 4.4 | 4.8 | 5.2 |
| Drying time (d) | 6 | 4.2 | 4.8 | 5.4 | 6.6 | 7.2 | 7.8 |
| Permeable area depression storage (mm) | 5 | 3.5 | 4 | 4.5 | 5.5 | 6 | 6.5 |
| Impermeable area Depression storage (mm) | 3 | 2.1 | 2.4 | 2.7 | 3.3 | 3.6 | 3.9 |
| Parameter Name | Sensitivity Discriminant Factor S1 of Total Runoff | |||
|---|---|---|---|---|
| 27 August 2022 (Light Rain) | 13 June 2022 (Moderate Rain) | 23 June 2022 (Heavy Rain) | 20 July 2022 (Rainstorm) | |
| Manning coefficient of impermeable zone | −0.019 | −0.120 | −0.170 | −0.004 |
| Manning coefficient of permeable zone | 0.000 | 0.000 | 0.000 | −0.013 |
| Impermeable area depression storage | −0.491 | −0.086 | −0.062 | −0.014 |
| Permeable area depression storage | 0.000 | 0.000 | −0.015 | −0.032 |
| Maximum infiltration rate | 0.000 | 0.000 | −0.021 | −0.084 |
| Minimum infiltration rate | 0.000 | 0.000 | −0.024 | −0.021 |
| Attenuation coefficient | 0.000 | 0.000 | 0.053 | 0.089 |
| Drying time | 0.000 | 0.000 | 0.000 | 0.000 |
| Parameter Name | Sensitivity Discriminant Factor S2 of Total Runoff | |||
|---|---|---|---|---|
| 27 August 2022 (Light Rain) | 13 June 2022 (Moderate Rain) | 23 June 2022 (Heavy Rain) | 20 July 2022 (Rainstorm) | |
| Manning coefficient of impermeable zone | 0.000 | −0.072 | −0.086 | −0.034 |
| Manning coefficient of permeable zone | 0.000 | 0.000 | −0.012 | −0.009 |
| Impermeable area depression storage | −0.354 | −0.287 | −0.030 | −0.000 |
| Permeable area depression storage | 0.000 | 0.000 | −0.003 | −0.046 |
| Maximum infiltration rate | 0.000 | 0.000 | 0.000 | −0.015 |
| Minimum infiltration rate | 0.000 | 0.000 | 0.000 | 0.000 |
| Attenuation coefficient | 0.000 | 0.000 | 0.012 | 0.072 |
| Drying time | 0.000 | 0.000 | 0.000 | 0.000 |
| Parameter Name | Initialization Value | The First Group | The Second Group | The Third Group | The Fourth Group | The Fifth Group | The Sixth Group |
|---|---|---|---|---|---|---|---|
| Manning coefficient of permeable zone | 0.24 | 0.23 | 0.22 | 0.22 | 0.21 | 0.2 | 0.2 |
| Manning coefficient of impermeable zone | 0.021 | 0.015 | 0.016 | 0.017 | 0.018 | 0.019 | 0.02 |
| Maximum infiltration rate (mm/h) | 79 | 79.5 | 80 | 80.5 | 81 | 81.5 | 82 |
| Minimum infiltration rate (mm/h) | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 3 | 3 |
| Attenuation coefficient (h−1) | 2 | 2 | 1.9 | 1.8 | 1.7 | 1.6 | 1.5 |
| Drying time (d) | 6 | 6 | 6 | 6 | 7 | 7 | 7 |
| Permeable area depression storage (mm) | 6 | 6.5 | 6.4 | 6.3 | 6.2 | 6.1 | 6.1 |
| Impermeable area Depression storage (mm) | 2.5 | 2.4 | 2.3 | 2.1 | 1.9 | 1.7 | 1.5 |
| Runoff coefficient | 0.645 | 0.643 | 0.633 | 0.624 | 0.615 | 0.607 | 0.599 |
| Comprehensive runoff coefficient | 0.599 | ||||||
| Recurrence Period (a) | Rainfall (mm) | Surface Runoff (mm) | Runoff Coefficient | Comprehensive Runoff Coefficient | Variable Coefficient |
|---|---|---|---|---|---|
| P = 0.5 a | 41.074 | 23.451 | 0.561 | 0.599 | 6.55 |
| P = 1 a | 52.825 | 30.762 | 0.575 | 4.09 | |
| P = 5 a | 80.111 | 50.729 | 0.633 | 5.52 | |
| P = 10 a | 93.863 | 61.358 | 0.654 | 8.78 | |
| P = 20 a | 106.612 | 72.674 | 0.681 | 12.81 |
| Recurrence Period (a) | Total Rainfall (mm) | Infiltration Loss (mm) | Surface Water Storage (mm) | Amount of Evaporation Loss (mm) | Surface Runoff (mm) |
|---|---|---|---|---|---|
| P = 0.5 a | 41.074 | 16.891 | 0.732 | 0 | 23.451 |
| P = 1 a | 52.825 | 21.250 | 0.813 | 0 | 30.762 |
| P = 2 a | 64.575 | 25.080 | 0.929 | 0 | 38.690 |
| P = 5 a | 80.111 | 28.134 | 1.248 | 0 | 50.729 |
| P = 10 a | 93.863 | 30.782 | 1.723 | 0 | 61.358 |
| P = 20 a | 106.612 | 31.699 | 1.899 | 0 | 72.674 |
| Recurrence Period (a) | Number of Overloaded Pipe Segments | Percentage | Number of Pipes Exceeding 30 min Overload Duration |
|---|---|---|---|
| P = 0.5 a | 0 | 0% | 0 |
| P = 1 a | 9 | 4.0% | 2 |
| P = 2 a | 17 | 7.6% | 9 |
| P = 5 a | 33 | 14.7% | 12 |
| P = 10 a | 36 | 16.1% | 18 |
| P = 20 a | 37 | 16.5% | 22 |
| Recurrence Period (a) | Number of Overflow Well Points | Number of Overloaded Well Points | Percentage of Total Nodes (%) |
|---|---|---|---|
| P = 0.5 a | 1 | 6 | 1.6 |
| P = 1 a | 9 | 8 | 4.0 |
| P = 2 a | 14 | 9 | 5.4 |
| P = 5 a | 32 | 13 | 10.5 |
| P = 10 a | 36 | 11 | 11.0 |
| P = 20 a | 37 | 13 | 11.7 |
| Rainwater Well | Corresponding Sub-Catchment Area | Peak Flow Rate (m3/s) | Amount of Water Accumulated at the Node (m3) |
|---|---|---|---|
| J47 | S2 | 1.458 | 2248 |
| J64 | S1 | 1.667 | 1828 |
| J154 | S11 | 1.250 | 1946 |
| J174 | S9 | 1.375 | 2276 |
| J130 | S20 | 1.375 | 1936 |
| J90 | S26 | 1.208 | 1579 |
| J86 | S29 | 1.458 | 2098 |
| J15 | S83 | 1.375 | 1248 |
| J118 | S74 | 1.292 | 1731 |
| J263 | S84 | 1.542 | 2766 |
| J388 | S65 | 1.417 | 1601 |
| J426 | S25 | 1.250 | 1628 |
| J423 | S38 | 1.292 | 1925 |
| Sub-Catchment Area | Area (m2) | Adjusted Volume (m3) | Sunken Green Area (m2) | Proportion of Sunken Green Space (%) | Reduction Rate of Accumulated Water Volume (%) |
|---|---|---|---|---|---|
| S2 | 429,907 | 2248 | 11,240 | 2.61 | 54.95% |
| S1 | 898,016 | 1828 | 9140 | 1.02 | 57.06% |
| S11 | 337,127 | 1946 | 9730 | 2.88 | 56.53% |
| S9 | 978,140 | 2276 | 11,380 | 1.16 | 57.50% |
| S20 | 187,756 | 1936 | 9680 | 5.15 | 56.70% |
| S26 | 517,411 | 1579 | 7895 | 1.52 | 58.05% |
| S29 | 385,656 | 2098 | 10,490 | 2.72 | 55.88% |
| S83 | 706,477 | 1248 | 6240 | 0.88 | 56.45% |
| S74 | 896,597 | 1731 | 8655 | 0.96 | 57.43% |
| S84 | 536,058 | 2766 | 13,830 | 2.58 | 55.63% |
| S65 | 439,807 | 1601 | 8005 | 1.82 | 56.76% |
| S25 | 271,957 | 1628 | 8140 | 2.99 | 56.47% |
| S38 | 338,762 | 1925 | 9625 | 2.84 | 58.44% |
| Pipe Number | Optimized Front Pipe Diameter (m) | Optimized Rear Pipe Diameter (m) |
|---|---|---|
| 126 | 0.8 | 2.5 |
| 137 | 1.0 | 2.0 |
| 138 | 1.2 | 2.0 |
| 139 | 1.2 | 2.5 |
| 140 | 1.5 | 2.0 |
| 143 | 0.8 | 2.4 |
| 145 | 0.8 | 2.0 |
| 147 | 1.0 | 2.8 |
| 148 | 0.8 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, Y.; Li, M.; Zhang, N.; Li, Y.; Huang, P.; Zhang, H.; Huang, H.; Wei, W.; Zhu, S. Overflow Simulation and Optimization of a Drainage System in an Urban Area in the Northern Anhui Plain. Water 2024, 16, 1781. https://doi.org/10.3390/w16131781
Wan Y, Li M, Zhang N, Li Y, Huang P, Zhang H, Huang H, Wei W, Zhu S. Overflow Simulation and Optimization of a Drainage System in an Urban Area in the Northern Anhui Plain. Water. 2024; 16(13):1781. https://doi.org/10.3390/w16131781
Chicago/Turabian StyleWan, Yun, Mingjun Li, Nan Zhang, Yuxuan Li, Peiqing Huang, Houkuan Zhang, Hao Huang, Wei Wei, and Shuguang Zhu. 2024. "Overflow Simulation and Optimization of a Drainage System in an Urban Area in the Northern Anhui Plain" Water 16, no. 13: 1781. https://doi.org/10.3390/w16131781
APA StyleWan, Y., Li, M., Zhang, N., Li, Y., Huang, P., Zhang, H., Huang, H., Wei, W., & Zhu, S. (2024). Overflow Simulation and Optimization of a Drainage System in an Urban Area in the Northern Anhui Plain. Water, 16(13), 1781. https://doi.org/10.3390/w16131781






