Enhancing Hydrodynamic Performance of Floating Breakwaters Using Wing Plates
Abstract
1. Introduction
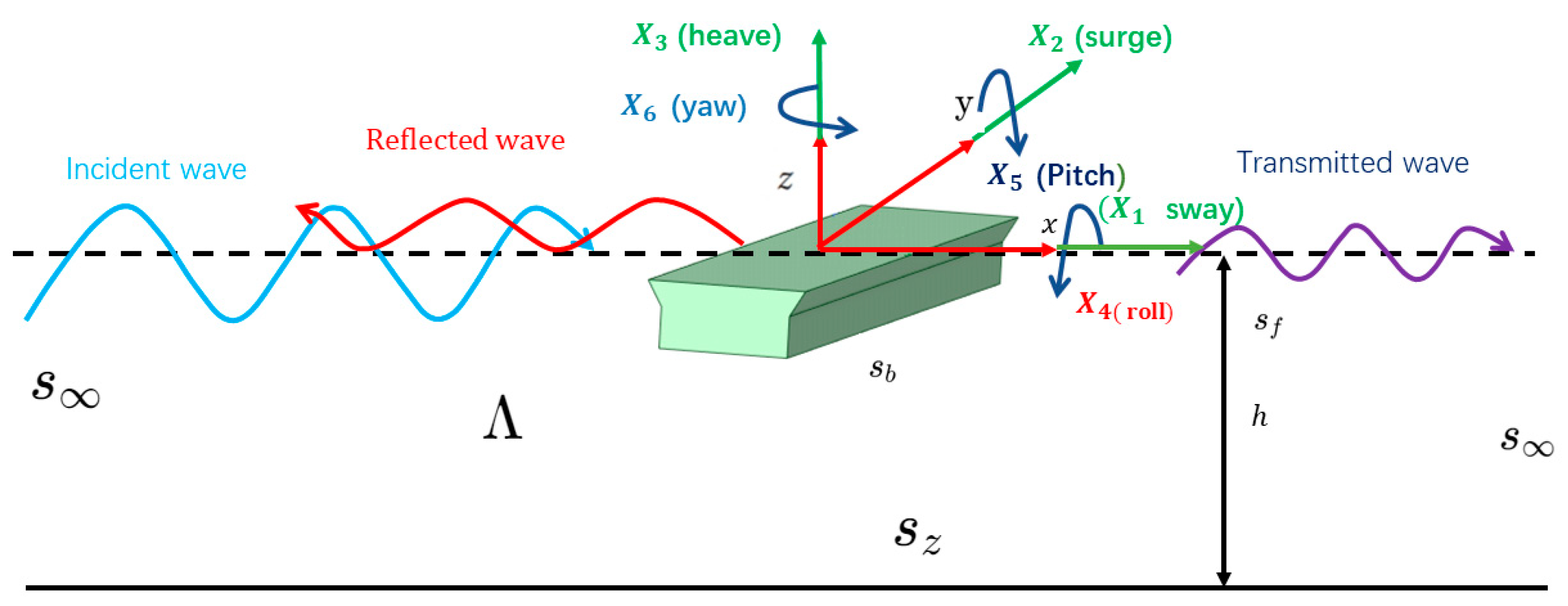
2. Theoretical Framework
2.1. Model Formulation
2.1.1. Governing Equations
- (i)
- The Laplace equation prevailing within the fluid domain [46]:
- (ii)
- Linear free surface () on z = 0:
- (iii)
- Body surface conditions ():
- (iv)
- Seabed surface condition () at z = −h:
- (v)
- For far-field conditions () where
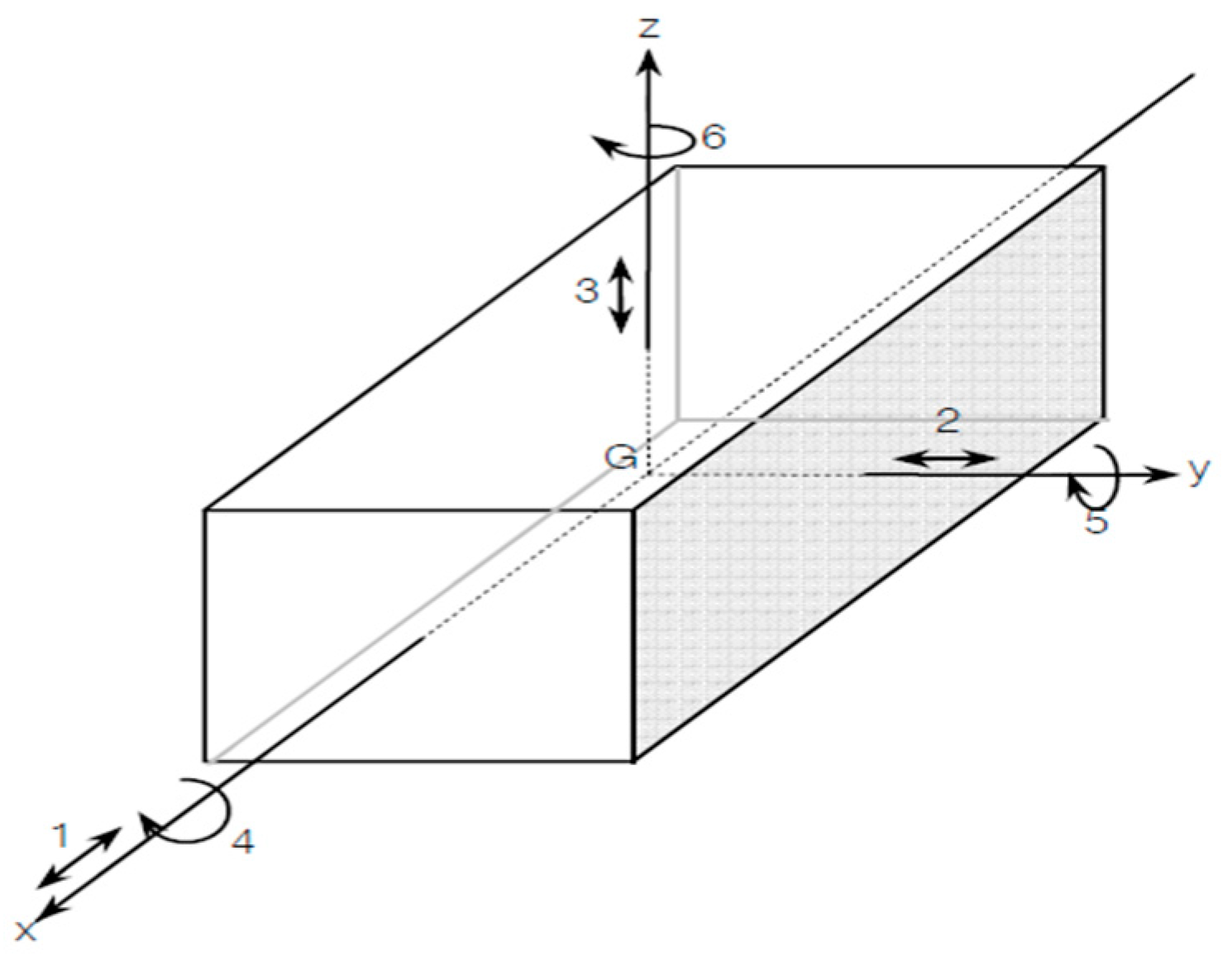
2.1.2. Equation of Motion and RAOs
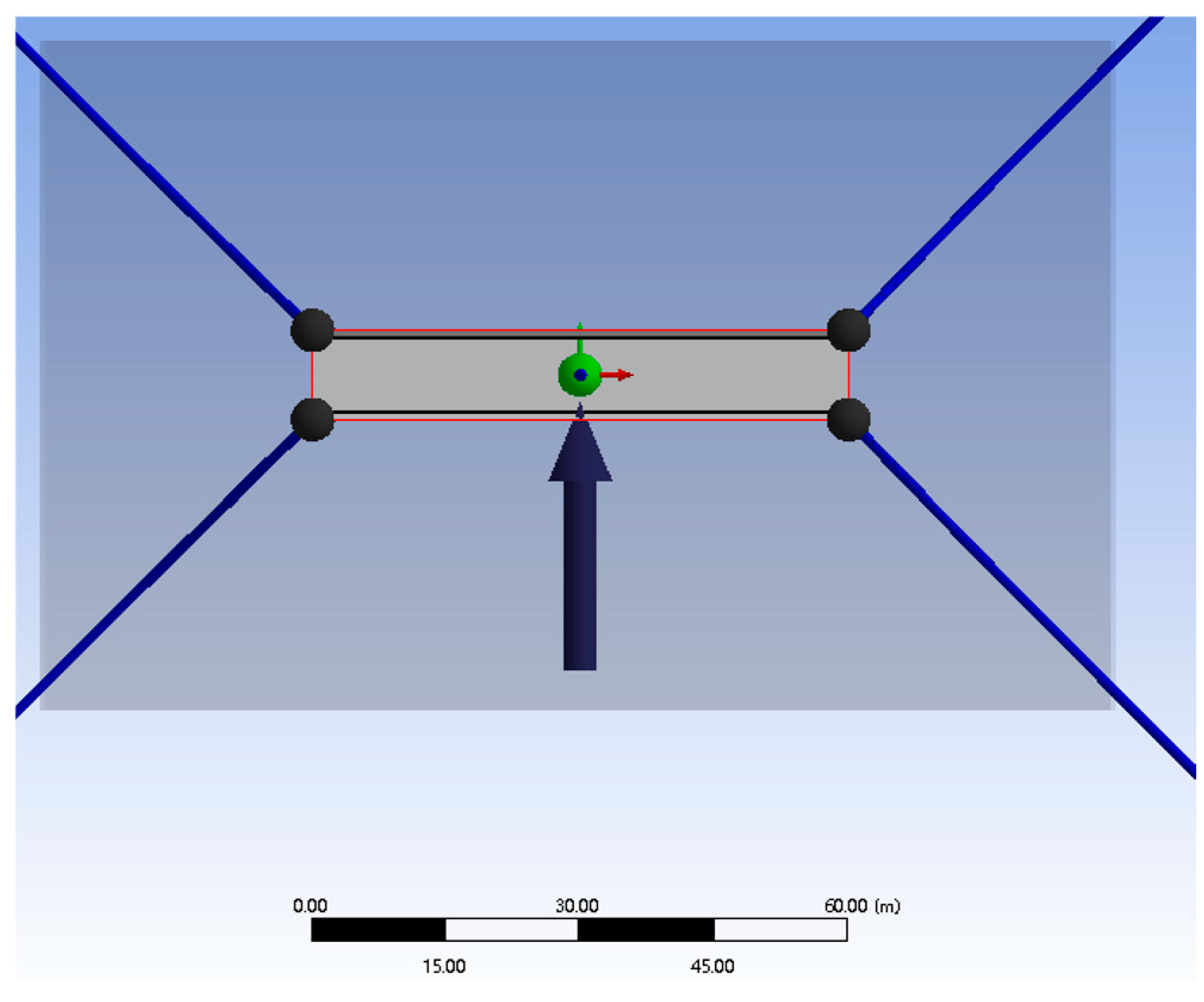
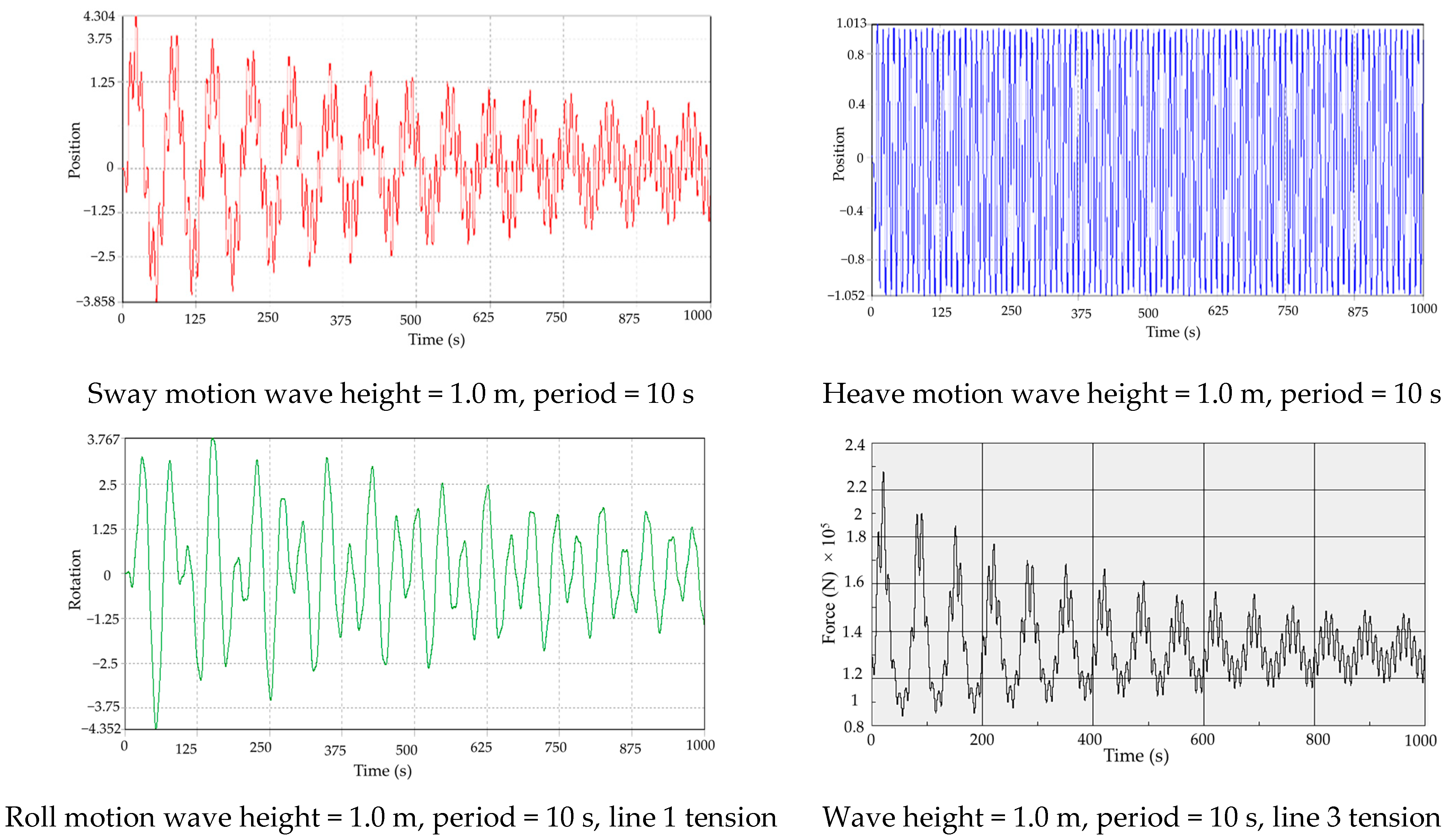
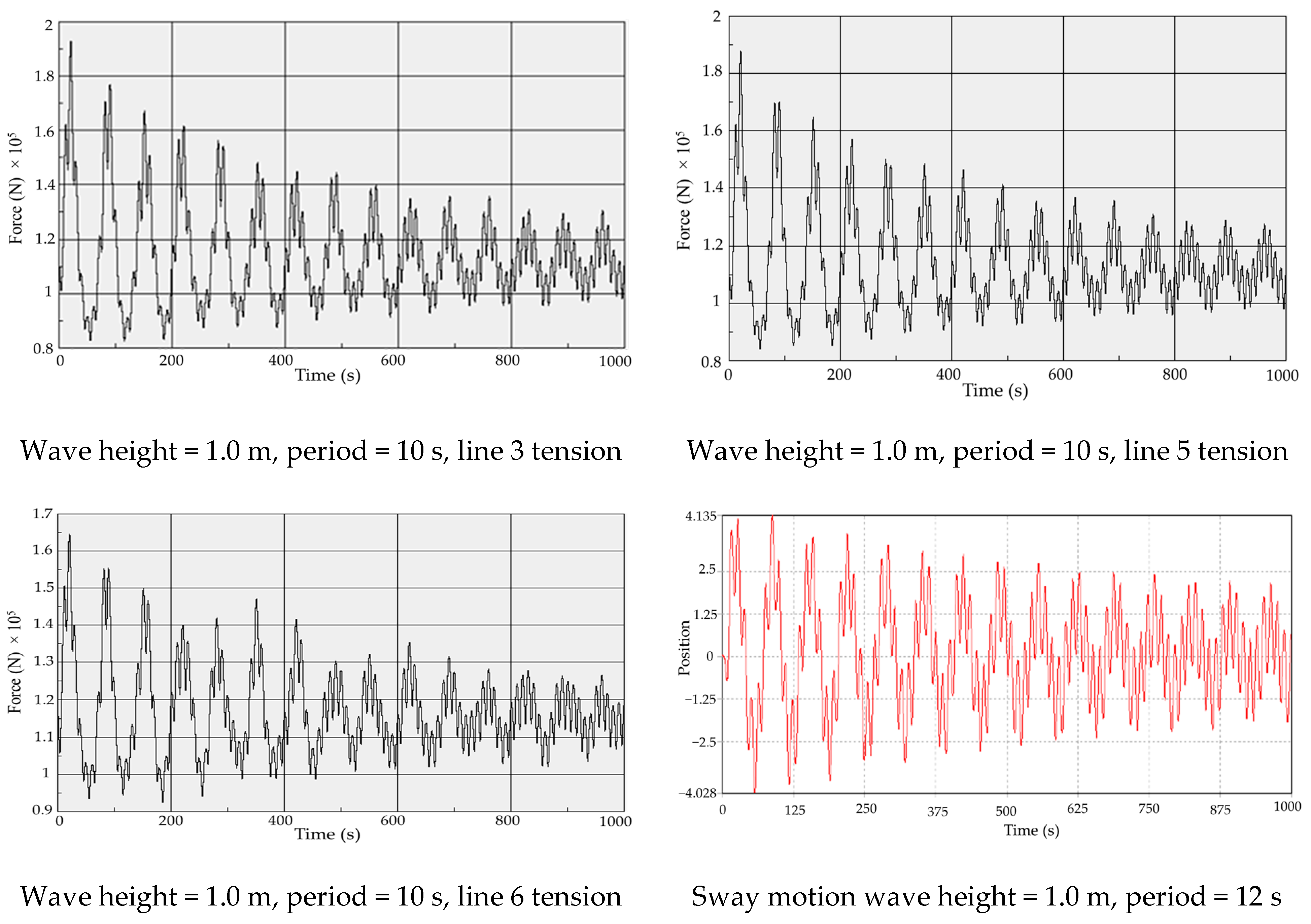
2.1.3. Mooring System
2.1.4. Wave Transmission and Reflection Coefficients
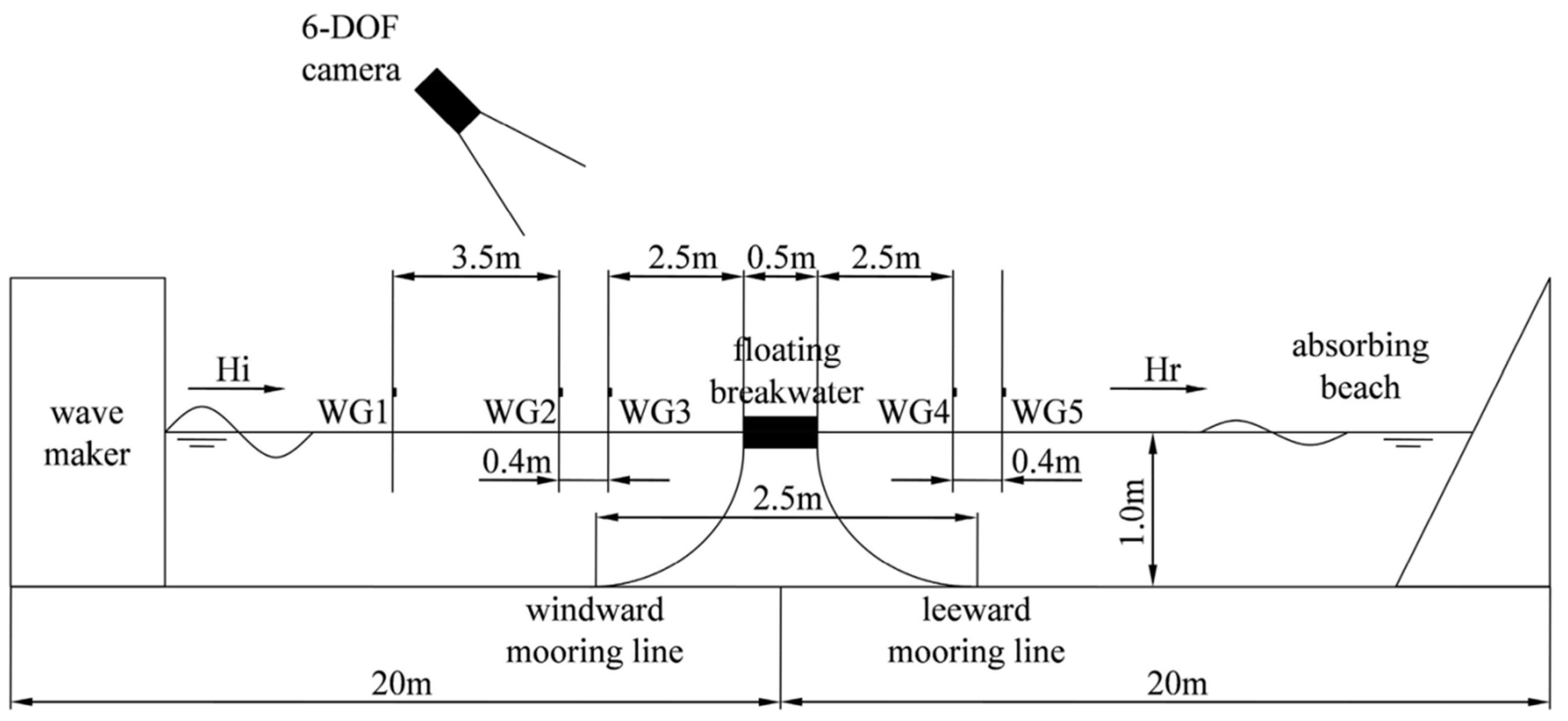
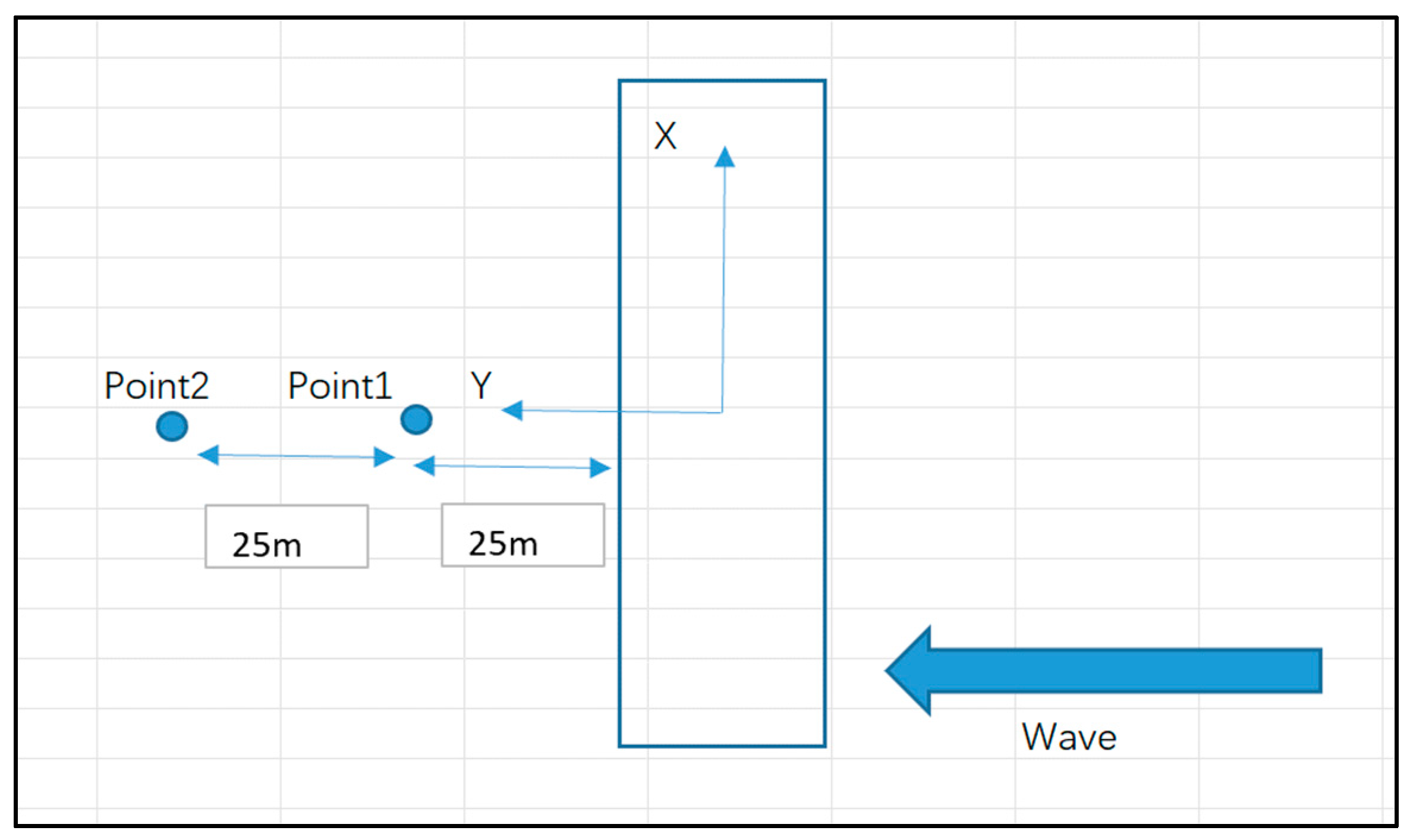
3. Case Study
4. Verification of Model
5. Results and Discussion
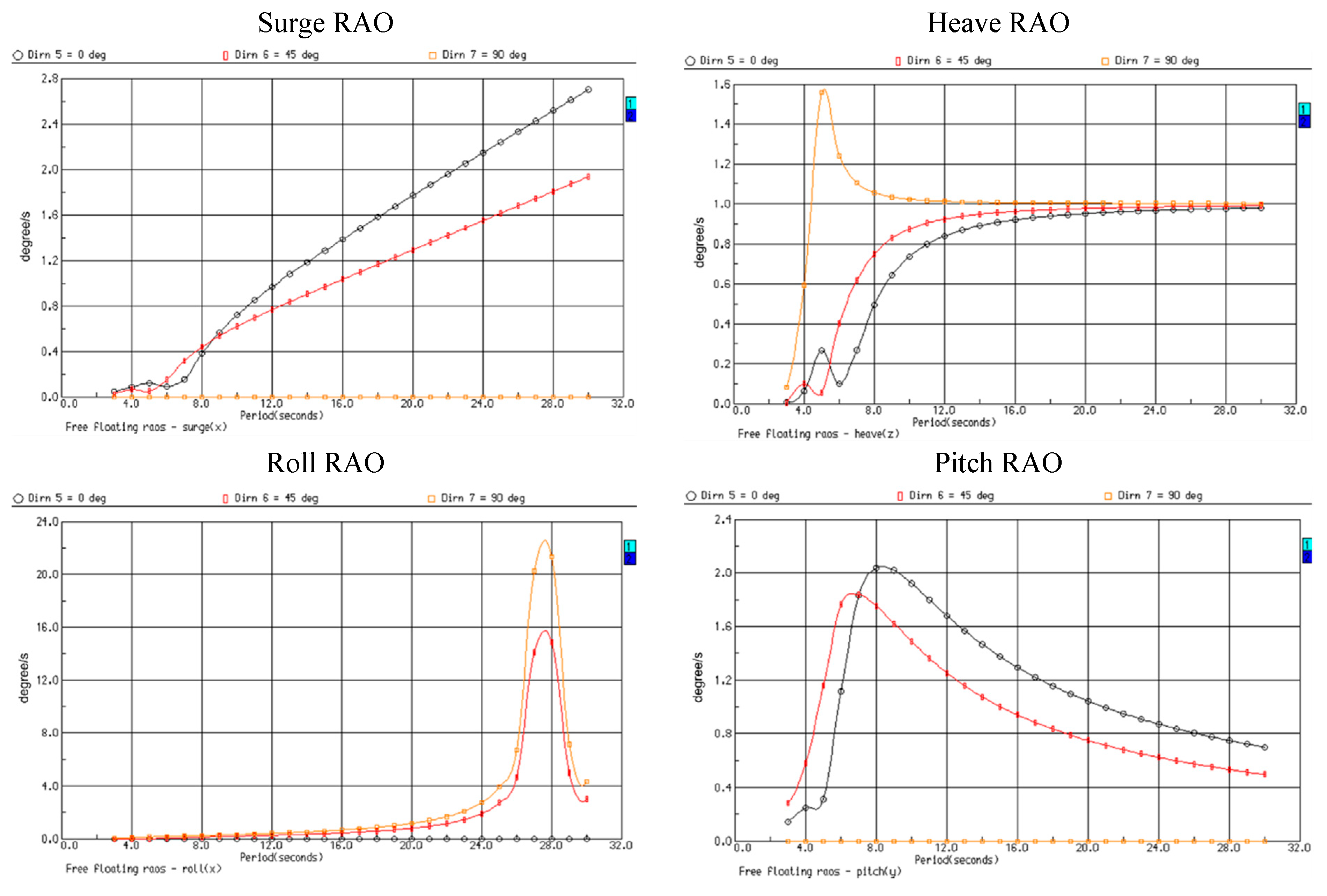
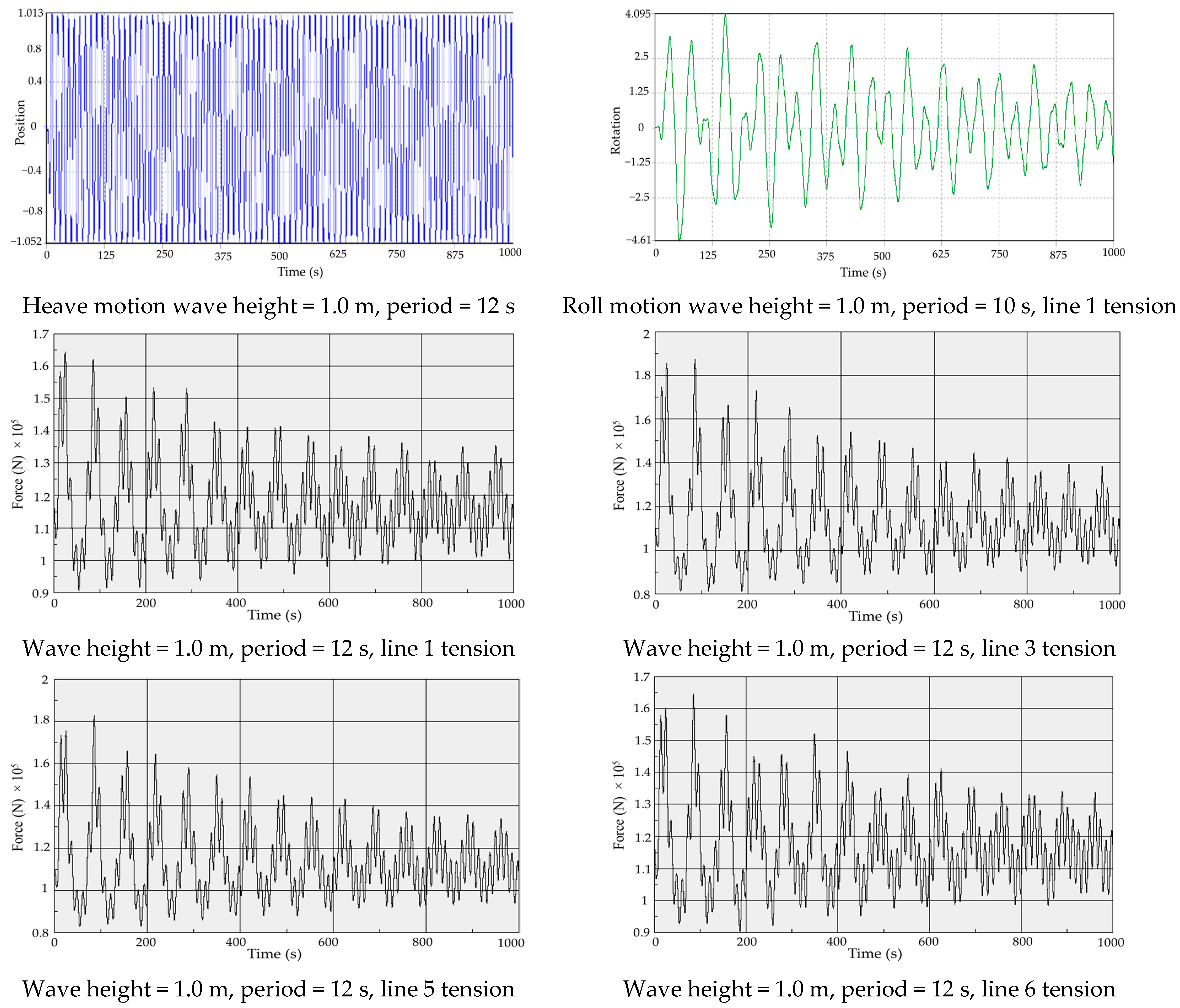
5.1. Motion RAO
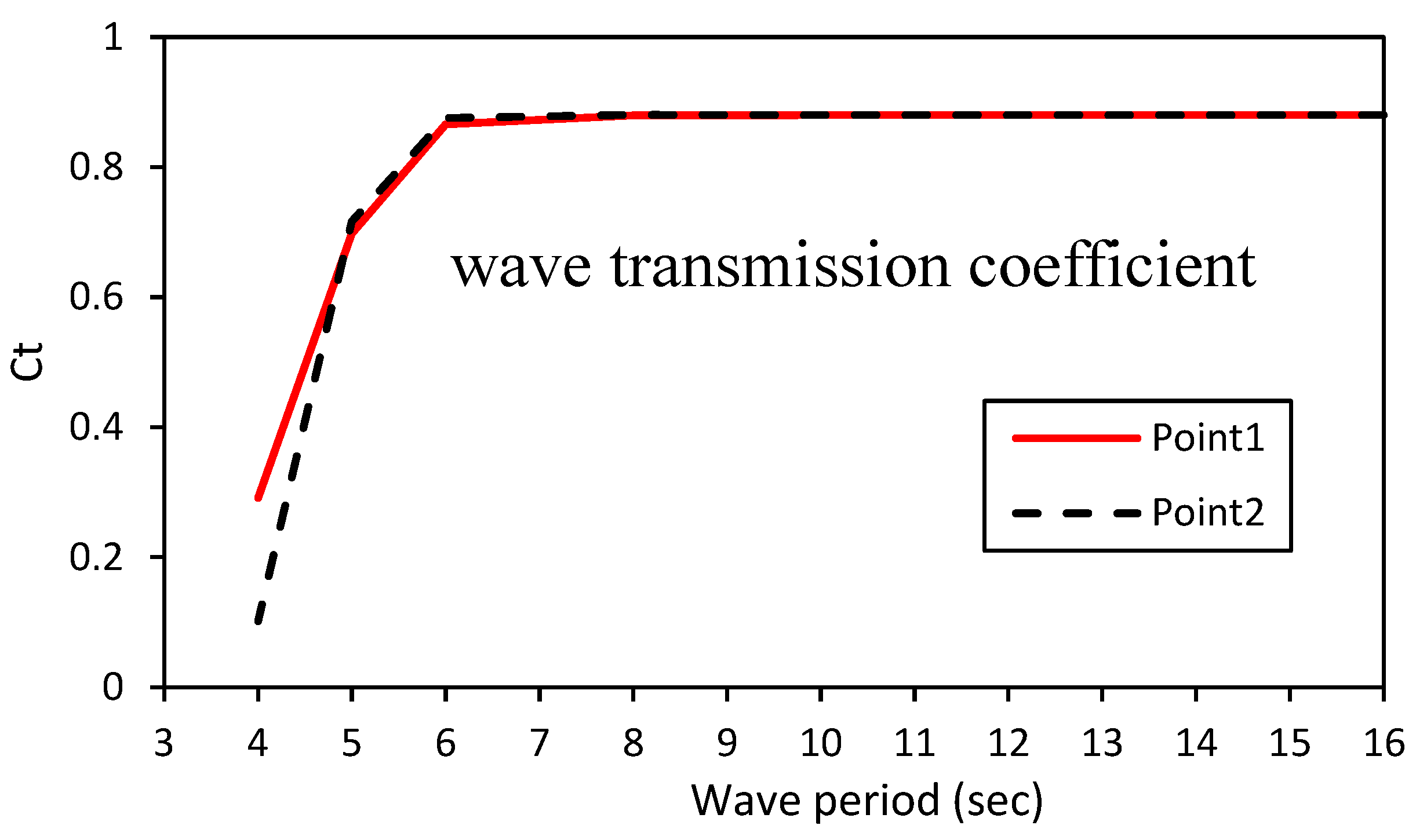
5.2. Transmission Coefficients
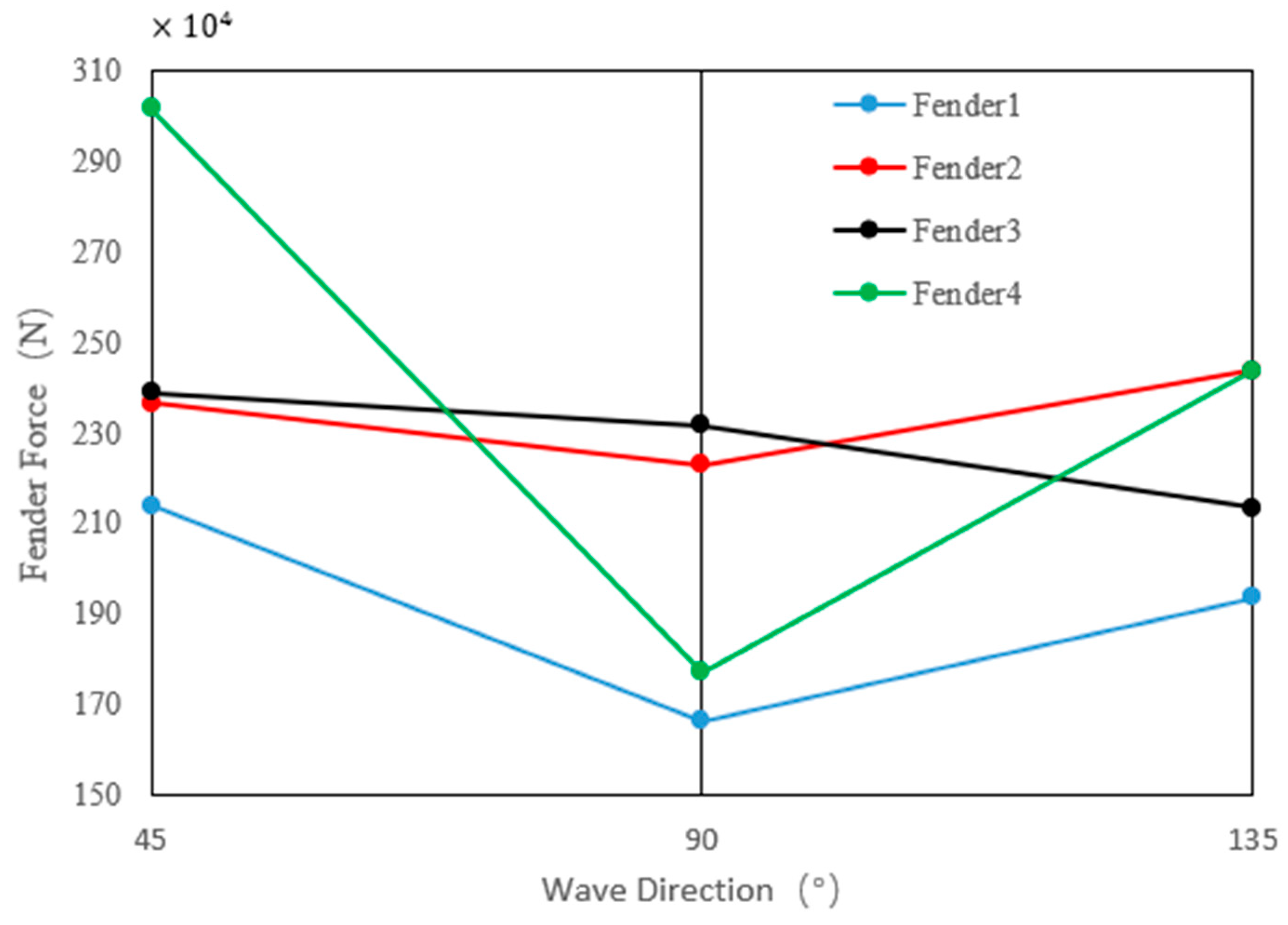
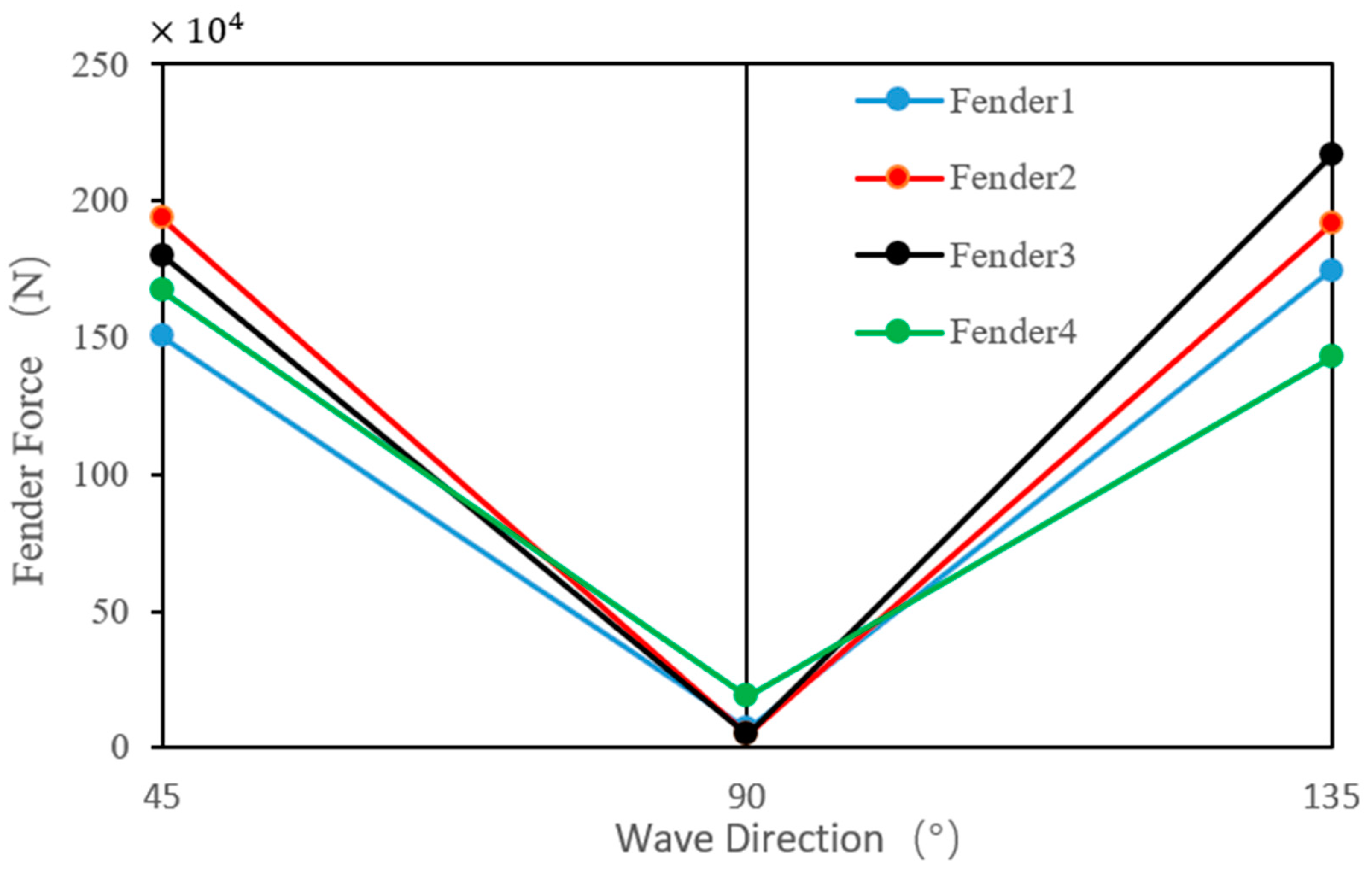
5.3. Connection Configuration
- (1)
- Anchor cables are used to connect single floating breakwaters, and their arrangement is of three types: parallel, single cross, and double cross. They can be divided into the power of parallel link anchor chains. The strength of an anchor chain is superior to that of a single-cross type and double-cross type.
- (2)
- The force generated when connecting the anchor chain and supporting it on the ball increases with increasing wave height. If the wave direction is 45 degrees or 135 degrees, the forces on the anchor chain and ball will be maximum, creating dangerous working conditions. If the direction of the waves is 90°, it is safer to connect the anchor chain and rely on the ball with minimal force.
- (3)
- When the wave height in the design state reaches the maximum value of 1 m, the maximum force of the connected anchor chain shall not exceed the breaking load. The maximum force on the ball does not exceed its reaction force. Both the ball and the anchor rope are safe.
6. Conclusions
- Successful development of a computer model that demonstrated good agreement with the physical model.
- The effectiveness of the breakwater diminishes if the natural period of the structure aligns with the period of the waves. Therefore, it is recommended that this factor is considered during breakwater construction.
- Modifying the breakwater design to increase the extinction coefficient or enhance wave reflection can improve its effectiveness.
- Among the investigated designs, the simple pontoon breakwater performed best in waves with a period of 16 s and a draft level of 3 m. Additionally, the step-pontoon breakwater exhibited superior performance under similar wave conditions.
- The force exerted on the anchor chain is greater than that of the single-cross type and the double-cross type.
- The force on the anchor chain and the ball increases with increasing wave height, with the most significant force occurring at wave directions of 45° or 135°, representing dangerous working conditions. Connecting the anchor chain and relying on the ball is safer when the wave direction is 90°.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Cui, J.; Li, M.Y. Numerical simulation and energy extraction power fitting of OWSCs under regular waves using SPH method. Ocean Eng. 2023, 283, 115077. [Google Scholar] [CrossRef]
- Cui, J.; Chen, X.; Sun, P.N.; Li, M.Y. Numerical investigation on the hydrodynamic behavior of a floating breakwater with moon pool through a coupling SPH model. Ocean Eng. 2022, 248, 110849. [Google Scholar] [CrossRef]
- Paotonan, C.; Rachman, T.; Ashury Putra, T.P. The Analytical Solution of Waves Transmission Coefficient on Semi Fixed Floating Breakwater. IOP Conf. Ser. Mater. Sci. Eng. 2020, 875, 012082. [Google Scholar] [CrossRef]
- Kit, A.Y.J.; Giap, S.G.E.; Ahmad, M.F. Experimental Study on Wave Transmission Coefficient of Double Cylindrical Floating Breakwater in a Wave Basin. J. Adv. Res. Fluid Mech. Therm. Sci. 2024, 112, 33–42. [Google Scholar] [CrossRef]
- Teh, H.M.; Mohammed, N.I. Wave interactions with a floating breakwater. In Proceedings of the 2012 IEEE Colloquium on Humanities, Science and Engineering (CHUSER), Kota Kinabalu, Malaysia, 3–4 December 2012; pp. 84–87. [Google Scholar] [CrossRef]
- Cui, J.; Chen, X.; Sun, P. Numerical investigation on the hydrodynamic performance of a new designed breakwater using smoothed particle hydrodynamic method. Eng. Anal. Bound. Elem. 2021, 130, 379–403. [Google Scholar] [CrossRef]
- Sujantoko; Pramestika, G.A.; Mustain, M.; Ikhwani, H.; Hadiwidodo, Y.S. Simulation of a Wave Hydrodynamic Numerical Model on a Single Vertical Porous Breakwater. IOP Conf. Ser. Earth Environ. Sci. 2024, 1298, 012007. [Google Scholar] [CrossRef]
- He, Y.; Han, B.; Ji, W.; Yan, L.; Han, X. Dynamic analysis of floating piers for curved bridge under wave load and effect of submerged annular rippled breakwater. Ocean Eng. 2022, 266, 112946. [Google Scholar] [CrossRef]
- Diwedar, A.I.; Abdelhaleem, F.S.; Ali, A.M. Wave parameters influence on breakwater stability. IOP Conf. Ser. Earth Environ. Sci. 2019, 326, 012013. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, J.; Mu, Y.; Zhang, Y.; Huang, S.; Shao, X. Numerical Study on Wave Dissipation Performance of OWC-Perforated Floating Breakwater under Irregular Waves. Sustainability 2023, 15, 11427. [Google Scholar] [CrossRef]
- Sarkar, B.; De, S.; Gayen, R. Water wave scattering by pair of porous barriers in the presence of a bottom-standing rectangular obstacle. Ships Offshore Struct. 2023, 19, 1–23. [Google Scholar] [CrossRef]
- Sujantoko; Rasman, I.F.; Mustain, M.; Pratikto, W.A.; Frestiqauli, S. Effect of Interparticle Distance on Smoothed Particle Hydrodynamics on Wave Transformation through Submerged Breakwater. IOP Conf. Ser. Earth Environ. Sci. 2024, 1298, 012001. [Google Scholar] [CrossRef]
- Kumar, U.V.; Saha, S.; Koley, S. A comparative study of wave scattering by non-porous and porous flexible plates in the presence of a submerged porous structure. Meccanica 2023, 58, 1329–1346. [Google Scholar] [CrossRef]
- He, M.; Liang, D.; Ren, B.; Li, J.; Shao, S. Wave interactions with multi-float structures: SPH model, experimental validation, and parametric study. Coast. Eng. 2023, 184, 104333. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, C.; Zhang, Q.; He, M.; Gao, X. Numerical study on the hydrodynamic characteristics of a double-row floating breakwater composed of a pontoon and an airbag. J. Mar. Sci. Eng. 2021, 9, 983. [Google Scholar] [CrossRef]
- Sujantoko; Djatmiko, E.B.; Wardhana, W.; Firmasyah, I.N.G. Numerical Modeling of Hydrodynamic Performance on Porous Slope Type Floating Breakwater. Nase More 2023, 70, 77–87. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, D.; Yu, G.; Xie, L. Wave Height Attenuation over a Nature-Based Breakwater of Floating Emergent Vegetation. Sustainability 2023, 15, 10749. [Google Scholar] [CrossRef]
- Vogel, J.R.; O’Brien, M.; Diallo, S.; Graves, G.M.; Strevett, K.; Storm, D.; Patterson, S. Optimizing and Implementing Floating Wetland Breakwaters to Reduce Shoreline Erosion in Reservoirs. In Soil Erosion Research Under a Changing Climate, Aguadilla, PR, USA, 8–13 January 2023; ASABE: St. Joseph, MI, USA, 2023; p. 1. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, H.; Li, C.; Li, Z. Research Progress and Prospect of Wave Attenuation Performance and Integration of Wave-Energy Converter of Floating Breakwater. J. Environ. Eng. 2023, 149, 03123001. [Google Scholar] [CrossRef]
- Krishna, K.R.A.; Karaseeri, A.G.; Karmakar, D. Oblique wave propagation through composite permeable porous structures. Mar. Syst. Ocean Technol. 2023, 17, 164–187. [Google Scholar] [CrossRef]
- Peng, N.N.; Lau, W.K.; Wai, O.W.H.; Chow, K.W. Computational and experimental studies of wave–structure interaction: Wave attenuation by a floating breakwater. Phys. Fluids 2023, 35, 45112. [Google Scholar] [CrossRef]
- Gayathri, R.; Khan, M.B.M.; Behera, H. Attenuation of wave force on a floating dock by multiple porous breakwaters. Eng. Anal. Bound. Elem. 2022, 143, 70–89. [Google Scholar] [CrossRef]
- Sawant, R.; Barve, K.H.; Ranganath, L.R.; Agrawal, J.D. A Numerical Approach for the Efficiency of Submerged Breakwater to Reduce Wave Impact on an Eroding Beach Adjacent to Estuary BT—Coastal, Harbour and Ocean Engineering. In Coastal, Harbour and Ocean Engineering. HYDRO 2021; Timbadiya, P.V., Deo, M.C., Singh, V.P., Eds.; Lecture Notes in Civil Engineering; Springer: Singapore, 2023; Volume 321, pp. 75–88. [Google Scholar]
- McCartney, B.; ASCE, M. Floating Breakwater Design. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 304–318. [Google Scholar] [CrossRef]
- Sannasiraj, S.A.; Sundar, V.; Sundaravadivelu, R. Mooring forces and motion responses of pontoon-type floating breakwaters. Ocean Eng. 1998, 25, 27–48. [Google Scholar] [CrossRef]
- Lee, H.H.; Chen, L.-Y.; Weng, W.-K.; Shyue, S.-W. The prediction of the dynamic and structural motions of a floating-pier system in waves. Ocean Eng. 2007, 34, 1044–1059. [Google Scholar] [CrossRef]
- Wang, H.Y.; Sun, Z.C. Experimental study of a porous floating breakwater. Ocean Eng. 2010, 37, 520–527. [Google Scholar] [CrossRef]
- Peña, E.; Ferreras, J.; Sanchez-Tembleque, F. Experimental study on wave transmission coefficient, mooring lines and module connector forces with different designs of floating breakwaters. Ocean Eng. 2011, 38, 1150–1160. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.; Law, A.W.-K. Hydrodynamic performance of a rectangular floating breakwater with and without pneumatic chambers: An experimental study. Ocean Eng. 2012, 51, 16–27. [Google Scholar] [CrossRef]
- Martin, T.; Kamath, A.; Bihs, H. Numerical simulation of interactions between water waves and a moored-floating breakwater. Coast. Eng. Proc. 2018, 1, 105. [Google Scholar] [CrossRef][Green Version]
- Cho, I.-H. Transmission coefficients of a floating rectangular breakwater with porous side plates. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 53–65. [Google Scholar] [CrossRef]
- Peng, W.; Lee, K.-H.; Shin, S.-H.; Mizutani, N. Numerical simulation of interactions between water waves and inclined moored submerged floating breakwaters. Coast. Eng. 2013, 82, 76–87. [Google Scholar] [CrossRef]
- Sannasiraj, S.A.; Sundar, V.; Sundaravadivelu, R. Wave transmission characteristics of a floating breakwater. Coast. Eng. 1996, 29, 137–153. [Google Scholar]
- Kim, D.S.; Kim, Y.J.; Kim, Y.S. Numerical study on the wave transmission characteristics of a floating breakwater. Ocean Eng. 2002, 29, 189–205. [Google Scholar]
- Kim, D.S.; Kim, Y.J.; Kim, Y.S. Wave transmission characteristics of a trapezoidal floating breakwater. Coast. Eng. 2004, 51, 563–579. [Google Scholar]
- Sannasiraj, S.A.; Sundar, V.; Sundaravadivelu, R. Wave transmission characteristics of a floating breakwater with a porous barrier. Ocean Eng. 2006, 33, 677–692. [Google Scholar]
- Kim, D.S.; Kim, Y.J.; Kim, Y.S. Experimental study on the wave transmission characteristics of a floating breakwater with a perforated barrier. Coast. Eng. 2008, 55, 1136–1150. [Google Scholar]
- Sannasiraj, S.A.; Sundar, V.; Sundaravadivelu, R. Wave transmission characteristics of a floating breakwater with a sloping front face. Ocean Eng. 2010, 37, 623–636. [Google Scholar]
- Kim, D.S.; Kim, Y.J.; Kim, Y.S. Numerical investigation on the wave transmission characteristics of a floating breakwater with a sloping front face. Coast. Eng. 2012, 65, 1–15. [Google Scholar]
- Sannasiraj, S.A.; Sundar, V.; Sundaravadivelu, R. Wave transmission characteristics of a floating breakwater with a wave absorber. Ocean Eng. 2014, 87, 1–14. [Google Scholar]
- Kim, D.S.; Kim, Y.J.; Kim, Y.S. Experimental study on the wave transmission characteristics of a floating breakwater with a wave absorber. Coast. Eng. 2016, 111, 1–14. [Google Scholar]
- Sannasiraj, S.A.; Sundar, V.; Sundaravadivelu, R. Wave transmission characteristics of a floating breakwater with a wave reflector. Ocean Eng. 2018, 158, 1–13. [Google Scholar]
- Lin, P. Numerical Modeling of Water Waves; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Jin, J. A Mixed Mode Function-Boundary Element Method for Very Large Floating Structure-Water Interaction Systems Excited by Airplane Landing Impacts. Doctoral Dissertation, University of Southampton, Southampton, UK, 2007. [Google Scholar]
- Barltrop, N.D. Floating Structures: A Guide for Design and Analysis, Vol. 1 and 2, Centre for Marine and Petroleum Technology; Oilfield Publications Ltd.: Herefordshire, UK, 1998; ISBN 1870553357. [Google Scholar]
- Newman, J.N. The theory of ship motions. Adv. Appl. Mech. 1979, 18, 221–283. [Google Scholar]
- Havelock, T.H. Waves due to a floating sphere making periodic heaving oscillations. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 231, 1–7. [Google Scholar]
- Cummins, W.E. Le Impulse Response Function and Ship Motions (No. DTMB-1661); David Taylor Model Basin: Washington, DC, USA, 1962. [Google Scholar]
- Duan, W.; Xu, S.; Xu, Q.; Ertekin, R.C.; Ma, S. Performance of an F-type floating breakwater: A numerical and experimental study. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 583–599. [Google Scholar] [CrossRef]
- Ji, C.; Deng, X.; Cheng, Y. An experimental study of double-row floating breakwaters. J. Mar. Sci. Technol. 2019, 24, 359–371. [Google Scholar] [CrossRef]


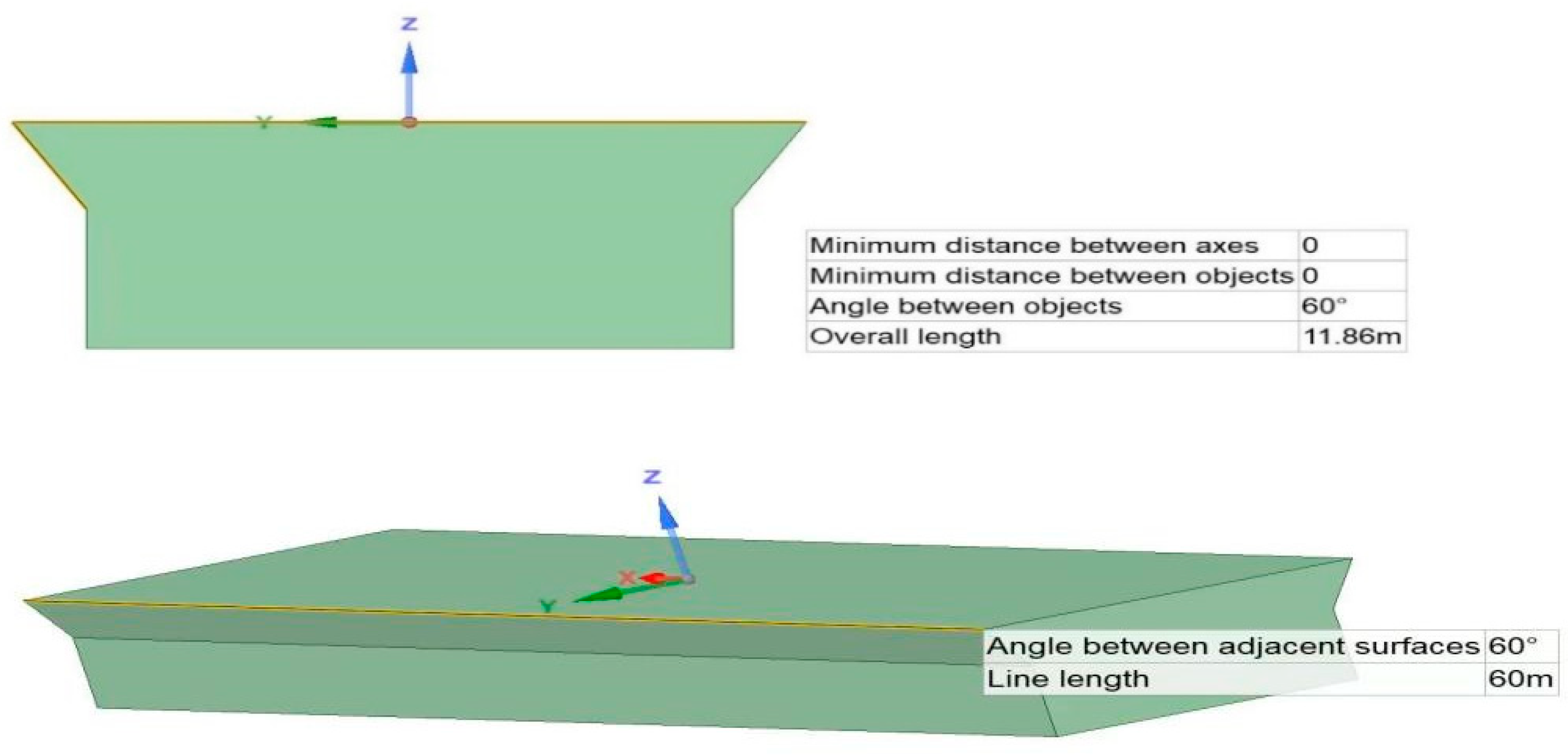


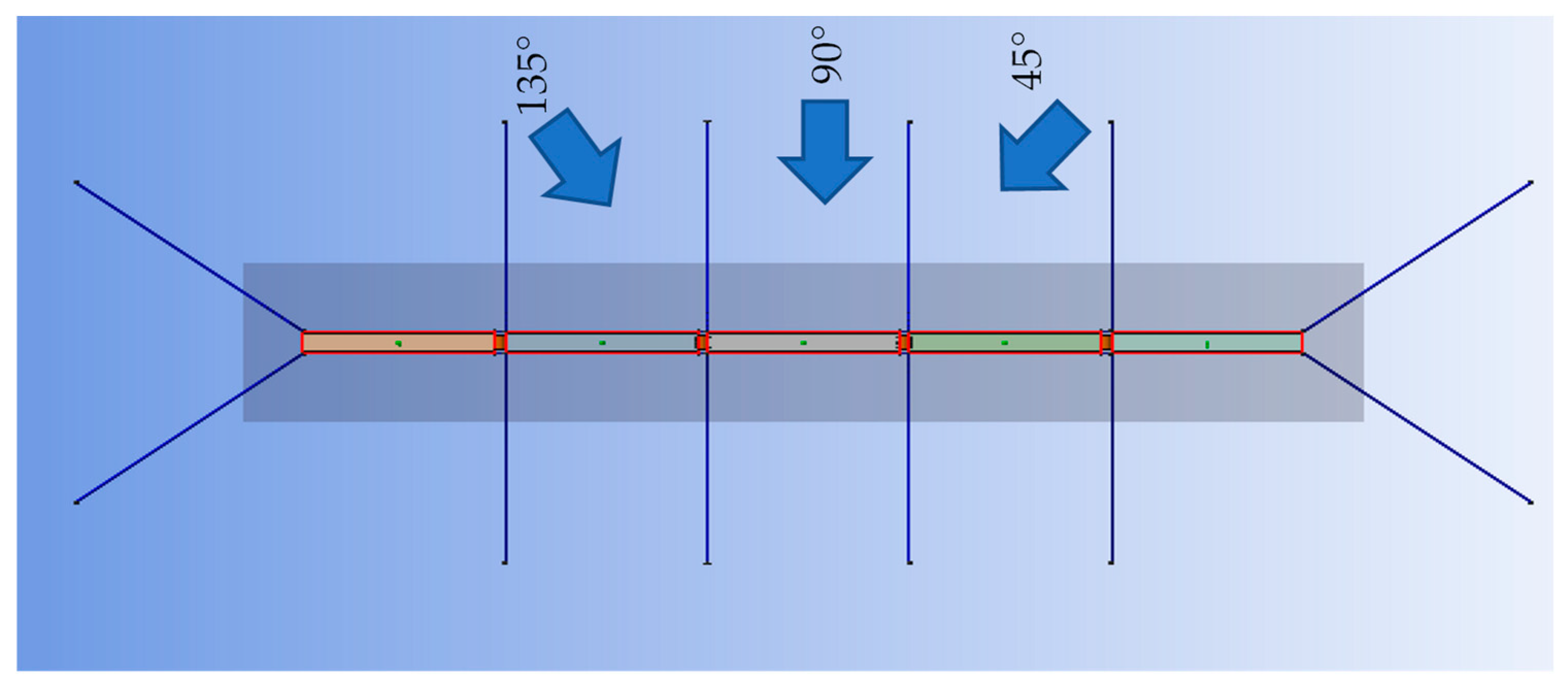
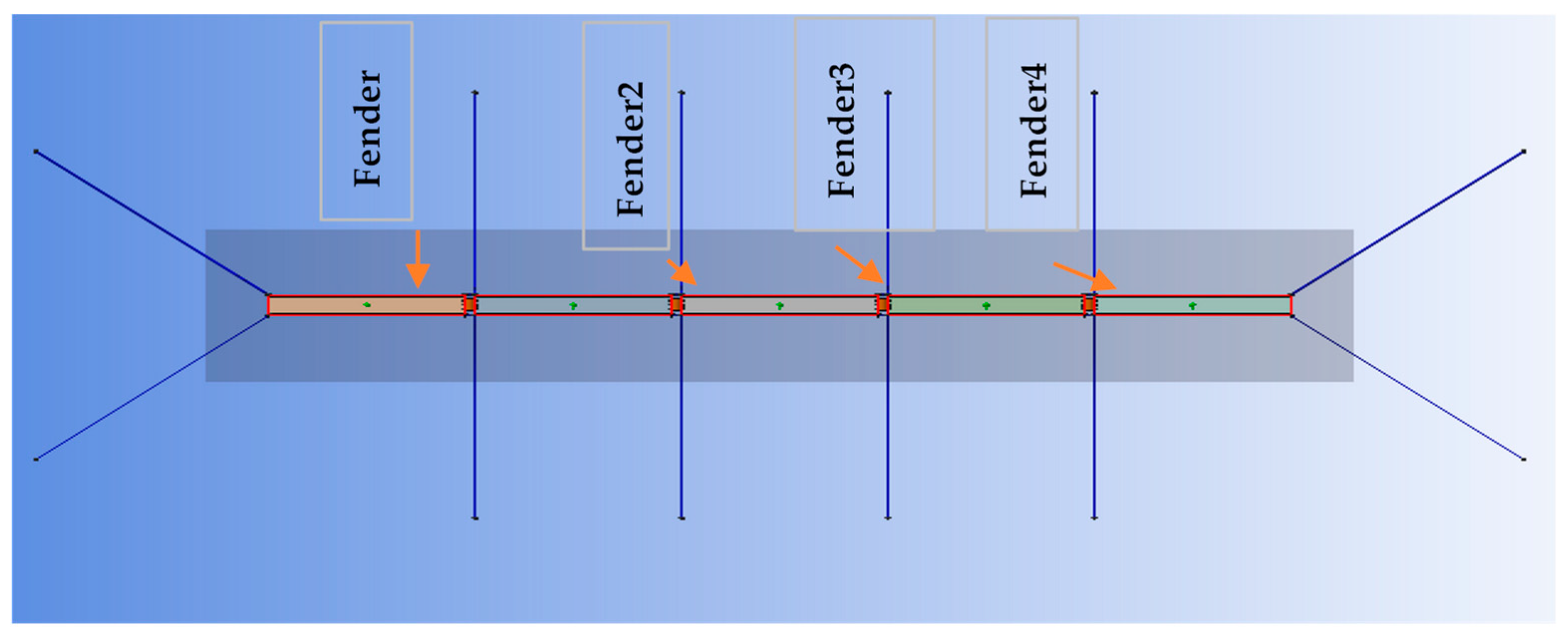

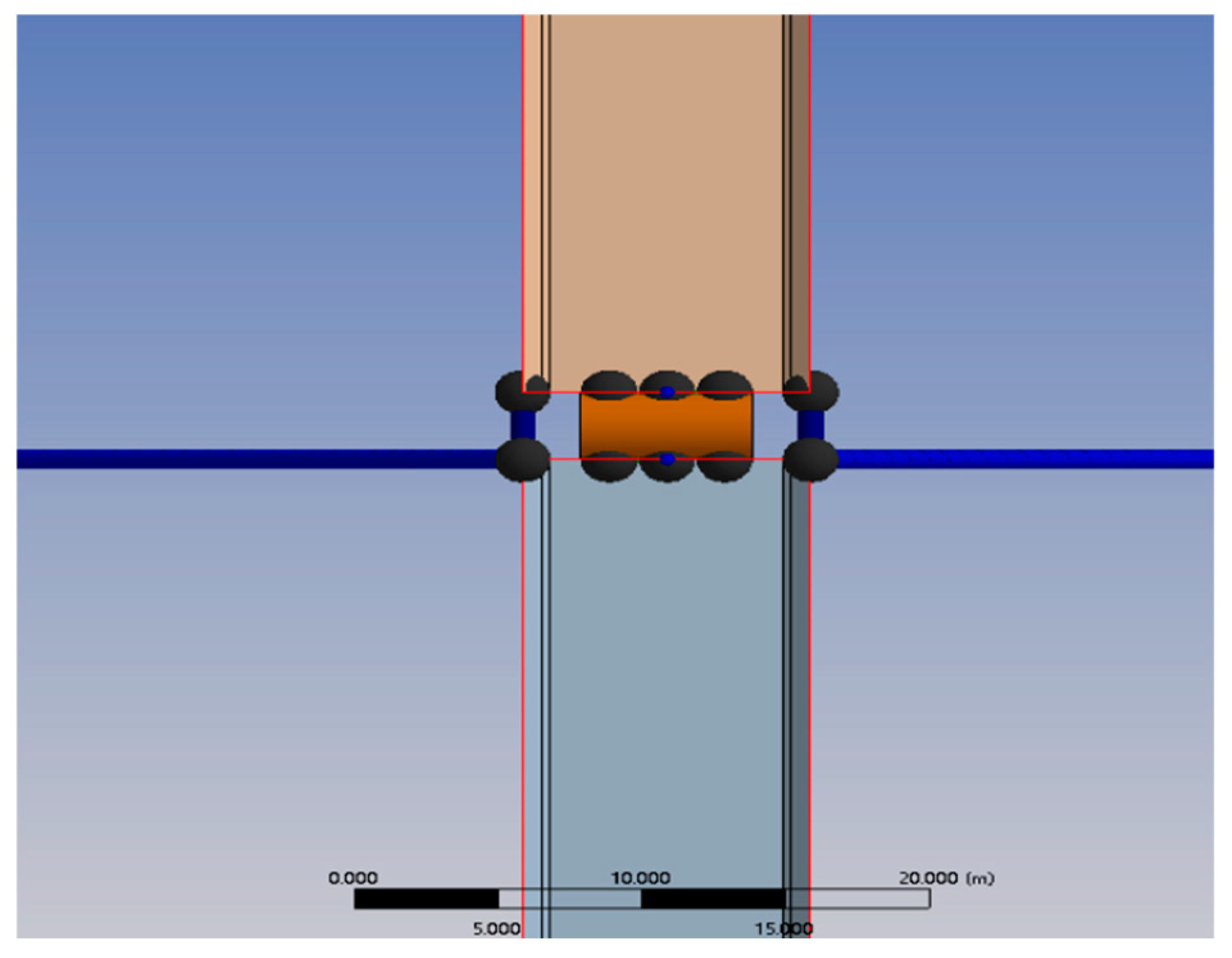
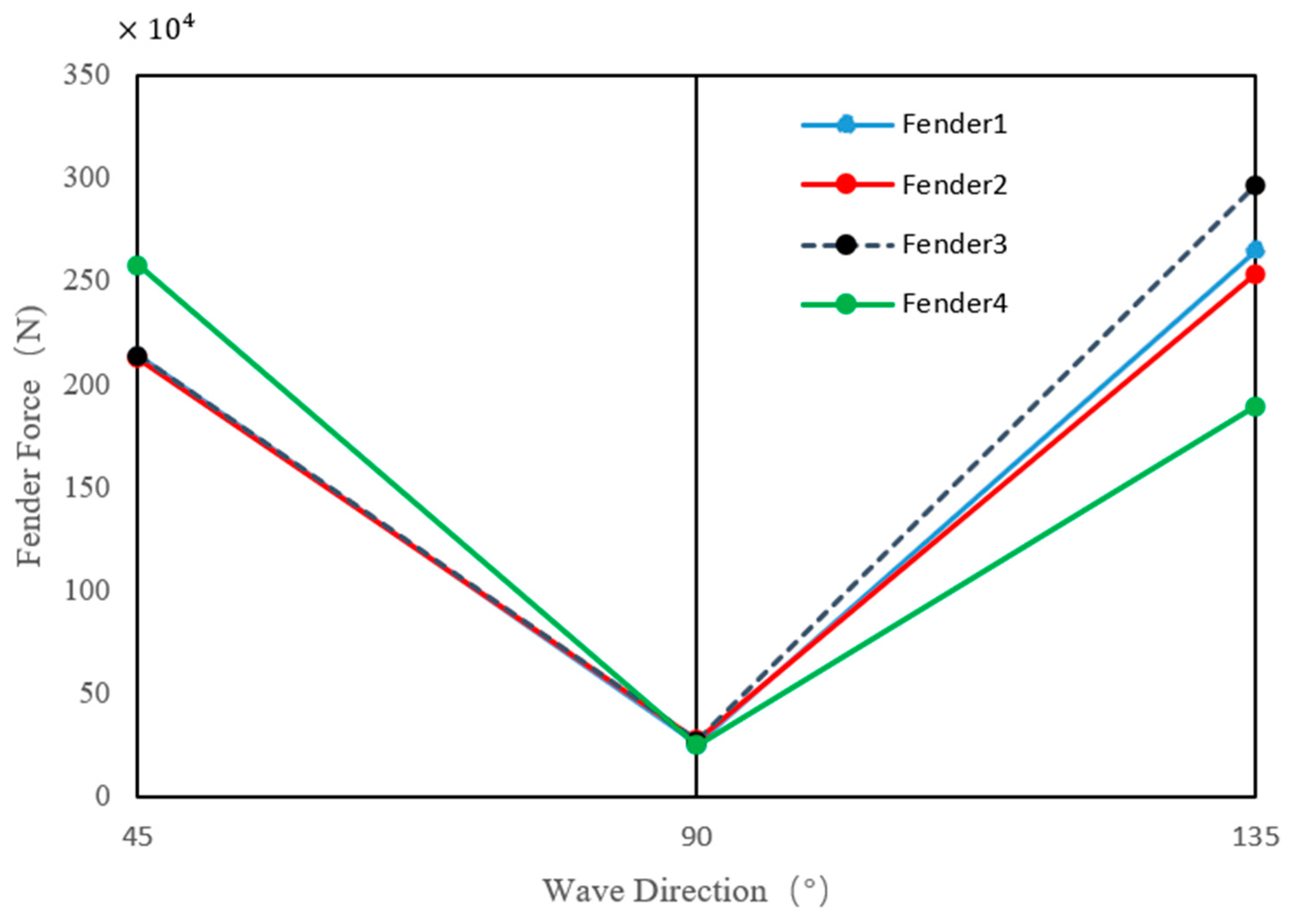
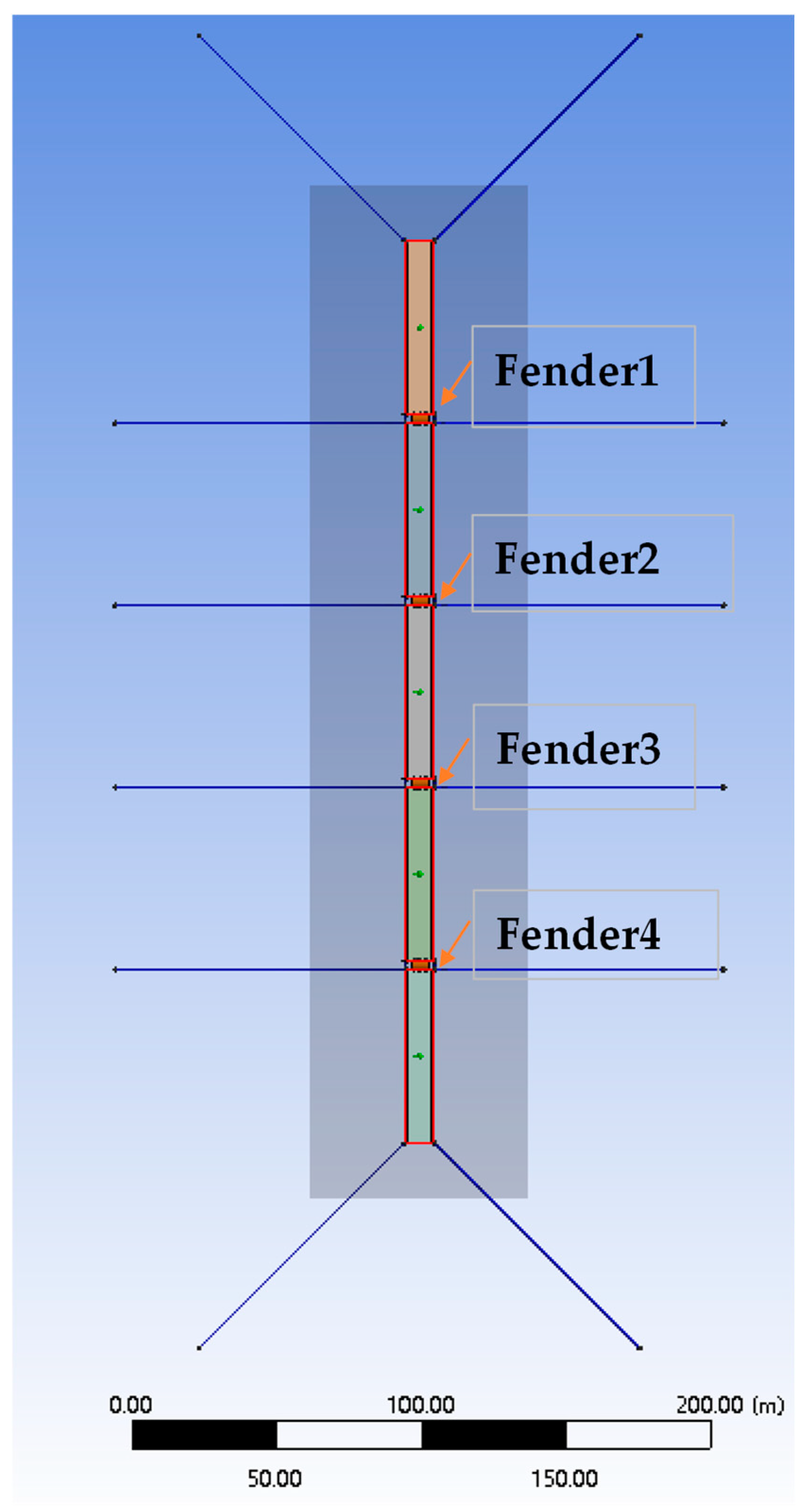
| Dimension | Value |
|---|---|
| Length | 60 m |
| Beam | 10 m |
| Depth | 4.21 m |
| Draft | 3 m |
| Radius of gyration, Rxx | 17.6 m |
| Radius of gyration, Ryy | 3.1 m |
| Radius of gyration, Rzz | 17.6 m |
| H = 1.0 m | Line Force [N] | |||
|---|---|---|---|---|
| Wave Direction | Line 1 | Line 2 | Line 3 | Line 4 |
| 45 | 467,800 | 488,400 | 470,400 | 423,800 |
| 90 | 69,330 | 96,300 | 85,300 | 68,290 |
| 135 | 458,500 | 386,600 | 409,300 | 411,000 |
| H = 1.0 m | Fender Force [N] | |||
|---|---|---|---|---|
| Wave Direction | Fender 1 | Fender 2 | Fender 3 | Fender 4 |
| 45 | 1,506,000 | 1,936,000 | 1,802,000 | 1,673,000 |
| 90 | 69,000 | 48,700 | 48,950 | 186,900 |
| 135 | 1,747,000 | 1,917,000 | 2,166,000 | 1,428,000 |
| H = 1.0 m | Line Force [N] | |||
|---|---|---|---|---|
| Wave Direction | Line 1 | Line 2 | Line 3 | Line 4 |
| 45 | 245,000 | 232,000 | 283,900 | 210,000 |
| 90 | 6700 | 12,000 | 8700 | 6600 |
| 135 | 175,000 | 277,000 | 248,800 | 186,600 |
| H = 1.0 m | Fender Force [N] | |||
|---|---|---|---|---|
| Wave Direction | Fender 1 | Fender 2 | Fender 3 | Fender 4 |
| 45 | 2,138,000 | 2,125,000 | 2,141,000 | 2,580,000 |
| 90 | 252,500 | 276,200 | 272,900 | 252,100 |
| 135 | 2,652,000 | 2,538,000 | 2,970,000 | 1,894,000 |
| H = 1.0 m | Line Force [N] | |||
|---|---|---|---|---|
| Wave Direction | Line 1 | Line 2 | Line 3 | Line 4 |
| 45 | 598,800 | 834,000 | 873,900 | 602,200 |
| 90 | 123,300 | 129,900 | 126,300 | 130,600 |
| 135 | 541,200 | 720,900 | 731,400 | 755,500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sairafi, F.A.; Zhang, J.; Jiang, C.; Almansour, A.I.; Saleh, B. Enhancing Hydrodynamic Performance of Floating Breakwaters Using Wing Plates. Water 2024, 16, 1779. https://doi.org/10.3390/w16131779
Al-Sairafi FA, Zhang J, Jiang C, Almansour AI, Saleh B. Enhancing Hydrodynamic Performance of Floating Breakwaters Using Wing Plates. Water. 2024; 16(13):1779. https://doi.org/10.3390/w16131779
Chicago/Turabian StyleAl-Sairafi, Fares Ali, Jisheng Zhang, Chaohua Jiang, Abdullah I. Almansour, and Bassiouny Saleh. 2024. "Enhancing Hydrodynamic Performance of Floating Breakwaters Using Wing Plates" Water 16, no. 13: 1779. https://doi.org/10.3390/w16131779
APA StyleAl-Sairafi, F. A., Zhang, J., Jiang, C., Almansour, A. I., & Saleh, B. (2024). Enhancing Hydrodynamic Performance of Floating Breakwaters Using Wing Plates. Water, 16(13), 1779. https://doi.org/10.3390/w16131779






