Abstract
The sediment transport along a coastal zone of Thermaikos Bay and the interaction with the coastline were studied in the present research. This study concerns the greater basin of an existing breakwater, for which the sand transport during the time periods 1950–1968 and 2009–2017, before and after the construction of the breakwater, were examined. The breakwater led to sand accumulation behind it, causing the well-known phenomenon of salient. It was revealed that climate change, in terms of wind conditions, significantly affected sediment transport; more specifically, the sand transport during 2009–2017 not only decreased significantly, but also changed its direction, in relation to 1950–1968. Based on the information obtained, technical interventions are proposed for the interception of sediment transport and the consequent accumulation of sand behind the breakwater.
1. Introduction
Alongshore sediment transport constitutes a process of highly significant scientific and engineering importance because of the continuous and developing interaction with the coastline and the possible technical interventions which are often designed via the structure of specific coastal projects.
It is well known that alongshore sand transport occurs mainly due to the oblique incidence of waves that break causing the generation of alongshore wave currents. The formation and development of these currents often cause undesirable coastal erosion phenomena, often intercepted by constructing a system of breakwaters or groins [1,2]. The construction of such structures aims to protect the coast from erosion, with the parallel development of deposition phenomena. Thus, there are cases where the enhancement of sand deposition phenomena is pursued, such as for the creation of a sandy beach. On the other hand, there are cases where the aim is to avoid deposition phenomena, in order to ensure sufficient water depths in a harbor’s basin. In all cases, erosion phenomena are undesirable. Therefore, it can be seen that erosion and deposition are two processes that work inversely and antagonistically, and the construction of a coastal project interacts with the coast in one direction or the other depending on the objective pursued and the correct design of the project. If the objective of a port project is to serve boats, then the construction of a breakwater could be undertaken with special care to avoid intense deposition phenomena. The deposition of a large amount of sediment behind a breakwater, starting from the shoreline and advancing offshore, creates the “Salient” phenomenon. If the deposited sand creates a strip of land that starts from the initial position and reaches the breakwater, the “TOMBOLO” effect is created. The two mechanisms associated with the above-described sandy strip [3] include (a) the field of currents that carry sediment from the sides of the breakwater to the centre, therefore contributing to the enhancement of the salient; and (b) the wave field that develops in the protected zone due to diffraction and generates currents that have a significant perpendicular component to the shore. It is the parallel interaction of these two mechanisms that results in the formation of a salient or tombolo.
Many researchers have worked on this issue over the last decades. Nata et al. [4] studied the effect of climate change on the design of horizontal composite breakwaters. A methodological framework was developed that integrates analytical solutions with numerical models towards the efficient design of the rubble-mound multi-layered part of the examined structures under the effect of climate change impacts (mean sea level rise and increase in wind speed), considering functionality/safety requirements and cost-related issues. The framework was applied to a recently damaged breakwater in Greece. By modifying specific design characteristics of the breakwater, different alternative cross-sections were designed and compared, and the best solution was proposed in terms of design requirements and cost-related issues.
According to Black and Andrews [5], salient and tombolo formations created by natural reefs and islands were investigated through aerial photographic records, for application to offshore coastal protection and surfing reefs. By analysing natural shoreline adjustment, all physical inputs that act to shape salients and tombolos over long time periods were integrated. Equations unique to natural obstructions were developed for prediction of the average salient cross-shore amplitude in the lee of both offshore islands and reefs.
Hieu et al. [6] presented the results of numerical study of the wave-induced currents and morphology changes due to the complicated interaction between waves and a sandy beach with shore-parallel breakwaters. The study was based on the SWASH wave model coupled with a developed sediment transport model. The simulated results of the coupling model were compared with the published laboratory experimental data. Good agreement was obtained for both wave-induced currents and the formation of salients and tombolos behind breakwaters. The numerical results of a shoreline response model were also compared with a published empirical formula, showing good agreement.
Coastal protection planning using offshore breakwater requires estimation of the formed salient. There are research results using physical models as well as field observations on the relation between the length of the breakwater and the position of the breakwater with the formed salient. The relation, however, is qualitative in nature. Previous research developed a calculation method for a formed salient in a single offshore breakwater as the result of a wave that is perpendicular to the breakwater. The model was developed based on the characteristic of a stable coastline, i.e., a stable coastline that is parallel to the wave crestline, whereas the salient equation was approached with polynomials. The equation provides a good result, i.e., the measurement of a salient that is very much in accordance with the result of previous research using a physical model or field measurements [7].
Mantatzi [8] studied the alongshore sediment transport and the shoreline changes in the area of Neoi Epivates Harbor, focusing on the description of the evolution of the depositional phenomena and the shoreline changes behind the breakwater. In that study, she applied some analytical relations by Silvester and Hsu [9], Karambas et al. [1,2], and Kemp et al. [10] in order to estimate the cross-shore length of the salient behind the breakwater. The method is empirical and was based on the analysis of shoreline data in parabolic bays and the perpendicular incidence of the waves in front of the breakwater.
The present research focuses on the following topics: (1) the study of the coastal sediment transport over time in the greater coastal area of the breakwater of Neoi Epivates of Thessaloniki, and (2) the ways to deal with the severe problems due to the sand deposition caused by the sediment transport and the interaction with the harbor project.
The fishing shelter of Neoi Epivates is located in the coastal zone of the Municipality of Thermaikos (Figure 1) in the community of Neoi Epivates. The study area falls under the administrative jurisdiction of the Municipality of Thermaikos, which belongs to the Region of Central Macedonia (Northern Greece) and is located approximately 20 km south of the city centre of Thessaloniki.
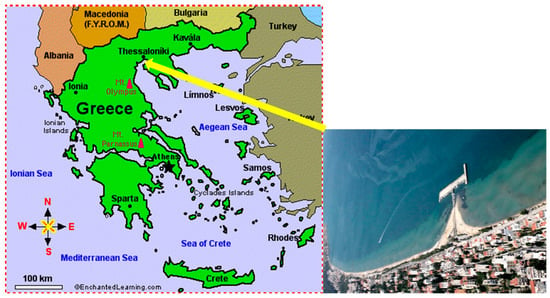
Figure 1.
A map of Greece [11] and the study area of the fishing shelter of Neoi Epivates [12].
This breakwater took its current form in 1997 in order to serve as a fishing shelter for the boats used by fishermen and residents of the area. The length of the breakwater was approximately 185 m. A small coastal bridge, built on piles (Figure 2), already existed perpendicular to the breakwater, connecting it to the coast and allowing the water and the sand to move freely under the deck. The initial length of the bridge was 120 m. Later it was extended by 55 m so that the current length of the bridge reached 175 m. The construction of the harbor project resulted in the deposition of large amounts of sandy materials, and the conversion of the area around the bridge and behind the breakwater into land. This process created two, roughly triangular-shaped new land surfaces, as shown in Figure 3 below, from the depositional material, and significantly reduced the water depths of a large part of the fishing shelter [13].

Figure 2.
Piles on which the pier is established. The arrow shows the piles [14].

Figure 3.
Formation of new land surfaces—the salient phenomenon in 2019 (Google Earth, 2023) [15].
The wind data of the period 1950–1968 and the period 2009–2017 were used for the study. The present work focused on the best possible diagnosis of the deposition problem due to coastal sediment transport (behind the breakwater at the fishing shelter of Neoi Epivates) that developed during the above two time periods; then, alternative ways of dealing with it are proposed. It is noted that the initial project of the bridge was undertaken much earlier and it took its final form in 1966–1968. The breakwater took its current form in 1997, i.e., after the first study period (1950–1968) of the present research and before the second study period (2009–2017). The first dredging was carried out in the year 2000, when an amount of 120,000 m3 of sand was removed by excavation and taken away from the site. In the next five years, the ongoing depositional processes refilled the area with sediments, creating a new strip of land beyond 120 m from the initial shoreline position. In the period 2000–2005, approximately 150,000 m3 of sand was deposited. No dredging was then carried out until September 2017, as a natural disaster occurring in the area of the Municipality of Thermaikos on 6–7 September 2016, resulted in the declaration of an emergency state in the municipality. Among the damage caused to the municipality was the accumulation of a large amount of sand and debris on the bottom of the fishing shelter, making any operations in the harbor impossible. The sand that was transported there originated from the intense erosion of the adjacent coastline [16].
The present study aimed to examine the alongshore sediment transport in the coastal zone of Neoi Epivates and the interaction of engineering works with the coast, via analytical relations and empirical equations. Special emphasis was given to the influence of climate change in terms of the effect of the change in wind conditions on the coastal sand transport.
2. Materials and Methods
This study required the application of a series of computational tools and methods that allowed the calculation of the wave climate of the area corresponding to the two periods under consideration, the coastal sediment transport induced, and, subsequently, the position and length of groins as a proposed measure to protect the shore against erosion and reduce the sediment transport, with the consequent depositional problems behind the breakwater. Only the winds that contribute to sediment transport were taken into account in this study, i.e., N, NE, NW, and W. A detailed description follows.
2.1. Step 1. Wind Wave Forecasting
On the map in Figure 4, the wind direction concerning the location of the port project and the Fi deployment lengths is plotted.

Figure 4.
Map of the Thermaikos Gulf. The star denotes the harbor of Neoi Epivates and the arrow denotes north (Google Earth, 2023) [15].
For the effective (or equivalent) deployment length:
where each Fi is a length in the direction forming an angle ai = 15°, 30°, 45° with the wind direction.
The nonlinear form of the relationship between wind speed and shear stress exerted on the sea surface necessitates the substitution of the parameter U10 with the adjusted wind speed:
UA = 0.71 ∙ U10 1.23
An average wind intensity of U10 = 7 m/s is taken into account for a moderate wind, U10 = 15 m/s for a strong wind, and U10 = 22 m/s for a rushing wind (storm).
The JONSWAP (Carter) and Pierson–Moskowitz (or PM) forecasting methods are applied, through which the significant wave height Hs and the period of maximum energy density Τp are calculated [17].
2.2. Step 2. Finding Period and Wavelength of Equivalent Waves
From the values of H and T calculated by the wave forecasting methods, the value of T of the equivalent waves is then estimated according to [18] from the relation:
and the equivalent waves from the relation:
These values of H and T are used to calculate the sediment transport.
More specifically, the significant wave height and period are calculated for all types of wind in different directions. Thus, for example, for the northerly wave we calculate the equivalent period from the formula (taking into account moderate, strong, and storm winds):
The equivalent wave height is then:
Equation (6) takes the following form:
The observations in the two tables below are used (Table 1 and Table 2) in order to examine whether there was a variation in the sediment transport over time (due to climate change).

Table 1.
Wind direction and intensity (observation period 1950–1968, Sedes Weather Station) [19].

Table 2.
Wind direction and intensity (Mikra Thessaloniki, 2009–2017) [20].
2.3. Step 3. Procedure for Wave Data Calculations in the Breaking Zone
From the previous step, the height (H) and period (T) of waves in the open sea due to the influence of winds of different directions are found. Only those winds that cause oblique wave incidence and, consequently, the generation of wave currents and sediment transport parallel to the coastline towards one direction or the other on the shoreline are taken into account. The angle of wave propagation (αο) is determined by the direction of the wind causing the wave relative to the direction of the shoreline, while the slope of the bottom (m) is determined by the topographic data of the coastal zone.
Then the wave-breaking elements, i.e., Hb, αb, and db, in the breaking line are found based on the diagrams in Figure 5 and Figure 6 below [17].
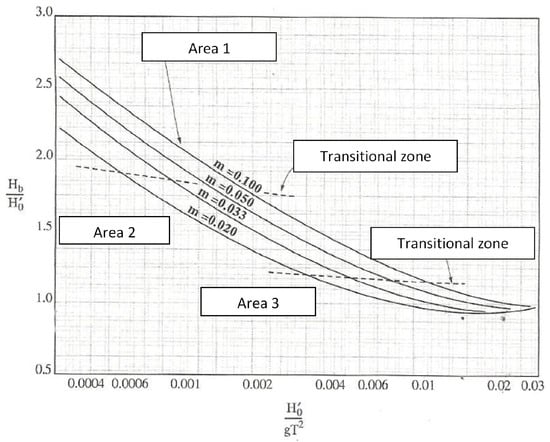
Figure 5.
Diagram for the determination of Hb.
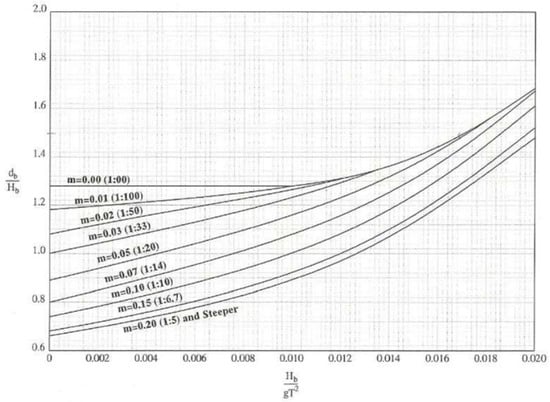
Figure 6.
Diagram for the determination of db.
2.4. Step 4. Calculation of the Annual Coastal Sediment Transport
A number of formulas have been developed during the recent decades for the calculation of the alongshore sediment transport.
More specifically, Bayram et al. [21] developed a new predictive formula of alongshore sediment transport in 2007. Six high-quality data sets on hydrodynamics and sediment transport, collected during both field and laboratory conditions, were employed to evaluate the predictive capability of the new formula. The new formula was well suited for practical applications in coastal areas, as well as for numerical modelling of sediment transport and shoreline changes.
Koutitas and Scarlatos [22] present a more generalised type of the alongshore sediment transport formula, which was found experimentally and can be written in the form below:
where Qs is the volumetric rate of transported sediments along the coast and inside the breaker zone, H is the wave height, φ is the wave-breaking angle with respect to the coastline, and m is an exponent varying between 2.0 and 3.5, and is an empirical coefficient incorporating the sediment particle diameter, beach slope, and wave period [23].
Qs = as ∙ Hm ∙ sin(2φ)
Here, the simple form of the mean annual alongshore sediment transport, Q in (), given by Koutitas [17] and CERC [24], is used as follows:
where Hb is the wave height, cgb = (db∙g)0.5 is the speed of propagation of the wave, and φ is the wave angle at the breaking line.
2.5. Step 5. Description—Presentation of the Sand Deposition Problem behind the Breakwater
A simple description of the sand deposition and the consequent salient development is follows. More specifically, the evolution over time of the salient behind the existing breakwater is shown, based on snapshots of Google Earth.
2.6. Step 6. Calculation of Length and Position of Proposed New Groins
The algebraic sum of the alongshore sediment transport components leads to a new volume of sediment transport Q. Then, a characteristic depth h is calculated according to the following formula [22].
h = 2.5 ∙ db
The length of the groin y, after t years in the vicinity (nearby area) of the breakwater, is then calculated by the following formula:
while the length x of the shoreline upstream of the groin on which sand is deposited is calculated by the equation
y = 2 ∙ (Q ∙ t ∙ ab /[π∙h]) 0.5
x = (3/ab) ∙ y
This length can be used to determine the approximate distance of the proposed groin from the bridge behind the breakwater.
Note that ab is the wave-breaking angle, here in rads [17,24,25].
3. Results
The data resulting from the present research are presented below.
Table 3 presents the characteristic wave data, derived from the JONSWAP (Carter) and Pierson–Moskowitz forecasting methods for the winds that cause alongshore wave induced currents, carrying small or large quantities of sand.

Table 3.
Results of method of prognosis of the wave characteristics.
The equivalent wave heights and equivalent wave periods for the time periods 1950–1968 and 2009–2017 are given in Table 4.

Table 4.
Equivalent wave heights and equivalent period for the periods 1950–1968 and 2009–2017.
The breaking waves’ characteristics for the time periods 1950–1968 and 2009–2017 are given in Table 5.

Table 5.
Data of the breaking waves for the periods 1950–1968 and 2009–2017.
The mean annual alongshore sediment transports for the periods 1950–1968 and 2009–2017 are given in Table 6.

Table 6.
Annual coastal sediment transport along the coast in the breakwater area for the periods 1950–1968 and 2009–2017.
After the calculation of the alongshore sediment transport for each one of the four winds that generate the coastal wave currents, the average alongshore sand transport is calculated for each direction along the shoreline from the sum of the corresponding volume sand transports. The transport towards the west is denoted with a negative sign, while the transport towards the east is denoted with a positive sign. Finally, the algebraic sum of the two volume transports lead to the mean total (overall) alongshore sand transport for the two time periods (Table 7).

Table 7.
Average annual alongshore sediment transport (m3) in periods 1950–1968 and 2009–2017.
The Sand Deposition Problem behind the Breakwater
According to step 5, in order to better determine the extent of the problem in the harbor of Neoi Epivates, the evolution over time of the salient behind the breakwater is shown based on snapshots of Google Earth (Figure 7). More specifically, 11 available images were collected, according to which the evolution of the problem over the years from 2003 to 2017 (Figure 7) can be understood. The cross-shore length of the salient is marked with the red line. During the period of September 2017, in order to reduce the salient phenomenon (sediment) after some intense meteorological phenomena and consequent disaster that happened in the area, dredging was carried out (removal of the transported materials behind the breakwater). With the help of Google Earth, the length of the developing cross-shore salient covered with transported sand was determined concerning the period from 2003 to 2017, as shown in the images of Figure 8 and the diagram of Figure 9.

Figure 7.
Evolution of the salient over the years from 2003 to 2017 (Google Earth, 2023) [15].
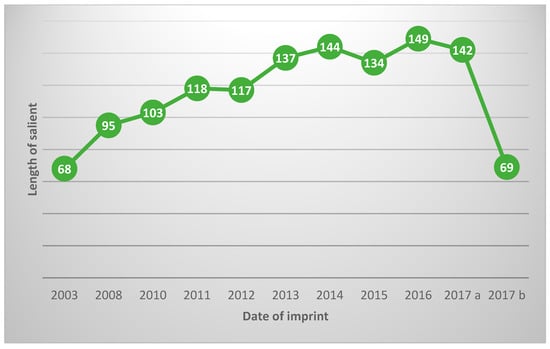
Figure 8.
Evolution over time of the cross-shore length of the salient. 2017a refers to April of 2017 and 2017b refers to September of 2017.

Figure 9.
Alongshore sand transport in periods 1950–1968 (left) and 2009–2017 (right).
Taking into account the data from the above images from Google Map and Figure 8, it seems that the increase in sand accretion behind the breakwater is nearly linear, starting in 2003 with a cross-shore length of the salient of 68 m, and reaching approximately 150 m in 2016 and 2017 (April); in 2017 (September), dredging works were conducted, reducing the salient by 73 m, i.e., by 51.7%.
Using the relations of step 6, the position x and the length y of the groin suggested for the interception of the sand transport can be found. Based on the calculations, it was found that after a time period of 5 years, the cross-shore length of the accumulated sand was ~75 m, while after a period of 20 years it was ~160 m; the distance from the breakwater at which the accretion of sand starts to occur along the shoreline was ~720 m and ~1500 m after a time period of 5 and 20 years, respectively.
It is worth noting that the rate of seawards sand accumulation at the upstream zone of the groin, which leads to the groin’s length calculation, is in very good agreement with the rate of advancement of the coastline (salient) behind the breakwater according to the mapping of the phenomenon through Google Earth. Thus, the abovementioned calculation of the cross-shore land projection seawards by 75 m for five years is in good agreement with the initial imprint of the salient shown in Figure 7 and Figure 8; more analytically, the cross-shore length of the salient in 2003 reached almost 70 m (68 m) away from the initial shore in 1997 i.e., approximately 5 to 6 years after the construction of the breakwater. Furthermore, as shown in Figure 7 and Figure 8, the length of the salient reached ~150 m in early 2017 m (i.e., twenty years after the breakwater’s construction) and, if no dredging occurred, the salient would normally exceed 150 m; this is in line with the calculations of the groins’ length of ~160 m. The small divergence between the calculated cross-shore lengths and the measured/imprinted ones are expected due to the fact that, behind the diffracted waves, the wave-induced current velocities are reformed with a consequent reduction in the magnitude of the length of the projected land.
4. Discussion
Alongshore sediment transport is of great importance for the study of coastal geomorphology. Coastal engineering works have a very significant impact on the environment and the conditions in the area where they are constructed. It is clear that if their presence reforms the hydrodynamic conditions, as well as the rate and manner of sediment transport, there will be a change in the coastline of the area. A highly characteristic example of alongshore sediment transport and the interactions of a breakwater with the shoreline is the case of Neoi Epivates harbor, situated in Northeast Thermaikos Bay (North Greece). As given in Table 7, it is obvious that in the period 2009–2017, which corresponds to the time period after the construction of the breakwater of Neoi Epivates, eastward movement was dominant, while in the period 1950–1968, which corresponds to the time period before the construction of the breakwater of Neoi Epivates, westward movement was dominant. These sand transports are shown with the arrows in Figure 9.
It is worth noting that the overall (total) westward alongshore sediment transport that corresponds to the period 1950–1968 is shown at the left side of Figure 8 with a larger arrow than the arrow of the overall eastward alongshore sediment transport that corresponds to the period 2009–2017, shown at the right side of the Figure 8. However, the length of the arrow is not given with a scale but only as an approximation. The change in the direction of sediment transport is due to climate change, which is related to the change in the meteorological regime. The different directions of the winds and their different frequencies of occurrence have a direct influence on the sediment transport. The sediment transport caused by alongshore wave currents generated by northerly and northeasterly waves (and winds) takes place in a westerly direction, and is reduced by 6%. Sediment transport caused by coastal wave currents generated by northwesterly and westerly waves (and winds) takes place in an easterly direction, and is reduced by 27.78%. These high reduction rates are due to the significant reduction in winds (in terms only of moderate, strong, and storm winds). It should be emphasised that climate changes directly affected the sediment transport, which is documented by the fact that not only did the magnitude of the sediment transport during the period 2009–2017 decrease significantly, but this transport also changed its direction compared to the period 1950–1968.
The predominance of the eastward sand transport is documented and confirmed by the image of the salient (Figure 10 and Figure 11), which clearly shows the eastward inclination of the salient ending.

Figure 10.
Formation of a salient [26].

Figure 11.
Erosion at the downstream side of the coast (Google Earth, 2023) [15].
The prevailing eastward sand transport in relation to the construction of the breakwater caused intense problems of sediment deposition and the accumulation of large quantities of sand behind the breakwater, with the consequent development of the salient. Intense sand accumulation was observed at the upstream side of the shore, while erosion of the coast was observed at the downstream side. This observation is quite clearly shown in Figure 10. It is obvious that in the case of westward sediment transport, erosion and deposition developed at the opposite sides in relation to the aforementioned case.
As far as the wind conditions in the study area are concerned, it is remarkable that the frequency of occurrence of moderate, strong, and stormy winds of the period 1950–1968 is different from the frequency of occurrence of the winds of the period 2009–2017. In more detail, the intensity of north winds decreased by 17.70%, while the intensity of northwest winds decreased by 33.10%. The intensity of northeast winds decreased by 5.88%, while the intensity of west winds decreased by 54.65%. The aforementioned data are given in Table 8 and Table 9.

Table 8.
Percentages of decrease in wind intensity for the periods 1950–1968 and 2009–2017.

Table 9.
Percentages of reduction in sediment transport for the periods 1950–1968 and 2009–2017.
The Breakwater, the Problems Related to the Salient, and an Engineering Proposed Solution
As far as the construction of a breakwater is concerned, the ratio of the length of the breakwater Ls to the distance from the shore Yo can be calculated for the estimation of the potential salient development. Concerning the breakwater in the Neoi Epivates Harbor, the length of the breakwater is Ls = 185 m and the distance from the shore is Yo = 175 m. Consequently, the ratio Ls/Yo is 185/175 = 1.06.
The interested reader can find relationships that correlate the aforementioned parameters to the potential development of salients in published papers and text books of the scientific community [2,27]. Thus, according to [2], for Ls/Yo > 2, a tombolo formation occurs; for Ls/Yo < 1.5, a salient is developed; for Ls/Yo < 0.5, a weak salient is formed; and for Ls/Yo < 0.2, minimal changes in the morphology of the coast are expected.
In this particular case, since the ratio of the two parameters is equal to 1.06, the breakwater appears to cause sand accumulation on the coastline due to its construction, i.e., a salient. This is not desirable, as the breakwater was built to protect the zone behind it, as well as the bridge that operates as a fishing shelter. The construction led to the intense salient phenomena, which reduced the number available docking vessels.
Ideally, the ratio of the length of the breakwater to its distance from the shore should be less than 0.2 so that salient formation could be avoided and a large part of the bridge could be utilised for the vessels’ mooring. This could be achieved by constructing the breakwater even further away from the shore.
Ultimately, the construction of the breakwater at Neoi Epivates caused problems with the docking of vessels and environmental degradation in the greater area, due to the deposited material that was created on either side of the breakwater. So, after the necessary calculations that have been completed, it was considered that a groin to the west of the breakwater could be examined. Regular monitoring of the environmental condition of the harbor and periodic dredging could be also necessary. Of course, it is well known that there are also other important soft engineering practices like beach nourishment and submerged breakwaters, or even floating breakwaters, which are often combined in order to successfully address problems of sand accumulation and consequent erosional processes in adjacent positions [2,28].
In order to address the problem of intense depositional phenomena, the construction of a groin on the west side of the breakwater can be proposed. According to the calculations, the groin can be constructed at 1500 m away from the breakwater. However, in the coastal zone west of the breakwater and at a distance of approximately 1850 m away from it, there is already a 120 m long bridge/pier with a deck on piles. Thus, the existing groin can be used to prevent sand from being transferred mainly from the west. The calculations showed that the necessary length of the groin should extend to ~160 m (for a long time period of two decades); therefore, the existing groin could be extended by 40 m. Furthermore, the bridge allows the free water circulation and transport of sediment below its main body on piles. Therefore, filling the empty space between the piles with stones could be proposed. This type of construction would prevent the sand transport. In this way, the existing coastal bridge is transformed into a conventional groin on the west side of the harbor.
It is noted that changes in the alongshore sediment transport concern only the magnitude and the direction of the sand transport during two time periods. The breakwater was constructed after the first time period of the study, so the effects of the breakwater on the shoreline concern only the sand transport that was developed during the second time period. However, some conclusions can be rationally drawn by combining and integrating the findings arising from the aforementioned study, which examines the two extended time periods. For example, it is obvious that if the breakwater had existed during the first time period, the inclination of the salient would have developed westwards, which means that a groin (if selected as a technical solution) to the east side of the breakwater should be designed.
Of course, it is the magnitude of the volume of transported sand that significantly affects the cross-shore length of the salient behind the breakwater. Furthermore, it is obvious that the direction of the alongshore sediment transport determines the side (right or left of the breakwater) at which the inhibition of sand transport should be pursued
5. Conclusions
The present study revealed that climate change, in terms of wind conditions, significantly affected alongshore sediment transport; more specifically, the sand transport during 2009–2017 not only significantly decreased, but also changed direction, in relation to 1950–1968. In more detail, an important reduction in the volume of sand transport due to the reduction in wind intensity, as well as the changes in the wind fields in the periods 1950–1968 and 2009–2017, were observed.
As far as the breakwater of the harbor of Neoi Epivates is concerned, the construction caused problems with the docking of vessels and environmental degradation in the greater area of the harbor, due to the disposition and the consequent sand accumulation on both sides of the bridge.
Based on this study, the building of a groin is proposed with an intervention on an existing bridge located at the west of the port. At the same time, regular monitoring of the environmental condition of the port and, when necessary, periodic dredging is necessary.
Author Contributions
Methodology, C.N. and Y.S.; Formal analysis, C.N.; Writing—review & editing, C.N.; Project administration, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Karambas, T.; Krestenitis, Y.; Koutitas, C. Coastal Engineering—Projects of Coastal Protection; Association of Greek Academic Libraries: Athens, Greece, 2016. (In Greek) [Google Scholar]
- Karambas, T.; Dimas, A.; Loukogeorgaki, E. Coastal Engineering and Port Works; DISIGMA: Thessaloniki, Greece, 2020. (In Greek) [Google Scholar]
- Ming, D.; Chiew, Y.M. Shoreline changes behind detached breakwater. J. Waterw. Port Coastal Ocean Eng. 2000, 126, 63–70. [Google Scholar] [CrossRef]
- Nata, S.; Charalampidou, A.; Loukogeorgaki, E.; Karampas, T. Design of breakwaters under the effect of climate change. In Proceedings of the Twenty-Sixth (2016) International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016; Volume 3, pp. 1436–1443, ISBN 13:978-1-880653-88-3. [Google Scholar]
- Black, K.P.; Andrews, C.J. Sandy Shoreline Response to Offshore Obstacles Part 1: Salient and Tombolo Geometry and Shape. J. Coastal Res. 2001, 29, 82–93. [Google Scholar]
- Hieu, P.D.; Vinh, P.N.; Viet, N.T.; Thanh, N.V. Numerical study of nearshore hydrodynamics and morphology changes behind offshore breakwaters under actions of waves using a sediment transport model coupled with the SWASH model. Coastal Eng. Jpn. 2020, 62, 553–565. [Google Scholar] [CrossRef]
- Hutahaean, S. Salient Calculation at the Single Offshore Breakwater for a Wave Perpendicular to Coastline using Polynomial Approach. Int. J. Adv. Eng. Res. Sci. 2020, 7, 156–161. [Google Scholar] [CrossRef]
- Mantatzi, G. Coastal Sand Transport and Change of Coastline along the area of Neoi Epivates Harbor (Thessaloniki Bay). Master’s Thesis, Department of Environmental Engineering, International Hellenic University, Thessaloniki, Greece, 2024. [Google Scholar]
- Silvester, R.; Hsu, J.R.C. Coastal Stabilization; World Scientific: Singapore, 1997. [Google Scholar]
- Kemp, J.; Vandeputte, B.; Eccleshall, T.; Simons, R.; Troch, P. A modified hyperbolic tangent equation to determine equilibrium shape of Headland Bay beaches. Coastal Eng. Proc. 2018, 1, 106. [Google Scholar] [CrossRef]
- Greece Information—Map of Greece. Available online: https://www.enchantedlearning.com/europe/greece/index.shtml (accessed on 7 May 2024).
- In the Parliament, the Erosion of the Coasts of the Municipality of Thermaikos. Available online: https://thermaikos.news/eidiseis/sth-boylh-h-diabrrwsh-twn-aktwn-toy-dimoy-thermaikoy/ (accessed on 7 May 2024).
- Dafloukas, C.; Savvidis, Y. Longshore sediment Transport in Relation to Climate Change and Interactions of Coastal Engineering Projects with the Shoreline: The Case of the Harbor of Neoi Epivates (Thermaikos Bay). In Proceedings of the 15th PanHellenic Conference of Hellenic Hydro-Technical Union, Thessaloniki, Greece, 2–3 June 2022. [Google Scholar]
- Georgakakis, K.; Pavlidou, E. Study for the Treatment of the Problem of Sand Deposition in the Fishing Harbor of New Epivates (East Thermaikos Gulf). Master’ Thesis, Alexander Technological Educational Institute of Thessaloniki, Sindos, Thessaloniki, Greece, 2018. [Google Scholar]
- Google Earth Pro. Version 7.3.6.9345. Available online: https://www.google.com/earth/versions/#earth-pro (accessed on 18 June 2023).
- Dafloukas, C. Coastal Sand Transport and Interactions of Coastal Engineering Works with the Shoreline. The Case of the Coastal Zone of Nea Epivates (Gulf of Thessaloniki). Master’ Thesis, International University of Greece, Sindos, Thessaloniki, Greece, 2021. [Google Scholar]
- Koutitas, C. Introduction in Coastal Engineering and Harbor Works; ZHTH: Thessaloniki, Greece, 1996. [Google Scholar]
- Borah, D.K.; Balloffet, A. Beach evolution caused by littoral drift barrier. J. Waterw. Port Coastal Ocean Eng. 1985, 111, 645–660. [Google Scholar] [CrossRef]
- Κatsoulis, D. Wind Conditions over the Aegean Sea. Ph.D. Thesis, University of Athens, Athens, Greece, 1970. (In Greek). [Google Scholar]
- Savvidis, Y.; Mamtsadeli, S. Environmental state of a harbor in terms of waters’ renewal. A case study for a fishery harbor of Thessaloniki Bay (NW Aegean Sea). J. Geosci. Environ. Prot. 2022, 10, 385–406. [Google Scholar] [CrossRef]
- Bayram, A.; Larson, M.; Hanson, H. A new formula for the total longshore sediment transport rate. Coastal Eng. 2007, 54, 700–710. [Google Scholar] [CrossRef]
- Koutitas, C.; Scarlatos, P. Computational Modelling in Hydraulic and Coastal Engineering; CRC Press: Boca Raton, FL, USA, 2015; p. 313. [Google Scholar] [CrossRef]
- Kamphuis, J.W. Alongshore Sediment Transport Rate. J. Waterw. Port Coastal Ocean Eng. 1991, 117, 624–640. [Google Scholar] [CrossRef]
- CERC (Coastal Engineering Research Center). Shore Protection Manual; Corps of Engineers, Waterways Experiment Station, Department of the Army: Vicksburg, MS, USA, 1984; Volume 1–2. [Google Scholar]
- Pelnard-Considere, R. Essai de Theorie de L’evolution des Formes de Rivage en Plages de Sable et de Galets. In Les Energies de la Mer: Compte Rendu Des Quatriemes Journees de L’hydraulique, Paris 13, 14 and 15 Juin 1956; Question III, Rapport 1, 74-1-10; Société hydrotechnique de France: Paris, France, 1956. [Google Scholar]
- Tsembekidis, G. Technical File for the Exemption from the Applicable Provisions of the Environmental Licensing Procedure of the “Rehabilitation Project of the Neoi Epivates Fishing Shelter of the Municipality of Thermaikos”; Thessaloniki Central Macedonia Region Services: Thessaloniki, Greece, 2017. (In Greek) [Google Scholar]
- de Macêdo, R.J.A.; Manso, V.D.A.V.; da Fontoura Klein, A.H. The geometric relationships of salients and tombolos alonga mesotidal tropical coast. Geomorphology 2022, 411, 108311. [Google Scholar] [CrossRef]
- Koutandos, E.V.; Karambas, T.H.V.; Koutitas, C.G.; Prinos, P.E. Shoreline changes in presence of a floating breakwater. In Proceedings of the International Conference ‘Protection and Restoration of the Environment VI’, Skiathos, Greece, 1–5 July 2002; Volume I; pp. 403–410. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).