Study on the Seepage Mechanism of Gaskets at the Joints of Shield Segments Based on Coupled Euler-Lagrangian Method
Abstract
1. Introduction
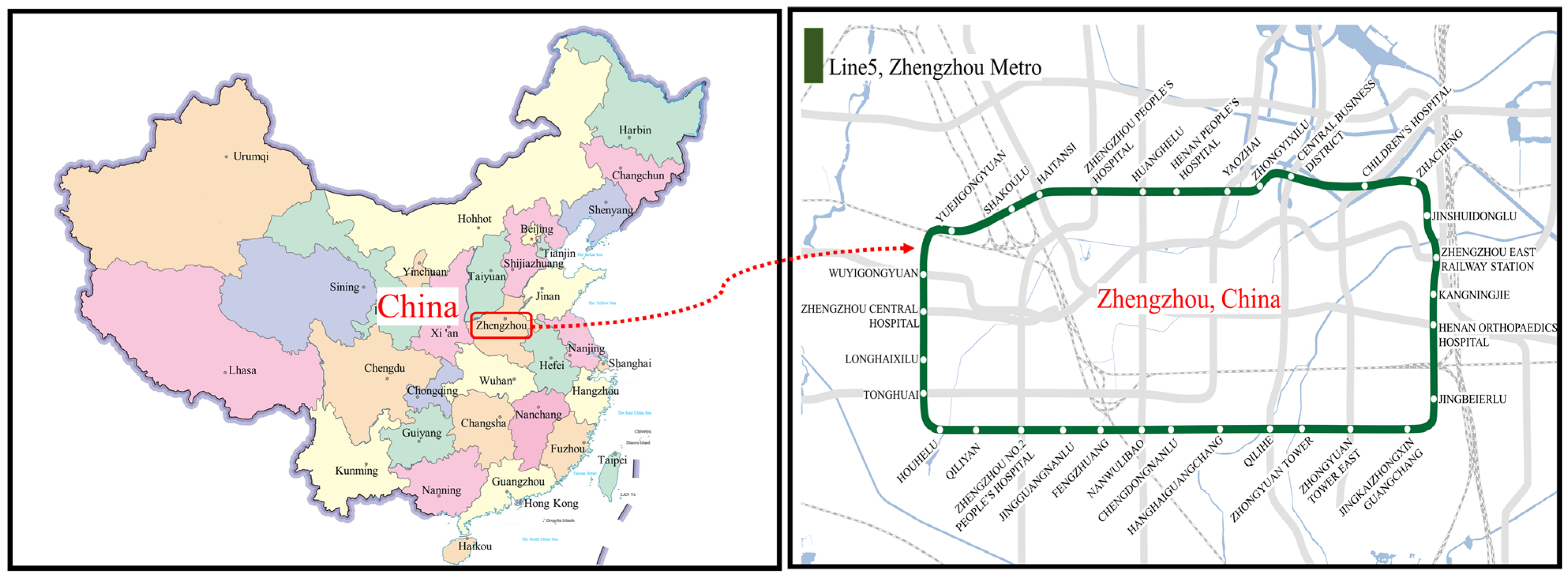
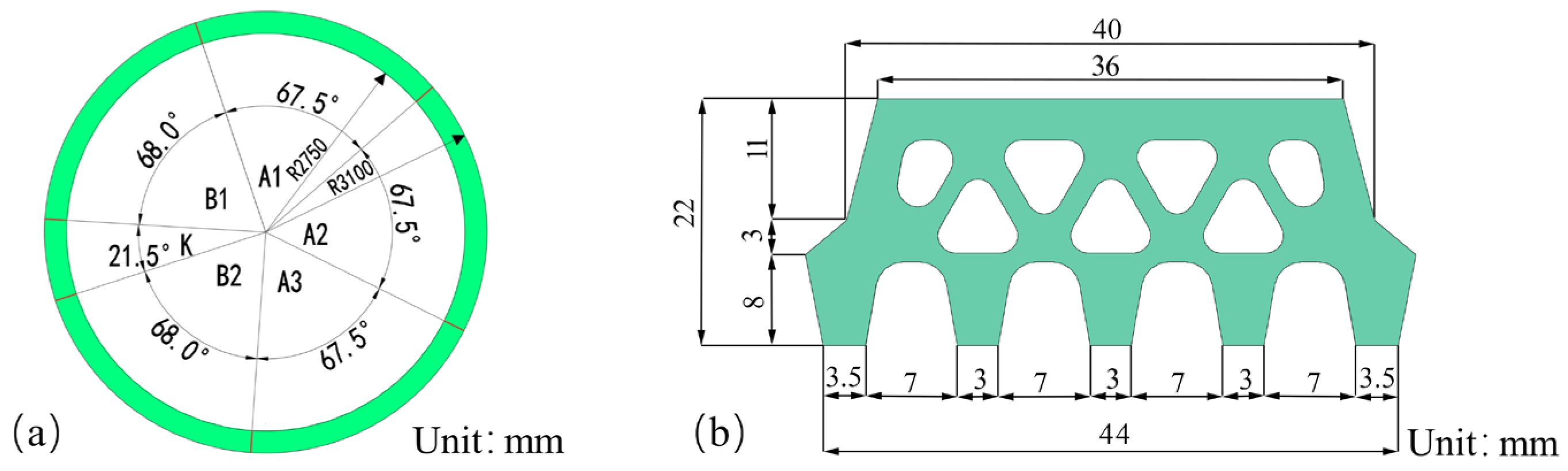
2. Project Overview
3. CEL Fluid-Solid Coupling and Numerical Modeling
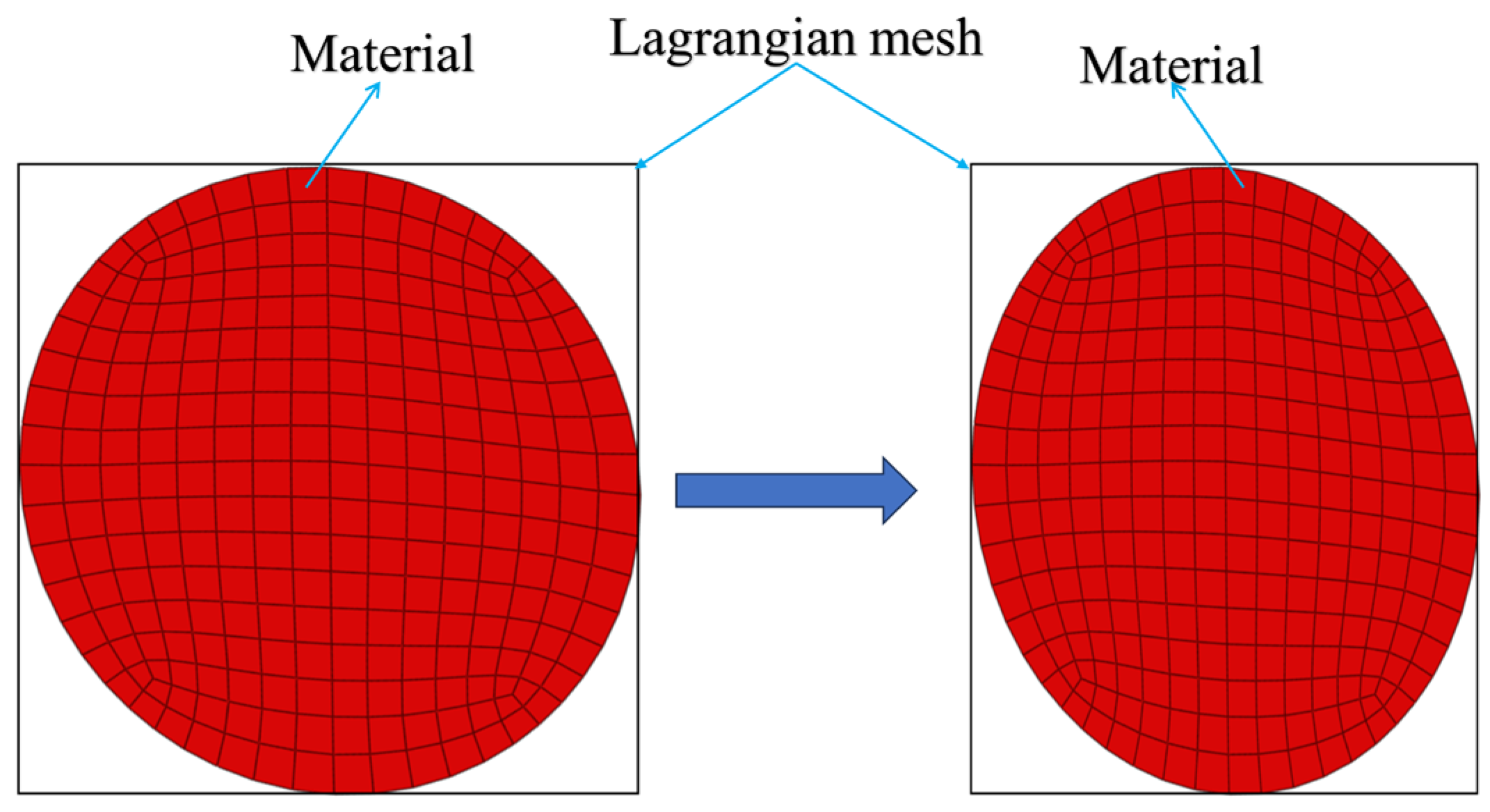
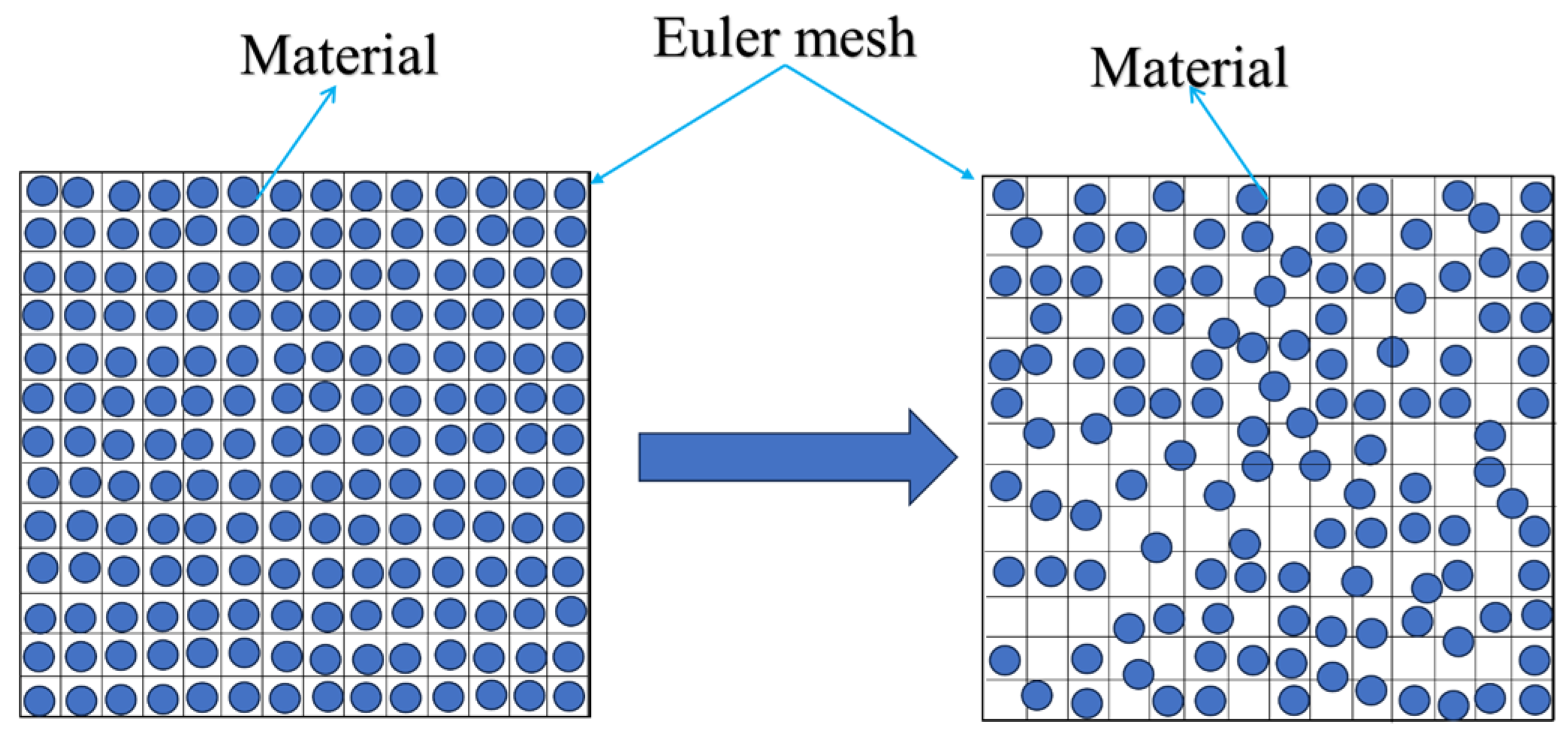
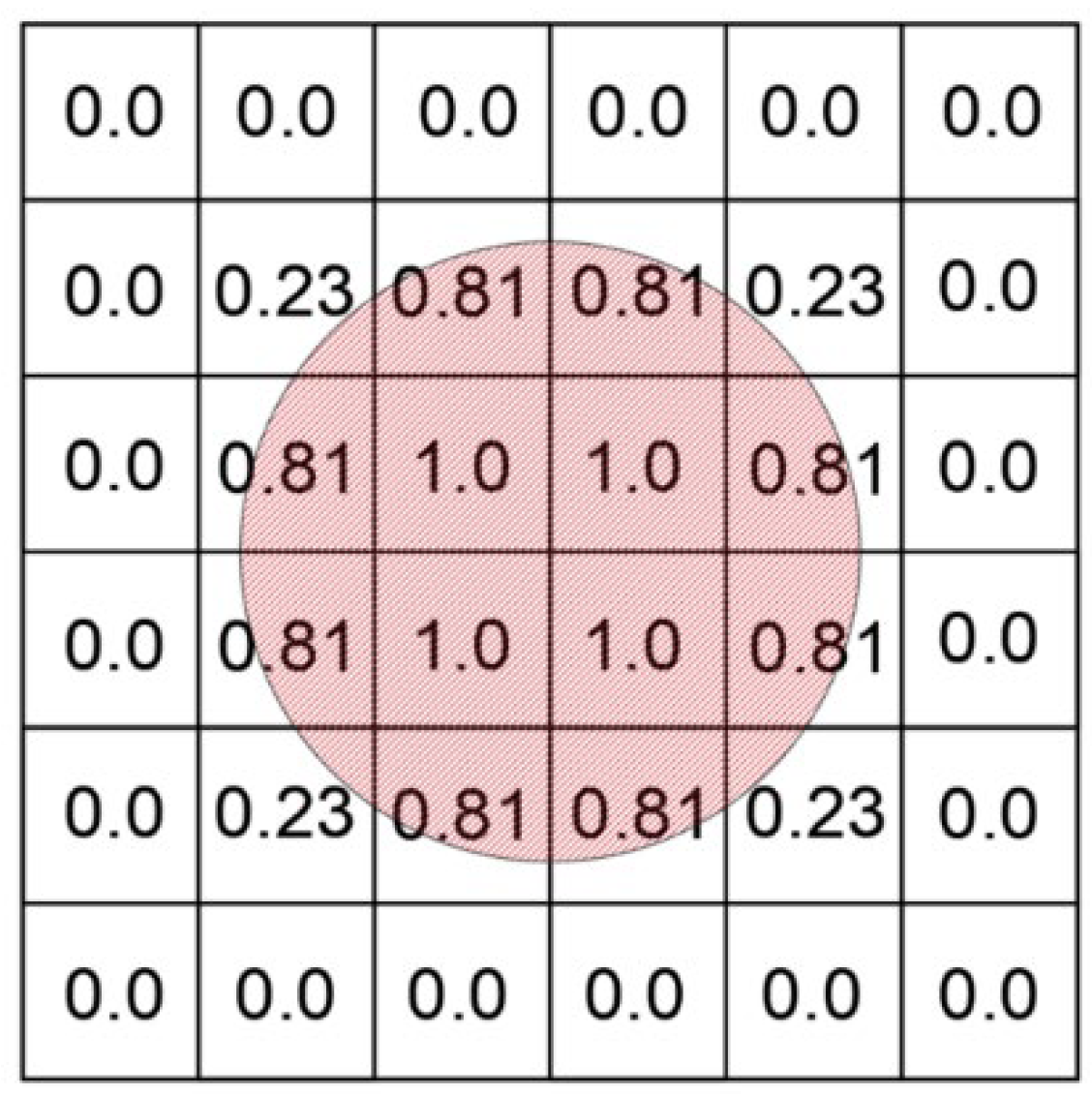
3.1. CEL Fluid-Sructure Coupling
3.2. Model Construction
3.2.1. Constitutive Relationship of Materials and Parameter Settings
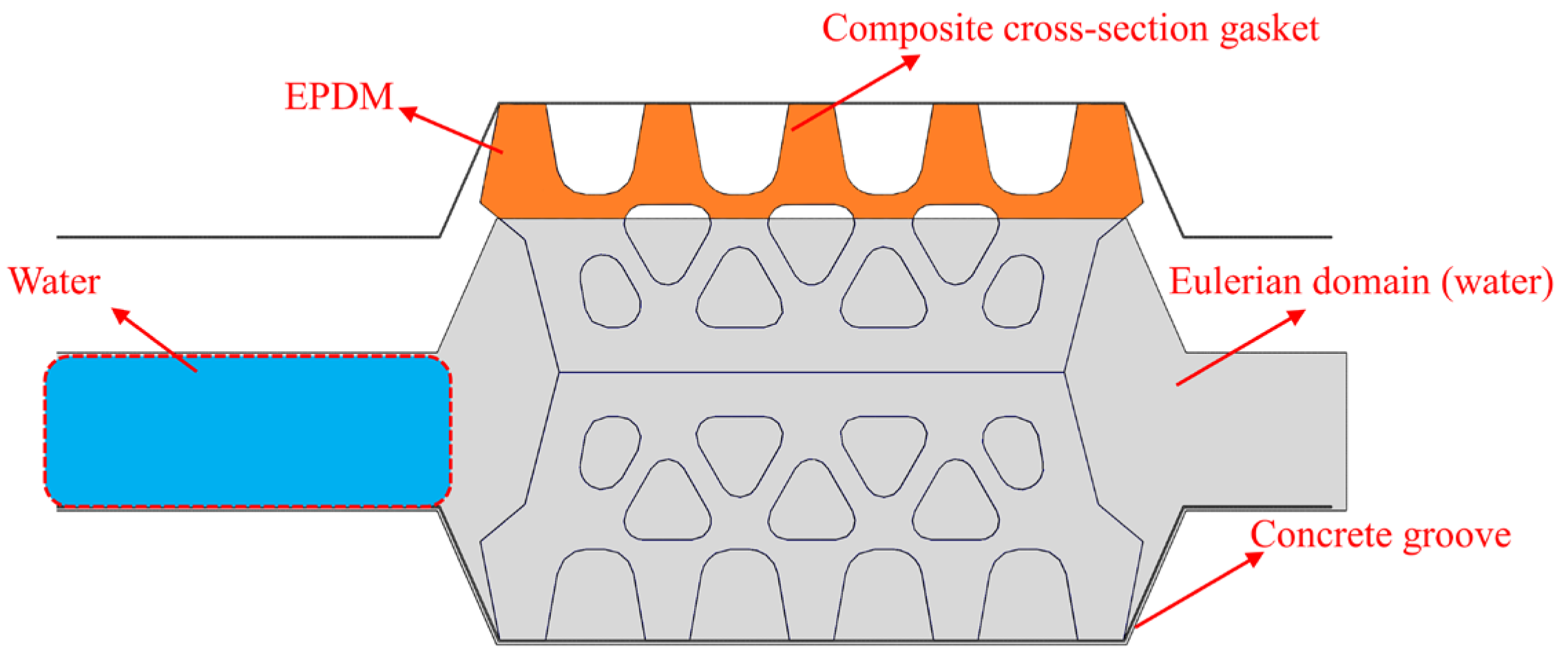
3.2.2. Setting of Eulerian Domain and Initial Material Assignment
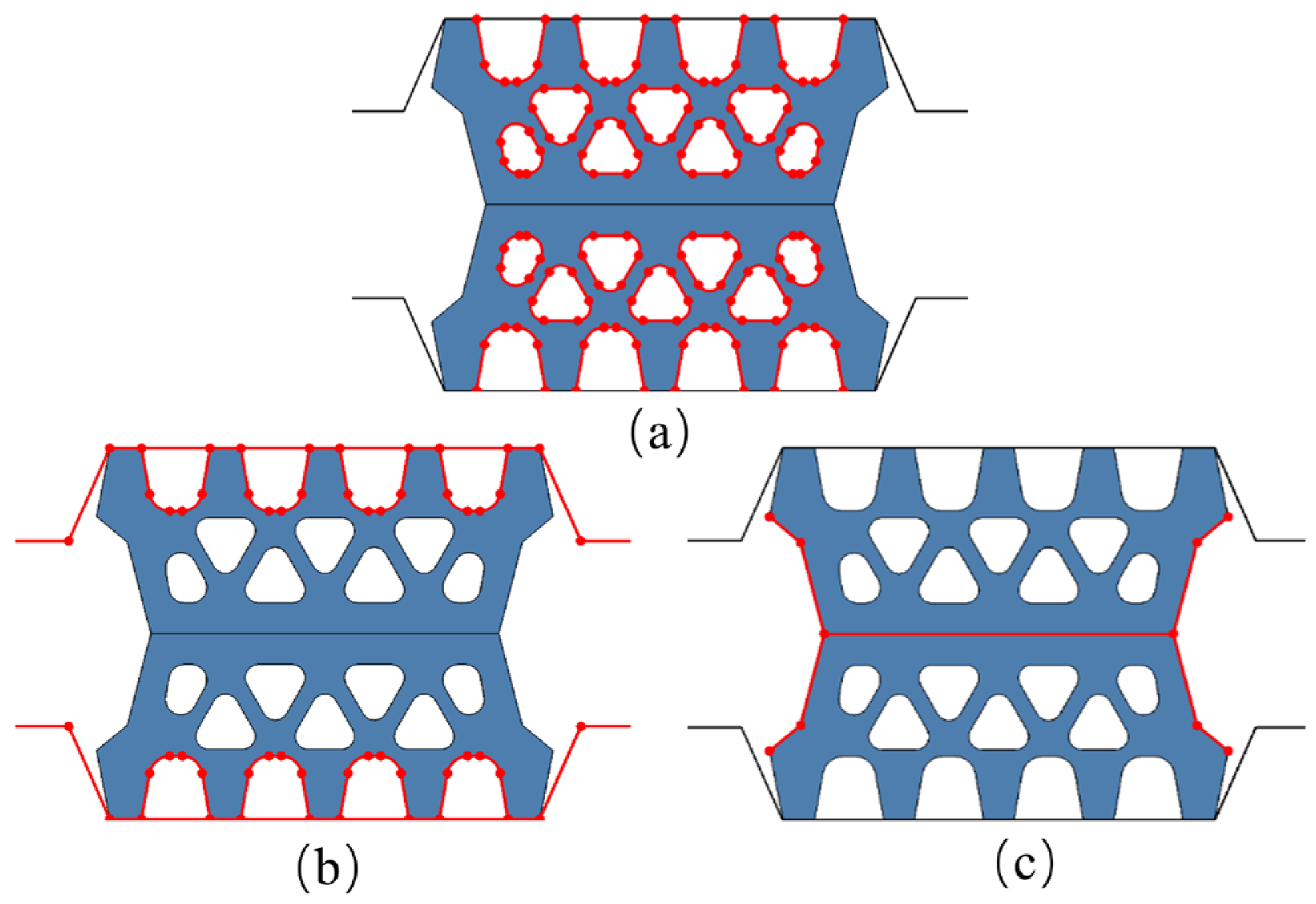
3.2.3. Contact Relations and Boundary Conditions
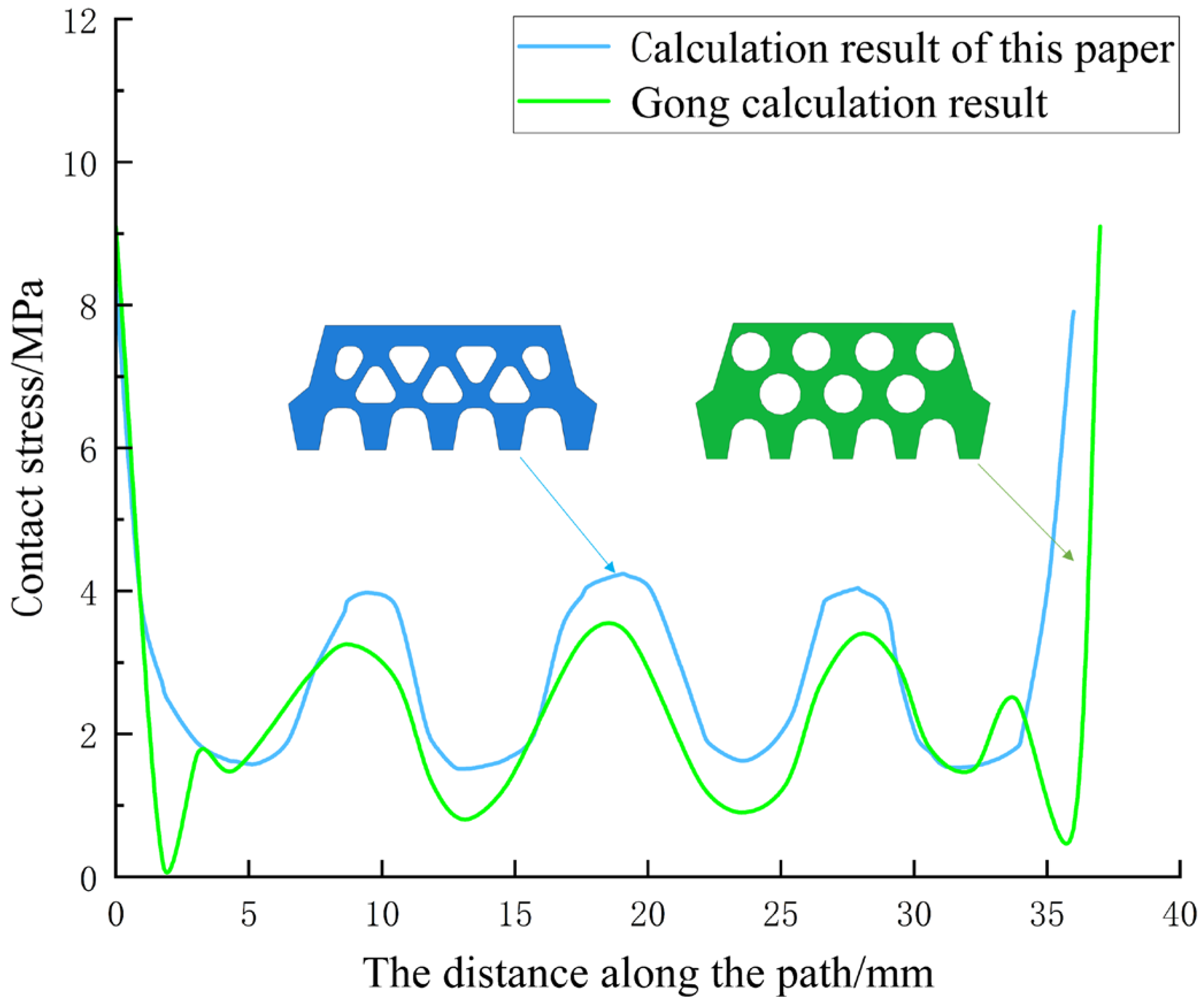
3.3. Model Verification
4. Leakage Mechanism of Sealing Gasket at Shield Segment Joint
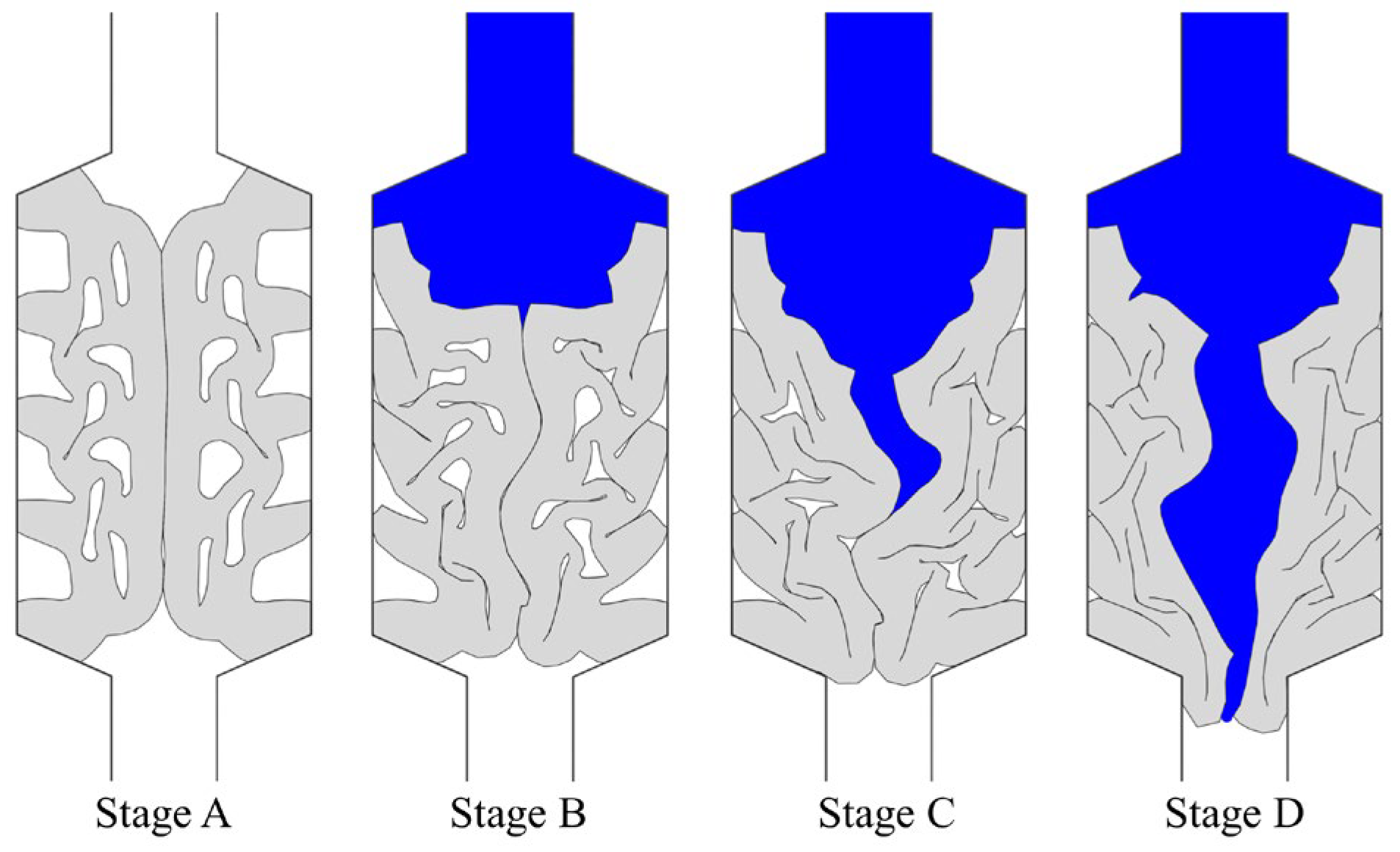
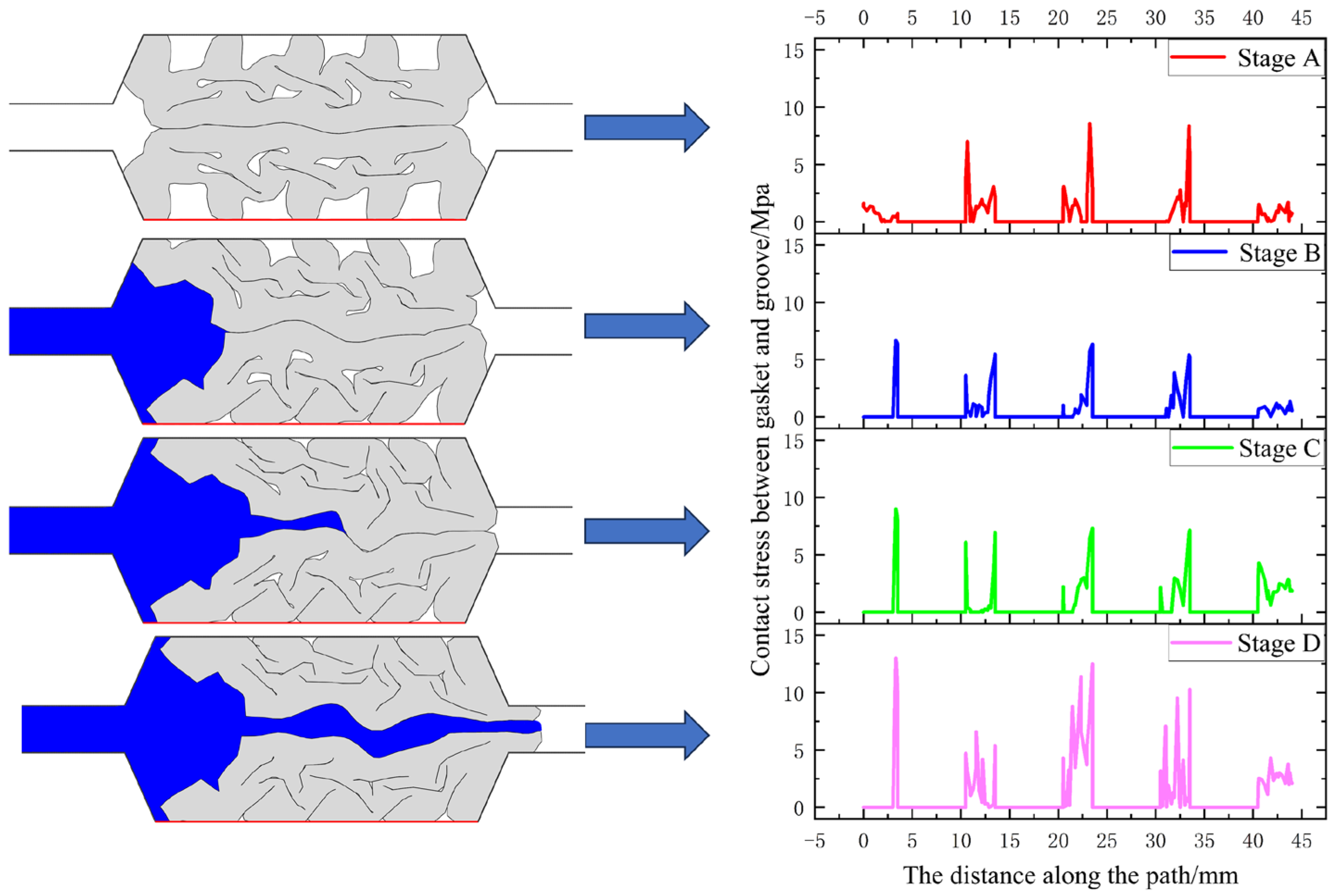
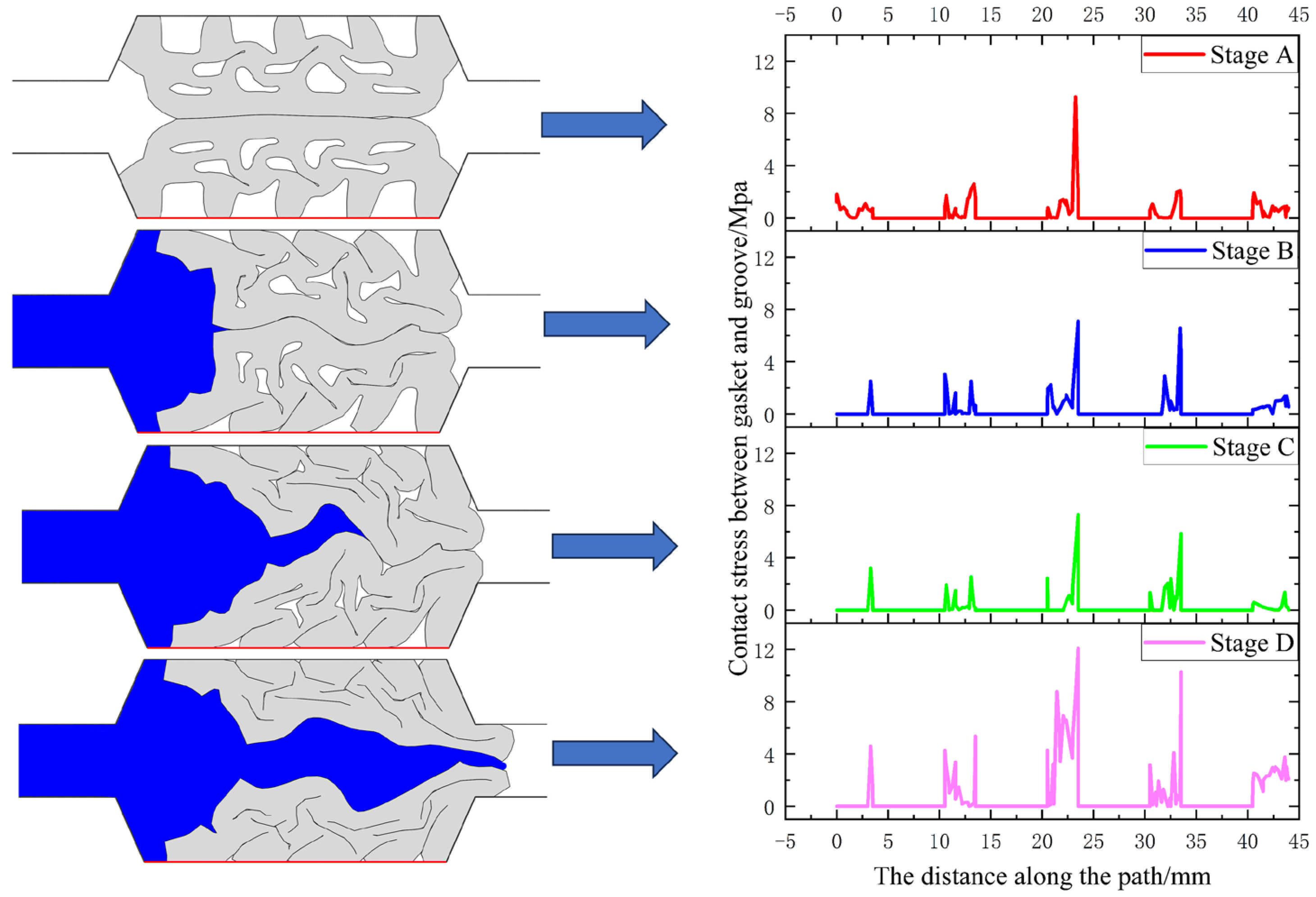
4.1. Leakage Process
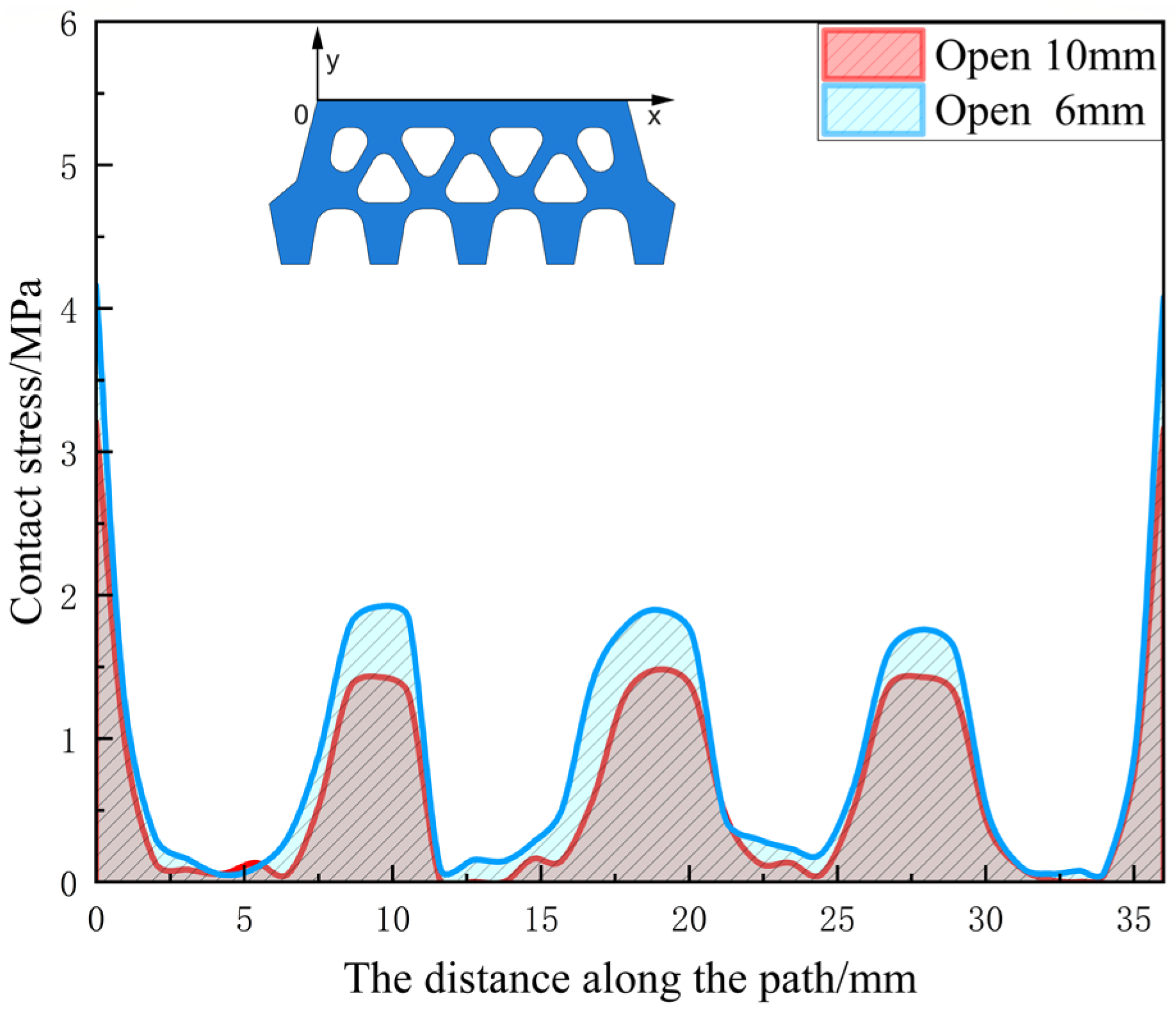
4.2. Seepage Stress Barrier
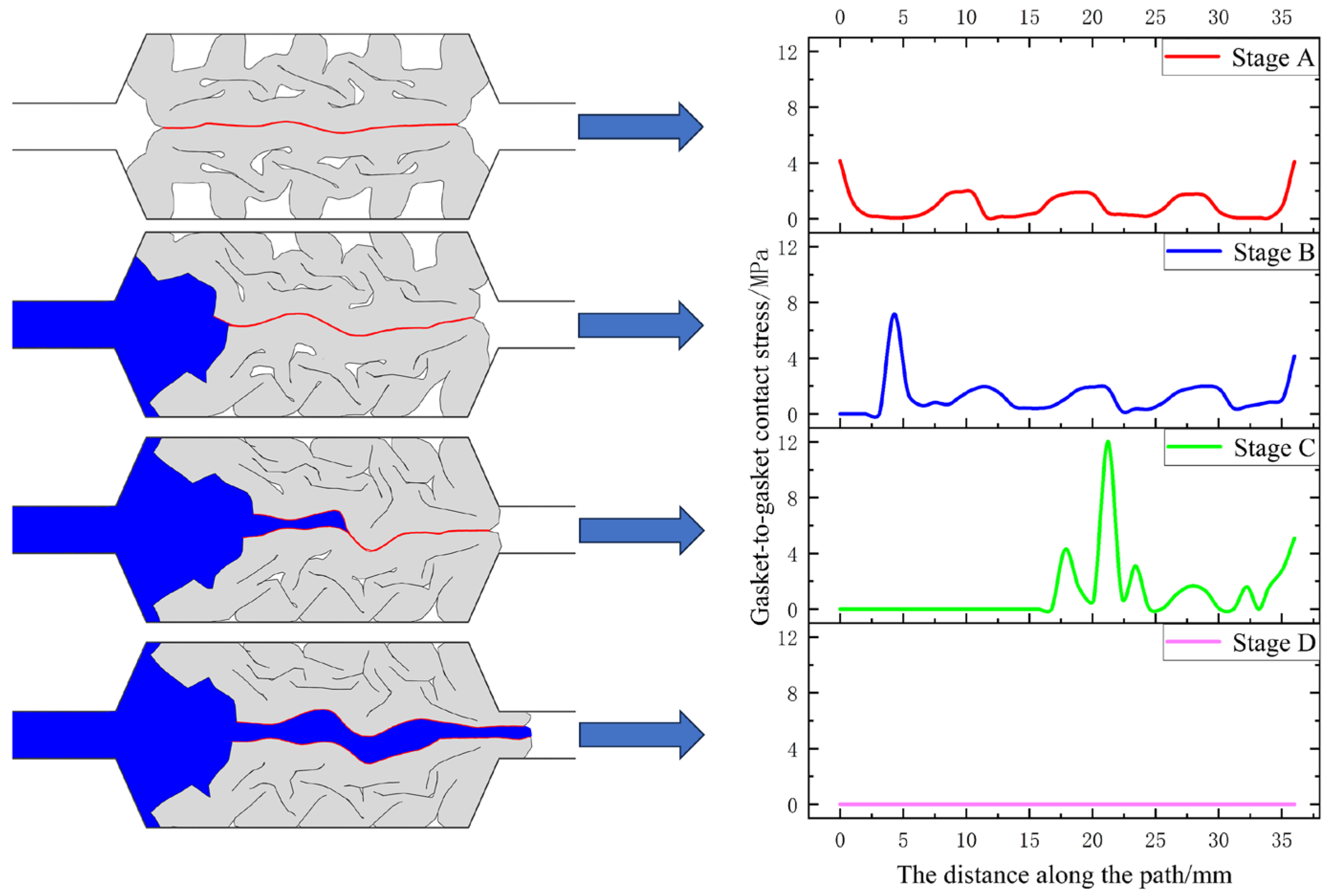
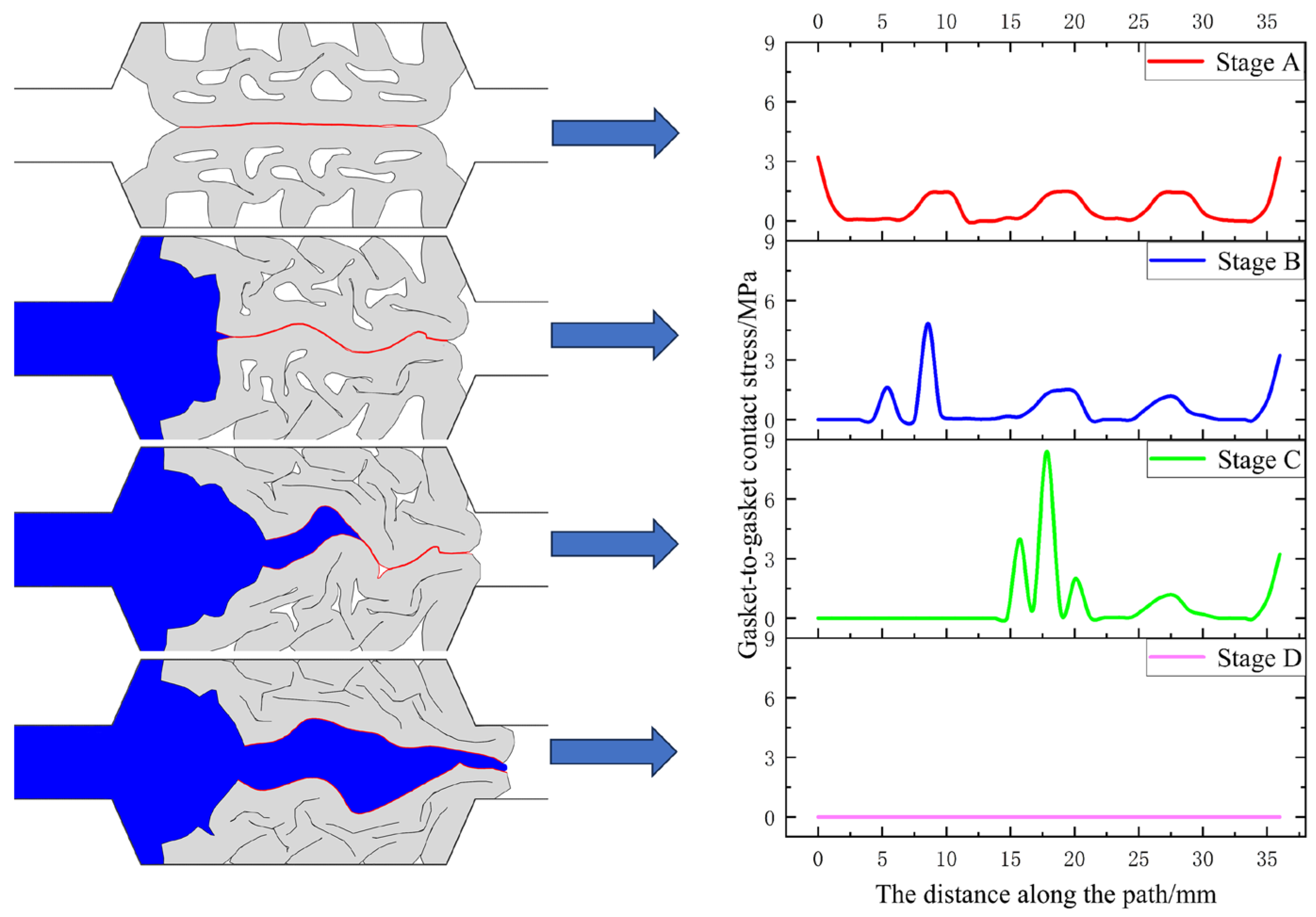
4.3. Dynamic Variation of Interface Stress
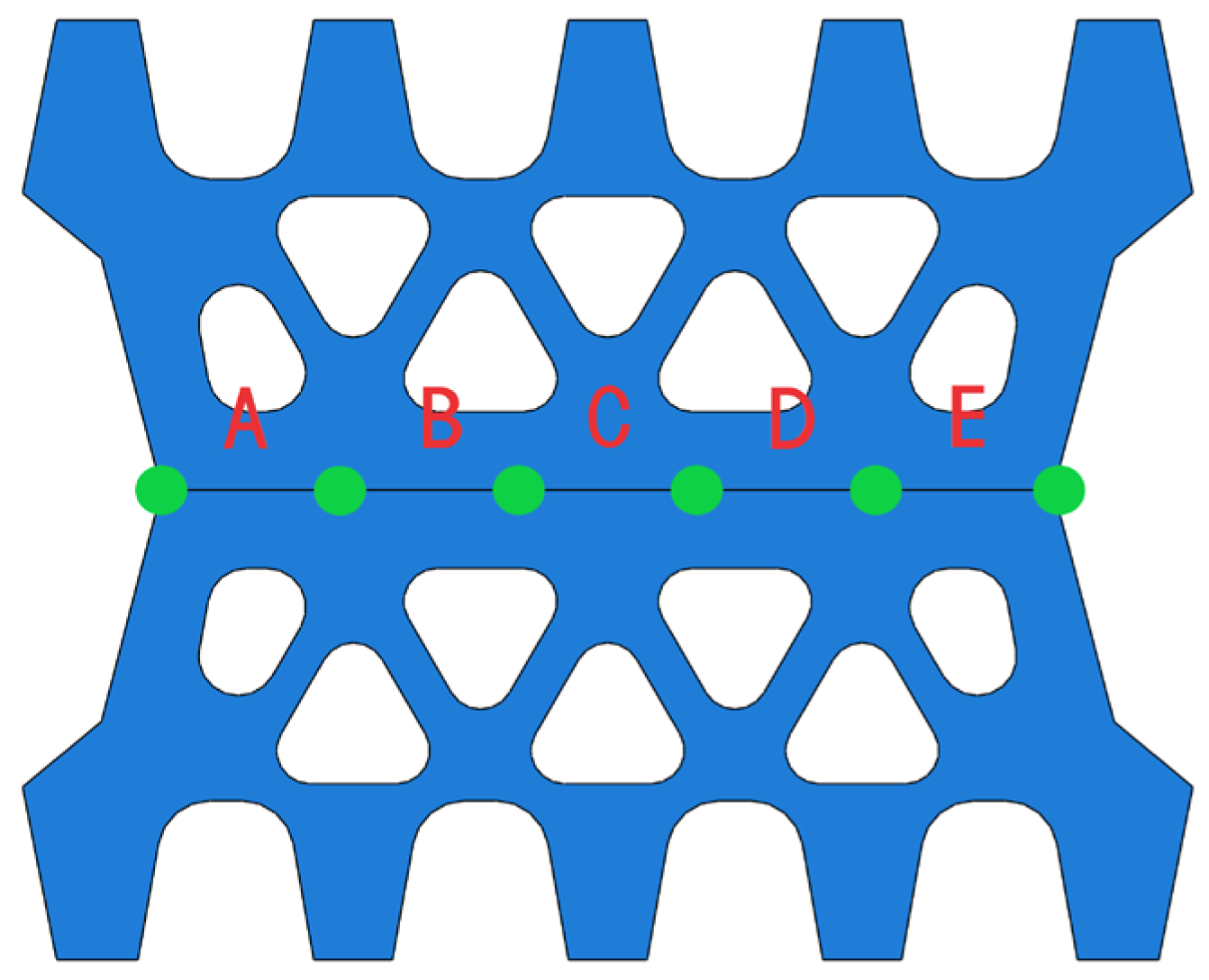
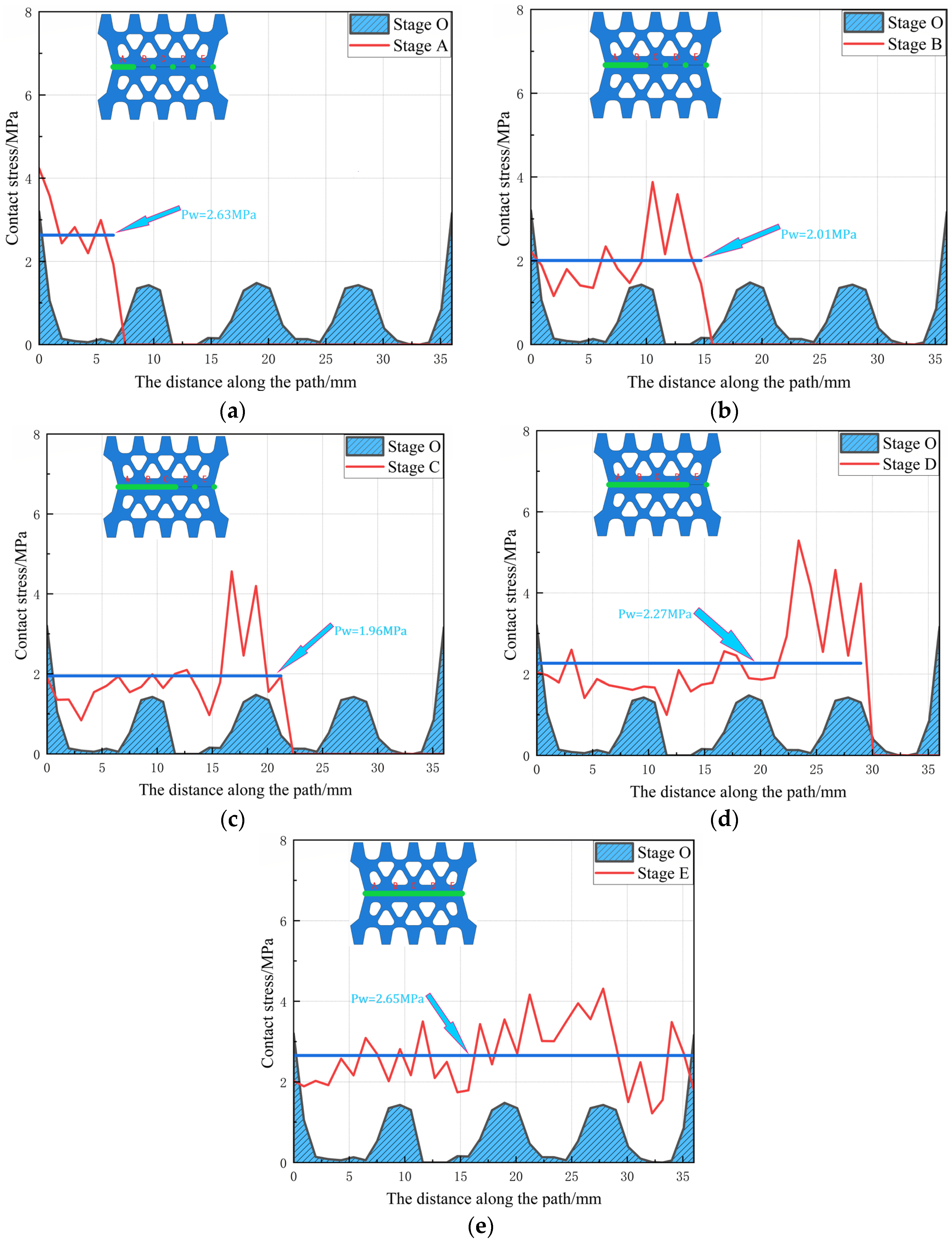
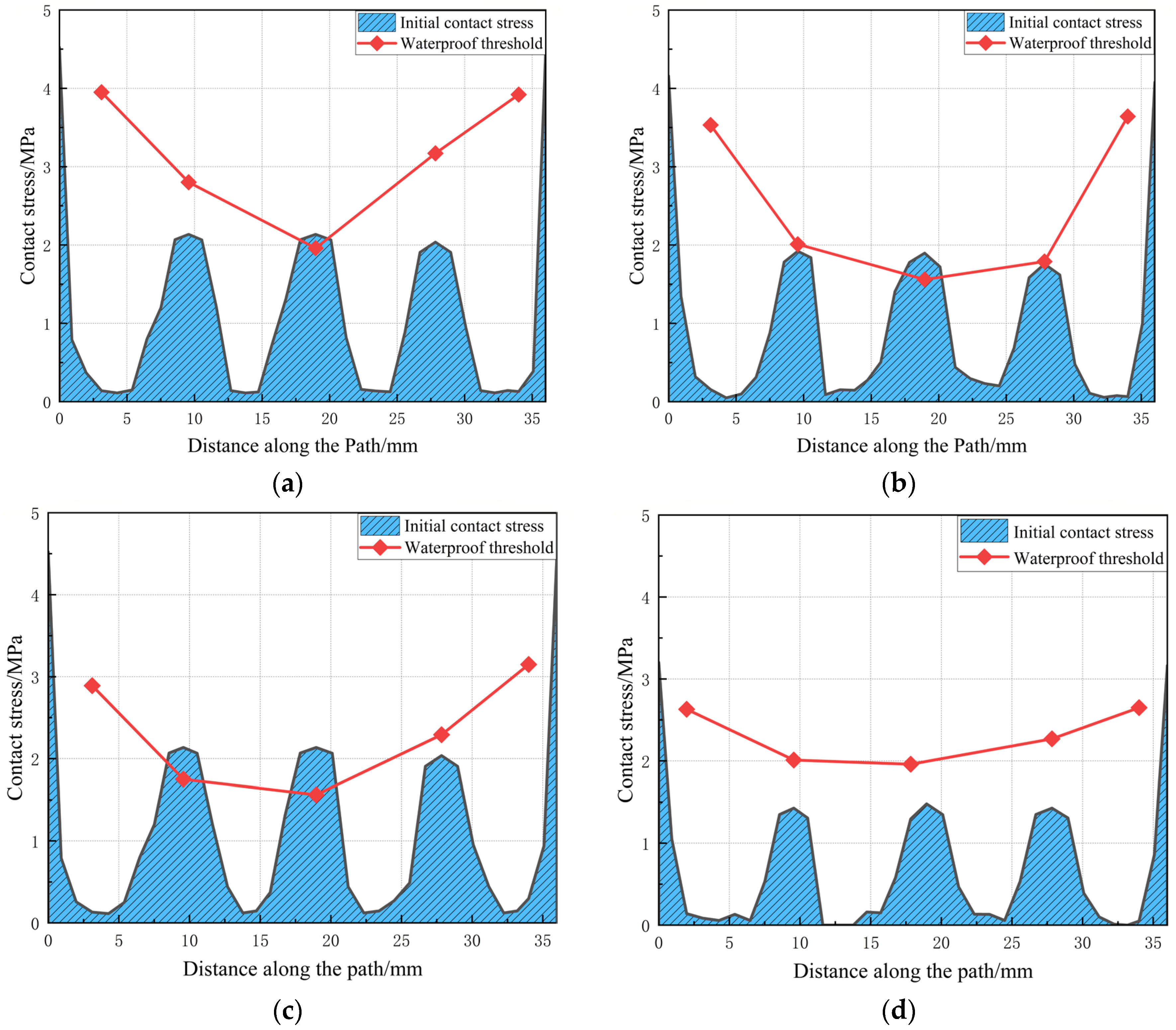
5. Waterproof Performance Analysis of Gasket under Water Pressure
6. Discussion and Conclusions
6.1. Discussion
- 1.
- Currently, this paper primarily focuses on the waterproof failure mechanism caused by water pressure acting on elastic rubber sealing pads in the open state. However, the waterproof failure mechanism of sealing pads in staggering situations has not been addressed. Future research could delve deeper into this aspect, conducting more extensive exploration and analysis to comprehensively understand the waterproof performance of sealing pads under different conditions.
- 2.
- When analyzing the waterproof failure mechanism of elastic rubber sealing pads, this paper has not yet considered the influence of long-term effects such as fatigue and stress relaxation that may occur during prolonged use. These long-term effects could significantly impact the waterproof performance of the sealing pads. Therefore, the next step in research could involve a deeper investigation into the waterproof failure mechanism of elastic rubber sealing pads under prolonged water pressure. This would further refine the theoretical framework of waterproof design and propose more accurate definitions and criteria for safety factors, providing more reliable guidance for waterproof design.
6.2. Conclusions
- 1.
- Throughout the entire process, from segment assembly to leakage at the joint, the elastic rubber sealing gasket undergoes four key stages: gasket compression, pressure water extrusion, water wedging, and final leakage. Under the action of pressure water, the interface between the sealing gaskets is initially separated, creating gaps. With increasing water pressure, the interface between the gaskets gradually opens until the pressure water finally breaches, resulting in leakage at the joint.
- 2.
- Analysis reveals that the permeation stress barrier formed by the initial contact stress exhibits a “W” symmetric distribution, with the contact stress peak at both ends of the interface approximately twice that of the middle. The contact stress at the gasket-groove interface undergoes intermittent changes throughout the entire water seepage process.
- 3.
- By using the weighted average of water pressure to determine the waterproof threshold at each stage of the gasket, it is observed that the waterproof threshold of the elastic rubber gasket is dependent on the seam opening size. The waterproof threshold of the elastic gasket decreases with increasing seam opening size; when the opening size of the elastic gasket is small, its waterproof threshold is larger, indicating stronger waterproofing capability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xue, Y.D.; Zhang, S.; Zhou, M.L.; Zhu, H.H. Novel SfM-DLT method for metro tunnel 3D reconstruction and Visualization. Undergr. Space 2021, 6, 134–141. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Y. Joint Waterproofing Design for River-crossing Shield Tunnel of Nanjing Subway, Line 10. China Build. Waterproofing 2013, 18–25. [Google Scholar] [CrossRef]
- Yang, J.S.; Fu, Q.; Yu, L.J.; Wang, T.; Wei, Q.; Li, W.; Wang, S.W. Research Progress of Rubber Modified Acrylate Pressure Sensitive Adhesive. J. Petrochem. Univ. 2023, 36, 8. [Google Scholar]
- Girnau, G. Lining and waterproofing techniques in Germany. Tunn. Tunn. Int. 1978, 10, 36–45. [Google Scholar]
- Paul, S.L. Hydraulic Pressure and Stiffness Tests of Gaskets for Precast Concrete Tunnel Liner Segments; Unpublished Report; Department of Civil Engineering, University of Illinois at Urbana-Champaign: Urbana, IL, USA, 1984. [Google Scholar]
- Liu, Y.K.; Wu, Y.; Li, W.H.; Zhang, Q.S.; Liu, R.T.; Bai, J.W.; Li, W. Development of a water leakage model test system and investigation of the water leakage behavior in subsea shield tunnels during operation. Measurement 2024, 233, 114691. [Google Scholar] [CrossRef]
- Zhang, G.L.; Zhang, W.J.; Cao, W.Z.; Wang, B.D.; Lai, T.T.; Guo, W.S.; Gao, P. A novel test setup for determining waterproof performance of rubber gaskets used in tunnel segmental joints: Development and application. Tunn. Undergr. Space Technol. 2021, 115, 104079. [Google Scholar] [CrossRef]
- Zhao, M.; Ding, W.Q.; Peng, Y.C.; Shen, B.W.; Guo, X.H.; Yang, L.S. Experimental Study on the Reliability of Shield Tunnel Segment Joints to Remain Watertight Under High Water Pressure. Mod. Tunn. Technol. 2013, 50, 87–93. [Google Scholar]
- Shalabi, F.I.; Cording, E.J.; Paul, S.L. Concrete segment tunnel lining sealant performance under earthquake loading. Tunn. Undergr. Space Technol. 2012, 31, 51–60. [Google Scholar] [CrossRef]
- Ding, W.Q.; Wang, Q.S.; Qiao, Y.F.; Jin, Y.L. Experimental investigation on waterproofing performance of segmental joint with double gaskets for shield tunnel. Undergr. Space 2022, 7, 898–910. [Google Scholar] [CrossRef]
- Karpenko, M.; Skačkauskas, P.; Prentkovskis, O. Methodology for the composite tire numerical simulation based on the frequency response analysis. Eksploat. Niezawodn. 2023, 25, 1–11. [Google Scholar] [CrossRef]
- Yan, Q.X.; Zhong, H.J.; Zhang, C.; Zhao, Z.C.; Wen, Y.X.; Wang, P. Novel numerical model to simulate water seepage through segmental gasketed joints of underwater shield tunnels considering the superimposed seepage squeezing effect. Undergr. Space 2023, 13, 104–120. [Google Scholar] [CrossRef]
- Xu, L.; Wu, G.Z. Some Forms of Strain Energy Function for Rubber with Finite Element Analysis. China Rubber Ind. 1999, 46, 707–711. [Google Scholar]
- Zhang, T.; Huo, Y.P.; Wu, Y.; Yin, Z.N.; Wen, Y.X.; Yan, Q.X. Test and Numerical Simulation of Mechanical Performance of Waterproof Gasket in Shiel Tunnel Under River. Railw. Eng. 2022, 62, 128–133. [Google Scholar]
- Ouyang, W.B. Mechanical Test and Numerical Analysis of Elastic Gaskets of Shield Tunnels. Tunn. Constr. 2013, 33, 933–936. [Google Scholar]
- Gong, C.J.; Ding, W.Q.; Soga, K.; Mosalam, K.M. Failure mechanism of joint waterproofing in precast segmental tunnel linings. Tunn. Undergr. Space Technol. 2019, 84, 334–352. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Feng, S.M.; You, G.G.; Wen, Z.J. Study on Waterproof Mechanism of Shield Tunnel Joints Considering Water Pressure Process. Tunn. Constr. 2020, 40, 1594–1601. [Google Scholar]
- Sun, L.W. Numerical Analysis of Waterproof Mechanism of Shield Tunnel Joint Based on Applied Water Pressure. Tunn. Constr. 2018, 38, 603–610. [Google Scholar]
- Zhang, J.W.; Chen, Y.Y.; Feng, Q.K. Characteristic parameters’ optimization based on contact pressure of sealing gasket for segmental joints. Adv. Mech. Eng. 2020, 12, 1687814020943360. [Google Scholar]
- Xie, J.C.; Huang, X.H.; Jin, G.L. Analytical model for the sealant performance of tunnel gasketed joints based on multi-scale contact and percolation theories. Undergr. Space 2024, 14, 319–337. [Google Scholar] [CrossRef]
- Karpenko, M.; Bogdevičius, M. Investigation of hydrodynamic processes in the system—“pipeline-fittings”. In Proceedings of the TRANSBALTICA XI: Transportation Science and Technology: Proceedings of the International Conference TRANSBALTICA, Vilnius, Lithuania, 2–3 May 2019; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 331–340. [Google Scholar]
- Zhang, J.H.; Li, Y.; Liu, X.W.; Sun, Z.B.; Cao, G.Q. Statistical analysis of shield tunnel disease based on horizontal convergence in soft clay. China Civ. Eng. J. 2020, 53, 124–130. [Google Scholar]
- Dai, X.Q.; Wang, J.; Li, Z.X.; Han, J.Y.; Wang, W.W.; Li, K.J. Research on current situation of causes and prevention measures of water leakage diseases in shield tunnels. Yangtze River 2022, 53, 186–192. [Google Scholar]
- Liu, Y.J. Study on Structural Safety of Shield Tunnel and Vehicle Dynamic Behavior under Disease Condition in Beijing Subway; Beijing Jiaotong University: Beijing, China, 2019. [Google Scholar]
- Shao, H.; Wang, R. Analysis of the Influence Factors and Its Characteristics of Metro Shield Tunnel Defects in Shanghai. Mod. Tunn. Technol. 2018, 55, 922–929. [Google Scholar]
- Li, P. Study on Waterproofing Mechanism and Design Method of the Double Sealing Gaskets for Shield Tunnel under High Water Pressure; Southwest Jiaotong University: Chengdu, China, 2021. [Google Scholar]
- Yao, X.H.; Huang, Y.T.; Ou, Z.C.; Liu, X.M.; Hu, B.R. CEL Algorithm-Based Analysis of Dynamic Characteristics of Amphibious Aircraft Landing on Water. J. South China Univ. Technol. (Nat. Sci. Ed.) 2015, 43, 110–115. [Google Scholar]
- Wang, W.C. Research on Ice-Soil-Pipeline Coupling Model Based on CEL Method; China University of Petroleum: Beijing, China, 2021. [Google Scholar]
- Yan, S.W.; Lin, S.; Huo, Z.L.; Chu, J.; Guo, W. Coupled Eulerian-Lagrangian finite element analysis of suction caisson penetration processes under hydraulic pressure. Rock Soil Mech. 2017, 38, 247–252. [Google Scholar]
- Zhang, Z.X.; Gu, G.S.; Huang, X.; Zhang, J.Q.; Zhang, C. Experimental Study on Waterproof Performance of Embedded Sealing Gasket of Segment Joint for a Shield Tunnel. Tunn. Constr. 2019, 39, 1402–1411. [Google Scholar]
- Zhang, Q.; Shi, J.W.; Suo, S.F.; Meng, G.Y. Finite element analysis of rubber materials based on Mooney-Rivlin models and Yeoh models. China Synth. Rubber Ind. 2020, 43, 468–471. [Google Scholar]
- Wang, H.K.; Yu, Y.; Sun, Z.Z.; Xu, W.S. Numerical study on the implosion of hollow slender cylindrical shells and the induced chain failure. J. Ship Mech. 2023, 27, 1208–1220. [Google Scholar]
- Gong, C.J.; Ding, W.Q.; Soga, K.; Mosalam, K.M. Sealant behavior of EPDM gaskets in TBM tunnel segmental joints. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017; p. ARMA-2017-0563. [Google Scholar]
- Zhou, W.F.; Liao, S.M.; Men, Y.Q. A fluid-solid coupled modeling on water seepage through gasketed joint of segmented tunnels. Tunn. Undergr. Space Technol. 2021, 114, 104008. [Google Scholar] [CrossRef]




| Type | Definition |
|---|---|
| Wet stained | Moist spots with noticeable color changes on the inner surface of tunnel segments. |
| Water seepage | Infiltration of water into segments, resulting in moisture on the inner surface of segments. |
| Dribbling | When the amount of water reaches a certain level, it drops from above. |
| Mud leakage sand | Water mixed with soil particles, sediment, and other materials from behind the segments flows out from the leakage area. |
| Leak Location | Leakage Quantity/Piece | Leakage Ratio/% |
|---|---|---|
| T-type seam | 10 | 50 |
| Circumferential seam | 3 | 15 |
| Transverse joint | 4 | 20 |
| Bolt hole | 2 | 10 |
| Reserved grouting hole | 1 | 5 |
| ) | ||
|---|---|---|
| 65 | 0.60 | 0.15 |
| 66 | 0.62 | 0.16 |
| 67 | 0.65 | 0.16 |
| 68 | 0.68 | 0.17 |
| 69 | 0.71 | 0.18 |
| 70 | 0.74 | 0.19 |
| 1.483 × 106 | 0 | 0 | 1.00 × 10−9 | 1.00 × 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Hou, D.; Li, S. Study on the Seepage Mechanism of Gaskets at the Joints of Shield Segments Based on Coupled Euler-Lagrangian Method. Water 2024, 16, 1661. https://doi.org/10.3390/w16121661
Wang X, Hou D, Li S. Study on the Seepage Mechanism of Gaskets at the Joints of Shield Segments Based on Coupled Euler-Lagrangian Method. Water. 2024; 16(12):1661. https://doi.org/10.3390/w16121661
Chicago/Turabian StyleWang, Xiaorui, Dazhao Hou, and Songfeng Li. 2024. "Study on the Seepage Mechanism of Gaskets at the Joints of Shield Segments Based on Coupled Euler-Lagrangian Method" Water 16, no. 12: 1661. https://doi.org/10.3390/w16121661
APA StyleWang, X., Hou, D., & Li, S. (2024). Study on the Seepage Mechanism of Gaskets at the Joints of Shield Segments Based on Coupled Euler-Lagrangian Method. Water, 16(12), 1661. https://doi.org/10.3390/w16121661






