Evaluation of Statistical PMP Considering RCP Climate Change Scenarios in Republic of Korea
Abstract
:1. Introduction
2. Study Area and Datasets
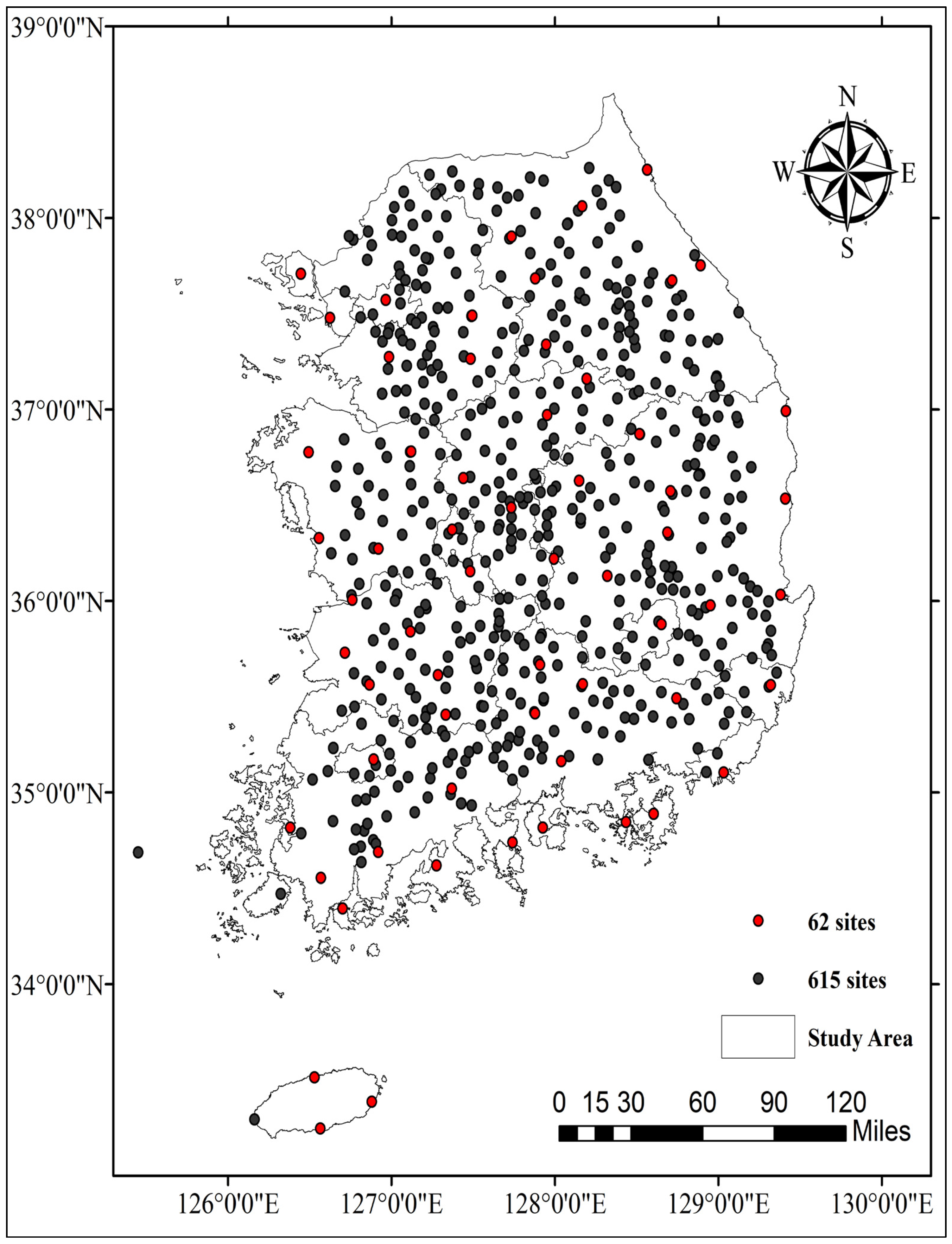
2.1. Study Area
2.2. Datasets
3. Methodology
3.1. Hershfield Method
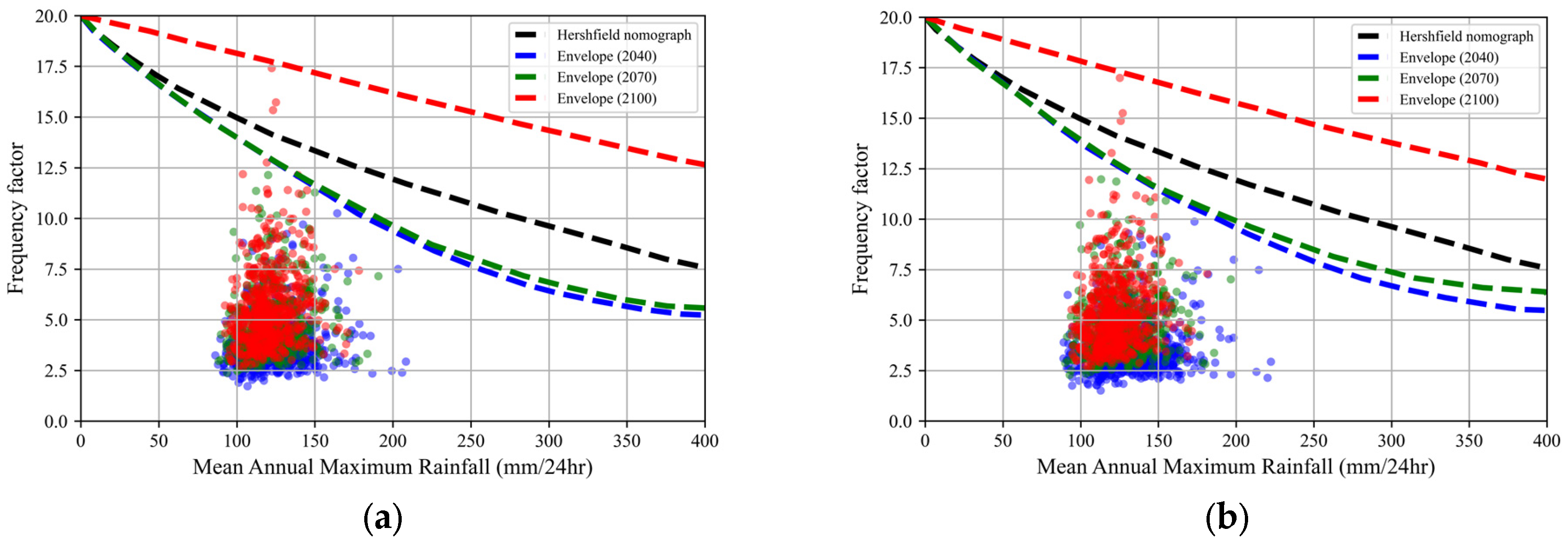
3.2. Hershfield’s Nomograph
3.3. Frequency Factor Method
3.4. Hydrometeorological Method
3.5. Statistical Measures
4. Application and Results
4.1. Statistical Probable Maximum Precipitation for Historical Period
4.2. PMP of Modified Hershfield’s Nomograph for Future Period
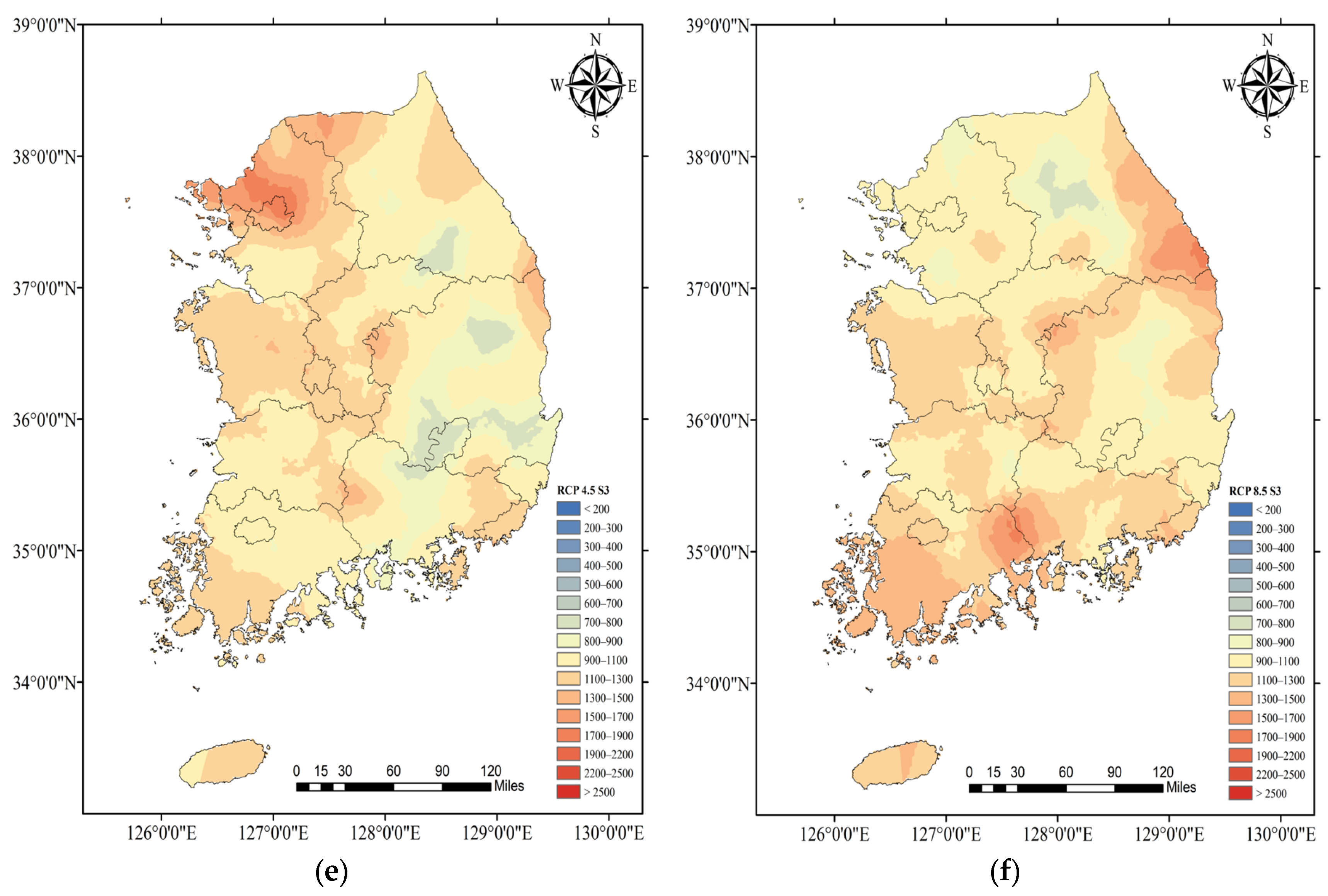
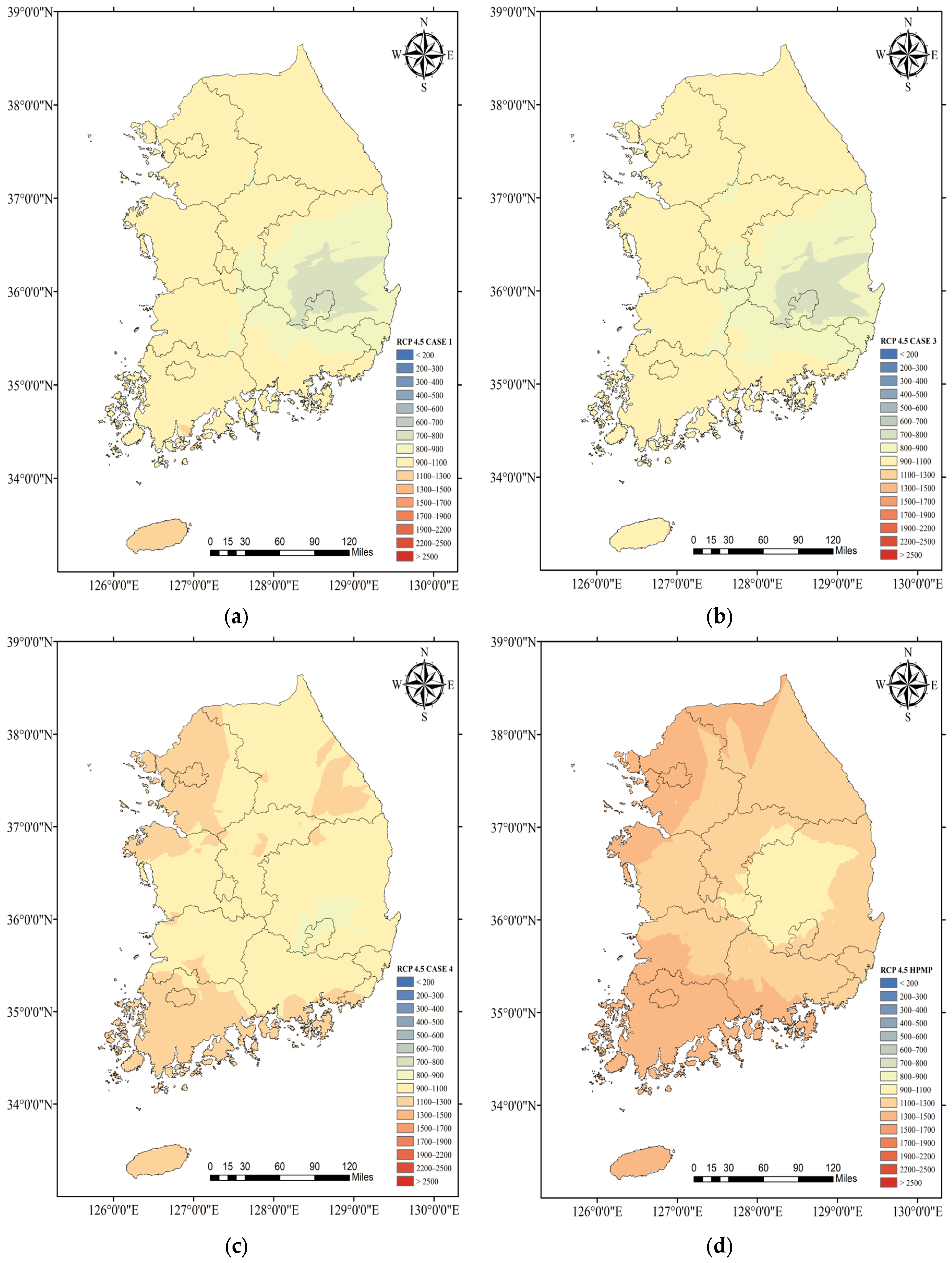
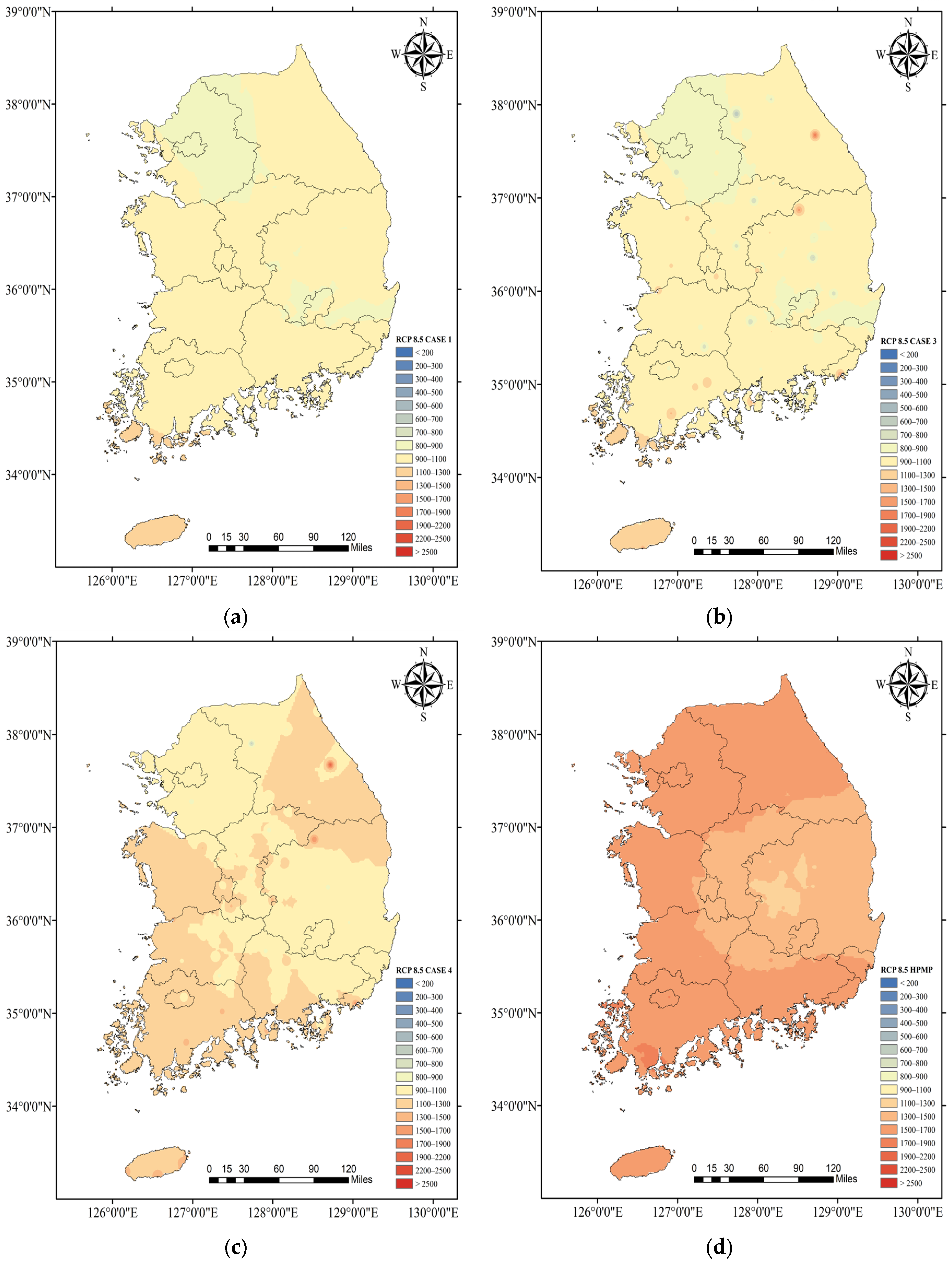
4.3. Comparision of SPMP by Each Method for Future Period
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Meteorological Organization. Manual for Estimation of Probable Maximum Precipitation, 2nd ed.; Operational Hydrology Report No. 1, WMO, No. 332; World Meteorological Organization: Geneva, Switzerland, 1986. [Google Scholar]
- World Meteorological Organization. Manual for Estimation of Probable Maximum Precipitation; WMO-No. 1045; World Meteorological Organization: Geneva, Switzerland, 2009; ISBN 978-92-63-11045-9. [Google Scholar]
- King, L.M.; Micovic, Z. Application of the British Columbia MetPortal for estimation of probable maximum precipitation and probable maximum flood for a coastal watershed. Water 2022, 14, 785. [Google Scholar] [CrossRef]
- Gonzalez-Alvarez, A.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Ramos, H.M. Effect of the non-stationarity of rainfall events on the design of hydraulic structures for runoff management and its applications to a case study at Gordo Creek Watershed in Cartagena de Indias. Colombia. Fluids 2018, 3, 27. [Google Scholar] [CrossRef]
- Johnson, K.A.; Smithers, J.C. Updating the estimation of 1-day probable maximum precipitation in South Africa. J. Hydrol. Reg. Stud. 2020, 32, 100736. [Google Scholar] [CrossRef]
- Ministry of Works. Estimation of Probable Maximum Precipitation in Korea: A Research Report on the Development of Water Resources Management Techniques; Ministry of Works: Seoul, Republic of Korea, 1988; Volume 3.
- Ministry of Land, Infrastructure and Transport. Estimation of Probable Maximum Precipitation in Korea; Ministry of Land, Infrastructure and Transport: Sejong-si, Republic of Korea, 2000.
- Ministry of Land, Infrastructure and Transport. Renewable Report of PMP Map in Korea; Ministry of Land, Infrastructure and Transport: Sejong-si, Republic of Korea, 2004.
- Ministry of Land, Infrastructure and Transport and K-water. PMP and PMF Calculation Procedure Guideline Establishment Service Report; Ministry of Land, Infrastructure and Transport and K-water: Sejong-si, Republic of Korea, 2008.
- Ministry of Environment. Re-Evaluation and Supplementary Research on Report the Probable Maximum Precipitation Calculation Procedure Report; Ministry of Environment: Sejong-si, Republic of Korea, 2020.
- Lee, O.; Kim, S. Estimation of future probable maximum precipitation in Korea using multiple regional climate models. Water 2018, 10, 637. [Google Scholar] [CrossRef]
- Beauchamp, J.; Leconte, R.; Trudel, M.; Brissette, F. Estimation of the summer-fall PMP and PMF of a northern watershed under a changed climate. Water Resour. Res. 2013, 49, 3852–3862. [Google Scholar] [CrossRef]
- Lee, K.; Singh, V.P. Analysis of uncertainty and non-stationarity in probable maximum precipitation in Brazos River basin. J. Hydrol. 2020, 590, 125526. [Google Scholar] [CrossRef]
- Micovic, Z.; Schaefer, M.G.; Taylor, G.H. Uncertainty analysis for probable maximum precipitation estimates. J. Hydrol. 2015, 521, 360–373. [Google Scholar] [CrossRef]
- Hershfield, D.M. Estimating the probable maximum precipitation. J. Hydraul. Div. 1961, 87, 99–116. [Google Scholar] [CrossRef]
- Lee, J.; Choi, J.; Lee, O.; Yoon, J.; Kim, S. Estimation of probable maximum precipitation in Korea using a regional climate model. Water 2017, 9, 240. [Google Scholar] [CrossRef]
- Desa, M.N.; Noriah, A.B.; Rakhecha, P. Probable maximum precipitation for 24 h duration over southeast Asian monsoon region—Selangor, Malaysia. J. Hydrol. 2001, 58, 41–54. [Google Scholar] [CrossRef]
- Sim, I.; Lee, O.; Jeong, S.; Kim, S. Estimating the return period for statistical probable maximum precipitation. J. Korean Soc. Hazard Mitig. 2019, 19, 373–382. [Google Scholar] [CrossRef]
- Sim, K.; Lee, O.; Kim, S.; Kim, E. Determination of minimum observation period for estimating probable maximum precipitation using statistical method. J. Korean Soc. Hazard Mitig. 2017, 17, 369–375. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A probabilistic view of Hershfield’s method for estimating probable maximum precipitation. Water Resour. Res. 1999, 35, 1313–1322. [Google Scholar] [CrossRef]
- Sarkar, S.; Maity, R. Increase in probable maximum precipitation in a changing climate over India. J. Hydrol. 2020, 585, 124806. [Google Scholar] [CrossRef]
- Hiraga, Y.; Iseri, Y.; Warner, M.D.; Frans, C.D.; Duren, A.M.; England, J.F.; Kavvas, M.L. Estimation of long-duration maximum precipitation during a winter season for large basins dominated by atmospheric rivers using a numerical weather model. J. Hydrol. 2021, 598, 126224. [Google Scholar] [CrossRef]
- Salas, J.D.; Anderson, M.L.; Papalexiou, S.M.; Frances, F. PMP and climate variability and change: A Review. J. Hydrol. Eng. 2020, 25, 03120002. [Google Scholar] [CrossRef]
- Rousseau, A.N.; Klein, I.M.; Freudiger, D.; Gagnon, P.; Frigon, A.; Ratté-Fortin, C. Development of a methodology to evaluate probable maximum precipitation (PMP) under changing climate conditions: Application to southern Quebec, Canada. J. Hydrol. 2014, 519 Pt D, 3094–3109. [Google Scholar] [CrossRef]
- Sarkar, S.; Maity, R. Estimation of probable maximum precipitation in the context of climate change. MethodX 2020, 7, 100904. [Google Scholar] [CrossRef]
- Rastogi, D.; Kao, S.-C.; Ashfaq, M.; Mei, R.; Kabela, E.D.; Gangrade, S.; Naz, B.S.; Preston, B.L.; Singh, N.; Anantharaj, V.G. Effects of climate change on probable maximum precipitation: A sensitivity study over the Alabama-Coosa-Tallapoosa River Basin. J. Geophys. Res. Atmos. 2017, 122, 4808–4828. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Karl, T.R.; Easterling, D.R.; Redmond, K.; Young, J.; Yin, X.; Hennon, P. Probable maximum precipitation and climate change. Geophys. Res. Lett. 2013, 40, 1402–1408. [Google Scholar] [CrossRef]
- Hershfield, D.M. Method for estimating the probable maximum precipitation. J. Am. Water Works Assoc. 1965, 57, 965–972. Available online: http://www.jstor.org/stable/41264521 (accessed on 13 March 2023). [CrossRef]
- Chow, V.T. A general formula for hydrologic frequency analysis. Trans. Am. Geophys. Union 1951, 32, 231–237. [Google Scholar] [CrossRef]
- Ministry of Environment. Flood Design Standard Guidelines; Ministry of Environment: Sejong-si, Korea, 2019.
- Lee, O.; Park, Y.; Kim, E.S.; Kim, S. Projection of Korean Probable Maximum Precipitation under Future Climate Change Scenarios. Adv. Meteorol. 2016, 2016, 3818236. [Google Scholar] [CrossRef]
- Kim, S.; Shin, J.-Y.; Ahn, H.; Heo, J.-H. Selecting Climate Models to Determine Future Extreme Rainfall Quantiles. J. Korean Soc. Hazard Mitig. 2019, 19, 55–69. [Google Scholar] [CrossRef]
- Kim, S.; Joo, K.; Kim, H.; Shin, J.-Y.; Heo, J.-H. Regional quantile delta mapping method using regional frequency analysis for regional climate model precipitation. J. Hydrol. 2021, 596, 125685. [Google Scholar] [CrossRef]
- Institute of Hydrology. Flood Studies Report: Hydrological Studies, Volume No. 1; National Environment Research Council: London, UK, 1975; ISBN 978-09-01-87525-9. [Google Scholar]




| Climate Scenario | Period (Year) |
|---|---|
| RCP 4.5 and 8.5 | Obs. start year~2040 |
| Obs. start year~2070 | |
| Obs. start year~2100 |
| Statistical Measure | Formula |
|---|---|
| Mean Absolute Error (MAE) | |
| Mean Absolute Percentage Error (MAPE) | |
| Root Mean Square Error (RMSE) |
| Case | Statistical Methods |
|---|---|
| Case 1 | ) |
| Case 2 | for each site |
| Case 3 | Hershfield’s original nomograph |
| Case 4 | Modified Hershfield’s nomograph |
| Case 5 | Chow’s frequency factor method (T = 60,000) |
| Estimation of PMP | SPMPs | HPMP (2020) | |||||
|---|---|---|---|---|---|---|---|
| Case 1 Hershfield’s | Case 2 for Each Site | Case 3 Hershfield’s Nomograph | Case 4 Modified Nomograph | Case 5 Chow’s T = 60,000 | |||
| PMP | Max. | 2083 | 1420 | 1608 | 1719 | 2966 | 1396 |
| Mean | 1035 | 357 | 909 | 955 | 1316 | 967 | |
| Min. | 395 | 141 | 403 | 411 | 437 | 598 | |
| Max. | 15.0 | 10.4 | 15.4 | 15.8 | 35.1 | - | |
| Mean | 15.0 | 3.4 | 13.1 | 13.8 | 19.8 | - | |
| Min. | 15.0 | 1.3 | 9.7 | 11.0 | 9.7 | - | |
| Evaluation | |||||||
| MAE | 184 | 613 | 150 | 149 | 372 | - | |
| MAPE | 19 | 63 | 16 | 15 | 39 | - | |
| RMSE | 249 | 634 | 194 | 189 | 487 | - | |
| SPMP/HPMP Ratio | 1.071 | 0.369 | 0.941 | 0.988 | 1.361 | - | |
| Scenario (Period) | RCP 4.5 | RCP 8.5 | |||||
|---|---|---|---|---|---|---|---|
| 2040 | 2070 | 2100 | 2040 | 2070 | 2100 | ||
| Max | 16.5 | 17.0 | 25.5 | 16.6 | 17.0 | 25.0 | |
| Mean | 12.7 | 12.9 | 17.7 | 12.4 | 12.8 | 17.3 | |
| Min | 9.1 | 10.0 | 16.5 | 8.8 | 9.9 | 16.1 | |
| PMP | Max | 1573 | 1904 | 2665 | 1810 | 1831 | 2614 |
| Mean | 633 | 763 | 1079 | 788 | 779 | 1101 | |
| Min | 377 | 444 | 594 | 393 | 432 | 622 | |
| Estimation of PMP | SPMPs | HPMP (2100) | ||||||
|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 for Each Site | Case 3 Hershfield’s Nomograph | Case 4 Modified Nomograph | Case 5 Chow’s T = 60,000 | ||||
| RCP 4.5 scenario | SPMP | Max. | 1823 | 1600 | 1643 | 2665 | 2795 | 1655 |
| Mean | 967 | 480 | 948 | 1118 | 1361 | 1273 | ||
| Min. | 514 | 172 | 535 | 599 | 611 | 856 | ||
| Max. | 15.0 | 12.6 | 18.9 | 25.5 | 27.4 | - | ||
| Mean | 15.0 | 4.9 | 12.6 | 17.7 | 18.5 | - | ||
| Min. | 15.0 | 1.4 | 7.3 | 16.5 | 9.9 | - | ||
| Evaluation | ||||||||
| MAE | 372 | 798 | 367 | 327 | 407 | - | ||
| MAPE | 29 | 62 | 28 | 25 | 32 | - | ||
| RMSE | 431 | 841 | 430 | 408 | 522 | - | ||
| SPMP/HPMP Ratio | 0.760 | 0.377 | 0.745 | 0.878 | 1.069 | - | ||
| RCP 8.5 scenario | SPMP | Max. | 1968 | 1017 | 1828 | 2316 | 3634 | 2136 |
| Mean | 1003 | 477 | 983 | 1137 | 1933 | 1566 | ||
| Min. | 563 | 212 | 567 | 626 | 912 | 1019 | ||
| Max. | 15.0 | 14.0 | 15.8 | 25.0 | 31.2 | - | ||
| Mean | 15.0 | 5.9 | 14.8 | 17.3 | 24.0 | - | ||
| Min. | 15.0 | 3.4 | 13.6 | 16.1 | 17.7 | - | ||
| Evaluation | ||||||||
| MAE | 594 | 1089 | 605 | 512 | 514 | - | ||
| MAPE | 37 | 69 | 38 | 32 | 34 | - | ||
| RMSE | 646 | 1122 | 656 | 565 | 744 | - | ||
| SPMP/HPMP Ratio | 0.641 | 0.304 | 0.628 | 0.726 | 1.234 | - | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, M.; Kim, S.; Kim, H.; Kim, H.; Shin, J.-Y.; Heo, J.-H. Evaluation of Statistical PMP Considering RCP Climate Change Scenarios in Republic of Korea. Water 2023, 15, 1756. https://doi.org/10.3390/w15091756
Seo M, Kim S, Kim H, Kim H, Shin J-Y, Heo J-H. Evaluation of Statistical PMP Considering RCP Climate Change Scenarios in Republic of Korea. Water. 2023; 15(9):1756. https://doi.org/10.3390/w15091756
Chicago/Turabian StyleSeo, Miru, Sunghun Kim, Heechul Kim, Hanbeen Kim, Ju-Young Shin, and Jun-Haeng Heo. 2023. "Evaluation of Statistical PMP Considering RCP Climate Change Scenarios in Republic of Korea" Water 15, no. 9: 1756. https://doi.org/10.3390/w15091756





