Adapted Water Quality Indices: Limitations and Potential for Water Quality Monitoring in Africa
Abstract
:1. Introduction
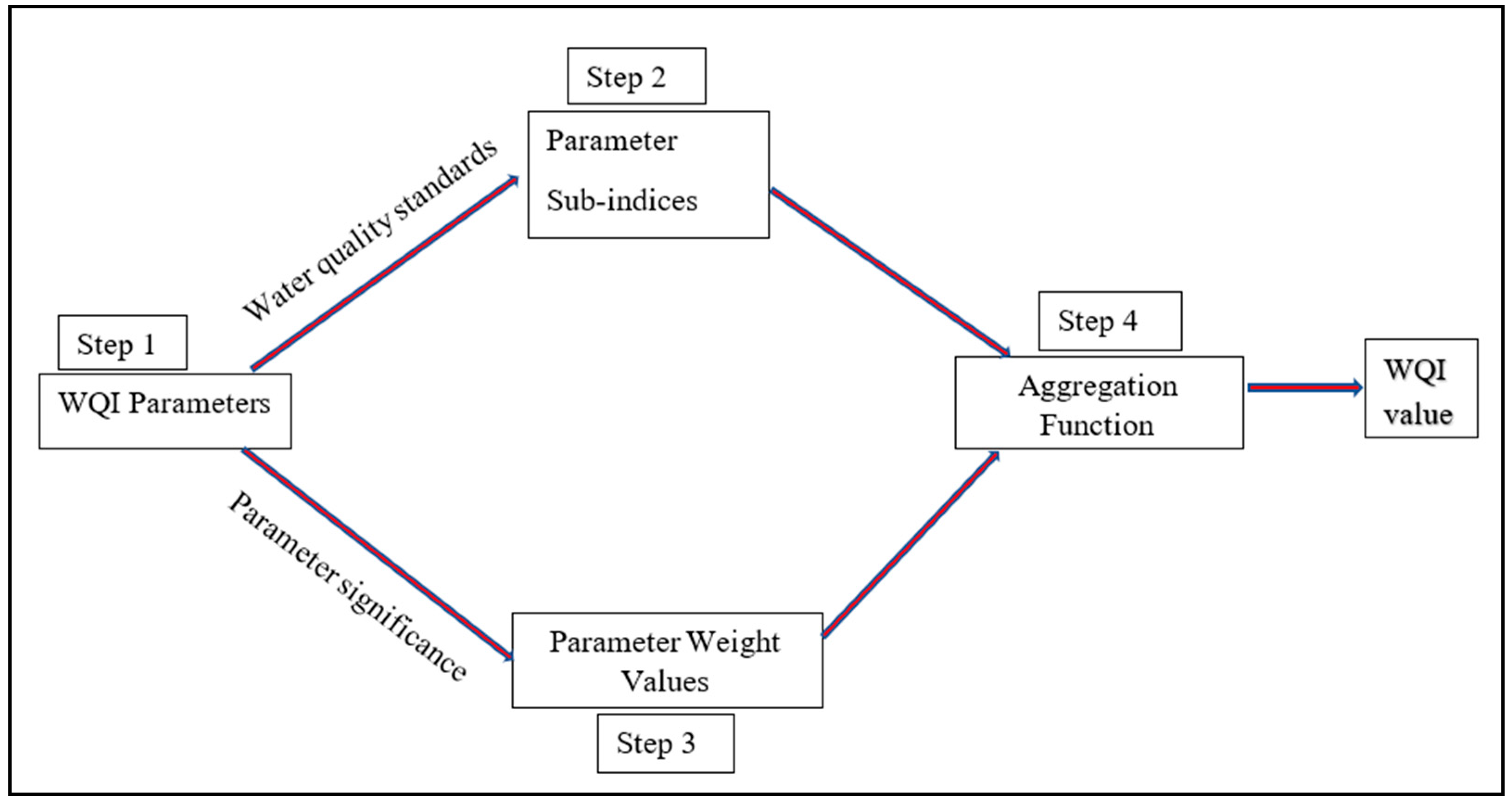
1.1. Development of a WQI
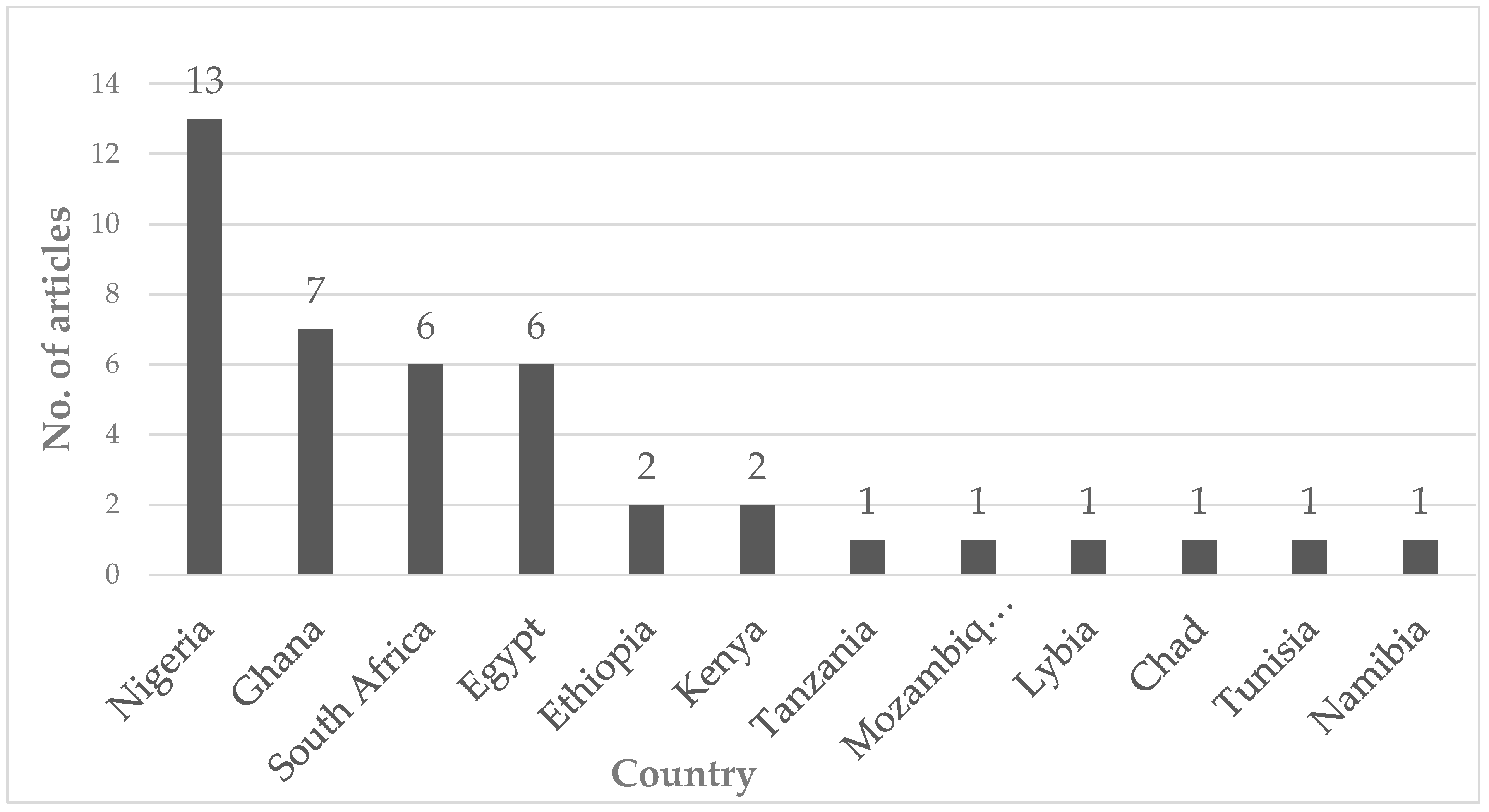
1.2. Application of WQIs: The African Perspective
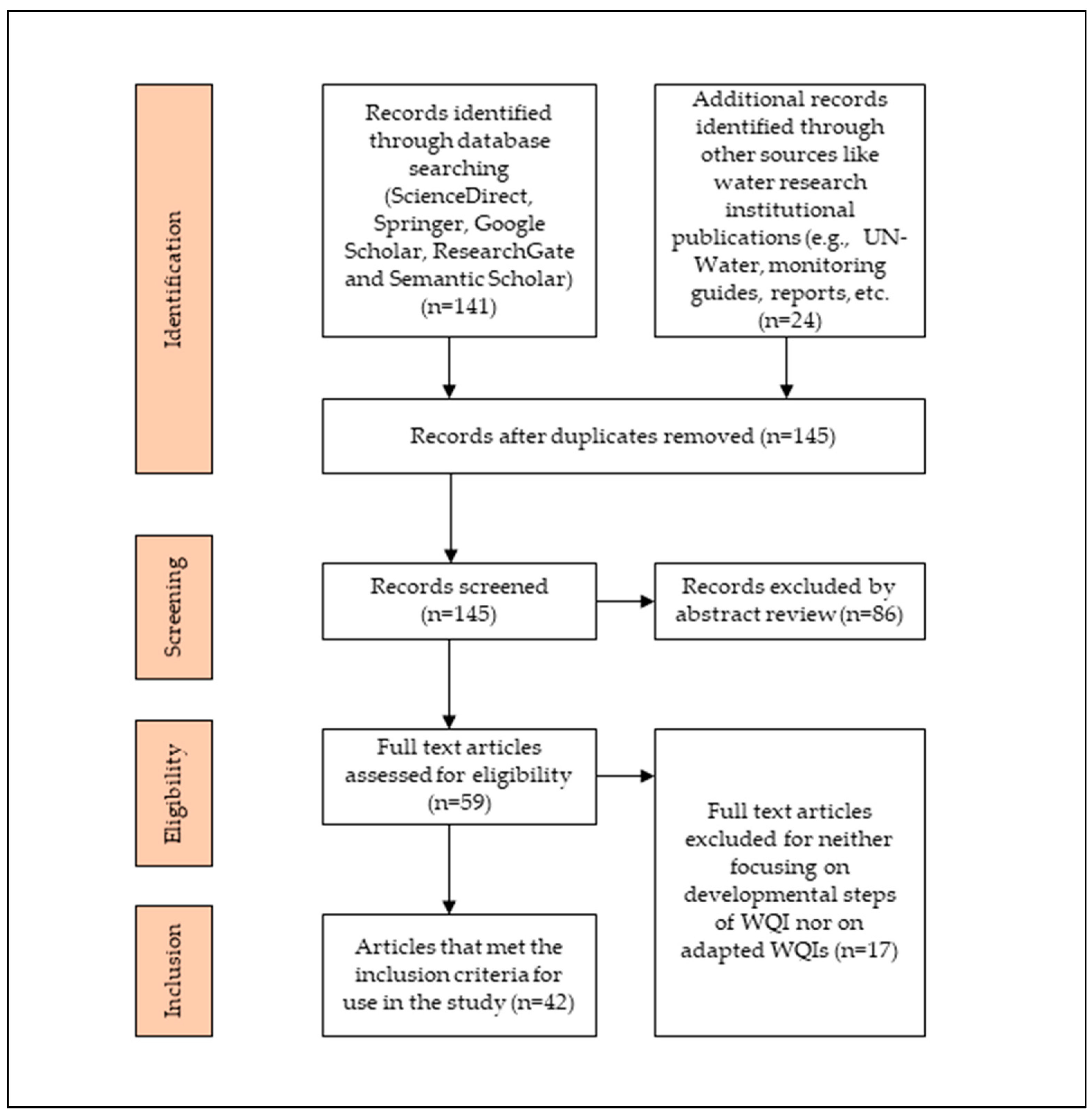
2. Materials and Methods
Data Sources, Inclusion and Exclusion Criteria, Analyses
3. Results and Discussion
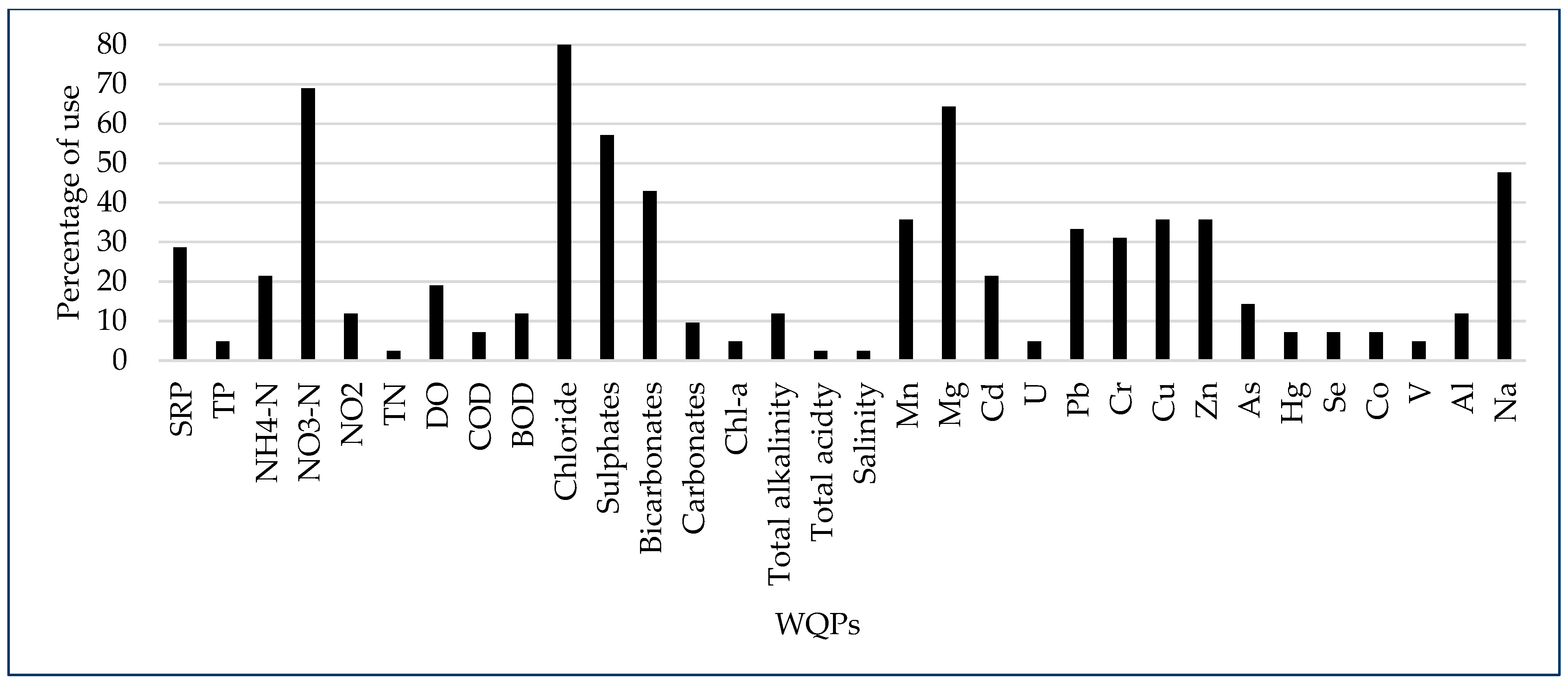
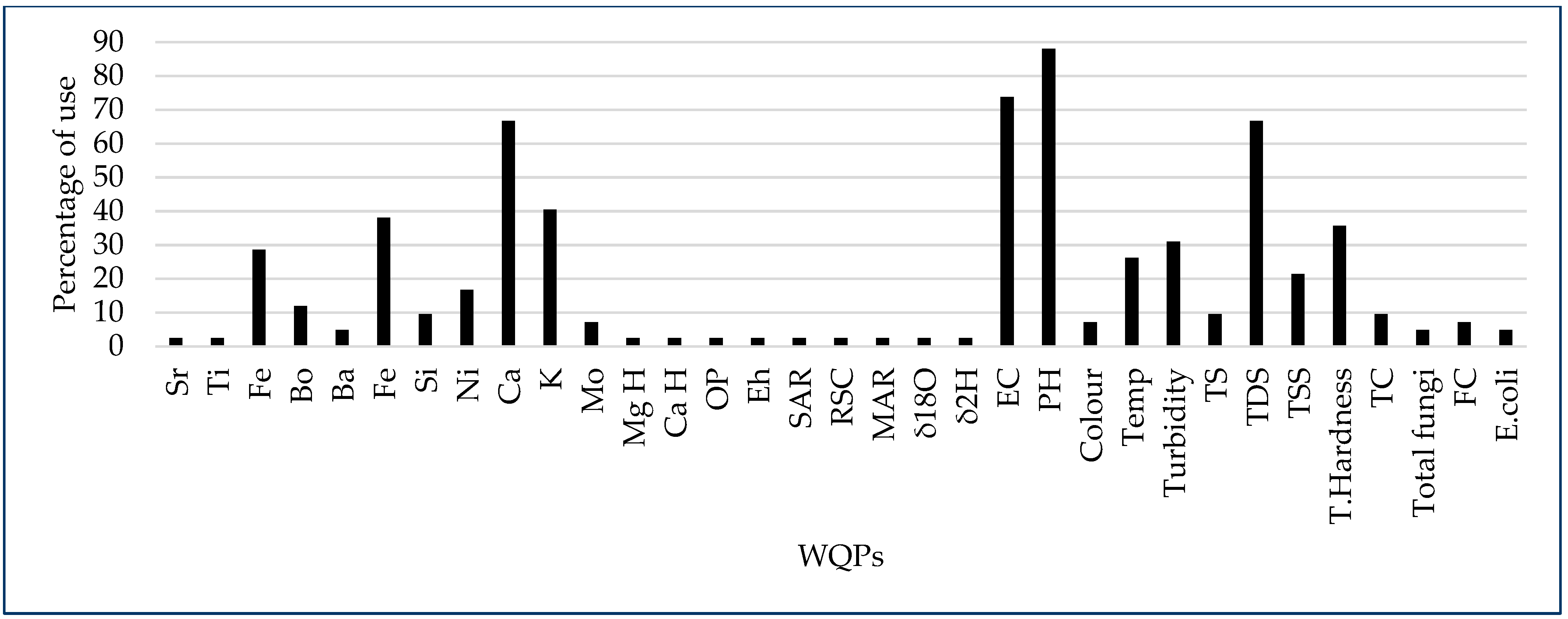
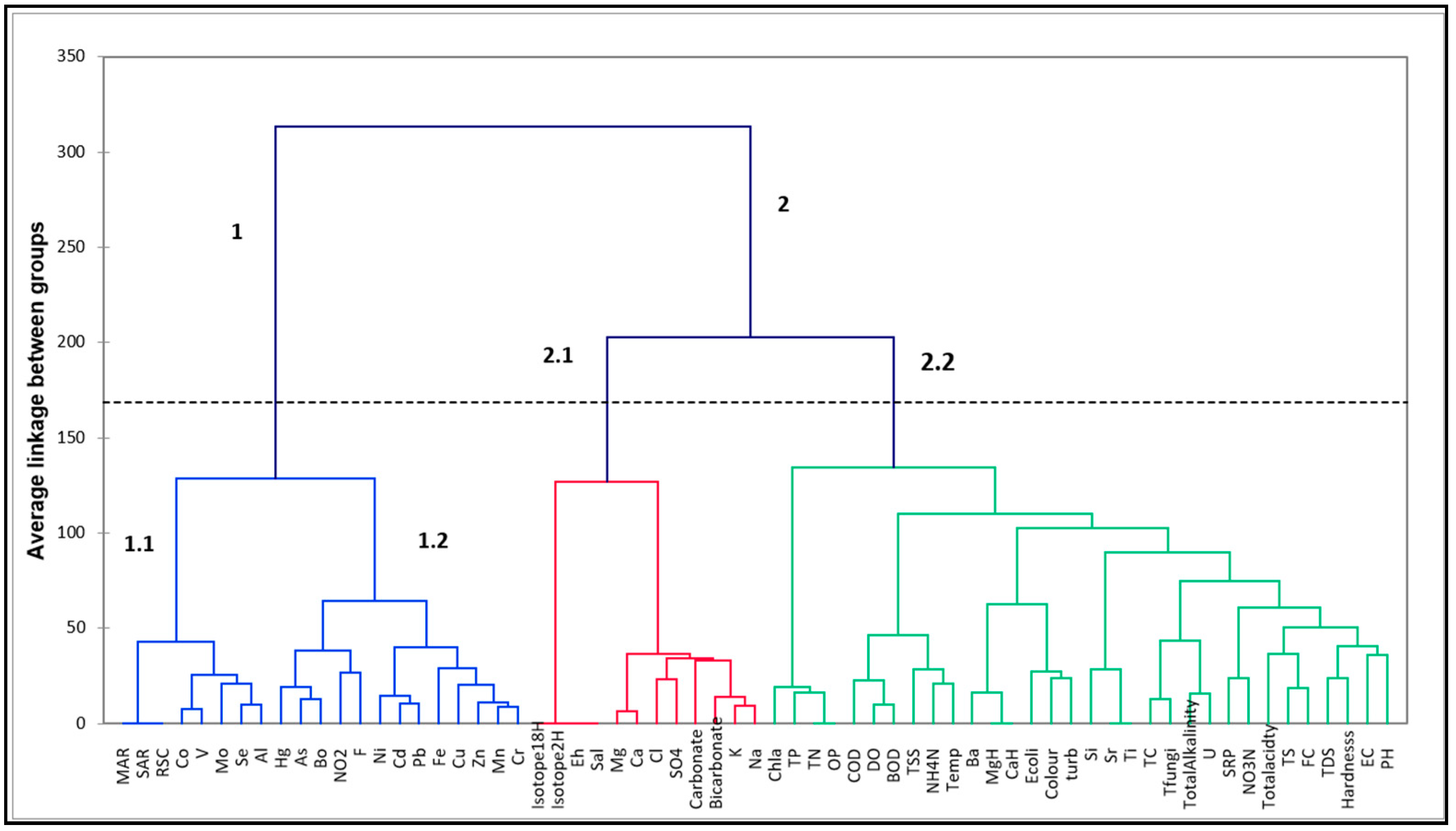
3.1. Parameter Selection Criteria in the Adapted WQIs
- Combination one; Zn2+, Mn, Cu 2+, Fe, Pb, Cd, Ni, Bo, As, Hg, Al, Se, Mo, and Co with Cr, V, MAR, SAR, and RSC as outliers.
- Combination two; Mg, Ca, Cl−, SO4, HCO3, K+, and Na+ with Eh, Sal, and the stable isotopes as outliers.
- Combination three; COD, DO, BOD, TSS, NH4-N, Temp, E. coli, colour, turbidity, TC, Total fungi, Total Alkalinity, SRP, NO3-N, Total acidity, TS, FC, TDS, Hardness, EC, and pH with outliers like OP, MgH, CaH, Sr, Ti, and U.
3.2. Generation of Parameter Sub-Indices
3.2.1. Use of Expert Judgment
3.2.2. Use of Water Quality Standards
- (a)
- Recommended standards—20, 30, 40, 80, 120
- (b)
- Sub-index ranges—100, 75, 50, 25, 1
- (c)
- Pairing—class 1 (20–100), class 2 (30–75), class 3 (40–50), class 4 (25–80), and class 5 (1–120) are used. The paired data are the bases for sub-index development since they are the key points of the rating curves. If the actual measured value falls between two classes, the sub-index value is obtained using mathematical equations. For example, Equation (1) is used when a parameter decreases the level of water quality with an increase in the parameter value.
- (a)
- Si = 0 if xi > recommended standard
- (b)
- Si = 1 if xi < recommended standard
3.2.3. Statistical Methods
3.3. Sub-Index Development in the Adapted Indices
3.4. Assignment of Parameter Weights
3.4.1. The Delphi Technique
3.4.2. AHP
3.5. Assignment of Parameter Weights in the Adapted Indices
3.6. Final Computation of the WQI
3.7. Aggregation Function for the Adapted CCMEWQI
- (i)
- Calculation of Excursion
- -
- When the test value must not exceed the objective.
- -
- When the test value must not fall below the objective.
- (ii)
- Calculation of Normalised Sum of Excursions
- (iii)
- Calculation of F3
3.8. Aggregation Function for the Adapted WAWQI
- (i)
- (ii)
3.9. Classification of WQIs and Index Scores
3.9.1. Classification of Water Quality in the Adapted WQIs
3.9.2. Limitations Identified in the Classification Scales of Adapted Indices in Reviewed Articles
3.10. Potential Solutions to Uncertainties Associated with Adapted Iindices
3.10.1. Parameter Selection Uncertainties
3.10.2. Eclipsing, Ambiguity and Rigidity
3.11. Applied Analysis and Comparison of Adapted WQIs and New Models
3.11.1. Water Quality Index Based on DEA: Application to Algerian Dams [113]
3.11.2. UWQI: South African Catchments [65]
Parameter Selection
Weight Coefficients
Formation of Sub-Indices
Aggregation Formula
Classification of WQI Scores in UWQI
3.11.3. The Surrogate Water Quality Index Based on Multivariate Statistical Analysis: South African Watersheds [66]
3.11.4. The Hounsinou Scale: Its Development and Use to Determine the Overall Quality of Groundwater Used for Drinking and Bathing in the Municipality of Abomey-Calavi in Benin [121]
4. Future Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Aljanabi, Z.Z.; Al-Obaidy, A.H.; Hassan, F.M. A brief review of water quality indices and their applications. IOP Conf. Ser. Earth Environ. Sci. 2021, 779, 012088. [Google Scholar] [CrossRef]
- Soumaila, K.I.; Niandou, A.S.; Naimi, M.; Mohamed, C.; Schimmel, K.; Luster-Teasley, S.; Sheick, N.N. A systematic review and meta-analysis of water quality indices. J. Agric. Sci. Technol. B 2019, 9, 1–14. [Google Scholar]
- Kachroud, M.; Trolard, F.; Kefi, M.; Jebari, S.; Bourrié, G. Water quality indices: Challenges and application limits in the literature. Water 2019, 11, 361. [Google Scholar] [CrossRef] [Green Version]
- Lumb, A.; Sharma, T.C.; Bibeault, J.F. A review of genesis and evolution of water quality index (WQI) and some future directions. Water Qual. Expo. Health 2011, 3, 11–24. [Google Scholar] [CrossRef]
- Zeinalzadeh, K.; Rezaei, E. Regional Studies Determining spatial and temporal changes of surface water quality using principal component analysis. J. Hydrol. 2017, 13, 1–10. [Google Scholar] [CrossRef]
- Tiwari, T.N.; Mishra, M.A. A preliminary assignment of water quality index of major Indian rivers. Indian J. Environ. Prot. 1985, 5, 276–279. [Google Scholar]
- Poonam, T.; Tanushree, P.; Sukalyan, C. Water quality indices—Important tools for water quality assessment. Int. J. Adv. Chem. 2013, 1, 15–18. [Google Scholar]
- Tyagi, S.; Sharma, B.; Singh, P.; Dobhal, R. Water Quality Assessment in Terms of Water Quality Index. Am. J. Water Resour. 2013, 1, 34–38. [Google Scholar] [CrossRef]
- Boyacioglu, H. Development of a water quality index based on a European classification scheme. Water SA 2007, 33, 101–106. [Google Scholar] [CrossRef] [Green Version]
- Banda, T.D.; Kumarasamy, V.M. Development of water quality indices (WQIs): A review. Pol. J. Environ. Stud. 2020, 29, 2011–2021. [Google Scholar] [CrossRef]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Tozer, R.G. A-Water-Quality-Index-Do-we-dare? Water Sew. Work. 1970, 117, 339–343. [Google Scholar]
- Banda, T.D. Developing an Equitable Raw Water Pricing Model: The Vaal Case Study. Ph.D. Thesis, Tshwane University of Technology, Pretoria, South Africa, October 2015. [Google Scholar] [CrossRef]
- Hallock, D.; Ehinger, W. Quality Assurance Monitoring Plan: Stream Ambient Water Quality Monitoring; Washington State Departament of Ecology: Olympia, WA, USA, 2003.
- Liu, W.C.; Yu, H.L.; Chung, C.E. Assessment of water quality in a subtropical alpine lake using multivariate statistical techniques and geostatistical mapping: A case study. Int. J. Environ. Res. Public Health 2011, 8, 1126–1140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horton, R. An index number system for rating water quality. J. Water Pollut. Control. Fed. 1965, 37, 300–305. [Google Scholar]
- Prati, L.; Pavanello, R.; Pesarin, F. Assessment of surface water quality by single index of pollution. Water Res. 1971, 5, 741–751. [Google Scholar] [CrossRef]
- Dinius, S.H. Social accounting system for evaluating water resources. Water Resour Res. 1972, 5, 1159–1177. [Google Scholar] [CrossRef]
- Brown, R.M.; McClelland, N.I.; Deininger, R.; Landwehr, J.M. Validating the WQI. In Proceedings of the National Meeting of American Society of Civil Engineers on Water Resources Engineering, Washington, DC, USA, 30 January 1973; Volume 29. [Google Scholar]
- Stoner, J.D. Water-Quality Indices for Specific Water Uses; US Geological Survey Circular: Arlington, VA, USA, 1978; pp. 154–196. [CrossRef] [Green Version]
- Dinius, S.H. Design of an Index of Water Quality. JAWRA 1987, 23, 833–843. [Google Scholar] [CrossRef]
- Bhargava, D.S. Expression for Drinking Water Supply Standards. J. Environ. Eng. 1985, 111, 304–316. [Google Scholar] [CrossRef]
- Smith, D.G. A better water quality indexing system for rivers and streams. Water Res. 1990, 24, 1237–1244. [Google Scholar] [CrossRef]
- Canadian Council of Ministers of the Environment. CCME. Canadian Water Quality Guidelines for the Protection of Aquatic Life: CCME Water Quality Index; Technical Report 1.0; Canadian Council of Ministers of the Environment: Quebec City, QC, Canada, 2001. [Google Scholar]
- Said, A.; Stevens, D.; Sehlke, G. Innovative Index for Evaluating Water Quality in Streams. Environ. Manag. 2004, 34, 406–414. [Google Scholar] [CrossRef]
- Ewaid, S.H.; Abed, S.A.; Al-Ansari, N.; Salih, R.M. Development and evaluation of a water quality index for the Iraqi rivers. Hydrology 2020, 7, 67. [Google Scholar] [CrossRef]
- Walsh, P.; Wheeler, W. Water Quality Index Aggregation and Cost Benefit Analysis: National Center for Environmental Economics Water Quality Index Aggregation and Cost Benefit Analysis; U.S. Environmental Protection Agency: Washington, DC, USA, 2012; p. 26.
- Swamee, P.K.; Tyagi, A. Describing water quality with aggregate index. J. Environ. Eng. 2000, 126, 451–455. [Google Scholar] [CrossRef]
- Ramesh, S.; Sukumaran, N.; Murugesan, A.G.; Rajan, M.P. An innovative approach of Drinking Water Quality Index—A case study from Southern Tamil Nadu, India. Ecol. Indic. 2010, 10, 857–868. [Google Scholar] [CrossRef]
- Kim, A.G.; Cardone, C. R.Scatterscore: A reconnaissance method to evaluate changes in water quality. Environ. Monit. Assess. 2005, 111, 277–295. [Google Scholar] [CrossRef] [PubMed]
- Liou, S.M.; Lo, S.L.; Wang, S.H. A generalized water quality index for Taiwan. Environ. Monit. Assess. 2004, 96, 35–52. [Google Scholar] [CrossRef] [PubMed]
- Sargaonkar, A.; Deshpande, V. Development of an overall index of pollution for surface water based on a general classification scheme in Indian context. Environ. Monit. Assess. 2003, 89, 43–67. [Google Scholar] [CrossRef] [PubMed]
- Tsegaye, T.; Sheppard, D.; Islam, K.R.; Tadesse, W.; Atalay, A.; Marzen, L. Development of chemical index as a measure of in-stream water quality in response to land-use and landcover changes. Water Air Soil Pollut. 2006, 174, 161–179. [Google Scholar] [CrossRef]
- Kumar, D.; Alappat, B.J. NSF-Water Quality Index: Does It Represent the Experts’ Opinion? Pract. Period. Hazard. Toxic Radioact. Waste Manag. 2009, 13, 75–79. [Google Scholar] [CrossRef]
- Manju, E.K.; George, A.V.; Rekha, V.B. A Comparative Study of Water Quality Index (WQI) of Vagamon and Peermade Sub-Watersheds of Meenachil and Pamba River Basins of Western Ghats, Kerala, South India. J. Environ. Sci. Toxilogy Food Technol. 2014, 8, 53–58. [Google Scholar] [CrossRef]
- Wills, M.; Irvine, K.N. Application of the National Sanitation Foundation Water Quality Index in the Ccazenovia Creek, NY, Pilot Watershed Management Project. Middle States Geogr. 1996, 95–104. Available online: http://msaag.aag.org/wp-content/uploads/2013/04/12_Wills_Irvine.pdf (accessed on 22 December 2022).
- Noori, R.; Berndtsson, H.R.M.; Adamowski, J.F.; Abyaneh, M.R. A critical review on the application of the National Sanitation Foundation Water Quality Index. Environ. Pollut. 2019, 244, 575–587. [Google Scholar] [CrossRef]
- Kalagbor, I.A.; Johnny, V.I.; Ogbolokot, I.E. Application of National Sanitation Foundation and Weighted Arithmetic Water Quality Indices for the Assessment of Kaani and Kpean Rivers in Nigeria. Am. J. Water Resour. 2019, 7, 11–15. [Google Scholar] [CrossRef]
- Abbasi, T.; Abbasi, S.A. Water quality indices based on bioassessment: The biotic indices. J. Water Health 2011, 9, 330–348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goher, M.E.; Mahdy, E.S.M.; Abdo, M.H.; El Dars, F.M.; Korium, M.A.; Elsherif, A.A.S. Water quality status and pollution indices of Wadi El-Rayan lakes, El-Fayoum, Egypt. Sustain. Water Resour. Manag. 2019, 5, 387–400. [Google Scholar] [CrossRef]
- Abukila, A.F. Assessing the drain estuaries’ water quality in response to pollution abatement. Water Sci. 2015, 29, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Miyittah, M.K.; Tulashie, S.K.; Tsyawo, F.W.; Sarfo, J.K.; Darko, A.A. Assessment of surface water quality status of the Aby Lagoon System in the Western Region of Ghana. Heliyon 2020, 6, e04466. [Google Scholar] [CrossRef]
- Egbi, C.D.; Anornu, G.; Appiah-Adjei, E.K.; Ganyaglo, S.Y.; Dampare, S.B. Evaluation of water quality using hydrochemistry, stable isotopes, and water quality indices in the Lower Volta River Basin of Ghana. Environ. Dev. Sustain. 2019, 21, 3033–3063. [Google Scholar] [CrossRef]
- Ligate, F.; Ijumulana, J.; Irunde, R.; Kimambo, V.; Mtamba, J.; Ahmad, A.; Hamisi, R.; Maity, J.P.; Mtalo, F.; Bhattacharya, P. Geogenic contaminants and groundwater quality around Lake Victoria goldfields in northwestern Tanzania. Chemosphere 2022, 307, 135732. [Google Scholar] [CrossRef] [PubMed]
- Terrado, M.; Barceló, D.; Tauler, R.; Borrell, E.; de Campos, S. Surface-water-quality indices for the analysis of data generated by automated sampling networks. TrAC Trends Anal. Chem. 2010, 29, 40–52. [Google Scholar] [CrossRef]
- Yogendra, K.; Puttaiah, E.T. Determination of Water Quality Index and Suitability of an Urban Waterbody in Shimoga Town, Karnataka. In Proceedings of the Taal2007: The 12th World Lake Conference, Jaipur, Rajasthan, India, 28 October–2 November 2007. [Google Scholar]
- Salem, M.A.; Sharif, O.A.; Alshofeir, A.A.; Assad, M.E.H. An evaluation of drinking water quality in five wells in Sebha city, Libya, using a water quality index and multivariate analysis. Arab. J. Geosci. 2022, 15, 1519. [Google Scholar] [CrossRef]
- Rabeiy, R.E.S. Assessment and modeling of groundwater quality using WQI and GIS in Upper Egypt area. Environ. Sci. Pollut. Res. 2018, 25, 30808–30817. [Google Scholar] [CrossRef]
- Hagage, M.; Madani, A.A.; Elbeih, S.F. Quaternary groundwater aquifer suitability for drinking in Akhmim, Upper Egypt: An assessment using water quality index and GIS techniques. Arab. J. Geosci. 2022, 15, 196. [Google Scholar] [CrossRef]
- Khmila, K.; Trabelsi, R.; Zouari, K.; Kumar, U.S. Application of geochemical and isotopic tracers for the evaluation of groundwater quality in the irrigated area of the Sbiba plain (Central West Tunisia). Agric. Ecosyst. Environ. 2021, 313, 107298. [Google Scholar] [CrossRef]
- Njuguna, S.M.; Onyango, J.A.; Githaiga, K.B.; Gituru, R.W.; Yan, X. Application of multivariate statistical analysis and water quality index in health risk assessment by domestic use of river water. Case study of Tana River in Kenya. Process. Saf. Environ. Prot. 2020, 133, 149–158. [Google Scholar] [CrossRef]
- Githaiga, K.B.; Njuguna, S.M.; Gituru, R.W.; Yan, X. Water quality assessment, multivariate analysis and human health risks of heavy metals in eight major lakes in Kenya. J. Environ. Manag. 2021, 297, 113410. [Google Scholar] [CrossRef]
- Chebet, E.B.; Kibet, J.K.; Mbui, D. The assessment of water quality in river Molo water basin, Kenya. Appl. Water Sci. 2020, 10, 92. [Google Scholar] [CrossRef] [Green Version]
- Robert, G.K.; Onyari, C.N.; Mbaka, J.G. Development of a Water Quality Assessment Index for the Chania River, Kenya. Afr. J. Aquat. Sci. 2020, 46, 142–152. [Google Scholar] [CrossRef]
- Teshome, F.B. Seasonal water quality index and suitability of the water body to designated uses at the eastern catchment of Lake Hawassa. Environ. Sci. Pollut. Res. 2020, 27, 279–290. [Google Scholar] [CrossRef]
- Berhe, B.A. Evaluation of groundwater and surface water quality suitability for drinking and agricultural purposes in Kombolcha town area, eastern Amhara region, Ethiopia. Appl. Water Sci. 2020, 10, 127. [Google Scholar] [CrossRef]
- Akoteyon, I.S.; Omotayo, A.O.; Soladoye, O.; Olaoye, H.O. Determination of water quality index and suitability of Urban River for municipal water supply in Lagos-Nigeria. Eur. J. Sci. Res. 2011, 54, 263–271. [Google Scholar]
- Nwanosike, A.A.; Olasehinde, P.I.; Okosun, E.; Yisa, J. Assessment of the Water Quality Index of Otamiri and Oramiriukwa Rivers Assessment of the Water Quality Index of Otamiri and Oramiriukwa Rivers. Phys. Int. 2010, 1, 102–109. [Google Scholar] [CrossRef]
- Ochelebe, I.; Kudamnya, E.A. Hydrochemistry and an appraisal of surface water and groundwater quality for domestic and irrigation use in parts of Southern Benue Trough, Nigeria. Sustain. Water Resour. Manag. 2022, 8, 159. [Google Scholar] [CrossRef]
- Oni, O.; Fasakin, O. The Use of Water Quality Index Method to Determine the Potability of Surface Water and Groundwater in the Vicinity of a Municipal Solid Waste Dumpsite in Nigeria. Am. J. Eng. Res. 2016, 5, 96–101. [Google Scholar]
- Yisa, J.; Oladejo, J.T. Analytical Studies on Water Quality Index of River Landzu Analytical Studies on Water Quality Index of River Landzu. Am. J. Appl. Sci. 2010, 7, 453–458. [Google Scholar] [CrossRef] [Green Version]
- Boah, D.K.; Pelig-ba, K.B.; Twum, S.B. Mathematical Computation of Water Quality Index of Vea Dam in Upper East Region of Ghana. Environ. Sci. 2015, 3, 11–16. [Google Scholar] [CrossRef] [Green Version]
- Akoto, O.; Adopler, A.; Tepkor, H.E.; Opoku, F. A comprehensive evaluation of surface water quality and potential health risk assessments of Sisa river, Kumasi. Groundw. Sustain. Dev. 2021, 15, 100654. [Google Scholar] [CrossRef]
- Boateng, T.K.; Opoku, F.; Acquaah, S.O.; Akoto, O. Groundwater quality assessment using statistical approach and water quality index in Ejisu-Juaben Municipality, Ghana. Environ. Earth Sci. 2016, 75, 489. [Google Scholar] [CrossRef]
- Bon, A.F.; Abderamane, H.; Ewodo, M.G.; Banakeng, L.A.; Bontsong, B.; Stephane, B.; Piih, S.L.; Wangbara, D.B. Parametrization of groundwater quality of the Quaternary aquifer in N’Djamena (Chad), Lake Chad Basin: Application of numerical and multivariate analyses. Environ. Sci. Pollut. Res. 2021, 28, 12300–12320. [Google Scholar] [CrossRef]
- Banda, T.D.; Kumarasamy, M. Development of a universal water quality index (UWQI) for South African river catchments. Water 2020, 12, 1534. [Google Scholar] [CrossRef]
- Banda, T.D.; Kumarasamy, M. Application of multivariate statistical analysis in the development of a surrogate water quality index (WQI) for South African watersheds. Water 2020, 12, 1584. [Google Scholar] [CrossRef]
- Belle, G.; Fossey, A.; Esterhuizen, L.; Moodley, R. Contamination of groundwater by potential harmful elements from gold mine tailings and the implications to human health: A case study in Welkom and Virginia, Free State Province, South Africa. Groundw. Sustain. Dev. 2021, 12, 100507. [Google Scholar] [CrossRef]
- Mandindi, W.Z.; Nyaba, L.; Mketo, N.; Nomngongo, P.N. Seasonal Variation of Drinking Water Quality and Human Health Risk Assessment: A Case Study in Rural Village of the Eastern Cape, South Africa. Water 2022, 14, 2013. [Google Scholar] [CrossRef]
- Molekoa, M.D.; Avtar, R.; Kumar, P.; Minh, H.V.T.; Kurniawan, T.A. Hydrogeochemical assessment of groundwater quality of Mokopane area, Limpopo, South Africa using statistical approach. Water 2019, 11, 1891. [Google Scholar] [CrossRef] [Green Version]
- Molekoa, M.D.; Avtar, R.; Kumar, P.; Minh, H.V.T.; Dasgupta, R.; Johnson, B.A.; Sahu, N.; Verma, R.L.; Yuus, A.P. Spatio-temporal analysis of surface water quality in mokopane area, Limpopo, South Africa. Water 2021, 13, 220. [Google Scholar] [CrossRef]
- Molekoa, M.D.; Kumar, P.; Chouldhary, B.K.; Yunus, A.P.; Kharrazi, A.; Khedher, K.M.; Al Shaib, M.; Singh, B.P.; Minh, H.V.T.; Kurniawan, T.A.; et al. Spatio-temporal variations in the water quality of the Doorndraai Dam, South Africa: An assessment of sustainable water resource management. Curr. Res. Environ. Sustain. 2022, 4, 100187. [Google Scholar] [CrossRef]
- Namugize, J.N.; Jewitt, G.P.W. Sensitivity analysis for water quality monitoring frequency in the application of a water quality index for the uMngeni River and its tributaries, KwaZulu-Natal, South Africa. Water SA 2018, 44, 516–527. [Google Scholar] [CrossRef] [Green Version]
- Sutadian, A.D.; Muttil, N.; Yilmaz, A.G.; Perera, B.J.C. Using the Analytic Hierarchy Process to identify parameter weights for developing a water quality index. Ecol. Indic. 2016, 75, 220–233. [Google Scholar] [CrossRef]
- Cude, C.G. Oregon Water Quality Index a tool for evaluating water quality management effectiveness. JAWRA 2001, 37, 125–137. [Google Scholar] [CrossRef]
- Swamee, P.K.; Tyagi, A. Improved Method for Aggregation of Water Quality Subindices. J. Environ. Eng. 2007, 133, 220–225. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, J.; Tetzlaff, J.; Altman, D.G. Reprint-Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. Ann. Intern. Med. 2009, 151, 264–269. Available online: http://www.annals.org/cgi/content/full/151/4/264 (accessed on 15 May 2022). [CrossRef] [Green Version]
- Sirunda, J.; Oberholster, P.; Wolfaardt, G. Assessing the Adverse Effects of Land Use Activities on the Water Quality of Selected Sub-Saharan Africa Reservoirs Using a Combination of Water Quality Indices. Water Air Soil Pollut. 2022, 233, 267. [Google Scholar] [CrossRef]
- Anim-Gyampo, M.; Anornu, G.; Appiah-Adjei, E.; Agodzo, S. Quality and health risk assessment of shallow groundwater aquifers within the Atankwidi basin of Ghana. Groundw. Sustain. Dev. 2019, 9, 100217. [Google Scholar] [CrossRef]
- Bankole, A.O.; Oluwasanya, G.; Odjegba, E.E. Evaluation of groundwater suitability in the Cretaceous Abeokuta Formation, Nigeria: Implications for water supply and public health. Groundw. Sustain. Dev. 2022, 19, 100845. [Google Scholar] [CrossRef]
- Marove, C.A.; Sotozono, R.; Tangviroon, P.; Tabelin, C.B.; Igarashi, T. Assessment of soil, sediment and water contaminations around open-pit coal mines in Moatize, Tete province, Mozambique. Environ. Adv. 2022, 8, 100215. [Google Scholar] [CrossRef]
- Solihu, H.; Bilewu, S.O. Assessment of anthropogenic activities impacts on the water quality of Asa river: A case study of Amilengbe area, Ilorin, Kwara state, Nigeria. Environ. Chall. 2022, 7, 100473. [Google Scholar] [CrossRef]
- Wali, S.U.; Alias, N.B.; Harun, S.B.; Gada, M.A.; Dankani, I.M.; Kaoje, I.U.; Usman, A.A. Water quality indices and multivariate statistical analysis of urban groundwater in semi-arid Sokoto Basin, Northwestern Nigeria. Groundw. Sustain. Dev. 2022, 18, 100779. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A review of water quality index models and their use for assessing surface water quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Ekere, N.R.; Agbazue, V.E.; Ngang, B.U.; Ihedioha, J.N. Hydrochemistry and Water Quality Index of groundwater resources in Enugu north district, Enugu, Nigeria. Environ. Monit. Assess. 2019, 191, 150. [Google Scholar] [CrossRef] [PubMed]
- Idehen, O. Geophysical and water quality index surveys of groundwater quality around Ugbor dumpsite in Benin city, Edo Sstate, Nigeria, West Africa. J. Adv. Phys. 2016, 12, 4383–4392. [Google Scholar] [CrossRef]
- Mgbenu, C.N.; Egbueri, J.C. The hydrogeochemical signatures, quality indices and health risk assessment of water resources in Umunya district, Southeast Nigeria. Appl. Water Sci. 2019, 9, 22. [Google Scholar] [CrossRef] [Green Version]
- Ibanga, O.A.; Ohwo, S.E.; Omonigho, G.M. Application of Water Quality Index in Assessment of Swimming Pools Water Quality in Hotels in Emerging Africa Littoral Metropolis of Warri, Delta State, Nigeria. Geosport Soc. 2020, 13, 91–107. [Google Scholar] [CrossRef]
- Misaghi, F.; Delgosha, F.; Razzaghmanesh, M.; Myers, B. Introducing a water quality index for assessing water for irrigation purposes: A case study of the Ghezel Ozan River. Sci. Total Environ. 2017, 589, 107–116. [Google Scholar] [CrossRef]
- Jagaba, A.H.; Kutty, S.R.M.; Hayder, G.; Abubakar, S.; Ghaleb, A.A.S.; Lawal, I.M.; Noor, A.; Umaru, I.; Almahbashi, N.M.Y. Water quality hazard assessment for hand dug wells in Rafin Zurfi, Bauchi State, Nigeria. Ain Shams Eng. J. 2020, 11, 983–999. [Google Scholar] [CrossRef]
- Bhargava, D.S. Use of a Water Quality Index for River Classification and Zoning of Ganga River. Environ. Pollut. Ser. B Chem. Phys. 1983, 6, 51–67. [Google Scholar] [CrossRef]
- Ayogu, C.N.; Maduka, R.I.; Ayogu, N.O.; Njoku, C.N.; Chinedu-Asogwa, N.C. Hydro-geochemical analysis and quality evaluation of surface water in the Mamu River basin, southeastern Nigeria. Appl. Water Sci. 2020, 10, 159. [Google Scholar] [CrossRef]
- Akakuru, O.C.; Akudinobi, B.; Opara, A.I.; Onyekuru, S.O.; Akakuru, O.U. Hydrogeochemical facies and pollution status of groundwater resources of Owerri and environs, Southeastern Nigeria,”. Environ. Monit. Assess. 2021, 193, 623. [Google Scholar] [CrossRef]
- Icaga, Y. Fuzzy evaluation of water quality classification. Ecol. Indic. 2007, 7, 710–718. [Google Scholar] [CrossRef]
- Mophin-Kani, K.; Murugesan, A.G. Evaluation and Classification of Water Quality of Perennial River Tamirabarani through Aggregation of Water Quality Index. Int. J. Environ. Prot. IJEP 2011, 1, 24–33. [Google Scholar] [CrossRef]
- Dunnette, D.A. A geographically variable water quality index used in Oregon. J. Water Pollut. Control Fed. 1979, 51, 53–61. [Google Scholar]
- Ramakrishnaiah, C.R.; Sadashivaiah, C.; Ranganna, G. Assessment of Water Quality Index for the Groundwater in Tumkur Taluk, Karnataka State, India. E-J. Chem. 2009, 6, 523–530. [Google Scholar] [CrossRef] [Green Version]
- Sahu, P.; Sikdar, P.K. Hydrochemical framework of the aquifer in and around East Kolkata Wetlands, West Bengal, India. Environ. Geol. 2008, 55, 823–835. [Google Scholar] [CrossRef]
- Shah, K.A.; Joshi, G.S. Evaluation of water quality index for River Sabarmati, Gujarat, India. Appl. Water Sci. 2017, 7, 1349–1358. [Google Scholar] [CrossRef] [Green Version]
- Abrahão, R.; Carvalho, M.; Da Silva, W.R.; Machado, T.T.V.; Gadelha, C.L.M.; Hernandez, M.I.M. Use of index analysis to evaluate the water quality of a stream receiving industrial effluents. Water SA 2007, 33, 459–465. [Google Scholar] [CrossRef] [Green Version]
- Rubio-Arias, H.; Contreras-Caraveo, M.; Quintana, R.M.; Saucedo-Teran, R.A.; Pinales-Munguia, A. An overall water quality index (WQI) for a man-made aquatic reservoir in Mexico. Int. J. Environ. Res. Public Health 2012, 9, 1687–1698. [Google Scholar] [CrossRef] [PubMed]
- Debels, P.; Figueroa, R.; Urrutia, R.; Barra, R.; Niell, X. Evaluation of water quality in the Chillán River (Central Chile) using physicochemical parameters and a modified Water Quality Index. Environ. Monit. Assess. 2005, 110, 301–322. [Google Scholar] [CrossRef]
- Kannel, P.R.; Lee, S.; Lee, Y.S.; Kanel, S.R.; Khan, S.P. Application of water quality indices and dissolved oxygen as indicators for river water classification and urban impact assessment. Environ. Monit. Assess. 2007, 132, 93–110. [Google Scholar] [CrossRef]
- World Health Organisation (WHO). Heavy Metals: Understanding the Science and Impacts; World Health Organisation (WHO): Geneva, Switzerland, 2011. [Google Scholar]
- Birniwa, A.H.; Abubakar, A.S.; Huq, A.O.; Mahmud, H.N.M.E. Polypyrrole-polyethyleneimine (PPy-PEI) nanocomposite: An effective adsorbent for nickel ion adsorption from aqueous solution. J. Macromol. Sci. Part A 2021, 58, 206–217. [Google Scholar] [CrossRef]
- Fang, J.; Lang, M.; Ye, X.; Zhang, W.; Zhu, K. Non-isothermal crystallization behavior of polypropylene/zinc oxide composites. Sci. Eng. Compos. Mater. 2016, 23, 505–510. [Google Scholar] [CrossRef]
- Jaishankar, M.; Tseten, T.; Anbalagan, N.; Mathew, B.B.; Beeregowda, K.N. Toxicity, mechanism and health effects of some heavy metals. Interdiscip. Toxicol. 2014, 7, 60–72. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nriagu, J. Zinc Toxicity in Humans. Encycl. Environ. Heal. 2011, 801–807. [Google Scholar] [CrossRef]
- Ongley, E.D.; Booty, W.G. Pollution Remediation Planning In Developing Countries Pollution Remediation Planning In Developing Countries. Water Int. 2009, 24, 31–38. [Google Scholar] [CrossRef]
- Abuzaid, A.S. Evaluating Surface Water Quality for Irrigation in Dakahlia Governorate Using Water Quality Index and GIS Soil Quality View Project. 2018. Available online: https://www.researchgate.net/publication/328282660 (accessed on 4 July 2022).
- Sheldon, J.; Alber, M. Recommended indicators of estuarine water quality for Georgia. In Proceedings of the 2011 Georgia Water Resources Conference, University of Georgia, Athens, Georgia, 11–13 April 2011. [Google Scholar]
- Odonkor, S.T.; Ampofo, J.K. Escherichia coli as an indicator of bacteriological quality of water: An overview. Microbiol. Res. 2013, 4, e2. [Google Scholar] [CrossRef] [Green Version]
- Ashbolt, N.J. Water Quality: Guidelines, Standards and Health. Assessment of Risk and Risk Management for Water-Related Infectious Disease; World Health Organisation (WHO): Geneva, Switzerland, 2001; p. 424. Available online: http://www.who.int/iris/handle/10665/42442 (accessed on 10 August 2022).
- Soltani, A.A.; Oukil, B.H.; Bermad, A.; Boulassel, M.R. A new methodology for assessing water quality, based on data envelopment analysis: Application to Algerian dams. Ecol. Indic. 2021, 121, 106952. [Google Scholar] [CrossRef]
- Al-Mezeini, N.K.; Oukil, A.; Al-Ismaili, A.M. Investigating the efficiency of greenhouse production in Oman: A two-stage approach based on Data Envelopment Analysis and double bootstrapping. J. Clean. Prod. 2020, 247, 119160. [Google Scholar] [CrossRef]
- Oukil, A.; Al-Zidi, A. Benchmarking the hotel industry in Oman through a threestage DEA-based procedure. J. Arts Soc. Sci. 2018, 9, 5–23. [Google Scholar] [CrossRef] [Green Version]
- Cook, W.D.; Tone, K.; Zhu, J. Data envelopment analysis: Prior to choosing a model. Omega 2014, 44, 1–4. [Google Scholar] [CrossRef]
- Sturges, H.A. The Choice of a Class Interval. J. Am. Stat. Assoc. 1926, 153, 65–66. [Google Scholar] [CrossRef]
- DWAF. South African Water Quality Guidelines:Volume 1: Domestic Water Use; Department of Water Affairs and Forestry: Pretoria, South Africa, 1996.
- Bouza-Deaño, R.; Ternero-Rodriguez, M.; Fernández-Espinosa, A. Trend study and assessment of surface water quality in the Ebro River (Spain). J. Hydrol. 2008, 361, 227–239. [Google Scholar] [CrossRef]
- Zhao, Y.; Xia, X.H.; Yang, Z.F.; Wang, F. Assessment of water quality in Baiyangdian Lake using multivariate statistical techniques. Procedia Environ. Sci. 2012, 13, 1213–1226. [Google Scholar] [CrossRef] [Green Version]
- Hounsinou, S.P. The Hounsinou scale: Its development and use to determine the overall quality of groundwater used for drinking and bathing in the municipality of Abomey-Calavi in Benin. J. Hydrol. Reg. Stud. 2021, 34, 100777. [Google Scholar] [CrossRef]

| WQI Model | Parameters | Standardisation | Weighting | Aggregation Function | Reference |
|---|---|---|---|---|---|
| Horton index | DO, pH, SC, Alk, temp, CCE, FC, Cl−, PP, OP | Parameters value used as sub-index value | Fixed and unequal system | Weighted Arithmetic Average QI = M1M2 | [15] |
| NSFWQI (1) | DO, BOD, pH, temp, FC, Turb, nitrates, phosphates, TDS | Rating curves; Experts’ opinion | Expert questionnaire | Weighted Arithmetic Average WQI = | [11] |
| Prati’s implicit index | BOD, pH, COD, DO, conc. of permanganate, ammonium, nitrates, Cl−, Fe, Mn, CCE, SS Alkyl Benzene sulphonates | Linear and parabolic function | No | Additive I = | [16] |
| Dinius index (1) | Temp, DO, pH, EC, colour, BOD, Alk, FC, Cl-, hardness, E. coli | Linear and nonlinear function | Delphi technique | Weighted DWQI = | [17] |
| NSFWQI (2) | DO, BOD, PH, temp, FC, Turb, nitrates, phosphates, TDS | Rating curves; Experts’ opinion | Expert questionnaire | Weighted Geometric Average WQI (M) = | [18] |
| Stoner’s index | Irrigation: EC, SAR, SC, Mn, B, As, Cd, Be, Al, Co, Cr, V, Ni, Cu, Zn, F Public water: Cl,MBAs, phenols, nitrates, ammonia, colour, pH, Cu, FC, F, Fe, Zi, sulphates | Limits classes: nonlinear functions | Researcher’s experience | Additive I = + | [19] |
| Dinius Index (2) | Temp, DO, pH, EC, colour, BOD, Alk, FC, Cl−, hardness, E. coli, nitrates | The linear and non-linear function | Delphi technique | Geometrical average IWQ = | [20] |
| Bhargava index | According to the use | Formulas | Weighted Product | Additive WQI = | [21] |
| Smith index | BOD, temp, Turb, SS, DO, ammonia, FC | Rating curves; Experts’ opinion | Delphi technique | Minimum operator I min = | [22] |
| CCME WQI | Minimum of 4, not specified | Standard values | No | Arithmetic average 100 − | [23] |
| New WQI | DO, TP, FC, Turb, SC | No need | Ranking | Logarithmic aggregation SAID WQI = log | [24] |
| Ewaid index | COD, TDS, DO, total hardness, Cl−, TC | Rating curves; Experts’ opinion | Expert opinion | Formula [(−0.019 TDS + 84.587) × 0.2] + [(−0.006 TC + 86.231) × 0.2] + [10 DO × 0.2] + [((−0.119 TH) + 113.68) × 0.15] + [(−5.886 COD +99.846) × 0.1] + [(−0.12 Cl+ 106.58) × 0.15] | [25] |
| Chemical Parameters (52) | Physical Parameters (9) | Microbiological Parameters (4) |
|---|---|---|
| Dissolved Oxygen (DO), pH, Total Phosphorus (TP), chloride (Cl−), Chemical Oxygen Demand (COD), Biochemical Oxygen Demand (BOD), manganese (Mn), Soluble Reactive Phosphorus (SRP), cadmium (Cd), lead (Pb), chromium (Cr), copper (Cu), zinc (Zn), sulphates , arsenic (As), fluoride (F−), mercury (Hg), selenium (Se), cobalt (Co), vanadium (V), magnesium (Mg), sodium adsorption ratio (SAR),Residual Sodium Carbonate (RSC), Magnesium Adsorption Ratio (MAR), nickel (Ni), calcium (Ca2+), nitrites , Total Nitrogen (TN), sodium (Na+), total acidity, total alkalinity, calcium hardness (Ca H), magnesium hardness (Mg H), silica (Si), salinity, boron (Bo), electrode potential (Eh), bicarbonate chlorophyll-a (Chl-a), iron oxide (Fe), Osmotic Potential (OP), barium (Ba), aluminium (Al), potassium (K+), molybdenum (Mo), strontium (Sr), Uranium (U), titanium (Ti), carbonates , ammonium nitrogen (NH4-N), nitrate nitrogen (NO3-N), Isotopes 2-H and 18-O. | Hardness, temperature, colour, total solids (TS), turbidity, suspended solids (SS), total dissolved solids (TDS), and electrical conductivity (EC). | Fecal coliform (FC), Escherichia coli (E. coli), Total Fungi (TF), Total Coliforms (TC). |
| Use | Parameters |
|---|---|
| Drinking | Temp, DO, BOD, TDS, TSS, EC, pH, hardness, colour, Alk, total acid, turb, F, Cl− Mn, , , SO4, NO2-N, NO3-N, PO4-P, NH4-N, Cu2+, Fe2+, Fe 3+, Cr, K+, Na+, Zn2+, Ca2+, Mg2+, Pb, As, Ar, Si, Al, Ba, B, U, Se, Mo, Bo, Cd, Hg, Ni, Co, V, E. coli, FC, TC |
| Domestic use | Temp, pH, turb, EC, TDS, TS, hardness, DO, BOD, COD, NO3-N, NH4-N, PO4-P, Cl−, SO4, Mg2+, B, Fe, F, As, Cd, Si, Cr, Sr, Ti, Pb, Ni, Hg, Se, Al, Mn, K+, Na+, Zn2+, Cu2+ Ca2+, Mg2+, , SO4, FC, Eh, salt, SiO2, Isotopes δ2H and δ18O |
| Agriculture and irrigation | Temp, EC, TDS, TS, pH, BOD, DO, Alk, turb, colour, K+, Na+, Zn2+, Ca2+, Mg2+, SO4, Cl−, SO4, , NO3-N, PO4-P, NH4-N, SAR, RSC, , MAR, hardness, B, Al, As, Cd, Co, Cr, Cu, Fe, Mn, Mo, Ni, Pb, Se, V, TC, FC, E. coli, Fungi |
| Protection of aquatic life | Temp, EC, pH, DO, turb, BOD, COD, TSS, TDS, Cl−, Chl-a, F, NH4-N, PO4-N, NO3-N, NO2-N, SO4, OP, Mn, Cu 2+, Zn2+, Pb, Cd, Cr, Ni, Fe, TC |
| Recreation | Temp, pH, turb, EC, Cl−, TSS, SRP, TP, NH4-N, NO3-N, E. coli |
| Class | a. CCME WQI | b. OWQI | ||
|---|---|---|---|---|
| Rank | Index Score | Rank | Index Score | |
| Class 1 | Excellent | 95–100 | Excellent | 90–100 |
| Class 2 | Good | 80–94 | Good | 85–89 |
| Class 3 | Fair | 60–79 | Fair | 80–84 |
| Class 4 | Marginal | 45–59 | Poor | 60–79 |
| Class 5 | Poor | 0–44 | Very poor | 0–59 |
| Class | a. TMWQI | b. RWQI | ||
|---|---|---|---|---|
| Rank | Index Score | Rank | Index Score | |
| Class 1 | Excellent | <26 | Excellent | <50 |
| Class 2 | Good | 26–50 | Good | 50–100 |
| Class 3 | Medium | 51–75 | Poor | 100–200 |
| Class 4 | Poor | 76–100 | Very poor | 200–300 |
| Class 5 | Unsuitable | >100 | Unsuitable | >100 |
| Colour | Rank | Index Value |
|---|---|---|
| Dark red | Very poor | 0–10 |
| Orange | Poor | * |
| Yellow | Medium/Average | 50 |
| Green | Good | ** |
| Dark blue | Excellent | 90–100 |
| Class | a. | b. | ||
|---|---|---|---|---|
| Rank | Index Score | Rank | Index Score | |
| Class 1 | <50 | Excellent | 0–25 | Excellent |
| Class 2 | 50–100 | Good | 26–50 | Good |
| Class 3 | 100–200 | Poor | 51–75 | Poor |
| Class 4 | 200–300 | Very poor | 76–100 | Very poor |
| Class 5 | >300 | Unsuitable for human consumption | >100 | Unsuitable for human consumption |
| Class | a. | b. | ||
|---|---|---|---|---|
| Rank | Index Score | Rank | Index Score | |
| Class 1 | 91 ≤ Index ≤ 100 | Good | >2.8 | Excellent |
| Class 2 | 61 ≤ Index < 91 | Acceptable | 2.3–2.8 | Good |
| Class 3 | 31 ≤ Index < 61 | Regular | <2.3 | Poor |
| Class 4 | 16 ≤ Index < 31 | Bad | ||
| Class 5 | 0 ≤ Index < 16 | Very bad | ||
| Metrics of Comparison | Adapted WQIs | The DEA Model | UWQI | Surrogate WQI | Hounsinou Scale |
|---|---|---|---|---|---|
| 1. Parameter selection | Researchers’ discretion | Value observation | Expert opinion | Delphi technique multivariate statistics | Researchers’ discretion |
| 2. No. of parameters | average: 14 | 10 | 13 | 4 | 27 |
| 3. Type of parameters | Physical, chemical, microbiological | Physical, chemical | Physical, chemical | Physical, chemical | Physical, chemical, microbiological |
| 4. Index development steps | Parameter selection, the establishment of parameter weights, the formation of sub-indices and the final aggregation function | Creation of input variables, classification to obtain optimistic closeness values, Banker Charnes Cooper, (BCC) model with a single output, WQI | Parameter selection, the establishment of weight coefficients, formation of sub-indices and aggregation formula | Delphi method, PCA, Hierarchical Cluster Analysis (HCA), Multivariate Regression Analysis (MRA), Regression model | Parameter selection, the establishment of parameter weights, formation of sub-indices and the final aggregation function |
| 5. Index aggregation function | Weighted Arithmetic function WQI = | WQI = | Modified weighted sum to to Final UWQI function WQI = to 1.0880563 | Surrogate WQI = f(x) = b0 + b1x1 + b2x2 + … + b4x4 + ε | CWQI = MWQI = 1/3 (10/9 TC + 20 FC + 1000 EI) |
| 6. Water quality standards | Sub-index development using FAO guidelines for irrigation, South African National Water Standards, etc. | Classification of each hydrochemical parameter into quality categories using WHO guidelines for drinking water, National agency for hydraulic resources, etc. | Sub-index development using South Africas water quality guidelines implemented by water and forestry depatment | - | Sub-index development usingWHO guidelines for drinking water quality |
| 7. Index categorisation scheme | Adapted CCMEWQI-increasing categorisation scale with 5 classes Adapted WAWQI- decreasing scale with 5 classes | Sturges’s rule I = 1 + 3.322log10(K) | Increasing categorisation scale with 5 classes, including logical linguistic descriptors | Increasing categorisation scale with 5 classes | CWQI-decreasing categorisation scale with 7 classes MWQI-decreasing categorisation scale with 8 classes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lukhabi, D.K.; Mensah, P.K.; Asare, N.K.; Pulumuka-Kamanga, T.; Ouma, K.O. Adapted Water Quality Indices: Limitations and Potential for Water Quality Monitoring in Africa. Water 2023, 15, 1736. https://doi.org/10.3390/w15091736
Lukhabi DK, Mensah PK, Asare NK, Pulumuka-Kamanga T, Ouma KO. Adapted Water Quality Indices: Limitations and Potential for Water Quality Monitoring in Africa. Water. 2023; 15(9):1736. https://doi.org/10.3390/w15091736
Chicago/Turabian StyleLukhabi, Dorothy Khasisi, Paul Kojo Mensah, Noble Kwame Asare, Tchaka Pulumuka-Kamanga, and Kennedy Ochieng Ouma. 2023. "Adapted Water Quality Indices: Limitations and Potential for Water Quality Monitoring in Africa" Water 15, no. 9: 1736. https://doi.org/10.3390/w15091736






