Ant-Inspired Metaheuristic Algorithms for Combinatorial Optimization Problems in Water Resources Management
Abstract
1. Introduction
2. Methodology
3. Ant Colony Optimization
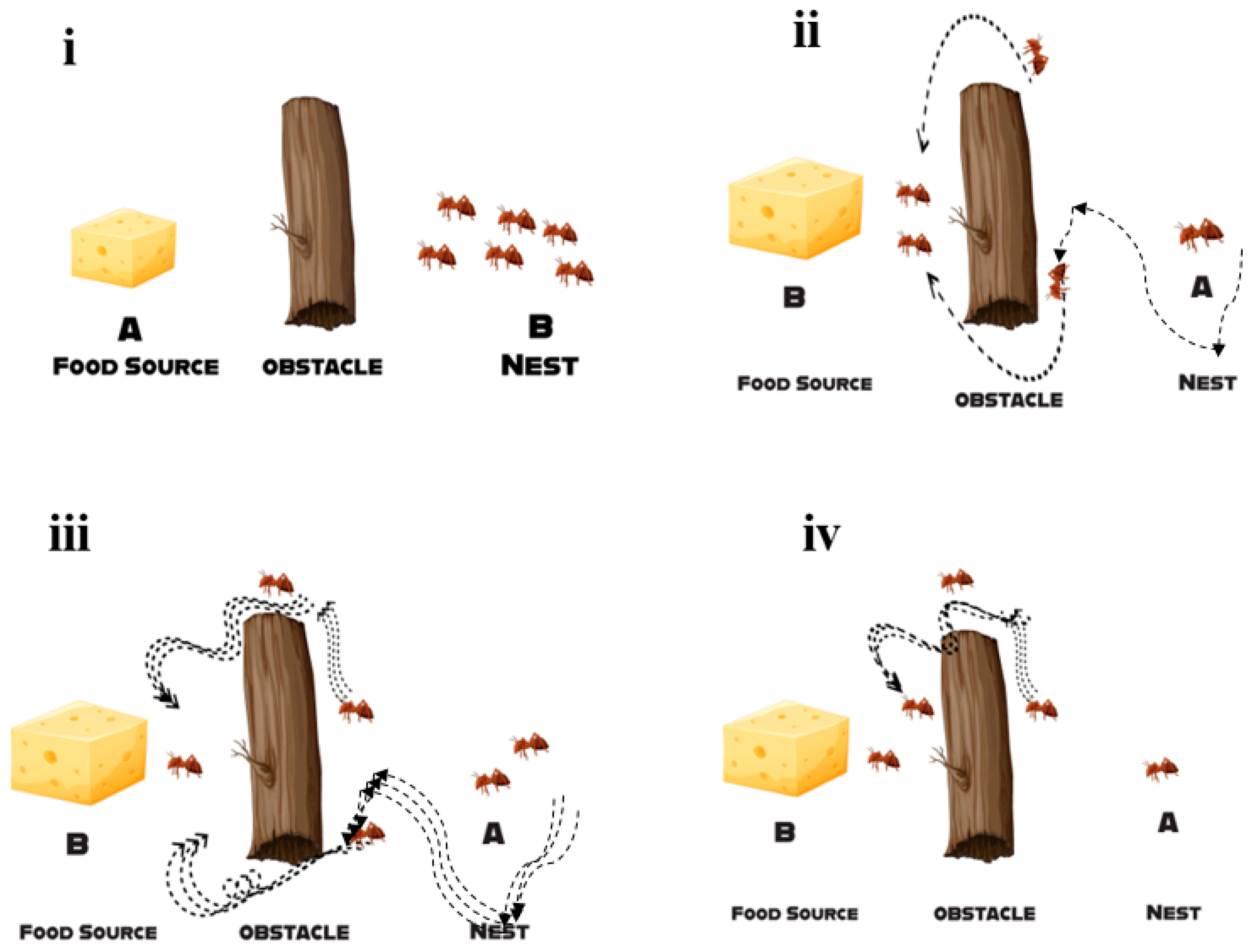
3.1. Clustering Behavior of Ants
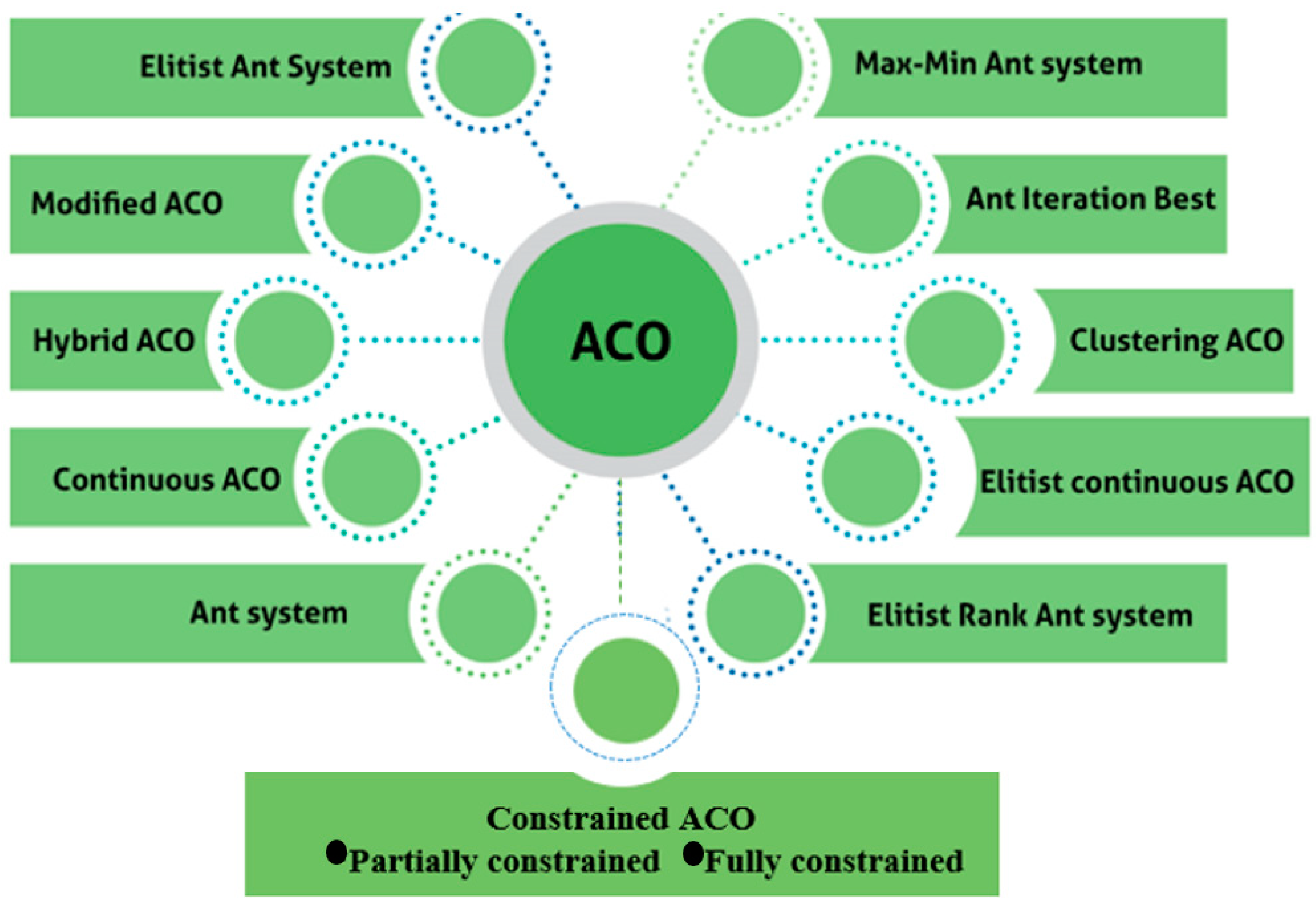
3.2. Variants of ACO
| Method & Logic | Advantages | Disadvantages |
|---|---|---|
| 1. Ant system [10] Inspired by the foraging behavior of real ant colonies | Capturing indirect communication among the individuals of a colony of ants | –No concrete proof of how many ants would be required for convergence –Stopping criteria not mentioned –Optimal value for the stagnation behavior is not clearly specified –Getting stuck in local optima –How to decide varying the values for the various parameters |
| 2. Ant density model [15,16] Leaves a defined trail of Q for unit length in its path | Requires extensive data on ant populations | |
| 3. Ant cycle model [16] Adaptation of the ant quantity model, which basically performs the process of reinforcement in accordance with the distance travelled | Limited scalability | |
| 4. Ant quantity model [16] Deposits a pheromone quantity of Q on the entire path. | Shorter paths will automatically have more pheromone deposits on them hence higher desirability | |
| 5. Ant colony system [11,17] –Fine-tuned version of ant system –The probability rule used to find the path to move in next area is different from AS | –Suitable for parallelization –The length of route covered is given priority | Convergence speed and solution accuracy when dealing with a large amount of data is not defined |
| 6. ACS–3 opt local search [18] Additional local search heuristics to improve the exploitation capability of the algorithm | –Overcomes the problem of getting stuck in local optima –Provides state transition rule, a global update rule and a local pheromone update rule | –Increased computational complexity –Risk of getting trapped in local optima |
| 7. Max–min ant system [19] Exploits the best solution found during the iteration | Limits the ant when it is about to choose an arc to travel by eliminating that arc if it does not fall between the interval | Getting stuck in local optima aggravates the problem of premature stagnation |
| 8. Elitist ant system [20] –Preserves fittest individual of a system to save genetic information –Additional reinforcement to the parts belonging to the best path found since the beginning of the solution procedure | Risk of beginning with poor initial solution is less | –Local search becomes more important than global search –Effect of emphasizing short paths reduces when destination comes closer, especially when ants travel on good but sub-optimal paths |
| 9. ASibest (asymmetric best-worst ant system) [21] Asymmetry in the pheromone updates, where ants differentiate between the best and worst solutions found so far, and update pheromones accordingly. | Faster convergence and improved solution quality compared to the basic AS algorithm | –Potential for over-optimization –Limited applicability –Asymmetry may cause trade-offs between exploitation and exploration |
| 10. Elitist ant rank system ASrank [22] Elitism and rank used to update trail weights considering the best ants’ rank-based system ranks the resultant paths according to their distance travelled and provides them with a rank value. | –Danger of over-emphasized pheromone trails using sub-optimal paths can be avoided –Emphasizing good paths and good ants equally, hence well balanced –The results of this approach provide a balanced exploration and exploitation of the search space | –Getting stuck in local optima –Potential premature convergence –Lack of diversity in solution exploration |
| 11. Hybrid ant system [23] Combines ant system with other optimization techniques to leverage their strengths | –Enhanced performance by combining the strengths of different optimization techniques –Increased versatility –Robustness to local optima –Synergy of multiple algorithms | –Higher computational cost –Increased complexity –Difficulty in parameter tuning –Increased risk of overfitting |
| 12. Fast ant system [24] Uses re-initialization of pheromones and does not consider pheromone evaporation | –Uses re-initialization of pheromones to avoid stagnation –Enhanced exploitation–exploration balance | Only one ant is used, not the population. Hence, becomes a biased approach |
| 13. Cooperative genetic ant system [25] Combines both the genetic algorithm and ant system | –Better chance of achieving global solution –The global best will be chosen and then pheromone is updated –More solution space is explored using GA which yields global optimum | –Iterations give good results only for particular parameter values –Increased complexity |
| 14. Improved ant system [26] Dynamically adjusts the pheromone density values to avoid local optima | –Pheromone density value set dynamically avoids the local optima –Efficient search –Reduced error accumulation | –Heavy computational burden with multiple algorithms –Minimal reduction of errors compared with previous algorithm |
| 15. (Hybrid) model induced max–min ant system [27] Adjusted transition probabilities are developed by replacing static biased weighting factors with dynamic ones. | Optimal arcs will be identified at each step of tour construction using dual information derived from solving associated assignment problem (AP) and the search will be discarded from future consideration | –Requires additional computational overhead –Influenced by the bias problem-specific model |
| 16. Cunning ant system [28] Introduces additional “cunning” behavior in ants to improve their search efficiency | –Improved convergence speed –Robustness to local optima | –Complexity in tuning parameters –Potential for bias or overfitting |
| 17. Population based ACO [29] Involves multiple ant colonies or populations working concurrently on the same problem | –Enhanced exploration and exploitation –Improved convergence speed | –Potential for interference among colonies –Increased computational overhead |
| 18. Beam ACO [30] Uses limited number of top-ranked ants, also known as the “beam width,” for pheromone update and solution construction. | –Faster convergence –Reduced memory usage –Better exploitation –Enhanced solution quality | –Sensitivity to beam width parameter –Limited solution diversity –Reduced exploration |
| 19. Hyper cube ACO [31] Uses hypercubes to represent the search space and facilitate exploration. | –Enhanced exploration as ants can search space concurrently –Robust to changes in problem characteristics | –Additional layer of complexity to the algorithm –Requires careful tuning of hypercube-related parameters |
| 20. Continuous ACO [32] Specifically designed for solving continuous optimization problems | –Can handle a wide range of continuous optimization problems –Robust to noise and can tolerate small perturbations in the objective function or constraints –Capable of performing global search in the continuous search space | –May face challenges in fine-tuning and exploiting solutions to achieve high-quality solutions –May have slower convergence speed compared to gradient-based optimization algorithms |
| 21. Constrained ACO [33] Specifically designed to solve optimization problems with constraints, where the feasible solution space is restricted. | –Capable of handling optimization problems with constraints, making it suitable for solving real-world problems –Versatile –Robust to constraints violations during the search process | –Computationally expensive, especially for complex optimization problems –Needs to strike a balance between exploration and exploitation –May face challenges in finding high-quality solutions that satisfy all the constraints |
| 22. Elitist ACO [34] Incorporates an elitist strategy to improve the exploitation of the best solutions found | Elitist ACO reinforces the global best solution during each iteration, thereby enabling faster convergence towards the optimal solution | –May converge prematurely to a suboptimal solution, especially if the elite solutions are not updated or diversified effectively |
| 23. Partially constrained ACO [35] Designed to handle optimization problems where some constraints are present but not strictly enforced | –Allows for flexibility in handling constraints by not strictly enforcing them –Can explore solutions that violate constraints | –Does not strictly enforce constraints, which can result in solutions that violate constraints –Uses a penalty-based approach to handle constraints, where violations are penalized –May lead to a trade-off between convergence speed and solution quality |
| 24. Fully constrained ACO [35] Optimization process takes into consideration the constraints of the problem and generates solutions that strictly adhere to all the constraints | –Guaranteed constraint satisfaction –Convergence to feasible solutions | –Strictly adheres to constraints, which may limit the exploration of the search space –Sensitivity to constraint changes |
| 25. Arc based ACO [36] Uses arcs, or directed edges, as the building blocks for constructing solutions | –Ants only need to select arcs instead of vertices or components, hence reduced solution space –Improved solution quality | –Less flexible compared to vertex-based ACO –More complex to implement and configure |
| 26. Ant colony clustering [37] Objective is to group a set of data points into clusters based on some similarity or distance measure | –Flexible algorithm that can be adapted to various types of clustering problems –Good scalability | –Converge to suboptimal clustering solutions if the search process becomes trapped in local optima |
| 27. Ant colony coupled differential evolution [38] Combines the principles of ant colony optimization (ACO) and differential evolution (DE) to solve optimization problems | –Benefits from the global search capability of both ACO and DE –Converges to high-quality solutions efficiently due to the use of both exploitation (DE) and exploration (ACO) mechanisms | –Computational complexity –Algorithm complexity |
| 28. Elitist continuous ACO [8] Designed for continuous optimization problems where the decision variables are continuous instead of discrete | –Good global search capability –Can converge to high-quality solutions efficiently | –Requires careful parameter tuning to achieve optimal performance –Limited exploitation capability |
| 29. Fuzzy-ACO [39] Incorporates fuzzy logic into the ACO algorithm. | –Robustness to uncertainty –Good exploitation–exploration balance | –Requires careful parameter tuning –Computationally expensive |
| 30. Hybrid ACO [40] Combines ACO with other optimization techniques to create a hybrid approach | –Combines the strengths of different optimization techniques to provide enhanced optimization performance | –Increased complexity –Computationally expensive |
| 31. Quantum ACO [41] Combines ACO with quantum computing principles, specifically utilizing quantum bits (qubits) and quantum gates to encode and manipulate information during the optimization process | –Quantum parallelism –Quantum entanglement –Overcomes energy barriers and access search spaces that are inaccessible using quantum tunneling | –High computational overhead –Limited quantum computing resources |
| 32. Induced max–min ACO [27] Uses additional heuristics and rules to update pheromone trails | –Uses “induced perturbation” technique to introduce additional randomness in the search process, which enhances exploration of the solution space –Improved convergence speed | –There is no guarantee that it will always find the global optimal solution –Induced perturbation technique adds additional computational overhead to the algorithm |
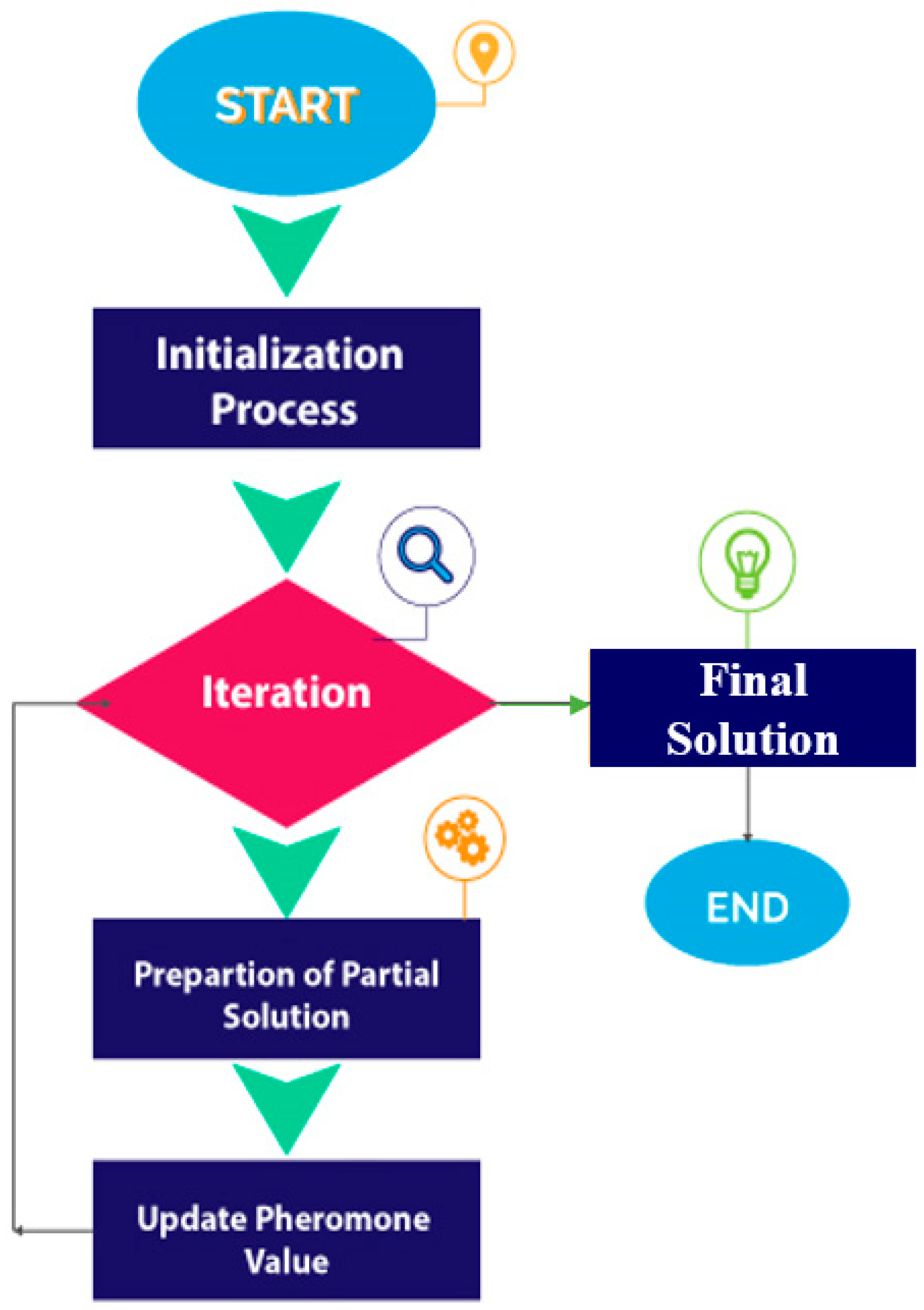
3.3. Workflow
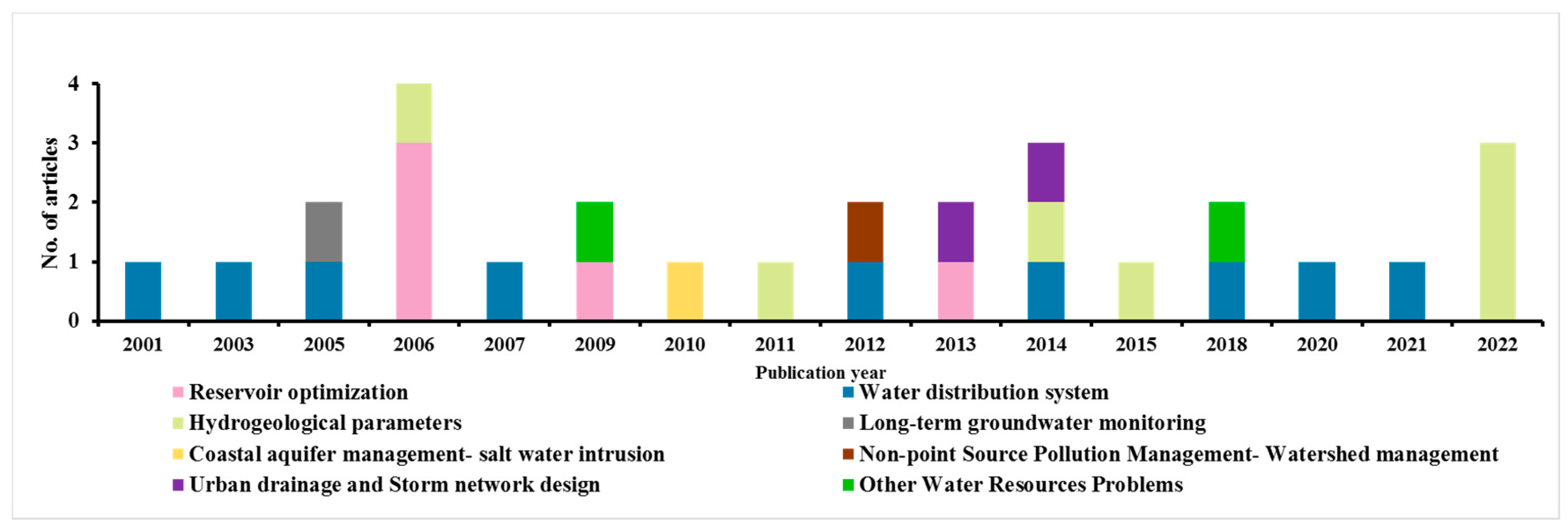
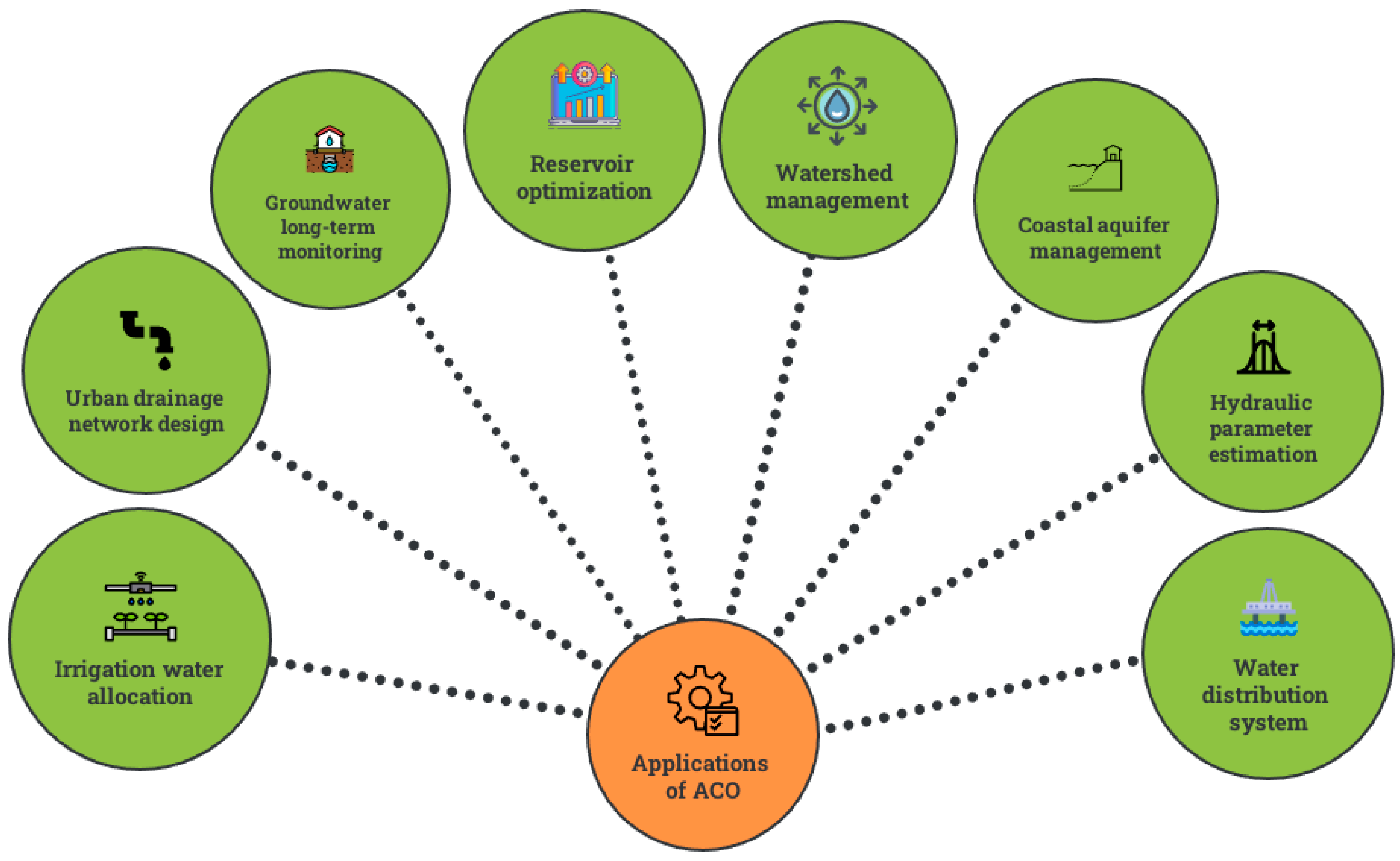
4. Applications of ACOs
4.1. Reservoir Optimization
| Year | ACO Variant | Application | Name of the Reservoir | Reference |
|---|---|---|---|---|
| 2006 | Improved ACO | Single purpose | Dez Reservoir, Iran | [43] |
| 2006 | ACO | Multi-purpose | Hirakud Reservoir, India | [45] |
| 2008 | ACO for continuous domains | Single purpose | Dez Reservoir, Iran | [44] |
| 2013 | CACOA, UCACO, PCACO, FCACO, max –min ant system | Multi-purpose | Theoretical study | [46] |
| 2018 | CACO & DACO | Single purpose | Dez Reservoir, Iran | [47] |
4.2. Water Distribution Systems
| Year | ACO Variant | Application | Reference |
|---|---|---|---|
| 2001 | ACO | Parameter selection | [49] |
| 2003 | ACO | Optimal design | [50] |
| 2005 | ACO, ASi-best | Optimal design | [51] |
| 2012 | ACO | Metric analysis for ACO search behavior | [52] |
| 2014 | Elitist AS, AS, ERAS, MMAS | Minimize design cost | [53] |
| 2017 | EA, GA, PSO, ACO, MA | Design and rehabilitation | [54] |
| 2018 | ACO | Planning of water delivery schedules | [55] |
| 2020 | Fuzzy SARSA learning and ACO | Water delivery scheduling under water shortage conditions | [56] |
4.3. Hydrogeological Parameter Estimation
| Year | ACO Variant | Application | Reference |
|---|---|---|---|
| 2006 | Hybrid ACO | Transmissivity and storage co-efficient for unsteady groundwater flow | [57] |
| 2012 | ACO-BP | Permeability analysis | [58] |
| 2014 | ACCO | Spatial evaluation of water quality | [59] |
| 2016 | Modified ACO | Flow modelling | [60] |
| 2021 | ACOR | Water quality management | [61] |
| 2022 | Improved ACO | Earth resistivity | [62] |
| 2022 | ACO | Groundwater salinity | [63] |
| 2022 | ACO | River water level forecasting | [64] |
| 2023 | ACO | Evapotranspiration | [65] |
| 2023 | ACO | Discharge | [66] |
4.4. Other Applications
| Year | ACO variant | Application | Reference |
|---|---|---|---|
| 2006 | ACO-LTM | Groundwater long-term monitoring | [67] |
| 2009 | ACDE | Water resource problems | [68] |
| 2010 | ECACO | Seawater intrusion management | [69] |
| 2012 | ACO + SWAT | Non-point source pollution management | [70] |
| 2016 | ABACO-TGA | Urban drainage network design | [71] |
| 2018 | ACO | Water management in irrigation areas | [72] |
4.4.1. Long-Term Groundwater Monitoring
4.4.2. ACDE-Water Resources Problems
4.4.3. Coastal Aquifer Management–Salt Water Intrusion
4.4.4. Non-Point Source Pollution Management–Watershed Management
4.4.5. Urban Drainage and Storm Network Design
4.4.6. Optimal Crop and Irrigation Water Allocation
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agarwal, P.; Mehta, S. Nature-Inspired Algorithms: State-of-Art, Problems and Prospects. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.678.3042&rep=rep1&type=pdf (accessed on 1 February 2023).
- Vassiliadis, V.; Dounias, G. Nature–Inspired Intelligence: A Review of Selected Methods and Applications. Int. J. Artif. Intell. Tools 2009, 18, 487–516. Available online: https://www.worldscientific.com/doi/pdf/10.1142/S021821300900024X (accessed on 9 January 2023). [CrossRef]
- Fister, I.; Yang, X.S.; Brest, J.; Fister, D. A brief review of nature-inspired algorithms for optimization. Elektrotech. Vestnik Electrotech. Rev. 2013, 80, 116–122. [Google Scholar]
- Ostfeld, A. Ant Colony Optimization for Water Resources Systems Analysis—Review and Challenges; InTech: Rijeka, Croatia, 2011; Available online: https://www.intechopen.com/books/ant-colony-optimization-methods-and-applications/ant-colony-optimization-for-water-resources-systems-analysis-review-and-challenges (accessed on 2 April 2021).
- Soto, R.; Crawford, B.; Olivares, R.; Taramasco, C.; Figueroa, I.; Gómez, Á.; Castro, C.; Paredes, F. Adaptive Black Hole Algorithm for Solving the Set Covering Problem. Math. Probl. Eng. 2018, 2018, 2183214. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant Colony Optimization, Book by Morco Dorigo and Thomas Stützle; MIT Press Direct: Cambridge, MA, USA, 2004; Available online: https://web2.qatar.cmu.edu/~gdicaro/15382/additional/aco-book.pdf (accessed on 15 August 2022).
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In European Conference of Artificial Life; SciSpace: Bangalore, India, 1991; pp. 134–142. [Google Scholar]
- Afshar, A.; Massoumi, A.; Afshar, A.; Mariño, A. State of the Art Review of Ant Colony Optimization Applications in Water Resource Management. Water Resour. Manag. 2015, 29, 3891–3904. [Google Scholar] [CrossRef]
- Bonabeau, E.; Corne, D.; Poli, R. Swarm intelligence: The state of the art special issue of natural computing. Nat. Comput. 2010, 9, 655–657. Available online: https://www.researchgate.net/publication/220132796_Swarm_intelligence_The_state_of_the_art_special_issue_of_natural_computing (accessed on 25 September 2021). [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant System: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. Available online: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4129846 (accessed on 1 June 2019). [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Franks, F.R.; Dornhaus, A.; Best, C.S.; Jones, E.L. Decision making by small and large house-hunting ant colonies: One size fits all. Anim. Behav. 2006, 72, 611–616. [Google Scholar] [CrossRef]
- Kube, C.R.; Bonabeau, E. Cooperative Transport by Ants and Robots. Robot. Auton. Syst. 1999, 30, 85–101. Available online: https://www.researchgate.net/publication/222658235_Cooperative_Transport_By_Ants_and_Robots (accessed on 16 November 2021).
- Dorigo, M.; Di Caro, G.; Gambardella, L.M. Ant algorithms for discrete optimization. Artif. Life 1999, 5, 137–172. [Google Scholar]
- SeonYoo, K. A modified ant colony optimization algorithm for dynamic topology optimization. Comput. Struct. 2013, 123, 68–78. [Google Scholar] [CrossRef]
- Prakasam, A.; Savarimuthu, N. Metaheuristic algorithms and probabilistic behaviour: A comprehensive analysis of Ant Colony Optimization and its variants. Artif. Intell. Rev. 2016, 45, 97–130. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the travelling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef]
- Mahi, M.; Baykan, Ö.K.; Kodaz, H. A new hybrid method based on Particle Swarm Optimization, Ant Colony Optimization and 3-Opt algorithms for Traveling Salesman Problem. Appl. Soft Comput. 2015, 30, 484–490. [Google Scholar] [CrossRef]
- Stützle, T.; Hoos, H.H. MAX–MIN Ant System. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Shtovba, S.D. Ant Algorithms: Theory and Applications. Progr. Comput. Softw. 2005, 31, 167–178. [Google Scholar] [CrossRef]
- Yan, Z.; Hao, W.; Yonghua, Z.; Yun, C. BEST-WORST Ant System. In Proceedings of the 3rd International Conference on Advanced Computer Control, Harbin, China, 18–20 January 2011. [Google Scholar] [CrossRef]
- Bernd, B.; Richard, H.; Christine, S. A New Rank Based Version of the Ant System—A Computational Study. Cent. Eur. J. Oper. Res. 1999, 7, 25–38. [Google Scholar]
- McKendall, A.R.; Shang, J. Hybrid ant systems for the dynamic facility layout problem. Comput. Oper. Res. 2006, 33, 790–803. [Google Scholar] [CrossRef]
- Taillard, E.D.; Gambardella, L.M. Adaptive Memories for the Quadratic Assignment Problem; Technical Report, IDSIA-87-97; IDSIA: Lugano, Switzerland, 1997. [Google Scholar]
- Abbattista, F.; Abbattista, N.; Caponetti, L. An evolutionary and cooperative agents model for optimization. In Proceedings of the 1995 IEEE International Conference on Evolutionary Computation, Perth, WA, Australia, 29 November–1 December 1995; Volume 2, pp. 668–671. [Google Scholar] [CrossRef]
- Pintea, C.M.; Dumitrescu, D. Improving ant systems using a local updating rule. In Proceedings of the Seventh International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC’05), Timisoara, Romania, 25–29 September 2005; p. 4. [Google Scholar] [CrossRef]
- Bai, J.; Yang, G.-K.; Chen, Y.-W.; Hu, L.-S.; Pan, C.-C. A model induced max-min ant colony optimization for asymmetric traveling salesman problem. Appl. Soft Comput. 2013, 13, 1365–1375. [Google Scholar] [CrossRef]
- Tsutsui, S. cAS: Ant Colony Optimization with Cunning Ants Parallel Problem Solving from Nature. In Proceedings of the PPSN IX, 9th International Conference, Reykjavik, Iceland, 9–13 September 2006; Volume 4193, ISBN 978-3-540-38990-3. [Google Scholar]
- Guntsch, M.; Middendorf, M. A Population Based Approach for ACO. In Applications of Evolutionary Computing—EvoWorkshops 2002; Lecture Notes in Computer Science; Cagnoni, S., Gottlieb, J., Hart, E., Middendorf, M., Raidl, G.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2279. [Google Scholar] [CrossRef]
- Blum, C. Beam-ACO—Hybridizing ant colony optimization with beam search: An application to open shop scheduling. Comput. Oper. Res. 2005, 32, 1565–1591. [Google Scholar] [CrossRef]
- Blum, C.; Dorigo, M. The hyper-cube framework for ant colony optimization. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 1161–1172. [Google Scholar] [CrossRef] [PubMed]
- Omran, M.G.H.; Al-Sharhan, S. Improved continuous Ant Colony Optimization algorithms for real-world engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 85, 818–829. [Google Scholar] [CrossRef]
- Meyer, B.; Ernst, A. Integrating ACO and Constraint Propagation. In Ant Colony Optimization and Swarm Intelligence—ANTS 2004; Lecture Notes in Computer Science; Dorigo, M., Birattari, M., Blum, C., Gambardella, L.M., Mondada, F., Stützle, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3172. [Google Scholar] [CrossRef]
- Aristidis, V. An Ant Colony Optimization (ACO) algorithm solution to Economic Load Dispatch (ELD) problem. WSEAS Trans. Syst. 2006, 5, 1763–1771. [Google Scholar]
- Thiruvady, D.; Singh, G.; Ernst, A.T.; Meyer, B. Constraint-based ACO for a shared resource constrained scheduling problem. Int. J. Prod. Econ. 2013, 141, 230–242. [Google Scholar] [CrossRef]
- Yaghini, M.; Foroughi, A. ACO-Based Neighborhoods for Fixed-charge Capacitated Multi-commodity Network Design Problem. Int. J. Transp. Eng. 2014, 1, 311–334. [Google Scholar] [CrossRef]
- Shelokar, P.S.; Jayaraman, V.K.; Kulkarni, B.D. An ant colony approach for clustering. Anal. Chim. Acta 2004, 509, 187–195. [Google Scholar] [CrossRef]
- dos Santos Coelho, L.; de Andrade Bernert, D.L. A modified ant colony optimization algorithm based on differential evolution for chaotic synchronization. Expert Syst. Appl. 2010, 37, 4198–4203. [Google Scholar] [CrossRef]
- Di Caprio, D.; Ebrahimnejad, A.; Alrezaamiri, H.; Santos-Arteaga, F.J. A novel ant colony algorithm for solving shortest path problems with fuzzy arc weights. Alexandria Eng. J. 2022, 61, 3403–3415. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, J.; Xuan, J.; Ren, Z.; Hu, Y. A Hybrid ACO algorithm for the Next Release Problem. In Proceedings of the The 2nd International Conference on Software Engineering and Data Mining, Chengdu, China, 23–25 June 2010; pp. 166–171. [Google Scholar]
- Ghosh, M.; Dey, N.; Mitra, D.; Chakrabarti, A. A novel quantum algorithm for ant colony optimisation. IET Quant. Comm. 2022, 3, 13–29. [Google Scholar] [CrossRef]
- Sakthipriya, N.; Kalaipriyan, T. Variants of Ant Colony Optimization—A State of an Art. Indian J. Sci. Technol. 2015, 8, 1–15. [Google Scholar] [CrossRef]
- Jalali, M.R.; Afshar, A.; Marino, M.A. Improved Ant Colony Optimization Algorithm for Reservoir Operation. Sci. Iran 2006, 13, 295–302. [Google Scholar]
- Kumar, D.N.; Reddy, M.J. Ant Colony Optimization for Multi-Purpose Reservoir Operation. Water Resour. Manag. 2006, 20, 879–898. [Google Scholar] [CrossRef]
- Dariane, A.B.; Moradi, A.M. Reservoir Operating by Ant Colony Optimization for Continuous Domains (ACOR) Case Study: Dez Reservoir. Int. J. Math. Phys. Eng. Sci. 2009, 3, 2. [Google Scholar]
- Moeini, R.; Afshar, M.H. Extension of the constrained ant colony optimization algorithms for the optimal operation of multi-reservoir systems. J. Hydroinf. 2013, 15, 155–173. [Google Scholar] [CrossRef]
- Mohammad, A.; Ketabchi, H.; Rasa, E. Elitist Continuous Ant Colony Optimization Algorithm: Application to Reservoir Operation Problems. Int. J. 2006, 4, 274–285. [Google Scholar]
- Sarbu, I.; Popa-Albu, S. Optimization of urban water distribution networks using heuristic methods: An overview. Water Int. 2022, 48, 120–148. [Google Scholar] [CrossRef]
- Simpson, A.R.; Maier, H.R.; Foong, W.K. Selection of parameters for ant colony optimization applied to the optimal design of water distribution systems. In Proceedings of the International Congress on Modelling and Simulation, Canberra, Australia, 10–13 December 2001; Australian National University: Perth, WA, Australia, 2001; pp. 1931–1936. [Google Scholar]
- Maier, H.R.; Simpson, A.R.; Zecchin, A.C.; Foong, W.K.; Phang, K.Y.; Seaha, H.Y.; Tan, C.L. Ant colony optimization for design of water distribution systems. J. Water Resour. Plan. Manag. 2003, 129, 200–208. [Google Scholar] [CrossRef]
- Zecchin, A.C.; Simpson, A.R.; Maier, H.R.; Nixon, J.B. Parametric study for an ant algorithm applied to water distribution system optimization. IEEE Trans. Evol. Comput. 2005, 9, 175–191. [Google Scholar] [CrossRef]
- Zecchin, A.C.; Simpson, A.R.; Maier, H.R. Improved understanding of the searching behavior of ant colony optimization algorithms applied to the water distribution design problem. Water Resour. Res. 2012, 48, 1–16. [Google Scholar] [CrossRef]
- Zecchin, A.C.; Maier, H.R.; Simpson, A.R. Ant Colony Optimization Applied to Water Distribution System Design: Comparative Study of Five Algorithms. J. Water Resour. Plan. Manag. 2007, 133, 87–92. [Google Scholar] [CrossRef]
- El-Ghandour, H.A.; Elbeltagi, M.E. Comparison of Five Evolutionary Algorithms for Optimization of Water Distribution Networks. J. Comput. Civil Eng. 2018, 32. Available online: https://ascelibrary.org/doi/abs/10.1061/%28ASCE%29CP.1943-5487.0000717 (accessed on 1 February 2023). [CrossRef]
- Liu, Y.; Yang, T.; Zhao, R.-H.; Li, Y.-B.; Zhao, W.-J.; Ma, X.-Y. Irrigation Canal System Delivery Scheduling Based on a Particle Swarm Optimization Algorithm. Water 2018, 10, 1281. [Google Scholar] [CrossRef]
- Omidzade, F.; Ghodousi, H.; Shahverdi, K. Comparing Fuzzy SARSA Learning and Ant Colony Optimization Algorithms in Water Delivery Scheduling under Water Shortage Conditions. J. Irrig. Drain. Eng. 2020, 146. Available online: https://ascelibrary.org/doi/10.1061/%28ASCE%29IR.1943-4774.0001496 (accessed on 1 February 2023). [CrossRef]
- Li, S.; Liu, Y.; Yu, H. Parameter Estimation Approach in Groundwater Hydrology Using Hybrid Ant Colony System. In Computational Intelligence and Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 182–191. [Google Scholar] [CrossRef]
- Irani, R.; Nasimi, R. An evolving neural network using an ant colony algorithm for a permeability estimation of the reservoir. Pet. Sci. Technol. 2011, 30, 375–384. [Google Scholar] [CrossRef]
- Hou, J.W.; Mi, W.B.; Li, L.T. Spatial quality evaluation for drinking water based on GIS and ant colony clustering algorithm. J. Cent. South Univ. 2014, 21, 1051–1057. [Google Scholar] [CrossRef]
- Dobre, G.; Drobot, R. Estimating soil hydraulic parameters using a metaheuristic algorithm. Model. Civil Eng. 2011, 102–111. [Google Scholar]
- Ghorbani, M.K.; Afshar, A.; Hamidifar, H. River water quality management using a fuzzy optimization model and the NSFWQI Index. Water SA 2021, 47, 45–53. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, H.; Bai, J.; Liu, B.; Wu, H.; Wu, Z.; He, Z. A Priori Constrained ACO Method Applied to Three-Dimensional Imaging of Subsurface Electrical Resistivity. Geotech. Geol. Eng. 2023, 41, 15–25. [Google Scholar] [CrossRef]
- Jamei, M.; Karbasi, M.; Malik, A.; Abualigah, L.; Islam, A.R.M.T.; Yaseen, Z.M. Computational assessment of groundwater salinity distribution within coastal multi-aquifers of Bangladesh. Sci. Rep. 2022, 12, 11165. [Google Scholar] [CrossRef]
- Ahmed, A.A.M.; Deo, R.C.; Ghahramani, A.; Feng, Q.; Raj, N.; Yin, Z.; Yang, L. New double decomposition deep learning methods for river water level forecasting. Sci. Total Environ. 2022, 831, 154722. [Google Scholar] [CrossRef]
- Ghorbani, M.K.; Afshar, A.; Hamidifar, H.; Reddy, M.J. Proceedings of the Institution of Civil Engineers. Water Manag. 2022, 175, 190–205. [Google Scholar]
- Eslamitabar, V.; Ahmadi, F.; Sharafati, A.; Rezaverdinejad, V. Bivariate simulation of river flow using hybrid intelligent models in sub-basins of Lake Urmia, Iran. Acta Geophys. 2023, 71, 873–892. [Google Scholar] [CrossRef]
- Li, Y.; Chan Hilton, A.B. Reducing Spatial Sampling in Long-Term Groundwater Monitoring Networks Using Ant Colony Optimization. Int. J. Comput. Intell. Res. 2010, 1, 19–28. [Google Scholar] [CrossRef]
- Ali, M.; Pant, M.; Abraham, A. A Hybrid Ant Colony Differential Evolution and its application to water resources problems. In Proceeding of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 1133–1138. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Ketabchi, H. Elitist Continuous Ant Colony Optimization Algorithm for Optimal Management of Coastal Aquifers. Water Resour. Manag. 2010, 25, 165–190. [Google Scholar] [CrossRef]
- Skardi, M.J.E.; Afshar, A.; Solis, S.S. Simulation-optimization model for non-point source pollution management in watersheds: Application of cooperative game theory. KSCE J. Civ. Eng. 2013, 17, 1232–1240. [Google Scholar] [CrossRef]
- Verdaguer, M.; Clara, N.; Gutiérrez, O.; Poch, M. Application of Ant-Colony-Optimization algorithm for improved management of first flush effects in urban wastewater systems. Sci. Total Environ. 2014, 485–486, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.C.H.; Dandy, G.C.; Maier, H.R.; Ascough, J.C., II. Improved Ant Colony Optimization for Optimal Crop and Irrigation Water Allocation by Incorporating Domain Knowledge. J. Water Resour. Plan. Manag. 2016, 142. Available online: https://ascelibrary.org/doi/10.1061/%28ASCE%29WR.1943-5452.0000662 (accessed on 1 February 2023). [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhavya, R.; Elango, L. Ant-Inspired Metaheuristic Algorithms for Combinatorial Optimization Problems in Water Resources Management. Water 2023, 15, 1712. https://doi.org/10.3390/w15091712
Bhavya R, Elango L. Ant-Inspired Metaheuristic Algorithms for Combinatorial Optimization Problems in Water Resources Management. Water. 2023; 15(9):1712. https://doi.org/10.3390/w15091712
Chicago/Turabian StyleBhavya, Ravinder, and Lakshmanan Elango. 2023. "Ant-Inspired Metaheuristic Algorithms for Combinatorial Optimization Problems in Water Resources Management" Water 15, no. 9: 1712. https://doi.org/10.3390/w15091712
APA StyleBhavya, R., & Elango, L. (2023). Ant-Inspired Metaheuristic Algorithms for Combinatorial Optimization Problems in Water Resources Management. Water, 15(9), 1712. https://doi.org/10.3390/w15091712







