Teaching Sprinkler Irrigation Engineering by a Spreadsheet Tool
Abstract
:1. Introduction
2. Background
2.1. Mathematical Model for Sprinkler Irrigation
2.2. Numerical Approach to Simulating Water Drops’ Trajectory and Velocity
2.3. Kinetic Energy and Power
2.4. Irrigation Performance Indices
3. Results
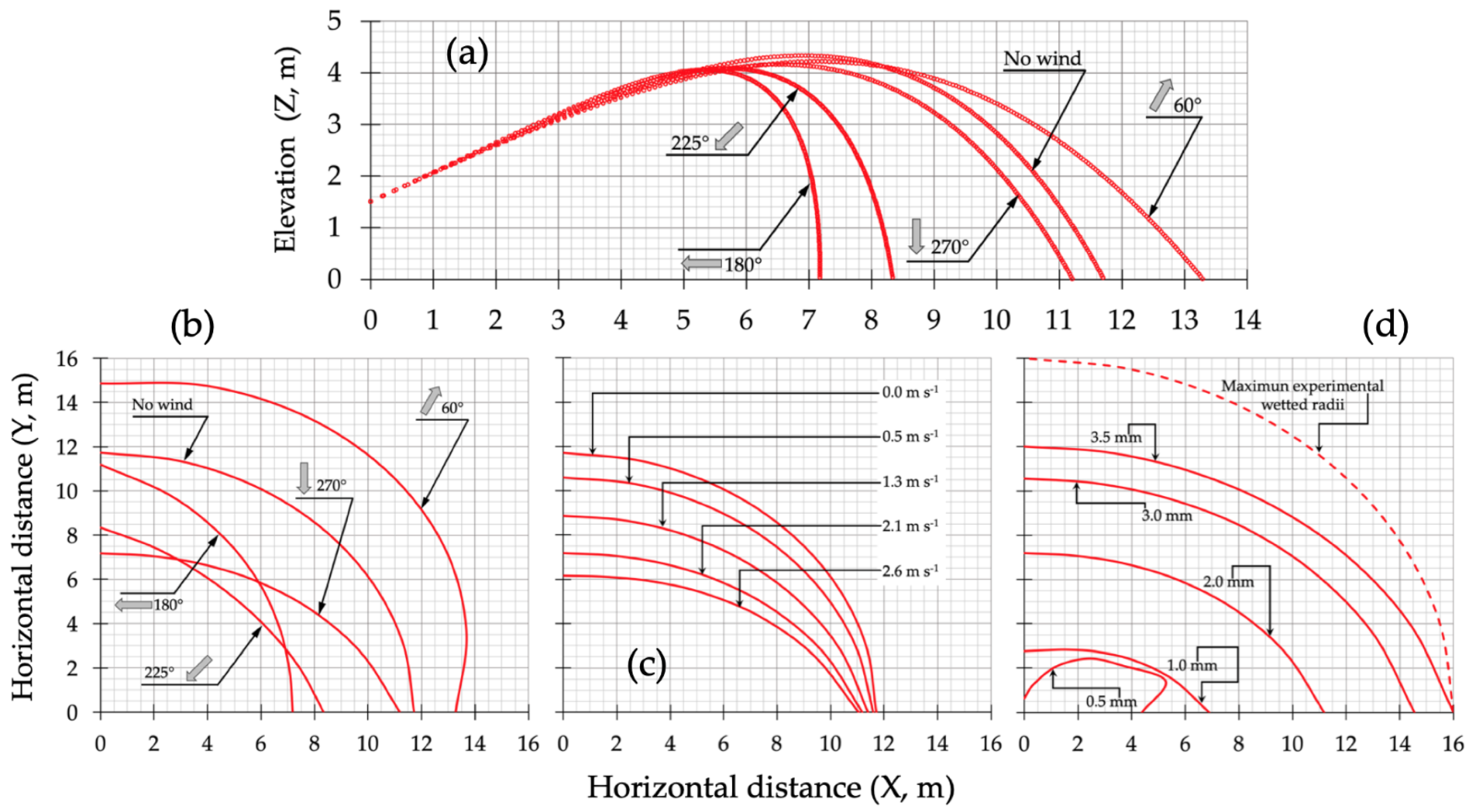
3.1. Sprinkler Irrigation Tool: Radial Patterns and Drop Diameter Frequency
3.2. Sprinkler Irrigation Tool: Drop Motion Simulation
3.3. Sprinkler Irrigation Tool: Add-On Resources
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Red de Indicadores de Ciencia y Tecnología (RICYT) 2021. El Estado de la Ciencia. Principales Indicadores de Ciencia y Tecnología Iberoamericanos/Interamericanos. Buenos Aires Argentina. 1968. Available online: www.ricyt.org (accessed on 12 December 2022).
- Feisel, L.D.; Rosa, A.J. The Role of the Laboratory in Undergraduate Engineering Education. J. Eng. Educ. 2005, 94, 121–130. [Google Scholar] [CrossRef]
- Fenton, J.D. Hydraulics: Science, knowledge, and culture. J. Hydraul. Res. 2016, 54, 485–501. [Google Scholar] [CrossRef]
- Jasanoff, S.; Markle, G.E.; Petersen, J.C.; Pinch, T. Handbook of Science and Technology Studies; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 1995; p. 832. [Google Scholar]
- Hunter, R. Highlights in the History of Hydraulics; University of Iowa: Iowa City, IA, USA, 1983; Available online: http://www.lib.uiowa.edu/spec-coll/bai/hydraul.htm (accessed on 5 January 2023).
- Feibleman, J.K. Pure Science, Applied Science, Technology, Engineering: An Attempt at Definitions Technology and Culture; The Johns Hopkins University Press and the Society for the History of Technology, Johns Hopkins University Press: Michigan, MA, USA, 1961; Volume 2, pp. 305–317. Available online: http://www.jstor.org/stable/3100886 (accessed on 10 January 2023).
- Playán, E.; Burguete, J.; Zapata, N.; Salvador, R.; Bautista-Capetillo, C.; Cavero, J.; Martínez-Cob, A.; Faci, J.; Dechmi, F. Mathematical problems and solutions in sprinkler irrigation. Monografías de la Real Academia de Ciencias de Zaragoza 2009, 31, 153–174. [Google Scholar]
- Merriam, J.L.; Keller, J. Farm Irrigation System Evaluation: A Guide for Management; Dept. of Agricultural and Irrigation Engineering, Utah State University: Logan, UT, USA, 1978. [Google Scholar]
- Basavaiah, J.; Arlene, A.A.; Mohan, P.C. Transformation of engineering education through student-centric learning. Int. J. Learn. Teach. 2021, 13, 32–41. [Google Scholar] [CrossRef]
- Wahba, E.M. An Improved Computational Algorithm for Teaching Hydraulics of Branching Pipes in Engineering Curricula. Comput. Appl. Eng. Educ. 2015, 23, 537–541. [Google Scholar] [CrossRef]
- López, P.A.; Mora, J.J.; Martínez, F.J.; Izquierdo, J. Computational Fluid Dynamics (CFD) Models in the Learning Process of Hydraulic Engineering. Comput. Appl. Eng. Educ. 2010, 18, 252–260. [Google Scholar] [CrossRef]
- Baldock, T.E.; Chanson, H. Undergraduate teaching of ideal and real fluid flows: The value of real-world experimental projects. Eur. J. Eng. Educ. 2006, 31, 729–739. [Google Scholar] [CrossRef]
- Hernandez-de-Menendez, M.; Morales-Menendez, R. Technological innovations and practices in engineering education: A review. Int. J. Interact. Des Manuf. 2019, 13, 713–728. [Google Scholar] [CrossRef]
- Barrón, C.A.; Alvarado, M.P.; Bautista-Capetillo, C.; Badillo-Almaraz, H. A computational tool to pipe network design. Acta Univ. Multidiscip. Sci. J. 2021, 31, e3093. [Google Scholar] [CrossRef]
- Saldarriaga, J.; Pulgarín, L.; Cuero, P.; Duque, N. Software para la Enseñanza de Hidráulica de Tuberías. In Proceedings of the XV Seminario Iberoamericano de Redes de Agua y Drenaje, SEREA2017, Bogota, Colombia, 27–30 November 2017; Volume 1, pp. 1–8. Available online: http://ssrn.com/abstract=3113745 (accessed on 17 January 2023).
- Ormsbee, L.E. The evolution of water distribution models. In Proceedings of the WDSA/CCWI Conference Proceedings, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]
- Ormsbee, L.E. The History of Water Distribution Network Analysis. In Proceedings of the Computer Age, 8th Annual Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Binning, C.D. Teaching Hydraulics without Water. In Proceedings of the World Water and Environmental Resources Congress, Philadelphia, PA, USA, 23–26 June 2003. [Google Scholar]
- Pandit, A. Water Engineering with the Spreadsheet A Workbook for Water Resources Calculations Using Excel; ASCE Press: Reston, VA, USA, 2016; pp. 3–129. ISBN 978-0-7844-7918-6. [Google Scholar]
- Oke, S.A. Spreadsheet Applications in Engineering Education: A Review. Int. J. Eng. Ed. 2004, 20, 893–901. [Google Scholar]
- Huddleston, A.H. Using Technology to Enrich Undergraduate Water Resources Instruction. In Proceedings of the World Water and Environmental Resources Congress, Philadelphia, PA, USA, 23–26 June 2003. [Google Scholar]
- El-Awad, M. and Al-Saidi, M. Excel as an Educational Platform for Design Analyses of Fluid-Thermal Systems. World J. Eng. Technol. 2022, 10, 434–443. [Google Scholar] [CrossRef]
- Gokyay, O. An easy MS Excel software to use for water distribution system design: A real case distribution network design solution. J. Appl. Water Eng. Res. 2020, 8, 290–297. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the Implicit Colebrook Equation for Flow Friction Using Excel. Spreadsheets Educ. Bond. Univ. 2017, 10, 2. Available online: https://hal.archives-ouvertes.fr/hal-01586190 (accessed on 21 January 2023).
- Coelho, B.; Andrade-Campos, A. Numerical tool for hydraulic modelling—An educational approach. Int. J. Mech. Eng. Educ. 2017, 45, 260–285. [Google Scholar] [CrossRef]
- Demir, S.; Demir, N.M.; Karadeniz, A. An MS Excel tool for water distribution network design in environmental engineering education. Wiley Comput. Appl. Eng. Educ. 2017, 26, 203–214. [Google Scholar] [CrossRef]
- Adedeji, K.B.; Hamam, Y.; Abe, B.T.; Abu-Mahfouz, A.M. A spreadsheet tool for the analysis of flows in small-scale water piping networks. In Proceedings of the IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 23–26 July 2017; Available online: https://ieeexplore.ieee.org/document/8104947 (accessed on 22 January 2023).
- Huddleston, D.H.; Alarcon, A.J.; Chen, W. Water Distribution Network Analysis Using Excel. J. Hydraul. Eng. 2004, 130, 1033–1035. [Google Scholar] [CrossRef]
- Washington State University. Irrigation in the Pacific-Northwest, Irrigation Schedule Tables; IAREC: Prosser, WA, USA, 2022; Available online: http://irrigation.wsu.edu/Content/Resources/Irrigation-Schedule-Tables.php (accessed on 25 January 2023).
- Karara, G.K.; Gathenya, J.M.; Home, P.G.; Ayugi, S. Modeling and Visualization of Irrigation Potential Using Microsoft Excel. Int. J. Nov. Res. Comput. Sci. Softw. Eng. 2016, 3, 52–57. [Google Scholar]
- Oki, L. Measuring Distribution Uniformity and Calculating Run Time. University of California Davis, Agricultural and Natural Resources, Plant Sciences Department. A Workshop for Landscape Professionals 4 October 2016, McMillan Center and Fair Oaks Horticulture Center 8020 Temple Park Rd, Fair Oaks, CA 95628, USA. Available online: https://ccuh.ucdavis.edu/sites/g/files/dgvnsk1376/files/inline-files/DU%20Run%20Time.pdf (accessed on 4 April 2023).
- El-Nemr, M.K. An interactive spreadsheet for drip irrigation system uniformity parameters evaluation. Int. J. Agric. Sci. 2012, 4, 216–220. [Google Scholar] [CrossRef]
- Steele, D.D.; Scherer, T.F.; Hopkins, D.G.; Tuscherer, S.R.; Wright, J. Spreadsheet implementation of irrigation scheduling by the checkbook method for north Dakota and Minnesota. ASABE Appl. Eng. Agric. 2010, 26, 983–995. [Google Scholar] [CrossRef]
- Microsoft. Excel for Mac, version 16.16.27 (201012); ID: 029881-001-1068342016, 2016 Commercial License.
- Vories, E.D.; von Bernuth, R.D.; Mickelson, R.H. Simulating sprinkler performance in wind. J. Irrig. Drain. Eng. 1987, 113, 119–130. [Google Scholar] [CrossRef]
- Carrión, P.; Tarjuelo, J.M.; Montero, J. SIRIAS: A simulation model for sprinkler irrigation: I. Description of the model. Irrig. Sci. 2001, 20, 73–84. [Google Scholar] [CrossRef]
- Dechmi, F. Gestión Del Agua en Sistemas de Riego Por Aspersión En El Valle de Ebro: Análisis de la Situación Actual Y Simulación de Escenarios. Ph.D. Thesis, Universitat de Lleida, Zaragoza, Spain, 2002. Available online: https://digital.csic.es/handle/10261/4810 (accessed on 30 January 2023).
- Robinson, G.; Robinson, I. The motion of an arbitrarily rotating spherical projectile and its application to ball games. Phys. Scr. 2013, 88, 018101. [Google Scholar] [CrossRef]
- Kincaid, D.C.; Solomon, K.H.; Oliphant, J.C. Drop size distributions for irrigation sprinklers. Trans. ASAE 1996, 39, 839–845. [Google Scholar] [CrossRef]
- Seginer, I.; Nir, D.; von Bernuth, D. Simulation of wind distorted sprinkler patterns. J. Irrig. Drain. Eng. ASCE 1991, 117, 285–306. [Google Scholar] [CrossRef]
- Von Bernuth, R.D.; Gilley, J.R. Sprinkler droplet size distribution estimation from single leg test data. Trans. ASAE 1984, 27, 1435–1441. [Google Scholar] [CrossRef]
- Seginer, I. Tangential Velocity of Sprinkler Drops. Trans. ASAE 1965, 8, 90–93. [Google Scholar] [CrossRef]
- Chapman, D.S.; Grey, A. Complex interactions between the wind and ballistic seed dispersal in Impatiens glandulifera (Royle). J. Ecol. 2012, 100, 874–883. [Google Scholar] [CrossRef]
- Fukui, Y.; Nakanishi, K.; Okamura, S. Computer evaluation of sprinkler irrigation uniformity. Irrig. Sci. 1980, 2, 23–32. [Google Scholar] [CrossRef]
- Okamura, S. Theoretical study on sprinkler sprays (I)~(III). Trans JSIDRE 1968, 26, 49. [Google Scholar]
- Park, S.W.; Mitchell, J.K.; Bubenzer, G.D. Splash Erosion Modeling: Physical Analyses. Trans. ASAE 1982, 25, 357–361. [Google Scholar] [CrossRef]
- Li, J.; Kawano, H. Simulating water-drop movement from noncircular sprinkler nozzles. Irrig. Drain. Eng. 1995, 121, 152–158. [Google Scholar] [CrossRef]
- Hills, D.; Gu, Y. Sprinkler volume mean droplet diameter as a function of pressure. Trans. ASAE 1989, 32, 471–476. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical recipes in C; Cambridge University Press: Cambridge, UK, 1988; p. 735. [Google Scholar]
- Zapata, N.; Playán, E.; Skhiri, A.; Burguete, J. Simulation of a collective solid-set sprinkler irrigation controller for optimum water productivity. J. Irrig. Drain. Eng. 2009, 135, 13–24. [Google Scholar] [CrossRef]
- Hull, T.E.; Enright, W.H.; Fellen, B.M.; Sedgwick, A.E. Comparing numerical methods for ordinary differential equations. SIAM J. Numer. Anal. 1972, 9, 603–637. [Google Scholar] [CrossRef]
- Makazaga Odria, J. Sobre Los Errores Locales y Globales de la Integración de Ecuaciones Diferenciales Ordinarias Mediante Métodos de Runge-Kutta Empíricos. Ph.D. Thesis, Universidad del País Vasco, Donostia, Spain, 2007. [Google Scholar]
- Vigueras Campuzano, A. Cálculo Numérico, Teoría, Problemas y Algunos Programas con Maxima; De Matemática Aplicada y Estadística, Escuela Técnica Superior de Ingeniería Industrial, Septo, Universidad Politécnica de Cartagena: Cartagena, Spain, 2016; ISBN 8-84-608-86-4. [Google Scholar]
- Rincon Bermúdez Rafael David. La extrapolación de Richardson, una forma de precisión para cálculos. Rev. Univ. Eafit 1991, 83, 85–92. Available online: https://publicaciones.eafit.edu.co/index.php/revista-universidad-eafit/article/view/1507/1379 (accessed on 5 March 2023).
- Tarjuelo Martín-Benito, J.M. El Riego Por Aspersión Y Su Tecnología,·, 3rd ed.; Ediciones MundiPrensa: Madrid, Spain, 2005; p. 491. ISBN 9788484762256. [Google Scholar]
- Kohl, R.A.; von Bernuth, R.D.; Huebner, G. Drop size distribution measurements problems using a laser unit. Trans. ASAE 1985, 28, 190–192. [Google Scholar] [CrossRef]
- King, B.A.; Bjorneberg, D.L. Characterizing droplet kinetic energy applied by moving spray-plate center-pivot irrigation sprinklers. Trans. ASABE 2013, 53, 137–145. [Google Scholar] [CrossRef]
- Christiansen, J.E. Irrigation by Sprinkling; Bulletin 670; Agricultural Experiment Station, College of Agriculture, University of California: Berkeley, CA, USA, 1942; p. 124. [Google Scholar]
- Bautista-Capetillo, C.; Salvador, R.; Burguete, J.; Montero, J.; Tarjuelo, J.M.; Zapata, N.; González, J.; Playán, E. Comparing methodologies for the characterization of water drops emitted by an irrigation sprinkler. Trans. ASABE 2009, 52, 1493–1504. [Google Scholar] [CrossRef]
- Salvador, R.; Bautista-Capetillo, C.; Burguete, J.; Zapata, N.; Serreta, A.; Playán, E. A photographic method for drop characterization in agricultural sprinklers. Irrig. Sci. 2009, 27, 307–317. [Google Scholar] [CrossRef]
- Timmerman, P.; van der Weele, J.P. On rise and fall of a ball with linear or quadratic drag. Am. J. Phys. 1999, 67, 538–546. [Google Scholar] [CrossRef]
- Grigore, I.; Miron, C.; Barna, E.S. Exploring excel spreadsheets to simulate the projectile motion in the gravitational field. Rom. Rep. Phys. 2017, 69, 1–14. [Google Scholar]
- Nave (2010) Hyperphysics (© C. R. Nave, 2010). Available online: http://hyperphysics.phy-astr.gsu.edu/hbasees/hframe.html (accessed on 14 November 2022).
- Thompson, A.L.; Gilley, G.R.; Norman, J.M. A sprinkler water droplet evaporation and plant canopy model: I. Model development. Trans. ASAE 1993, 36, 735–741. [Google Scholar] [CrossRef]
- Lorenzini, G. Simplified modeling of sprinkler droplet dynamics. Biosyst. Eng. 2004, 87, 1–11. [Google Scholar] [CrossRef]
- Deboer, D.W. Drop energy characteristics of a rotating spray-plate sprinkler. J. Irrig. Drain. Eng. 2002, 128, 137–146. [Google Scholar] [CrossRef]
- DeBoer, D.W.; Monnens, M.J. Estimation of drop size and kinetic energy from a rotating spray-plate sprinkler. Trans ASAE 2001, 44, 1571–1580. [Google Scholar] [CrossRef]
- Kuma Katoch, S. MS-Excel spreadsheet applications in introductory under- graduate physics-a review. J. Sci. Technol. 2020, 5, 48–52. [Google Scholar] [CrossRef]
- Bermúdez, M.; Puertas, J.; Cea, L. Introducing Excel spreadsheet calculations and numerical simulations with professional software into an undergraduate hydraulic engineering course. Comput. Appl. Eng. Educ. Wiley 2019, 1–14. [Google Scholar] [CrossRef]
- Garcés Cobos, L.; Montaluisa Vivas, Á.; Salas Jaramillo, E. El aprendizaje significativo y su relación con los estilos de aprendizaje. Anales de la Universidad Central del Ecuador 2018, 1, 231–248. [Google Scholar] [CrossRef]
- Niazkar, M.; Hosein, A.S. Application of Excel spreadsheet in engineering education. In Proceedings of the First International & Fourth National Conference on Engineering Education, Shiraz University, Shiraz, Iran, 10–12 November 2015; pp. 1–7. [Google Scholar]
- González Regaña, A.J. La hoja de cálculo para la resolución de problemas matemáticos por el método de polya. 3cTIC 2016, 5, 13–27. [Google Scholar] [CrossRef]
- Denton, D.W. Enhancing instruction through constructivism, cooperative learning, and cloud computing. TechTrends 2012, 56, 34–41. [Google Scholar] [CrossRef]
- Hernández, S. El modelo constructivista con las nuevas tecnologías: Aplicado en el proceso de aprendizaje, RUSC. Univ. Knowl. Soc. J. 2008, 5, 26–35. [Google Scholar] [CrossRef]
- Baker, J.E.; Sugden, S.J. Spreadsheets in Education–The First 25 Years. Spreadsheets Educ. (eJSiE) 2003, 1, 18–43. [Google Scholar]
- Jonassen, D.H. Evaluating Constructivistic Learning. Educ. Technol. 1991, 31, 28–33. [Google Scholar]
- Bautista-Capetillo, C.; Robles, O.; Salinas, H.; Playán, E. A particle tracking velocimetry technique for drop characterization in agricultural sprinklers. Irrig Sci. 2014, 32, 437–447. [Google Scholar] [CrossRef]
- Keller, J.; Bliesner, R.D. Sprinkler and Trickle Irrigation; Champan and Hall: Logan, UT, USA, 1990; ISBN 0-412-07951-1. [Google Scholar]
- Bautista-Capetillo, C.; Zavala, M.; Playán, E. Kinetic energy in sprinkler irrigation: Different sources of drop diameter and velocity. Irrig. Sci. 2012, 30, 29–41. [Google Scholar] [CrossRef]
- Salinas-Tapia, H.; Robles-Rovelo, C.O.; Chávez Carlos, D.; Bautista-Capetillo, C.F. Geometric and kinematic characterization of a spray using the PTV optical technique. Water Technol. Sci. 2014, 5, 125–140. (In Spanish) [Google Scholar]
- Lowe, E.J. Rain drops. Q. J. R. Meteorol. Soc. 1892, 18, 242–245. [Google Scholar] [CrossRef]
- Laws, J.O.; Parsons, D.A. The relation of raindrop size to intensity. Am. Geophys. Union Trans. 1943, 26, 452–460. [Google Scholar] [CrossRef]
- Magarvey, R.H. Stain method of drop size determination. J. Meteorol. 1956, 14, 182–184. [Google Scholar] [CrossRef]
- Kohl, R.A. Drop size distribution for medium-sized agricultural sprinklers. Trans. ASAE 1974, 17, 690–693. [Google Scholar] [CrossRef]
- Eigel, J.D.; Moore, I.D. A simplified technique for measuring raindrop size and distribution. Trans ASAE 1983, 24, 1079–1083. [Google Scholar] [CrossRef]
- Adrian, R.J. Particle Imaging Techniques for Experimental Fluid Mechanics; Annual Reviews Inc., Fluid Mechanics; Department of Theoretical and Applied Mechanics, University of Illinois: Urban, IL, USA, 1991; Volume 23, pp. 261–304. [Google Scholar]
- Cruvinel, P.E.; Minatel, E.; Mucheroni, M.; Vieira, S.; Crestana, S. An automatic method based on image processing for measurements of drop size distribution from agricultural sprinklers. Anais do IX SIBIGRAPI 1996, 3, 39–46. [Google Scholar]
- Sudheer, K.P.; Panda, R.K. Digital image processing for determining drop sizes from irrigation spray nozzles. Agric. Water Manage. 2000, 45, 159–167. [Google Scholar] [CrossRef]
- Blanquies, J.; Scharff, M.; Hallock, B. The design and construction of a rainfall simulator. International Erosion Control Association (IECA). In Proceedings of the 34th Annual Conference and Expo, Las Vegas, NV, USA, 24–28 February 2003. [Google Scholar]
- Jensen, K.D. Flow Measurements. J. Braz. Soc. Mech. Sci. Eng. 2004, 26, 400–419. [Google Scholar] [CrossRef]
- Salinas, T.H.; García, A.J.; Moreno, H.D.; Barrientos, G.B. Particle Tracking Velocimetry (PTV) Algorithm for Non-Uniform and Non-Spherical Particles. In Proceedings of the Electronics, Robotics and Automotive Mechanics Conference (CERMA’06), Cuernavaca, Mexico, 26–29 September 2006; pp. 322–327. [Google Scholar]
- Abudi, I.; Carmi, G.; Berliner, P. Rainfall simulator for field runoff studies. J. Hydrol. 2012, 454–455, 76–81. [Google Scholar] [CrossRef]
- Playán, E.; Zapata, N.; Faci, J.M.; Tolosa, D.; Lacueva, J.L.; Pelegrín, J.; Salvador, R.; Sánchez, I.; Lafita, A. Assessing sprinkler irrigation uniformity using a ballistic simulation model. Agric. Water Manag. 2006, 84, 89–100. [Google Scholar] [CrossRef]
- Beard, V.K.; Bringi, V.N.; Thurai, M. A new understanding of raindrop shape. Atmos. Res. 2010, 97, 396–415. [Google Scholar] [CrossRef]
- Burguete, J.; Playán, E.; Montero, J.; Zapata, N. Improving drop size and velocity estimates of an optical disdrometer: Implications for sprinkler irrigation simulation. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 2103–2116. [Google Scholar] [CrossRef]
- Mohammed, D.; Kohl, R.A. Infiltration response to kinetic energy. Trans. ASAE 1987, 86–2106, 108–111. [Google Scholar] [CrossRef]
- King, B.A.; Bjorneberg, D.L. Infiltration model for center pivot irrigation on bare soil. In Proceedings of the ASABE Annual International Meeting, Dallas, TX, USA, 29 July–1 August 2012; Paper No. 12-1336890. pp. 1–20. [Google Scholar]
- Montero, J.; Tarjuelo, J.M.; Carrión, P. Sprinkler droplet size distribution measured with an optical spectropluviometer. Irrig. Sci. 2003, 22, 47–56. [Google Scholar] [CrossRef]
- Li, Y.; Bai, G.; Yan, H. Development and validation of a modified model to simulate the sprinkler water distribution. Comput. Electron. Agric. 2015, 111, 38–47. [Google Scholar] [CrossRef]


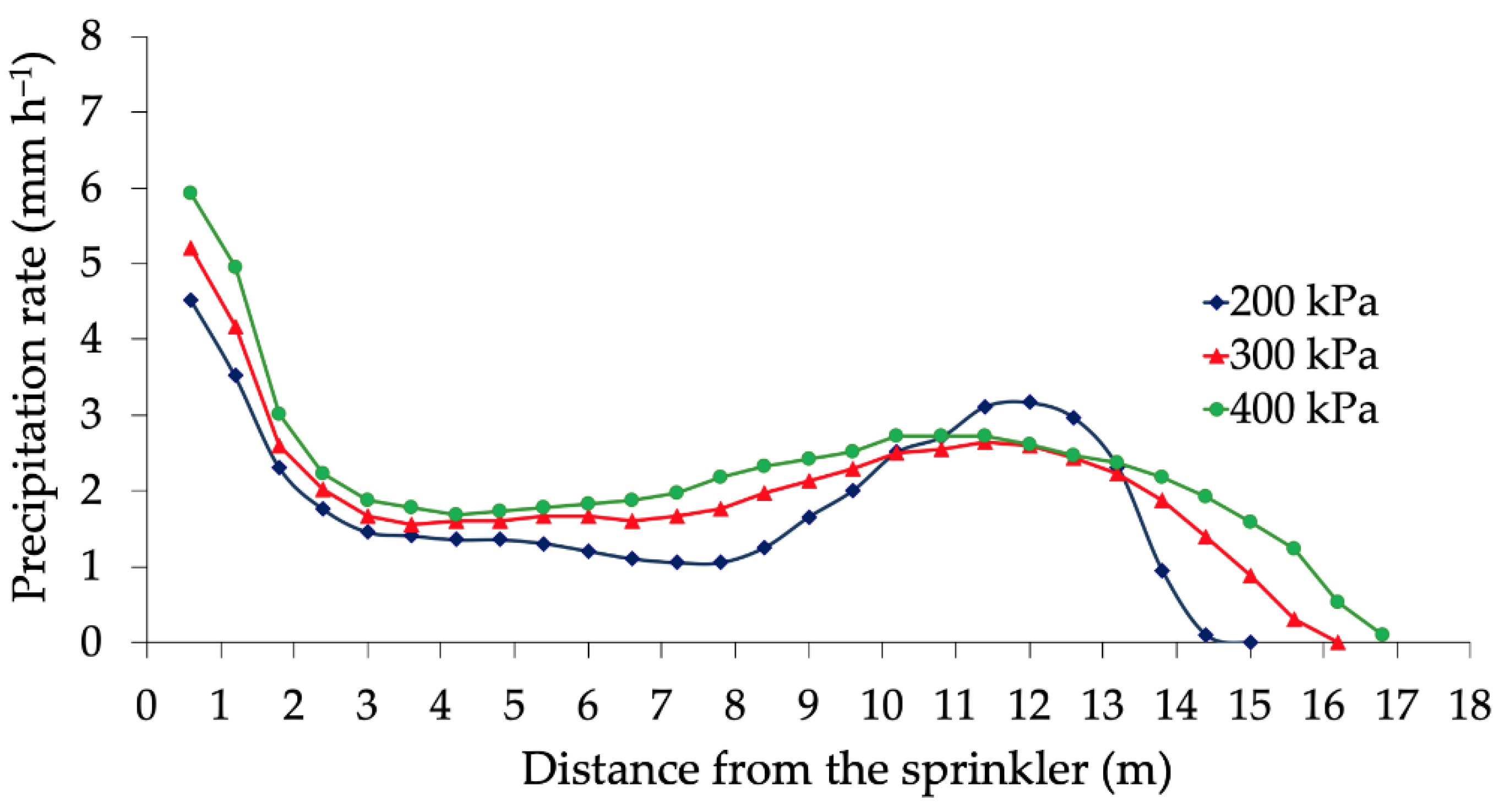
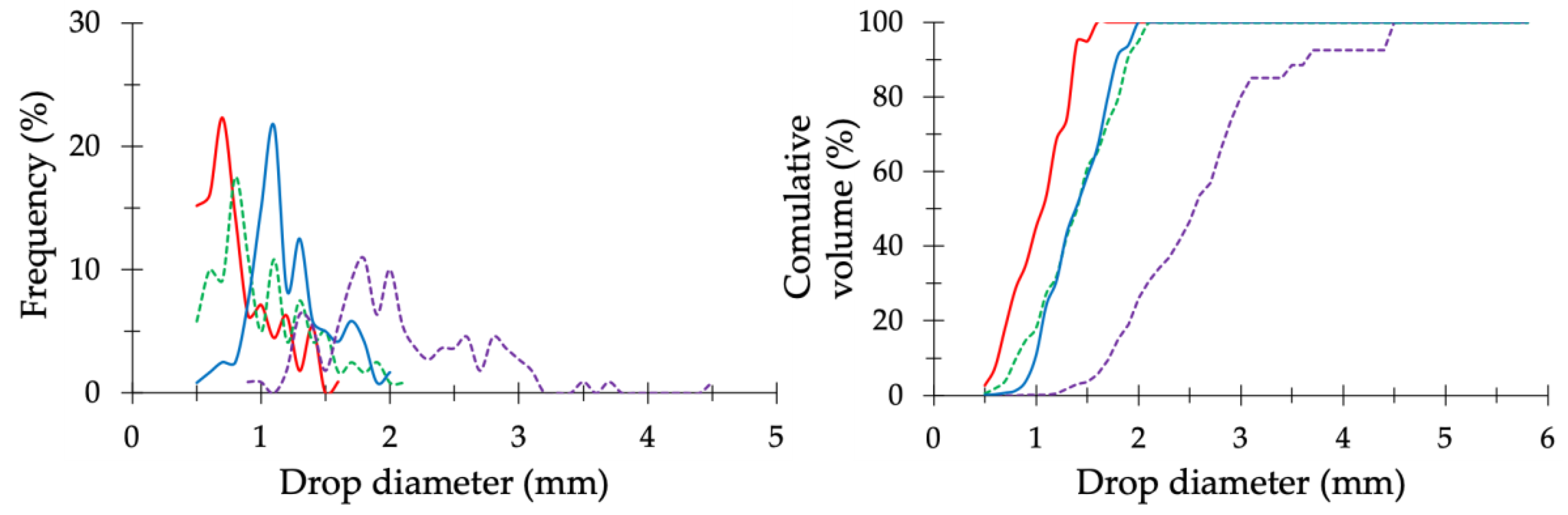
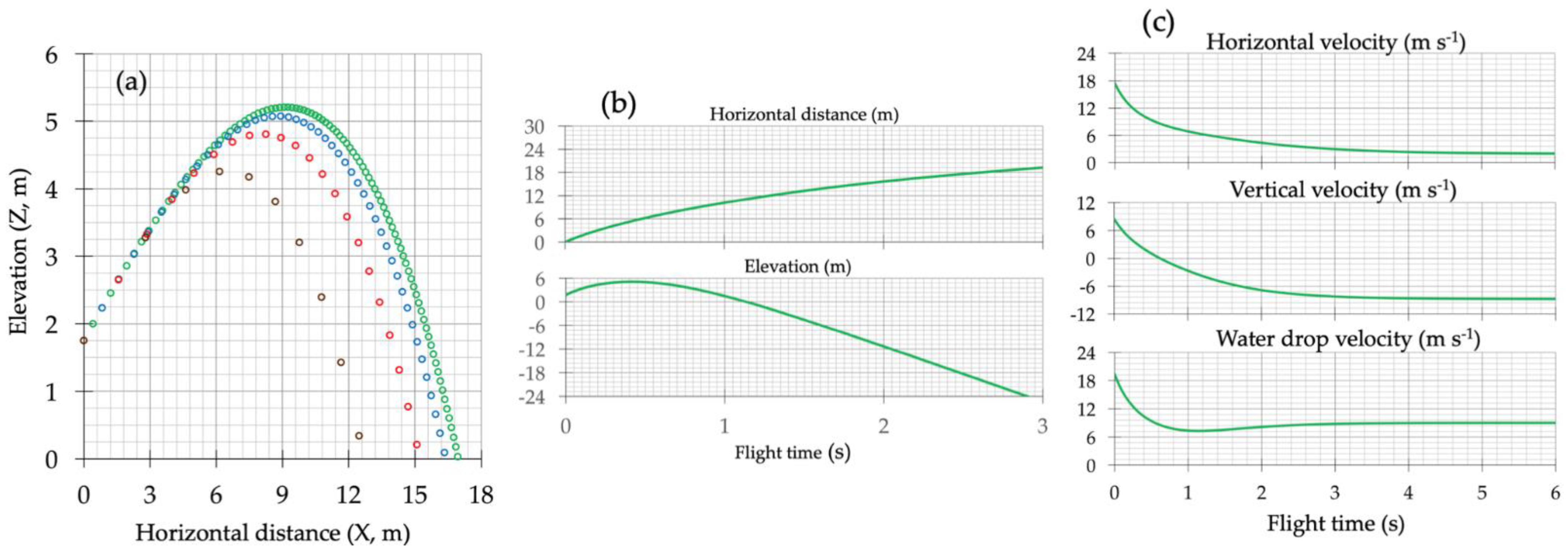
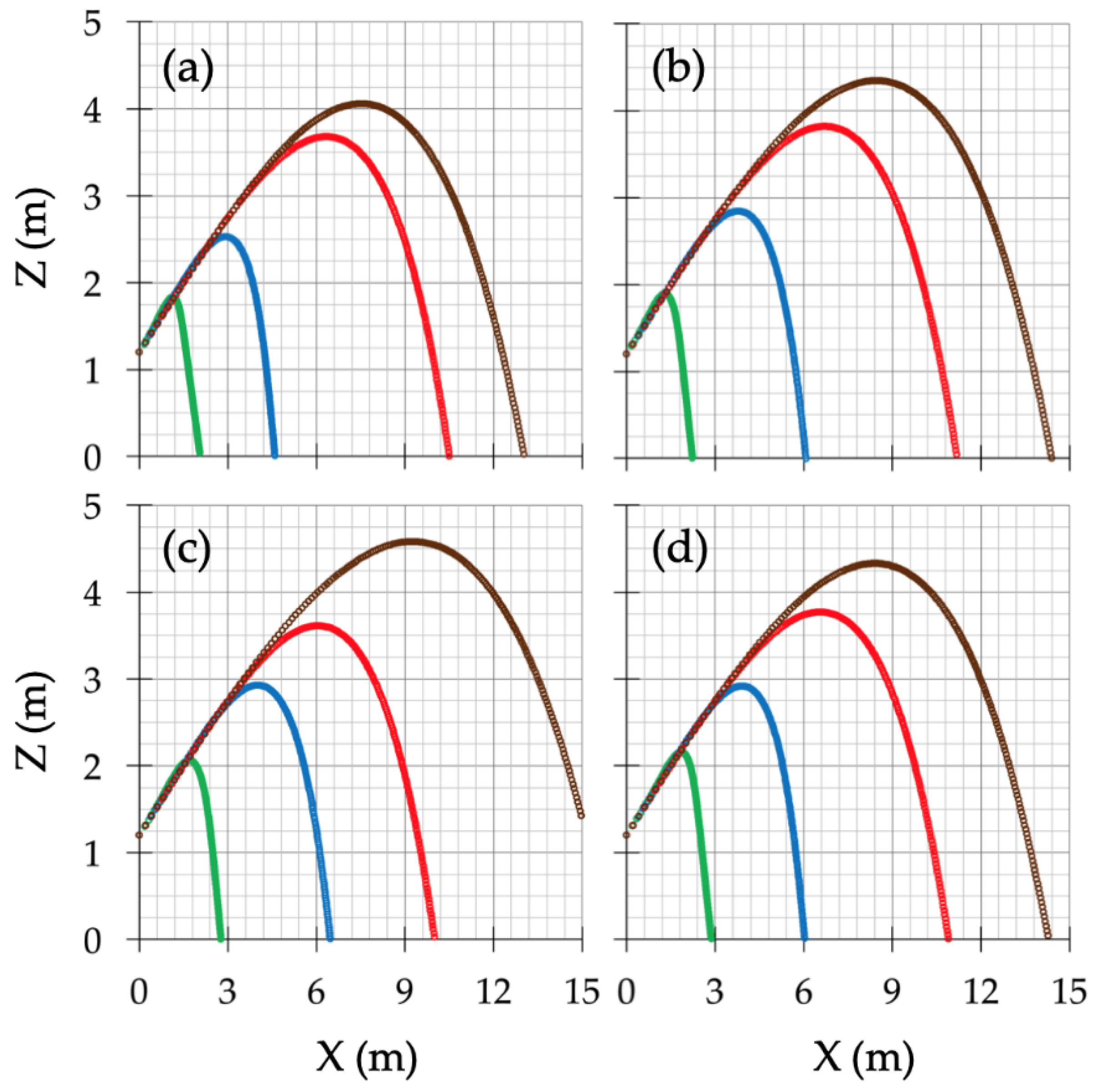
| Precipitation rate (l s−1) | |||||||||||
| Pluviometer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Distance (m) | 0.6 | 1.2 | 1.8 | 2.4 | 3.0 | 3.6 | 4.2 | 4.8 | 5.4 | 6.0 | |
| Operating pressure (kPa) | 200 | 90.0 | 70.0 | 46.0 | 35.0 | 29.0 | 28.0 | 27.0 | 27.0 | 26.0 | 24.0 |
| 300 | 100.0 | 80.0 | 50.0 | 39.0 | 32.0 | 30.0 | 31.0 | 31.0 | 32.0 | 32.0 | |
| 400 | 120.0 | 100.0 | 61.0 | 45.0 | 38.0 | 36.0 | 34.0 | 35.0 | 36.0 | 37.0 | |
| Precipitation rate (l s−1) | |||||||||||
| Pluviometer | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| Distance (m) | 6.6 | 7.2 | 7.8 | 8.4 | 9.0 | 9.6 | 10.2 | 10.8 | 11.4 | 12.0 | |
| Operating pressure (kPa) | 200 | 22.0 | 21.0 | 21.0 | 25.0 | 33.0 | 40.0 | 50.0 | 54.0 | 62.0 | 63.0 |
| 300 | 31.0 | 32.0 | 34.0 | 38.0 | 41.0 | 44.0 | 48.0 | 49.0 | 51.0 | 50.0 | |
| 400 | 38.0 | 40.0 | 44.0 | 47.0 | 49.0 | 51.0 | 55.0 | 55.0 | 55.0 | 53.0 | |
| Precipitation rate (l s−1) | |||||||||||
| Pluviometer | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| Distance (m) | 12.6 | 13.2 | 13.8 | 14.4 | 15.0 | 15.6 | 16.2 | 16.8 | 17.4 | 18.0 | |
| Operating pressure (kPa) | 200 | 59.0 | 46.0 | 19.0 | 2.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 300 | 47.0 | 43.0 | 36.0 | 27.0 | 17.0 | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 400 | 50.0 | 48.0 | 44.0 | 39.0 | 32.0 | 25.0 | 11.0 | 2.0 | 0.0 | 0.0 | |
| Operating Pressures (kPa) | Variable | Distance from Irrigation Sprinkler (m) | |||
|---|---|---|---|---|---|
| 3 | 6 | 9 | 12 | ||
| 200 | Diameter (mm) | 0.86 | 1.04 | 1.50 | 3.08 |
| Velocity (m s−1) | 2.72 | 3.06 | 4.19 | 6.06 | |
| 300 | Diameter (mm) | 0.81 | 1.03 | 1.22 | 2.06 |
| Velocity (m s−1) | 2.45 | 2.92 | 3.82 | 5.13 | |
| 400 | Diameter (mm) | 0.86 | 0.96 | 1.19 | 1.45 |
| Velocity (m s−1) | 2.43 | 2.96 | 3.72 | 4.42 | |
| Drag Coefficient Model | Drop Diameter (mm) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time of Flight (s) | Travel Distance (m) | Error (m) | Terminal Velocity (ms−1) | |||||||||||||
| 0.5 | 1.0 | 2.0 | 3.0 | 0.5 | 1.0 | 2.0 | 3.0 | 0.5 | 1.0 | 2.0 | 3.0 | 0.5 | 1.0 | 2.0 | 3.0 | |
| Okamura, [45] | 2.74 | 1.93 | 1.92 | 2.02 | 2.87 | 6.03 | 10.90 | 14.29 | 0.24 | 0.10 | 0.09 | 0.11 | 2.21 | 4.01 | 6.45 | 7.82 |
| Park et al., [46] | 3.37 | 1.89 | 1.92 | 1.92 | 2.05 | 4.59 | 10.49 | 13.02 | 0.38 | 0.34 | 0.13 | 0.10 | 1.97 | 3.54 | 6.34 | 7.74 |
| Li and Kawano, [47] | 2.48 | 1.82 | 1.93 | 2.02 | 2.23 | 6.07 | 11.19 | 14.39 | 0.12 | 0.12 | 0.08 | 0.07 | 2.18 | 4.31 | 6.57 | 7.87 |
| Hills and Gu, [48] | 2.13 | 1.82 | 1.90 | 2.05 | 2.77 | 6.46 | 10.01 | 15.91 | 0.22 | 0.14 | 0.11 | 0.12 | 2.56 | 4.49 | 6.08 | 8.45 |
| Drops | Distance from the Sprinkler (m) | |||
|---|---|---|---|---|
| 3 | 6 | 9 | 12 | |
| Number | 114 | 106 | 102 | 98 |
| ϕrange (mm) | 0.50–1.70 | 0.50–1.90 | 0.50–2.20 | 0.80–2.50 |
| ∀m | 1.19 | 1.25 | 1.46 | 1.78 |
| Vrange (m s−1) | 1.55–3.55 | 1.96–4.39 | 2.20–5.35 | 3.28–5.79 |
| Vm (m s−1) | 2.43 | 2.96 | 3.72 | 4.42 |
| Ekϕrange (J × 10−7) | 0.62–134.53 | 1.03–359.08 | 1.77–711.99 | 19.37–1422.98 |
| EkΩ (JL−1) | 3.640 | 5.530 | 8.880 | 12.150 |
| Prate (mm h−1) | 1.880 | 1.830 | 2.420 | 2.620 |
| PkΩ (W × 10−6) | 0.002 | 0.003 | 0.006 | 0.009 |
| δp (W m−2 × 10−3) | 1.900 | 2.800 | 6.000 | 8.800 |
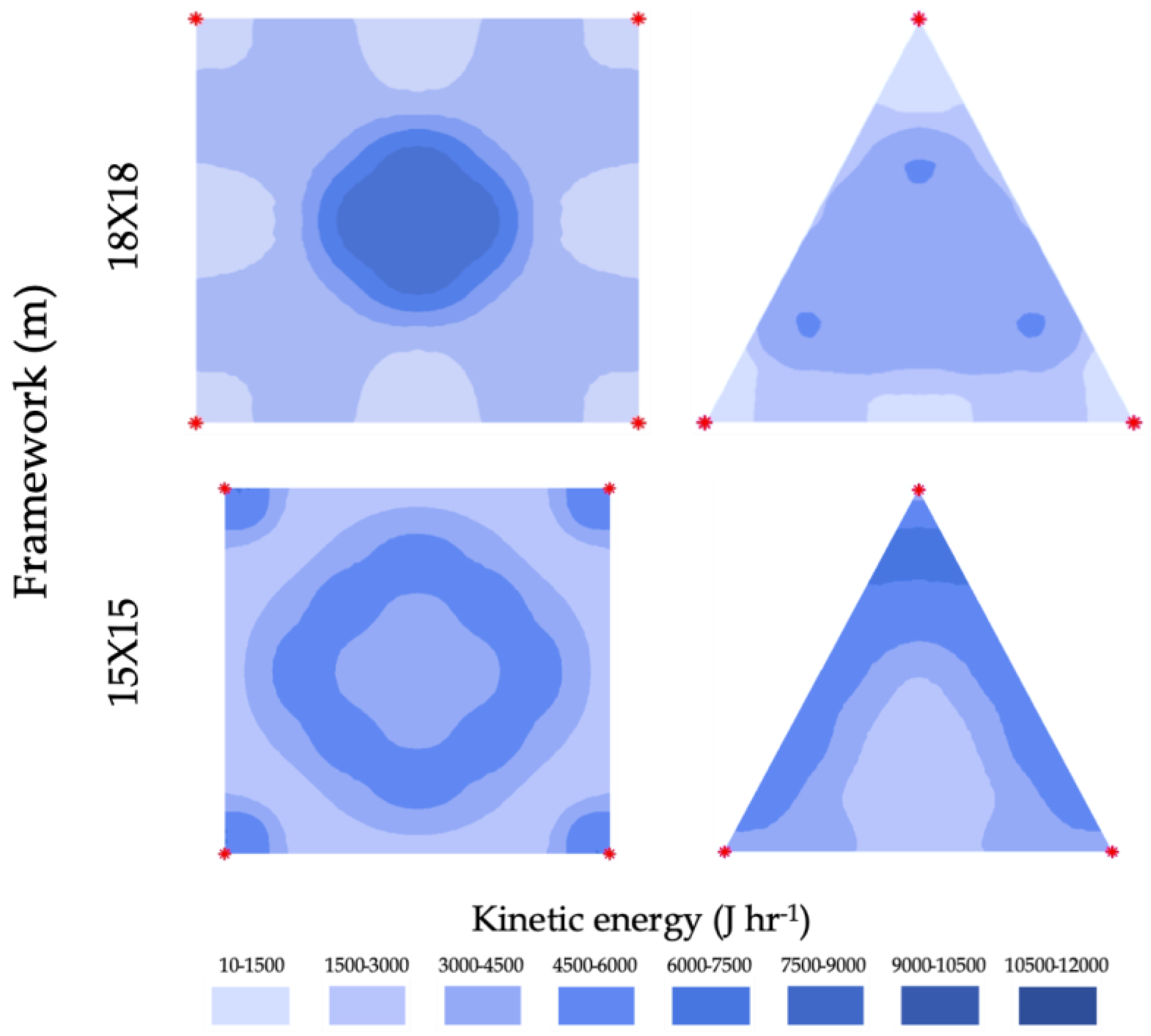
| Framework (m × m) | Operating Pressure (kPa) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 200 | 300 | 400 | 200 | 300 | 400 | 200 | 300 | 400 | 200 | 300 | 400 | |
| CU (%) | DU (%) | CUKϕ (%) | DUKϕ (%) | |||||||||
| R15 × 15 | 83.4 | 79.7 | 66.1 | 88.6 | 77.4 | 67.5 | 57.2 | 53.4 | 27.8 | 44.1 | 38.1 | 10.8 |
| R18 × 18 | 68.2 | 75.9 | 76.3 | 67.4 | 77.9 | 81.2 | 22.9 | 22.1 | 45.6 | 20.3 | 40.3 | 31.9 |
| T15 × 15 | 63.8 | 78.3 | 84.5 | 64.5 | 73.9 | 85.1 | 60.2 | 62.1 | 52.8 | 19.1 | 64.4 | 47.2 |
| T18 × 18 | 66.0 | 80.3 | 87.3 | 67.5 | 82.0 | 87.9 | 47.7 | 73.3 | 41.4 | 37.0 | 21.2 | 22.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bautista-Capetillo, C.; Robles Rovelo, C.O.; González-Trinidad, J.; Pineda-Martínez, H.; Júnez-Ferreira, H.E.; García-Bandala, M. Teaching Sprinkler Irrigation Engineering by a Spreadsheet Tool. Water 2023, 15, 1685. https://doi.org/10.3390/w15091685
Bautista-Capetillo C, Robles Rovelo CO, González-Trinidad J, Pineda-Martínez H, Júnez-Ferreira HE, García-Bandala M. Teaching Sprinkler Irrigation Engineering by a Spreadsheet Tool. Water. 2023; 15(9):1685. https://doi.org/10.3390/w15091685
Chicago/Turabian StyleBautista-Capetillo, Carlos, Cruz Octavio Robles Rovelo, Julián González-Trinidad, Hugo Pineda-Martínez, Hugo Enrique Júnez-Ferreira, and Martín García-Bandala. 2023. "Teaching Sprinkler Irrigation Engineering by a Spreadsheet Tool" Water 15, no. 9: 1685. https://doi.org/10.3390/w15091685







