Pipeline-Burst Detection on Imbalanced Data for Water Supply Networks
Abstract
:1. Introduction
- ➀
- The transfer learning paradigm is adopted for the first time to transfer the hydraulic model knowledge to an actual water supply network with a low cost.
- ➁
- A specific domain adaptation model is proposed to solve the data imbalance problem in actual pipeline-burst detection.
- ➂
- A closed form solution is deduced for the proposed model.
- ➃
- A three-point-positioning method is presented for pipeline-burst location.
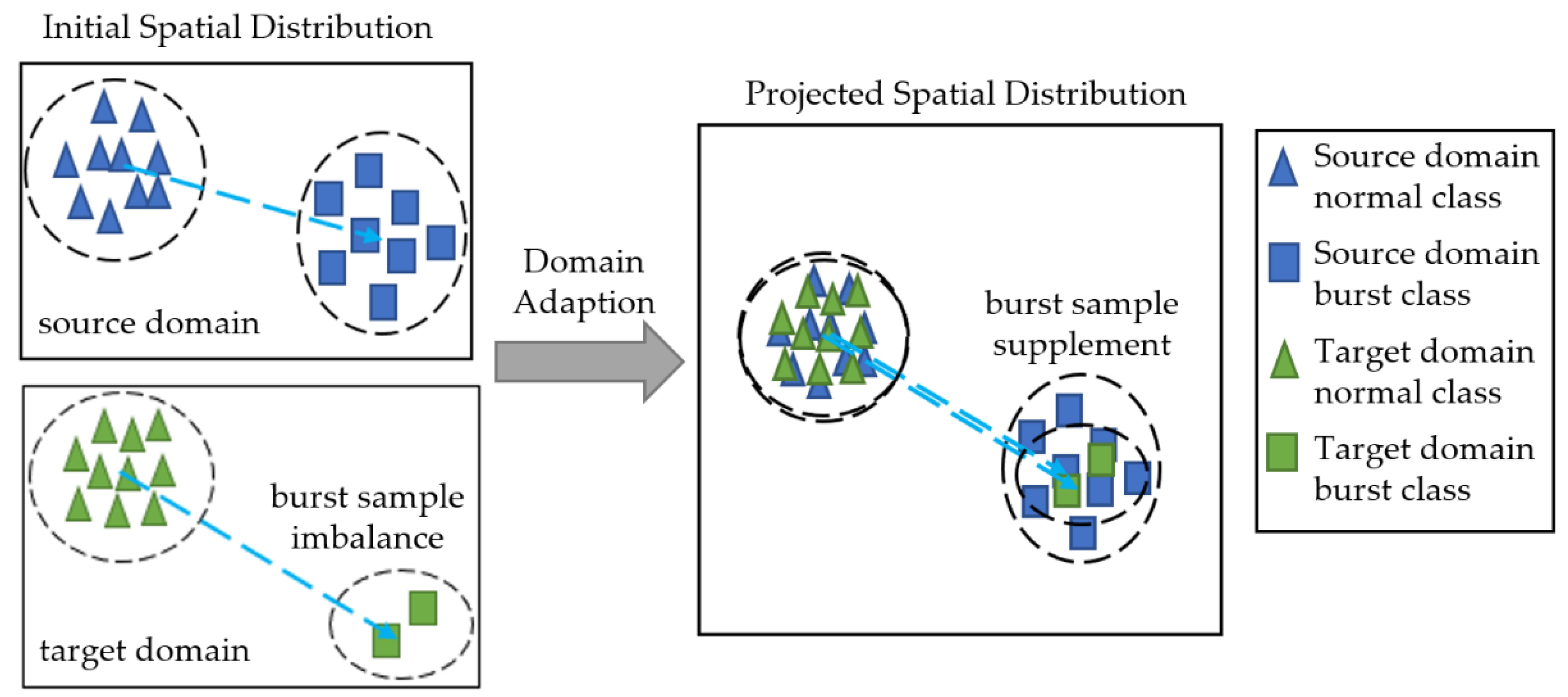
2. Method
2.1. Motivation
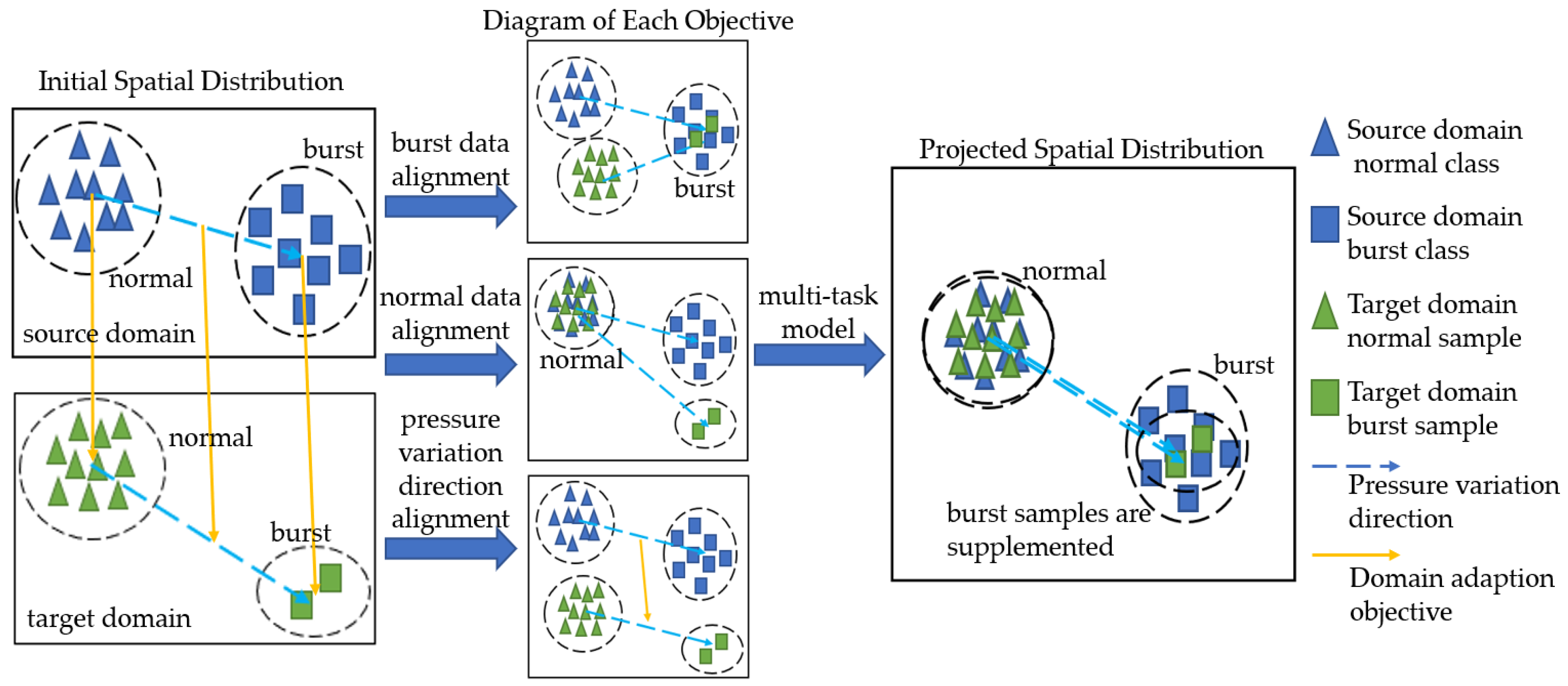
2.2. Proposed Method
2.2.1. Maximum Mean Difference
2.2.2. Model Formulation
2.2.3. Model Solution
| Algorithm 1: Algorithm steps of proposed method. |
| Input: |
| The source domain data matrix XS |
| The target domain data matrix XT |
| The trade-off parameter α, β and γ |
| Output: |
| Full data matrix X |
| Procedure: |
| 1: Calculate the mean vectors of normal and pipeline-burst samples and in the source domain XS. |
| 2: Calculate the mean vectors of normal and pipeline-burst samples and in the target domain XT. |
| 3: Calculate the projection matrix P according to Formula (8). |
| 4: Obtain transferred data matrix by PTXS. |
| 5: Form the Full Data matrix X = [PTXS, XT] for classifier training. |
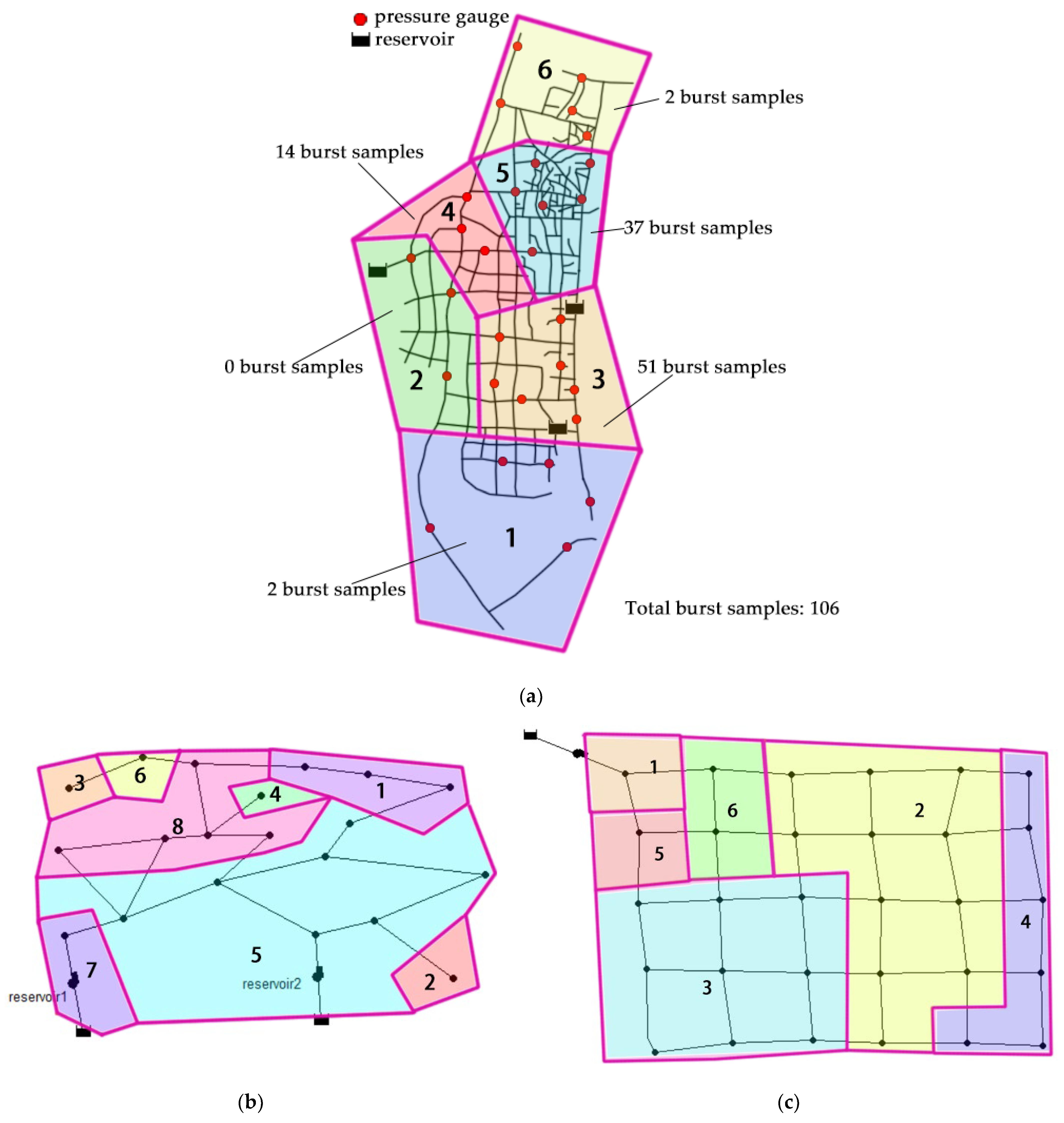
3. Dataset Description
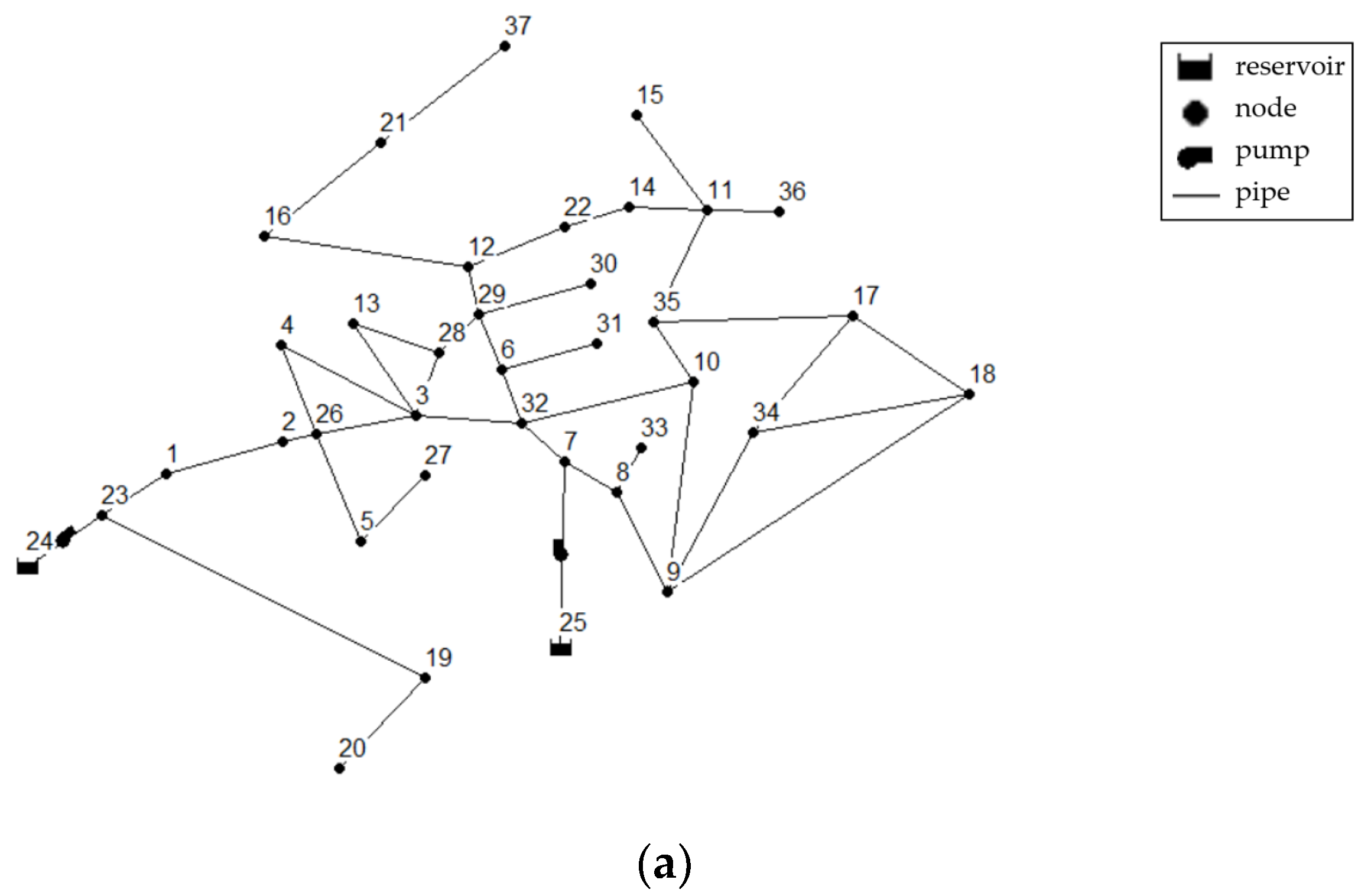
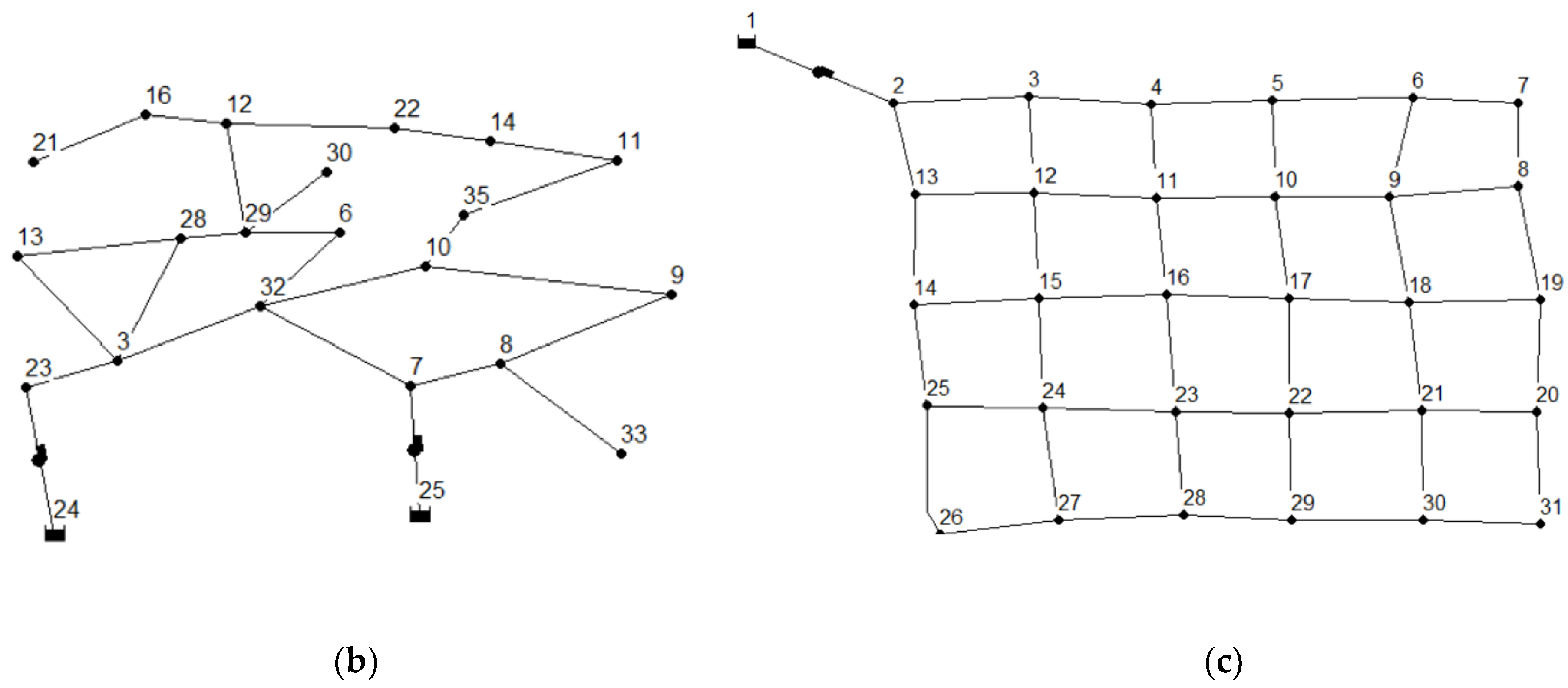
3.1. Actual Water Supply Network
3.2. Virtual Water Supply Networks
4. Experimental Settings
4.1. Scenario Settings
4.2. Partition Settings
4.3. Model Settings
4.4. Hardware Configuration
- CPU: Intel(R) Core(TM) i7-9750H
- Memory: 16.0 GB
- Hard disk: 256 GB SSD + 1 TB HDD
5. Results and Discussion
5.1. Results on Partition-Level Identification
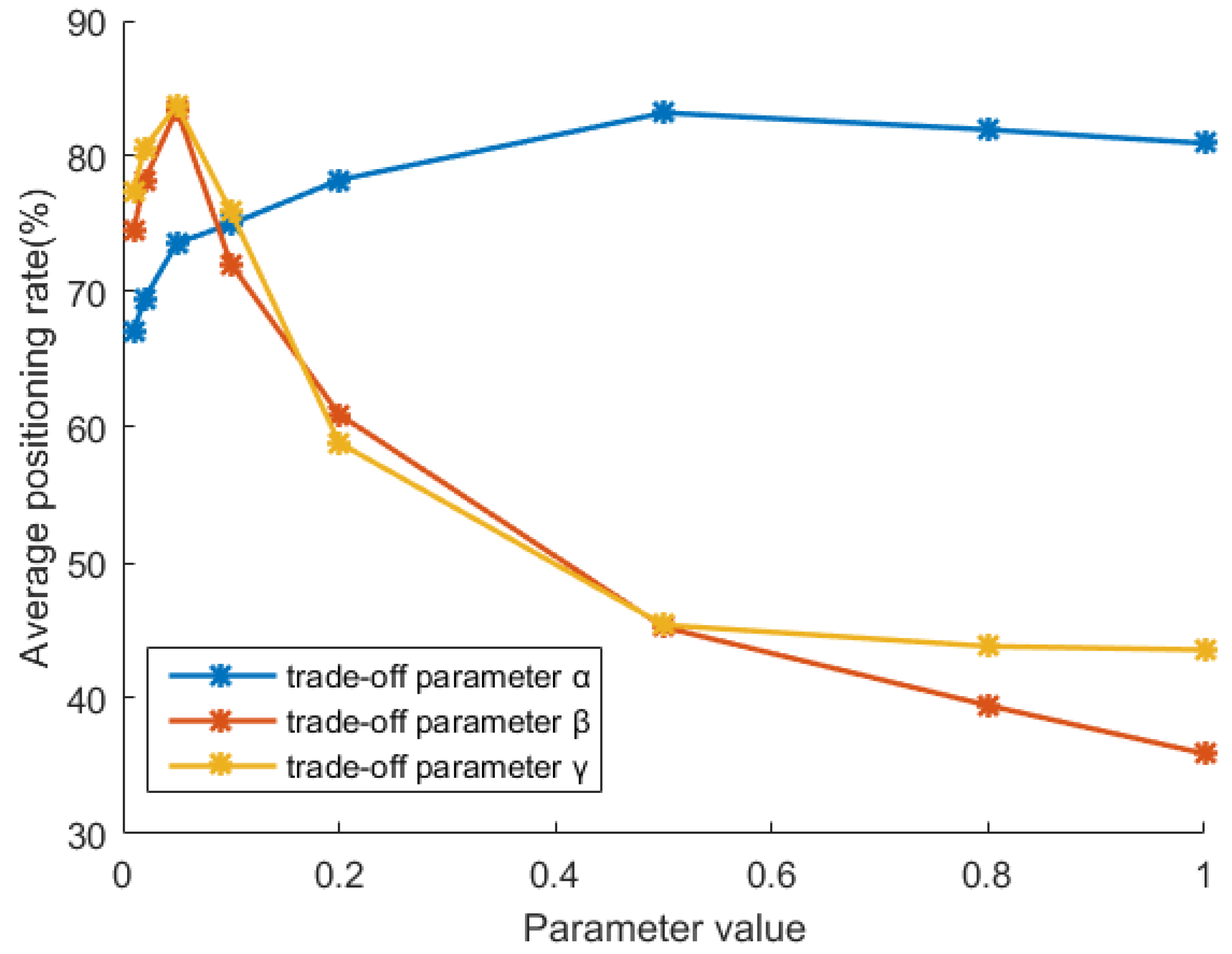
5.2. Sensitivity Analysis
5.3. Time Efficiency
5.4. Coordinate Location
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Wu, Y. A Model-Based Bayesian Framework for Pipeline Leakage Enumeration and Location Estimation. Water Resour. Manag. 2021, 35, 4381–4397. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S. A Review of Data-driven Approaches for Burst Detection in Water Distribution Systems. Urban Water J. 2017, 14, 972–983. [Google Scholar] [CrossRef]
- Romano, M.; Kapelan, Z. Automated Detection of Pipe Bursts and Other Events in Water Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140, 457–467. Available online: https://www.researchgate.net/publication/273369337 (accessed on 15 December 2022). [CrossRef] [Green Version]
- Borges, A.; Jung, D.; Kim, J.H. Smart WDS Management: Pipe Burst Detection Using Real-time Monitoring Data. In Proceedings of the SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI, San Francisco, CA, USA, 4–8 August 2017. [Google Scholar]
- Haghighi, A.; Covas, D.; Ramos, H. Direct Backward Transient Analysis for Leak Detection in Pressurized Pipelines: From Theory to Real Application. J. Water Supply Res. Technol. 2012, 61, 189–200. [Google Scholar] [CrossRef]
- Xie, X.; Hou, D.; Tang, X. Leakage Identification in Water Distribution Networks with Error Tolerance Capability. Water Resour. Manag. 2019, 33, 1233–1247. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Wu, X. Burst Detection in District Metering Areas Using a Data Driven Clustering Algorithm. Water Res. 2016, 100, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.K.; Chin, C.S.; Zhong, X. Review of Current Technologies and Proposed Intelligent Methodologies for Water Distributed Network Leakage Detection. IEEE Access 2018, 6, 78846–78867. [Google Scholar] [CrossRef]
- Cheng, W.; Fang, H.; Xu, G. Using SCADA to Detect and Locate Bursts in a Long-Distance Water Pipeline. Water 2018, 10, 1727. [Google Scholar] [CrossRef] [Green Version]
- Laucelli, D.; Romano, M.; Savi, D. Detecting Anomalies in Water Distribution Networks Using EPR Modelling Paradigm. J. Hydroinform. 2015, 18, 409–427. Available online: http://iwaponline.com/jh/article-pdf/18/3/409/478927/jh0180409.pdf (accessed on 15 December 2022). [CrossRef] [Green Version]
- Abdulshaheed, A.; Mustapha, F.; Ghavamian, A. A Pressure-based Method for Monitoring Leaks in a Pipe Distribution System: A Review. Renew. Sustain. Energy Rev. 2017, 69, 902–911. [Google Scholar] [CrossRef]
- Srirangarajan, S.; Allen, M.; Preis, A. Wavelet-based Burst Event Detection and Localization in Water Distribution Systems. J. Signal Process. Syst. 2013, 72, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Tang, Z.; Xu, W. Deep Learning Identifies Accurate Burst Locations in Water Distribution Networks. Water Res. 2019, 166, 115058. [Google Scholar] [CrossRef] [PubMed]
- Okeya, I.; Kapelan, Z.; Hutton, C. Online Burst Detection in a Water Distribution System Using the Kalman Filter and Hydraulic Modelling. Procedia Eng. 2014, 89, 418–427. [Google Scholar] [CrossRef] [Green Version]
- Santos-Ruiz, I.; Bermúdez, J.R.; López-Estrada, F.R. Online Leak Diagnosis in Pipelines Using an EKF-Based and Steady-State Mixed Approach. Control Eng. Pract. 2018, 81, 55–64. [Google Scholar] [CrossRef]
- Ye, G.; Fenner, R.A. Kalman Filtering of Hydraulic Measurements for Burst Detection in Water Distribution Systems. J. Pipeline Syst. Eng. Pract. 2011, 2, 14–22. [Google Scholar] [CrossRef]
- Jung, D.; Kang, D.; Liu, J.; Lansey, K. Improving the Rapidity of Responses to Pipe Burst in Water Distribution Systems: A Comparison of Statistical Process Control Methods. J. Hydroinform. 2015, 17, 307–328. Available online: https://www.researchgate.net/publication/276786519 (accessed on 15 December 2022). [CrossRef]
- Lee, S.J.; Lee, G.; Suh, J.C. Online Burst Detection and Location of Water Distribution Systems and Its Practical Applications. J. Water Resour. Plan. Manag. 2016, 142, 4015033. [Google Scholar] [CrossRef]
- Mounce, S.R.; Boxall, J.B.; Machell, J. Development and Verification of an Online Artificial Intelligence System for Detection of Bursts and Other Abnormal Flows. J. Water Resour. Plan. Manag. 2010, 136, 309–318. Available online: https://www.researchgate.net/publication/221936175 (accessed on 15 December 2022). [CrossRef]
- Shukla, H.; Piratla, K.R. Leakage Detection in Water Pipelines Using Supervised Classification of Acceleration Signals. Autom. Constr. 2020, 117, 103256. [Google Scholar] [CrossRef]
- Soldevila, A.; Fernandez-Canti, R.M.; Blesa, J. Leak localization in water distribution networks using Bayesian classifiers. J. Process Control 2017, 55, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Salam, A.; Tola, M.; Selintung, M. A leakage detection system on the Water Pipe Network through Support Vector Machine method. In Proceedings of the Makassar International Conference on Electrical Engineering and Informatics, Macassar, India, 26–30 November 2014. [Google Scholar]
- Hindy, H.; Brosset, D.; Bayne, E. Improving SIEM for Critical SCADA Water Infrastructures Using Machine Learning. In Computer Security: CyberICPS 2018, 1st ed.; Katsikas, S.K., Cuppens, F., Cuppens, N., Lambrinoudakis, C., Antón, A., Gritzalis, S., Mylopoulos, J., Kalloniatis, C., Eds.; Springer: Cham, Switzerland, 2019; pp. 3–19. [Google Scholar]
- Phan, H.C.; Dhar, A.S. Predicting Pipeline Burst Pressures with Machine Learning Models. Int. J. Press. Vessel. Pip. 2021, 191, 104384. [Google Scholar] [CrossRef]
- Mounce, S.R.; Machell, J. Burst Detection Using Hydraulic Data from Water Cistribution Systems with Artificial Neural Networks. Urban Water J. 2006, 3, 21–31. [Google Scholar] [CrossRef]
- Mounce, S.R.; Mounce, R.B.; Boxall, J.B. Novelty Detection for Time Series Data Analysis in Water Distribution Systems Using Support Vector Machines. J. Hydroinform. 2011, 13, 672–686. [Google Scholar] [CrossRef]
- Levinas, D.; Perelman, G.; Ostfeld, A. Water Leak Localization Using High-Resolution Pressure Sensors. Water 2021, 13, 591. [Google Scholar] [CrossRef]
- Sun, C.; Parellada, B.; Puig, V. Leak Localization in Water Distribution Networks Using Pressure and Data-Driven Classifier Approach. Water 2020, 12, 54. Available online: https://www.researchgate.net/publication/338104420 (accessed on 15 December 2022). [CrossRef] [Green Version]
- Tao, T.; Huang, H.; Li, F. Burst Detection Using an Artificial Immune Network in Water-Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140, 4014027. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.Y.; Zhao, M. Leakage Zone Identification in Large-Scale Water Distribution Systems Using Multiclass Support Vector Machines. J. Water Resour. Plan. Manag. 2016, 142, 4016042. [Google Scholar] [CrossRef]
- Meier, R.W.; Barkdoll, B.D. Sampling Design for Network Model Calibration Using Genetic Algorithms. J. Water Resour. Plan. Manag. 2000, 126, 245–250. [Google Scholar] [CrossRef]
- Schaetzen, D.; Walters, F. Optimal Sampling Design for Model Calibration Using Shortest Path, Genetic and Entropy Algorithms. Urban Water J. 2000, 2, 141–152. [Google Scholar] [CrossRef]
- Kapelan, Z.; Savic, D.; Walters, G. Optimal Sampling Design Methodologies for Water Distribution Model Calibration. J. Hydraul. Eng. 2005, 131, 190–200. [Google Scholar] [CrossRef]
- Bush, C.A.; Uber, J.G. Sampling Design Methods for Water Distribution Model Calibration. J. Water Resour. Plan. Manag. 1998, 124, 334–344. [Google Scholar] [CrossRef]
- Pan, S.J.; Qiang, Y. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Duan, L.; Tsang, I.W.; Xu, D. Domain Transfer Multiple Kernel Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 465–479. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.; Lu, J. Heterogeneous domain adaptation: An unsupervised approach. IEEE Trans. Neural Netw. Learn. Syst. 2017, 31, 5588–5602. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Chen, Y.; Li, D. Drift Compensation for an Electronic Nose by Adaptive Subspace Learning. IEEE Sens. J. 2019, 20, 337–347. [Google Scholar] [CrossRef]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2011, 22, 199–210. [Google Scholar] [CrossRef] [Green Version]
- Long, M.; Wang, J.; Ding, G. Transfer Feature Learning with Joint Distribution Adaptation. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 4–6 December 2018. [Google Scholar]
- Morosini, A.; Caruso, O. Identification of Measurement Points for Calibration of Water Distribution Network Models. In Proceedings of the 16th Conference on Water Distribution System Analysis, WDSA 2014, Bari, Italy, 14–17 July 2014. [Google Scholar]
- Shalaby, M.; Shokair, M.; Messiha, N.W. Performance Enhancement of TOA Localized Wireless Sensor Networks. Wirel. Pers. Commun. 2017, 95, 4667–4679. [Google Scholar] [CrossRef]
- Kim, J. Hybrid TOA–DOA techniques for maneuvering underwater target tracking using the sensor nodes on the sea surface. Ocean. Eng. 2021, 242, 110110. [Google Scholar] [CrossRef]


| Definition | Amount | Attribute 1 | Attribute 2 | ||
|---|---|---|---|---|---|
| Definition | Parameter | Definition | Parameter | ||
| reservoir | 3 | reservoir head | 20–100 m | ||
| pump | 6 | pump curve flow | 100–600 LPS | pump curve head | 20–100 m |
| pressure gauge | 29 | pressure | (0–1.2) Mpa | ||
| network node | 2924 | elevation | 0–120 ft | flow demand | 40–700 L/S |
| tubulation | 10,976 | pipe diameter | DN200–DN400 | pipe length | 50–200 m |
| Pipe Network | Definition | Amount | Attribute 1 | Attribute 2 | ||
|---|---|---|---|---|---|---|
| Definition | Parameter | Definition | Parameter | |||
| Virtual Network A | reservoir | 2 | reservoir head | 10–20 m | ||
| pump | 2 | pump curve flow | 400–600 LPS | pump curve head | 100–200 m | |
| pressure gauge | 35 | pressure | (0–2) Mpa | |||
| network node | 37 | elevation | 5–30 m | flow demand | 3–30 LPS | |
| tubulation | 42 | pipe diameter | DN100–DN400 | pipe length | 100–2000 m | |
| Virtual Network B | reservoir | 2 | reservoir head | 10–20 m | ||
| pump | 2 | pump curve flow | 200–300 LPS | pump curve head | 100–200 m | |
| pressure gauge | 21 | pressure | (1–2) Mpa | |||
| network node | 23 | elevation | 5–30 m | flow demand | 3–30 LPS | |
| tubulation | 25 | pipe diameter | DN100–DN400 | pipe length | 100–2000 m | |
| Virtual Network C | reservoir | 1 | reservoir head | 200 m | ||
| pump | 1 | pump curve flow | 700 LPS | pump curve head | 300 m | |
| pressure gauge | 30 | pressure | (2–5) Mpa | |||
| network node | 31 | elevation | 5–30 m | flow demand | 5–15 LPS | |
| tubulation | 23 | pipe diameter | DN200–DN300 | pipe length | 500–800 m | |
| Classifier | Main Parameter Setting |
|---|---|
| KNN | Neighbors k = 7 |
| RBF-SVM | Standard deviation σ = 10 Penalty coefficient C = 1 |
| LIN-SVM | Penalty coefficient C = 0.5 |
| BPNN | First hide layer = 20 Second hide layer = 15 |
| RF | Tree number = 20 |
| Method | Classifier | Burst Sample Retention Degree r | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | 0.3 | 0.5 | 1 | Average | ||
| Proposed method | KNN | 57.13 | 60.47 | 69.22 | 82 | 93.12 | 99.56 | 99.87 | 100 | 82.67 |
| RBF-SVM | 40.4 | 63.56 | 64.41 | 72.29 | 74.15 | 76.11 | 76.46 | 77 | 68.05 | |
| LIN-SVM | 51.97 | 86.77 | 97.48 | 99.63 | 99.87 | 100 | 100 | 100 | 91.97 | |
| BPNN | 40.14 | 46.35 | 56.18 | 83.08 | 94.97 | 99.98 | 100 | 100 | 77.59 | |
| RF | 48.69 | 52.77 | 61.43 | 86.1 | 93.72 | 99.21 | 99.56 | 99.83 | 80.16 | |
| No-processing approach | KNN | 0 | 9.32 | 23.74 | 53.92 | 81.62 | 97.95 | 99.87 | 100 | 58.3 |
| RBF-SVM | 10.94 | 12.37 | 15.24 | 26.93 | 45.26 | 60.57 | 66.53 | 68.45 | 38.29 | |
| LIN-SVM | 11.07 | 14.95 | 20.94 | 68.86 | 97.19 | 100 | 100 | 100 | 64.13 | |
| BPNN | 9.3 | 20.68 | 28.86 | 68.66 | 92.88 | 99.88 | 100 | 100 | 65.03 | |
| RF | 11.4 | 27.52 | 40.27 | 76.75 | 89.68 | 98.35 | 99.25 | 99.67 | 67.86 | |
| Kalman filtering method | None | 48.65 | 54.51 | 54.77 | 54.88 | 54.92 | 54.75 | 54.83 | 54.82 | 54.02 |
| Method | Classifier | Burst Sample Retention Degree r | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | 0.3 | 0.5 | 1 | Average | ||
| Proposed method | KNN | 49.46 | 51.24 | 64.99 | 81.71 | 90.85 | 98.16 | 99.67 | 99.95 | 79.5 |
| RBF-SVM | 47.54 | 48.4 | 52.71 | 64.73 | 67.5 | 68.13 | 69.34 | 72.97 | 61.42 | |
| LIN-SVM | 81.09 | 86.33 | 91.53 | 95.04 | 97.69 | 99.91 | 100 | 100 | 93.95 | |
| BPNN | 42.03 | 45.67 | 60.24 | 90.18 | 96.43 | 100 | 100 | 100 | 79.32 | |
| RF | 46.13 | 56.01 | 65.17 | 87.4 | 94.41 | 98.3 | 98.81 | 99.21 | 80.68 | |
| No-processing approach | KNN | 0.42 | 26.82 | 32.91 | 70.45 | 84.03 | 97.37 | 99.48 | 99.95 | 63.93 |
| RBF-SVM | 8.93 | 22.44 | 22.56 | 34.82 | 46.45 | 56.37 | 59.97 | 61.56 | 39.14 | |
| LIN-SVM | 7.95 | 17.61 | 29.66 | 86.63 | 98.32 | 100 | 100 | 100 | 67.52 | |
| BPNN | 19.3 | 35.05 | 45.88 | 84.67 | 97.1 | 99.81 | 100 | 100 | 72.73 | |
| RF | 22.24 | 39.67 | 49.59 | 84.53 | 92.77 | 97.92 | 98.45 | 99.18 | 73.04 | |
| Kalman filtering method | None | 43.61 | 47.03 | 47.09 | 47.21 | 47.28 | 47.34 | 47.43 | 47.42 | 46.80 |
| Method | Classifier | Burst Sample Retention Degree r | |||||
|---|---|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.3 | 0.5 | 1 | Average | ||
| Proposed method | KNN | 64.79 | 81.46 | 90.88 | 95.84 | 96.64 | 85.92 |
| RBF-SVM | 72.12 | 90.66 | 97.62 | 98.97 | 100 | 91.87 | |
| LIN-SVM | 57.49 | 86.25 | 95.27 | 97 | 99.56 | 87.11 | |
| BPNN | 93.77 | 94.89 | 96.3 | 99.07 | 98.26 | 96.46 | |
| RF | 22.04 | 30.37 | 51.95 | 70.18 | 79.63 | 50.83 | |
| No-processing approach | KNN | 0 | 0 | 7.83 | 26.8 | 66.39 | 20.2 |
| RBF-SVM | 12.34 | 23.3 | 53.68 | 70.99 | 85.17 | 49.1 | |
| LIN-SVM | 12.34 | 23.3 | 23.3 | 70.99 | 85.17 | 43.02 | |
| BPNN | 29.01 | 45.49 | 80.94 | 88.86 | 95.3 | 67.92 | |
| RF | 2.21 | 5.8 | 27.81 | 42.82 | 70.35 | 29.8 | |
| Kalman filtering method | None | 23.58 | 33.4 | 55 | 35.09 | 36.79 | 32.77 |
| Classifier | Burst Sample Retention Degree r | ||||
|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.3 | 0.5 | 1 | |
| KNN | 0.72 | 0.87 | 0.77 | 0.73 | 0.77 |
| RBF-SVM | 0.65 | 0.94 | 0.76 | 0.76 | 0.76 |
| LIN-SVM | 0.70 | 0.87 | 0.76 | 0.77 | 0.75 |
| ANN | 0.86 | 0.88 | 0.73 | 0.85 | 0.74 |
| RF | 0.84 | 0.57 | 0.66 | 0.65 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, T.; Zhang, L. Pipeline-Burst Detection on Imbalanced Data for Water Supply Networks. Water 2023, 15, 1662. https://doi.org/10.3390/w15091662
Wang H, Liu T, Zhang L. Pipeline-Burst Detection on Imbalanced Data for Water Supply Networks. Water. 2023; 15(9):1662. https://doi.org/10.3390/w15091662
Chicago/Turabian StyleWang, Hongjin, Tao Liu, and Lingxi Zhang. 2023. "Pipeline-Burst Detection on Imbalanced Data for Water Supply Networks" Water 15, no. 9: 1662. https://doi.org/10.3390/w15091662





