Estimating Hydraulic Parameters of Aquifers Using Type Curve Analysis of Pumping Tests with Piecewise-Constant Rates
Abstract
:1. Introduction
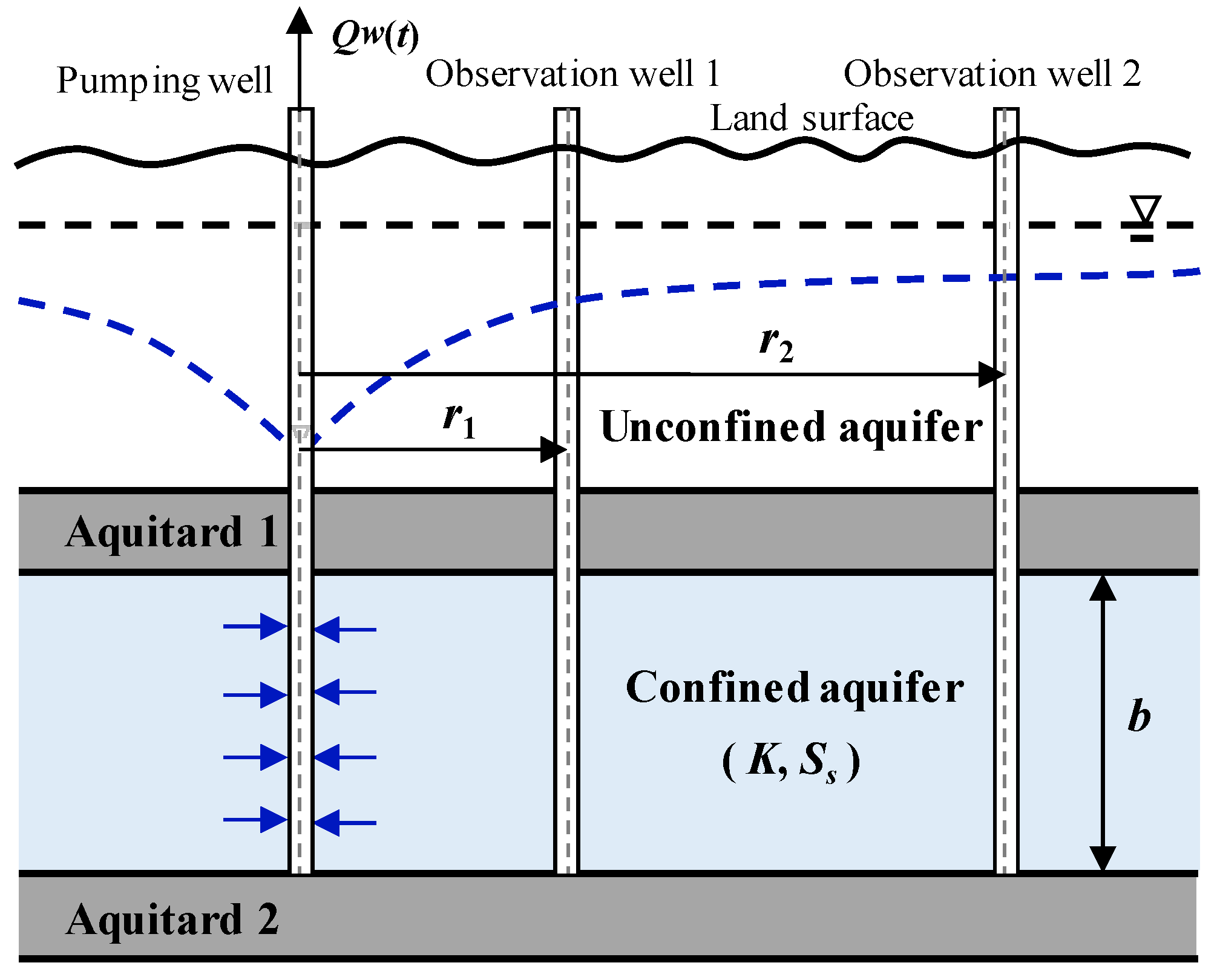
2. Methodology
2.1. Analytical Solution
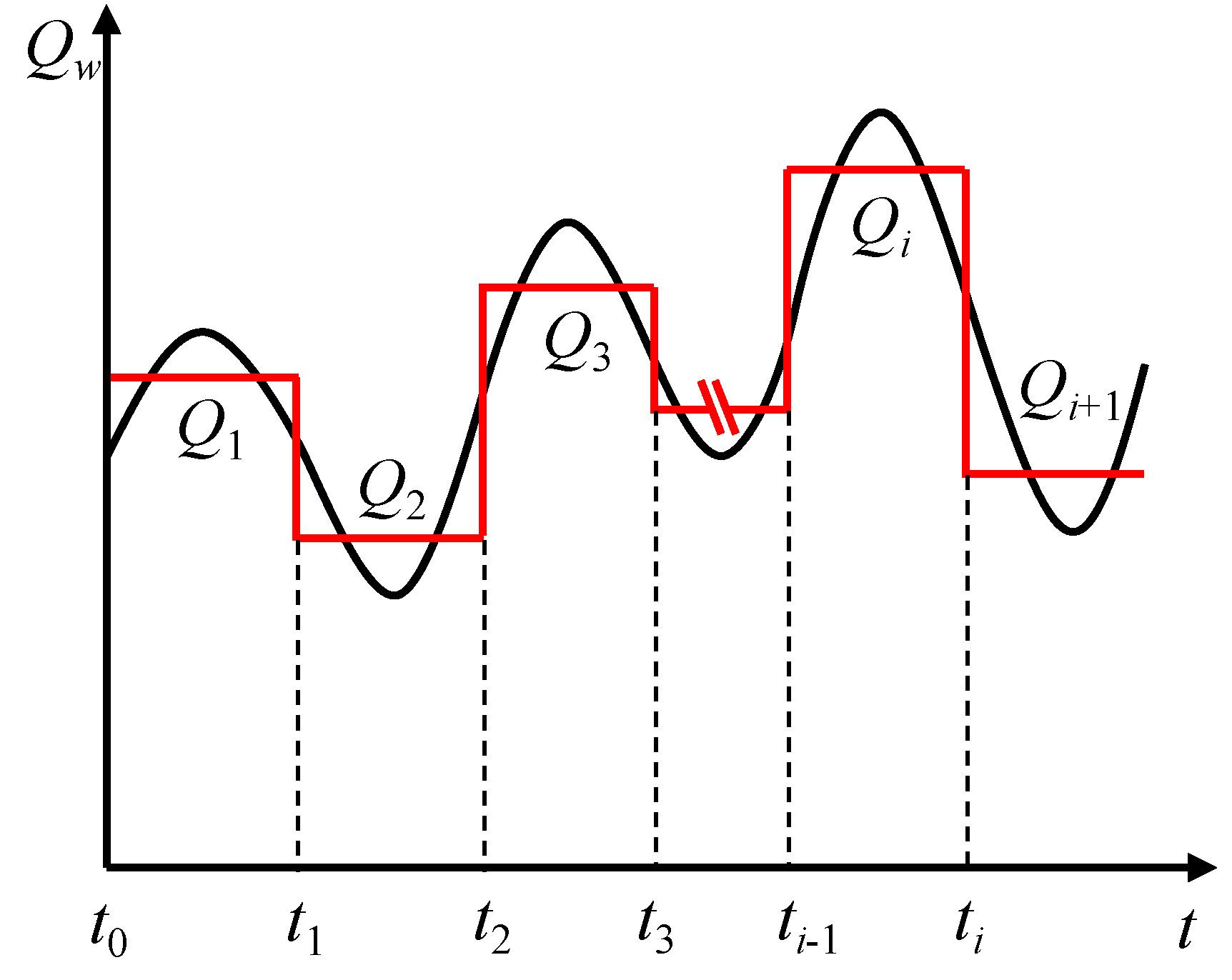
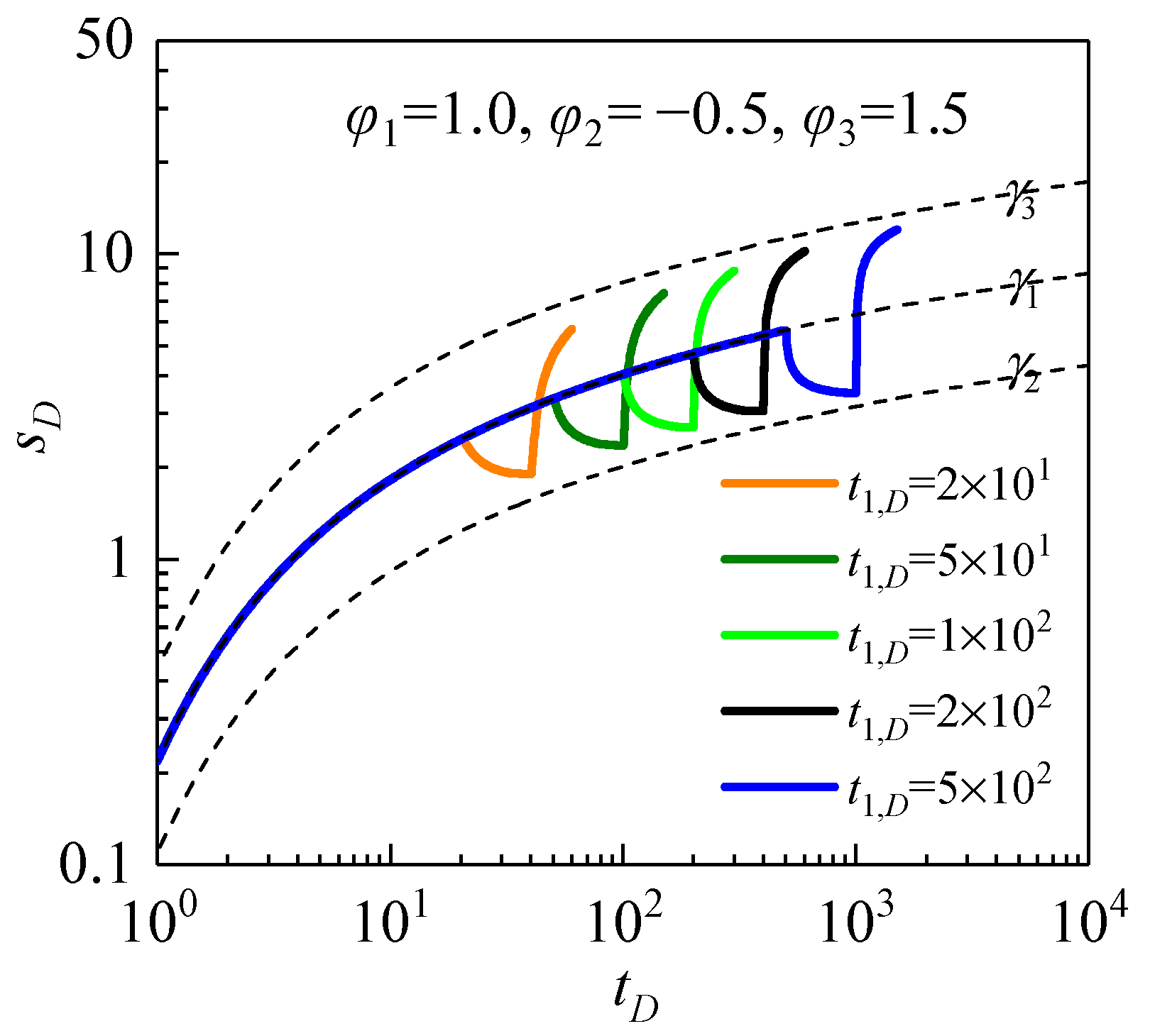
2.2. Type Curve Method
- (1)
- Plot the measured drawdown–time curve in a log–log graph.
- (2)
- Determine φi and βi, and prepare a series of type curves with different t1,D values in a log–log graph of the same scale as the measured curve.
- (3)
- Similar to Theis’s matching technique, match the measured drawdown–time curve with one of the type curves and choose the best matching curve.
- (4)
- Record the corresponding t1,D value, select a match point, and read the corresponding coordinates of s, t, sD, and tD.
3. Field Application
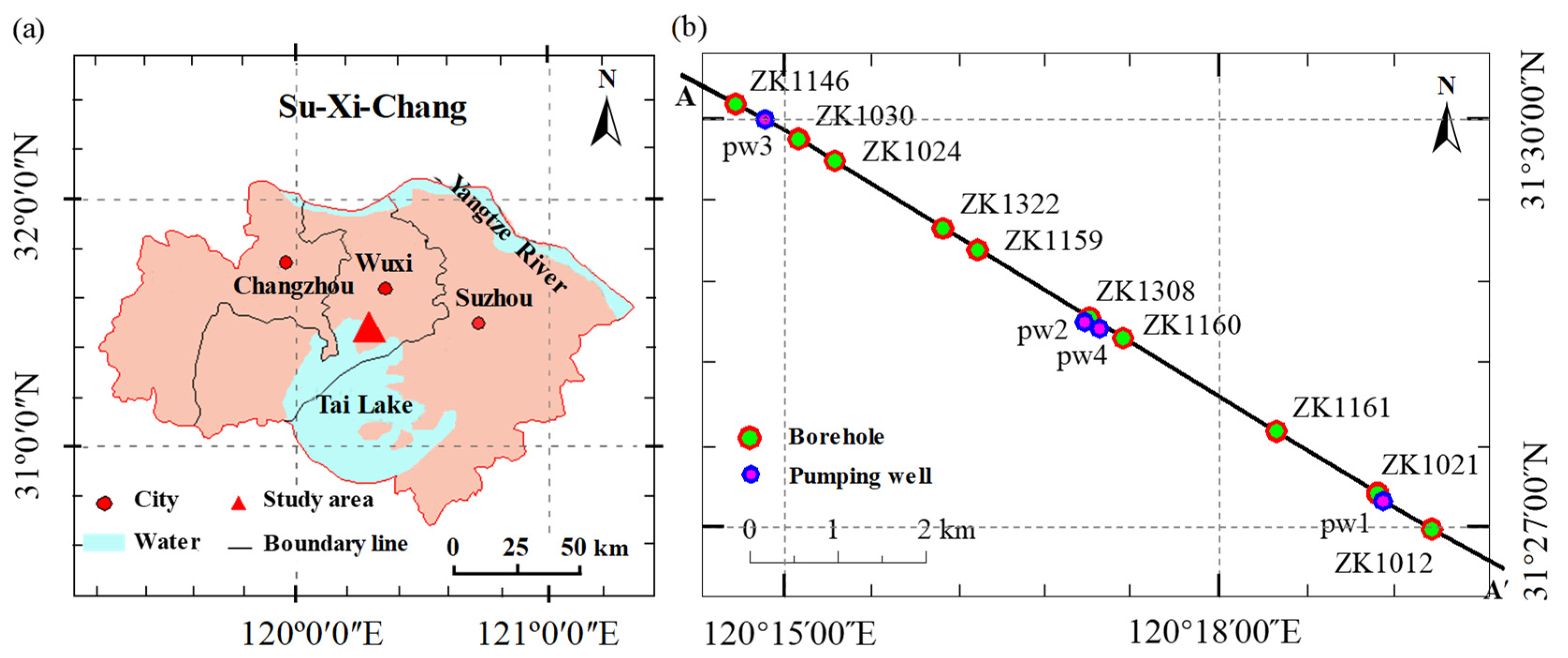
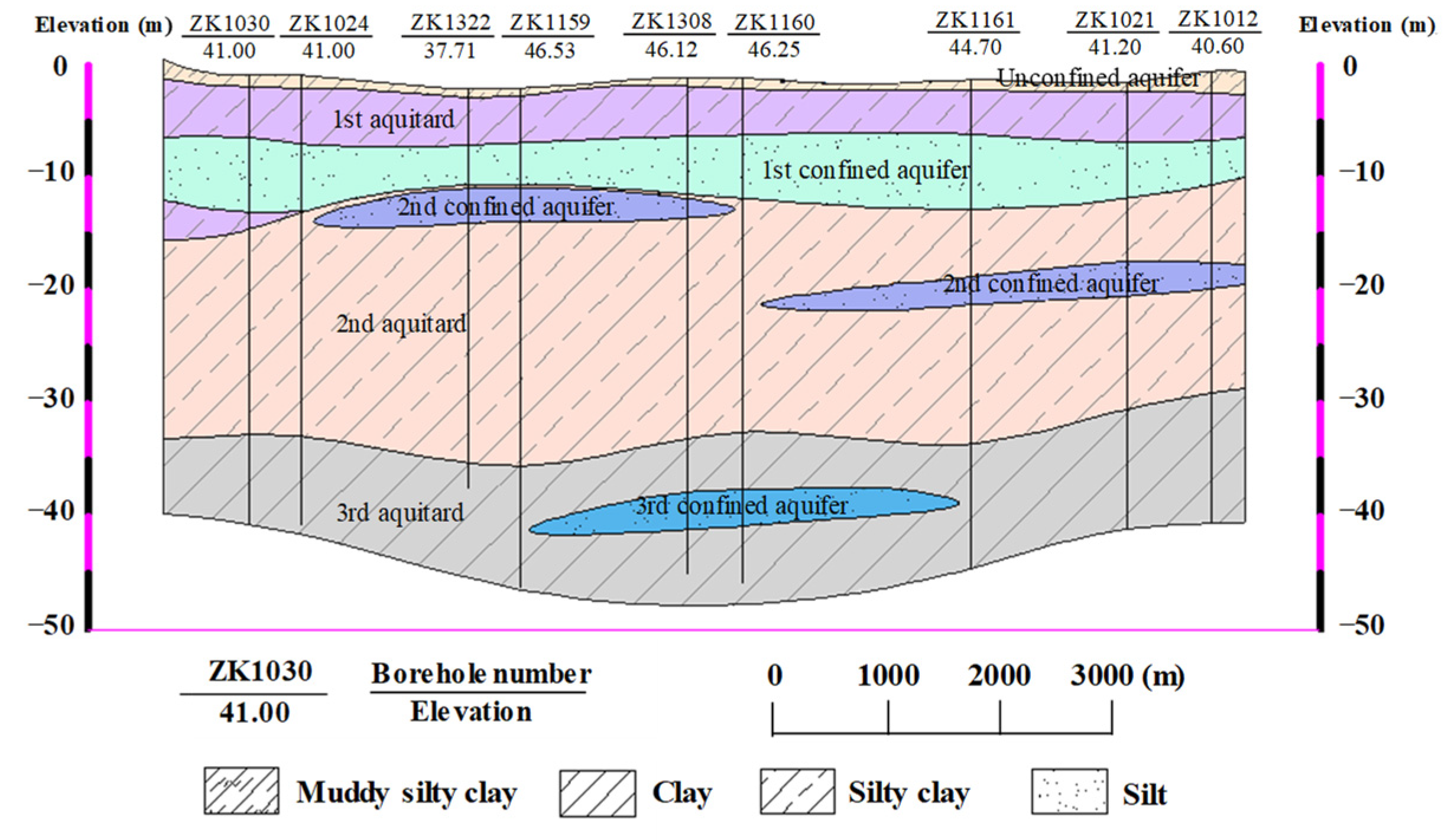
3.1. Background
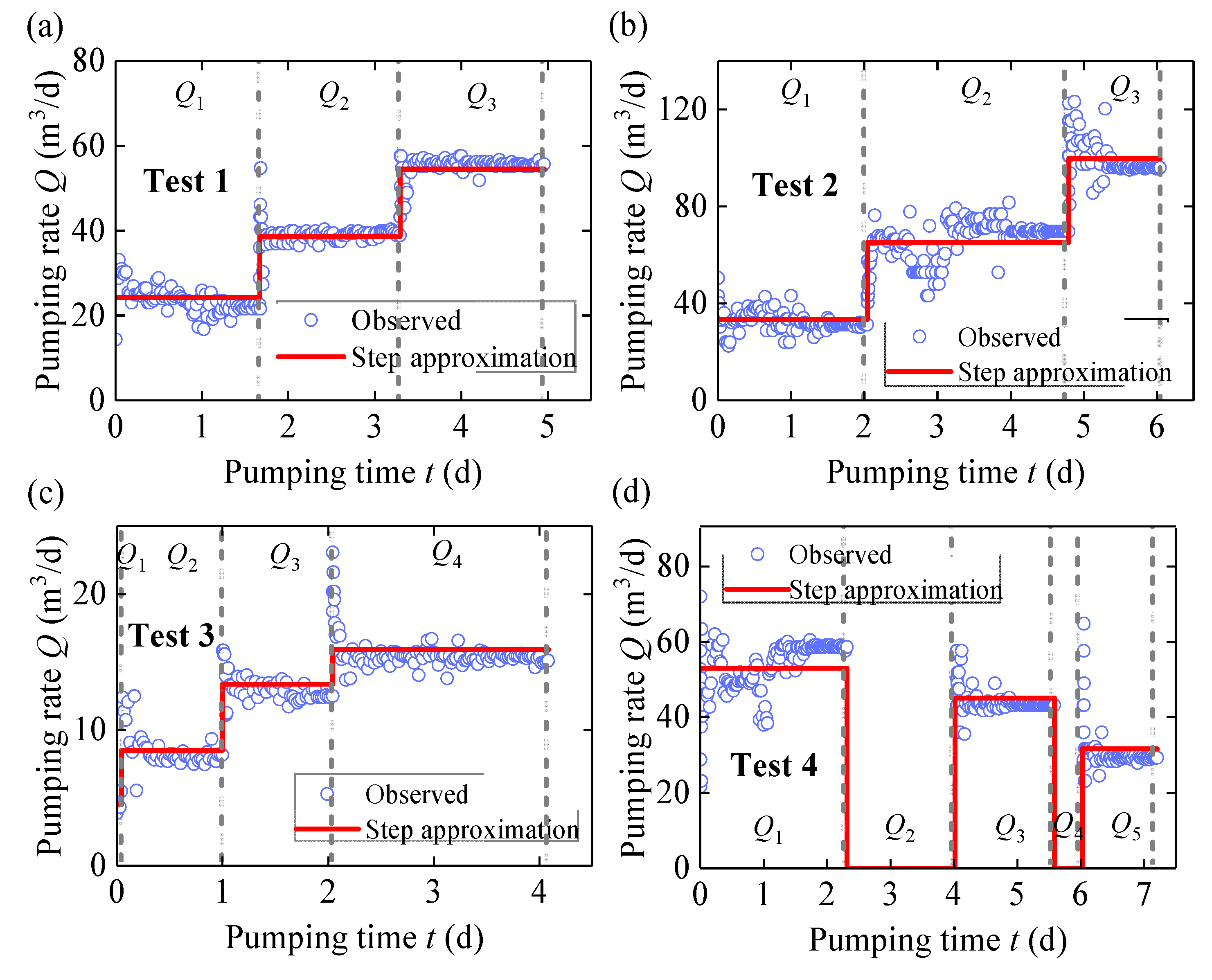
3.2. Analysis of In Situ Pumping Test
4. Discussion
5. Conclusions
- (1)
- The study introduced a new dimensionless transformation formula to simplify the analytical solution of variable-rate pumping tests, and a piecewise-constant function was further used to approximate the time-varying pumping rate records. Type curve analyses revealed that the time–drawdown curve of the first step was consistent with the Theis curve. However, the type curves of the subsequent steps deviated from the Theis curve and were associated with the first dimensionless inflection time (t1,D), which depended on the K and Ss of the confined aquifers. A large t1,D resulted in a faster time for a sudden turn in the drawdown.
- (2)
- A new type curve method was proposed to handle situations where the real pumping rate varies in a complicated pattern over time. One unique feature of this method is that the type curves depend on the pumping conditions rather than the observation conditions, making it applicable to drawdown data collected from various observation wells during a single pumping test. Furthermore, this new method could also be used to analyze recovery drawdown data by setting a zero pumping rate value for the corresponding shutdown period.
- (3)
- The hydraulic conductivity (K) and specific storage (Ss) of the first and second confined aquifers at the field site were estimated using the pumping rate and drawdown records from four real pumping tests. The estimation results showed that the hydraulic parameters obtained from the newly proposed type curve method were close to the calibrated results reported by PEST, indicating the reliability and robustness of this new method. Moreover, the K estimates were further verified by comparing them with lithology-based results. The geometric means of K and Ss were 6.62 m/d and 3.16 × 10−5 m−1 for the first confined aquifer and 0.92 m/d and 2.34 × 10−4 m−1 for the second confined aquifer.
- (4)
- The field pumping test results showed that the actual pumping rate may have an uncontrollable and short-duration decreasing trend at the early times of each step, resulting in uncertainty in the evaluation of aquifer hydraulic parameters. In addition, the heterogeneity of natural aquifers and the non-uniformity of their thickness also led to differences in the estimated hydraulic parameters of different observation wells in the same pumping test. Future studies will focus on characterizing the heterogeneity of aquifer systems from multiple pumping test data based on more realistic and refined pumping models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Banks, D.; Odling, N.E.; Skarphagen, H.; Rohr-Torp, E. Permeability and stress in crystalline rocks. Terra Nova 1996, 8, 223–235. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y.; Tan, T.; Zhang, L.; Zhu, S.; Xu, F. Evolution and modeling of mine water inflow and hazard characteristics in southern coalfields of China: A case of Meitanba mine. Int. J. Min. Sci. Technol. 2022, 32, 513–524. [Google Scholar] [CrossRef]
- Manoutsoglou, E.; Lazos, I.; Steiakakis, E.; Vafeidis, A. The Geomorphological and Geological Structure of the Samaria Gorge, Crete, Greece-Geological Models Comprehensive Review and the Link with the Geomorphological Evolution. Appl. Sci. 2022, 12, 10670. [Google Scholar] [CrossRef]
- Stober, I.; Bucher, K. Origin of salinity of deep groundwater in crystalline rocks. Terra Nova 1999, 11, 181–185. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhao, J.; Li, S.; Jiang, Z.; Huang, F.A. Unified Solution for Surrounding Rock of Roadway Considering Seepage, Dilatancy, Strain-Softening and Intermediate Principal Stress. Sustainability 2022, 14, 8099. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Zhao, Y.; Luo, S.; Wang, Y.; Wang, W.; Zhang, L.; Wan, W. Numerical Analysis of Karst Water Inrush and a Criterion for Establishing the Width of Water-resistant Rock Pillars. Mine Water Environ. 2017, 36, 508–519. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Aubertin, M. On the use of the Kozeny–Carman equation to predict the hydraulic conductivity of soils. Can. Geotech. J. 2003, 40, 616–628. [Google Scholar] [CrossRef]
- Ren, X.; Zhao, Y.; Deng, Q.; Li, D.; Wang, D. A relation of hydraulic conductivity-Void ratio for soils based on Kozeny-carman equation. Eng. Geol. 2016, 213, 89–97. [Google Scholar] [CrossRef]
- Gallage, C.; Kodikara, J.; Uchimura, T. Laboratory measurement of hydraulic conductivity functions of two unsaturated sandy soils during drying and wetting processes. Soils Found. 2013, 53, 417–430. [Google Scholar] [CrossRef]
- Masrouri, F.; Bicalho, K.V.; Kawai, K. Laboratory Hydraulic Testing in Unsaturated Soils. Geotech. Geol. Eng. 2008, 26, 691–704. [Google Scholar] [CrossRef]
- Abdalla, F.; Mubarek, K. Assessment of well performance criteria and aquifer characteristics using step-drawdown tests and hydrogeochemical data, west of Qena area, Egypt. J. Afr. Earth. Sci. 2018, 138, 336–347. [Google Scholar] [CrossRef]
- Hendrayanto; Kosugi, K.I.; Mizuyama, T. Field Determination of Unsaturated Hydraulic Conductivity of Forest Soils. J. For. Res. 1998, 3, 11–17. [Google Scholar] [CrossRef]
- Neuman, S.P.; Witherspoon, P.A. Field determination of the hydraulic properties of leaky multiple aquifer systems. Water Resour. Res. 1972, 8, 1284–1298. [Google Scholar] [CrossRef]
- Sethi, R. A dual-well step drawdown method for the estimation of linear and non-linear flow parameters and wellbore skin factor in confined aquifer systems. J. Hydrol. 2011, 400, 187–194. [Google Scholar] [CrossRef]
- Butt, M.A.; Mcelwee, C.D. Aquifer-Parameter Evaluation from Variable-Rate Pumping Tests Using Convolution and Sensitivity Analysis. Groundwater 1985, 23, 212–219. [Google Scholar] [CrossRef]
- Theis, C.V. The relation between the lowering of the Piezometric surface and the rate and duration of discharge of a well using ground-water storage. EOS Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Cooper, H.H.; Jacob, C.E. A generalized graphical method for evaluating formation constants and summarizing well-field history. EOS Trans. Am. Geophys. Union 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Hantush, M.S. Nonsteady Flow to Flowing Wells in Leaky Aquifers. J. Geophys. Res. 1959, 64, 1043–1052. [Google Scholar] [CrossRef]
- Neuman, S.P. Theory of Flow in Unconfined Aquifers Considering Delayed Response of the Water Table. Water Resour. Res. 1972, 8, 1031–1045. [Google Scholar] [CrossRef]
- Rorabaugh, M. Graphical and theoretical analysis of step-drawdown test of artesian well. Proc. Am. Soc. Civ. Eng. 1953, 79, 1–23. [Google Scholar]
- Sen, Z.; Altunkaynak, A. Variable discharge type curve solutions for confined aquifers. J. Am. Water Resour. Assoc. 2004, 40, 1189–1196. [Google Scholar] [CrossRef]
- Butler, J.J.; McElwee, C.D. Variable-rate pumping tests for radially symmetric nonuniform aquifers. Water Resour. Res. 1990, 26, 291–306. [Google Scholar] [CrossRef]
- Hantush, M.S. Drawdown around Wells of Variable Discharge. J. Geophys. Res. 1964, 69, 4221–4235. [Google Scholar] [CrossRef]
- Singh, S.K. Well Loss Estimation: Variable Pumping Replacing Step Drawdown Test. J. Hydraul. Eng. 2002, 128, 343–348. [Google Scholar] [CrossRef]
- Wen, Z.; Zhan, H.; Wang, Q.; Liang, X.; Ma, T.; Chen, C. Well hydraulics in pumping tests with exponentially decayed rates of abstraction in confined aquifers. J. Hydrol. 2017, 548, 40–45. [Google Scholar] [CrossRef]
- Zhang, G. Type curve and numerical solutions for estimation of Transmissivity and Storage coefficient with variable discharge condition. J. Hydrol. 2013, 476, 345–351. [Google Scholar] [CrossRef]
- Zhuang, C.; Zhou, Z.; Zhan, H.; Wang, J.; Li, Y. New graphical methods for estimating aquifer hydraulic parameters using pumping tests with exponentially decreasing rates. Hydrol. Process 2019, 33, 2314–2322. [Google Scholar] [CrossRef]
- Luo, N.; Zhanfeng, Z.; Walter, A.I.; Steven, J.B. Comparative study of transient hydraulic tomography with varying parameterizations and zonations: Laboratory sandbox investigation. J. Hydrol. 2017, 554, 758–779. [Google Scholar] [CrossRef]
- Doherty, J. PEST: Model Independent Parameter Estimation; Watermark Computing: Corinda, Australia, 2008. [Google Scholar]
- Copty, N.K.; Trinchero, P.; Sanchez-Vila, X.; Sarioglu, M.S.; Findikakis, A.N. Influence of heterogeneity on the interpretation of pumping test data in leaky aquifers. Water Resour. Res. 2008, 44, 2276–2283. [Google Scholar] [CrossRef]
- Demir, M.T.; Copty, N.K.; Trinchero, P.; Sanchez-Vila, X. Bayesian Estimation of the Transmissivity Spatial Structure from Pumping Test Data. Adv. Water Resour. 2017, 104, 174–182. [Google Scholar] [CrossRef]
- Sudicky, E.A.; Illman, W.A.; Goltz, I.K.; Adams, J.J.; Mclaren, R.G. Heterogeneity in hydraulic conductivity and its role on the macroscale transport of a solute plume: From measurements to a practical application of stochastic flow and transport theory. Water Resour. Res. 2010, 46, 489–496. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models: I. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Chen, C.; Tao, Q.; Wen, Z.; Wörman, A.; Jakada, H. Step-drawdown test for identifying aquifer and well loss parameters in a partially penetrating well with irregular (non-linear increasing) pumping rates. J. Hydrol. 2022, 614, 128652. [Google Scholar] [CrossRef]
- Ren, X.W.; Santamarina, J.C. The hydraulic conductivity of sediments: A pore size perspective. Eng. Geol. 2018, 233, 48–54. [Google Scholar] [CrossRef]
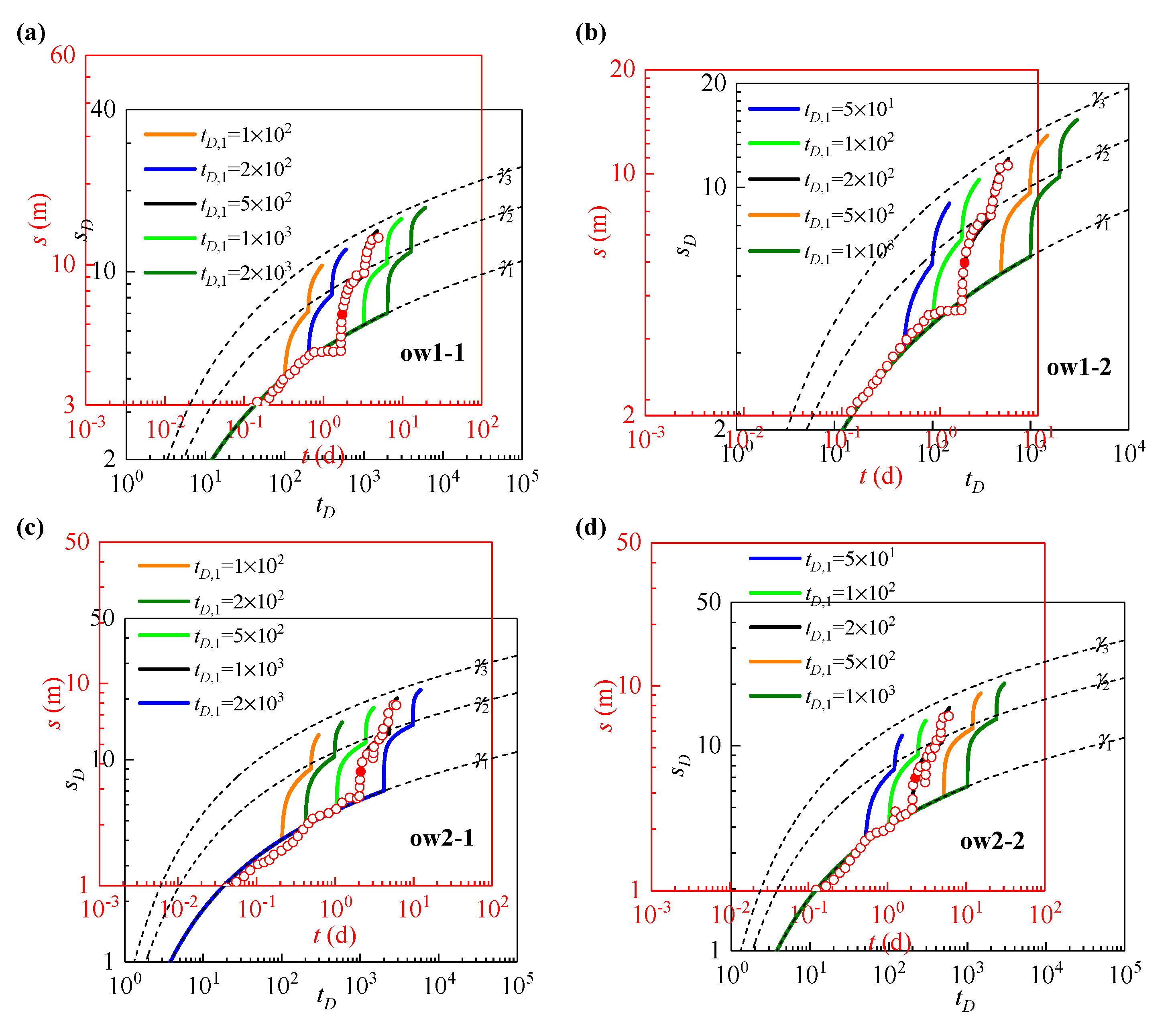
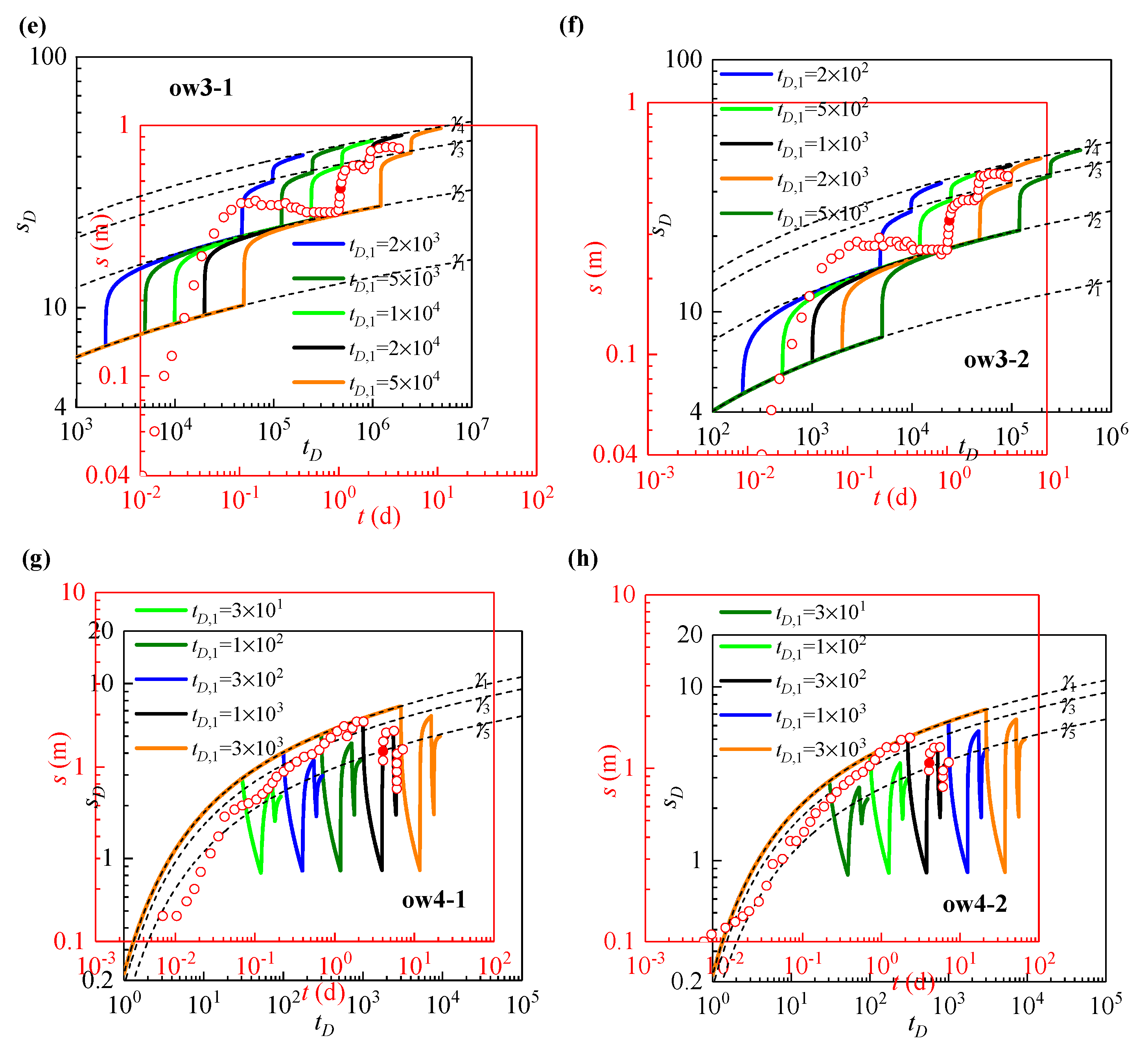
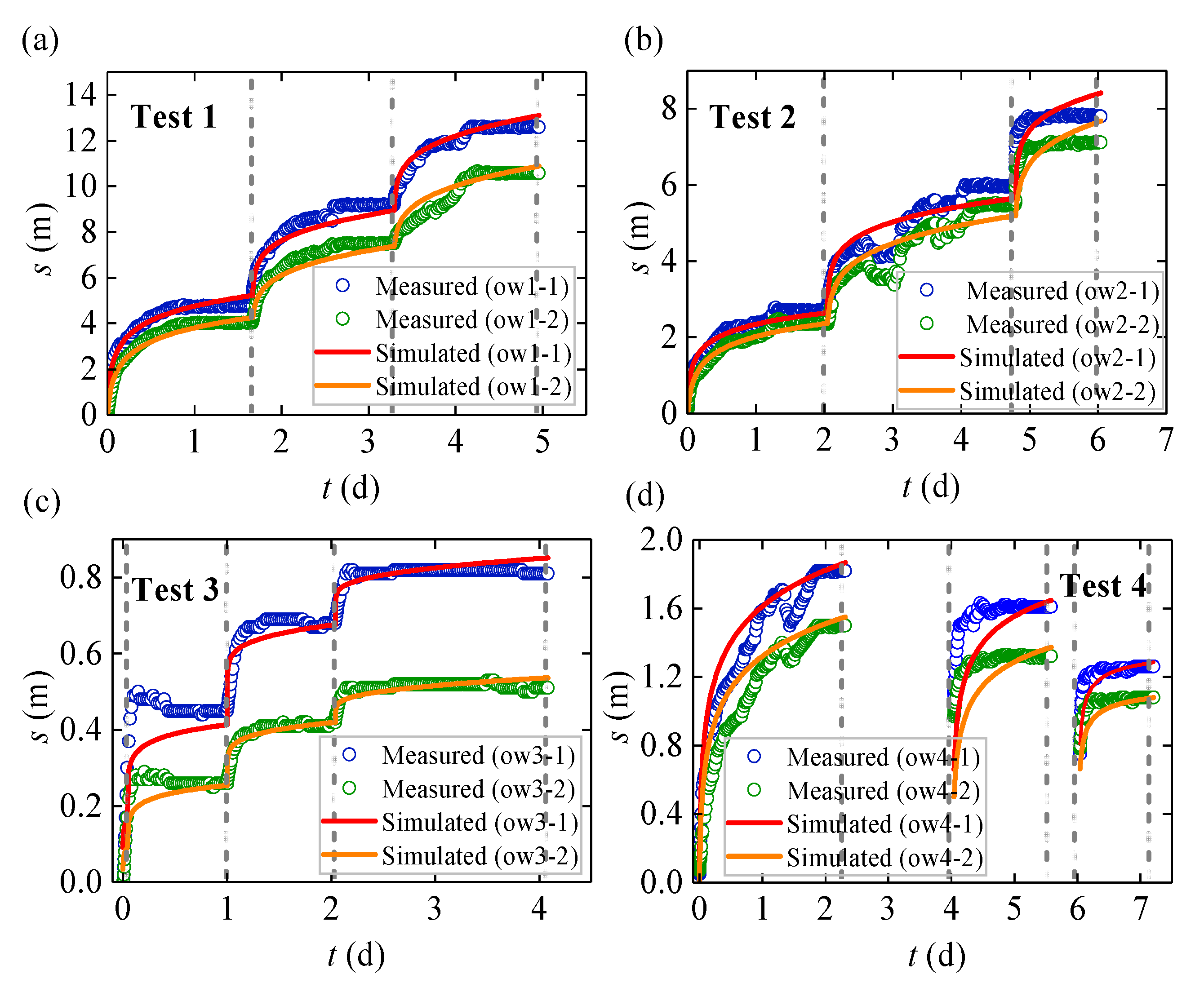
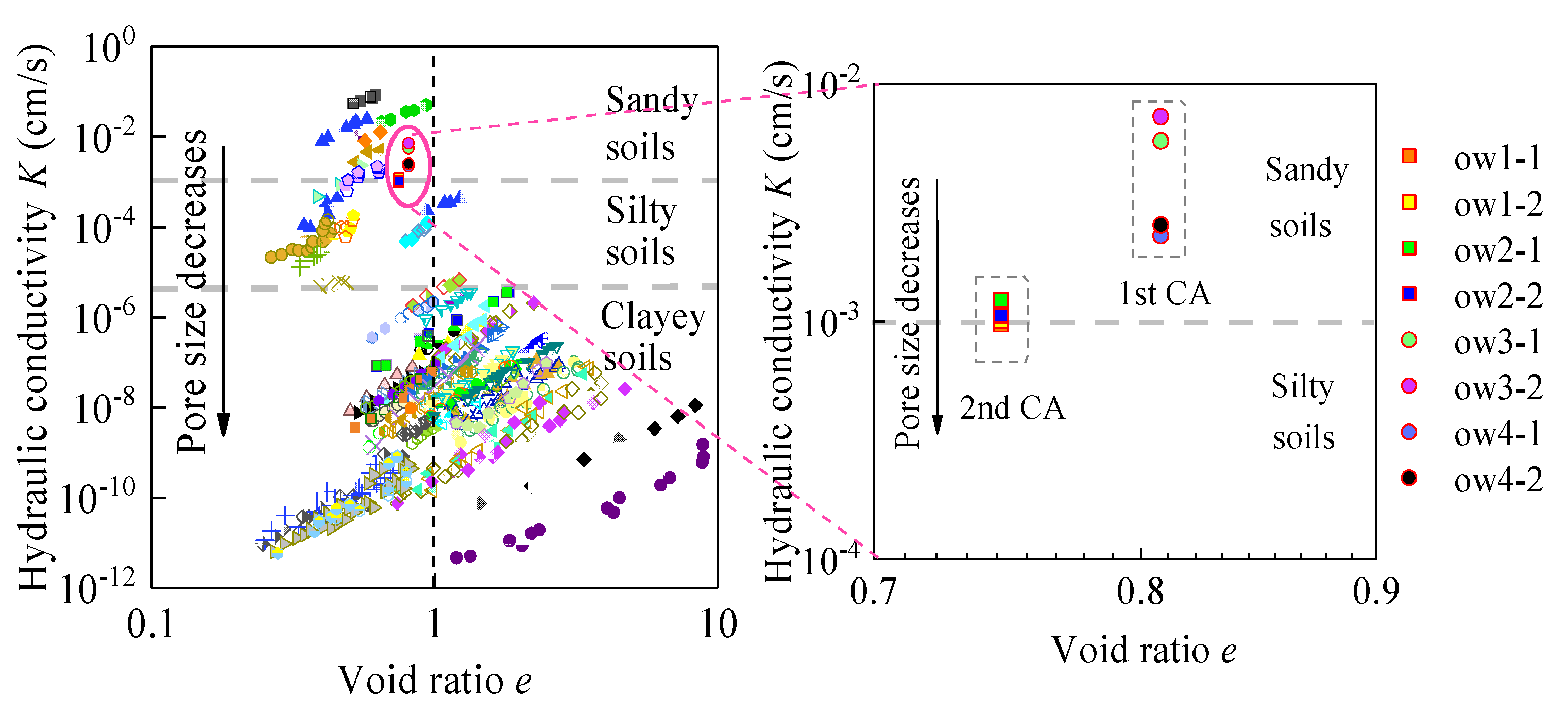
| Test No. (Aquifer) | Obs. Well | t1,D | Coordinate Values | K | Ss | |||
|---|---|---|---|---|---|---|---|---|
| tD | sD | t (d) | s (m) | |||||
| 1 (2nd CA *) | ow1-1 | 500 | 516.72 | 7.04 | 1.74 | 6.53 | 0.83 | 4.47 |
| ow1-2 | 200 | 213.26 | 6.02 | 1.79 | 5.53 | 0.84 | 1.26 | |
| 2 (2nd CA) | ow2-1 | 1000 | 1020.38 | 8.73 | 2.13 | 3.66 | 1.07 | 3.58 |
| ow2-2 | 200 | 217.55 | 7.05 | 2.27 | 3.55 | 0.89 | 1.66 | |
| 3 (1st CA) | ow3-1 | 20,000 | 481,359.64 | 30.96 | 1.06 | 0.54 | 4.98 | 0.02 |
| ow3-2 | 1000 | 24,185.94 | 23.10 | 1.06 | 0.34 | 5.90 | 0.05 | |
| 4 (1st CA) | ow4-1 | 1000 | 1754.08 | 4.11 | 4.06 | 1.23 | 2.01 | 7.47 |
| ow4-2 | 300 | 569.65 | 3.56 | 4.07 | 1.07 | 2.01 | 2.55 | |
| Test No. (Aquifer) | Observation Well | K (m/d) | Ss (×10−4 m−1) | CE |
|---|---|---|---|---|
| 1 | ow1-1 | 0.84 [0.81,0.87] a | 4.28 [3.67,4.99] | 0.993 |
| (2nd CA *) | ow1-2 | 0.87 [0.83,0.91] | 1.22 [1.03,1.44] | 0.988 |
| 2 | ow2-1 | 1.07 [0.99,1.14] | 3.75 [2.66,5.28] | 0.973 |
| (2nd CA) | ow2-2 | 0.92 [0.85,0.98] | 1.53 [1.17,2.01] | 0.972 |
| 3 | ow3-1 | 4.96 [4.30,5.62] | 0.02 [0.004,0.08] | 0.933 |
| (1st CA) | ow3-2 | 6.28 [5.73,6.83] | 0.04 [0.02,0.08] | 0.958 |
| 4 | ow4-1 | 1.98 [1.85,2.11] | 8.85 [6.63,11.81] | 0.819 |
| (1st CA) | ow4-2 | 2.20 [2.03,2.37] | 1.78 [1.30,2.43] | 0.743 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhou, Z.; Zhuang, C.; Dou, Z. Estimating Hydraulic Parameters of Aquifers Using Type Curve Analysis of Pumping Tests with Piecewise-Constant Rates. Water 2023, 15, 1661. https://doi.org/10.3390/w15091661
Li Y, Zhou Z, Zhuang C, Dou Z. Estimating Hydraulic Parameters of Aquifers Using Type Curve Analysis of Pumping Tests with Piecewise-Constant Rates. Water. 2023; 15(9):1661. https://doi.org/10.3390/w15091661
Chicago/Turabian StyleLi, Yabing, Zhifang Zhou, Chao Zhuang, and Zhi Dou. 2023. "Estimating Hydraulic Parameters of Aquifers Using Type Curve Analysis of Pumping Tests with Piecewise-Constant Rates" Water 15, no. 9: 1661. https://doi.org/10.3390/w15091661




