Evaluation of Snowmelt Impacts on Flood Flows Based on Remote Sensing Using SRM Model
Abstract
1. Introduction
2. Materials and Methods
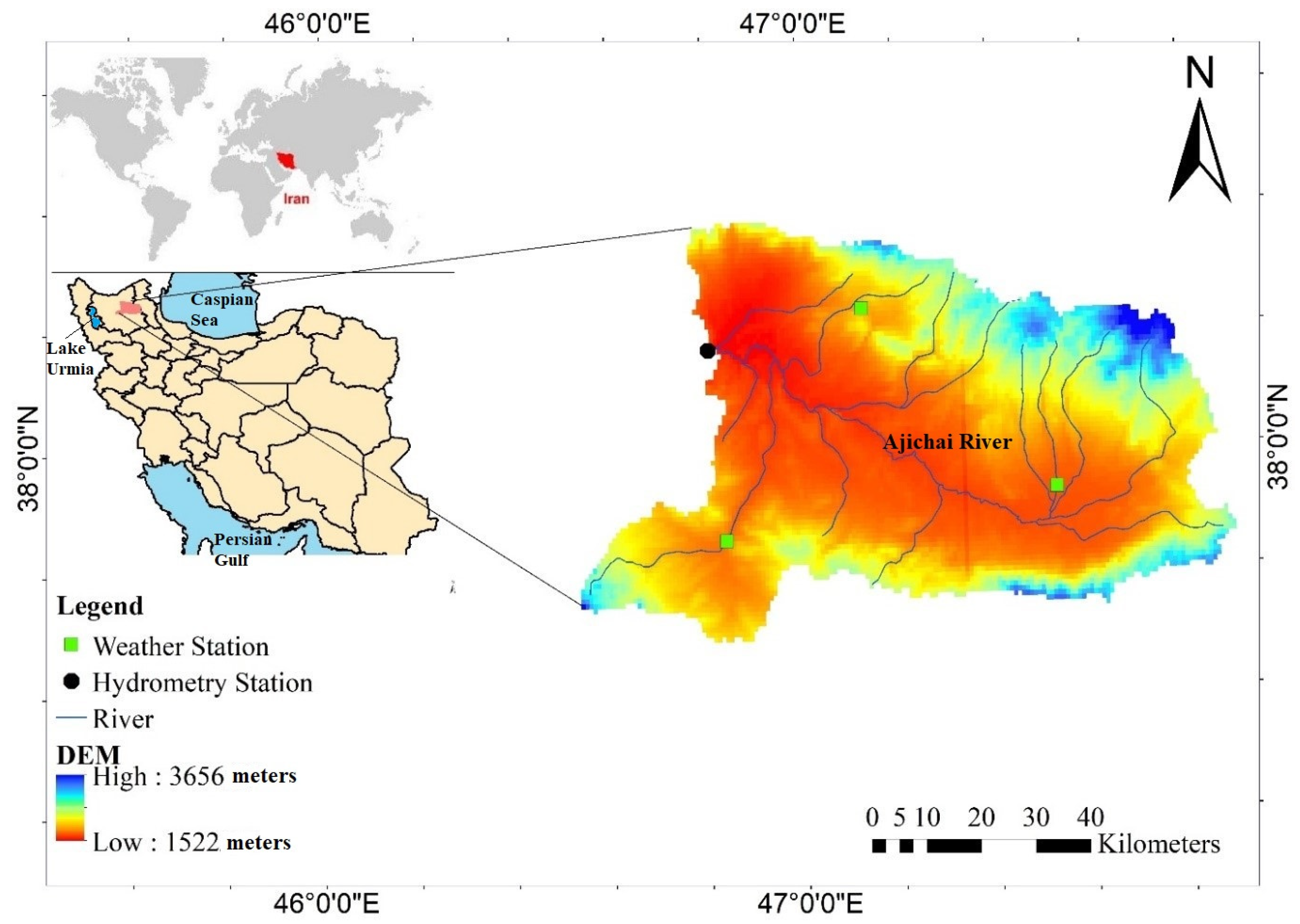
2.1. Study Area
2.2. Methodology
2.2.1. SCA Estimation by Remote Sensing
2.2.2. Google Earth Engine
2.3. SRM
2.3.1. Model Structure
2.3.2. Input Data
2.3.3. Model Input Parameters
2.3.4. Model Accuracy Evaluation
3. Results
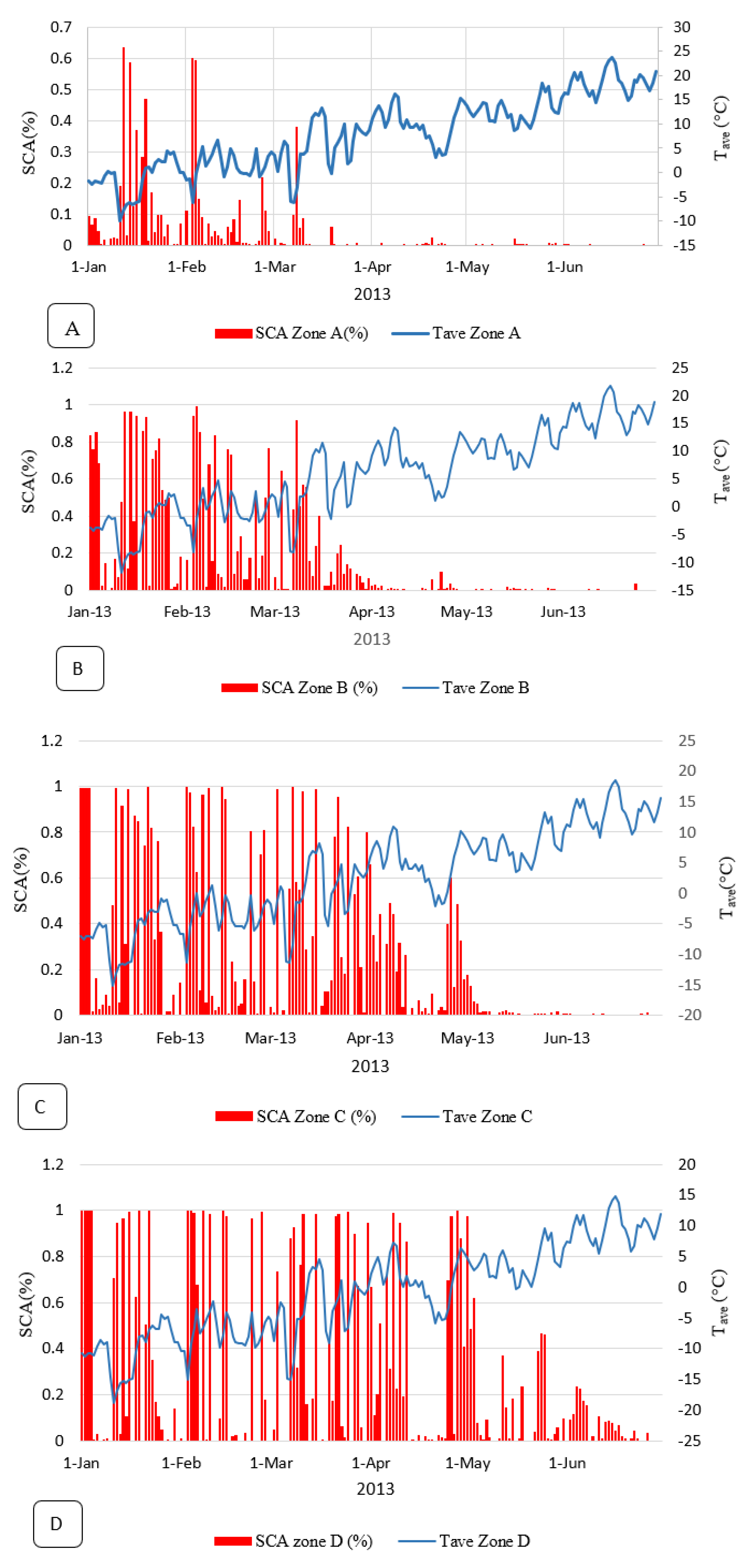
3.1. Comparison of Model Inputs
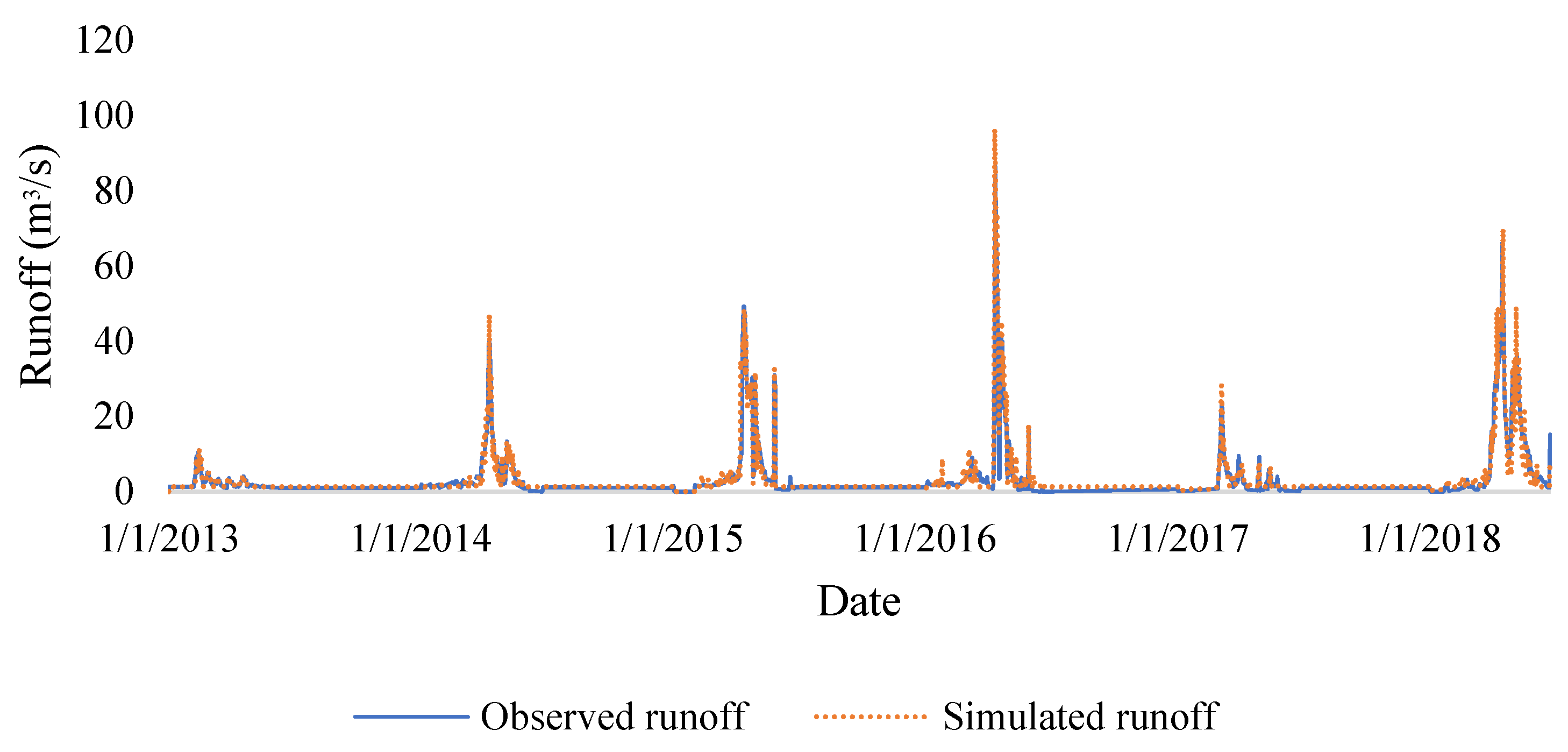
3.2. SRM Results
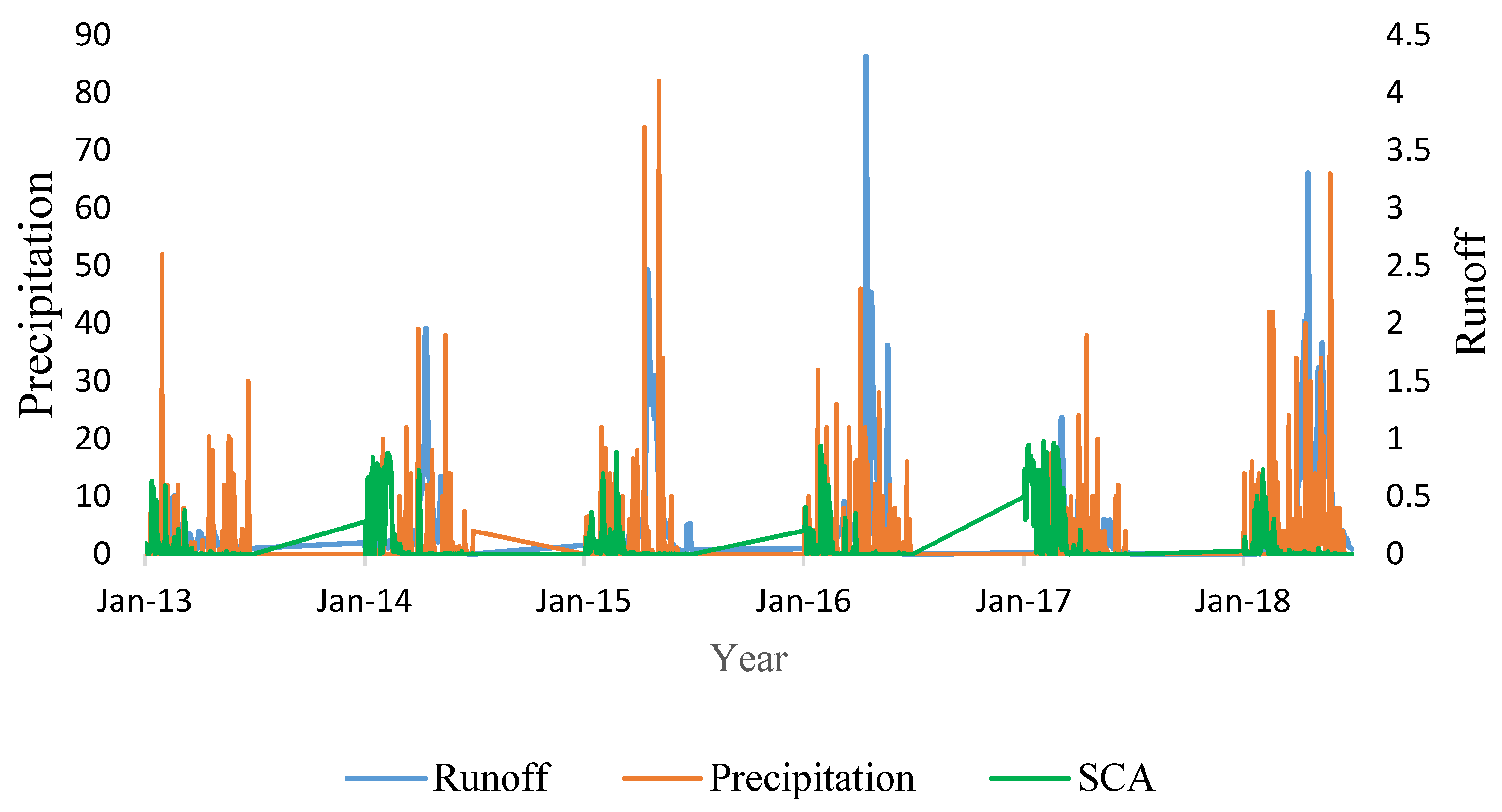
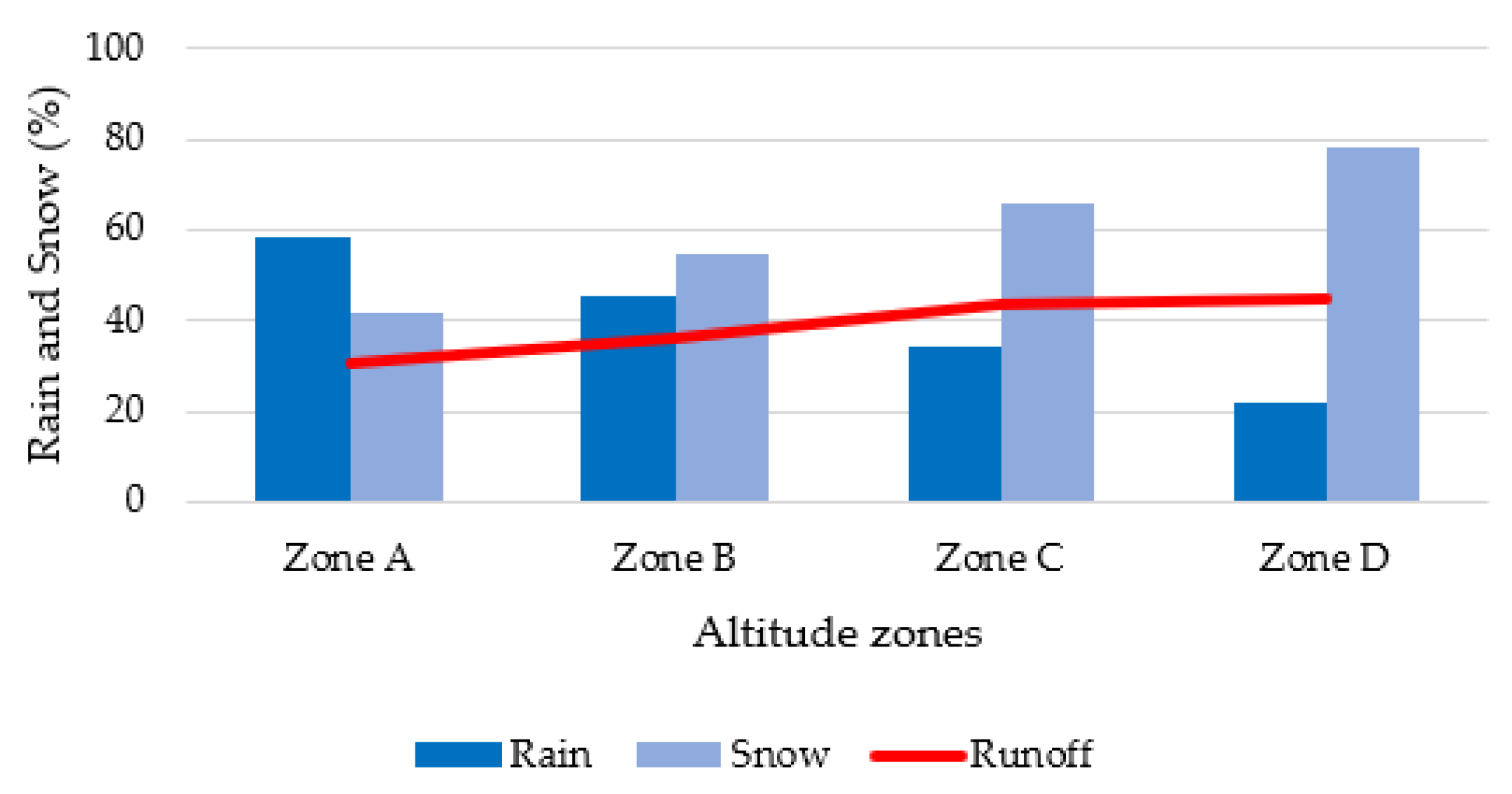
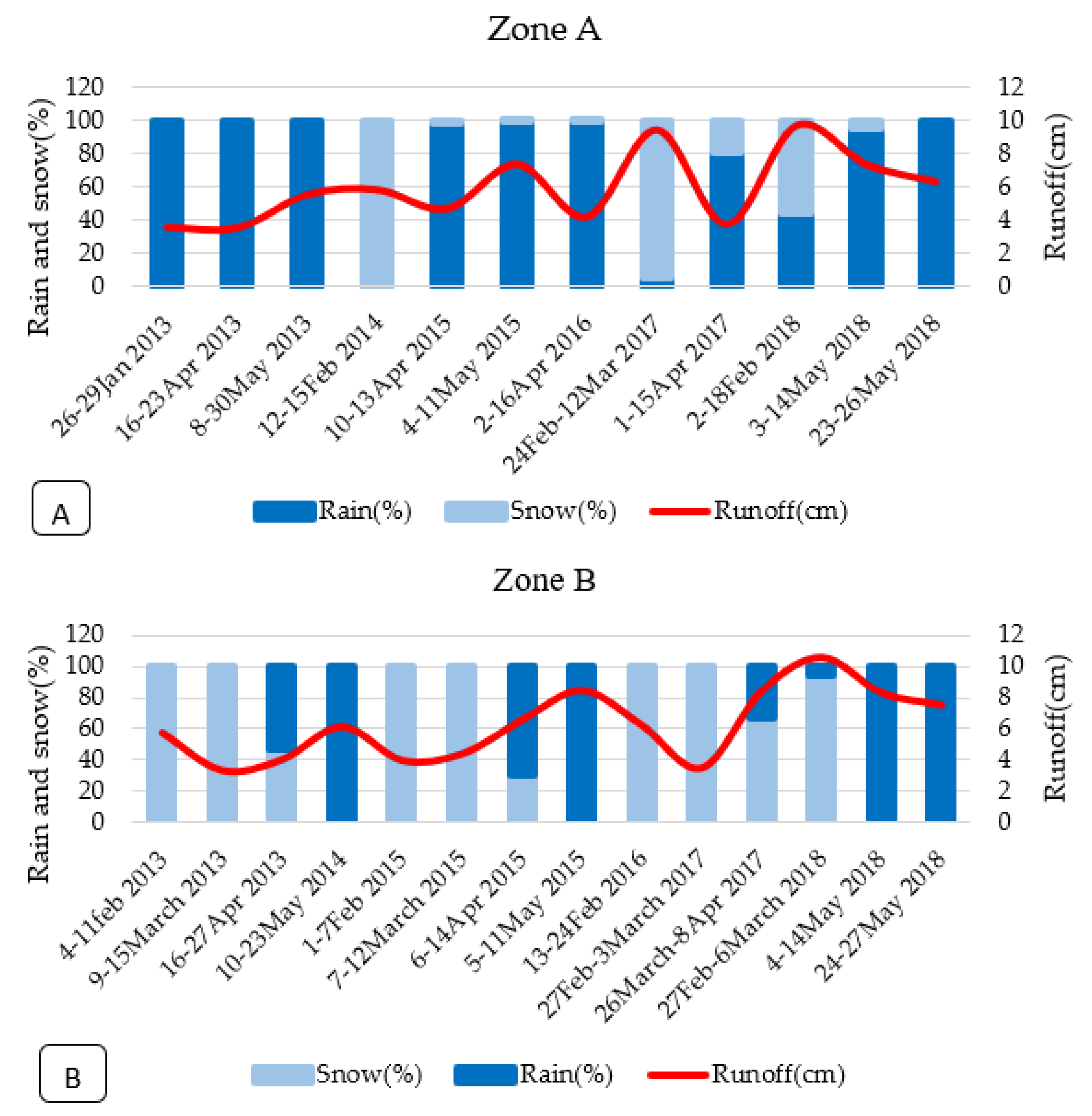
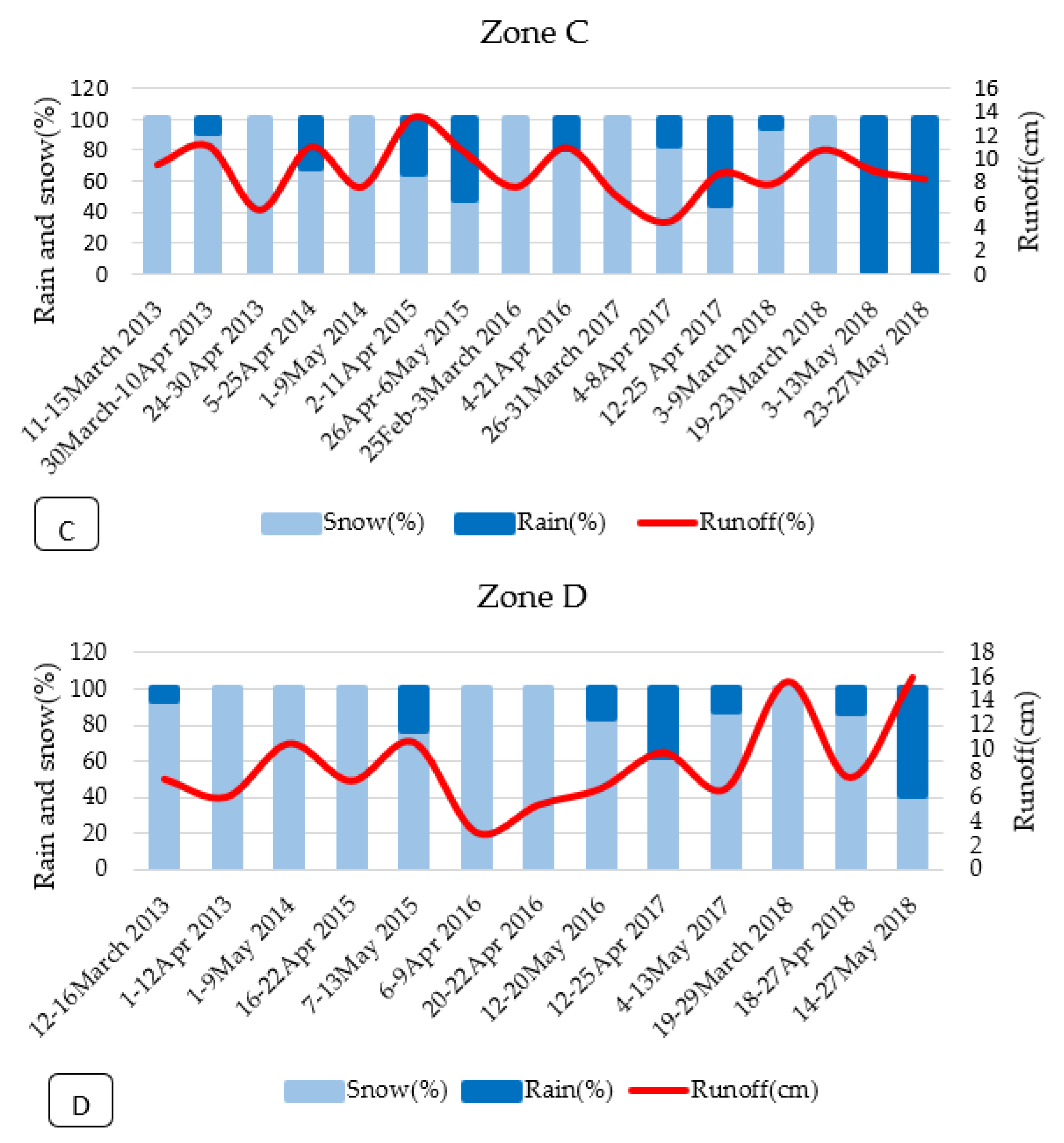
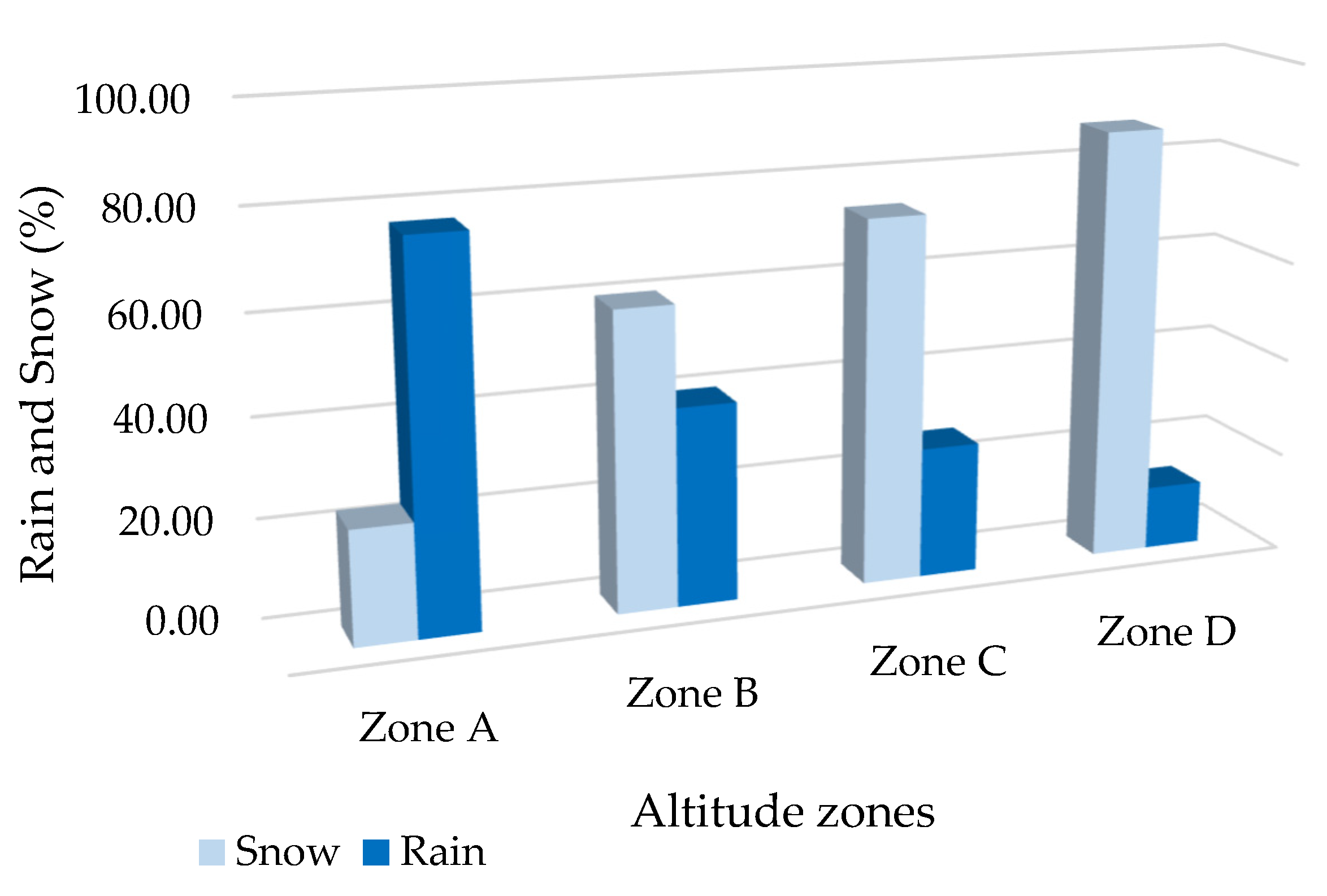
3.3. Impact of Snowmelt on Flooding
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow–a review of available methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Dong, C. Remote sensing, hydrological modeling and in situ observations in snow cover research: A review. J. Hydrol. 2018, 561, 573–583. [Google Scholar] [CrossRef]
- Hennessy, K.; Whetton, P.; Smith, I.; Bathols, J.; Hutchinson, M.; Sharples, J. The Impact of Climate Change on Snow Conditions in Mainland Australia; CSIRO Aspendale: Victoria, Australia, 2003. [Google Scholar]
- Hennessy, K.; Whetton, P.; Walsh, K.; Smith, I.; Bathols, J.; Hutchinson, M.; Sharples, J. Climate change effects on snow conditions in mainland Australia and adaptation at ski resorts through snowmaking. Clim. Res. 2008, 35, 255–270. [Google Scholar] [CrossRef]
- Javadinejad, S.; Dara, R.; Jafary, F. Climate change scenarios and effects on snow-melt runoff. Civ. Eng. J. 2020, 6, 1715–1725. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Fatehifar, A.; Moradi, A. Predicting future flood frequency under climate change using Copula function. Water Environ. J. 2020, 34, 710–727. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Sabaghzadeh, M.; Mokhtari, M.H. Impacts of aspect on snow characteristics using remote sensing from 2000 to 2020 in Ajichai-Iran. Cold Reg. Sci. Technol. 2022, 204, 103682. [Google Scholar] [CrossRef]
- Qiu, C.; Hattori, Y.; Kaji, M.; Onodera, M.; Hitokoto, M. Development of a river flow forecast model by coupling a snow accumulation/melt model with a distributed run-off model. J. Flood Risk Manag. 2014, 7, 89–99. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Pooladi, R.; Niazkar, M. Evaluation of Satellite-Based and Reanalysis Precipitation Datasets with Gauge-Observed Data over Haraz-Gharehsoo Basin, Iran. Sustainability 2022, 14, 13051. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Qin, Y.; Wang, W.; Zhang, M.; Zhang, K. Adaptability of MODIS Daily Cloud-Free Snow Cover 500 m Dataset over China in Hutubi River Basin Based on Snowmelt Runoff Model. Sustainability 2022, 14, 4067. [Google Scholar] [CrossRef]
- Graybeal, D.Y.; Leathers, D.J. Snowmelt-related flood risk in Appalachia: First estimates from a historical snow climatology. J. Appl. Meteorol. Climatol. 2006, 45, 178–193. [Google Scholar] [CrossRef]
- Zakharova, E.; Kouraev, A.; Biancamaria, S.; Kolmakova, M.; Mognard, N.; Zemtsov, V.; Kirpotin, S.; Decharme, B. Snow cover and spring flood flow in the Northern Part of Western Siberia (the Poluy, Nadym, Pur, and Taz Rivers). J. Hydrometeorol. 2011, 12, 1498–1511. [Google Scholar] [CrossRef]
- Nester, T.; Kirnbauer, R.; Parajka, J.; Blöschl, G. Evaluating the snow component of a flood forecasting model. Hydrol. Res. 2012, 43, 762–779. [Google Scholar] [CrossRef]
- Qiao, C.; Huang, Q.; Chen, T.; Chen, Y. Study on snowmelt flood disaster model based on remote sensing and gis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 709–713. [Google Scholar] [CrossRef]
- Uwamahoro, S.; Liu, T.; Nzabarinda, V.; Habumugisha, J.M.; Habumugisha, T.; Harerimana, B.; Bao, A. Modifications to Snow-Melting and Flooding Processes in the Hydrological Model—A Case Study in Issyk-Kul, Kyrgyzstan. Atmosphere 2021, 12, 1580. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Barnes, W.; Masuoka, E.J. Introduction to MODIS and an overview of associated activities. Earth Sci. Satell. Remote Sens. 2006, 12–32. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Appel, I. Development of the Aqua MODIS NDSI fractional snow cover algorithm and validation results. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1747–1756. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, H.; Lu, N.; Yao, T.; Liang, T. Toward advanced daily cloud-free snow cover and snow water equivalent products from Terra–Aqua MODIS and Aqua AMSR-E measurements. J. Hydrol. 2010, 385, 23–35. [Google Scholar] [CrossRef]
- Clement, M.A.; Kilsby, C.; Moore, P. Multi-temporal synthetic aperture radar flood mapping using change detection. J. Flood Risk Manag. 2018, 11, 152–168. [Google Scholar] [CrossRef]
- Mutanga, O.; Kumar, L. Google earth engine applications. Remote Sens. 2019, 11, 591. [Google Scholar] [CrossRef]
- Gorelick, N. Google earth engine. In EGU General Assembly Conference Abstracts; American Geophysical Union: Vienna, Austria, 2013; p. 11997. [Google Scholar]
- Martinec, J. Snowmelt-runoff model for stream flow forecasts. Hydrol. Res. 1975, 6, 145–154. [Google Scholar] [CrossRef]
- Martinec, J.; Rango, A.; Major, E. The Snowmelt-Runoff Model (SRM) User’s Manual; College of Agriculture and Home Economics, NM State University: Las Cruces, NM, USA, 1983. Available online: https://ntrs.nasa.gov/citations/19830015389 (accessed on 9 March 2023).
- Martinec, J.; Rango, A.; Roberts, R. Snowmelt Runoff Model (SRM) User’s Manual. Geogr. Bernensia P 2008, 35. [Google Scholar]
- Martinec, J.; Rango, A. Parameter values for snowmelt runoff modelling. J. Hydrol. 1986, 84, 197–219. [Google Scholar] [CrossRef]
- Abudu, S.; Cui, C.-l.; Saydi, M.; King, J.P. Application of snowmelt runoff model (SRM) in mountainous watersheds: A review. Water Sci. Eng. 2012, 5, 123–136. [Google Scholar] [CrossRef]
- Huang, J.B.; Wen, J.W.; Wang, B.; Hinokidani, O. Parameter sensitivity analysis for a physically based distributed hydrological model based on Morris’ screening method. J. Flood Risk Manag. 2020, 13, e12589. [Google Scholar] [CrossRef]
- Niazkar, M. Chapter 19—Multigene genetic programming and its various applications. In Handbook of Hydroinformatics; Es-lamian, S., Eslamian, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 321–332. [Google Scholar]
- Niazkar, M.; Goodarzi, M.R.; Fatehifar, A.; Abedi, M.J. Machine learning-based downscaling: Application of multi-gene genetic programming for downscaling daily temperature at Dogonbadan, Iran, under CMIP6 scenarios. Theor. Appl. Climatol. 2023, 151, 153–168. [Google Scholar] [CrossRef]
- Boudhar, A.; Hanich, L.; Boulet, G.; Duchemin, B.; Berjamy, B.; Chehbouni, A. Evaluation of the snowmelt runoff model in the Moroccan High Atlas Mountains using two snow-cover estimates. Hydrol. Sci. J. 2009, 54, 1094–1113. [Google Scholar] [CrossRef]
- Lee, S.; Klein, A.G.; Over, T.M. A comparison of MODIS and NOHRSC snow-cover products for simulating streamflow using the Snowmelt Runoff Model. Hydrol. Process. 2005, 19, 2951–2972. [Google Scholar] [CrossRef]
- Ma, H.; Cheng, G. A test of Snowmelt Runoff Model (SRM) for the Gongnaisi River basin in the western Tianshan Mountains, China. Chin. Sci. Bull. 2003, 48, 2253–2259. [Google Scholar] [CrossRef]
- Jain, S.K.; Goswami, A.; Saraf, A.K. Role of elevation and aspect in snow distribution in Western Himalaya. Water Resour. Manag. 2009, 23, 71–83. [Google Scholar] [CrossRef]
- Singh, D.K.; Gusain, H.S.; Dewali, S.K.; Tiwari, R.K.; Taloor, A.K. Analysis of snow dynamics in Beas river basin, western Himalaya using combined terra–aqua MODIS improved snow product and in situ data during twenty-first century. In Water, Cryosphere, and Climate Change in the Himalayas; Springer: Berlin/Heidelberg, Germany, 2021; pp. 115–128. [Google Scholar]
- Meshyk, A.; Barushka, M.; Marozava, V. Snow as a contributor to spring flooding in Belarus. Environ. Sci. Pollut. Res. 2021, 28, 18826–18836. [Google Scholar] [CrossRef]
- Freudiger, D.; Kohn, I.; Stahl, K.; Weiler, M. Large-scale analysis of changing frequencies of rain-on-snow events with flood-generation potential. Hydrol. Earth Syst. Sci. 2014, 18, 2695–2709. [Google Scholar] [CrossRef]
- Li, D.; Lettenmaier, D.P.; Margulis, S.A.; Andreadis, K. The role of rain-on-snow in flooding over the conterminous United States. Water Resour. Res. 2019, 55, 8492–8513. [Google Scholar] [CrossRef]
- Musselman, K.N.; Lehner, F.; Ikeda, K.; Clark, M.P.; Prein, A.F.; Liu, C.; Barlage, M.; Rasmussen, R. Projected increases and shifts in rain-on-snow flood risk over western North America. Nat. Clim. Chang. 2018, 8, 808–812. [Google Scholar] [CrossRef]
- Ahmad, N.; Khan, S.; Ehsan, M.; Rehman, F.U.; Al-Shuhail, A. Estimating the total volume of running water bodies using geographic information system (GIS): A case study of Peshawar Basin (Pakistan). Sustainability 2022, 14, 3754. [Google Scholar] [CrossRef]
- Manzoor, Z.; Ehsan, M.; Khan, M.B.; Manzoor, A.; Akhter, M.M.; Sohail, M.T.; Hussain, A.; Shafi, A.; Abu-Alam, T.; Abioui, M. Floods and flood management and its socio-economic impact on Pakistan: A review of the empirical literature. Front. Environ. Sci. 2022, 10, 2480. [Google Scholar] [CrossRef]
- Idowu, D.; Zhou, W. Land use and land cover change assessment in the context of flood hazard in Lagos State, Nigeria. Water 2021, 13, 1105. [Google Scholar] [CrossRef]
- Massari, C.; Camici, S.; Ciabatta, L.; Brocca, L. Exploiting satellite-based surface soil moisture for flood forecasting in the Mediterranean area: State update versus rainfall correction. Remote Sens. 2018, 10, 292. [Google Scholar] [CrossRef]
- Gude, V.; Corns, S.; Long, S. Flood prediction and uncertainty estimation using deep learning. Water 2020, 12, 884. [Google Scholar] [CrossRef]
- Fenner, R.; O’Donnell, E.; Ahilan, S.; Dawson, D.; Kapetas, L.; Krivtsov, V.; Ncube, S.; Vercruysse, K. Achieving urban flood resilience in an uncertain future. Water 2019, 11, 1082. [Google Scholar] [CrossRef]
- Stephens, T.; Bledsoe, B. Simplified Uncertainty Bounding: An Approach for Estimating Flood Hazard Uncertainty. Water 2022, 14, 1618. [Google Scholar] [CrossRef]
| Satellite Products | ||||
|---|---|---|---|---|
| Data product | Band name | Resolution | Data period | Data |
| MOD10A1.006 Terra Snow Cover Daily Global 500 m | NDSI_Snow_Cover | 500 m | 2013–2018 | Snow cover |
| Ground station observation | ||||
| Station name | Elevation | Longitude | Latitude | Zone |
| Heris | 1950 | 47°7′48″ | 38°13′47″ | A |
| Sarab | 1682 | 47°31′48″ | 37°55′47″ | A |
| Bostanabad | 1736 | 37°51′0″ | 46°50′24″ | A |
| Merkid | 1532 | 46°47′59″ | 38°9′35″ | Zone |
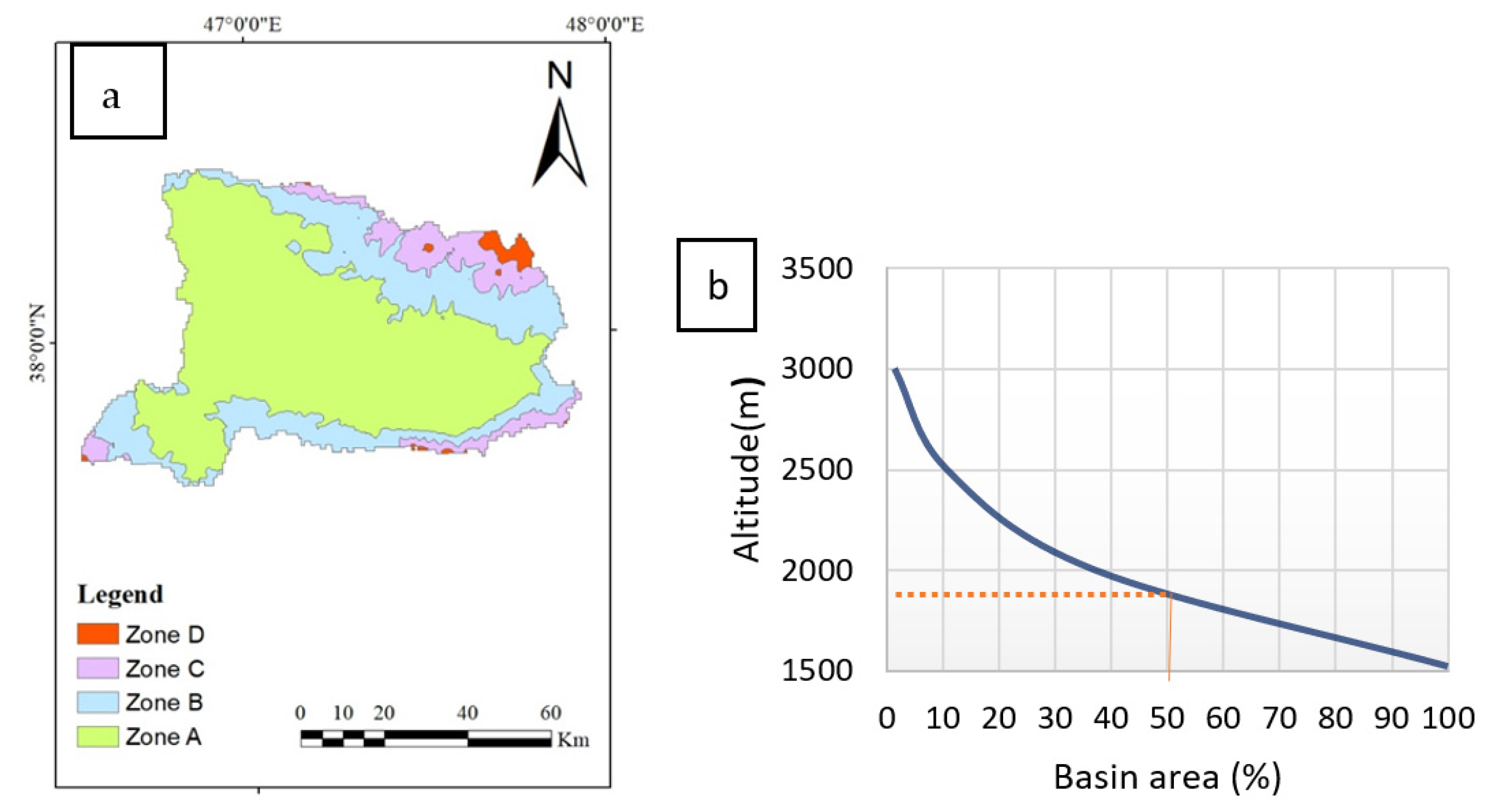
| Zone | Elevation Range (m) | Hypsometric Average Elevation (m) | Area (km2) | Area Percent (%) |
|---|---|---|---|---|
| A | 1522–2000 | 1761 | 3563 | 62.89 |
| B | 2000–2500 | 2250 | 1498 | 26.44 |
| C | 2500–3000 | 2750 | 527 | 9.3 |
| D | 3000–3656 | 3328 | 77 | 1.36 |
| Parameter | x | y | a | Tcrit (°C) | Cs | Cs | Cr | Lag Time |
|---|---|---|---|---|---|---|---|---|
| Value | 1.3 | 0.96 | 0.3–0.5 | 2 | 0.01–0.9 | 0.01–0.9 | 0.01–0.9 | 3 |
| Date | Volume Observed Runoff (Million m3) | Volume Simulated Runoff (Million m3) | R2 | Dv | NSE | Ep | Etp | |
|---|---|---|---|---|---|---|---|---|
| Calibration period | 2013 | 32.161 | 31.948 | 0.76 | 0.66 | 0.774 | 0.03 | 0.022 |
| 2014 | 65.295 | 62.775 | 0.84 | 3.85. | 0.856 | 0.17 | 0 | |
| 2015 | 93.766 | 95.259 | 0.86 | −1.59 | 0.86 | −0.01 | 0 | |
| 2016 | 91.772 | 104.83 | 0.82 | −14.22 | 0.82 | 0.11 | 0.022 | |
| Validation period | 2017 | 31.372 | 36.486 | 0.85 | −16.29 | 0.83 | 0.2 | 0.022 |
| 2018 | 136.141 | 137.15 | 0.85 | −0.74 | 0.85 | 0.05 | 0.022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goodarzi, M.R.; Sabaghzadeh, M.; Niazkar, M. Evaluation of Snowmelt Impacts on Flood Flows Based on Remote Sensing Using SRM Model. Water 2023, 15, 1650. https://doi.org/10.3390/w15091650
Goodarzi MR, Sabaghzadeh M, Niazkar M. Evaluation of Snowmelt Impacts on Flood Flows Based on Remote Sensing Using SRM Model. Water. 2023; 15(9):1650. https://doi.org/10.3390/w15091650
Chicago/Turabian StyleGoodarzi, Mohammad Reza, Maryam Sabaghzadeh, and Majid Niazkar. 2023. "Evaluation of Snowmelt Impacts on Flood Flows Based on Remote Sensing Using SRM Model" Water 15, no. 9: 1650. https://doi.org/10.3390/w15091650
APA StyleGoodarzi, M. R., Sabaghzadeh, M., & Niazkar, M. (2023). Evaluation of Snowmelt Impacts on Flood Flows Based on Remote Sensing Using SRM Model. Water, 15(9), 1650. https://doi.org/10.3390/w15091650







