Application of Analytical Probabilistic Models in Urban Runoff Control Systems’ Planning and Design: A Review
Abstract
:1. Introduction
2. Design of Urban Runoff Control Systems
3. Analytical Probabilistic Models (APMs)
- i.
- Selection of a case study of urban catchment and determination of its physiographic information (catchment area, slope, proportion of imperviousness, drainage length, depression storage, runoff coefficient);
- ii.
- Discretization of the long-term continuous rainfall data into individual events using the minimum inter-event time definition;
- iii.
- Use of probability distributions, such as Exponential, Weibull, etc., to fit rainfall depth, duration and intervention time;
- iv.
- Development of APM parameters for the rainfall station;
- v.
- Development of APMs for stormwater characteristics such as runoff volume and peak runoff captured by the facility, total runoff, pollutants captured and treated by the facility, volume of spilled runoff, etc.
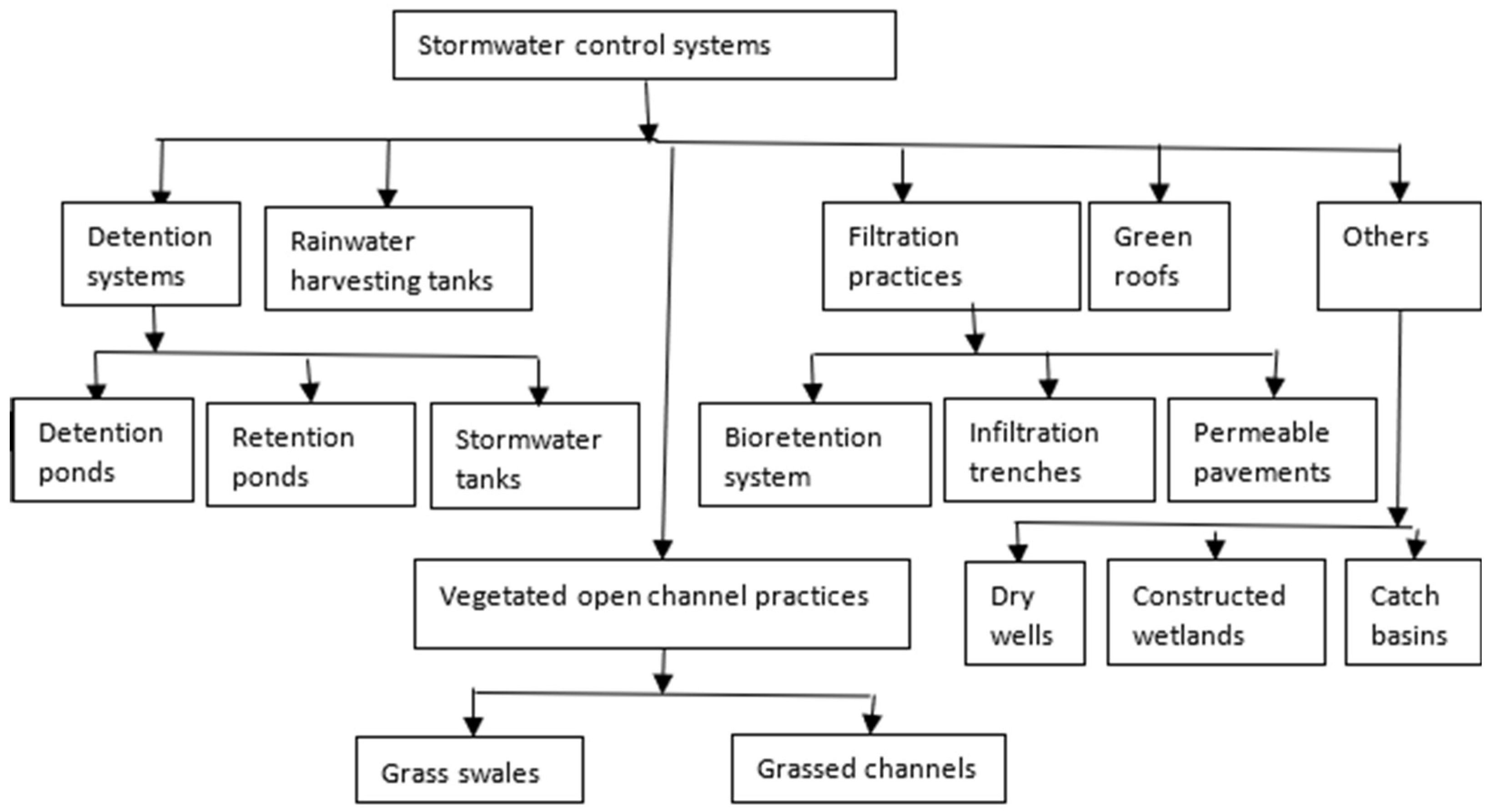
4. APM Application to Urban Runoff Control Systems
4.1. Detention Ponds/Stormwater Tanks
4.2. Rainwater Harvesting System/Rainwater Tanks
4.3. Green Roofs
4.4. Filtration Practices
4.4.1. Bioretention Cells/Biofilters/Rain Gardens/Impervious Area Disconnection
4.4.2. Infiltration Trenches/Basins
4.4.3. Permeable Pavements
4.5. Vegetated Open Channel Practices
4.6. Other Stormwater BMPs
5. Recommendations for Future Direction
- (a)
- The APM parameters were obtained from analyses of the long-term data on rainfall depth, duration and inter-event time. To make them more applicable, it is necessary to develop a comprehensive database of APM parameters describing rainfall characteristics in cities across the world, for the purpose of runoff control systems design;
- (b)
- Most rain-gauge stations, particularly in developing countries, record daily rainfall only. Urban catchments have shorter times of concentration, and studies in these parts of the world have to rely on rainfall disaggregation techniques, whereby daily rainfall is broken down to an hourly or even sub-hourly time scale, which may raise some reliability problems. There is a need for a database of finer-resolution rainfall data. The provision of a large network of hourly and sub-hourly rain-gauge data will not only be useful to urban hydrologists, but also to other professionals. It will also help in reducing the uncertainties caused by rainfall disaggregation. Another source of uncertainty is the spatial distribution of rain-gauge stations used to develop rainfall characteristics and APM parameters. Research is required into the effects of the spatial distribution of rain-gauge stations on the reliability of rainfall characteristics;
- (c)
- The APM parameters were derived based on minimum inter-event times of 2 h, 6 h, 12 h and 24 h. In the case of small urban catchments, with faster concentration, it is recommended that a database of APM parameters based on a smaller discretized inter-event time, such as 5 min, 15 min, 30 min or 1 h, be developed. This requires the archiving of rainfall data at a sub-hourly resolution, which could then be used to develop its own database;
- (d)
- There is uncertainty about the inter-event time value to be used in rainfall event aggregation from a continuous time series. This calls for further research on its reliability;
- (e)
- The APMs are mostly based on the exponential distribution of rainfall characteristics. Rainfall characteristics were also found to follow other distributions, such as Gamma, Weibull, and log-normal. A distribution fit test for other PDFs needs to be undertaken in different climates;
- (f)
- A decision support system that incorporates meteorological, catchment and runoff control systems’ characteristics altogether needs to be developed, which can then eventually be used in the design and real-time control of these systems;
- (g)
- The design of some systems, such as rainwater tanks, involves the consideration of rainfall variability vis-à-vis water demand and the cost of municipal water consumption. Likewise, designing detention ponds for runoff quantity and pollution control involves conflicting objectives. There is a need for studies that embed APMs into optimization techniques so as to derive optimum benefits from the runoff control systems at the least cost;
- (h)
- Climate change is known to affect the design of stormwater conveyance and storage systems. There is a research gap regarding the effect of climate change on runoff control systems designed using APMs. The impact of climate change on the reliability of the systems needs to be investigated, so as to ensure their design functions are met;
- (i)
- There is a research gap regarding the APMs related to the runoff reduction efficiency and pollution control performance of vegetated open channel technologies, such as swales, grass channel, etc.;
- (j)
- Different runoff control systems have been reviewed in this paper. Some systems may be more suitable to specific climates. There is a research gap in the determination of the best system for each specific geographical area.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ACRU | Agricultural Catchments Research Unit |
| APM | Analytical Probabilistic Models |
| ASM | Analytical Stochastic Models |
| ASTORM | Analytical STORM |
| BMPs | Best Management Practices |
| CDF | Cumulative Distribution Function |
| COD | Chemical Oxygen Demand |
| DP | Dynamic Programming |
| EMC | Event Mean Concentration |
| EX-SUDS | Extended Sustainable Urban Drainage System |
| GA | Genetic Algorithm |
| HEC-HMS | Hydrologic Engineering Center’s Hydrologic Modeling System |
| IDF | Intensity–Duration–Frequency |
| MIDUSS | Microcomputer Interactive Design of Urban Stormwater Drainage Systems |
| NLP | Non-Linear Programming |
| NSE | Nash–Sutcliff Efficiency |
| OTTHYMO | Ottawa Hydrological Model |
| PC-SWMM | Personal Computer–Storm Water Management Model |
| Probability Density Function | |
| PSO | Particle Swam Optimization |
| RMSE | Root Mean Square Error |
| SCN-CN | Soil Conservation Service–Curve Number |
| STORM | Stormwater Management Software |
| SUDS | Sustainable Urban Drainage system |
| SWMM | Storm Water Management Model |
References
- Steg, R. Summary of the Stormwater Sources in the Flatheadd Lake Basin; Montana Operations Office, USEPA: Montana, WY, USA, 2010.
- McCuen, R.H. Hydrologic Analysis and Design; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Birkinshaw, S.J.; Kilsby, C.; O’donnell, G.; Quinn, P.; Adams, R.; Wilkinson, M.E. Stormwater Detention Ponds in Urban Catchments—Analysis and Validation of Performance of Ponds in the Ouseburn Catchment, Newcastle upon Tyne, UK. Water 2021, 13, 2521. [Google Scholar] [CrossRef]
- GSMM. General Application Structural Stormwater Controls. Georgia Stormwater Management Manual, Vol. 2. Atlanta Re-gional Commission, GA, 2016. Available online: http://www.georgiastormwater.com/ (accessed on 3 October 2022).
- Guo, Y. Hydrologic Design of Urban Flood Control Detention Ponds. J. Hydrol. Eng. 2001, 6, 472–479. [Google Scholar] [CrossRef]
- Methods, H.; Durrans, S.R. Stormwater Conveyance Modeling and Design; Bently Institute Press: Exton, PA, USA, 2001. [Google Scholar]
- Jia, H.; Hu, J.; Huang, T.; Chen, A.S.; Ma, Y. Urban Runoff Control and Sponge City Construction. Water 2022, 14, 1910. [Google Scholar] [CrossRef]
- Jeng, H.A.C.; Englande, A.J.; Bakeer, R.M.; Bradford, H.B. Impact of urban stormwater runoff on estuarine environmental quality. Estuar. Coast. Shelf Sci. 2005, 63, 513–526. [Google Scholar] [CrossRef]
- Todeschini, S. Hydrologic and Environmental Impacts of Imperviousness in an Industrial Catchment of Northern Italy. J. Hydrol. Eng. 2016, 21, 05016013. [Google Scholar] [CrossRef]
- Schütte, S.; Schulze, R. Projected impacts of urbanisation on hydrological resource flows: A case study within the uMngeni Catchment, South Africa. J. Environ. Manag. 2017, 196, 527–543. [Google Scholar] [CrossRef] [PubMed]
- USEPA. Preliminary Data Summary of Urban Stormwater Best Management Practices; Report No EPA-821-R-99-012; United States Environmental Protection Agency: Washington, DC, USA, 1999.
- Sharifi, S.; Massoudieh, A.; Kayhanian, M. A Stochastic Stormwater Quality Volume-Sizing Method with First Flush Emphasis. Water Environ. Res. 2011, 83, 2025–2035. [Google Scholar] [CrossRef]
- Daly, E.; Deletic, A.; Hatt, B.E.; Fletcher, T.D. Modelling of stormwater biofilters under random hydrologic variability: A case study of a car park at Monash University, Victoria (Australia). Hydrol. Process. 2011, 26, 3416–3424. [Google Scholar] [CrossRef]
- Li, Y.; Babcock, R.W. Green roof hydrologic performance and modeling: A review. Water Sci. Technol. 2013, 69, 727–738. [Google Scholar] [CrossRef]
- Krasnogorskaya, N.; Longobardi, A.; Mobilia, M.; Khasanova, L.F.; Shchelchkova, A.I. Hydrological Modeling of Green Roofs Runoff by Nash Cascade Model. Open Civ. Eng. J. 2019, 13, 163–171. [Google Scholar] [CrossRef]
- Berndtsson, J.C. Green roof performance towards management of runoff water quantity and quality: A review. Ecol. Eng. 2010, 36, 351–360. [Google Scholar] [CrossRef]
- Qi, W.; Ma, C.; Xu, H.; Chen, Z.; Zhao, K.; Han, H. A review on applications of urban flood models in flood mitigation strategies. Nat. Hazards 2021, 108, 31–62. [Google Scholar] [CrossRef]
- Ellis, J. Sustainable surface water management and green infrastructure in UK urban catchment planning. J. Environ. Plan. Manag. 2013, 56, 24–41. [Google Scholar] [CrossRef]
- Maes, J. and Jacobs, S. Nature-based solutions for Europe’s sustainable development. Conserv. Lett. 2017, 10, 121–124. [Google Scholar] [CrossRef]
- O’Donnell, E.; Thorne, C.; Ahilan, S.; Arthur, S.; Birkinshaw, S.; Butler, D.; Dawson, D.; Everett, G.; Fenner, R.; Glenis, V.; et al. The blue-green path to urban flood resilience. Blue-Green Syst. 2019, 2, 28–45. [Google Scholar] [CrossRef]
- Yin, D.; Xu, C.; Jia, H.; Yang, Y.; Sun, C.; Wang, Q.; Liu, S. Sponge City Practices in China: From Pilot Exploration to Systemic Demonstration. Water 2022, 14, 1531. [Google Scholar] [CrossRef]
- Jia, H.; Wang, Z.; Zhen, X.; Clar, M.; Yu, S.L. China’s sponge city construction: A discussion on technical approaches. Front. Environ. Sci. Eng. 2017, 11, 18. [Google Scholar] [CrossRef]
- Debo, T.N.; Reese, A.J. Municipal Stormwater Management; Lewis Publishers: Boca Raton, FL, USA, 2003. [Google Scholar]
- Chen, J.; Adams, B.J. A derived probability distribution approach to stormwater quality modeling. Adv. Water Resour. 2007, 30, 80–100. [Google Scholar] [CrossRef]
- Adams, B.J.; Papa, F. Urban Stormwater Management Planning with Analytical Probabilistic Models; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Chen, J.; Adams, B.J. Development of analytical models for estimation of urban stormwater runoff. J. Hydrol. 2007, 336, 458–469. [Google Scholar] [CrossRef]
- Todeschini, S.; Papiri, S.; Ciaponi, C. Performance of stormwater detention tanks for urban drainage systems in northern Italy. J. Environ. Manag. 2012, 101, 33–45. [Google Scholar] [CrossRef]
- Mobley, J.T.; Culver, T.B. Design of outlet control structures for ecological detention ponds. J. Water Res. Plan. Manag. ASCE 2014, 140, 250–257. [Google Scholar] [CrossRef]
- Souza, F.P.; Costa, M.E.L.; Koide, S. Hydrological Modelling and Evaluation of Detention Ponds to Improve Urban Drainage System and Water Quality. Water 2019, 11, 1547. [Google Scholar] [CrossRef]
- Mielke, P.W.; Benjamin, J.R.; Cornell, C.A. Probability, Statistics and Decision for Civil Engineers. J. Am. Stat. Assoc. 1971, 66, 923. [Google Scholar] [CrossRef]
- Eagleson, P.S. Dynamics of flood frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]
- Adams, B.J.; Fraser, H.G.; Howard, C.D.D.; Hanafy, M.S. Meteorological Data Analysis for Drainage System Design. J. Environ. Eng. 1986, 112, 827–848. [Google Scholar] [CrossRef]
- Bacchi, B.; Balistrocchi, M.; Grossi, G. Proposal of a semi-probabilistic approach for storage facility design. Urban Water J. 2008, 5, 195–208. [Google Scholar] [CrossRef]
- Branham, T.L.; Behera, P.K. Development of a Rainfall Statistical Analysis Tool for Analytical Probabilistic Models for Urban Stormwater Management Analysis. In Proceedings of the World Environmental and Water Resources Congress, Providence, RI, USA, 16–20 May 2010. [Google Scholar] [CrossRef]
- Dan’azumi, S.; Shamsudin, S.; Aris, A. Development of analytical probabilistic model parameters for urban stormwater management. Sains Malays. 2013, 42, 325–332. [Google Scholar]
- Guo, Y.; Adams, B.J. Hydrologic analysis of urban catchment with event based probabilistic models, Runoff volume. Water Resour. Res. 1998, 34, 3421–3432. [Google Scholar] [CrossRef]
- Guo, Y.; Adams, B.J. Hydrologic analysis of urban catchment with event based probabilistic models, 2. Peak discharge rate. Water Resour. Res. 1998, 34, 3433–3443. [Google Scholar] [CrossRef]
- Chen, J.; Adams, B.J. Urban Storm Water Control Evaluation with Analytical Probabilistic Models. J. Water Resour. Plan. Manag. 2005, 131, 362–374. [Google Scholar] [CrossRef]
- Chen, J.; Adams, B.J. Analysis of storage facilities for urban stormwater quantity control. Adv. Water Resour. 2005, 28, 377–392. [Google Scholar] [CrossRef]
- Chen, J.; Adams, B.J. Analytical urban storm water quality models based on pollutant buildup and wash-off processes. J. Environ. Eng. ASCE 2006, 132, 1314–1330. [Google Scholar] [CrossRef]
- Chen, J.; Adams, B.J. Urban stormwater quality control analysis with detention ponds. Water Environ. Res. 2006, 78, 744–753. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Adams, B.J. An analytical probabilistic approach to sizing flood control detention facilities. Water Resour. Res. 1999, 35, 2457–2468. [Google Scholar] [CrossRef]
- Guo, Y.; Adams, B.J. Analysis of detention ponds for stormwater quality control. Water Resour. Res. 1999, 35, 2447–2456. [Google Scholar] [CrossRef]
- Li, J.Y.; Adams, B.J. Probabilistic Models for Analysis of Urban Runoff Control Systems. J. Environ. Eng. 2000, 126, 217–224. [Google Scholar] [CrossRef]
- Behera, P.K.; Adams, B.J.; Li, J.Y. Runoff Quality Analysis of Urban Catchments with Analytical Probabilistic Models. J. Water Resour. Plan. Manag. 2006, 132, 4–14. [Google Scholar] [CrossRef]
- Quader, A.; Guo, Y. Peak Discharge Estimation Using Analytical Probabilistic and Design Storm Approaches. J. Hydrol. Eng. 2006, 11, 46–54. [Google Scholar] [CrossRef]
- Hassini, S.; Guo, Y. Exponentiality Test Procedures for Large Samples of Rainfall Event Characteristics. J. Hydrol. Eng. 2016, 21, 04016003. [Google Scholar] [CrossRef]
- Balistrocchi, M.; Grossi, G.; Bacchi, B. An analytical probabilistic model of the quality efficiency of a sewer tank. Water Resour. Res. 2009, 45, W12420. [Google Scholar] [CrossRef]
- Palynchuk, B.; Guo, Y. Threshold analysis of rainstorm depth and duration statistics at Toronto, Canada. J. Hydrol. 2008, 348, 535–545. [Google Scholar] [CrossRef]
- Andrés-Doménech, I.; Montanari, A.; Marco, J.B. Stochastic rainfall analysis for storm tank performance evaluation. Hydrol. Earth Syst. Sci. 2010, 14, 1221–1232. [Google Scholar] [CrossRef]
- Szeląg, B.; Suligowski, R.; Studziński, J.; De Paola, F. Application of logistic regression to simulate the influence of rainfall genesis on storm overflow operations: A probabilistic approach. Hydrol. Earth Syst. Sci. 2020, 24, 595–614. [Google Scholar] [CrossRef]
- Lee, M.; An, H.; Jeon, S.; Kim, S.; Jung, K.; Park, D. Development of an analytical probabilistic model to estimate runoff event volumes in South Korea. J. Hydrol. 2022, 612, 128129. [Google Scholar] [CrossRef]
- Kim, S.; Han, S. Urban Stormwater Capture Curve Using Three-Parameter Mixed Exponential Probability Density Function and NRCS Runoff Curve Number Method. Water Environ. Res. 2010, 82, 43–50. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, S.; Baetz, B.W. Probabilistic rainfall-runoff transformation considering both infiltration and saturation excess runoff generation processes. Water Resour. Res. 2012, 48, W06513. [Google Scholar] [CrossRef]
- Hassini, S.; Guo, Y. Derived flood frequency distributions considering individual event hydrograph shapes. J. Hydrol. 2017, 547, 296–308. [Google Scholar] [CrossRef]
- Hassini, S.; Guo, Y. Analytical Hydrological Model for the Planning and Design of Low-Impact Development Practices. In Recent Advances in Environmental Science from the Euro-Mediterranean and Surrounding Regions, 2nd ed.; EMCEI 2019. Environmental Science and Engineering; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Hassini, S.; Guo, Y. Analytical Derivation of Urban Flood Frequency Models Accounting Saturation-Excess Runoff Generation. J. Hydrol. 2020, 584, 124713. [Google Scholar] [CrossRef]
- Hassini, S.; Guo, Y. Analytical Derivation of Urban Runoff-Volume Frequency Models. J. Sustain. Water Built Environ. 2022, 8, 04021022. [Google Scholar] [CrossRef]
- Guo, Y.; Zhuge, Z. Analytical probabilistic flood routing for urban stormwater management purposes. Can. J. Civ. Eng. 2008, 35, 487–499. [Google Scholar] [CrossRef]
- Guo, Y.; Hansen, D.; Li, C. Probabilistic approach to estimating the effects of channel reaches on flood frequencies. Water Resour. Res. 2009, 45, W08404. [Google Scholar] [CrossRef]
- Guo, Y.; Markus, M. Analytical Probabilistic Approach for Estimating Design Flood Peaks of Small Watersheds. J. Hydrol. Eng. 2011, 16, 847–857. [Google Scholar] [CrossRef]
- Guo, Y.; Dai, J. Expanded analytical probabilistic stormwater models for use in watershed and master drainage planning. Can. J. Civ. Eng. 2009, 36, 933–943. [Google Scholar] [CrossRef]
- Shishegar, S.; Duchesne, S.; Pelletier, G. Optimization methods applied to stormwater management problems: A review. Urban Water J. 2018, 15, 276–286. [Google Scholar] [CrossRef]
- Gayer, J. Managing Urban Runoff in the Light of Integrated Water Resources Management. Ph.D. Thesis, Faculty of Water Management and Melioration, Corvinus University of Budapest, Budapest, Hungary, 2004. [Google Scholar]
- Drake, J.; Young, D.; McIntosh, N. Performance of an Underground Stormwater Detention Chamber and Comparison with Stormwater Management Ponds. Water 2016, 8, 211. [Google Scholar] [CrossRef]
- Chin, D. Water Resources Engineering; Prentice Hall: Hoboken, NJ, USA, 2006. [Google Scholar]
- Shishegar, S.; Duchesne, S.; Pelletier, G. An integrated optimization and rule-based approach for predictive real time control of urban stormwater management systems. J. Hydrol. 2019, 577, 124000. [Google Scholar] [CrossRef]
- Hogan, D.M.; Walbridge, M.R. Best Management Practices for Nutrient and Sediment Retention in Urban Stormwater Runoff. J. Environ. Qual. 2007, 36, 386–395. [Google Scholar] [CrossRef]
- Papa, F.; Adams, B.J.; Guo, Y. Detention time selection for stormwater quality control ponds. Can. J. Civ. Eng. 1999, 26, 72–82. [Google Scholar] [CrossRef]
- Wang, G.-T.; Chen, S.; Barber, M.E.; Yonge, D.R. Modeling Flow and Pollutant Removal of Wet Detention Pond Treating Stormwater Runoff. J. Environ. Eng. 2004, 130, 1315–1321. [Google Scholar] [CrossRef]
- Papa, F.; Adams, B.J.; Bryant, G.J. Models for Wwater Qquality Ccontrol by Sstonnwater Pponds. J. Water Manag. Model. 1997, 5, R195-01. [Google Scholar] [CrossRef]
- Becciu, G.; Raimondi, A. Probabilistic analysis of spills from stormwater detention facilities. Urban Water II 2014, 139, 159–170. [Google Scholar] [CrossRef]
- Raimondi, A.; Becciu, G. On pre-filling probability of flood control detention facilities. Urban Water J. 2013, 12, 344–351. [Google Scholar] [CrossRef]
- Becciu, G.; Raimondi, A. Probabilistic Analysis of the Retention Time in Stormwater Detention Facilities. Procedia Eng. 2015, 119, 1299–1307. [Google Scholar] [CrossRef]
- Becciu, G.; Raimondi, A.; Brebbia, C. Probabilistic modeling of the efficiency of a stormwater detention facility. Int. J. Sustain. Dev. Plan. 2015, 10, 1–11. [Google Scholar] [CrossRef]
- Raimondi, A.; Di Chiano, M.G.; Marchioni, M.; Sanfilippo, U.; Becciu, G. Probabilistic modeling of sustainable urban drainage systems. Urban Ecosyst. 2022, 1–10. [Google Scholar] [CrossRef]
- Ross, S.M. Introduction to Probability Models; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Guo, Y.; Baetz, B.W. Sizing of Rainwater Storage Units for Green Building Applications. J. Hydrol. Eng. 2007, 12, 197–205. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y. Analytical Probabilistic Model for Evaluating the Hydrologic Performance of Green Roofs. J. Hydrol. Eng. 2013, 18, 19–28. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y. Explicit Equation for Estimating Storm-Water Capture Efficiency of Rain Gardens. J. Hydrol. Eng. 2013, 18, 1739–1748. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y. Stochastic analysis of storm water quality control detention ponds. J. Hydrol. 2019, 571, 573–584. [Google Scholar] [CrossRef]
- Parolari, A.J.; Pelrine, S.; Bartlett, M.S. Stochastic water balance dynamics of passive and controlled stormwater basins. Adv. Water Resour. 2018, 122, 328–339. [Google Scholar] [CrossRef]
- Becciu, G.; Raimondi, A. Factors affecting the pre-filling probability of water storage tanks. WIT Trans. Ecol. Environ. 2012, 164, 473–484. [Google Scholar] [CrossRef]
- De Paola, F.; Ranucci, A. Analysis of Spatial Variability for Stormwater Capture Tank Assessment. Irrig. Drain. 2012, 61, 682–690. [Google Scholar] [CrossRef]
- Papa, F.; Adams, B.J. Application of derived probability and dynamic programming techniques to planning regional storm-water management systems. Water Sci. Technol. 1997, 36, 227–234. [Google Scholar] [CrossRef]
- Shamsudin, S.; Dan’azumi, S.; Aris, A.; Yusop, Z. Optimum combination of pond volume and outlet capacity of a storm-water detention pond using particle swarm optimization. Urban Water J. 2014, 11, 127–136. [Google Scholar] [CrossRef]
- Dan’Azumi, S.; Shamsudin, S.; Aris, A. Optimization of pollution control performance of wet detention ponds in tropical urban catchments using particle swarm optimization. J. Hydroinform. 2012, 15, 529–539. [Google Scholar] [CrossRef]
- Behera, P.K.; Teegavarapu, R.S.V. Optimization of a Stormwater Quality Management Pond System. Water Resour. Manag. 2014, 29, 1083–1095. [Google Scholar] [CrossRef]
- Raimondi, A.; Becciu, G. Probabilistic Modeling of Rainwater Tanks. Procedia Eng. 2014, 89, 1493–1499. [Google Scholar] [CrossRef]
- Raimondi, A.; Becciu, G. Probabilistic Design of Multi-use Rainwater Tanks. Procedia Eng. 2014, 70, 1391–1400. [Google Scholar] [CrossRef]
- Becciu, G.; Raimondi, A.; Dresti, C. Semi-probabilistic design of rainwater tanks: A case study in Northern Italy. Urban Water J. 2016, 15, 192–199. [Google Scholar] [CrossRef]
- De Paola, F.; De Martino, F. Stormwater Tank Performance: Design and Management Criteria for Capture Tanks Using a Continuous Simulation and a Semi-Probabilistic Analytical Approach. Water 2013, 5, 1699–1711. [Google Scholar] [CrossRef]
- Kim, H.; Han, M.; Lee, J.Y. The application of an analytical probabilistic model for estimating the rainfall–runoff reductions achieved using a rainwater harvesting system. Sci. Total. Environ. 2012, 424, 213–218. [Google Scholar] [CrossRef] [PubMed]
- Di Chiano, M.G.; Marchioni, M.; Raimondi, A.; Sanfilippo, U.; Becciu, G. Probabilistic Approach to Tank Design in Rainwater Harvesting Systems. Hydrology 2023, 10, 59. [Google Scholar] [CrossRef]
- Guo, R.; Guo, Y. Stochastic modelling of the hydrologic operation of rainwater harvesting systems. J. Hydrol. 2018, 562, 30–39. [Google Scholar] [CrossRef]
- Pelak, N.; Porporato, A. Sizing a rainwater harvesting cistern by minimizing costs. J. Hydrol. 2016, 541, 1340–1347. [Google Scholar] [CrossRef]
- Sim, I.; Kim, S. Probabilistic solution to rainwater harvesting system and its impact on climate change. Desalination Water Treat. 2020, 200, 407–421. [Google Scholar] [CrossRef]
- Cheng, G.; Huang, G.; Guo, Y.; Baetz, B.W.; Dong, C. Stochastic Rainwater Harvesting System Modeling Under Random Rainfall Features and Variable Water Demands. Water Resour. Res. 2021, 57, e2021WR029731. [Google Scholar] [CrossRef]
- USEPA. Using Green Roofs to Reduce Heat Islands. 2023. Available online: https://www.epa.gov/heatislands/using-green-roofs-reduce-heat-islands (accessed on 14 March 2023).
- Raimondi, A.; Becciu, G. Performance of Green Roofs for Rainwater Control. Water Resour. Manag. 2020, 35, 99–111. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, S.; Liu, S. Runoff Reduction Capabilities and Irrigation Requirements of Green Roofs. Water Resour. Manag. 2014, 28, 1363–1378. [Google Scholar] [CrossRef]
- Guo, Y. Stochastic Analysis of Hydrologic Operation of Green Roofs. J. Hydrol. Eng. 2016, 21, 04016016. [Google Scholar] [CrossRef]
- Raimondi, A.; Marchioni, M.; Sanfilippo, U.; Stroppa, F.F.; Becciu, G. Probabilistic estimation of runoff from green roofs. Int. J. Comput. Methods Exp. Meas. 2022, 10, 13–25. [Google Scholar] [CrossRef]
- Raimondi, A.; Marchioni, M.; Sanfilippo, U.; Becciu, G. Vegetation Survival in Green Roofs without Irrigation. Water 2021, 13, 136. [Google Scholar] [CrossRef]
- Guo, R.; Guo, Y.; Liu, S. Analytical Equations for Direct Quantification of Green Roofs’ Hydrologic Performance Statistics. J. Hydrol. Eng. 2022, 27, 04022003. [Google Scholar] [CrossRef]
- Raimondi, A.; Sanfilippo, U.; Marchioni, M.; Di Chiano, M.; Becciu, G. Influence of climatic parameters on the probabilistic design of green roofs. Sci. Total Environ. 2023, 865, 161291. [Google Scholar] [CrossRef]
- FHWA. Stormwater Best Management Practices in Ultra-Urban Setting: Selection and Monitoring. Washington DC, Federal Highway Administration, U.S. Department of Transportation, 2000. Available online: https://rosap.ntl.bts.gov/view/dot/25727. (accessed on 12 November 2022).
- Błażejewski, R.; Murat-Błażejewska, S. Analytical solutions of a routing problem for storm water in a detention basin. Hydro-Log. Sci. J. 2003, 48, 665–671. [Google Scholar] [CrossRef]
- Weiss, P.T.; Gulliver, J.; Erickson, A.J. Cost and Pollutant Removal of Storm-Water Treatment Practices. J. Water Resour. Plan. Manag. 2007, 133, 218–229. [Google Scholar] [CrossRef]
- VASM. Virginia Stormwater Handbook; Virginia Department of Conservation and Recreation, Division of Soil and Water Conservation: Richmond, VA, USA, 1999; Volume II. Available online: http://observatoriaigua.uib.es/repositori/suds_virginiab.pdf (accessed on 5 October 2022).
- Zhang, S.; Guo, Y. Stormwater Capture Efficiency of Bioretention Systems. Water Resour. Manag. 2013, 28, 149–168. [Google Scholar] [CrossRef]
- Guo, R.; Guo, Y.; Zhang, S.; Zhu, D.Z. A Tool for Water Balance Analysis of Bioretention Cells. J. Sustain. Water Built Environ. 2020, 6, 04020013. [Google Scholar] [CrossRef]
- Islam, A.; Hassini, S.; El-Dakhakhni, W. Resilience Quantification of Low-Impact Development Systems Using SWMM and a Probabilistic Approach. J. Sustain. Water Built Environ. 2022, 8, 04022013. [Google Scholar] [CrossRef]
- Fach, S.; Dierkes, C. On-site infiltration of road runoff using pervious pavements with subjacent infiltration trenches as source control strategy. Water Sci. Technol. 2011, 64, 1388–1397. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Gao, T. Analytical Equations for Estimating the Total Runoff Reduction Efficiency of Infiltration Trenches. J. Sustain. Water Built Environ. 2016, 2, 06016001. [Google Scholar] [CrossRef]
- Guo, R.; Guo, Y. Analytical Equations for Use in the Planning of Infiltration Facilities. J. Sustain. Water Built Environ. 2018, 4, 06018001. [Google Scholar] [CrossRef]
- Fadhelab, S.; Rico, M.A.; Hana, D. Sensitivity of peak flow to the change of rainfall temporal pattern due to warmer climate. J. Hydrol. 2018, 560, 546–559. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y. Proper Sizing of Infiltration Trenches Using Closed-Form Analytical Equations. Water Resour. Manag. 2020, 34, 1–13. [Google Scholar] [CrossRef]
- Butler, D.; Davies, J.W. Urban Drainage, 2nd ed.; Spon Press, Tailor & Francis Group: New York, NY, USA, 2004. [Google Scholar]
- Zhang, S.; Guo, Y. An analytical equation for evaluating the stormwater capture efficiency of permeable pavement systems. J. Irrig. Drain. Eng. ASCE 2015, 131, 06014004-1–06014004-9. [Google Scholar]
- Guo, R.; Guo, Y.; Wang, J. Stormwater capture and antecedent moisture characteristics of permeable pavements. Hydrol. Process. 2018, 32, 2708–2720. [Google Scholar] [CrossRef]
- Zeng, J.; Huang, G.; Mai, Y.; Chen, W. Optimizing the cost-effectiveness of low impact development (LID) practices using an analytical probabilistic approach. Urban Water J. 2020, 17, 136–143. [Google Scholar] [CrossRef]
- SMRC. Assorted Fact Sheets: Stormwater Management Practices; Stormwater Manager’s Resource Center, Center for Watershed Protection: Ellicot City, MD, USA, 2020; Available online: http://www.stormwatercenter.net (accessed on 5 July 2020).
- USEPA. Free Water Surface Wetlands for Wastewater Treatments: A Technology Assessment; EPA 832 S 99 032; Office of Water, USEPA: Washington, DC, USA, 1999. Available online: http://www.epa.gov/owow/wetlands/pdf/FW_Surface_Wetlands.pdf. (accessed on 9 August 2020).
- AWWA. National Water Quality Management Strategy: Australian Guidelines for Urban Stormwater Management; Australia and New-Zealand; Australian Water Works Association: St. Leonards, NSW, Australia, 2000. [Google Scholar]
- Perez-Pedini, C.; Limbrunner, J.F.; Vogel, R.M. Optimal Location of Infiltration-Based Best Management Practices for Storm Water Management. J. Water Resour. Plan. Manag. 2005, 131, 441–448. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldrees, A.; Dan’azumi, S. Application of Analytical Probabilistic Models in Urban Runoff Control Systems’ Planning and Design: A Review. Water 2023, 15, 1640. https://doi.org/10.3390/w15091640
Aldrees A, Dan’azumi S. Application of Analytical Probabilistic Models in Urban Runoff Control Systems’ Planning and Design: A Review. Water. 2023; 15(9):1640. https://doi.org/10.3390/w15091640
Chicago/Turabian StyleAldrees, Ali, and Salisu Dan’azumi. 2023. "Application of Analytical Probabilistic Models in Urban Runoff Control Systems’ Planning and Design: A Review" Water 15, no. 9: 1640. https://doi.org/10.3390/w15091640





