Distrust Behavior in Social Network Large-Scale Group Decision Making and Its Application in Water Pollution Management
Abstract
:1. Introduction
- (1)
- The AHC method is utilized to decrease the complexity of LSGDM-SN with the FPR, in which both the trust relationships and distrust relationships among experts are incorporated into the clustering method. Then, the concept of preference similarity, trust similarity, and distrust similarity are proposed to compute the degree of overall similarity among experts. Meanwhile, the algorithm for the AHC of LSGDM-SN is presented.
- (2)
- Consensus feedback based on distrust behavior and social network analysis (SNA) is presented to encourage the subset to modify its FPR based on different distrust types. In the identification process, both the distrust score and the degree of difference are incorporated to measure the distrust degree of the subset. Based on the cases of distrust behaviors, two pieces of feedback advice are provided to the subset to adjust its FPR.
- (3)
- A score function of FPR is designed to choose the best alternative for water pollution management. By calculating the final score of the collective FPR, we rank all alternatives. Then, the one with the highest score is selected as the best solution for water pollution management. Finally, a framework for the proposed LSGDM-SN considering distrust behavior is depicted to visualize the decision process.
2. Preliminaries
2.1. Fuzzy Preference Relation
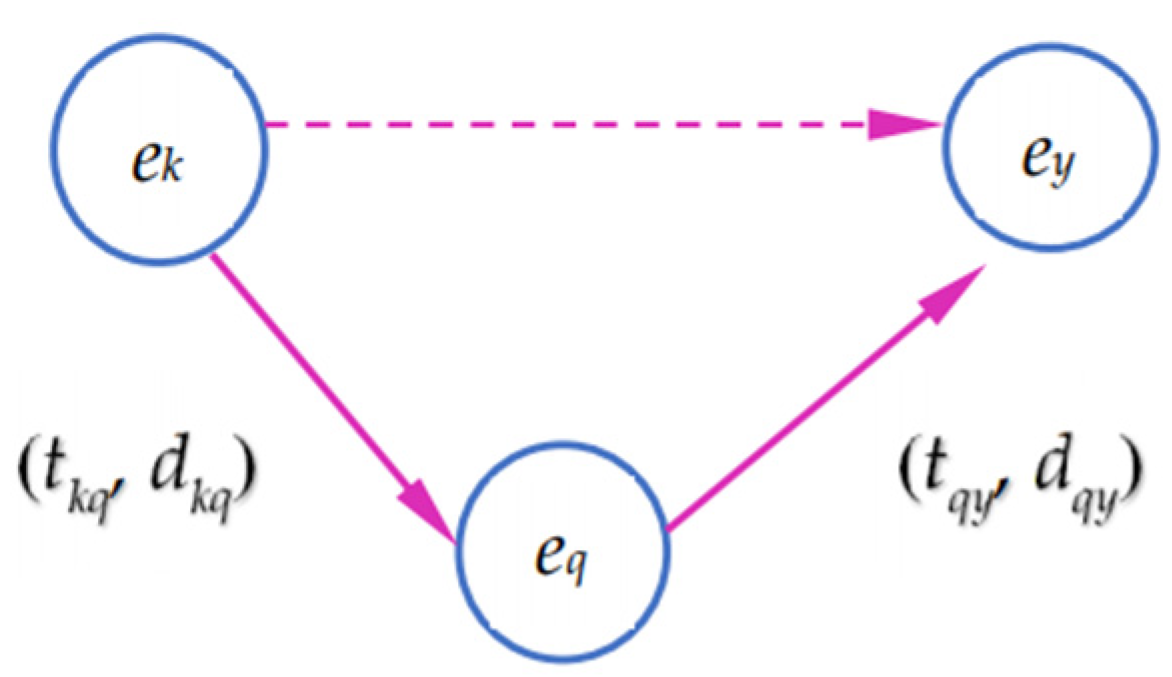
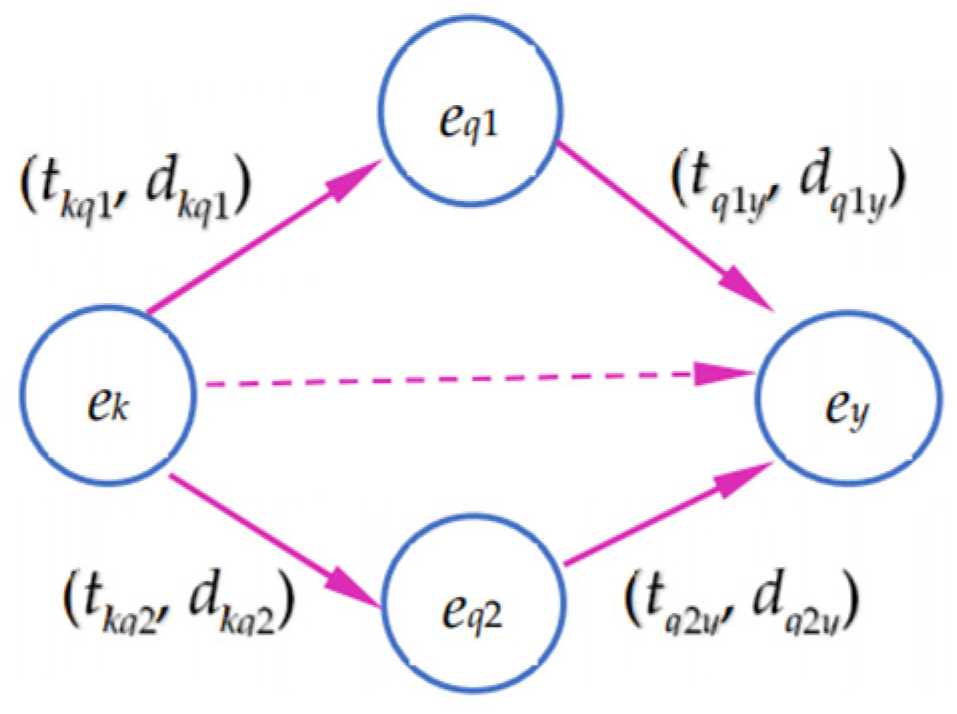
2.2. SNA
- (1)
- Socio-matrix: The matrix G = (gkq)m×m is utilized to present the relationships data among experts. If expert ek has no relationship with eq, the value of gkq is equal to 0. Otherwise, the value of gkq is 1 if there is an existing relationship between ek and eq.
- (2)
- Graph: Social networks can also be represented by a graph, where the points are connected by straight lines. In the network diagram, ek→eq indicates that there is a direct relationship from ek to eq.
- (3)
- Algebraic: The algebraic can denote the social relationships among experts and the relationship combinations.
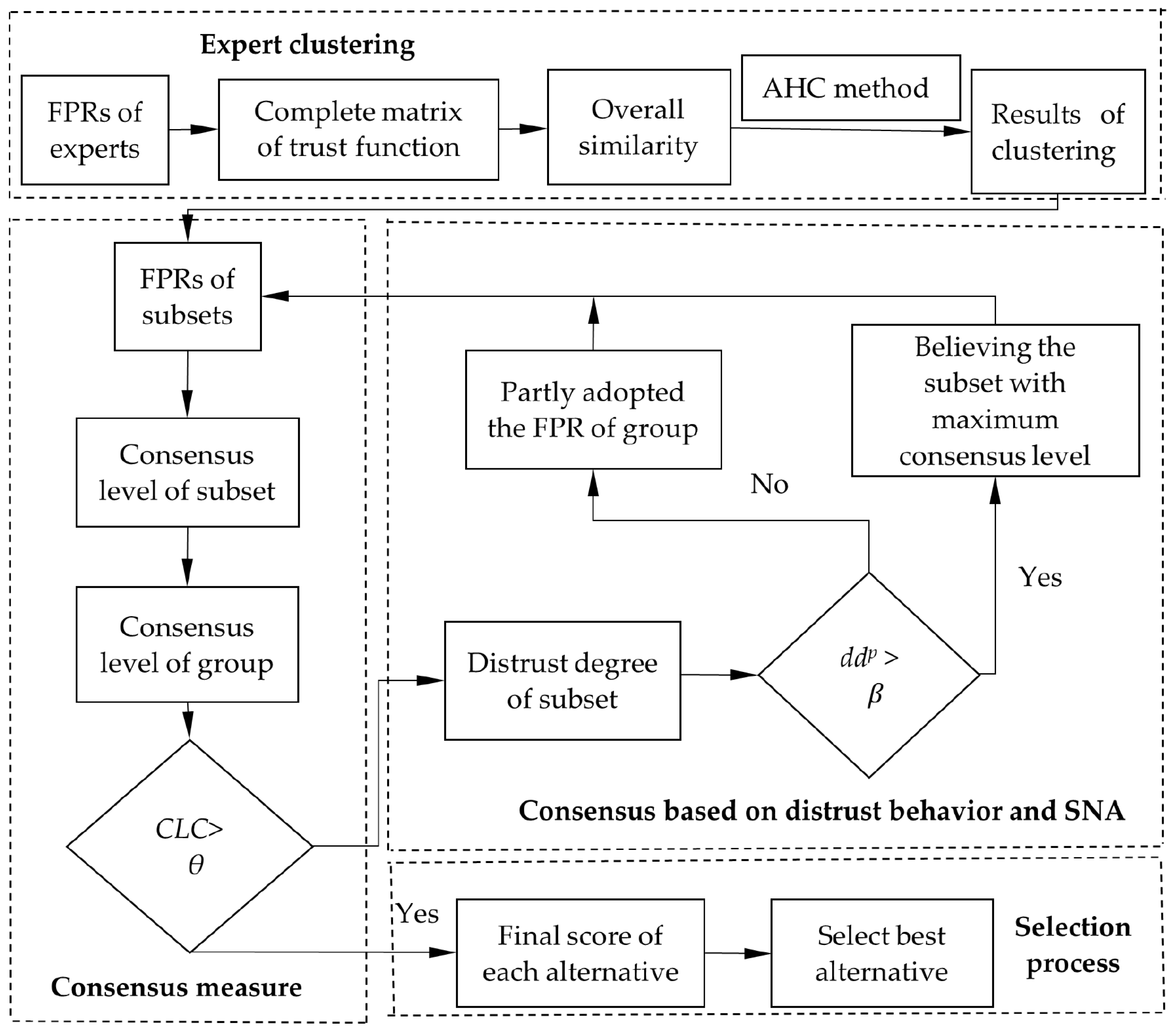
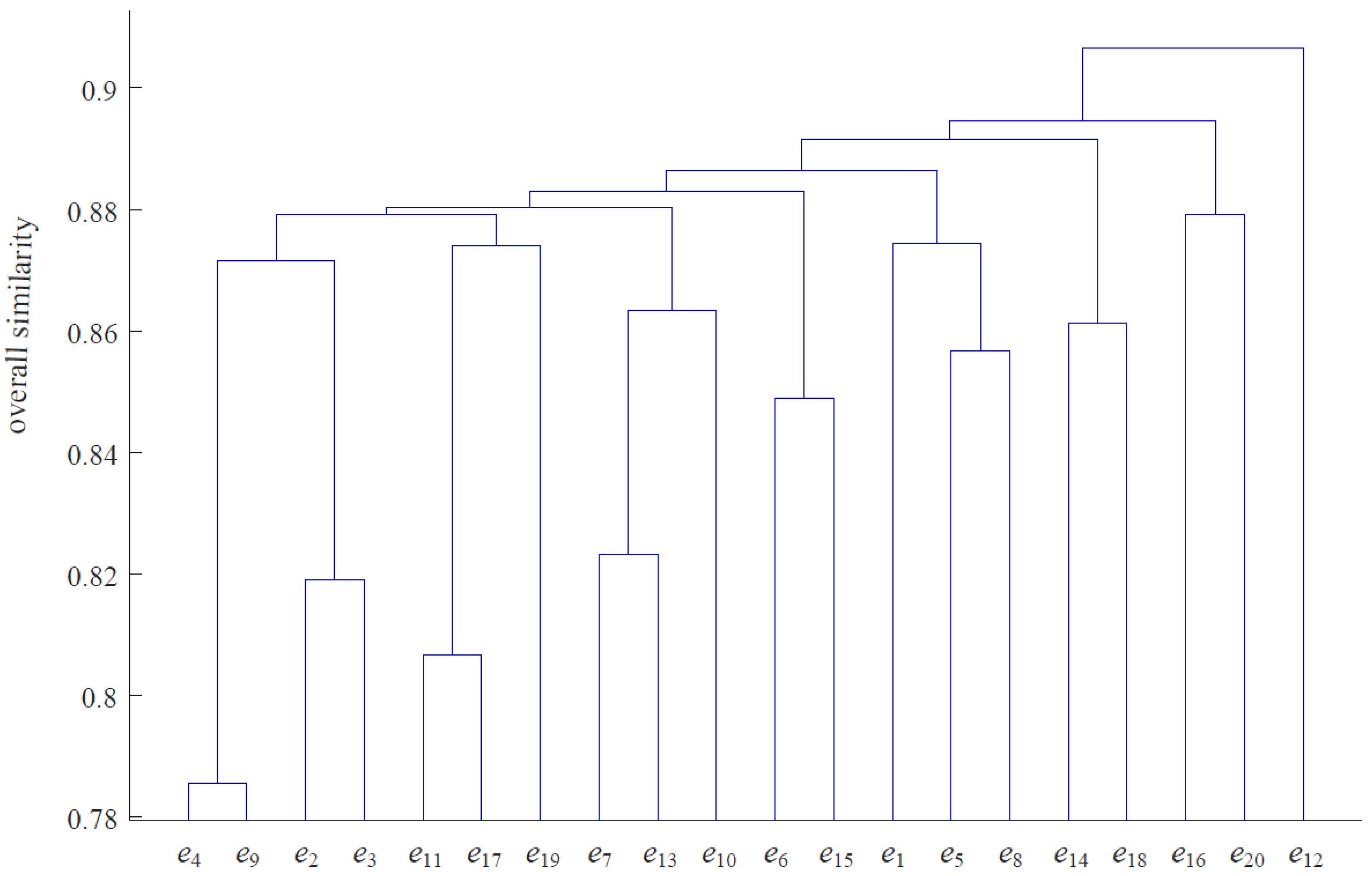
3. Large-Scale Expert Clustering Based on AHC Approach
| Algorithm 1. The detailed AHC method. |
| Input. Output: subsets su1, …, sup, …, suυ. Step 1: Regard each expert ek (k =1, …, m) as one initial subset. Step 2: Calculating the values of pskq, tskq, dskq and oskq for each initial subset based on Equations (8)–(11). Step 3: Selecting the maximum oskq, then classify initial subsets eq and ek into one new subset. Step 4: Deleting subsets eq and ek in Step 3, the overall similarity is recalculated based on Definition 9. Step 5: Steps 3 and 4 are repeated constantly. If all subsets are merged into one subset, the process is ended. Step 6: Setting the number of subsets, output the clustering result su1, …, sup, …, suυ. |
4. Consensus of LSGDM-SN Based on Distrust Behavior and SNA
4.1. Consensus Measure
4.2. Consensus Feedback Based on Distrust Behavior and SNA
4.3. Selection Process
4.4. The Proposed Framework of LSGDM-SN
5. Case Study
6. Comparative Analysis and Discussion
6.1. The Impact of Distrust Behavior on Alternative Ranking
6.2. The Impact of Weight Determination on Decision Result
6.3. Sensitivity Analysis of Consensus Threshold
6.4. The Comparison with Other Related Studies
7. Conclusions
- (1)
- A novel AHC method considering preference similarity and social similarity is proposed to decrease the complexity of LSGDM-SN with FPRs. Several definitions, including preference similarity, trust similarity, and distrust similarity, are proposed to compute the degree of overall similarity among experts. Subsequently, the AHC algorithm dealing with the LSGDM-SN problem is designed.
- (2)
- The consensus feedback for detecting and managing distrust behavior is presented, which encourages the subset to modify its FPR based on different distrust types. To identify the distrust behavior, both the distrust score and the degree of difference are incorporated to measure the distrust degree of the subset. Based on the value of distrust degree, two pieces of modification advice are provided to subset to modify it FPR.
- (3)
- A score function is defined to derive the alternatives ranking in water pollution management. After computing the values of scores for all alternatives, we rank them. The optimal alternative is obtained based on the maximum value score. Finally, the LSGDM-SN framework considering distrust behavior is described to visualize the decision process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, P.D.; Li, Y.Y.; Wang, P. Opinion dynamics and minimum adjustment-driven consensus model for multi-criteria large-scale group decision making under a novel social trust propagation mechanism. IEEE Trans. Fuzzy Syst. 2023, 31, 307–321. [Google Scholar] [CrossRef]
- Liang, X.; Guo, J.; Liu, P.D. A large-scale group decision-making model with no consensus threshold based on social network analysis. Inf. Sci. 2022, 612, 361–383. [Google Scholar] [CrossRef]
- Li, Y.H.; Kou, G.; Li, G.X.; Peng, Y. Consensus reaching process in large-scale group decision making based on bounded confidence and social network. Eur. J. Oper. Res. 2022, 303, 790–802. [Google Scholar] [CrossRef]
- Meng, F.Y.; Chen, B.C.; Wang, Z.R. A trust-based large-scale group decision making consensus reaching framework for intercity railway public-private partnership model selection. Neural Comput. Appl. 2022, 34, 19091–19115. [Google Scholar] [CrossRef]
- Lu, Y.L.; Xu, Y.J.; Herrera-Viedma, E. Consensus progress for large-scale group decision making in social networks with incomplete probabilistic hesitant fuzzy information. Appl. Soft Comput. 2022, 126, 109249. [Google Scholar] [CrossRef]
- Bai, S.Z.; He, H.; Ge, M.K.; Yang, R.B.; Luo, D.; Bi, X.R. Large-scale group decision-making model with cooperative behavior based on social network analysis considering propagation of decision-makers’ preference. J. Math. 2022, 2022, 2842601. [Google Scholar] [CrossRef]
- Peng, J.J.; Chen, X.G.; Tian, C.; Zhang, Z.Q.; Song, H.Y.; Dong, F. Picture fuzzy large-scale group decision-making in a trust- relationship-based social network environment. Inf. Sci. 2022, 608, 1675–1701. [Google Scholar] [CrossRef]
- Zhu, Y.C.; Xu, X.H.; Pan, B. A method for the dynamic collaboration of the public and experts in large-scale group emergency decision-making: Using social media data to evaluate the decision-making quality. Comput. Ind. Eng. 2023, 176, 108943. [Google Scholar] [CrossRef]
- Sun, X.L.; Zhu, J.J. Large-scale group classification decision making method and its application with trust-interest dual factors in social network. Appl. Soft Comput. 2023, 133, 109890. [Google Scholar] [CrossRef]
- Wang, Y.M.; He, S.F.; Zamora, D.G.; Pan, X.H.; Martínez, L. A large scale group three-way decision-based consensus model for site selection of new energy vehicle charging stations. Expert Syst. Appl. 2023, 214, 119107. [Google Scholar] [CrossRef]
- Pan, X.H.; Wang, Y.M.; He, S.F.; Chin, K.S. A dynamic programming algorithm based clustering model and its application to interval type-2 fuzzy large-scale group decision-making problem. IEEE Trans. Fuzzy Syst. 2022, 30, 108–120. [Google Scholar] [CrossRef]
- Yu, S.M.; Du, Z.J.; Zhang, X.Y.; Luo, H.Y.; Lin, X.D. Trust cop-kmeans clustering analysis and minimum-cost consensus model considering voluntary trust loss in social network large-scale decision-making. IEEE Trans. Fuzzy Syst. 2022, 30, 2634–2648. [Google Scholar] [CrossRef]
- Wu, X.L.; Liao, H.C.; Tang, M. Decision making towards large-scale alternatives from multiple online platforms by a multivariate time-series-based method. Expert Syst. Appl. 2023, 212, 118838. [Google Scholar] [CrossRef]
- Meng, F.Y.; Zhao, D.Y.; Tan, C.Q.; Li, Z.J. Ordinal-cardinal consensus analysis for large-scale group decision making with uncertain self-confidence. Inf. Fusion 2023, 93, 344–362. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.J.; Gong, Z.W.; Herrera, F. Democratic consensus reaching process for multi-person multi-criteria large scale decision making considering participants’ individual attributes and concerns. Inf. Fusion 2022, 77, 220–232. [Google Scholar] [CrossRef]
- Tang, M.; Liao, H.C.; Fujita, H. Delegation mechanism-based large-scale group decision making with heterogeneous experts and overlapping communities. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3542–3555. [Google Scholar] [CrossRef]
- Xiong, K.; Dong, Y.C.; Zha, Q.B. A large-scale consensus model to manage non-cooperative behaviors in group decision making: A perspective based on historical data. Expert Syst. Appl. 2023, 214, 119163. [Google Scholar] [CrossRef]
- Wu, P.; Li, F.G.; Zhao, J.; Zhou, L.G.; Martfnez, L. Consensus reaching process with multiobjective optimization for large-scale group decision making with cooperative game. IEEE Trans. Fuzzy Syst. 2023, 31, 293–306. [Google Scholar] [CrossRef]
- Yao, S.B.; Gu, M. An influence network-based consensus model for large-scale group decision making with linguistic information. Int. J. Comput. Int. Sys. 2022, 15, 3. [Google Scholar] [CrossRef]
- Gai, T.T.; Cao, M.S.; Chiclana, F.; Zhang, Z.; Dong, Y.C.; Herrera-Viedma, E.; Wu, J. Consensus-trust driven bidirectional feedback mechanism for improving consensus in social network large-group decision making. Group Decis. Negot. 2023, 32, 45–74. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Zhou, M.; Liu, X.B.; Cheng, B.Y.; Herrera-Viedma, E. Consensus reaching mechanism with parallel dynamic feedback strategy for large-scale group decision making under social network analysis. Comput. Ind. Eng. 2022, 174, 108818. [Google Scholar] [CrossRef]
- Liu, W.Q.; Zhu, J.J.; Chiclana, F. Large-scale group consensus hybrid strategies with three-dimensional clustering optimisation based on normal cloud models. Inf. Fusion 2023, 94, 66–91. [Google Scholar] [CrossRef]
- Wang, S.; Wu, J.; Chiclana, F.; Sun, Q.; Herrera-Viedma, E. Two stage feedback mechanism with different power structures for consensus in large-scale group decision-making. IEEE Trans. Fuzzy Syst. 2022, 30, 4177–4189. [Google Scholar] [CrossRef]
- Dong, Y.C.; Zha, Q.B.; Zhang, H.J.; Herrera, F. Consensus reaching and strategic manipulation in group decision making with trust relationships. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6304–6318. [Google Scholar] [CrossRef]
- Wu, J.; Cao, M.S.; Chiclana, F.; Dong, Y.C.; Herrera-Viedma, E. An optimal feedback model to prevent manipulation behavior in consensus under social network group decision making. IEEE Trans. Fuzzy Syst. 2021, 29, 1750–1763. [Google Scholar] [CrossRef]
- Xu, X.Z.; Zhang, Y.; Wu, L. The layout and the spatio-temporal evolution of water-polluting enterprises in Zhejiang under regulation. Front. Environ. Sci. 2023, 11, 1121598. [Google Scholar] [CrossRef]
- Xiao, J.; Gao, D.D.; Zhang, H.; Shi, H.L.; Chen, Q.; Li, H.F.; Ren, X.N.; Chen, Q.S. Water quality assessment and pollution source apportionment using multivariate statistical techniques: A case study of the Laixi River Basin, China. Environ. Monit. Assess. 2023, 195, 287. [Google Scholar] [CrossRef]
- Zhang, M.H.; Wang, L.; Huang, X.D.; Zhang, X.F. Pollution contribution response in governance and potential pollution factors in Licun river. Sustainability 2022, 14, 3547. [Google Scholar] [CrossRef]
- Pan, D.; Fan, W.C. Benefits of environmental information disclosure in managing water pollution: Evidence from a quasi-natural experiment in China. Environ. Sci. Pollut. Res. 2021, 28, 14764–14781. [Google Scholar] [CrossRef]
- Han, H.Y.; Xia, S.; Jiang, Y. Challenging issues over sustainable water management in coastal area from China. J. Coast Res. 2018, 83, 946–958. [Google Scholar]
- Wang, Y.J.; Zhang, M.; Yang, C.G.; He, Y.; Ju, M.T. Regional water pollution management pathways and effects under strengthened policy constraints: The case of Tianjin, China. Environ. Sci. Pollut. Res. 2022, 29, 77026–77046. [Google Scholar] [CrossRef]
- Tanino, T. Fuzzy preference orderings in group decision making. Fuzzy Sets Syst. 1984, 12, 117–131. [Google Scholar] [CrossRef]
- Tanino, T. Fuzzy preference relations in group decision making. In Non-Conventional Preference Relations in Decision Making; Kacprzyk, J., Roubens, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; Volume 301, pp. 54–71. [Google Scholar]
- Ma, J.; Fan, Z.P.; Jiang, Y.P.; Mao, J.Y.; Ma, L. A method for repairing the inconsistency of fuzzy preference relations. Fuzzy Sets Syst. 2006, 157, 20–33. [Google Scholar] [CrossRef]
- Xu, Y.J.; Liu, X.; Wang, H.M. The additive consistency measure of fuzzy reciprocal preference relations. Int. J. Mach. Learn. Cybern. 2018, 9, 1141–1152. [Google Scholar] [CrossRef]
- Wu, J.; Xiong, R.Y.; Chiclana, F. Uninorm trust propagation and aggregation methods for group decision making in social network with four tuple information. Knowl.-Based Syst. 2016, 96, 29–39. [Google Scholar] [CrossRef]
- Baraldi, A.; Blonda, P. A survey of fuzzy clustering algorithms for pattern recognition. I. IEEE Trans. Syst. Man Cybern. Part B 1999, 29, 778–785. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.J.; Yu, S.M.; Luo, H.Y.; Lin, X.D. Consensus convergence in large-group social network environment: Coordination between trust relationship and opinion similarity. Knowl.-Based Syst. 2021, 217, 106828. [Google Scholar] [CrossRef]
- Li, S.L.; Wei, C.P. A two-stage dynamic influence model-achieving decision-making consensus within large scale groups operating with incomplete information. Knowl.-Based Syst. 2020, 189, 105132. [Google Scholar] [CrossRef]
- Lu, Y.L.; Xu, Y.J.; Herrera-Viedma, E.; Han, Y.F. Consensus of large-scale group decision making in social network: The minimum cost model based on robust optimization. Inf. Sci. 2021, 547, 910–930. [Google Scholar] [CrossRef]
- Ahmed, D.; Dai, B.X.; Khalil, A.M. Possibility Fermatean fuzzy soft set and its application in decision-making. J. Intell. Fuzzy Syst. 2023, 44, 1565–1574. [Google Scholar] [CrossRef]
- Mishra, A.R.; Chen, S.M.; Rani, P. Multicriteria decision making based on novel score function of Fermatean fuzzy numbers, the CRITIC method, and the GLDS method. Inf. Sci. 2023, 623, 915–931. [Google Scholar] [CrossRef]
- Riaz, M.; Hashmi, M.R.; Karaaslan, F.; Sezgin, A.; Shamiri, M.M.A.A.; Khalaf, M.M. Emerging trends in social networking systems and generation gap with neutrosophic crisp soft mapping. CMES-Comput. Model. Eng. Sci. 2023, 136, 1759–1783. [Google Scholar] [CrossRef]
- Malik, A.S.; Yasin, S.A.; Mahmood, A. The demographic differences in perception of university students towards the use of social networking sites as a smart e-learning system. Ann. Hum. Soc. Sci. 2023, 4, 34–45. [Google Scholar]
| Socio-Matrix | Graph | Algebraic |
|---|---|---|
| G = | 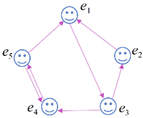 | e1Be3 e2Be1 e3Be2, e3Be4 e1Be5 e5Be4, e5Be1 |
| Experts | FPR | Experts | FPR |
|---|---|---|---|
| e1 | e2 | ||
| e3 | e4 | ||
| e5 | e6 | ||
| e7 | e8 | ||
| e9 | e10 | ||
| e11 | e12 | ||
| e13 | e14 | ||
| e15 | e16 | ||
| e17 | e18 | ||
| e19 | e20 |
| e1 | e2 | e3 | … | e18 | e19 | e20 | |
|---|---|---|---|---|---|---|---|
| e1 | (1, 0) | (0.9, 0.3) | (0.8, 0.7) | (0.6, 1.0) | (-, -) | (-, -) | |
| e2 | (-, -) | (1, 0) | (0.8, 0.3) | (-, -) | (0.7, 0.9) | (-, -) | |
| e3 | (0.3, 0.3) | (0.1, 0.6) | (1, 0) | (0.8, 0.4) | (-, -) | (-, -) | |
| … | |||||||
| e18 | (-, -) | (-, -) | (-, -) | (1, 0) | (0.1, 0.1) | (0.8, 0.5) | |
| e19 | (-, -) | (-, -) | (0.7, 1.0) | (0.4, 0.9) | (1, 0) | (-, -) | |
| e20 | (-, -) | (0.7, 0.2) | (0.1, 0.7) | (0.3, 0.4) | (-, -) | (1, 0) |
| τ | CLC (τ) | sup,(τ) | sup,(τ) < β | FPR |
|---|---|---|---|---|
| 0 | 0.92 | su7,(0) | No | |
| 1 | 0.93 | su5,(0) | Yes | |
| 2 | 0.94 | su6,(0) | Yes | |
| 3 | 0.94 | su3,(0) | No | |
| 4 | 0.95 |
| Collective FPR | fs(xi) | Ranking of Alternatives |
|---|---|---|
| fs(x1) = 0.505 fs(x2) = 0.523 fs(x3) = 0.453 fs(x4) = 0.520 | x2 > ≻x4 > ≻x1 > ≻x3 |
| Consensus Iteration | fs(xi) | Ranking of Alternatives |
|---|---|---|
| 5 | fs(x1) = 0.511 fs(x2) = 0.519 fs(x3) = 0.451 fs(x4) = 0.518 | x2 > ≻x4 > ≻x1 > ≻x3 |
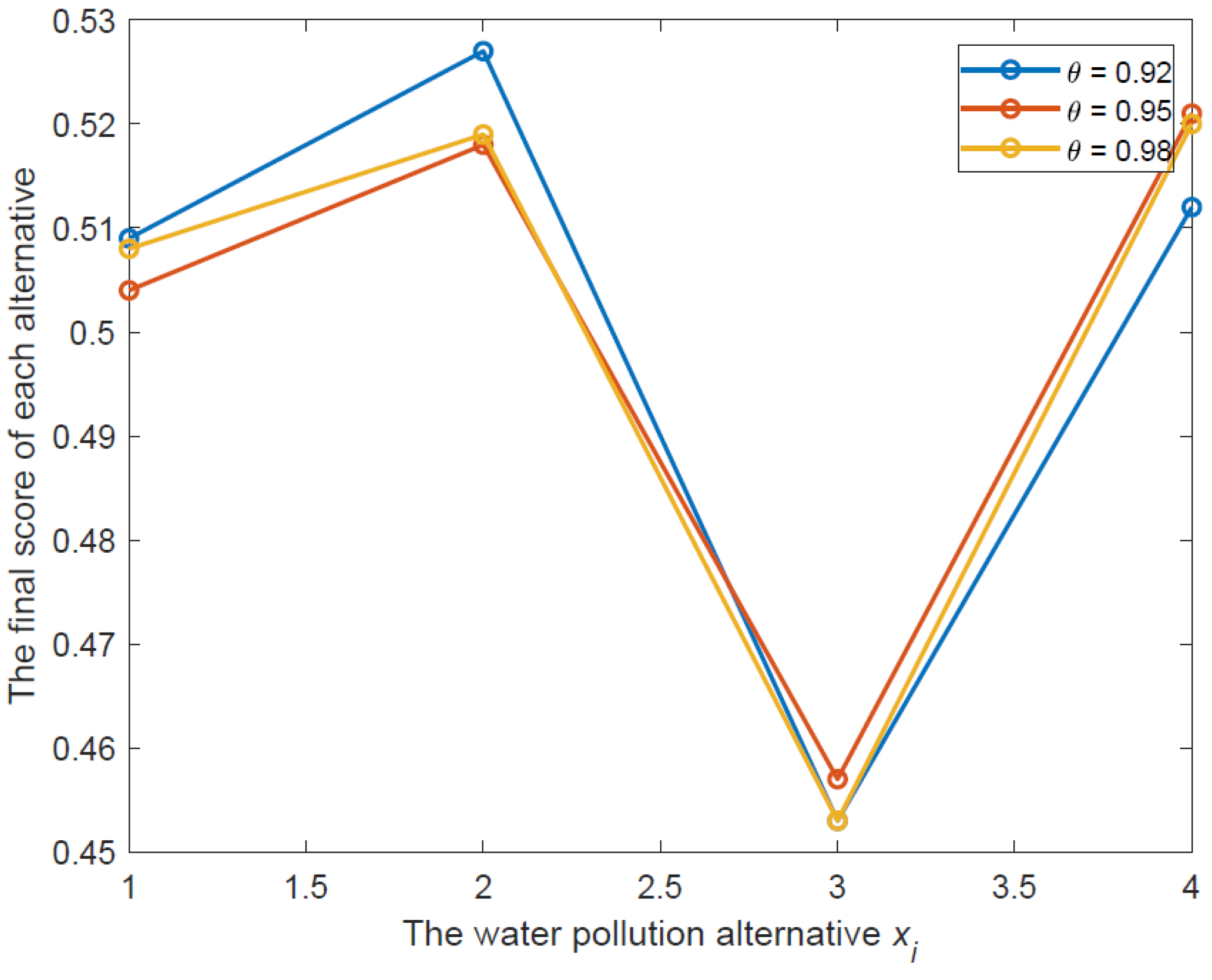
| θ | τ | fs(x1) | fs(x2) | fs(x3) | fs(x4) | Ranking of Alternatives |
|---|---|---|---|---|---|---|
| 0.92 | 0 | 0.509 | 0.527 | 0.453 | 0.512 | x2 > ≻x4 > ≻x1 > ≻x3 |
| 0.93 | 1 | 0.506 | 0.526 | 0.448 | 0.520 | x2 > ≻x4 > ≻x1 > ≻x3 |
| 0.94 | 3 | 0.509 | 0.519 | 0.455 | 0.517 | x2 > ≻x4 > ≻x1 > ≻x3 |
| 0.95 | 4 | 0.504 | 0.518 | 0.457 | 0.521 | x4 > ≻x2 >≻x1 > ≻x3 |
| 0.96 | 7 | 0.509 | 0.518 | 0.453 | 0.520 | x4 > ≻x2 > ≻x1 > ≻x3 |
| 0.97 | 10 | 0.508 | 0.520 | 0.454 | 0.518 | x2 > ≻x4 > ≻x1 > ≻x3 |
| 0.98 | 14 | 0.508 | 0.519 | 0.453 | 0.520 | x4 > ≻x2 > ≻x1 > ≻x3 |
| 0.99 | 22 | 0.507 | 0.520 | 0.453 | 0.519 | x2 > ≻x4 > ≻x1 > ≻x3 |
| 1 | 344 | 0.508 | 0.519 | 0.453 | 0.520 | x4 > x2 > x1 > x3 |
| Method | Clustering Method | Social Relationship | FPR | Distrust Behavior | Water Pollution Problem |
|---|---|---|---|---|---|
| Lu et al. [40] | K-means clustering | √ | × | × | × |
| Liu et al. [15] | DM clustering | × | × | × | × |
| Wang et al. [23] | Louvain algorithm | √ | × | × | × |
| Meng et al. [4] | Trust-based density peaks clustering | √ | × | × | × |
| Our method | AHC method | √ | √ | √ | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Liu, G.; Xu, Y. Distrust Behavior in Social Network Large-Scale Group Decision Making and Its Application in Water Pollution Management. Water 2023, 15, 1638. https://doi.org/10.3390/w15091638
Lu Y, Liu G, Xu Y. Distrust Behavior in Social Network Large-Scale Group Decision Making and Its Application in Water Pollution Management. Water. 2023; 15(9):1638. https://doi.org/10.3390/w15091638
Chicago/Turabian StyleLu, Yanling, Gaofeng Liu, and Yejun Xu. 2023. "Distrust Behavior in Social Network Large-Scale Group Decision Making and Its Application in Water Pollution Management" Water 15, no. 9: 1638. https://doi.org/10.3390/w15091638






