Assessing the Effect of Conduit Pattern and Type of Recharge on the Karst Spring Hydrograph: A Synthetic Modeling Approach
Abstract
:Highlights:
- The network maze conduit pattern is generated based on a newly developed code.
- A synthetic modeling approach is applied to characterize the shape of the spring hydrograph.
- The interaction of conduit patterns and recharge types mainly affects the spring hydrograph.
- Peak discharge and time are controlled by conduit patterns and recharge events, respectively.
- The recession coefficient is mainly affected by the density of conduits.
1. Introduction
2. Methods
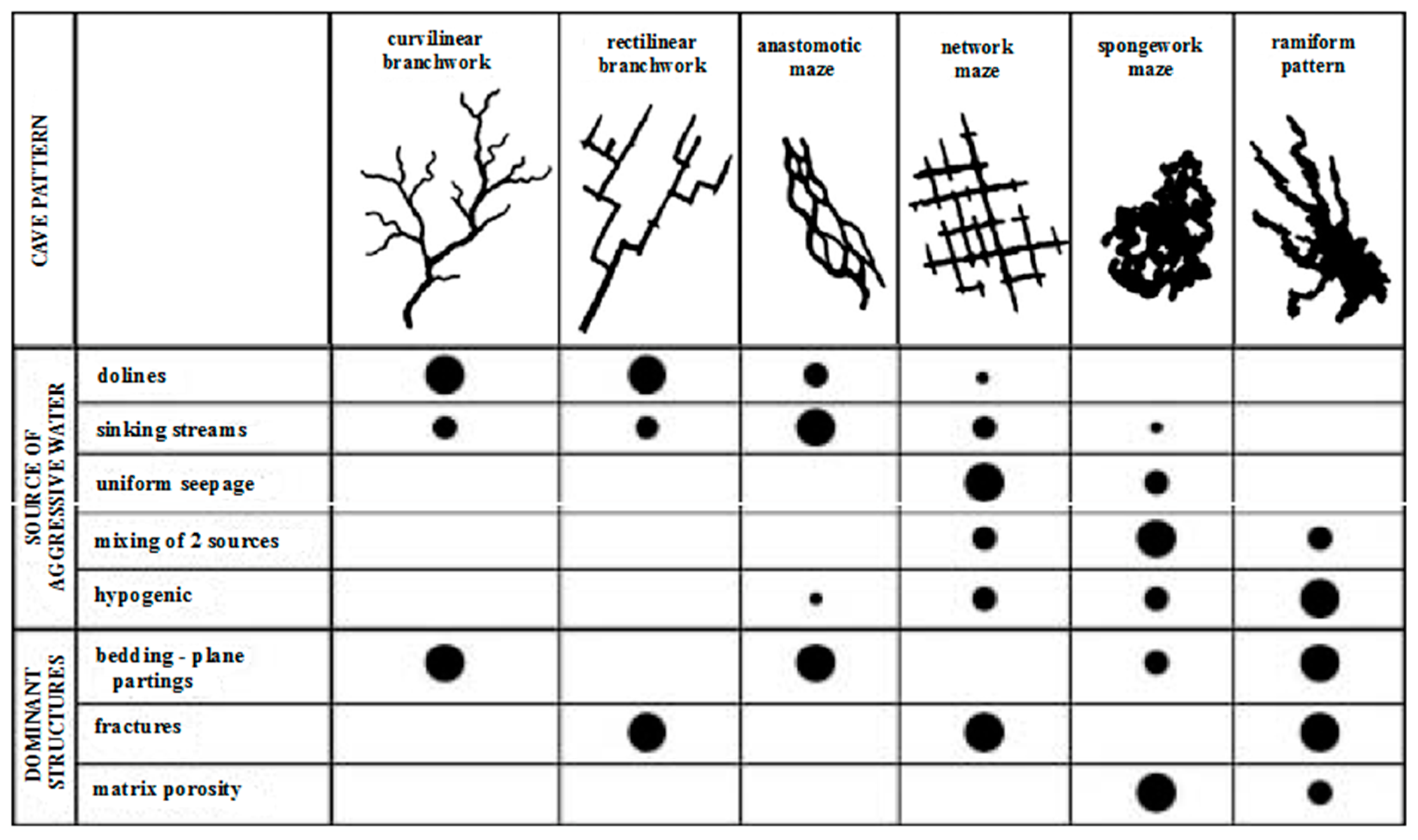
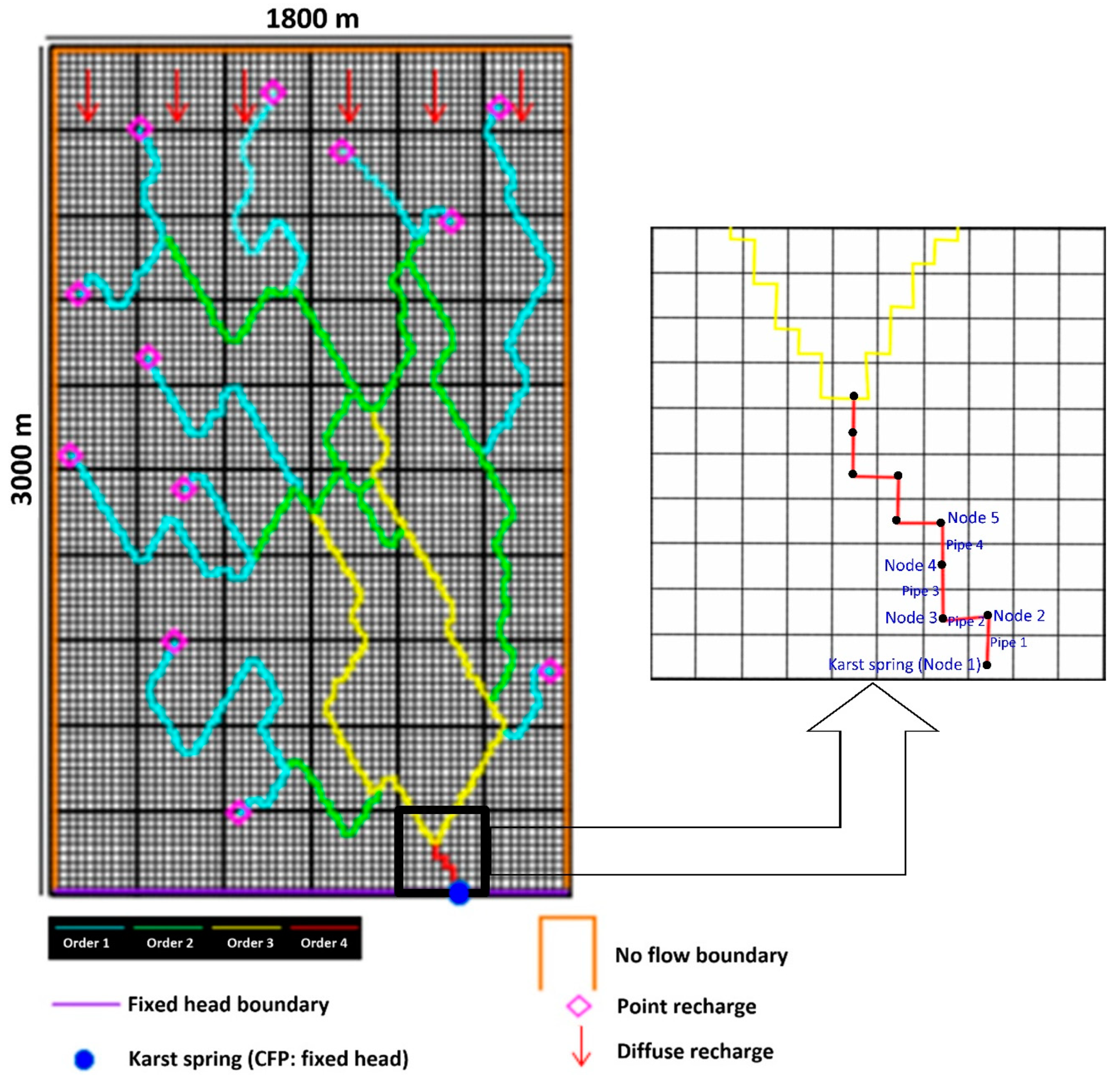
2.1. Generation of Conduit Networks
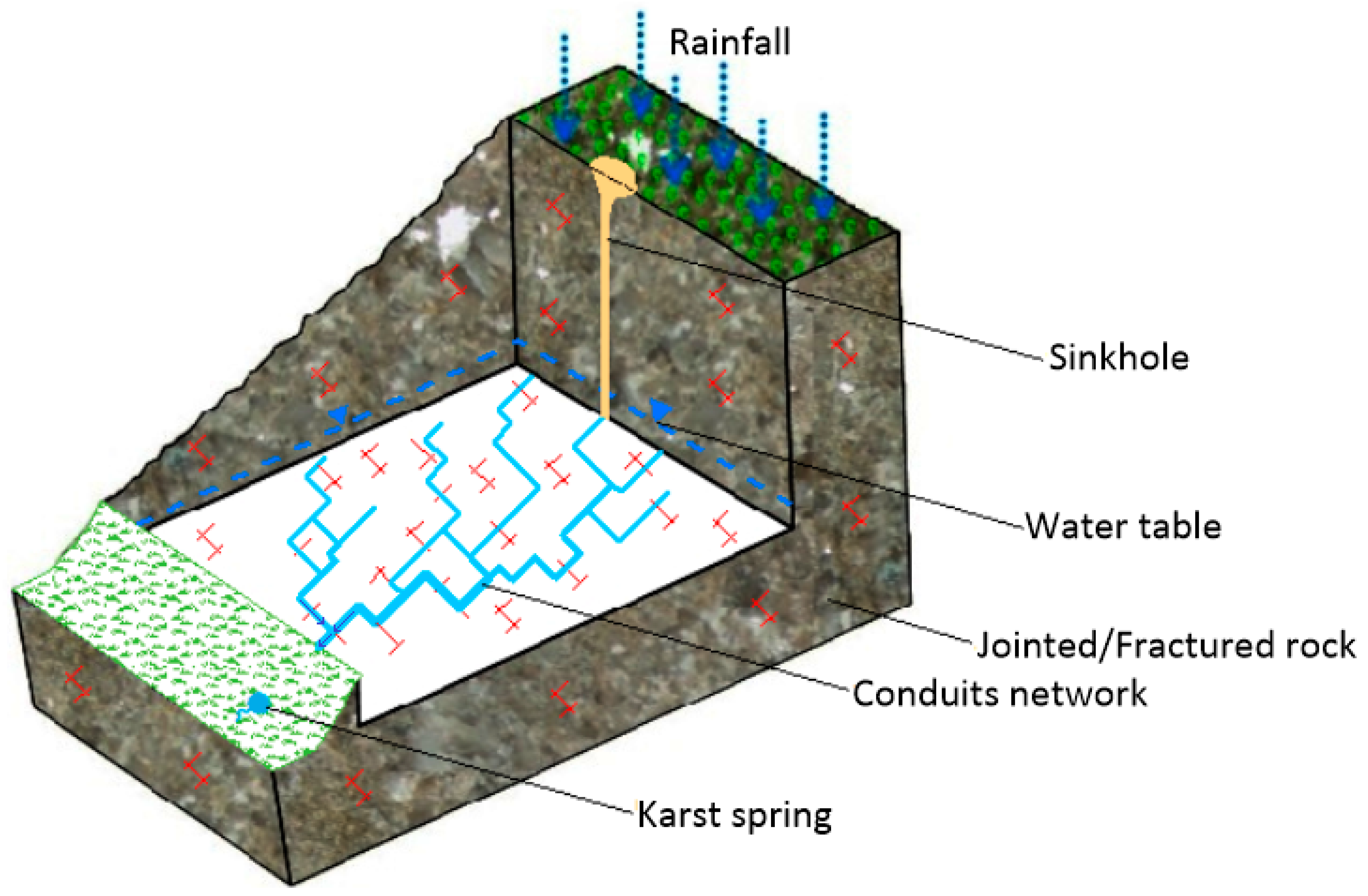
2.2. Conceptual Model and Model Description
2.3. Simulation Scenarios
3. Results and Discussion
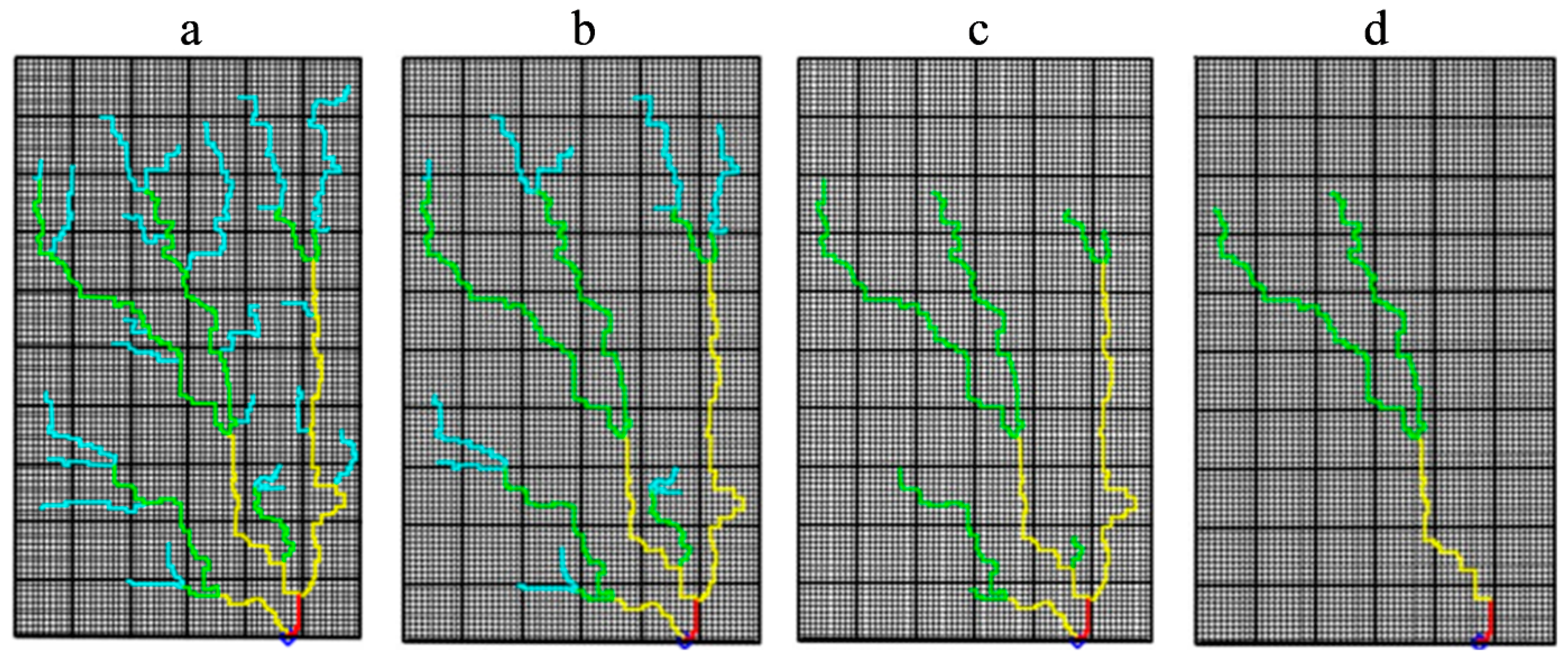
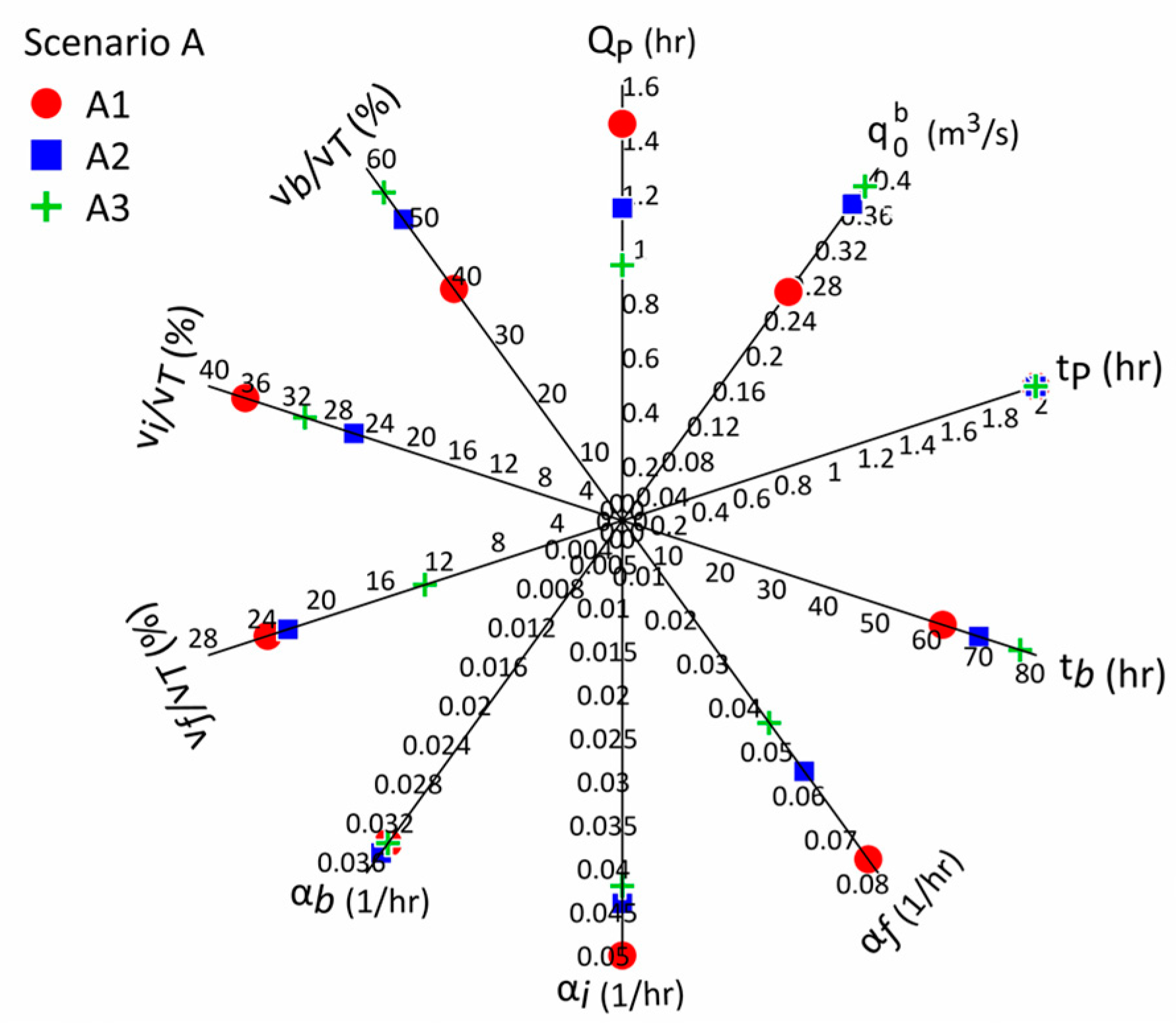
3.1. The Effect of the Conduit Pattern
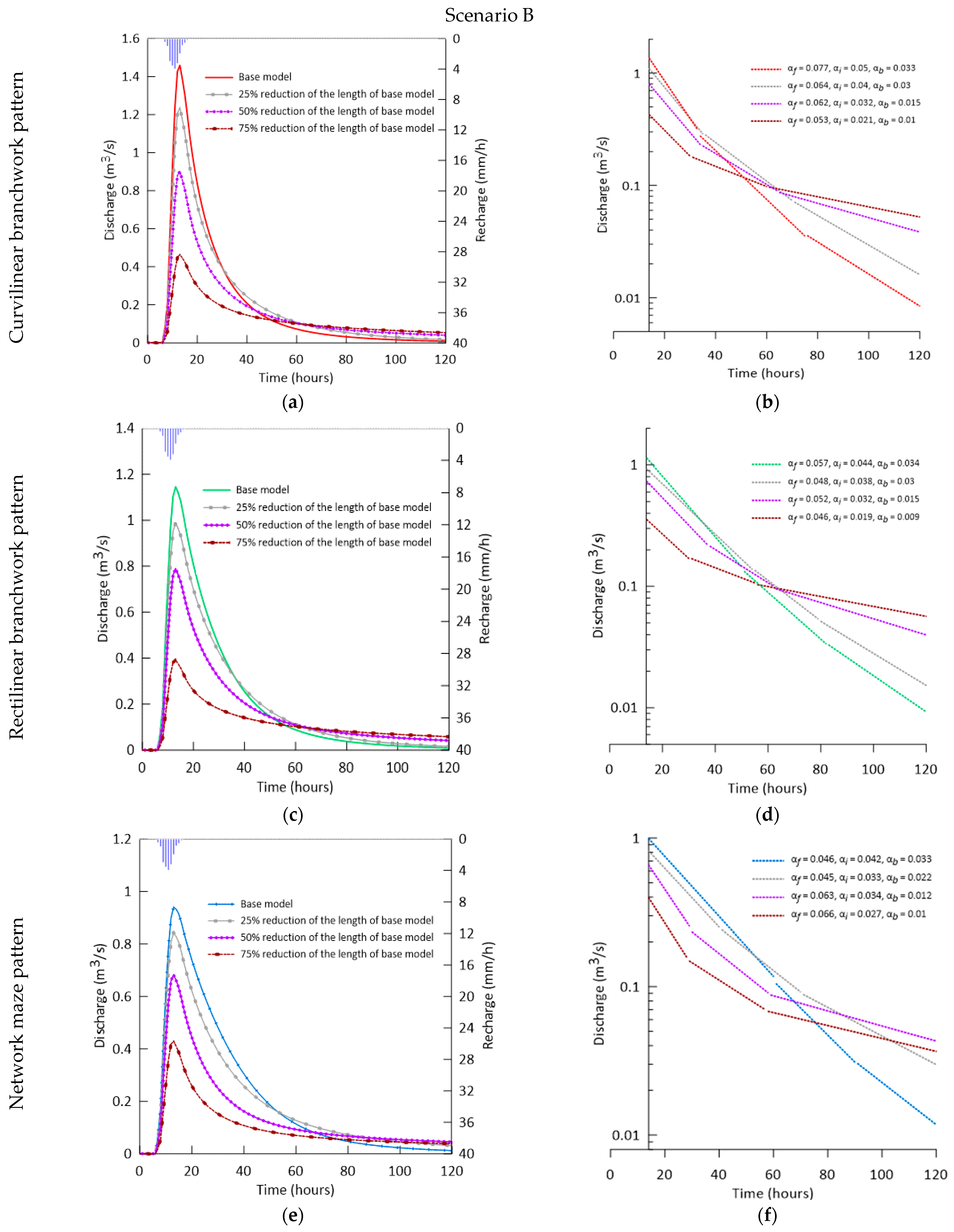
3.2. The Effect of the Conduit Density
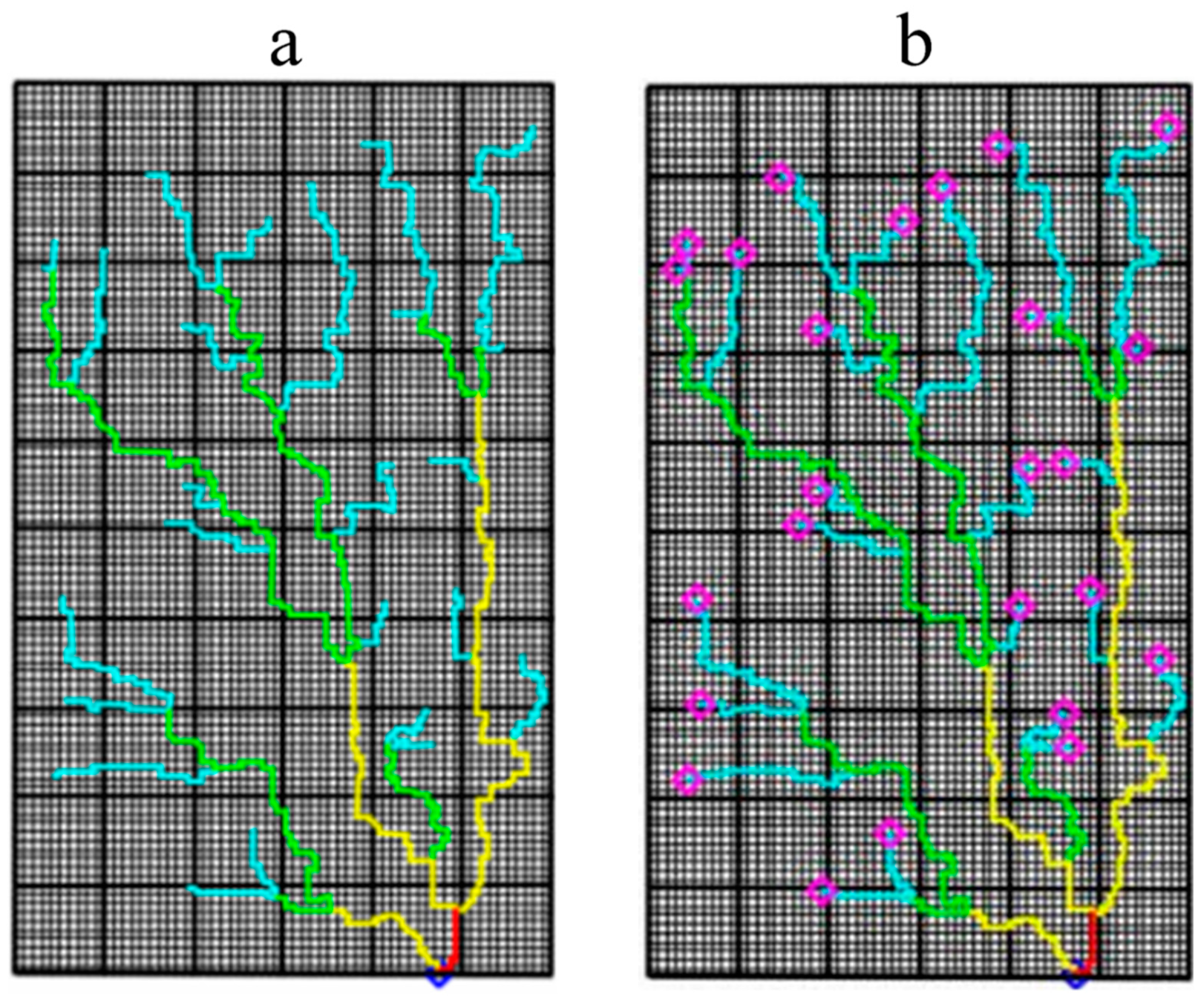
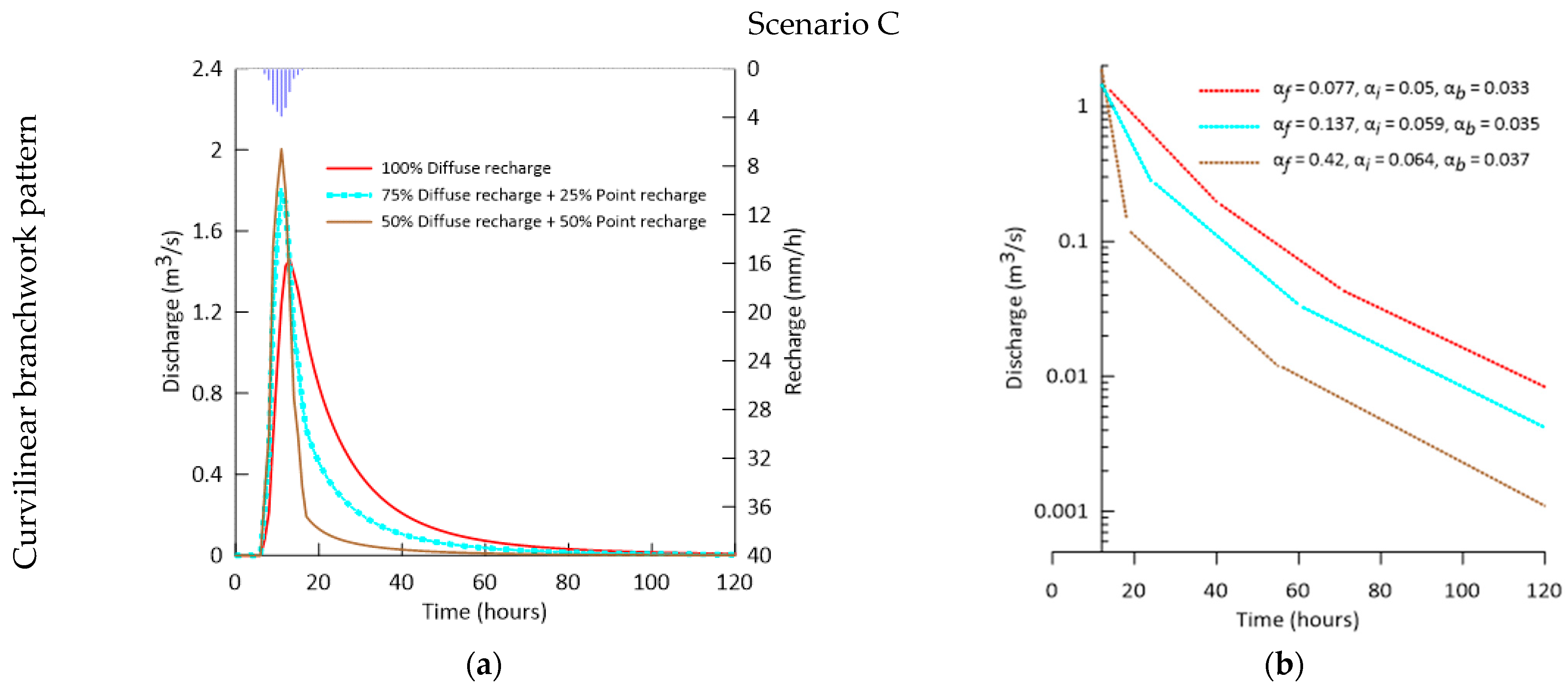
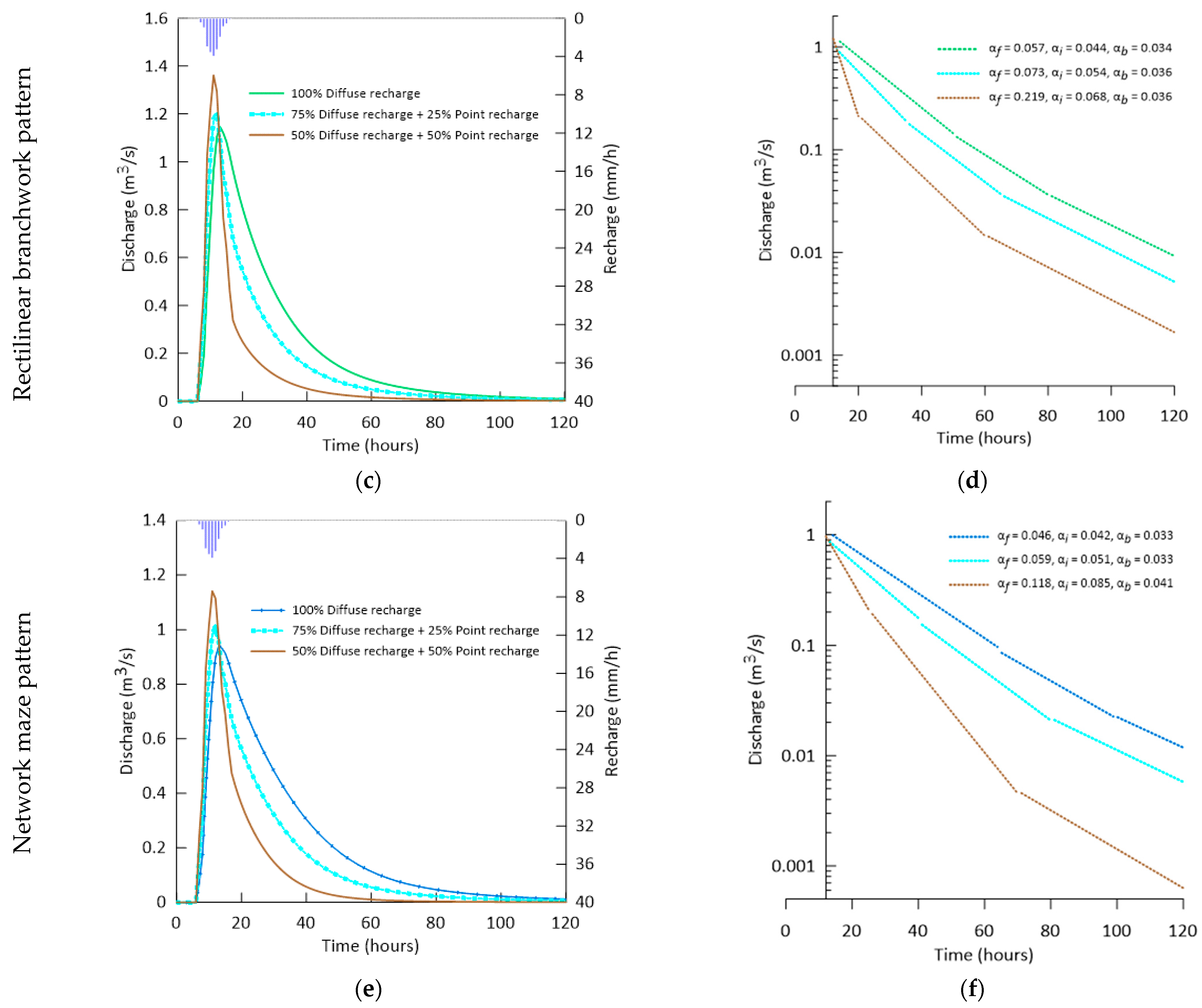
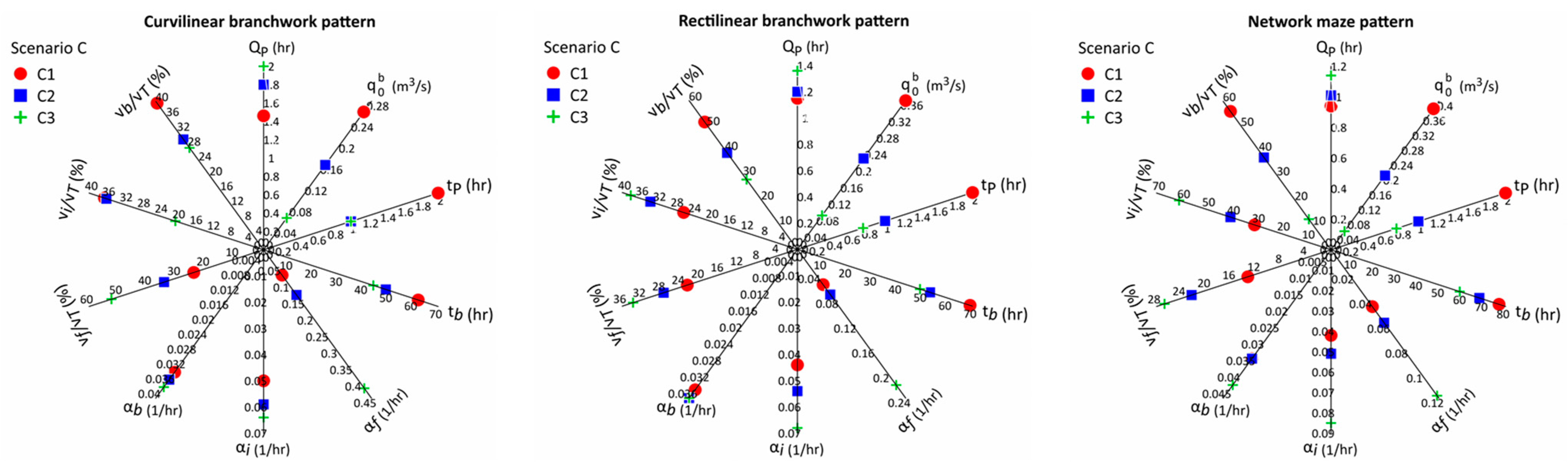
3.3. The Effect of Recharge Type
4. Field Examples to Verify the Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ford, D.; Williams, P.D. Karst Hydrogeology and Geomorphology; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 0-470-84997-5. [Google Scholar]
- White, W.B. Geomorphology and Hydrology of Karst Terrains; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Ghasemizadeh, R.; Yu, X.; Butscher, C.; Padilla, I.Y.; Alshawabkeh, A. Improved regional groundwater flow modeling using drainage features: A case study of the central northern karst aquifer system of Puerto Rico (USA). Hydrogeol. J. 2016, 24, 1463. [Google Scholar] [CrossRef] [PubMed]
- Andriani, G.F.; Parise, M. On the applicability of geomechanical models for carbonate rock masses interested by karst processes. Environ. Earth Sci. 2015, 74, 7813–7821. [Google Scholar] [CrossRef]
- Chang, Y.; Wu, J.; Liu, L. Effects of the conduit network on the spring hydrograph of the karst aquifer. J. Hydrol. 2015, 527, 517–530. [Google Scholar] [CrossRef]
- Worthington, S.R. Groundwater residence times in unconfined carbonate aquifers. J. Cave Karst Stud. 2007, 69, 94–102. [Google Scholar]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Padilla, A.; Pulido-Bosch, A.; Mangin, A. Relative importance of baseflow and quickflow from hydrographs of karst spring. Groundwater 1994, 32, 267–277. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Raeisi, E.; Bakalowicz, M. Method of leakage study at the karst dam site. A case study: Khersan 3 Dam, Iran. Environ. Geol. 2007, 52, 1053–1065. [Google Scholar] [CrossRef]
- Jourde, H.; Massei, N.; Mazzilli, N.; Binet, S.; Batiot-Guilhe, C.; Labat, D.; Steinmann, M.; Bailly-Comte, V.; Seidel, J.-L.; Arfib, B.; et al. SNO KARST: A French network of observatories for the multidisciplinary study of critical zone processes in karst watersheds and aquifers. Vadose Zone J. 2018, 17, 1–18. [Google Scholar] [CrossRef]
- Eisenlohr, L.; Király, L.; Bouzelboudjen, M.; Rossier, Y. Numerical simulation as a tool for checking the interpretation of karst spring hydrographs. J. Hydrol. 1997, 193, 306–315. [Google Scholar] [CrossRef]
- Fiorillo, F. The recession of spring hydrographs, focused on karst aquifers. Water Resour. Manag. 2014, 28, 1781–1805. [Google Scholar] [CrossRef]
- Kovács, A.; Perrochet, P. A quantitative approach to spring hydrograph decomposition. J. Hydrol. 2008, 352, 16–29. [Google Scholar] [CrossRef]
- Bonacci, O. Karst springs hydrographs as indicators of karst aquifers. Hydrol. Sci. J. 1993, 38, 51–62. [Google Scholar] [CrossRef]
- Kiraly, L.; Perrochet, P.; Rossier, Y. Effect of the epikarst on the hydrograph of karst springs: A numerical approach. Bull. Cent. Hydrogéol. 1995, 14, 199–220. [Google Scholar]
- Mohammadi, Z.; Shoja, A. Effect of annual rainfall amount on characteristics of karst spring hydrograph. Carbonates Evaporites 2014, 29, 279–289. [Google Scholar] [CrossRef]
- Shirafkan, M.; Mohammadi, Z.; Sivelle, V.; Labat, D. The effects of exchange flow on the Karst spring hydrograph under the different flow regimes: A synthetic modeling approach. Water 2021, 13, 1189. [Google Scholar] [CrossRef]
- Amit, H.; Lyakhovsky, V.; Katz, A.; Starinsky, A.; Burg, A. Interpretation of spring recession curves. Groundwater 2002, 40, 543–551. [Google Scholar] [CrossRef]
- Dewandel, B.; Lachassagne, P.; Bakalowicz, M.; Weng, P.; Al-Malki, A. Evaluation of aquifer thickness by analysing recession hydrographs. Application to the Oman ophiolite hard-rock aquifer. J. Hydrol. 2003, 274, 248–269. [Google Scholar] [CrossRef]
- Florea, L.J.; Vacher, H. Springflow hydrographs: Eogenetic vs. telogenetic karst. Groundwater 2006, 44, 352–361. [Google Scholar] [CrossRef]
- Palmer, A.N. Origin and morphology of limestone caves. Geol. Soc. Am. Bull. 1991, 103, 1–21. [Google Scholar] [CrossRef]
- Al-Halbouni, D.; Watson, R.A.; Holohan, E.P.; Meyer, R.; Polom, U.; Dos Santos, F.M.; Comas, X.; Alrshdan, H.; Krawczyk, C.M.; Dahm, T. Dynamics of hydrological and geomorphological processes in evaporite karst at the eastern Dead Sea–a multidisciplinary study. Hydrol. Earth Syst. Sci. 2021, 25, 3351–3395. [Google Scholar] [CrossRef]
- Jeannin, P.-Y.; Groves, C.; Häuselmann, P. Speleological investigations. Methods Karst Hydrogeol. Int. Contrib. Hydrogeol. IAH 2007, 26, 25–44. [Google Scholar]
- Pardo-Igúzquiza, E.; Dowd, P.A.; Xu, C.; Durán-Valsero, J.J. Stochastic simulation of karst conduit networks. Adv. Water Resour. 2012, 35, 141–150. [Google Scholar] [CrossRef]
- Palmer, A.N. Speleogenesis in carbonate rocks. In Evolution of Karst: From Prekarst to Cessation; Inštitut za Raziskovanje Krasa, ZRC SAZU: Ljubljana, Slovenia, 2002; pp. 43–59. [Google Scholar]
- Collon, P.; Bernasconi, D.; Vuilleumier, C.; Renard, P. Statistical metrics for the characterization of karst network geometry and topology. Geomorphology 2017, 283, 122–142. [Google Scholar] [CrossRef]
- Hendrick, M.; Renard, P. Subnetworks of percolation backbones to model karst systems around Tulum, Mexico. Front. Phys. 2016, 4, 43. [Google Scholar] [CrossRef]
- Ronayne, M.J. Influence of conduit network geometry on solute transport in karst aquifers with a permeable matrix. Adv. Water Resour. 2013, 56, 27–34. [Google Scholar] [CrossRef]
- Borghi, A.; Renard, P.; Jenni, S. A pseudo-genetic stochastic model to generate karstic networks. J. Hydrol. 2012, 414, 516–529. [Google Scholar] [CrossRef]
- Jaquet, O.; Siegel, P.; Klubertanz, G.; Benabderrhamane, H. Stochastic discrete model of karstic networks. Adv. Water Resour. 2004, 27, 751–760. [Google Scholar] [CrossRef]
- Lafare, A. Modélisation Mathématique de la Spéléogenèse: Une Approche Hybride à Partir de Réseaux de Fractures Discrets et de Simulations Hydrogéologiques. Ph.D. Thesis, Université Montpellier II, Montpellier, France, 2011. [Google Scholar]
- De Rooij, R.; Graham, W. Generation of complex karstic conduit networks with a hydrochemical model. Water Resour. Res. 2017, 53, 6993–7011. [Google Scholar] [CrossRef]
- Henson, W.R.; de Rooij, R.; Graham, W. What Makes a First-Magnitude Spring?: Global Sensitivity Analysis of a Speleogenesis Model to Gain Insight into Karst Network and Spring Genesis. Water Resour. Res. 2018, 54, 7417–7434. [Google Scholar] [CrossRef]
- Kaufmann, G.; Romanov, D.; Hiller, T. Modeling three-dimensional karst aquifer evolution using different matrix-flow contributions. J. Hydrol. 2010, 388, 241–250. [Google Scholar] [CrossRef]
- Reimann, T.; Hill, M.E. MODFLOW-CFP: A new conduit flow process for MODFLOW–2005. Groundwater 2009, 47, 321–325. [Google Scholar] [CrossRef]
- Ghasemizadeh, R.; Hellweger, F.; Butscher, C.; Padilla, I.; Vesper, D.; Field, M.; Alshawabkeh, A. Groundwater flow and transport modeling of karst aquifers, with particular reference to the North Coast Limestone aquifer system of Puerto Rico. Hydrogeol. J. 2012, 20, 1441. [Google Scholar] [CrossRef] [PubMed]
- Sauter, M.; Geyer, T.; Kovács, A.; Teutsch, G. Modellierung der hydraulik von karstgrundwasserleitern–eine übersicht. Grundwasser 2006, 11, 143–156. [Google Scholar] [CrossRef]
- Ronayne, M.J. Understanding Groundwater Dynamics in Structurally Heterogeneous Aquifers. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2008. [Google Scholar]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Alghalandis, Y. DFNE Practices with ADFNE; Alghalandis Computing: Toronto, ON, Canada, 2018. [Google Scholar]
- Gleyzer, A.; Denisyuk, M.; Rimmer, A.; Salingar, Y. A Fast Recursive Gis Algorithm for Computing Strahler Stream Order in Braided and Nonbraided Networks 1. JAWRA J. Am. Water Resour. Assoc. 2004, 40, 937–946. [Google Scholar] [CrossRef]
- Winston, R.B. ModelMuse Version 4: A graphical user interface for MODFLOW 6. In Scientific Investigations Report-US Geological Survey; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2019. [Google Scholar]
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a Conduit Flow Process (CFP) for MODFLOW-2005; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2008; Volume 6.
- Reimann, T.; Rehrl, C.; Shoemaker, W.B.; Geyer, T.; Birk, S. The significance of turbulent flow representation in single-continuum models. Water Resour. Res. 2011, 47, W09503. [Google Scholar] [CrossRef]
- Liedl, R.; Sauter, M.; Hückinghaus, D.; Clemens, T.; Teutsch, G. Simulation of the development of karst aquifers using a coupled continuum pipe flow model. Water Resour. Res. 2003, 39, 1057. [Google Scholar] [CrossRef]
- Hubinger, B.; Birk, S. Influence of initial heterogeneities and recharge limitations on the evolution of aperture distributions in carbonate aquifers. Hydrol. Earth Syst. Sci. 2011, 15, 3715–3729. [Google Scholar] [CrossRef]
- Doctor, D.H.; Alexander, E.C., Jr. Interpretation of water chemistry and stable isotope data from a karst aquifer according to flow regimes identified through hydrograph recession analysis. In US Geological Survey Karst Interest Group Proceedings, Rapid City, South Dakota; BiblioGov: Singapore, 2005; pp. 82–92. [Google Scholar]
- Jakada, H.; Chen, Z.; Luo, M.; Zhou, H.; Wang, Z.; Habib, M. Watershed characterization and hydrograph recession analysis: A comparative look at a karst vs. non-karst watershed and implications for groundwater resources in Gaolan River Basin, Southern China. Water 2019, 11, 743. [Google Scholar] [CrossRef]
- Şen, Z. General modeling of karst spring hydrographs and development of a dimensionless karstic hydrograph concept. Hydrogeol. J. 2020, 28, 549–559. [Google Scholar] [CrossRef]
- Király, L.; Morel, G. Remarques sur l’hydrogramme des sources karstiques simulé par modèles mathématiques: Avec 15 figures. Bull. Cent. Hydrogéol. 1976, 1, 37–60. [Google Scholar]
- Fiorillo, F. Tank-reservoir drainage as a simulation of the recession limb of karst spring hydrographs. Hydrogeol. J. 2011, 19, 1009. [Google Scholar] [CrossRef]
- Abirifard, M.; Birk, S.; Raeisi, E.; Sauter, M. Dynamic volume in karst aquifers: Parameters affecting the accuracy of estimates from recession analysis. J. Hydrol. 2022, 612, 128286. [Google Scholar] [CrossRef]
- Geyer, T.; Birk, S.; Liedl, R.; Sauter, M. Quantification of temporal distribution of recharge in karst systems from spring hydrographs. J. Hydrol. 2008, 348, 452–463. [Google Scholar] [CrossRef]
- Kovács, A.; Perrochet, P.; Darabos, E.; Lénárt, L.; Szűcs, P. Well hydrograph analysis for the characterisation of flow dynamics and conduit network geometry in a karst aquifer, Bükk Mountains, Hungary. J. Hydrol. 2015, 530, 484–499. [Google Scholar] [CrossRef]
- Kovács, A.; Perrochet, P.; Király, L.; Jeannin, P.-Y. A quantitative method for the characterisation of karst aquifers based on spring hydrograph analysis. J. Hydrol. 2005, 303, 152–164. [Google Scholar] [CrossRef]
- Kovács, A.; Perrochet, P. Well Hydrograph Analysis for the Estimation of Hydraulic and Geometric Parameters of Karst and Connected Water Systems; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 3-319-06138-0. [Google Scholar]
- Kincaid, T.R. Morphologic and Fractal Characterization of Saturated Karstic Caves; University of Wyoming: Laramie, WY, USA, 1999; ISBN 0-599-44583-1. [Google Scholar]
- Kaufmann, G. Modelling karst geomorphology on different time scales. Geomorphology 2009, 106, 62–77. [Google Scholar] [CrossRef]
- Kincaid, T.; Werner, C.L.; GeoHydros, L. Karst Hydrogeology of the Woodville Karst Plain Florida. In Sinkholes and the Engineering and Environmental Impacts of Karst, Edition: Geotechnical Special Publication; Geo-Institute: Fairfax, VA, USA, 2008. [Google Scholar]
- Gilbert, D. Nutrient (Biology) TMDL for the Upper Wakulla River (WBID 1006); Florida Department of Environmental Protection Technical Report; Florida Department of Environmental Protection: Tallahassee, FL, USA, 2012.
- Kincaid, T.R.; Hazlett, T.J.; Davies, G.J. Quantitative groundwater tracing and effective numerical modeling in karst: An example from the Woodville Karst Plain of North Florida. In Sinkholes and the Engineering and Environmental Impacts of Karst; Geo-Institute: Fairfax, VA, USA, 2005; pp. 114–121. [Google Scholar]
- DeHan, R.; Loper, D. Hydrogeologic Characterization and Modeling of the Woodville Karst Plain, North Florida Report of Investigations: 2005–2006; Hazlett-Kincaid, Inc.: Reno, NV, USA, 2007. [Google Scholar]
- Rodríguez-Martínez, J. Characterization of Springflow in the North Coast Limestone of Puerto Rico Using Physical, Chemical, and Stable Isotopic Methods; US Geological Survey: Reston, VA, USA, 1997.







| Conduit Pattern Characteristics | Diameter of Conduit (m) | |||
|---|---|---|---|---|
| Order | Conduit Node | Curvilinear Branchwork | Rectilinear Branchwork | Network Maze |
| 1 | 371 | 0.5 | 0.7 | 0.8 |
| 2 | 246 | 1 | 0.9 | 0.88 |
| 3 | 147 | 1.5 | 1.2 | 1 |
| 4 | 10 | 2 | 1.5 | 1.25 |
| Scenario | Constant Parameters | Variable Parameters | Assumed Conduit Network | Recharge Type | The Number of Models Run | |
|---|---|---|---|---|---|---|
| Scenario A | Hydrogeological characteristics of the aquifer (K, T, and S), K-exchange, Volume of conduit network, Boundary conditions (No flow boundary, Fixed head boundary, Karst spring), and Type of recharge | Conduit pattern | A1: Curvilinear branchwork | Diffuse Recharge (100%) | Point Recharge (0%) | 3 |
| A2: Rectilinear branchwork | ||||||
| A3: Network maze | ||||||
| Scenario B | Hydrogeological characteristics of the aquifer (K, T, and S), K-exchange, Conduit pattern, Boundary conditions (No flow boundary, Fixed head boundary, Karst spring), and Type of recharge | Conduit density | B1: the base model, including A1, A2, and A3 | Diffuse Recharge (100%) | Point Recharge (0%) | 9 |
| B2: 25% reduction in the length of the base model, including A1, A2, and A3 | ||||||
| B3: 50% reduction in the length of the base model including A1, A2, and A3 | ||||||
| B4: 75% reduction in the length of the base model, including A1, A2, and A3 | ||||||
| Scenario C | Hydrogeological characteristics of the aquifer (K, T, and S), K-exchange, Volume of conduit network, Boundary conditions (No flow boundary, Fixed head boundary, Karst spring), and Conduit pattern | Recharge type and amount | C1 (same as A1 or A2 or A3) | Diffuse Recharge (100%) | Point Recharge (0%) | 6 |
| C2 (A1 or A2 or A3) | Diffuse Recharge (75%) | Point Recharge (25%) | ||||
| C3 (A1 or A2 or A3) | Point Recharge (50%) | Diffuse Recharge (50%) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostad, H.; Mohammadi, Z.; Fiorillo, F. Assessing the Effect of Conduit Pattern and Type of Recharge on the Karst Spring Hydrograph: A Synthetic Modeling Approach. Water 2023, 15, 1594. https://doi.org/10.3390/w15081594
Ostad H, Mohammadi Z, Fiorillo F. Assessing the Effect of Conduit Pattern and Type of Recharge on the Karst Spring Hydrograph: A Synthetic Modeling Approach. Water. 2023; 15(8):1594. https://doi.org/10.3390/w15081594
Chicago/Turabian StyleOstad, Hadi, Zargham Mohammadi, and Francesco Fiorillo. 2023. "Assessing the Effect of Conduit Pattern and Type of Recharge on the Karst Spring Hydrograph: A Synthetic Modeling Approach" Water 15, no. 8: 1594. https://doi.org/10.3390/w15081594





