An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models
Abstract
:1. Introduction
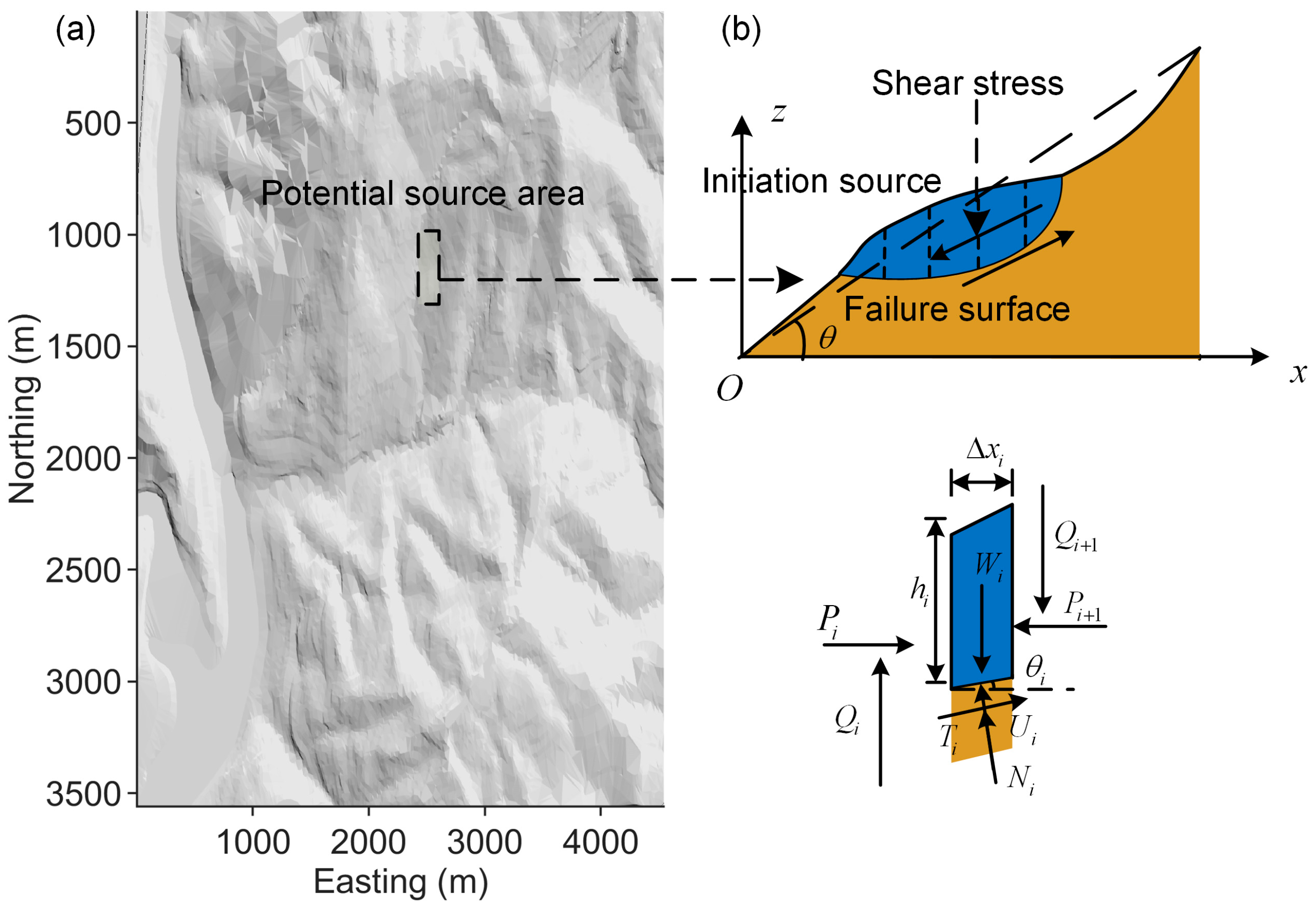
2. Physically Based Initiation Model of the Debris Flow Sources
2.1. Limit Equilibrium Method for Slope Stability Analysis
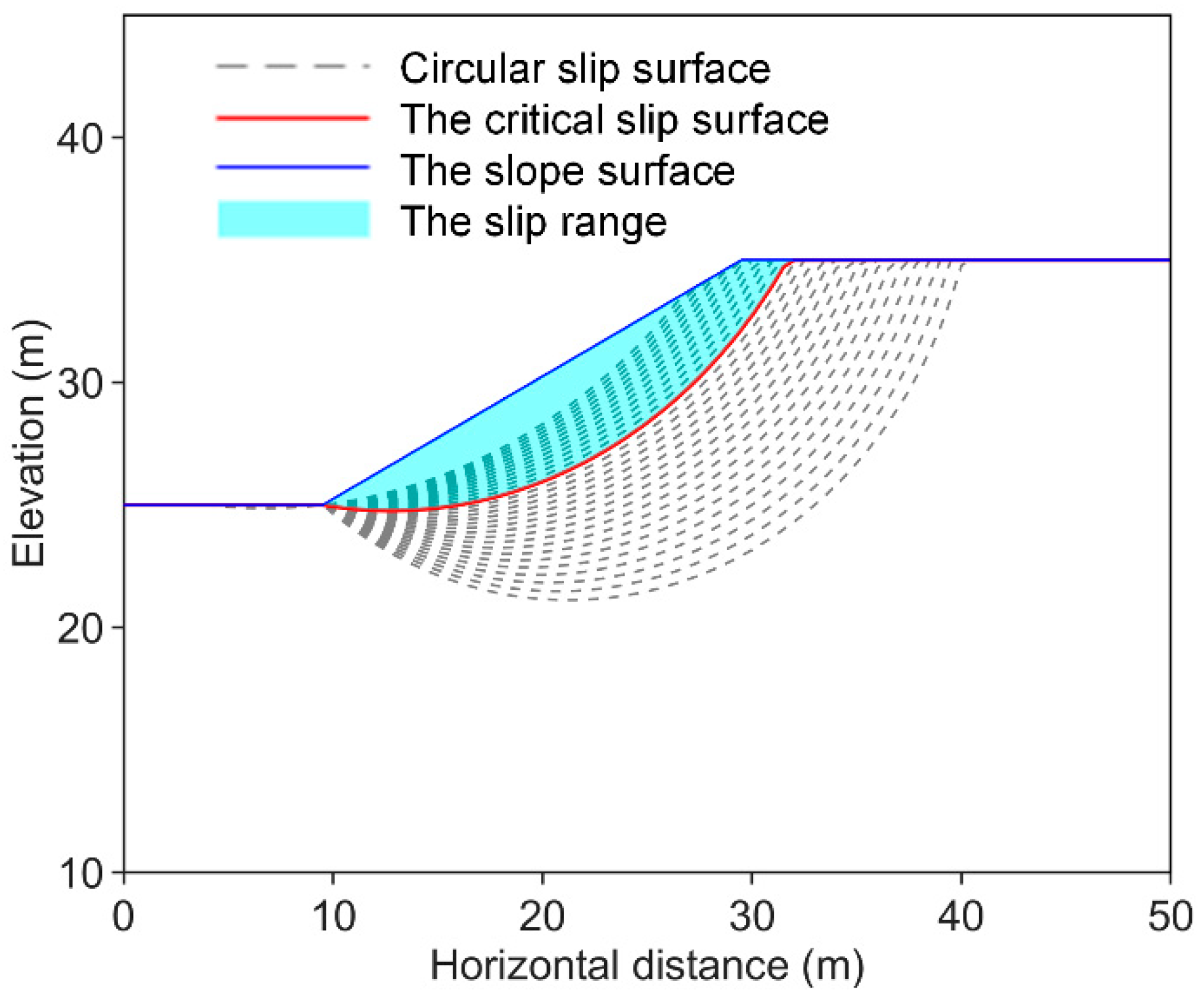
2.2. Critical Slip Surface Determination Incorporated with the Monte Carlo Method
- (1)
- Composite critical slip surface determination.
- The slip surface should be located entirely within the slope body range, and the shear inlet and shear outlet are on the slope surface;
- There should be smooth transitions between adjacent slip slice segments and no sharp corners. The angle between two adjacent slip slice segments should be greater than 90°;
- The horizontal spacing of adjacent nodes should be greater than the minimum horizontal spacing to avoid overlap of the slice division nodes.
- (2)
- Considering the spatial variability of the soil, calculate the range of the critical slip surface and the initiation source volume.
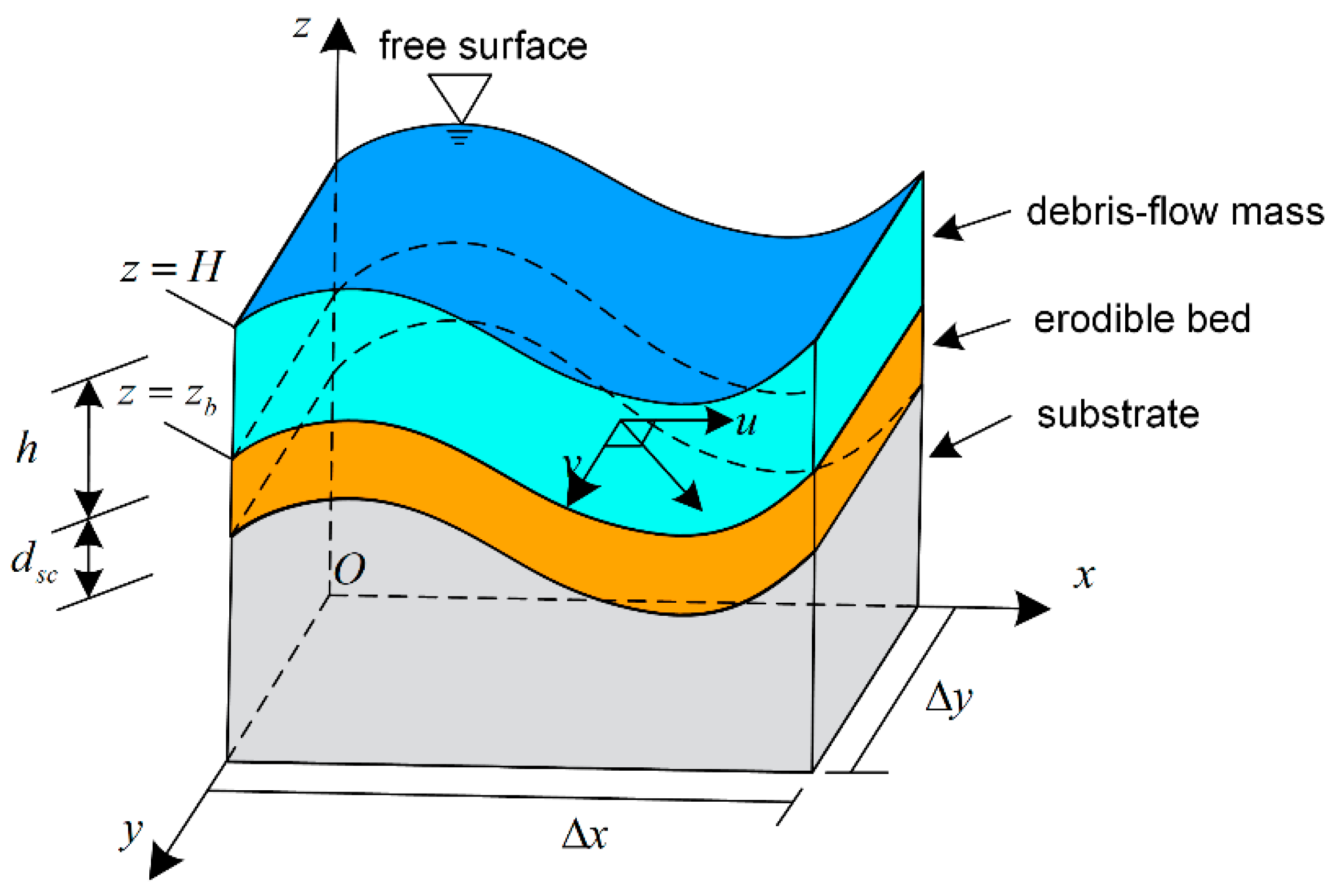
3. Entrainment-Incorporated Numerical Model
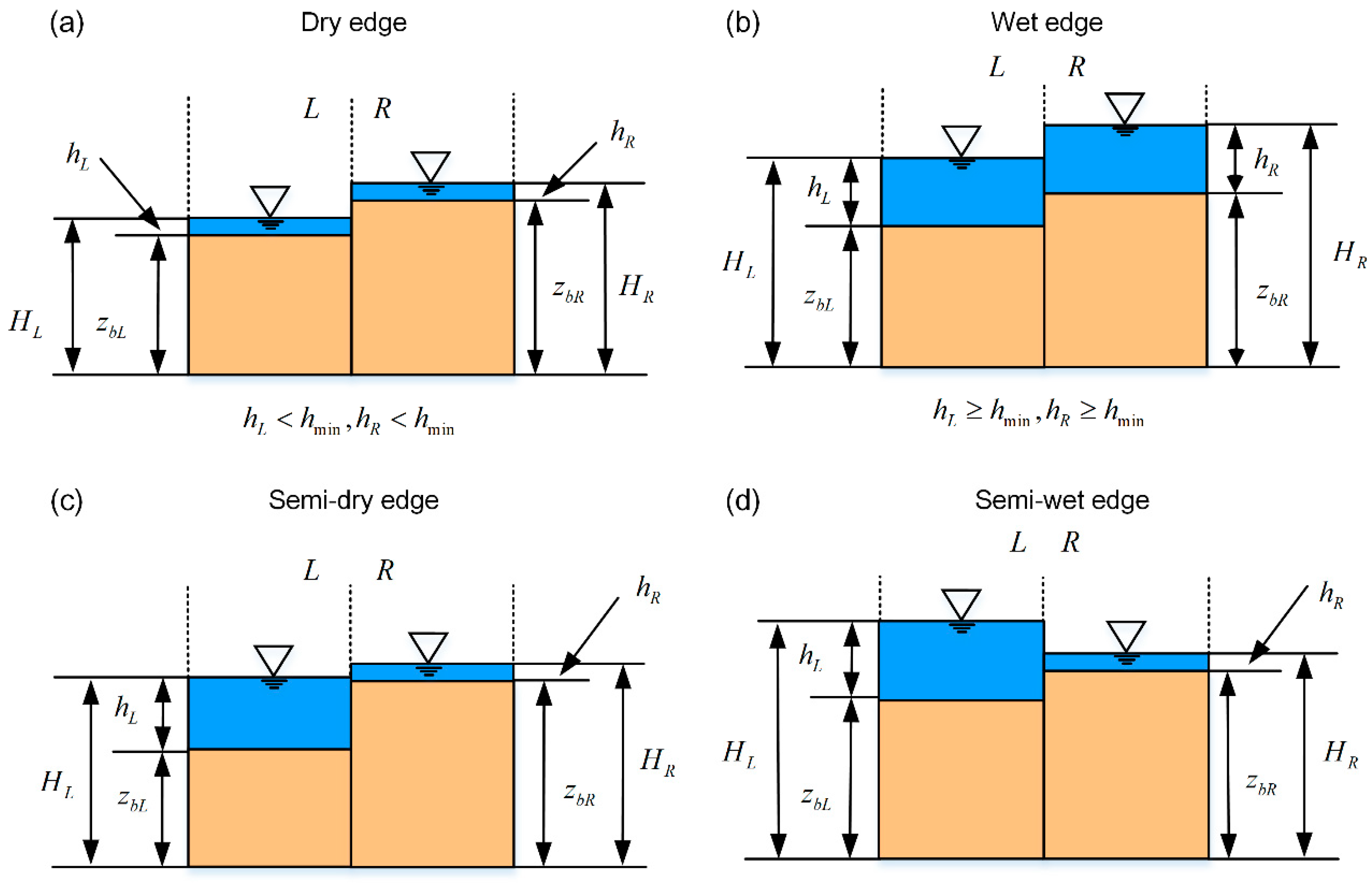
4. Wet/Dry Front Treatment over Complex Topography
- Dry edge. The flow depths of both neighboring cells are smaller than , which is mathematically expressed as , as shown in Figure 5a.
- Wet edge: in contrast to the dry edge, the flow depths of both neighboring cells are greater than , which is , as shown in Figure 5b.
- Semi-dry edge: the flow depth of one neighboring cell is greater than while the other one is less than , and the flow surface level of the dry side is higher than that of the wet side. For example, , and , as shown in Figure 5c;
- Semi-wet edge: the flow depth condition of the cells on both sides is the same as that of the semi-dry edge, but the flow surface level of the wet side is higher than that of the dry side—for example, , and , as shown in Figure 5d.
5. Case Study: The 2010 Hongchun Debris-Flow Event in the Yingxiu Town, China
5.1. The Overview of the 2010 Hongchun Debris-Flow Event
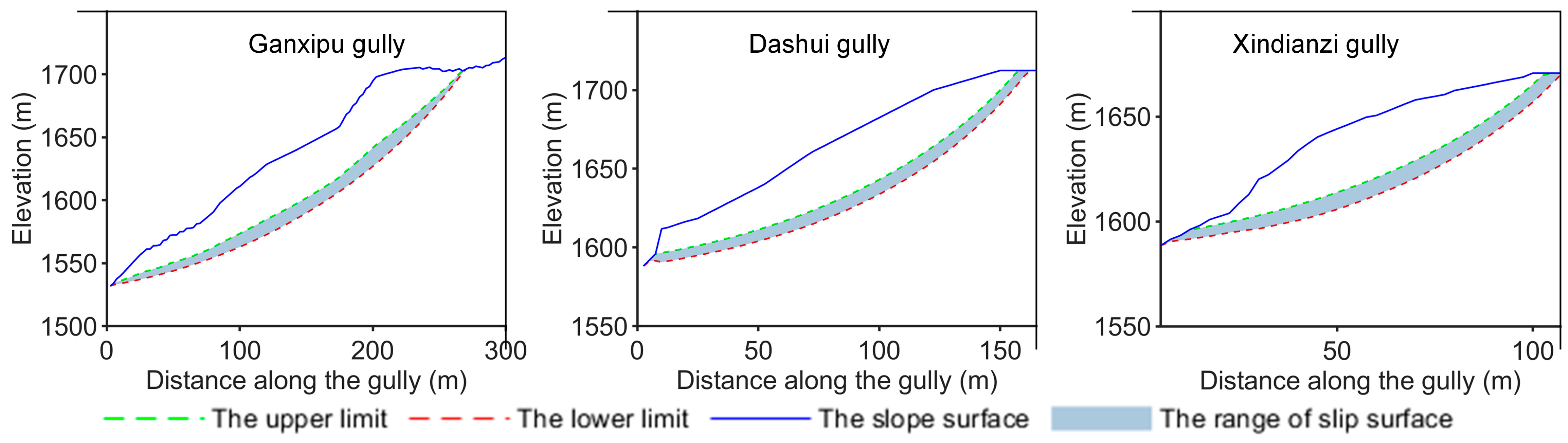
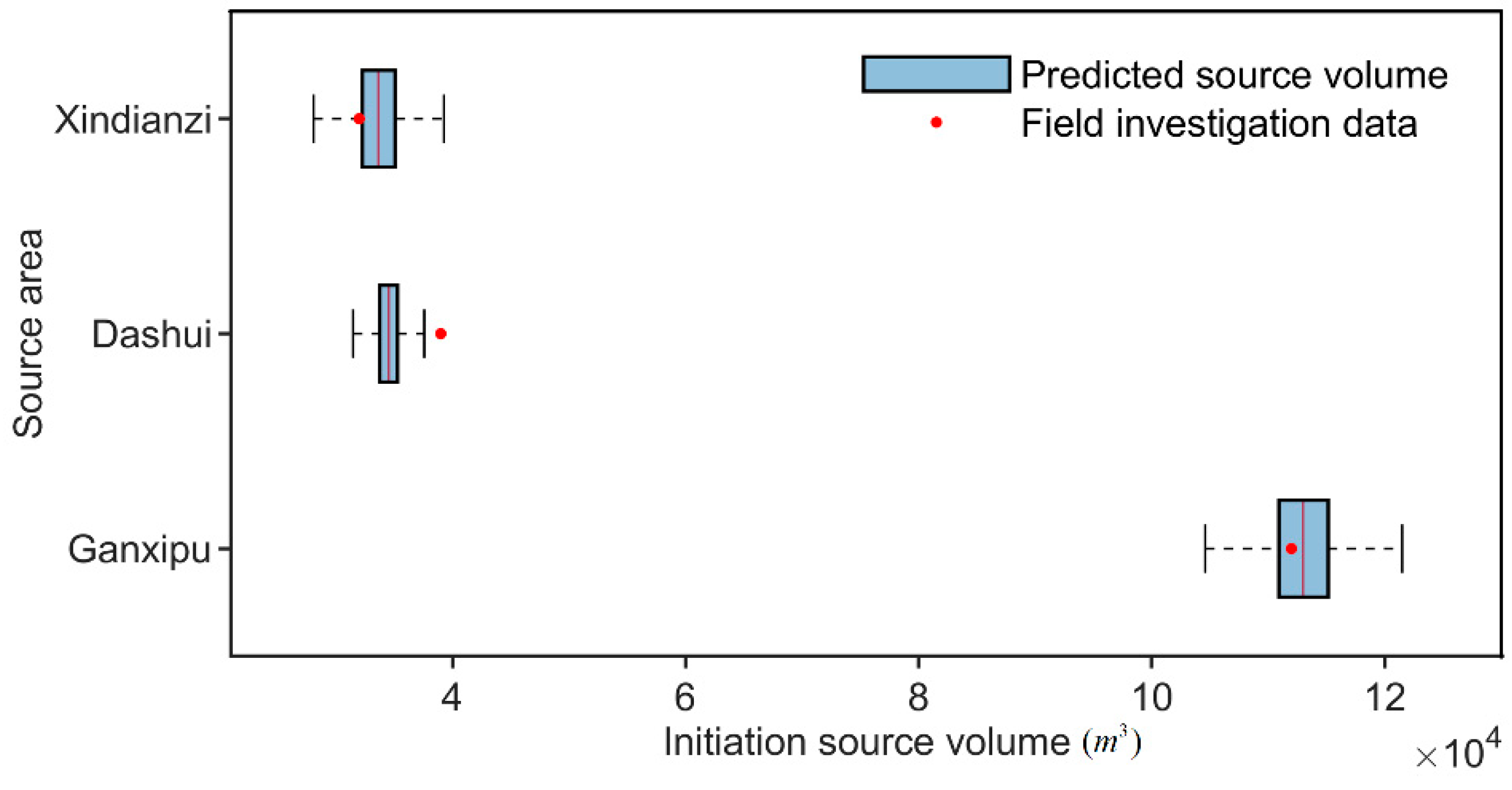
5.2. The Physically Based Estimation of the Slope Initiation Source
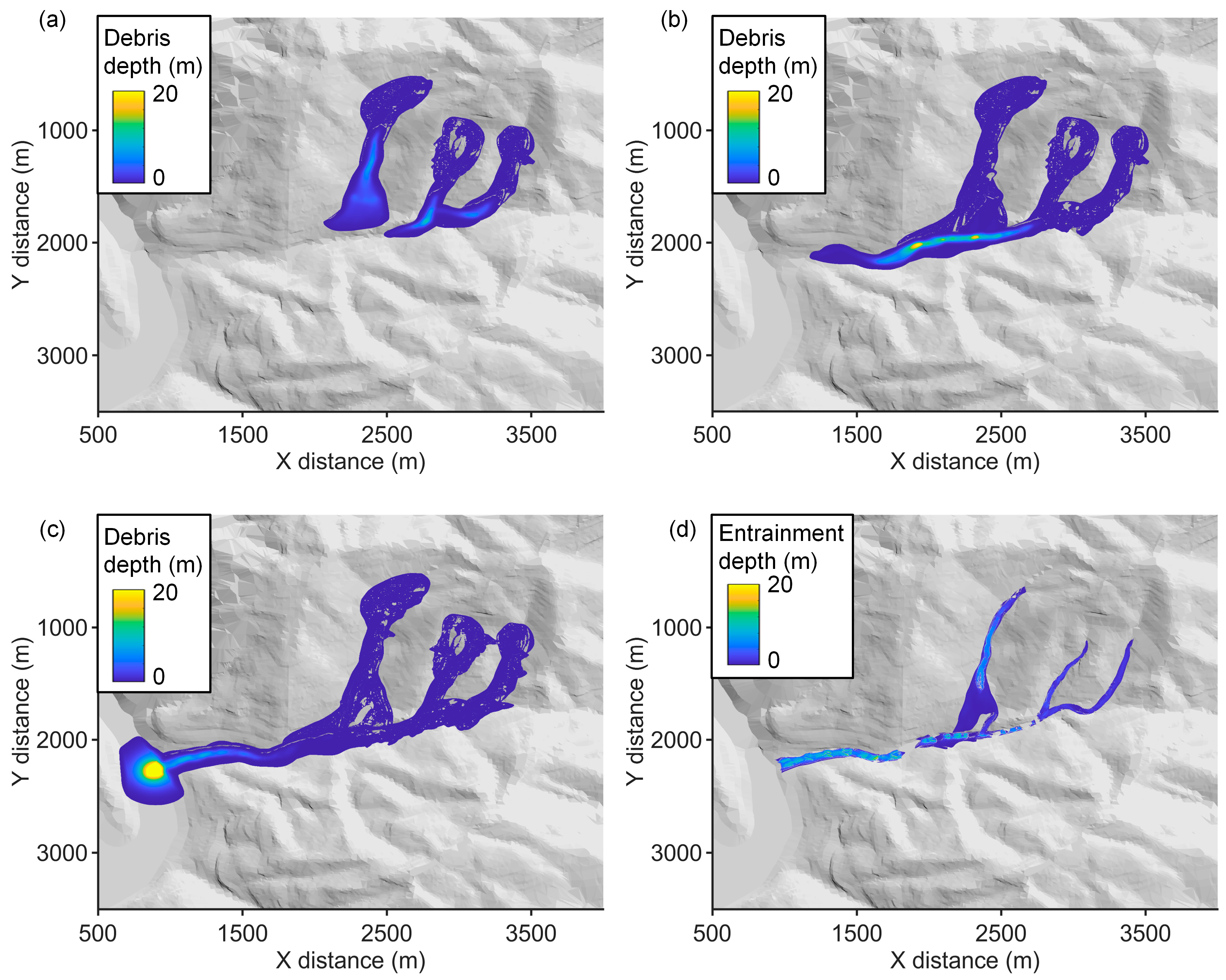
5.3. Numerical Simulation of the Debris-Flow Dynamic Process
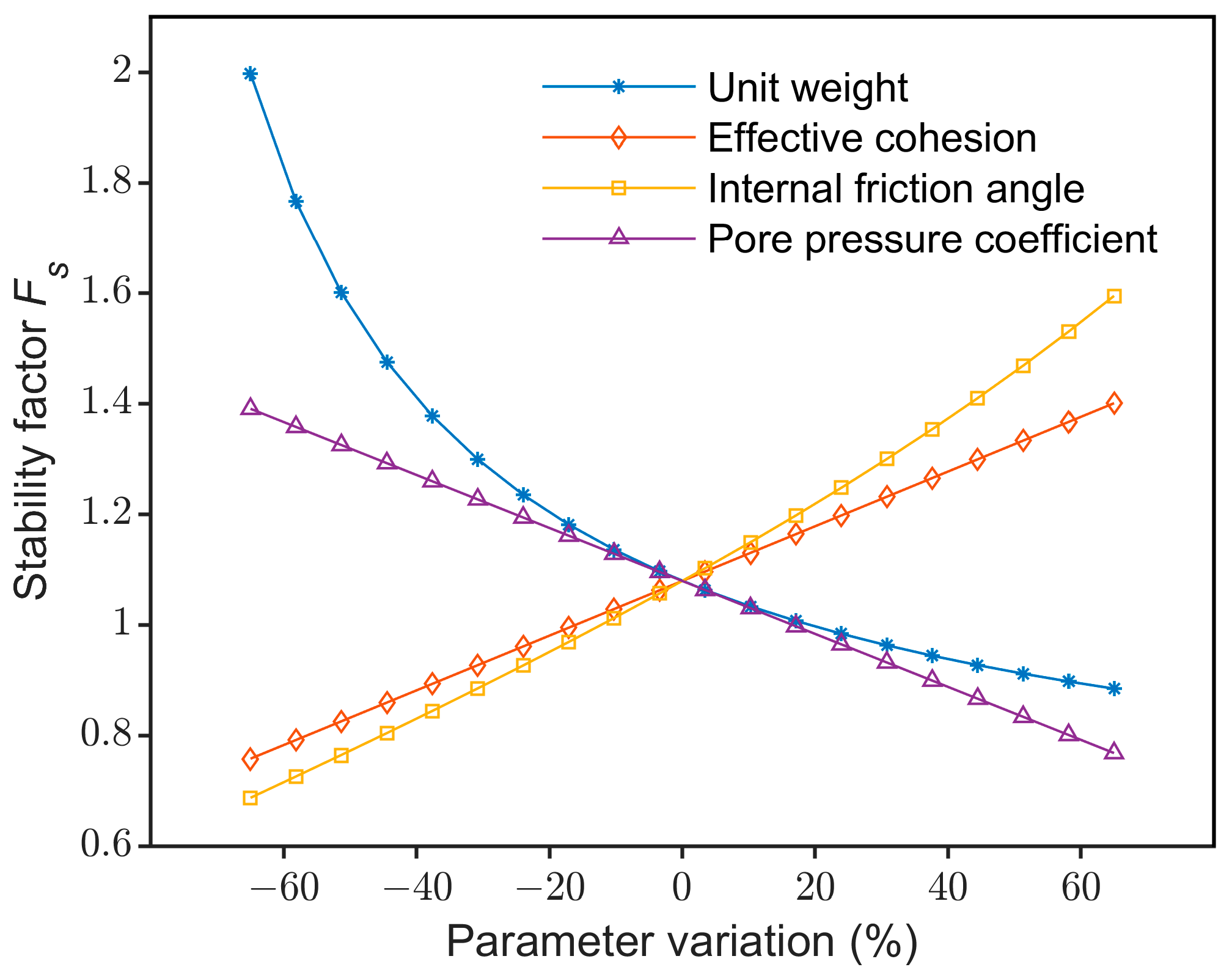
6. Discussion
6.1. Advantages
6.2. Limitations and Future Works
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pudasaini, S.P. A general two-phase debris flow model. J. Geophys. Res. Earth Surf. 2012, 117, F03010. [Google Scholar] [CrossRef]
- Dowling, C.A.; Santi, P.M. Debris flows and their toll on human life: A global analysis of debris-flow fatalities from 1950 to 2011. Nat. Hazards 2014, 71, 203–227. [Google Scholar] [CrossRef]
- Han, Z.; Ma, Y.; Li, Y.; Zhang, H.; Chen, N.; Hu, G.; Chen, G. Hydrodynamic and topography based cellular automaton model for simulating debris flow run-out extent and entrainment behavior. Water Res. 2021, 193, 116872. [Google Scholar] [CrossRef] [PubMed]
- Scheidl, C.; Rickenmann, D. Empirical prediction of debris-flow mobility and deposition on fans. Earth Surf. Process. Landforms 2010, 35, 157–173. [Google Scholar] [CrossRef]
- Du, J.; Fan, Z.J.; Xu, W.T.; Dong, L.Y. Research progress of initial mechanism on debris flow and related discrimination methods: A review. Front. Earth Sci. 2021, 9, 629567. [Google Scholar] [CrossRef]
- Liu, X.; Wang, F.; Nawnit, K.; Lv, X.; Wang, S. Experimental study on debris flow initiation. Bull. Eng. Geol. Environ. 2020, 79, 1565–1580. [Google Scholar] [CrossRef]
- Tang, H.; McGuire, L.A.; Rengers, F.K.; Kean, J.W.; Staley, D.M.; Smith, J.B. Evolution of debris-flow initiation mechanisms and sediment sources during a sequence of postwildfire rainstorms. J. Geophys. Res. Earth Surf. 2019, 124, 1572–1595. [Google Scholar] [CrossRef]
- Chen, H.X.; Zhang, L.M.; Zhang, S.; Xiang, B.; Wang, X.F. Hybrid simulation of the initiation and runout characteristics of a catastrophic debris flow. J. Mt. Sci. 2013, 10, 219–232. [Google Scholar] [CrossRef]
- Zhong, W.; He, N.; Cosgrove, T.; Zhu, Y.J.; Fu, L. Analysis of the correlation between fractal dimension of gravelly soil and debris-flow initiation through in-situ experiments. Appl. Ecol. Environ. Res. 2019, 17, 7573–7589. [Google Scholar] [CrossRef]
- Zhou, J.W.; Cui, P.; Yang, X.G. Dynamic process analysis for the initiation and movement of the Donghekou landslide-debris flow triggered by the Wenchuan earthquake. J. Asian Earth Sci. 2013, 76, 70–84. [Google Scholar] [CrossRef]
- Hu, M.J.; Wang, R.; Chen, Z.X.; Wang, Z.B. Initiation process simulation of debris deposit based on particle flow code. Rock Soil Mech. 2010, 31, 394–397. (In Chinese) [Google Scholar]
- Liu, J.; Nakatani, K.; Mizuyama, T. Effect assessment of debris flow mitigation works based on numerical simulation by using Kanako 2D. Landslides 2013, 10, 161–173. [Google Scholar] [CrossRef]
- Lin, D.G.; Hsu, S.Y.; Chang, K.T. Numerical simulations of flow motion and deposition characteristics of granular debris flows. Nat. Hazards 2009, 50, 623–650. [Google Scholar] [CrossRef]
- Wang, C.; Li, S.; Esaki, T. GIS-based two-dimensional numerical simulation of rainfall-induced debris flow. NHESS 2008, 8, 47–58. [Google Scholar] [CrossRef]
- Luna, B.Q.; Remaître, A.; Van Asch, T.W.; Malet, J.P.; Van Westen, C.J. Analysis of debris flow behavior with a one dimensional run-out model incorporating entrainment. Eng. Geol. 2012, 128, 63–75. [Google Scholar] [CrossRef]
- Cannon, S.H.; Gartner, J.E.; Wilson, R.C.; Bowers, J.C.; Laber, J.L. Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California. Geomorph 2008, 96, 250–269. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Yang, S.; Wang, M.; Shi, X.; Yao, S.; Mitri, H.S. Slope stability prediction for circular mode failure using gradient boosting machine approach based on an updated database of case histories. Saf. Sci. 2019, 118, 505–518. [Google Scholar] [CrossRef]
- Hazari, S.; Sharma, R.P.; Ghosh, S. Swedish circle method for pseudo-dynamic analysis of slope considering circular failure mechanism. Geotech. Geol. Eng. 2020, 38, 2573–2589. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, W.; Zheng, H. Searching for critical slip surfaces of slopes using stress fields by numerical manifold method. JRMGE 2020, 12, 1313–1325. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.Q.; Cao, Z.J.; Wang, Y. Adaptive Monte Carlo simulation method for system reliability analysis of slope stability based on limit equilibrium methods. Eng. Geol. 2020, 264, 105384. [Google Scholar] [CrossRef]
- Crosta, G.B.; Imposimato, S.; Roddeman, D. Numerical modeling of 2-D granular step collapse on erodible and nonerodible surface. J. Geophys. Res. Earth Surf. 2009, 114, F03020. [Google Scholar] [CrossRef]
- Horton, P.; Jaboyedoff, M.; Rudaz, B.E.A.; Zimmermann, M. Flow-R, a model for susceptibility mapping of debris flows and other gravitational hazards at a regional scale. Nat. Hazards Earth Syst. Sci. 2013, 13, 869–885. [Google Scholar] [CrossRef]
- Iverson, R.M.; George, D.L. A depth-averaged debris-flow model that includes the effects of evolving dilatancy. I. Proc. R. Soc. A 2014, 470, 20130819. [Google Scholar] [CrossRef]
- Han, Z.; Chen, G.; Li, Y.; Tang, C.; Xu, L.; He, Y.; Wang, W. Numerical simulation of debris-flow behavior incorporating a dynamic method for estimating the entrainment. Eng. Geol. 2015, 190, 52–64. [Google Scholar] [CrossRef]
- Ouyang, C.; He, S.; Tang, C. Numerical analysis of dynamics of debris flow over erodible beds in Wenchuan earthquake-induced area. Eng. Geol. 2015, 194, 62–72. [Google Scholar] [CrossRef]
- Armanini, A.; Fraccarollo, L.; Rosatti, G. Two-dimensional simulation of debris flows in erodible channels. Comput. Geosci. 2009, 35, 993–1006. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Chanson, H. Ritter’s dry-bed dam-break flows: Positive and negative wave dynamics. Environ. Fluid Mech. 2017, 17, 665–694. [Google Scholar] [CrossRef]
- Chen, C.; Qi, J.; Li, C.; Beardsley, R.C.; Lin, H.; Walker, R.; Gates, K. Complexity of the flooding/drying process in an estuarine tidal-creek salt-marsh system: An application of FVCOM. J. Geophys. Res. Ocean. 2008, 113, C07052. [Google Scholar] [CrossRef]
- Liang, D.; Lin, B.; Falconer, R.A. A boundary-fitted numerical model for flood routing with shock-capturing capability. J. Hydrol. 2007, 332, 477–486. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Hagen, S.C. Review of wetting and drying algorithms for numerical tidal flow models. Int. J. Numer. Meth. Fluids 2013, 71, 473–487. [Google Scholar] [CrossRef]
- Liu, D.; Tang, J.; Wang, H.; Cao, Y.; Bazai, N.A.; Chen, H.; Liu, D. A new method for wet-dry front treatment in outburst flood simulation. Water 2021, 13, 221. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, N.; Pei, Y. Well-balanced finite volume scheme for shallow water flooding and drying over arbitrary topography. Eng. Appl. Comput. Fluid Mech. 2013, 7, 40–54. [Google Scholar] [CrossRef]
- Le, H.A.; Lambrechts, J.; Ortleb, S.; Gratiot, N.; Deleersnijder, E.; Soares-Frazão, S. An implicit wetting–drying algorithm for the discontinuous Galerkin method: Application to the Tonle Sap, Mekong River Basin. Environ. Fluid Mech. 2020, 20, 923–951. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing river model set-up for 2-D dynamic flood modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Baeza, A.; Donat, R.; Martinez-Gavara, A. A numerical treatment of wet/dry zones in well-balanced hybrid schemes for shallow water flow. Appl. Numer. Math. 2012, 62, 264–277. [Google Scholar] [CrossRef]
- Zhou, X.P.; Cheng, H. Stability analysis of three-dimensional seismic landslides using the rigorous limit equilibrium method. Eng. Geol. 2014, 174, 87–102. [Google Scholar] [CrossRef]
- Han, Z.; Chen, G.; Li, Y.; He, Y. Assessing entrainment of bed material in a debris-flow event: A theoretical approach incorporating Monte Carlo method. ESPL 2015, 40, 1877–1890. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhang, J.M. Extended algorithm using Monte Carlo techniques for searching general critical slip surface in slope stability analysis. Yantu Gongcheng Xuebao (Chin. J. Geotech. Eng.) 2006, 28, 857–862. (In Chinese) [Google Scholar] [CrossRef]
- Naef, D.; Rickenmann, D.; Rutschmann, P.; McArdell, B.W. Comparison of flow resistance relations for debris flows using a one-dimensional finite element simulation model. NHESS 2006, 6, 155–165. [Google Scholar] [CrossRef]
- Han, Z.; Su, B.; Li, Y.; Dou, J.; Wang, W.; Zhao, L. Modeling the progressive entrainment of bed sediment by viscous debris flows using the three-dimensional SC-HBP-SPH method. Water Res. 2020, 182, 116031. [Google Scholar] [CrossRef]
- Iverson, R.M.; Reid, M.E.; Logan, M.; LaHusen, R.G.; Godt, J.W.; Griswold, J.P. Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nat. Geosci. 2011, 4, 116–121. [Google Scholar] [CrossRef]
- Hungr, O.; McDougall, S. Two numerical models for landslide dynamic analysis. Comput. Geosci. 2009, 35, 978–992. [Google Scholar] [CrossRef]
- Bingham, H.B.; Zhang, H. On the accuracy of finite-difference solutions for nonlinear water waves. J. Eng. Math. 2007, 58, 211–228. [Google Scholar] [CrossRef]
- Zhao, D.H.; Shen, H.W.; Tabios, G.Q., III; Lai, J.S.; Tan, W.Y. Finite-volume two-dimensional unsteady-flow model for river basins. J. Hydraul. Eng. 1994, 120, 863–883. [Google Scholar] [CrossRef]
- Xia, J.; Falconer, R.A.; Lin, B.; Tan, G. Modelling flood routing on initially dry beds with the refined treatment of wetting and drying. IJRBM 2010, 8, 225–243. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, S.; Li, W.L.; Van Asch, T.W. The 13 August 2010 catastrophic debris flows after the 2008 Wenchuan earthquake, China. Nat. Hazards Earth Syst. Sci. 2012, 12, 201–216. [Google Scholar] [CrossRef]
- Shen, W.; Wang, D.; Qu, H.; Li, T. The effect of check dams on the dynamic and bed entrainment processes of debris flows. Landslides 2019, 16, 2201–2217. [Google Scholar] [CrossRef]
- Li, D.; Xu, X.; Ji, F.; Cao, N. Engineering management and its effect of large debris flow at Hongchun valley in Yingxiu town, Wenchuan County. J. Eng. Geol. 2013, 21, 260–268. [Google Scholar]
- Zhao, T.Y.; Yan, K.; Li, H.W.; Wang, X. Study on theoretical modeling and vibration performance of an assembled cylindrical shell-plate structure with whirl motion. Appl. Math. Model. 2022, 110, 618–632. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Li, K.; Ma, H. Study on dynamic characteristics of a rotating cylindrical shell with uncertain parameters. Anal. Math. Phys. 2022, 12, 97. [Google Scholar] [CrossRef]
- Li, W.; Zhu, J.; Fu, L.; Zhu, Q.; Xie, Y.; Hu, Y. An augmented representation method of debris flow scenes to improve public perception. Int. J. Geogr. Inf. Sci. 2021, 35, 1521–1544. [Google Scholar] [CrossRef]
- He, S.; Wang, D.; Zhao, P.; Chen, W.; Li, Y.; Chen, X.; Jamali, A.A. Dynamic simulation of debris flow waste-shoal land use based on an integrated system dynamics-geographic information systems model. LAND DEGRAD DEV 2022, 33, 2062–2075. [Google Scholar] [CrossRef]

| Parameter | Unit Weight | Effective Cohesion | Pore Pressure Coefficient | Internal Friction Angle |
|---|---|---|---|---|
| Notation | c | |||
| Unit | ||||
| Value range | ||||
| Coefficient of variation | 0 | 0.25 |
| Module | Parameter | Notation | Units | Value |
|---|---|---|---|---|
| Debris-flow material (rheology) | Debris flow density | 2020 | ||
| Dynamic viscosity | 0.15 | |||
| Bulk basal friction angle of the flowing mass | ° | 12 | ||
| Chezy coefficient | / | 12 | ||
| Control parameters (simulation) | Fitting parameter of the velocity profile | / | 0.50 | |
| Grid size | 2.5 | |||
| Time increment | 0.001 | |||
| The minimum depth | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Li, M.; Li, Y.; Zhao, M.; Li, C.; Xie, W.; Ding, H.; Ma, Y. An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models. Water 2023, 15, 1592. https://doi.org/10.3390/w15081592
Han Z, Li M, Li Y, Zhao M, Li C, Xie W, Ding H, Ma Y. An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models. Water. 2023; 15(8):1592. https://doi.org/10.3390/w15081592
Chicago/Turabian StyleHan, Zheng, Ming Li, Yange Li, Mingyue Zhao, Changli Li, Wendu Xie, Haohui Ding, and Yangfan Ma. 2023. "An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models" Water 15, no. 8: 1592. https://doi.org/10.3390/w15081592






