An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models
Abstract
1. Introduction
2. Physically Based Initiation Model of the Debris Flow Sources
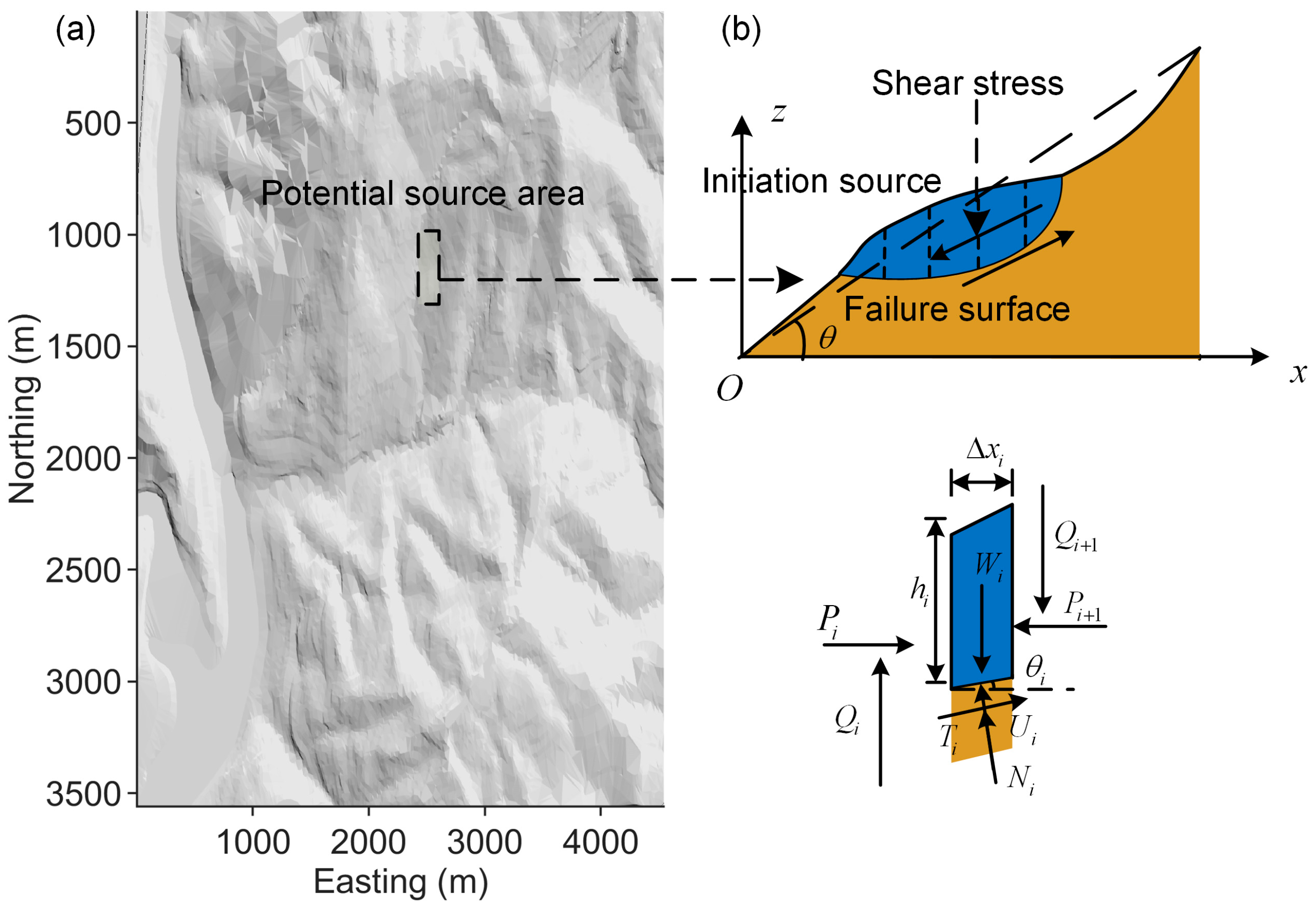
2.1. Limit Equilibrium Method for Slope Stability Analysis
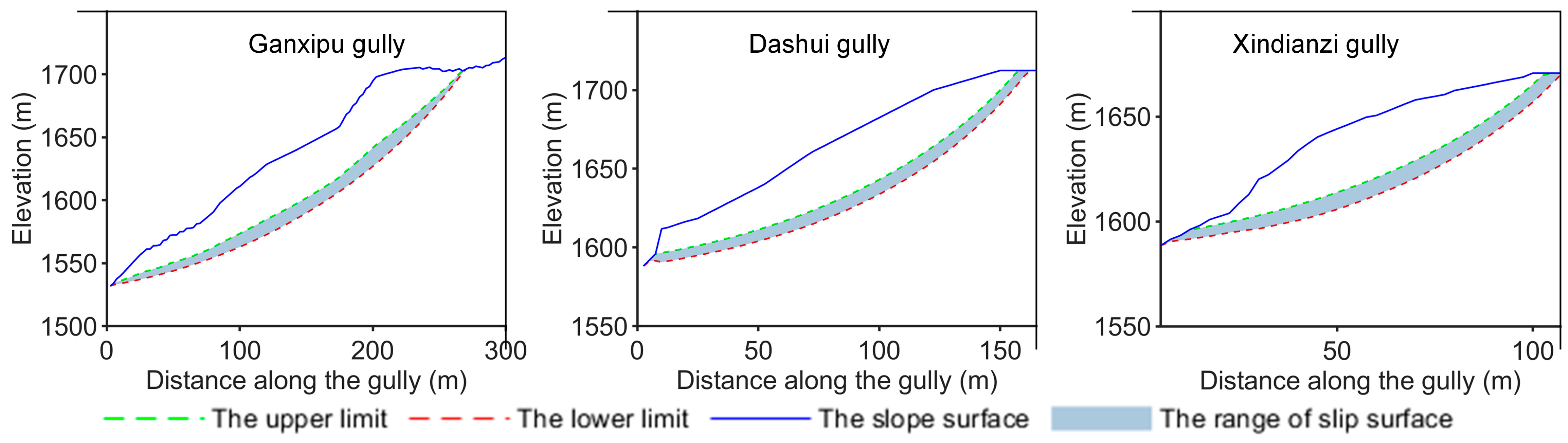
2.2. Critical Slip Surface Determination Incorporated with the Monte Carlo Method
- (1)
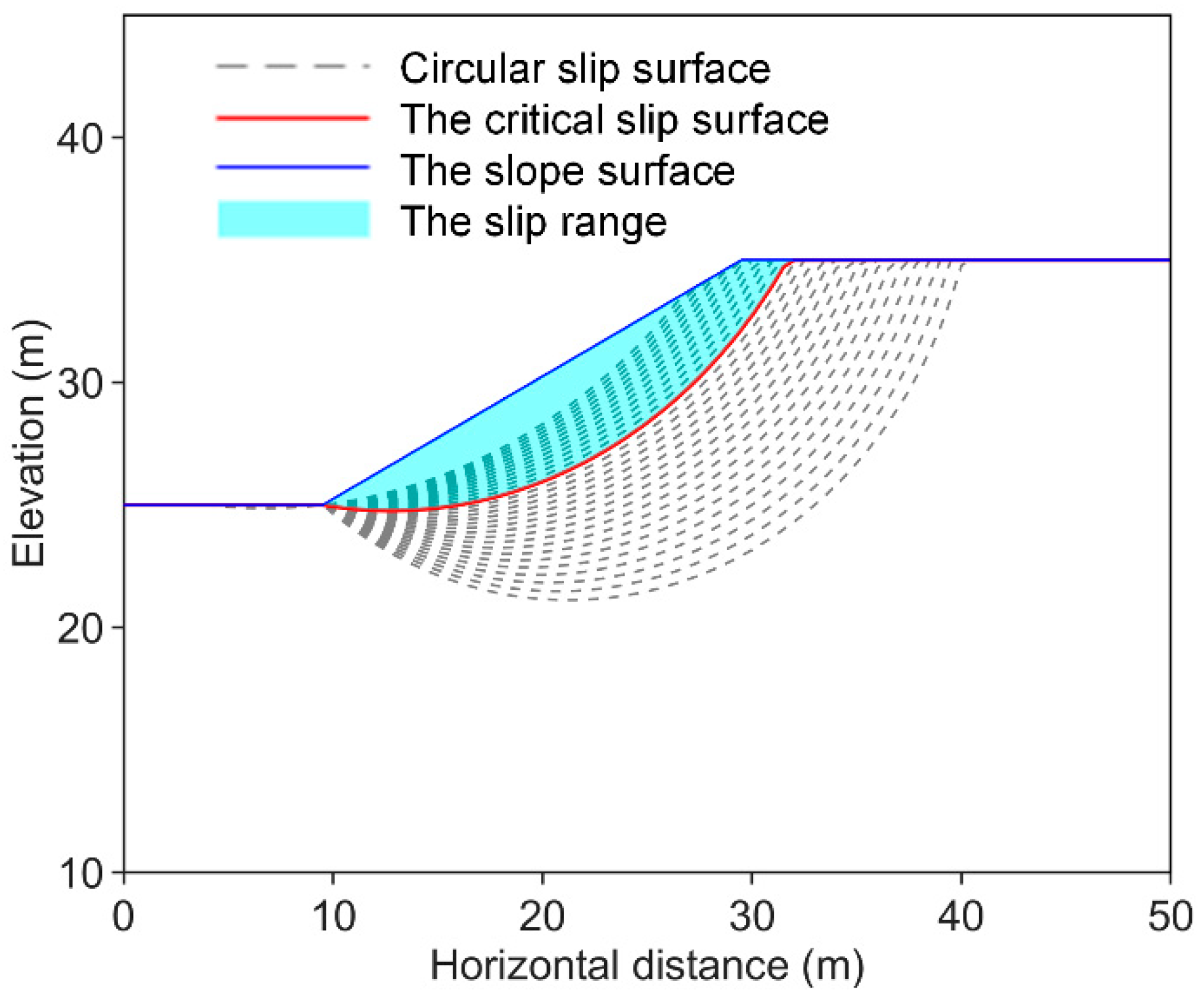
- Composite critical slip surface determination.
- The slip surface should be located entirely within the slope body range, and the shear inlet and shear outlet are on the slope surface;
- There should be smooth transitions between adjacent slip slice segments and no sharp corners. The angle between two adjacent slip slice segments should be greater than 90°;
- The horizontal spacing of adjacent nodes should be greater than the minimum horizontal spacing to avoid overlap of the slice division nodes.
- (2)
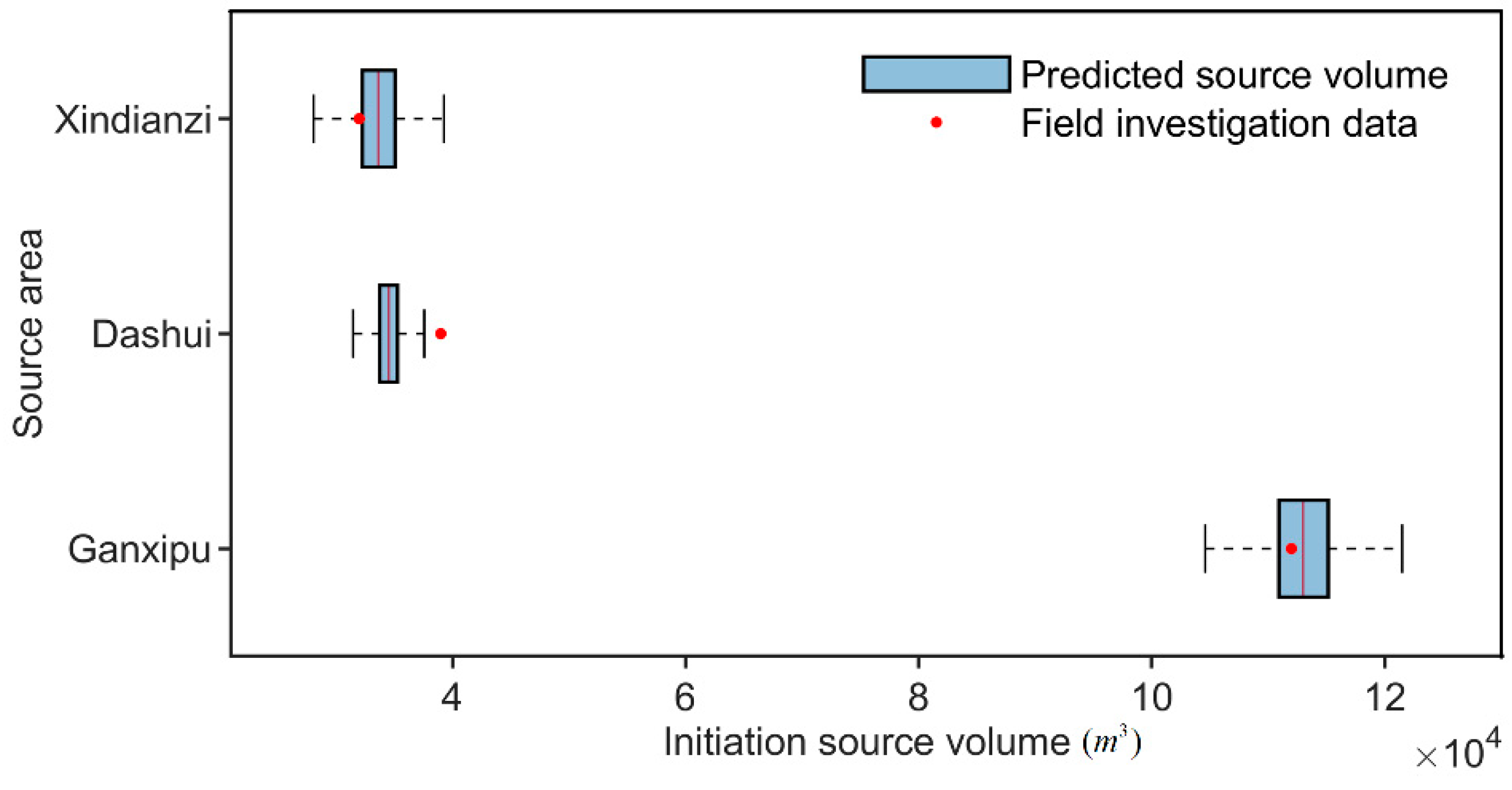
- Considering the spatial variability of the soil, calculate the range of the critical slip surface and the initiation source volume.
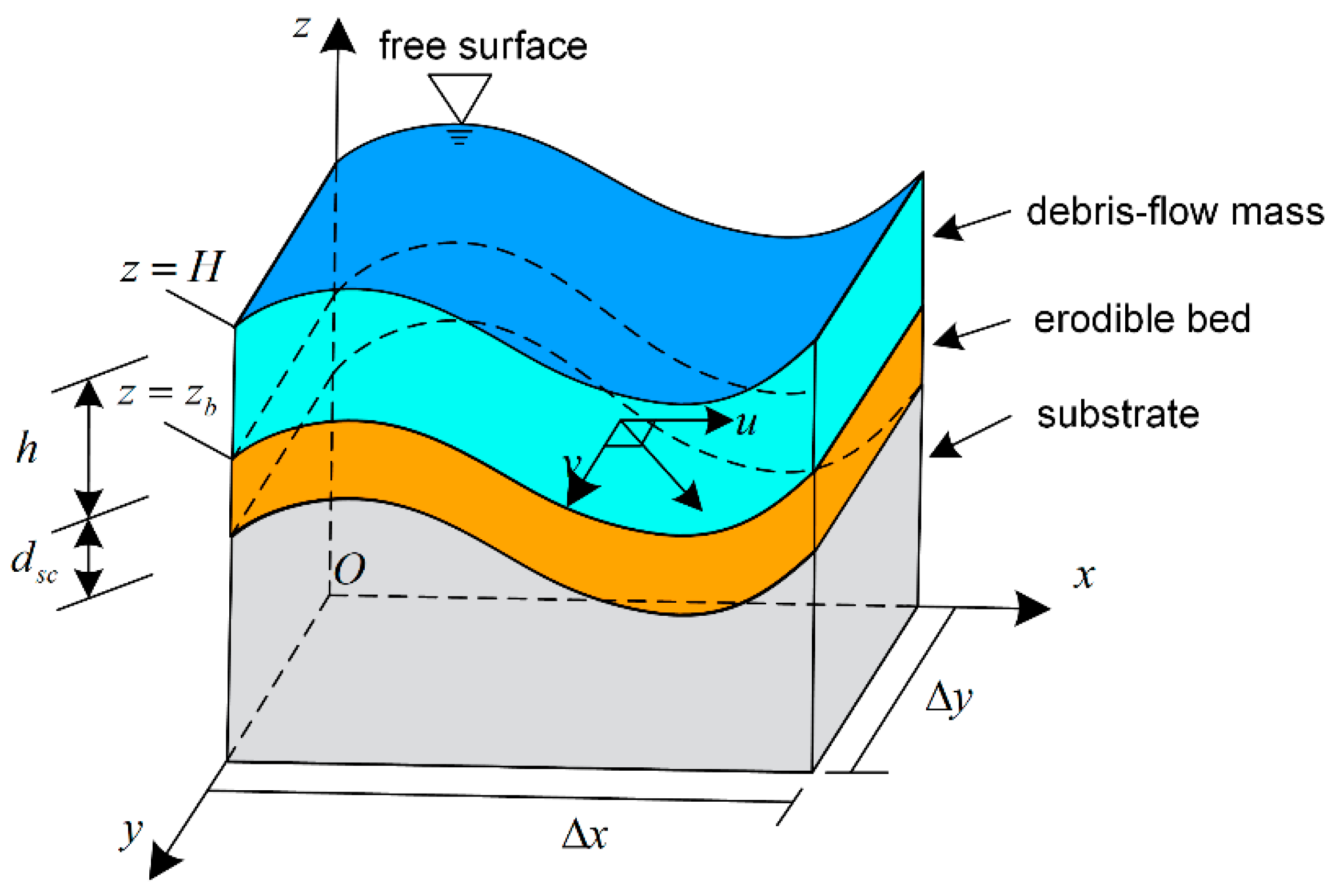
3. Entrainment-Incorporated Numerical Model
4. Wet/Dry Front Treatment over Complex Topography
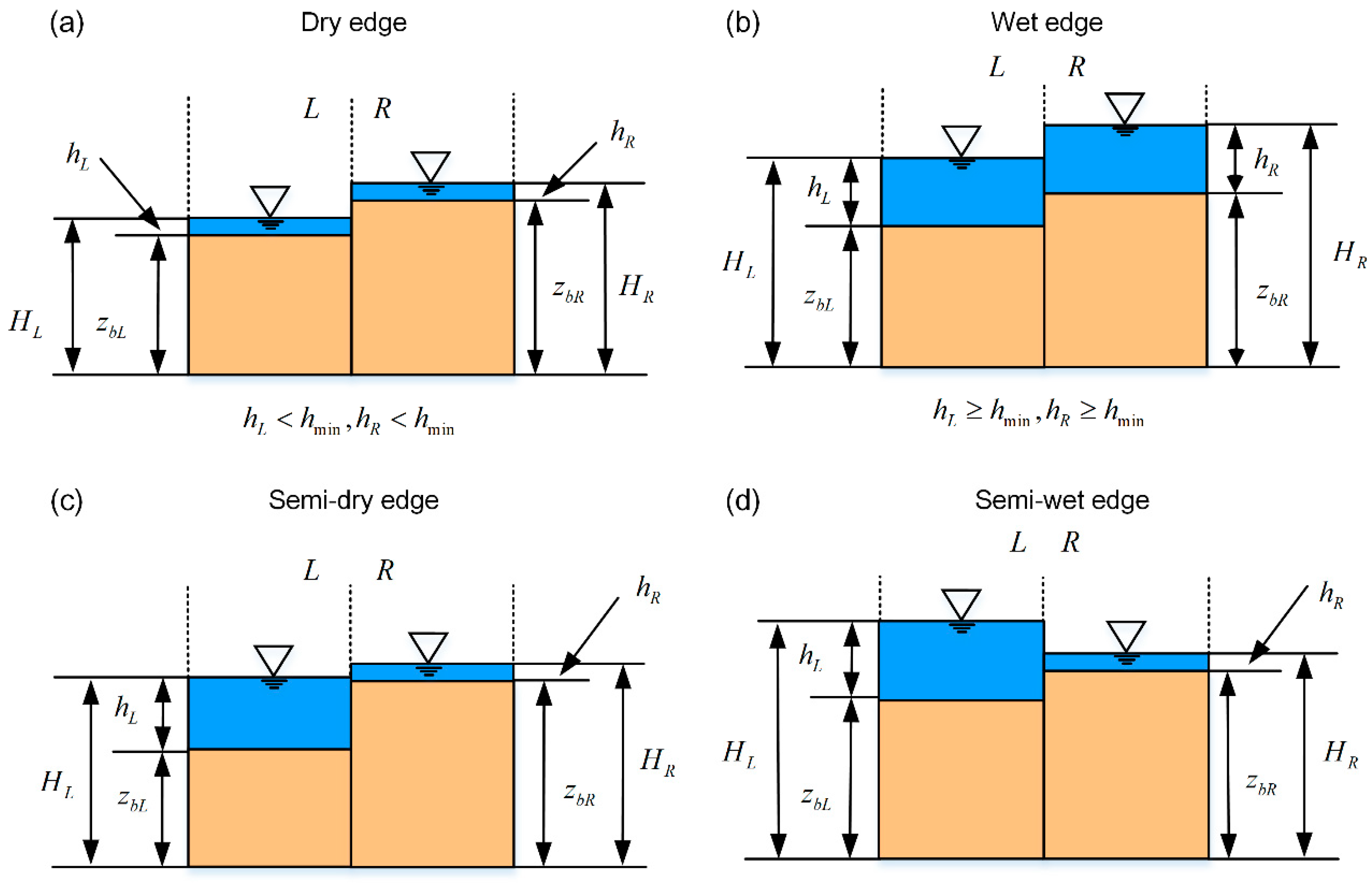
- Dry edge. The flow depths of both neighboring cells are smaller than , which is mathematically expressed as , as shown in Figure 5a.
- Wet edge: in contrast to the dry edge, the flow depths of both neighboring cells are greater than , which is , as shown in Figure 5b.
- Semi-dry edge: the flow depth of one neighboring cell is greater than while the other one is less than , and the flow surface level of the dry side is higher than that of the wet side. For example, , and , as shown in Figure 5c;
- Semi-wet edge: the flow depth condition of the cells on both sides is the same as that of the semi-dry edge, but the flow surface level of the wet side is higher than that of the dry side—for example, , and , as shown in Figure 5d.
5. Case Study: The 2010 Hongchun Debris-Flow Event in the Yingxiu Town, China
5.1. The Overview of the 2010 Hongchun Debris-Flow Event
5.2. The Physically Based Estimation of the Slope Initiation Source
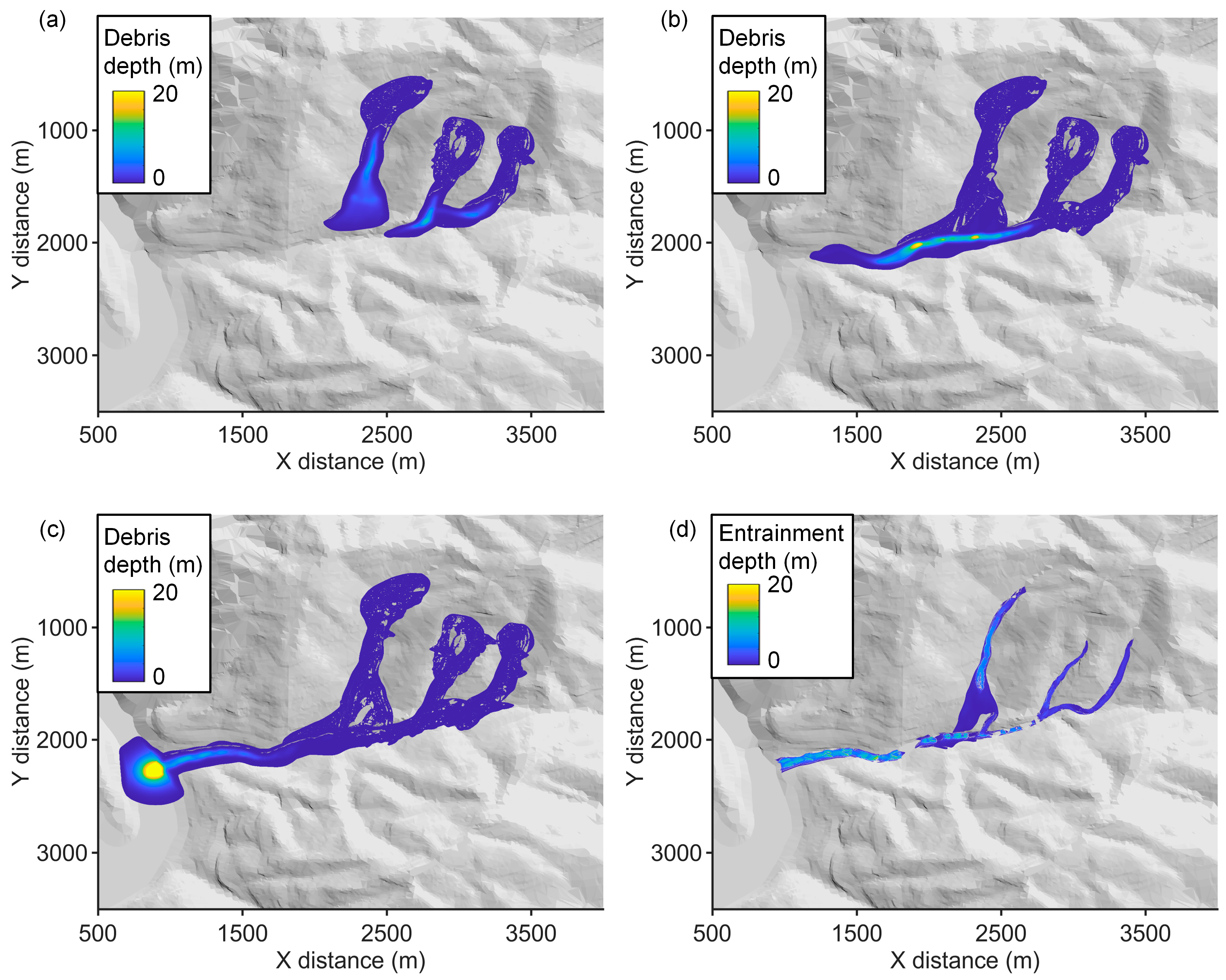
5.3. Numerical Simulation of the Debris-Flow Dynamic Process
6. Discussion
6.1. Advantages
6.2. Limitations and Future Works
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pudasaini, S.P. A general two-phase debris flow model. J. Geophys. Res. Earth Surf. 2012, 117, F03010. [Google Scholar] [CrossRef]
- Dowling, C.A.; Santi, P.M. Debris flows and their toll on human life: A global analysis of debris-flow fatalities from 1950 to 2011. Nat. Hazards 2014, 71, 203–227. [Google Scholar] [CrossRef]
- Han, Z.; Ma, Y.; Li, Y.; Zhang, H.; Chen, N.; Hu, G.; Chen, G. Hydrodynamic and topography based cellular automaton model for simulating debris flow run-out extent and entrainment behavior. Water Res. 2021, 193, 116872. [Google Scholar] [CrossRef] [PubMed]
- Scheidl, C.; Rickenmann, D. Empirical prediction of debris-flow mobility and deposition on fans. Earth Surf. Process. Landforms 2010, 35, 157–173. [Google Scholar] [CrossRef]
- Du, J.; Fan, Z.J.; Xu, W.T.; Dong, L.Y. Research progress of initial mechanism on debris flow and related discrimination methods: A review. Front. Earth Sci. 2021, 9, 629567. [Google Scholar] [CrossRef]
- Liu, X.; Wang, F.; Nawnit, K.; Lv, X.; Wang, S. Experimental study on debris flow initiation. Bull. Eng. Geol. Environ. 2020, 79, 1565–1580. [Google Scholar] [CrossRef]
- Tang, H.; McGuire, L.A.; Rengers, F.K.; Kean, J.W.; Staley, D.M.; Smith, J.B. Evolution of debris-flow initiation mechanisms and sediment sources during a sequence of postwildfire rainstorms. J. Geophys. Res. Earth Surf. 2019, 124, 1572–1595. [Google Scholar] [CrossRef]
- Chen, H.X.; Zhang, L.M.; Zhang, S.; Xiang, B.; Wang, X.F. Hybrid simulation of the initiation and runout characteristics of a catastrophic debris flow. J. Mt. Sci. 2013, 10, 219–232. [Google Scholar] [CrossRef]
- Zhong, W.; He, N.; Cosgrove, T.; Zhu, Y.J.; Fu, L. Analysis of the correlation between fractal dimension of gravelly soil and debris-flow initiation through in-situ experiments. Appl. Ecol. Environ. Res. 2019, 17, 7573–7589. [Google Scholar] [CrossRef]
- Zhou, J.W.; Cui, P.; Yang, X.G. Dynamic process analysis for the initiation and movement of the Donghekou landslide-debris flow triggered by the Wenchuan earthquake. J. Asian Earth Sci. 2013, 76, 70–84. [Google Scholar] [CrossRef]
- Hu, M.J.; Wang, R.; Chen, Z.X.; Wang, Z.B. Initiation process simulation of debris deposit based on particle flow code. Rock Soil Mech. 2010, 31, 394–397. (In Chinese) [Google Scholar]
- Liu, J.; Nakatani, K.; Mizuyama, T. Effect assessment of debris flow mitigation works based on numerical simulation by using Kanako 2D. Landslides 2013, 10, 161–173. [Google Scholar] [CrossRef]
- Lin, D.G.; Hsu, S.Y.; Chang, K.T. Numerical simulations of flow motion and deposition characteristics of granular debris flows. Nat. Hazards 2009, 50, 623–650. [Google Scholar] [CrossRef]
- Wang, C.; Li, S.; Esaki, T. GIS-based two-dimensional numerical simulation of rainfall-induced debris flow. NHESS 2008, 8, 47–58. [Google Scholar] [CrossRef]
- Luna, B.Q.; Remaître, A.; Van Asch, T.W.; Malet, J.P.; Van Westen, C.J. Analysis of debris flow behavior with a one dimensional run-out model incorporating entrainment. Eng. Geol. 2012, 128, 63–75. [Google Scholar] [CrossRef]
- Cannon, S.H.; Gartner, J.E.; Wilson, R.C.; Bowers, J.C.; Laber, J.L. Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California. Geomorph 2008, 96, 250–269. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Yang, S.; Wang, M.; Shi, X.; Yao, S.; Mitri, H.S. Slope stability prediction for circular mode failure using gradient boosting machine approach based on an updated database of case histories. Saf. Sci. 2019, 118, 505–518. [Google Scholar] [CrossRef]
- Hazari, S.; Sharma, R.P.; Ghosh, S. Swedish circle method for pseudo-dynamic analysis of slope considering circular failure mechanism. Geotech. Geol. Eng. 2020, 38, 2573–2589. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, W.; Zheng, H. Searching for critical slip surfaces of slopes using stress fields by numerical manifold method. JRMGE 2020, 12, 1313–1325. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.Q.; Cao, Z.J.; Wang, Y. Adaptive Monte Carlo simulation method for system reliability analysis of slope stability based on limit equilibrium methods. Eng. Geol. 2020, 264, 105384. [Google Scholar] [CrossRef]
- Crosta, G.B.; Imposimato, S.; Roddeman, D. Numerical modeling of 2-D granular step collapse on erodible and nonerodible surface. J. Geophys. Res. Earth Surf. 2009, 114, F03020. [Google Scholar] [CrossRef]
- Horton, P.; Jaboyedoff, M.; Rudaz, B.E.A.; Zimmermann, M. Flow-R, a model for susceptibility mapping of debris flows and other gravitational hazards at a regional scale. Nat. Hazards Earth Syst. Sci. 2013, 13, 869–885. [Google Scholar] [CrossRef]
- Iverson, R.M.; George, D.L. A depth-averaged debris-flow model that includes the effects of evolving dilatancy. I. Proc. R. Soc. A 2014, 470, 20130819. [Google Scholar] [CrossRef]
- Han, Z.; Chen, G.; Li, Y.; Tang, C.; Xu, L.; He, Y.; Wang, W. Numerical simulation of debris-flow behavior incorporating a dynamic method for estimating the entrainment. Eng. Geol. 2015, 190, 52–64. [Google Scholar] [CrossRef]
- Ouyang, C.; He, S.; Tang, C. Numerical analysis of dynamics of debris flow over erodible beds in Wenchuan earthquake-induced area. Eng. Geol. 2015, 194, 62–72. [Google Scholar] [CrossRef]
- Armanini, A.; Fraccarollo, L.; Rosatti, G. Two-dimensional simulation of debris flows in erodible channels. Comput. Geosci. 2009, 35, 993–1006. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Chanson, H. Ritter’s dry-bed dam-break flows: Positive and negative wave dynamics. Environ. Fluid Mech. 2017, 17, 665–694. [Google Scholar] [CrossRef]
- Chen, C.; Qi, J.; Li, C.; Beardsley, R.C.; Lin, H.; Walker, R.; Gates, K. Complexity of the flooding/drying process in an estuarine tidal-creek salt-marsh system: An application of FVCOM. J. Geophys. Res. Ocean. 2008, 113, C07052. [Google Scholar] [CrossRef]
- Liang, D.; Lin, B.; Falconer, R.A. A boundary-fitted numerical model for flood routing with shock-capturing capability. J. Hydrol. 2007, 332, 477–486. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Hagen, S.C. Review of wetting and drying algorithms for numerical tidal flow models. Int. J. Numer. Meth. Fluids 2013, 71, 473–487. [Google Scholar] [CrossRef]
- Liu, D.; Tang, J.; Wang, H.; Cao, Y.; Bazai, N.A.; Chen, H.; Liu, D. A new method for wet-dry front treatment in outburst flood simulation. Water 2021, 13, 221. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, N.; Pei, Y. Well-balanced finite volume scheme for shallow water flooding and drying over arbitrary topography. Eng. Appl. Comput. Fluid Mech. 2013, 7, 40–54. [Google Scholar] [CrossRef]
- Le, H.A.; Lambrechts, J.; Ortleb, S.; Gratiot, N.; Deleersnijder, E.; Soares-Frazão, S. An implicit wetting–drying algorithm for the discontinuous Galerkin method: Application to the Tonle Sap, Mekong River Basin. Environ. Fluid Mech. 2020, 20, 923–951. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing river model set-up for 2-D dynamic flood modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Baeza, A.; Donat, R.; Martinez-Gavara, A. A numerical treatment of wet/dry zones in well-balanced hybrid schemes for shallow water flow. Appl. Numer. Math. 2012, 62, 264–277. [Google Scholar] [CrossRef]
- Zhou, X.P.; Cheng, H. Stability analysis of three-dimensional seismic landslides using the rigorous limit equilibrium method. Eng. Geol. 2014, 174, 87–102. [Google Scholar] [CrossRef]
- Han, Z.; Chen, G.; Li, Y.; He, Y. Assessing entrainment of bed material in a debris-flow event: A theoretical approach incorporating Monte Carlo method. ESPL 2015, 40, 1877–1890. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhang, J.M. Extended algorithm using Monte Carlo techniques for searching general critical slip surface in slope stability analysis. Yantu Gongcheng Xuebao (Chin. J. Geotech. Eng.) 2006, 28, 857–862. (In Chinese) [Google Scholar] [CrossRef]
- Naef, D.; Rickenmann, D.; Rutschmann, P.; McArdell, B.W. Comparison of flow resistance relations for debris flows using a one-dimensional finite element simulation model. NHESS 2006, 6, 155–165. [Google Scholar] [CrossRef]
- Han, Z.; Su, B.; Li, Y.; Dou, J.; Wang, W.; Zhao, L. Modeling the progressive entrainment of bed sediment by viscous debris flows using the three-dimensional SC-HBP-SPH method. Water Res. 2020, 182, 116031. [Google Scholar] [CrossRef]
- Iverson, R.M.; Reid, M.E.; Logan, M.; LaHusen, R.G.; Godt, J.W.; Griswold, J.P. Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nat. Geosci. 2011, 4, 116–121. [Google Scholar] [CrossRef]
- Hungr, O.; McDougall, S. Two numerical models for landslide dynamic analysis. Comput. Geosci. 2009, 35, 978–992. [Google Scholar] [CrossRef]
- Bingham, H.B.; Zhang, H. On the accuracy of finite-difference solutions for nonlinear water waves. J. Eng. Math. 2007, 58, 211–228. [Google Scholar] [CrossRef]
- Zhao, D.H.; Shen, H.W.; Tabios, G.Q., III; Lai, J.S.; Tan, W.Y. Finite-volume two-dimensional unsteady-flow model for river basins. J. Hydraul. Eng. 1994, 120, 863–883. [Google Scholar] [CrossRef]
- Xia, J.; Falconer, R.A.; Lin, B.; Tan, G. Modelling flood routing on initially dry beds with the refined treatment of wetting and drying. IJRBM 2010, 8, 225–243. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, S.; Li, W.L.; Van Asch, T.W. The 13 August 2010 catastrophic debris flows after the 2008 Wenchuan earthquake, China. Nat. Hazards Earth Syst. Sci. 2012, 12, 201–216. [Google Scholar] [CrossRef]
- Shen, W.; Wang, D.; Qu, H.; Li, T. The effect of check dams on the dynamic and bed entrainment processes of debris flows. Landslides 2019, 16, 2201–2217. [Google Scholar] [CrossRef]
- Li, D.; Xu, X.; Ji, F.; Cao, N. Engineering management and its effect of large debris flow at Hongchun valley in Yingxiu town, Wenchuan County. J. Eng. Geol. 2013, 21, 260–268. [Google Scholar]
- Zhao, T.Y.; Yan, K.; Li, H.W.; Wang, X. Study on theoretical modeling and vibration performance of an assembled cylindrical shell-plate structure with whirl motion. Appl. Math. Model. 2022, 110, 618–632. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Li, K.; Ma, H. Study on dynamic characteristics of a rotating cylindrical shell with uncertain parameters. Anal. Math. Phys. 2022, 12, 97. [Google Scholar] [CrossRef]
- Li, W.; Zhu, J.; Fu, L.; Zhu, Q.; Xie, Y.; Hu, Y. An augmented representation method of debris flow scenes to improve public perception. Int. J. Geogr. Inf. Sci. 2021, 35, 1521–1544. [Google Scholar] [CrossRef]
- He, S.; Wang, D.; Zhao, P.; Chen, W.; Li, Y.; Chen, X.; Jamali, A.A. Dynamic simulation of debris flow waste-shoal land use based on an integrated system dynamics-geographic information systems model. LAND DEGRAD DEV 2022, 33, 2062–2075. [Google Scholar] [CrossRef]

| Parameter | Unit Weight | Effective Cohesion | Pore Pressure Coefficient | Internal Friction Angle |
|---|---|---|---|---|
| Notation | c | |||
| Unit | ||||
| Value range | ||||
| Coefficient of variation | 0 | 0.25 |
| Module | Parameter | Notation | Units | Value |
|---|---|---|---|---|
| Debris-flow material (rheology) | Debris flow density | 2020 | ||
| Dynamic viscosity | 0.15 | |||
| Bulk basal friction angle of the flowing mass | ° | 12 | ||
| Chezy coefficient | / | 12 | ||
| Control parameters (simulation) | Fitting parameter of the velocity profile | / | 0.50 | |
| Grid size | 2.5 | |||
| Time increment | 0.001 | |||
| The minimum depth | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Li, M.; Li, Y.; Zhao, M.; Li, C.; Xie, W.; Ding, H.; Ma, Y. An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models. Water 2023, 15, 1592. https://doi.org/10.3390/w15081592
Han Z, Li M, Li Y, Zhao M, Li C, Xie W, Ding H, Ma Y. An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models. Water. 2023; 15(8):1592. https://doi.org/10.3390/w15081592
Chicago/Turabian StyleHan, Zheng, Ming Li, Yange Li, Mingyue Zhao, Changli Li, Wendu Xie, Haohui Ding, and Yangfan Ma. 2023. "An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models" Water 15, no. 8: 1592. https://doi.org/10.3390/w15081592
APA StyleHan, Z., Li, M., Li, Y., Zhao, M., Li, C., Xie, W., Ding, H., & Ma, Y. (2023). An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models. Water, 15(8), 1592. https://doi.org/10.3390/w15081592








