A Review on the Research Advances in Groundwater–Surface Water Interaction with an Overview of the Phenomenon
Highlights
- This article discussed GW-SW interaction mechanisms and interdependency, flux exchange, and contaminant transport.
- This article also highlighted groundwater–surface water interactions via translatory, macropore, groundwater ridging, and return flows.
- A scale-dependent interaction behaviour based on large-scale or hyporheic/sediment-scale processes was noted.
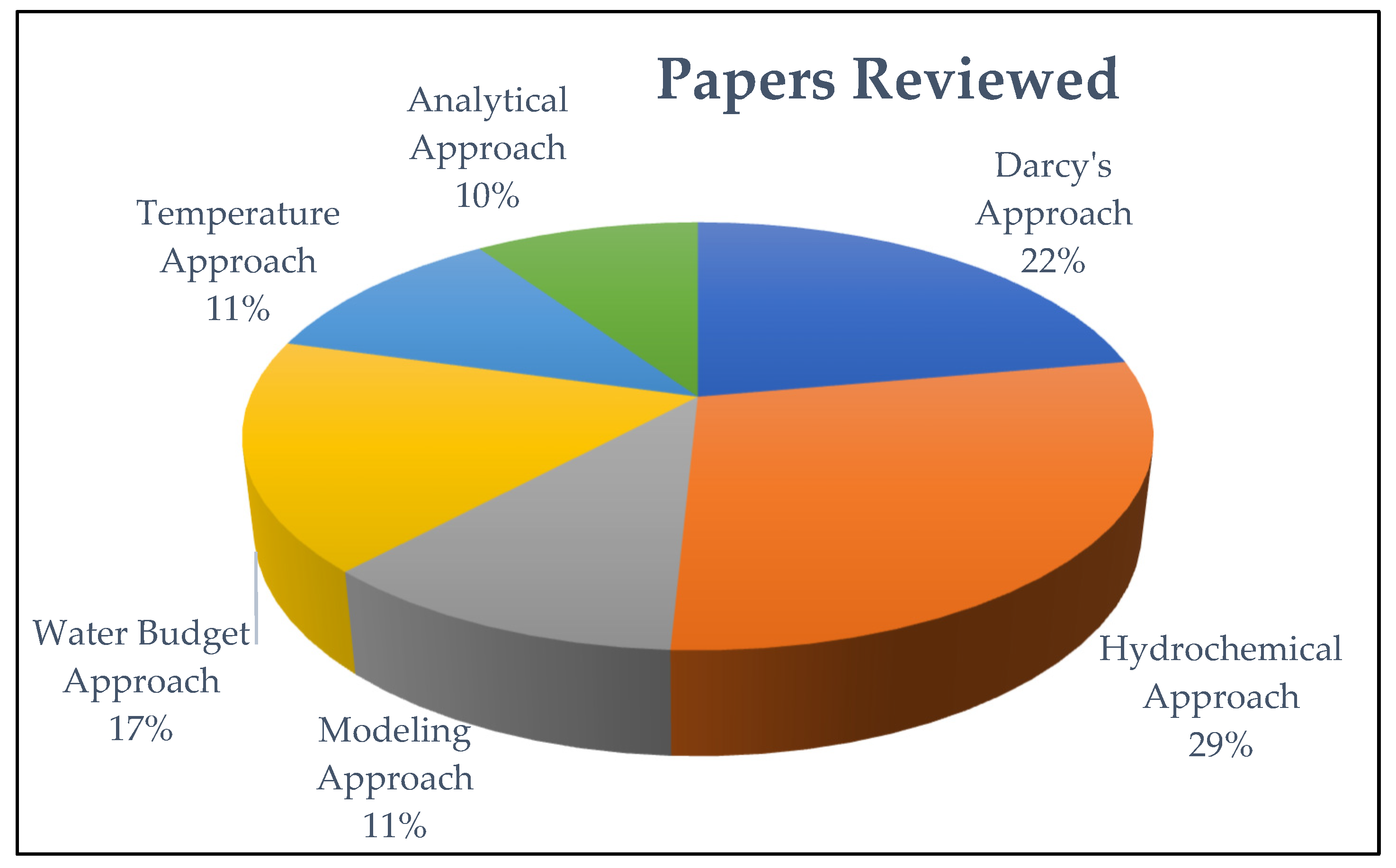
- The authors provided a detailed review on experimental, analytical, numerical, and semi-analytical methods for estimating interaction.
- Finally, the method for GW-SW interaction estimation depends on the study context; guidance on choosing the right approach is provided in this article.
Abstract
:1. Introduction
2. Importance of SW–GW Interaction
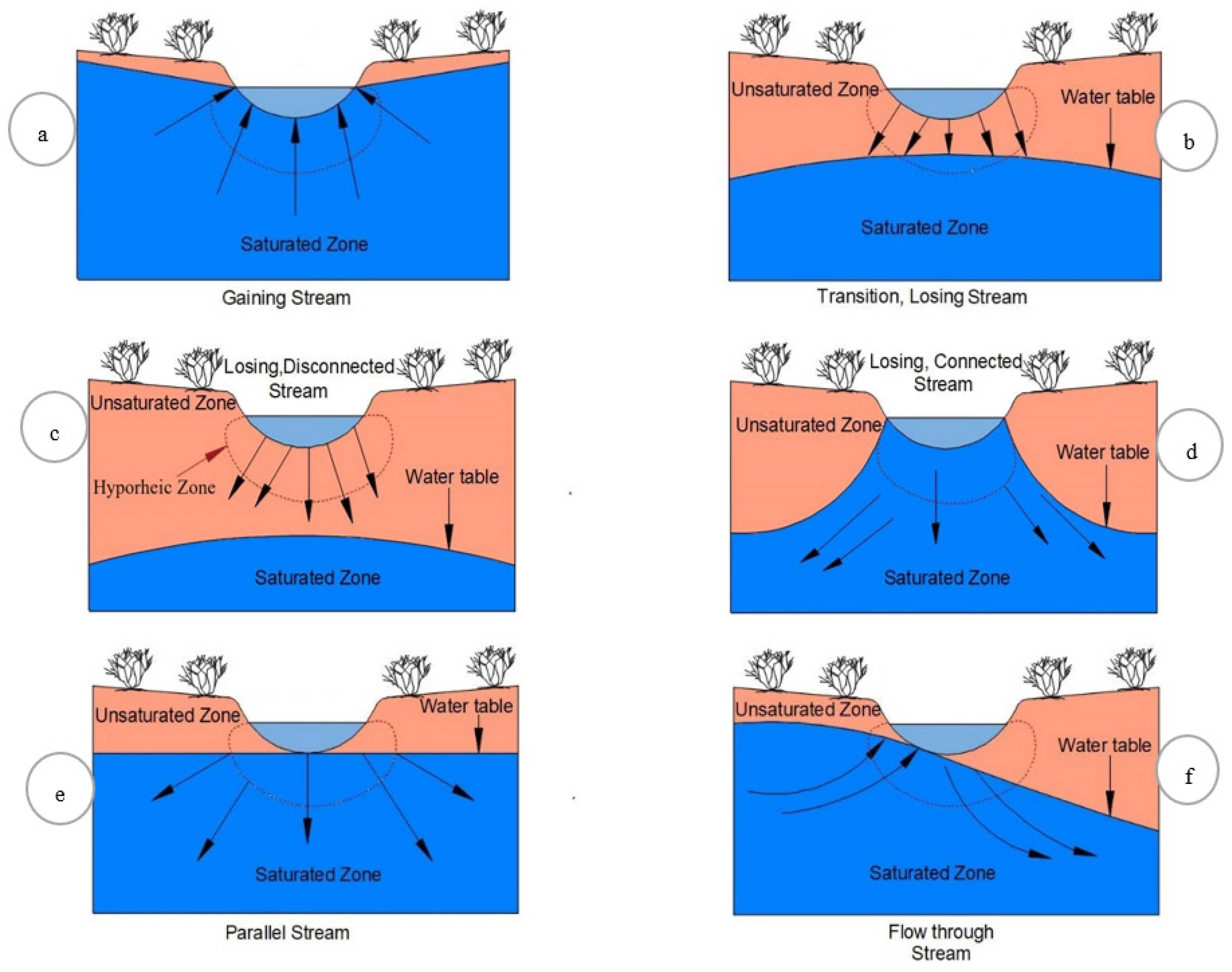
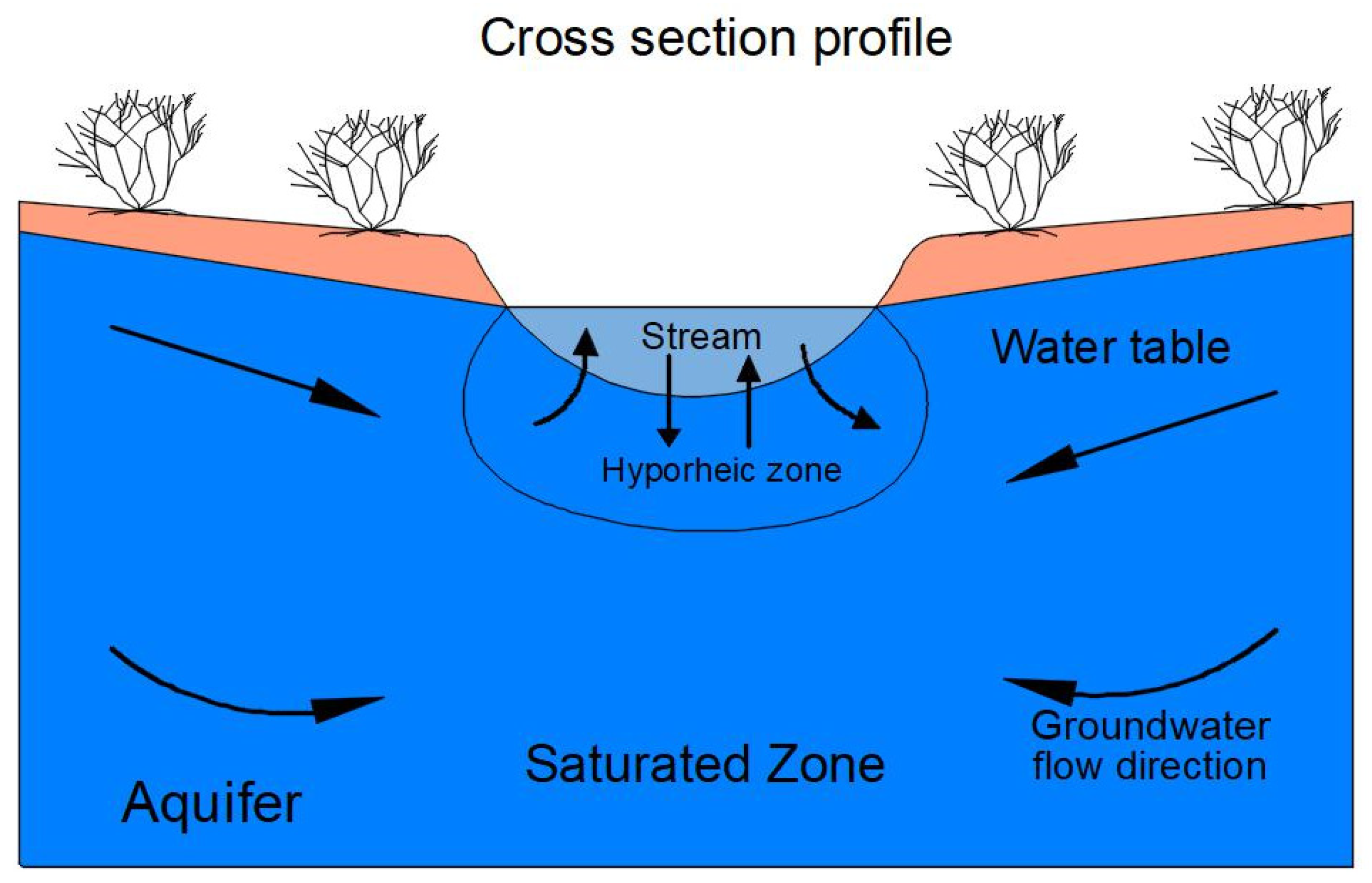
3. Mechanisms of GW–SW Interaction
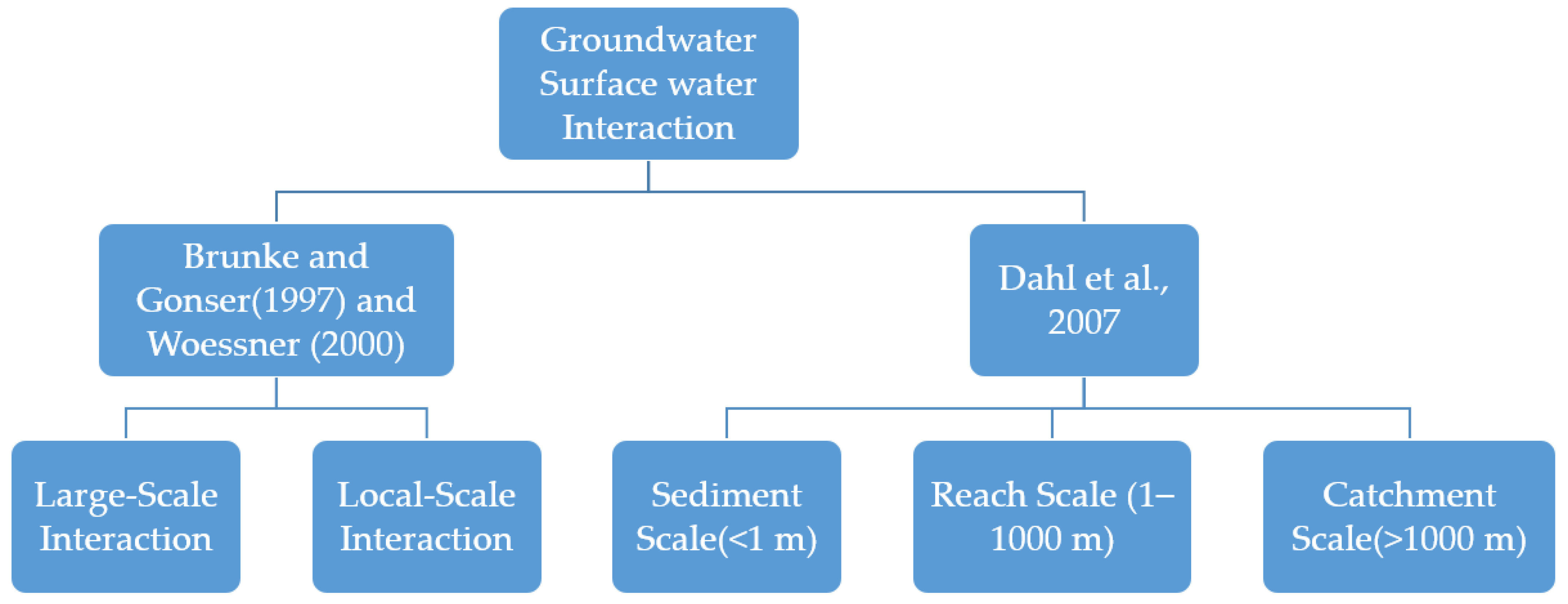
4. Scales of GW–SW Interactions
- (a)
- Large-scale Interaction
- (b) Hyporheic interaction or sediment scale interaction
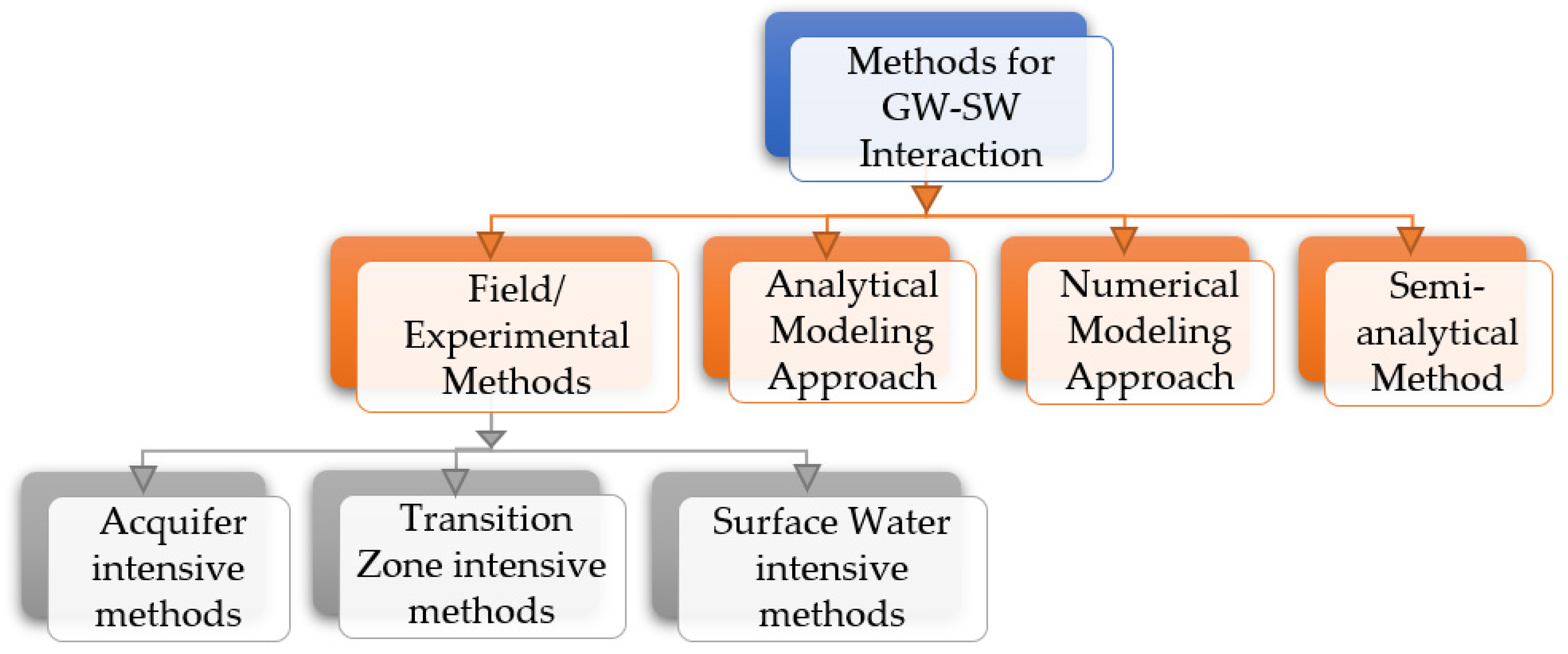
5. Methods for Analyzing GW–SW Interaction
5.1. Field/Experimental Methods
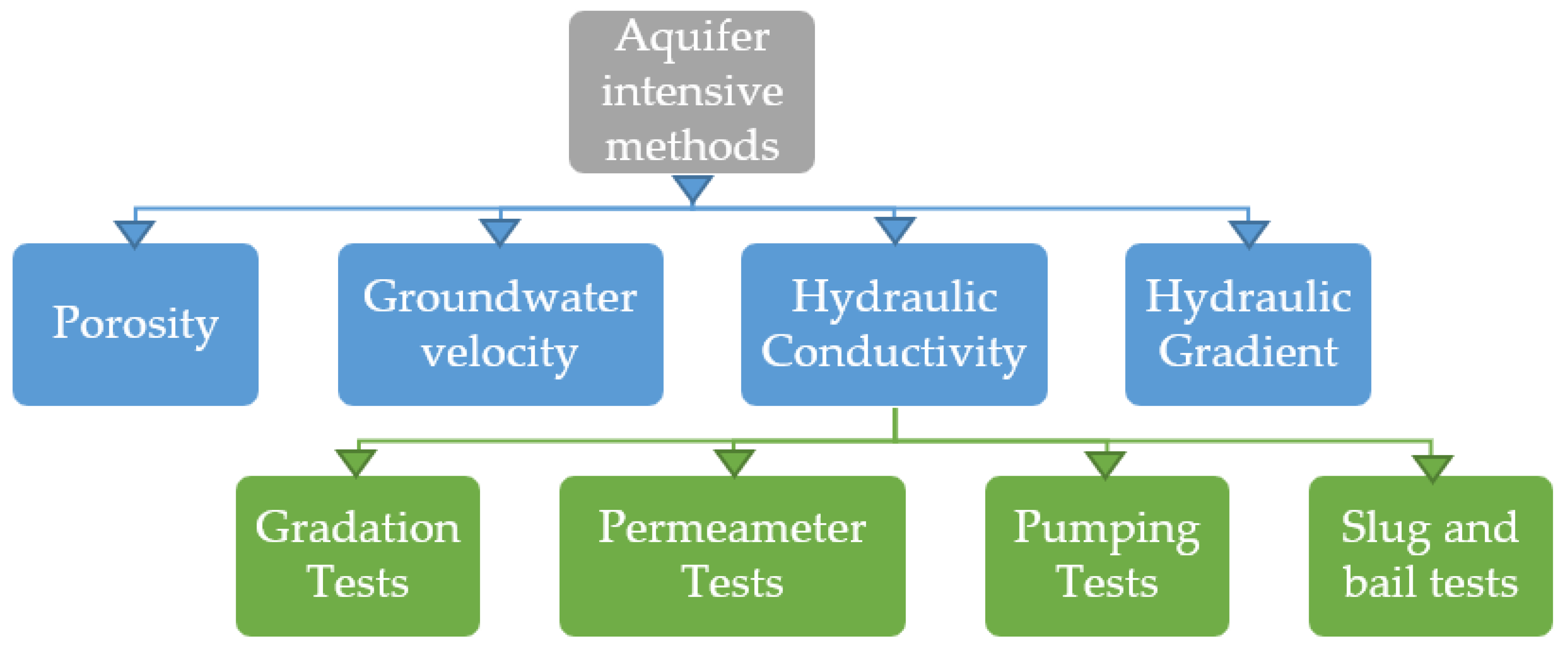
5.1.1. Aquifer Intensive Methods
5.1.2. Surface Water Intensive Methods
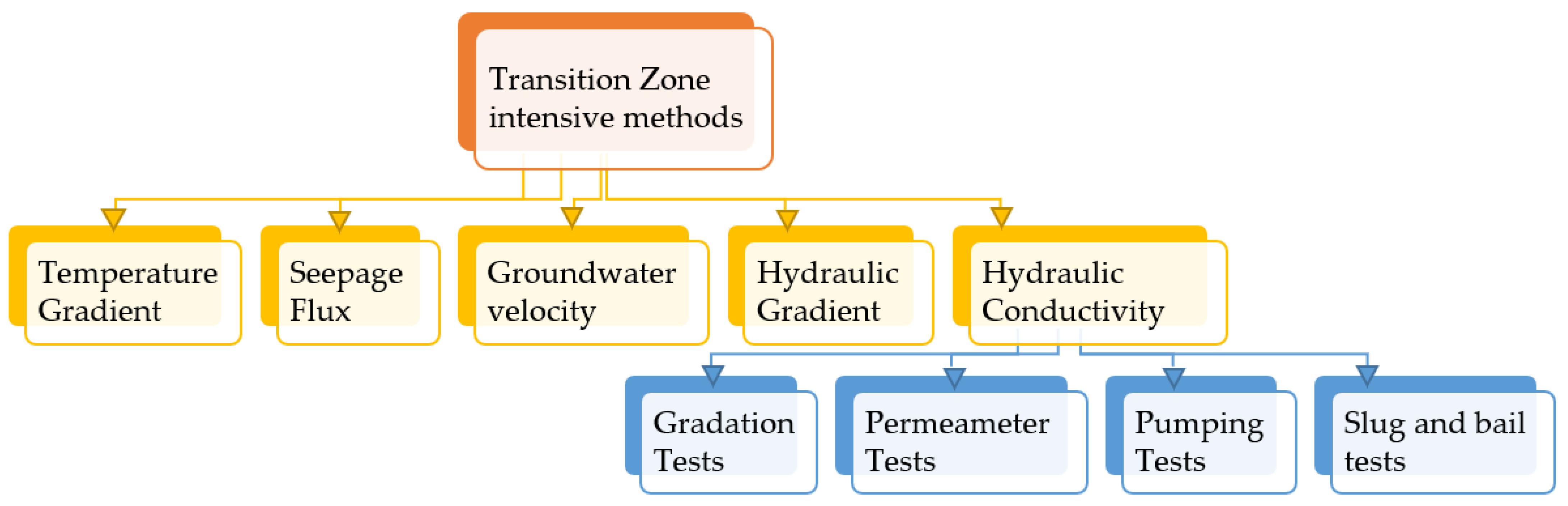
5.1.3. Transition Zone Intensive Methods
5.2. Analytical Modeling Methods
5.3. Numerical Modeling Methods
- (i)
- Runoff simulations using hydrological models;
- (ii)
- Simulations of groundwater systems using hydrogeological models;
- (iii)
- Physical properties based ISSHM (Integrated Surface–Subsurface Hydrological Models).
5.4. Semi-Analytical Methods
6. Discussion and Applicability of the Methods
| Sr. No. | Method Applied | Fundamental Mechanism | Related Studies |
|---|---|---|---|
| 1. | Darcy approach | Measure components of Darcy Law experimentally and use Darcy’s Law | Kebede et al. (2021) [100], Sadat-Noori et al. (2021) [103], Larned et al. (2015) [114], Doering et al. (2013) [99], Banks et al. (2009) [4], Coluccio (2018) [102], Burbery and Ritson (2010) [113], Menció et al. (2014) [106], Acuña and Tockner (2009) [109], Cremeans et al. (2020) [101], Freitas et al. (2019) [107]. |
| 2. | Hydrochemistry | Quantify different chemical ions in the samples of groundwater and surface water to understand their extent of interaction | Longa and Koontanakulvong (2020) [115], Kebede et al. (2021) [100], Sadat-Noori et al. (2021) [103], Larned et al. (2015) [114], Doering et al. (2013) [99], Banks et al. (2009) [4], Coluccio (2018) [102], Burbery and Ritson (2010) [113], Guggenmos et al. (2011) [111], Acuña and Tockner (2009) [109], Navarro-Martínez et al. (2020) [112], Carol et al. (2020) [108], Ferreira et al. (2018) [110], Freitas et al. (2019) [107]. |
| 3. | Heat (Temperature) approach | The difference in the temperature between groundwater and surface water | Thomas (2021) [118], Sadat-Noori et al. (2021) [103], Doering et al. (2013) [99], Banks et al. (2009) [4], Coluccio (2018) [102], Acuña and Tockner (2009) [109], Passadore et al. (2015) [117]. |
| 4. | Numerical modeling | Replicate the actual scenario into a software environment with some inputs taken through experimentations e.g., hydraulic conductivity | Tran et al. (2020) [122], Deb et al. (2019) [104], Waseem et al. (2020) [121], Ghysels et al. (2021) [120]. |
| 5. | Water Budget | Any increase or decrease in the quantity or quality of surface water is due to its source, which is the groundwater | Kebede et al. (2021) [100], Li et al. (2020) [116], Larned et al. (2015) [114], Doering et al. (2013) [99], Banks et al. (2009) [4], Burbery and Ritson (2010) [113], Guggenmos et al. (2011) [111], Menció et al. (2014) [106], Acuña and Tockner (2009) [109] |
| 6. | Analytical/semi-analytical modeling and other approaches | Use equations of groundwater flow and different conditions to get nearer to the actual phenomenon | Ghysels et al. (2021) [120], El-Rawy et al. (2020) [124], Keery et al. (2006) [125], Thomle et al. (2020) [126], Johnson (2012) [119], Nawalany et al. (2020) [82]. |
- (a)
- Choosing the scale to be considered for measurement
- (b) Choosing the appropriate method for estimation of the process
7. Conclusions and the Way Forward
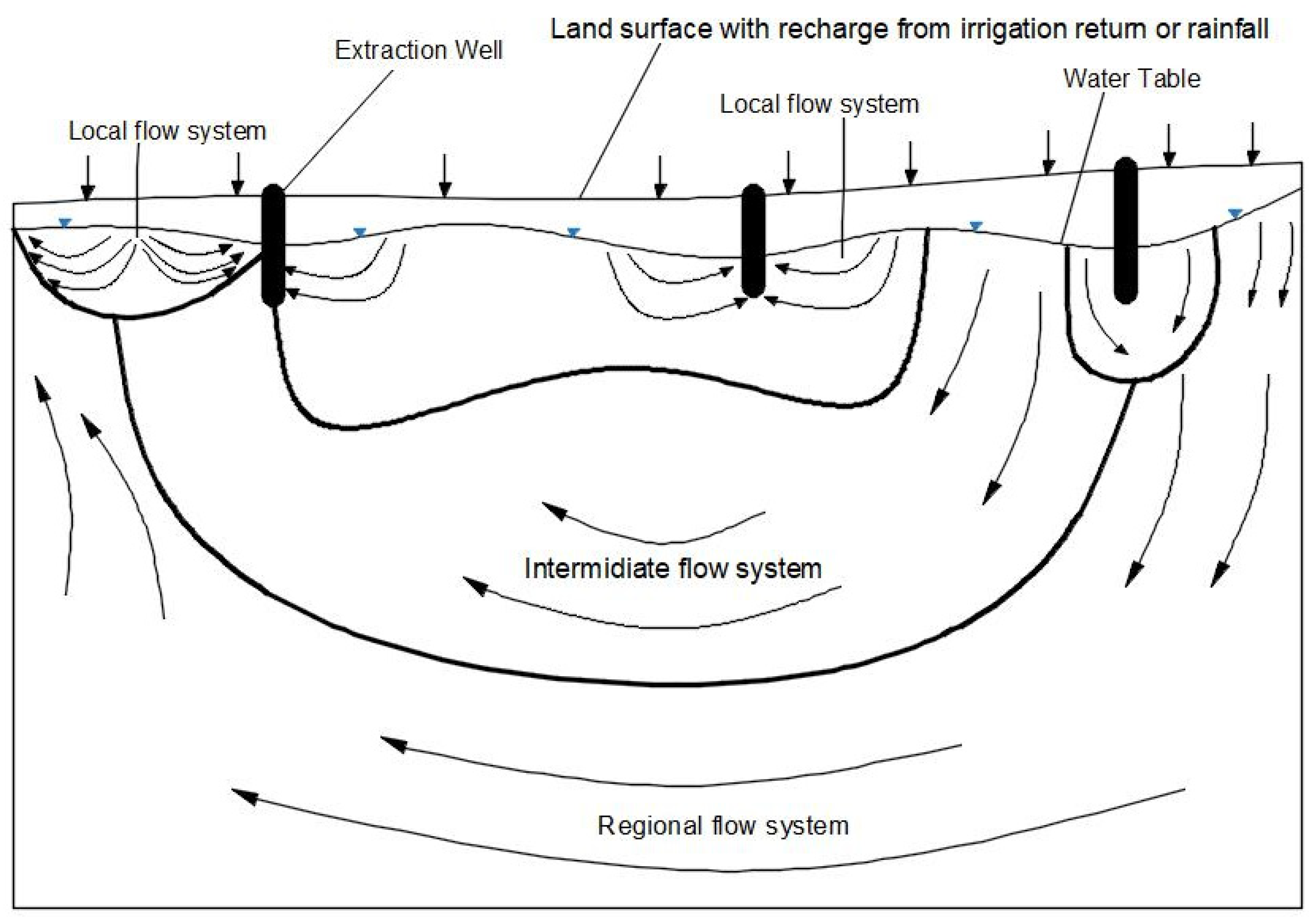
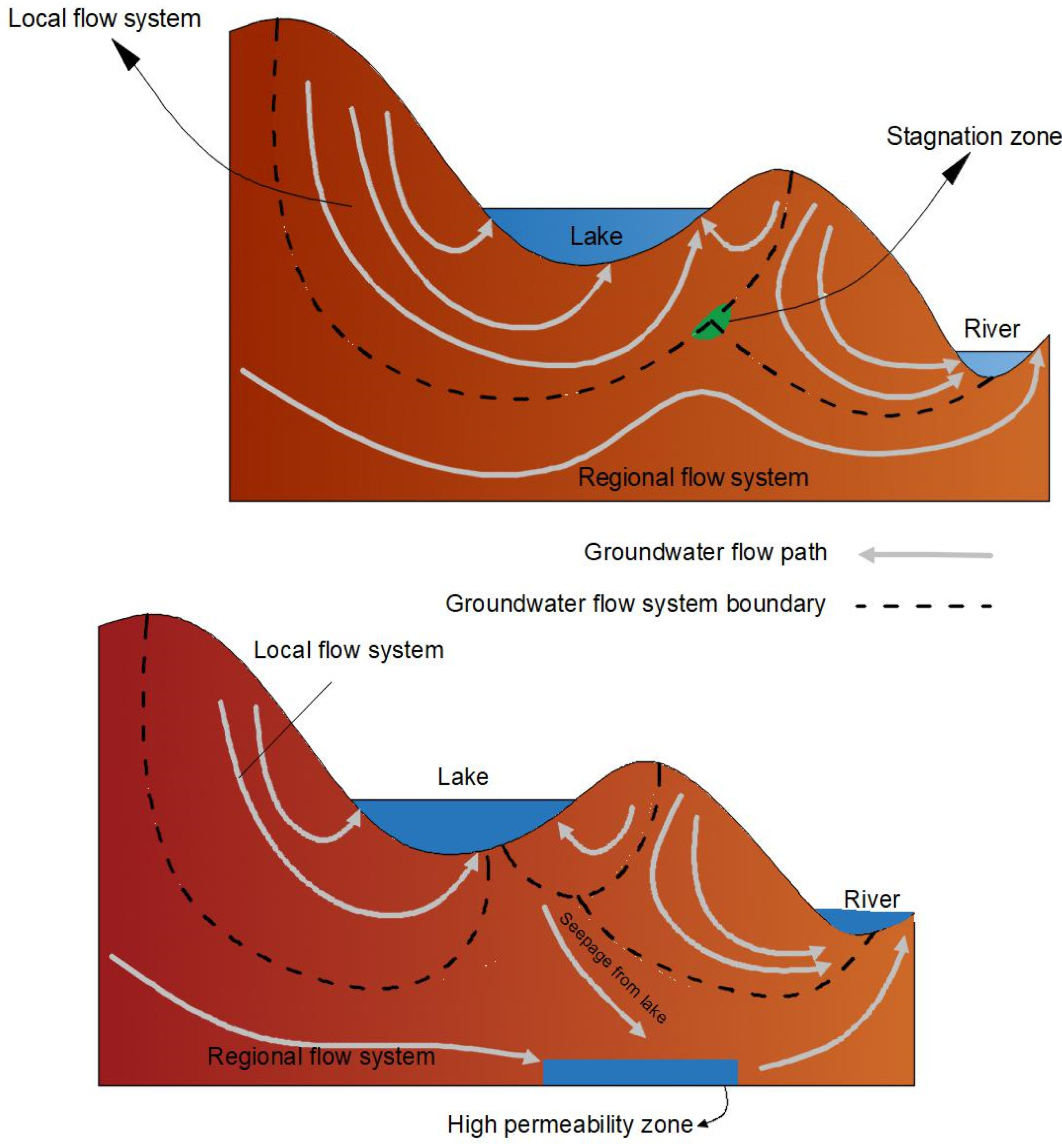
- The interaction mechanisms were shown to be dependent on base flows and interflows in general, along with flows like translatory, macropore, groundwater ridging, and return flow for a quick response after a storm event. Alongside this, the dependency of the interaction process on the scale of interaction was explored as an overview of the local, intermediate, and regional flow systems.
- It was observed that the large-scale interactions explained how seepage from the channel bed would take place in the absence of a continuous groundwater flow system boundary. The hyporheic zone dependency on stream bed materials’ hydraulic conductivity and bed topography was proven.
- The methods of interaction and instruments used were found to be dependent on the scale in which the process needs to be quantified. Aquifer zone methods used Darcy’s Law as the basis of estimation, but due to the variability of different parameters used in this method, it was found highly prone to errors.
- For surface water, there are several methods like the Environmental Tracer Method, Heat Tracer Method, Hydrograph Separation Method, and Incremental Streamflow. Of these, the Environmental Tracer Method was found to be the most widely and successfully used technique for interaction estimation. In the transition zone, most of the measuring parameters resembled that of surface water.
- Taking into account the strengths of analytical and numerical modeling techniques, 2-D and 3-D semi-analytical solutions can be used to simulate the complex physical and mathematical phenomenon of groundwater–surface water interaction. These methods are efficient even to solve and simulate those typical interaction problems without the use of grids as at many locations meshing cause the solution to deviate from the actual process taking place.
- The most important factors in achieving an accurate interaction quantification are the scales and methods chosen. It is always better to get results through both large-scale and small-scale measurements since adhering to a single scale may ignore the intricacies that are detectable in the other. Further, the methods are suggested to be used in conjunction with another technique to avoid any error in the result.
Funding
Data Availability Statement
Conflicts of Interest
References
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water—A Single Resource; U.S. Geological Survey: Reston, VA, USA, 1998. [Google Scholar]
- Valett, H.M.; Hakenkamp, C.C.; Boulton, A.J. Perspectives on the hyporheic zone: Integrating hydrology and biology. In-troduction. J. North Am. Benthol. Soc. 1993, 12, 40–43. [Google Scholar] [CrossRef]
- Triska, F.J.; Kennedy, V.C.; Avanzino, R.J.; Zellweger, G.W.; Bencala, K.E. Retention and transport of nutrients in a third-order stream in northwestern California: Hyporheic processes. Ecology 1989, 70, 1893–1905. [Google Scholar] [CrossRef]
- Banks, E.W.; Simmons, C.T.; Love, A.J.; Cranswick, R.; Werner, A.D.; Bestland, E.A.; Wood, M.; Wilson, T. Fractured bedrock and saprolite hydrogeologic controls on groundwater/surface-water interaction: A conceptual model. Hydrogeol. J. 2009, 17, 1969–1989. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Winter, T.C. Recent advances in understanding the interaction of groundwater and surface water. Rev. Geophys. 1995, 33, 985–994. [Google Scholar] [CrossRef]
- Williamson, W.H. Groundwater Resources of the Upper Hunter Valley, New South Wales; University of N.S.W.: Kensington, Australia, 1957. [Google Scholar] [CrossRef]
- Barlow, P.M.; Ahlfeld, D.P.; Dickerman, D.C. Conjunctive-management models for sustained yield of stream-aquifer systems. J. Water Resour. Plan. Manag. 2003, 29, 35–48. [Google Scholar] [CrossRef]
- Barlow, P.M.; Granato, G.E. Simulation-Optimization Modeling to Assist Conjunctive Management of Stream-Aquifer Systems of Rhode Island. Ground Water News and Views AGWSE Division. 2007. Available online: http://info.ngwa.org/newsletters/newsviews/index.html (accessed on 15 February 2023).
- Lee, D.R.; Cherry, J.A. A Field Exercise on Groundwater Flow Using Seepage Meters and Mini-Piezometers. J. Geol. Educ. 1978, 27, 6–10. [Google Scholar] [CrossRef]
- Woessner, W.W.; Sullivan, K.E. Results of Seepage Meter and Mini-Piezometer Study, Lake Mead, Nevada. Ground Water 1984, 22, 561–568. [Google Scholar] [CrossRef]
- Wroblicky, G.J.; Campana, M.E.; Valett, H.M.; Dahm, C.N. Seasonal variation in surface-subsurface water exchange and lateral hyporheic area of two stream-aquifer systems. Water Resour. Res. 1998, 34, 317–328. [Google Scholar] [CrossRef]
- González-Pinzón, R.; Ward, A.S.; Hatch, C.E.; Wlostowski, A.N.; Singha, K.; Gooseff, M.N.; Haggerty, R.; Harvey, J.W.; Cirpka, O.A.; Brock, J.T. A field comparison of multiple techniques to quantify groundwater–surface-water interactions. Freshw. Sci. 2015, 34, 139–160. [Google Scholar] [CrossRef]
- Lapworth, D.J.; Dochartaigh, B.; Nair, T.; Keeffe, J.; Krishan, G.; MacDonald, A.M.; Khan, M.; Kelkar, N.; Choudhary, S.; Krishnaswamy, J.; et al. Characterizing groundwater-surface water connectivity in the lower Gandak catchment, a barrage regulated biodiversity hotspot in the mid- Gangetic basin. J. Hydrol. 2021, 594, 125923. [Google Scholar]
- Negrel, P.; Petelet-Giraud, E.; Barbier, J.; Gautier, E. Surface water-groundwater interactions in an alluvial plain: Chemical and isotopic systematics. J. Hydrol. 2003, 277, 248–267. [Google Scholar] [CrossRef]
- Grodzka-Łukaszewska, M.; Pawlak, S.; Sinicyn, G. Spatial distribution of the water exchange through river cross-section–measurements and the numerical model. Arch. Environ. Prot. 2023, 47, 69–79. [Google Scholar] [CrossRef]
- Grodzka-Łukaszewska, M.; Sinicyn, G.; Grygoruk, M.; Mirosław-Świątek, D.; Kardel, I.; Okruszko, T. The role of the river in the functioning of marginal fen: A case study from the Biebrza Wetlands. PeerJ 2022, 10, e13418. [Google Scholar] [CrossRef]
- Anibas, C.; Verbeiren, B.; Buis, K.; Chormański, J.; Doncker, L.D.; Okruszko, T.; Meire, P.; Batelaan, O. A hierarchical approach on groundwater-surface water interaction in wetlands along the upper Biebrza River, Poland. Hydrol. Earth Syst. Sci. 2012, 16, 2329–2346. [Google Scholar] [CrossRef]
- Binley, A. Tools and Techniques: Electrical Methods. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; Volume 11, pp. 233–259. [Google Scholar] [CrossRef]
- McLachlan, P.J.; Chambers, J.E.; Uhlemann, S.S.; Binley, A. Geophysical characterisation of the groundwater-surface water interface. Adv. Water Resour. 2017, 109, 302–319. [Google Scholar] [CrossRef]
- Telford, W.M.; Geldart, R.E.; Sheriff, R.E. Applied Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hayashi, M.; Rosenberry, D.O. Effects of Ground Water Exchange on the Hydrology and Ecology of Surface Water. Ground Water 2002, 40, 309–316. [Google Scholar] [CrossRef]
- Jordan, T.E.; Correll, D.L.; Weller, D.E. Relating nutrient discharges from watersheds to land use and streamflow variability. Water Resour. Res. 1997, 33, 2579–2590. [Google Scholar] [CrossRef]
- Svhindler, D.W. Effects of acid rain on freshwater ecosystems. Science 1988, 239, 149–157. [Google Scholar] [CrossRef] [PubMed]
- Zektser, I.S.; Loaiciga, H.A. Groundwater fluxes in the global hydrologic cycle: Past, present and future. J. Hydrol. 1993, 144, 405–427. [Google Scholar] [CrossRef]
- Kwon, E.Y.; Kim, G.; Primeau, F.; Moore, W.S.; Cho, H.M.; DeVries, T.; Sarmiento, J.L.; Charette, M.A.; Cho, Y.K. Global estimate of submarine groundwater discharge based on an observationally constrained radium isotope model. Geophys. Res. Lett. 2014, 41, 8438–8444. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; Lewandowski, J.; Meinikmann, K.; Nützmann, G. Groundwater-the disregarded component in lake water and nutrient budgets. Part 1: Effects of groundwater on hydrology. Hydrol. Process. 2014, 29, 2895–2921. [Google Scholar] [CrossRef]
- Dubrovsky, N.M.; Burow, K.R.; Clark, G.M. The Quality of Our Nation’s Waters-Nutrients in the Nation’s Streams and Groundwater; U.S. Geological Survey: Reston, VA, USA, 2010. [Google Scholar]
- Sebestyen, S.D.; Boyer, E.W.; Shanley, J.B.; Kendall, C.; Doctor, D.H.; Aiken, G.R.; Ohte, N. Sources, transformations, and hydrological processes that control stream nitrate and dissolved organic matter concentrations during snowmelt in an upland forest. Water Resour. Res. 2008, 44, W12410. [Google Scholar] [CrossRef]
- Kazmierczak, J.; Nilsson, B.; Postma, D.; Sebok, E.; Karan, S.; Müller, S.; Czekaj, J.; Engesgaard, P. Transport of geogenic phosphorus to a groundwater-dominated eutrophic lake. J. Hydrol. 2021, 598, 126175. [Google Scholar] [CrossRef]
- Ramesh, R.; Purvaja, G.R.; Ika, R.V. The Problem of Groundwater Pollution: A Case Study from Madras City, India. 1995. Available online: http://www.iomenvis.in/rramesh/publications/1995-1.pdf (accessed on 15 February 2023).
- Bear, J.; Cheng, A.H.D.; Sorek, S.; Ouazar, D.; Herrera, I. (Eds.) Seawater Intrusion in Coastal Aquifers: Concepts, Methods and Practices; Springer Science & Business Media: Berlin, Germany, 1999; Volume 14. [Google Scholar]
- Werner, A.D.; Bakker, M.; Post, V.E.A.; Vandenbohede, A.; Lu, C.; Ataie-Ashtiani, B.; Simmons, C.T.; Barrye, D.A. Seawater intrusion processes, investigation and management: Recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Singh, G.; Singh, D.D.; Sharma, S.K. Effect of Polluted Surface Water on Groundwater: A Case Study of Budha Nullah. IOSR J. Mech. Civ. Eng. (IOSR-JMCE) 2013, 5, 1–8. [Google Scholar] [CrossRef]
- Maeng, S.K.; Sharma, S.K.; Lekkerkerker-Teunissen, K.; Amy, G.L. Occurrence and fate of bulk organic matter and pharmaceutically active compounds in managed aquifer recharge: A review. Water Res. 2011, 45, 3015–3033. [Google Scholar] [CrossRef]
- Li, C.; Gao, X.; Wang, W.; Zhang, X.; Zhang, Z.; Jiang, C.; Wang, Y. Hydro-biogeochemical processes of surface water leakage into groundwater in large scale karst water system: A case study at Jinci, northern China. J. Hydrol. 2021, 596, 125691. [Google Scholar] [CrossRef]
- Prakash, R.; Srinivasamoorthy, K.; Sundarapandian, S.M.; Nanthakumar, C.; Gopinath, S.; Saravanan, K.; Vinnarasi, F. Submarine Groundwater Discharge from an Urban Estuary to Southeastern Bay of Bengal, India: Revealed by Trace Element Fluxes. Arch. Environ. Contam. Toxicol. 2021, 80, 208–233. [Google Scholar] [CrossRef] [PubMed]
- Guevara-Ochoa, C.; Medina-Sierra, A.; Vivesa, L. Spatio-temporal effect of climate change on water balance and interactions between groundwater and surface water in plains. Sci. Total Environ. 2020, 722, 137886. [Google Scholar] [CrossRef] [PubMed]
- Abdelhalim, A.; Sefelnasr, A.; Ismail, E. Response of the interaction between surface water and groundwater to climate change and proposed megastructure. J. Afr. Earth Sci. 2019, 162, 103723. [Google Scholar] [CrossRef]
- Beven, K.J. Interflow. In Unsaturated Flow in Hydrologic Modeling: Theory and Practice; Morel-Seytoux, H.J., Ed.; Springer: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Hewlett, J.D.; Hibbert, A.R. Factors affecting the response of small watersheds to precipitation in humid areas. In Forest Hydrology; Sopper, W.E., Lull, H.W., Eds.; Pergamon Press: Oxford, UK, 1967. [Google Scholar]
- Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring methods for groundwater and surface water interactions: A review. Hydrol. Earth Syst. Sci. 2006, 10, 873–887. [Google Scholar] [CrossRef]
- Ranjith, M.; Rao, K.J.; Sridevi, S.; Ramesh, T.; Bhave, M.H.V. Groundwater Quality and Fluoride Contamination in Kalwakurthy Mandal of Mahabubnagr District, Telangana State, India. Int. J. Pure Appl. Biosci. 2017, 5, 1397–1405. [Google Scholar] [CrossRef]
- Taylor, S.A.; Ashcroft, G.L. Physical Edaphology: The Physics of Irrigated and Non-Irrigated Soils; WH. Freeman: San Francisco, CA, USA, 1972. [Google Scholar]
- CGWB. Manual on Artificial Recharge of Groundwater; CGWB, Government of India: Jaipur, India, 2007. [Google Scholar]
- Rossetto, R.; Barbagli, A.; De Filippis, G.; Marchina, C.; Vienken, T.; Mazzanti, G. Importance of the Induced Recharge Term in Riverbank Filtration: Hydrodynamics, Hydrochemical, and Numerical Modelling Investigations. Hydrology 2020, 7, 96. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhai, Y.; Teng, Y.; Wang, G.; Du, Q.; Wang, J.; Yang, G. Water supply safety of riverbank filtration wells under the impact of surface water-groundwater interaction: Evidence from long-term field pumping tests. Sci. Total Environ. 2019, 711, 135141. [Google Scholar] [CrossRef]
- Tóth, J. A theoretical analysis of groundwater flow in small drainage basins. J. Geophys. Res. 1963, 68, 4795–4812. [Google Scholar] [CrossRef]
- Tripathi, M.; Yadav, P.K.; Chahar, B.R.; Dietrich, P. A review on groundwater–surface water interaction highlighting the significance of streambed and aquifer properties on the exchanging flux. Environ. Earth Sci. 2021, 80, 604. [Google Scholar] [CrossRef]
- Dahl, M.; Nilsson, B.; Langhoff, J.H.; Refsgaard, J.C. Review of classification systems and new multi-scale typology of groundwater–surface water interaction. J. Hydrol. 2007, 344, 1–16. [Google Scholar] [CrossRef]
- Woessner, W.W. Stream and fluvial plain groundwater interactions: Rescaling hydrogeological thought. Ground Water 2000, 38, 423–429. [Google Scholar] [CrossRef]
- Brunke, M.; Gonser, T.O.M. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef]
- Winter, T.C. Numerical Simulation Analysis of the Interaction of Lakes & Groundwater; USGS Professional Paper 1001; U.S. Government Printing Office: Washington, DC, USA, 1976. [Google Scholar]
- Harvey, J.W.; Bencala, K.E. The effect of streambed topography on surface-subsurface water exchange in mountain catchments. Water Resour. Res. 1993, 29, 89–98. [Google Scholar] [CrossRef]
- Cardenas, M.B. A model for lateral hyporheic flow based on valley slope and channel sinuosity. Water Resour. Res. 2009, 45, W01501. [Google Scholar] [CrossRef]
- Lone, S.A.; Jeelani, G.; Deshpande, R.D.; Mukherjee, A. Stable isotope (δ18O and δD) dynamics of precipitation in a high-altitude Himalayan cold desert and its surroundings in Indus river basin, Ladakh. Atmos Res. 2019, 221, 46–57. [Google Scholar] [CrossRef]
- Katz, A.; Stein, M.; Starinsky, A.; Goldstein, S.L.; Machlus, M.; Schramm, A. Strontium isotopic, chemical, and sedimentological evidence for the evolution of Lake Lisan and the Dead Sea. Geochim. Et Cosmochim. Acta 1997, 61, 3975–3992. [Google Scholar]
- Gates, J.B.; Edmunds, W.M.; Darling, W.G.; Ma, J.; Pang, Z.; Young, A.A. Conceptual model of recharge to southeastern Badain Jaran Desert groundwater and lakes from environmental tracers. Appl. Geochem. 2008, 23, 3519–3534. [Google Scholar] [CrossRef]
- Wang, Y.G.; Guo, H.Y.; Li, J.; Huang, Y.; Liu, Z.Y.; Liu, C.E. Investigation and Evaluation of Groundwater Resources and Environmental Problems in the Qaidam Basin; Geological Publishing House: Beijing, China, 2008. [Google Scholar]
- Harvey, F.E.; Lee, D.R.; Rudolph, D.L.; Frape, S.K. Locating groundwater discharge 25 in large lakes using bottom sediment electrical conductivity mapping. Water Resour. Res. 1997, 33, 2609–2615. [Google Scholar] [CrossRef]
- Hornberger, G.M.; Raffensperger, J.P.; Wiberg, P.L.; Eshleman, K.N. Elements of Physical Hydrology; The John Hopkins University Press: Baltimore, MA, USA, 1998. [Google Scholar]
- Linsley, R.K.; Kohler, M.A.; Paulhus, J.L.H. Hydrology for Engineers; McGraw-Hill Book Company: London, UK, 1988. [Google Scholar]
- Hannula, S.R.; Esposito, K.J.; Chermak, J.A.; Runnells, D.D.; Keith, D.C.; Hall, L.E. Estimating ground water discharge by hydrograph separation. Ground Water 2003, 41, 368–375. [Google Scholar] [CrossRef]
- Pettyjohn, W.A.; Henning, R. Preliminary Estimate of Ground-Water Recharge Rates, Related Streamflow and Water Quality in Ohio; Ohio State University Water Resources Center Project Completion Report Number 552; Ohio State University, Water Resources Center: Columbus, OH, USA, 1979. [Google Scholar]
- Nathan, R.J.; McMahon, T.A. Evaluation of automated techniques for base flow and recession analysis. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Muttiah, R.; Bernhardt, G. Automated Base-Flow Separation and Recession Analysis Techniques. Ground Water 1995, 33, 1010–1018. [Google Scholar] [CrossRef]
- Carter, R.W.; Davidian, J. General Procedures for Gaging Streams; United States Geological Survey Techniques of Water Resources Investigations; US Government Printing Office: Washington, DC, USA, 1968. [Google Scholar]
- Kilpatrick, F.A.; Schneider, V.R. Use of Flumes in Measuring Discharge; United States Geological Survey techniques of Water-Resources Investigations; US Government Printing Office: Washington, DC, USA, 1983. [Google Scholar]
- Kilpatrick, F.A.; Cobb, E.D. Measurement of Discharge Using Tracers; United States Geological Survey Techniques of Water-Resources Investigations; US Government Printing Office: Washington, DC, USA, 1985. [Google Scholar]
- Harvey, J.W.; Wagner, B.J. Quantifying hydrologic interactions between streams and their subsurface hyporheic zones. In Streams and Groundwaters; Jones, J.B., Mulholland, P.J., Eds.; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Zachara, J.M.; Chen, X.; Murray, C.; Hammond, G. River stage influences on uranium transport in a hydrologically dynamic groundwater-surface water transition zone. Water Resour. Res. 2016, 52, 1568–1590. [Google Scholar] [CrossRef]
- Mugunthan, P.; Russell, K.T.; Gong, B.; Riley, M.J.; Chin, A.; McDonald, B.G.; Eastcott, L.J. A Coupled Groundwater–Surface Water Modeling Framework for Simulating Transition Zone Processes. Groundwater 2017, 55, 302–315. [Google Scholar] [CrossRef] [PubMed]
- Biksey, T.M.; Gross, E.D. The hyporheic zone: Linking groundwater and surface water—Understanding the paradigm. Remediation 2001, 12, 55–62. [Google Scholar] [CrossRef]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 1998. [Google Scholar]
- Silliman, S.E.; Ramirez, J.; McCabe, R.L. Quantifying downflow through creek sediments using temperature time series: One-dimensional solution incorporating measured surface temperature. J. Hydrol. 1995, 167, 99–119. [Google Scholar] [CrossRef]
- Lee, D.R. Device for Measuring Seepage Flux in Lakes and Estuaries. Limnol. Oceanogr 1977, 22, 140–147. [Google Scholar] [CrossRef]
- Isiorho, S.A.; Meyer, J.H. The effects of bag type and meter size on seepage meter measurements. Ground Water 1999, 37, 411–413. [Google Scholar] [CrossRef]
- Landon, M.K.; Rus, D.L.; Harvey, F.E. Comparison of instream methods for measuring hydraulic conductivity in sandy streambeds. Ground Water 2001, 39, 870–885. [Google Scholar] [CrossRef]
- Duque, C.; Russoniello, C.J.; Rosenberry, D. History and evolution of seepage meters for quantifying flow between groundwater and surface water: Part 2–Marine settings and submarine groundwater discharge. Earth Sci. Rev. 2020, 204, 103168. [Google Scholar] [CrossRef]
- Martinez, C.J. Seepage Meters for Measuring Groundwater–Surface Water Exchange; Institute of Food and Agricultural Sciences (IFAS): Gainesville, FL, USA, 2019. [Google Scholar]
- Grodzka-Łukaszewska, M.; Nawalany, M.; Zijl, W. A Velocity-Oriented Approach for Modflow. Transp. Porous Media 2017, 119, 373–390. [Google Scholar] [CrossRef]
- Nawalany, M.; Sinicyn, G.; Grodzka-Łukaszewska, M.; Mirosław-Świątek, D. Groundwater–surface water interaction—Analytical approach. Water 2020, 12, 1792. [Google Scholar] [CrossRef]
- Anderson, M.P.; Woessner, W.W. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Ameli, A.A. Semi-Analytical Methods for Simulating the Groundwater-Surface Water Interface; University of Waterloo: Waterloo, ON, Canada, 2014. [Google Scholar]
- Tóth, J. A conceptual model of the groundwater regime and the hydrogeologic environment. J Hydrol. 1970, 10, 164–176. [Google Scholar] [CrossRef]
- Darcy, H.P.G. Les Fountaines Publiques de la Ville de Dijon; Victon Dalmont: Paris, France, 1856. [Google Scholar]
- Werner, A.D.; Gallagher, M.R.; Weeks, S.W. Regional-scale, fully coupled modelling of stream–aquifer interaction in a tropical catchment. J. Hydrol. 2006, 328, 497–510. [Google Scholar] [CrossRef]
- An, H.; Ichikawa, Y.; Tachikawa, Y.; Shiiba, M. Three-dimensional finite difference saturated-unsaturated flow modeling with nonorthogonal grids using a coordinate transformation method. Water Resour. Res. 2010, 46, W11521. [Google Scholar] [CrossRef]
- Patel, H.; Eldho, T.; Rastogi, A. Simulation of radial collector well in shallow alluvial riverbed aquifer using analytic element method. J. Irrig. Drain. Eng. 2010, 136, 107–119. [Google Scholar] [CrossRef]
- Rushton, K.R.; Brassington, F.C. Hydraulic behaviour and regional impact of a horizontal well in a shallow aquifer: Example from the Sefton Coast, northwest England (UK). Hydrogeol. J. 2013, 21, 1117–1128. [Google Scholar] [CrossRef]
- Craig, J.R. Analytical solutions for 2D topography-driven flow in stratified and syncline aquifers. Adv. Water Resour. 2008, 31, 1066–1073. [Google Scholar] [CrossRef]
- Mishra, P.K.; Neuman, S.P. Improved forward and inverse analyses of saturated-unsaturated flow toward a well in a compressible unconfined aquifer. Water Resour. Res. 2010, 46, W07508. [Google Scholar] [CrossRef]
- Mishra, P.K.; Vessilinov, V.; Gupta, H. On simulation and analysis of variable-rate pumping tests. Ground Water 2013, 51, 469–473. [Google Scholar] [CrossRef] [PubMed]
- Tartakovsky, G.D.; Neuman, S.P. Three-dimensional saturated-unsaturated flow with axial symmetry to a partially penetrating well in a compressible unconfined aquifer. Water Resour. Res. 2007, 43, 86. [Google Scholar] [CrossRef]
- Tristscher, P.; Read, W.; Broadbridge, P.; Knight, J. Steady saturated-unsaturated flow in irregular porous domains. Math. Comput. Model. 2001, 34, 177–194. [Google Scholar] [CrossRef]
- Wong, S.; Craig, J.R. Series solutions for flow in stratified aquifers with natural geometry. Adv. Water Resour. 2010, 33, 48–54. [Google Scholar] [CrossRef]
- Haitjema, H. Analytic Element Modeling of Groundwater Flow; Academic Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Ward, N.D.; Lough, H. Stream depletion from pumping a semiconfined aquifer in a two-layer leaky aquifer system. J. Hydrol. Eng. 2011, 16, 955–959. [Google Scholar] [CrossRef]
- Doering, M.; Uehlinger, U.; Tockner, K. Vertical hydrological exchange, and ecosystem properties and processes at two spatial scales along a floodplain river (Tagliamento, Italy). Freshw. Sci. 2013, 32, 12–25. [Google Scholar] [CrossRef]
- Kebede, S.; Charles, K.; Godfrey, S.; MacDonald, A.; Taylor, R.G. Regional-scale interactions between groundwater and surface water under changing aridity: Evidence from the River Awash Basin, Ethiopia. Hydrol. Sci. J. 2021, 66, 450–463. [Google Scholar] [CrossRef]
- Cremeans, M.M.; Devlin, J.F.; Osorno, T.C.; McKnight, U.S.; Bjerg, P.L. A Comparison of Tools and Methods for Estimating Groundwater-Surface Water Exchange. Natl. Ground Water Assoc. 2020, 40, 24–34. [Google Scholar] [CrossRef]
- Coluccio, K. A Comparison of Methods for Estimating Groundwater-Surface Water Interactions in Braided Rivers. Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 2018. [Google Scholar]
- Sadat-Noori, M.; Anibas, C.; Andersen, M.S.; Glamore, W. A comparison of radon, heat tracer and head gradient methods to quantify surface water-groundwater exchange in a tidal wetland (Kooragang Island, Newcastle, Australia). J. Hydrol. 2021, 598, 126281. [Google Scholar] [CrossRef]
- Deb, P.; Kiem, A.S.; Willgoose, G.R. Mechanisms influencing non-stationarity in rainfall-runoff relationships in southeast Australia. J. Hydrol. 2019, 571, 749–764. [Google Scholar] [CrossRef]
- Tweed, S.; Leblanc, M.; Cartwright, I. Groundwater–surface water interaction and the impact of a multi-year drought on lakes conditions in South-East Australia. J. Hydrol. 2009, 379, 41–53. [Google Scholar] [CrossRef]
- Menció, A.; Galán, M.; Boix, D.; Mas-Pla, J. Analysis of stream–aquifer relationships: A comparison between mass balance and Darcy’s law approaches. J. Hydrol. 2014, 517, 157–172. [Google Scholar] [CrossRef]
- Freitas, J.G.; Furquim, S.A.C.; Aravena, R.; Cardoso, E.L. Interaction between lakes’ surface water and groundwater in the Pantanal wetland. Braz. Environ. Earth Sci. 2019, 78, 139. [Google Scholar] [CrossRef]
- Carol, E.; Alvarez, M.P.; Candanedo, I.; Saavedra, S.; Arcia, M.; Franco, A. Surface water– groundwater interactions in the Matusagaratı´ wetland, Panama. Wetl. Ecol Manag. 2020, 28, 971–982. [Google Scholar] [CrossRef]
- Acuña, V.; Tockner, K. Surface–subsurface water exchange rates along alluvial river reaches control the thermal patterns in an Alpine River network. Freshw. Biol. 2009, 54, 306–320. [Google Scholar] [CrossRef]
- Ferreira, V.V.M.; Moreira, R.M.; Rocha, Z.; Chagas, C.J.; Fonseca, R.L.M.; Santos, T.O.; Rodrigues, P.C.H.; Menezes, M.A.B.C. Use of radon isotopes, gamma radiation and dye tracers to study water interactions in a small stream in Brazil. Environ. Earth Sci. 2018, 77, 699. [Google Scholar] [CrossRef]
- Guggenmos, M.R.; Jackson, B.M.; Daughney, C.J. Investigation of groundwater-surface water interaction using hydrochemical sampling with high temporal resolution, Mangatarere catchment, New Zealand. Hydrol. Earth Syst. Sci. Discuss. 2011, 8, 10225–10273. [Google Scholar]
- Navarro-Martínez, F.; Sánchez-Martosa, F.; Garcíab, A.S.; Gallegoa, J.G. The use of major, trace elements and uranium isotopic ratio (234U/238U) for tracing of hydrogeochemical evolution of surface waters in the Andarax River catchment (SE Spain). J. Geochem. Explor. 2020, 213, 106533. [Google Scholar] [CrossRef]
- Burbery, L.; Ritson, J. Integrated Study of Surface Water and Shallow Groundwater Resources of the Orari Catchment; Environment Canterbury Regional Council: Kaikoura, New Zealand, 2010. [Google Scholar]
- Larned, S.T.; Unwin, M.J.; Boustead, N.C. Ecological dynamics in the riverine aquifers of a gaining and losing river. Freshw. Sci. 2015, 34, 245–262. [Google Scholar] [CrossRef]
- Longa, T.T.; Koontanakulvong, S. Groundwater and River Interaction Impact to Aquifer System in Saigon River Basin, Vietnam. Eng. J. 2020, 24, 15–24. [Google Scholar] [CrossRef]
- Li, M.; Liang, X.; Xiao, C.; Cao, Y. Quantitative Evaluation of Groundwater–Surface Water Interactions: Application of Cumulative Exchange Fluxes Method. Water 2020, 12, 259. [Google Scholar] [CrossRef]
- Passadore, G.; Sottani, A.; Altissimo, L.; Putti, M.; Rinaldo, A. Groundwater thermal monitoring to characterize streambed water fluxes of the Brenta river (Northern Italy). Procedia Environ. Sci. 2015, 25, 199–205. [Google Scholar] [CrossRef]
- Thomas, E.O. Effect of temperature on D. O and T.D.S: A measure of Ground and Surface Water Interaction. Water Sci. 2021, 35, 11–21. [Google Scholar]
- Johnson, T.C.; Slater, L.D.; Ntarlagiannis, D.; Day-Lewis, F.D.; Elwaseif, M. Monitoring groundwater-surface water interaction using time-series and time-frequency analysis of transient three-dimensional electrical resistivity changes. Water Resour. Res. 2012, 48, 1–13. [Google Scholar] [CrossRef]
- Ghysels, G.; Anibas, C.; Awol, H.; Tolche, A.D.; Schneidewind, U.; Huysmans, M. The Significance of Vertical and Lateral Groundwater–Surface Water Exchange Fluxes in Riverbeds and Riverbanks: Comparing 1D Analytical Flux Estimates with 3D Groundwater Modeling. Water 2021, 13, 306. [Google Scholar] [CrossRef]
- Waseem, M.; Kachholz, F.; Klehr, W.; Tränckner, J. Suitability of a Coupled Hydrologic and Hydraulic Model to Simulate SurfaceWater and Groundwater Hydrology in a Typical North-Eastern Germany Lowland Catchment. Appl. Sci. 2020, 10, 1281. [Google Scholar] [CrossRef]
- Tran, Q.D.; Ni, C.F.; Lee, I.H.; Truong, M.H.; Liu, C.J. Numerical Modeling of Surface Water and Groundwater Interactions Induced by Complex Fluvial Landforms and Human Activities in the Pingtung Plain Groundwater Basin, Taiwan. Appl. Sci. 2020, 10, 7152. [Google Scholar] [CrossRef]
- Reeves, J.; Hatch, C.E. Impacts of three-dimensional nonuniform flow on quantification of groundwater-surface water interactions using heat as a tracer. Water Resour. Res. 2016, 52, 6851–6866. [Google Scholar] [CrossRef]
- El-Rawy, M.; Batelaan, O.; Buis, K.; Anibas, C.; Mohammed, G.; Zijl, W.; Salem, A. Analytical and Numerical Groundwater Flow Solutions for the FEMME-Modeling Environment. Hydrology 2020, 7, 27. [Google Scholar] [CrossRef]
- Keery, J.; Binley, A.; Crook, N.; Smith, J.W.N. Temporal and spatial variability of groundwater– surface water fluxes: Development and application of an analytical method using temperature time series. J. Hydrol. 2007, 336, 1–16. [Google Scholar] [CrossRef]
- Thomle, J.; Strickland, C.; Johnson, T.C.; Zhu, Y.; Stegen, J. A Flux Detection Probe to Quantify Dynamic Groundwater-Surface Water Exchange in the Hyporheic Zone. Natl. Ground Water Assoc. 2020, 58, 892–900. [Google Scholar] [CrossRef]
- Akhtar, N.; Syakir, M.I.; Ahmad, M.I.; Anees, M.T.; Bakar, A.F.B.A.; Mizan, S.A.; Alsaadi, S.F.; Khan, M.M.A.; Yusuff, M.S.M. Upscaling of Surface Water and Groundwater Interactions in Hyporheic Zone from Local to Regional Scale. Water 2022, 14, 647. [Google Scholar] [CrossRef]
- Khan, H.H.; Khan, A. Groundwater-surface water interaction along river Kali, near Aligarh, India. HydroResearch 2019, 2, 119–128. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; LaBaugh, J.W.; Hunt, R.J. Use of Monitoring Wells, Portable Piezometers, and Seepage Meters to Quantify Flow Between Surface Water and Ground Water; Techniques and Methods Chapter 4–D2; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 2008. [Google Scholar]


| Model Name | Discretization/Equations Solved | Applications | |
|---|---|---|---|
| For GW | For SW | ||
| CATHY | 3D Finite Element | 1D Finite Difference |
|
| MODFLOW-MODHMS | MODFLOW (3D Finite Difference) | 1D Saint Venant |
|
| MODBRANCH | MODFLOW (3D Finite Difference) | BRANCH (1D Saint-Venant) |
|
| MIKE SHE | 3D Finite Difference | 2D Saint-Venant |
|
| SWAT-MODFLOW | MODFLOW (3D Finite Difference) | SWAT |
|
| Approach | Advantages | Disadvantages |
|---|---|---|
| Darcy approach |
|
|
| Numerical modeling approach |
|
|
| Hydrochemistry (Use of isotopes) |
|
|
| Temperature studies |
|
|
| Water Budget |
|
|
| Analytical/semi-analytical and other approaches |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banerjee, D.; Ganguly, S. A Review on the Research Advances in Groundwater–Surface Water Interaction with an Overview of the Phenomenon. Water 2023, 15, 1552. https://doi.org/10.3390/w15081552
Banerjee D, Ganguly S. A Review on the Research Advances in Groundwater–Surface Water Interaction with an Overview of the Phenomenon. Water. 2023; 15(8):1552. https://doi.org/10.3390/w15081552
Chicago/Turabian StyleBanerjee, Dolon, and Sayantan Ganguly. 2023. "A Review on the Research Advances in Groundwater–Surface Water Interaction with an Overview of the Phenomenon" Water 15, no. 8: 1552. https://doi.org/10.3390/w15081552
APA StyleBanerjee, D., & Ganguly, S. (2023). A Review on the Research Advances in Groundwater–Surface Water Interaction with an Overview of the Phenomenon. Water, 15(8), 1552. https://doi.org/10.3390/w15081552






