3D CFD Study of Scour in Combined Wave–Current Flows around Rectangular Piles with Varying Aspect Ratios
Abstract
:1. Introduction
2. Numerical Model
2.1. Hydrodynamic Model
2.2. Free Surface Model
2.3. Modelling of Sediment Transport
Suspended Sediment Load Transportation
3. Model Validation
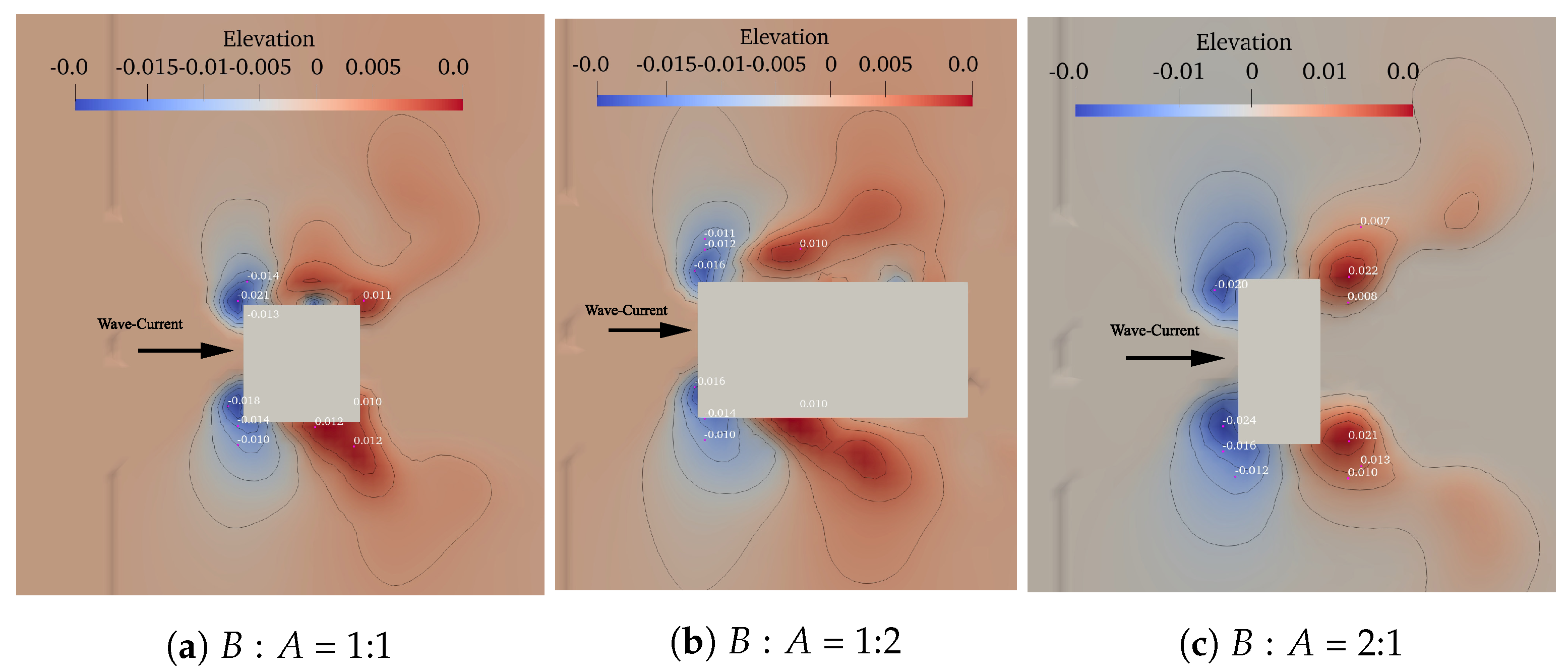
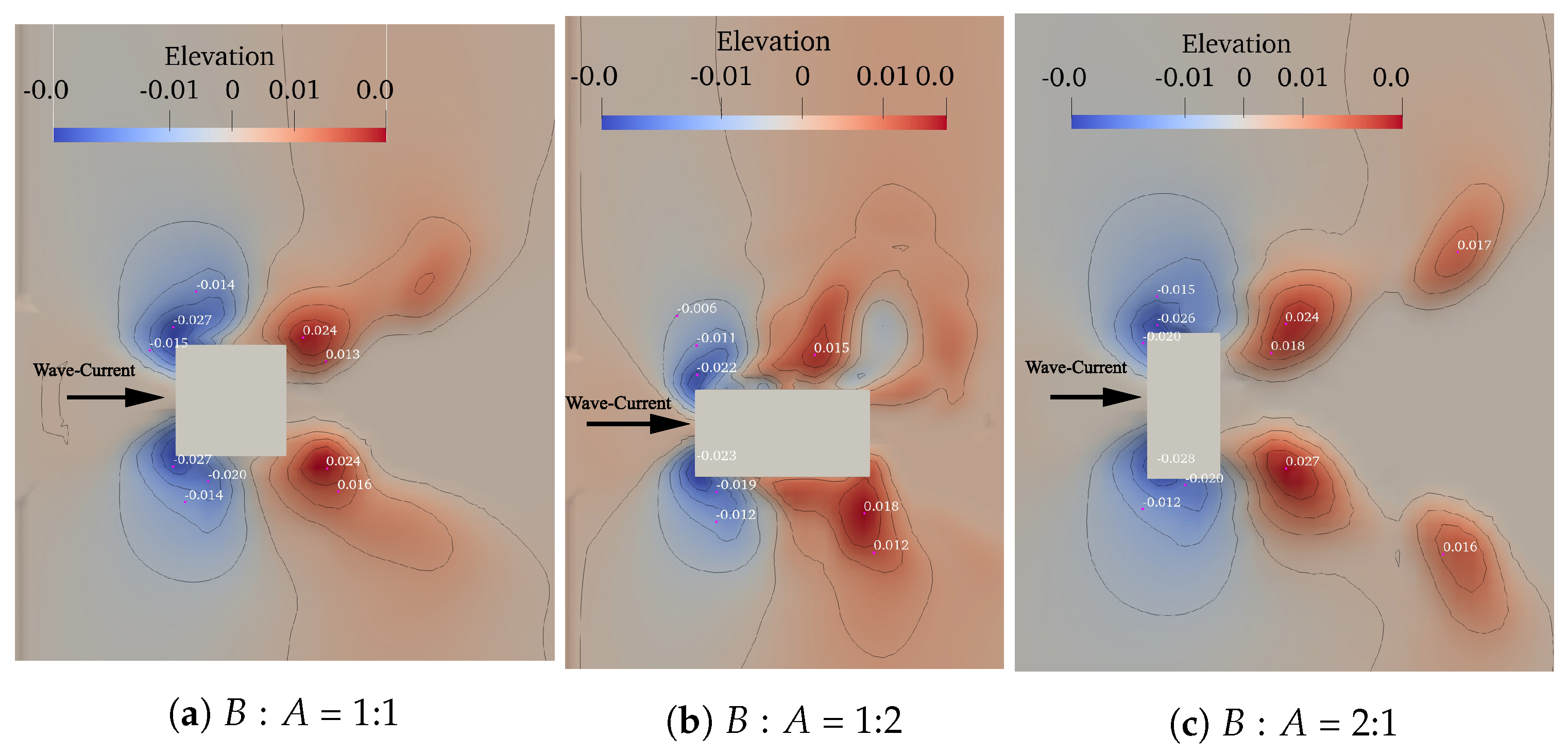
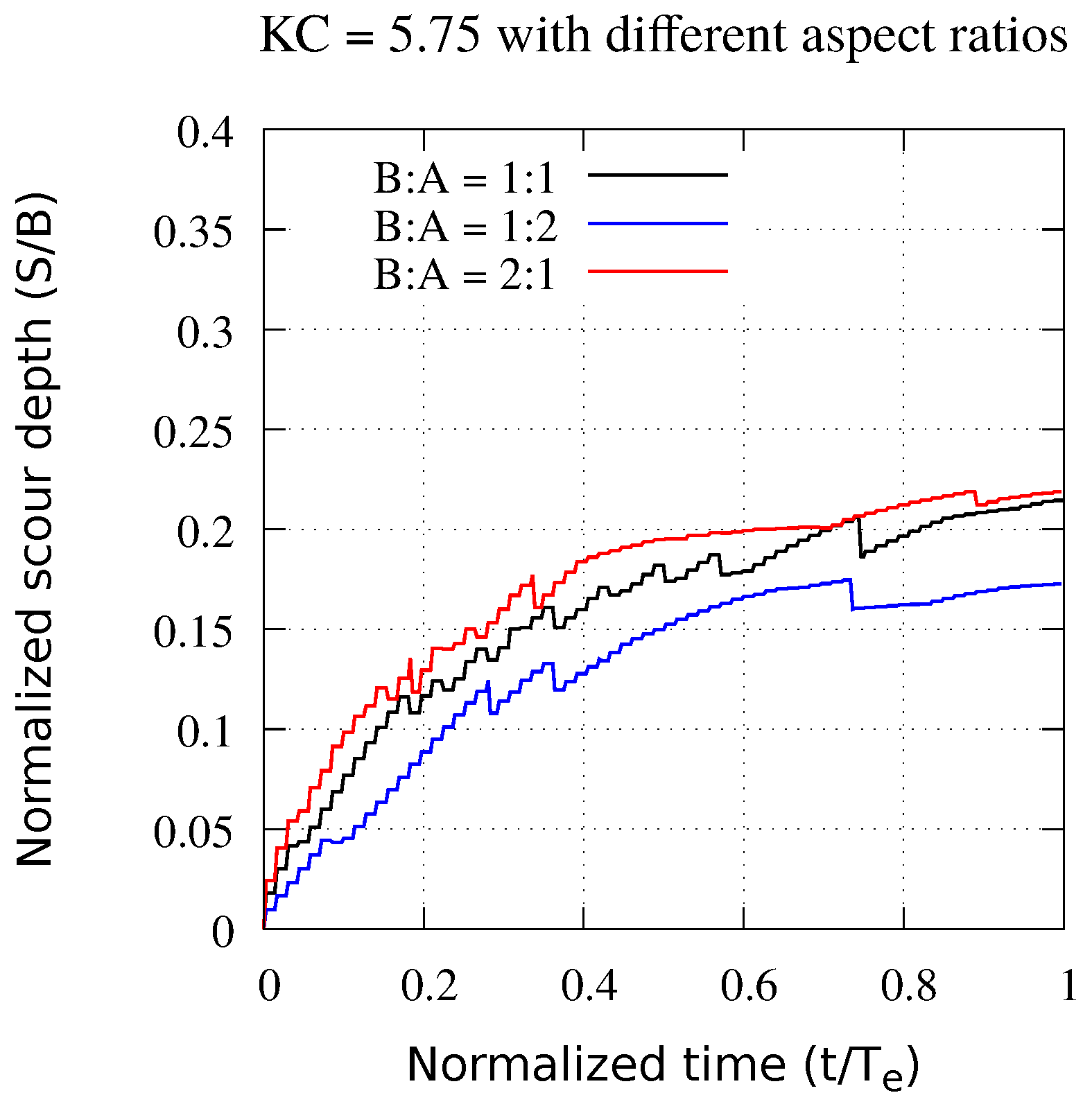
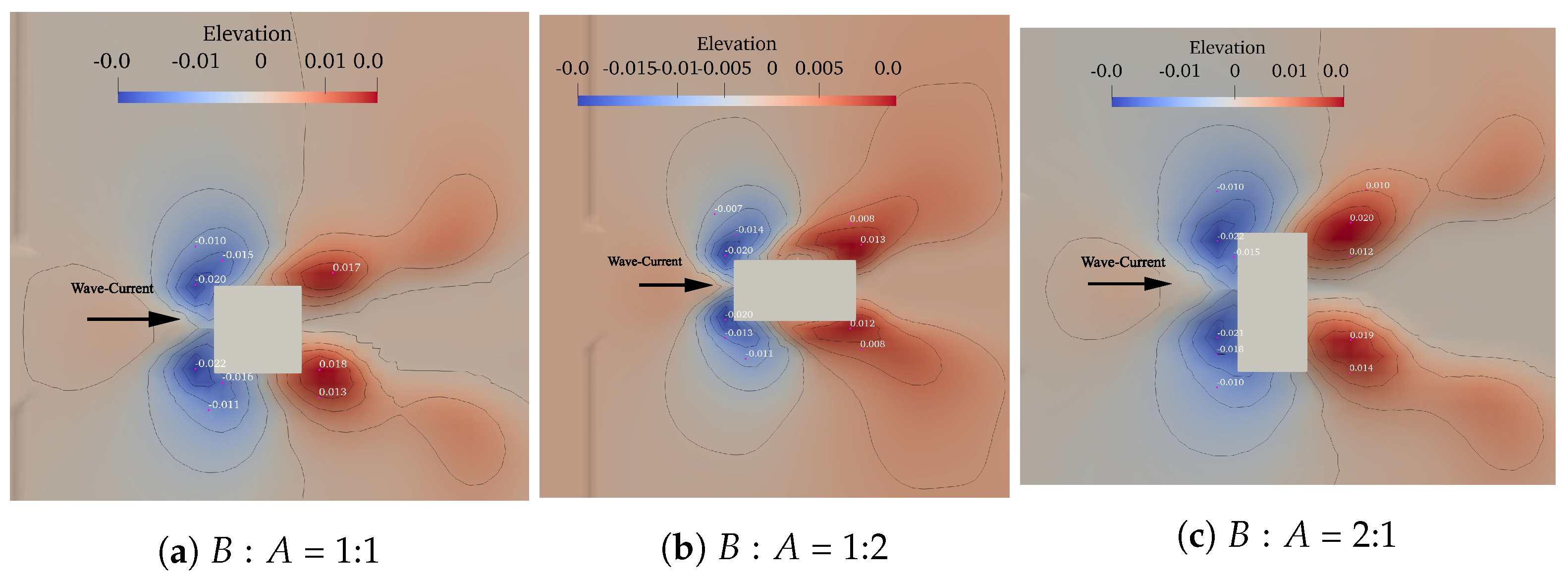
4. Results And Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sumer, B.M. The Mechanics of Scour in the Marine Environment; World Scientific: Singapore, 2002. [Google Scholar]
- Whitehouse, R. Scour at Marine Structures: A Manual for Practical Applications; Thomas Telford: London, UK, 1998. [Google Scholar]
- Chiew, Y.M.; Melville, B.W. Local scour around bridge piers. J. Hydraul. Res. 1987, 25, 15–26. [Google Scholar] [CrossRef]
- Richardson, J.E.; Panchang, V.G. Three-dimensional simulation of scour-inducing flow at bridge piers. J. Hydraul. Eng. 1998, 124, 530–540. [Google Scholar] [CrossRef]
- Olsen, N.R.; Kjellesvig, H.M. Three-dimensional numerical flow modeling for estimation of maximum local scour depth. J. Hydraul. Res. 1998, 36, 579–590. [Google Scholar] [CrossRef]
- Liu, X.; García, M.H. Three-dimensional numerical model with free water surface and mesh deformation for local sediment scour. J. Waterw. Port Coast. Ocean. Eng. 2008, 134, 203–217. [Google Scholar] [CrossRef]
- Ahmad, N.; Afzal, S.; Bihs, H.; Arntsen, ØA. Three-dimensional numerical modeling of local scour around a non-slender cylinder under varying wave conditions. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Saud Afzal, M.; Bihs, H.; Kamath, A.; Arntsen, ØA. Three-dimensional numerical modeling of pier scour under current and waves using level-set method. J. Offshore Mech. Arct. Eng. 2015, 137, 032001. [Google Scholar] [CrossRef]
- Kim, H.S.; Nabi, M.; Kimura, I.; Shimizu, Y. Numerical investigation of local scour at two adjacent cylinders. Adv. Water Resour. 2014, 70, 131–147. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of marine sands: A manual for practical applications. Oceanogr. Lit. Rev. 1997, 9, 947. [Google Scholar]
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Zhang, Y.; Jeng, D.S.; Gao, F.; Zhang, J.S. An analytical solution for response of a porous seabed to combined wave and current loading. Ocean Eng. 2013, 57, 240–247. [Google Scholar] [CrossRef]
- Alhaddad, S.; Labeur, R.J.; Uijttewaal, W. Breaching flow slides and the associated turbidity current. J. Mar. Sci. Eng. 2020, 8, 67. [Google Scholar] [CrossRef]
- Alhaddad, S.; Labeur, R.J.; Uijttewaal, W. Large-scale Experiments on Breaching Flow Slides and the Associated Turbidity Current. J. Geophys. Res. Earth Surf. 2020, 125, e2020JF005582. [Google Scholar] [CrossRef]
- Alhaddad, S.; de Wit, L.; Labeur, R.J.; Uijttewaal, W. Modeling of Breaching-Generated Turbidity Currents Using Large Eddy Simulation. J. Mar. Sci. Eng. 2020, 8, 728. [Google Scholar] [CrossRef]
- Alhaddad, S.; Weij, D.; van Rhee, C.; Keetels, G. Stabilizing and Destabilizing Breaching Flow Slides. J. Mar. Sci. Eng. 2023, 11, 560. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Scour around pile in combined waves and current. J. Hydraul. Eng. 2001, 127, 403–411. [Google Scholar] [CrossRef]
- Umeyama, M. Reynolds stresses and velocity distributions in a wave-current coexisting environment. J. Waterw. Port Coast. Ocean Eng. 2005, 131, 203–212. [Google Scholar] [CrossRef]
- Umeyama, M. Changes in turbulent flow structure under combined wave-current motions. J. Waterw. Port Coast. Ocean Eng. 2009, 135, 213–227. [Google Scholar] [CrossRef]
- Umeyama, M. Coupled PIV and PTV measurements of particle velocities and trajectories for surface waves following a steady current. J. Waterw. Port, Coast. Ocean Eng. 2011, 137, 85–94. [Google Scholar] [CrossRef]
- Sumer, B.; Christiansen, N.; Fredsøe, J. Influence of cross section on wave scour around piles. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 477–495. [Google Scholar] [CrossRef]
- Diab, R.; Link, O.; Zanke, U. Geometry of developing and equilibrium scour holes at bridge piers in gravel. Can. J. Civ. Eng. 2010, 37, 544–552. [Google Scholar] [CrossRef]
- Yao, W.; An, H.; Draper, S.; Cheng, L.; Harris, J.M. Experimental investigation of local scour around submerged piles in steady current. Coast. Eng. 2018, 142, 27–41. [Google Scholar] [CrossRef]
- Omara, H.; Ookawara, S.; Nassar, K.A.; Masria, A.; Tawfik, A. Assessing local scour at rectangular bridge piers. Ocean Eng. 2022, 266, 112912. [Google Scholar] [CrossRef]
- Ismael, A.; Gunal, M.; Hussein, H. Effect of bridge pier position on scour reduction according to flow direction. Arab. J. Sci. Eng. 2015, 40, 1579–1590. [Google Scholar] [CrossRef]
- Al-Shukur, A.H.K.; Obeid, Z.H. Experimental study of bridge pier shape to minimize local scour. Int. J. Civ. Eng. Technol. 2016, 7, 162–171. [Google Scholar]
- Mir, B.H.; Lone, M.A.; Bhat, J.A.; Rather, N.A. Effect of gradation of bed material on local scour depth. Geotech. Geol. Eng. 2018, 36, 2505–2516. [Google Scholar] [CrossRef]
- Gazi, A.H.; Purkayastha, S.; Afzal, M.S. The Equilibrium Scour Depth around a Pier under the Action of Collinear Waves and Current. J. Mar. Sci. Eng. 2020, 8, 36. [Google Scholar] [CrossRef]
- Abbasnia, A.H.; Ghiassi, R. Improvements on bed-shear stress formulation for pier scour computation. Int. J. Numer. Methods Fluids 2011, 67, 383–402. [Google Scholar] [CrossRef]
- Ghiassi, R.; Abbasnia, A.H. Investigation of vorticity effects on local scouring. Arab. J. Sci. Eng. 2013, 38, 537–548. [Google Scholar] [CrossRef]
- Bihs, H.; Kamath, A.; Chella, M.A.; Aggarwal, A.; Arntsen, Ø.A. A new level set numerical wave tank with improved density interpolation for complex wave hydrodynamics. Comput. Fluids 2016, 140, 191–208. [Google Scholar] [CrossRef]
- Dutta, D.; Bihs, H.; Afzal, M.S. Computational Fluid Dynamics modelling of hydrodynamic characteristics of oscillatory flow past a square cylinder using the level set method. Ocean Eng. 2022, 253, 111211. [Google Scholar] [CrossRef]
- Qi, W.G.; Li, Y.X.; Xu, K.; Gao, F.P. Physical modelling of local scour at twin piles under combined waves and current. Coast. Eng. 2019, 143, 63–75. [Google Scholar] [CrossRef]
- Qi, W.G.; Gao, F.P. Physical modeling of local scour development around a large-diameter monopile in combined waves and current. Coast. Eng. 2014, 83, 72–81. [Google Scholar] [CrossRef]
- Gautam, S.; Dutta, D.; Bihs, H.; Afzal, M.S. Three-dimensional Computational Fluid Dynamics modelling of scour around a single pile due to combined action of the waves and current using Level-Set method. Coast. Eng. 2021, 170, 104002. [Google Scholar] [CrossRef]
- Afzal, M.S.; Bihs, H.; Kumar, L. Computational fluid dynamics modeling of abutment scour under steady current using the level set method. Int. J. Sediment Res. 2020, 35, 355–364. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Jiang, G.S.; Peng, D. Weighted ENO schemes for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 2000, 21, 2126–2143. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modelling for CFD; DCW Industries Inc.: La Canada, CA, USA, 1994. [Google Scholar]
- Naot, D.; Rodi, W. Calculation of secondary currents in channel flow. J. Hydraul. Div. 1982, 108, 948–968. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef]
- Durbin, P. Limiters and wall treatments in applied turbulence modeling. Fluid Dyn. Res. 2009, 41, 012203. [Google Scholar] [CrossRef]
- Jiang, G.S. Efficient Implementation of Weighted ENO Schemes; Department of Mathematics, University of California: Los Angeles, CA, USA, 1995. [Google Scholar]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef]
- Griebel, M.; Dornseifer, T.; Neunhoeffer, T. Numerical Simulation in Fluid Dynamics: A Practical Introduction; Siam: Philadelphia, PA, USA, 1997; Volume 3. [Google Scholar]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Peng, D.; Merriman, B.; Osher, S.; Zhao, H.; Kang, M. A PDE-based fast local level set method. J. Comput. Phys. 1999, 155, 410–438. [Google Scholar] [CrossRef]
- Kraft, S.; Wang, Y.; Oberlack, M. Large eddy simulation of sediment deformation in a turbulent flow by means of level-set method. J. Hydraul. Eng. 2011, 137, 1394–1405. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Engelund, F.; Fredsøe, J. A sediment transport model for straight alluvial channels. Hydrol. Res. 1976, 7, 293–306. [Google Scholar] [CrossRef]
- Shields, A. Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Ph.D. Thesis, Technical University, Berlin, Germany, 1936. [Google Scholar]
- Hunt, J. The turbulent transport of suspended sediment in open channels. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1954, 224, 322–335. [Google Scholar]
- Rijn, L.C.v. Sediment transport, part II: Suspended load transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Rouse, H. Modern conceptions of the mechanics of fluid turbulence. Trans. ASCE 1937, 102, 463–505. [Google Scholar] [CrossRef]
- Lane, E.W. Design of stable channels. Trans. Am. Soc. Civ. Eng. 1955, 120, 1234–1260. [Google Scholar] [CrossRef]
- Kovacs, A.; Parker, G. A new vectorial bedload formulation and its application to the time evolution of straight river channels. J. Fluid Mech. 1994, 267, 153–183. [Google Scholar] [CrossRef]
- Ikeda, S. Incipient motion of sand particles on side slopes. J. Hydraul. Div. 1982, 108, 95–114. [Google Scholar] [CrossRef]
- Dey, S. Experimental study on incipient motion of sediment particles on generalized sloping fluvial beds. Int. J. Sediment Res. 2001, 16, 391–398. [Google Scholar]
- Dey, S. Threshold of sediment motion on combined transverse and longitudinal sloping beds. J. Hydraul. Res. 2003, 41, 405–415. [Google Scholar] [CrossRef]
- Burkow, M.; Griebel, M. A full three dimensional numerical simulation of the sediment transport and the scouring at a rectangular obstacle. Comput. Fluids 2016, 125, 1–10. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351. [Google Scholar] [CrossRef]
- Sumer, B.M.; Christiansen, N.; Fredsøe, J. The horseshoe vortex and vortex shedding around a vertical wall-mounted cylinder exposed to waves. J. Fluid Mech. 1997, 332, 41–70. [Google Scholar] [CrossRef]
- Hunt, J.C.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. 1988. Available online: https://ntrs.nasa.gov/citations/19890015184 (accessed on 15 March 2023).
- Ettema, R.; Melville, B.W.; Barkdoll, B. Scale effect in pier-scour experiments. J. Hydraul. Eng. 1998, 124, 639–642. [Google Scholar] [CrossRef]
- Faruque, M. Studying the Effect of Froude Number and Densimetric Froude Number on Local Scours around Circular Bridge Piers. Int. J. Archit. Civ. Constr. Sci. 2018, 11, 1–7. [Google Scholar]
- Ettema, R.; Kirkil, G.; Muste, M. Similitude of large-scale turbulence in experiments on local scour at cylinders. J. Hydraul. Eng. 2006, 132, 33–40. [Google Scholar] [CrossRef]
- Qi, W.; Gao, F. Equilibrium scour depth at offshore monopile foundation in combined waves and current. Sci. China Technol. Sci. 2014, 57, 1030–1039. [Google Scholar] [CrossRef]
- Sumer, B.M.; Petersen, T.U.; Locatelli, L.; Fredsøe, J.; Musumeci, R.E.; Foti, E. Backfilling of a scour hole around a pile in waves and current. J. Waterw. Port Coast. Ocean. Eng. 2013, 139, 9–23. [Google Scholar] [CrossRef]
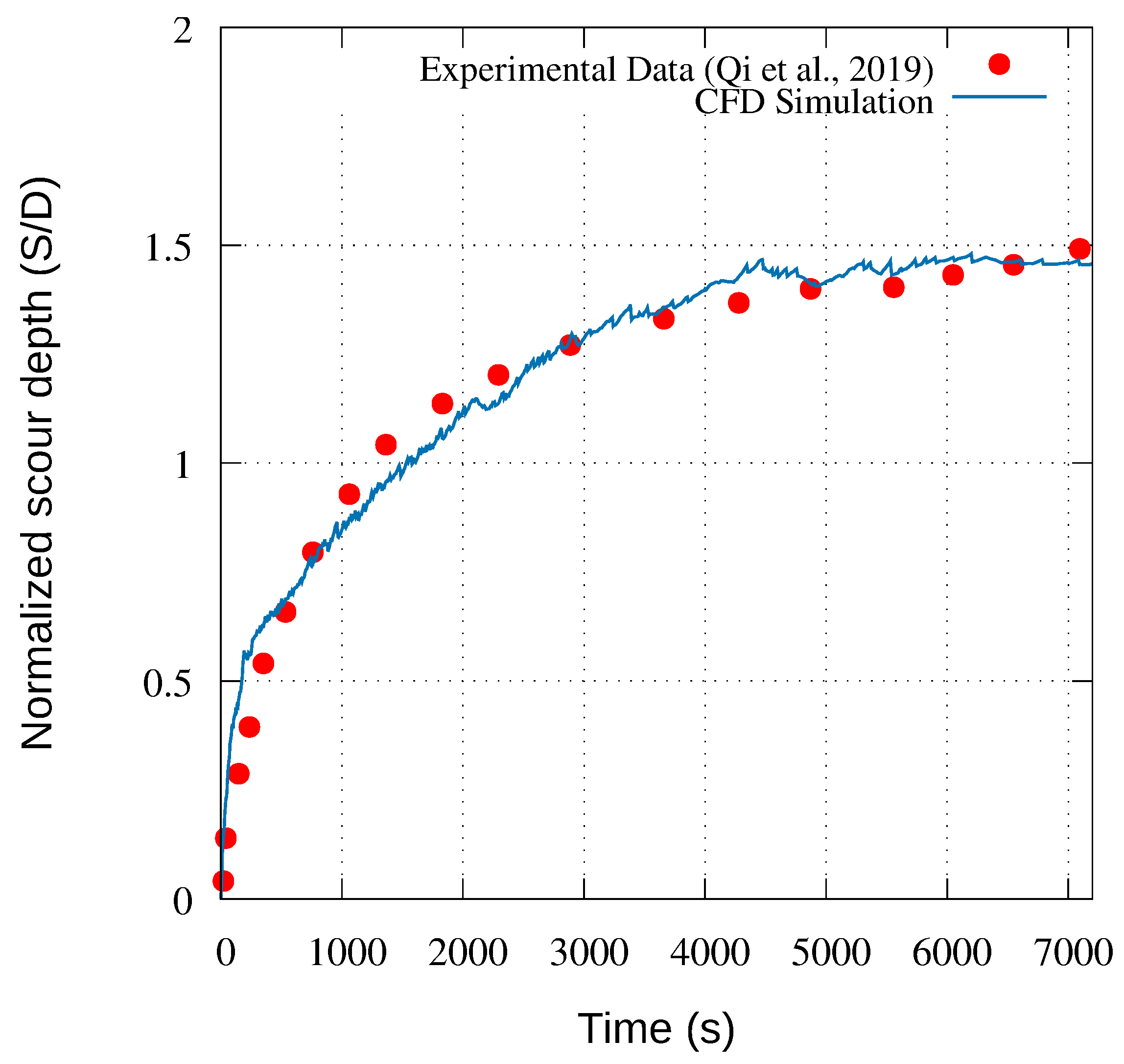
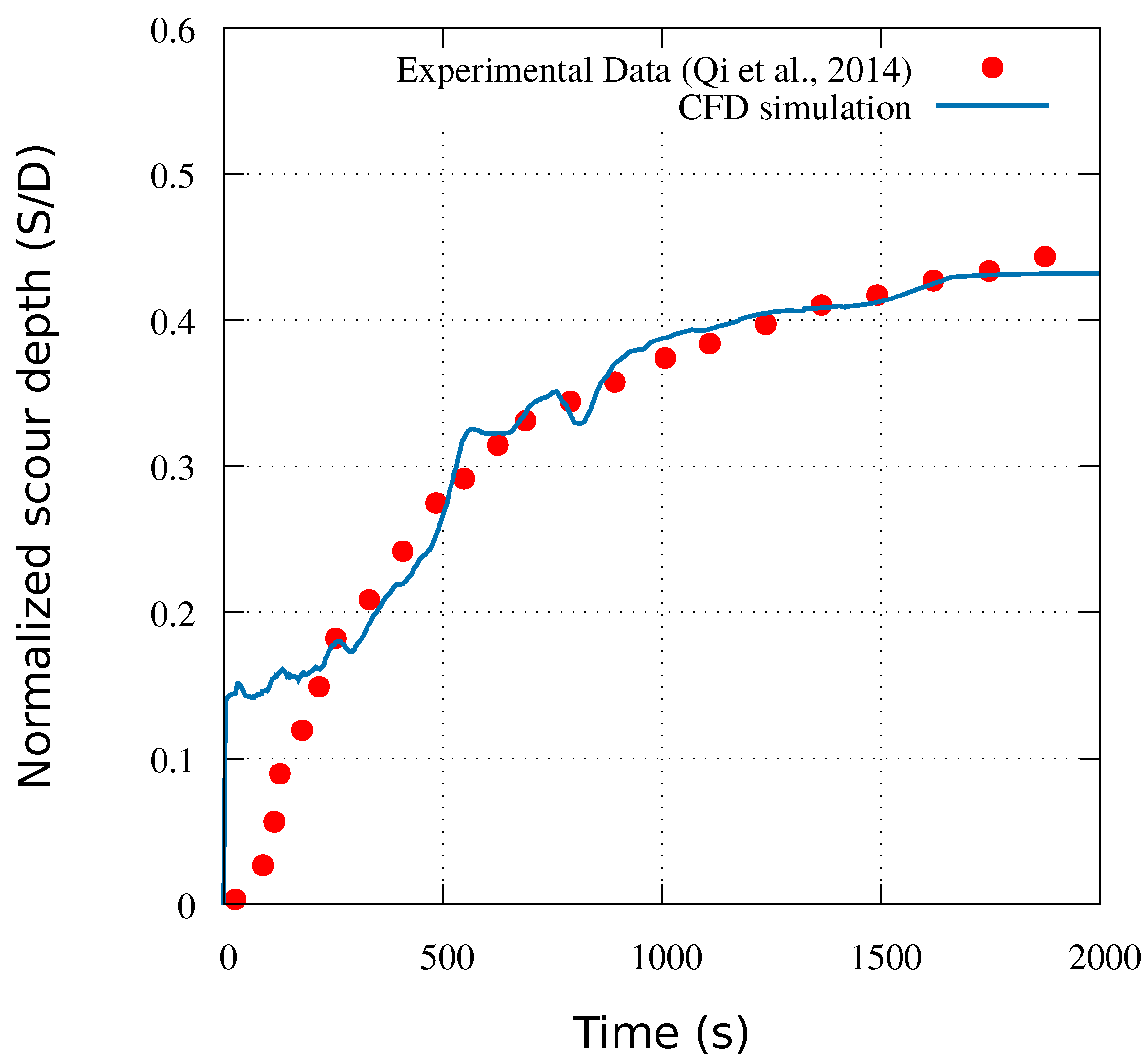
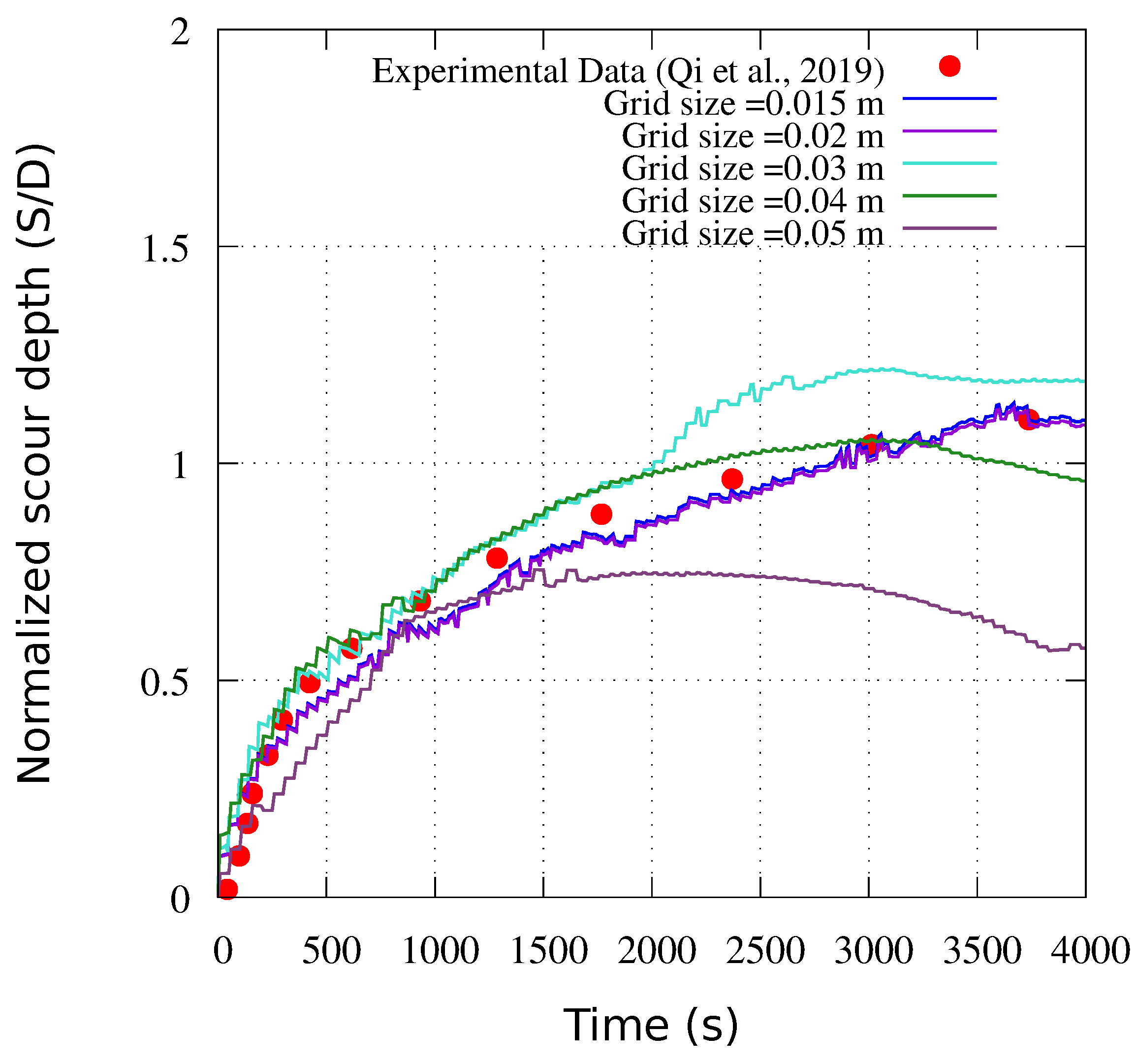





| Cases | (-) | (mm) | (-) | (-) | (KN/m) |
|---|---|---|---|---|---|
| Validation 1 (Figure 1) | 0.409 | 0.15 | 0.35 | 0.62 | 10.65 |
| Validation 2 (Figure 2) | 0.045 | 0.38 | 0.435 | 0.352 | 9.03 |
| Validation 3 (Figure 3) | 0.409 | 0.15 | 0.35 | 0.62 | 10.65 |
| Cases | Run | Time Period (s) | (m/s) | (m/s) | S/D | ||
|---|---|---|---|---|---|---|---|
| Validation | W-C scour (Figure 1) | 1.8 | 0.25 | 0.23 | 0.48 | 5.63 | 1.5 |
| W-C scour (Figure 2) | 1.4 | 0.303 | 0.23 | 0.43 | 1.28 | 0.41 | |
| W-C scour (Figure 3) | 1.8 | 0.25 | 0.23 | 0.48 | 5.63 | 1.08 | |
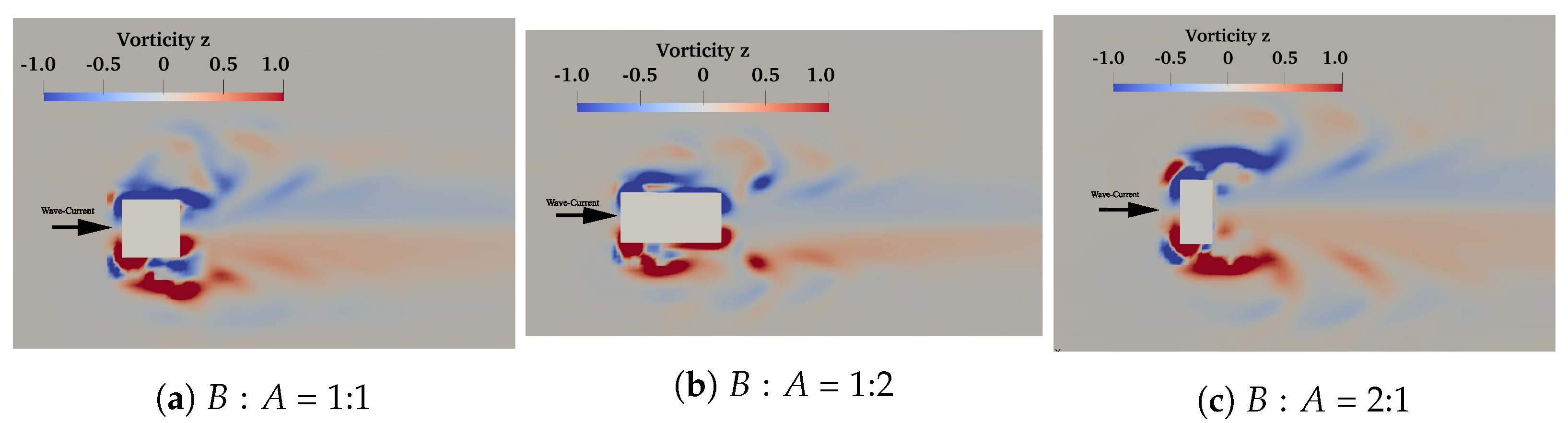
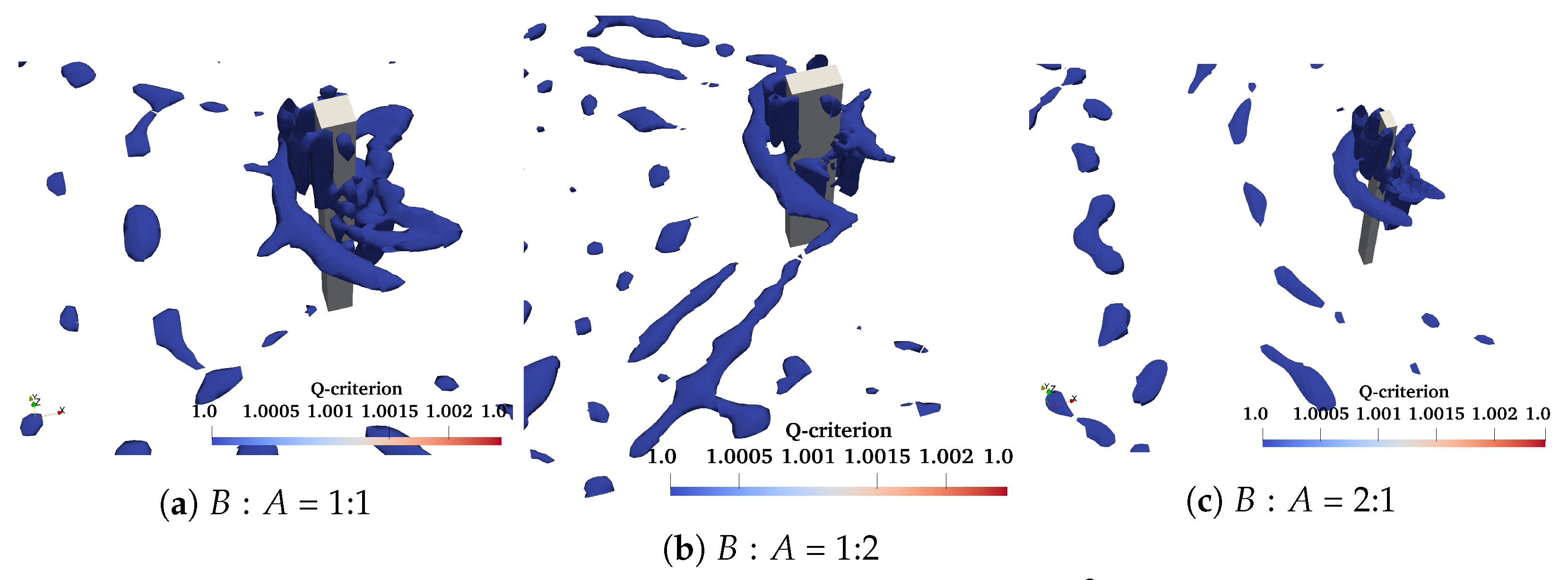
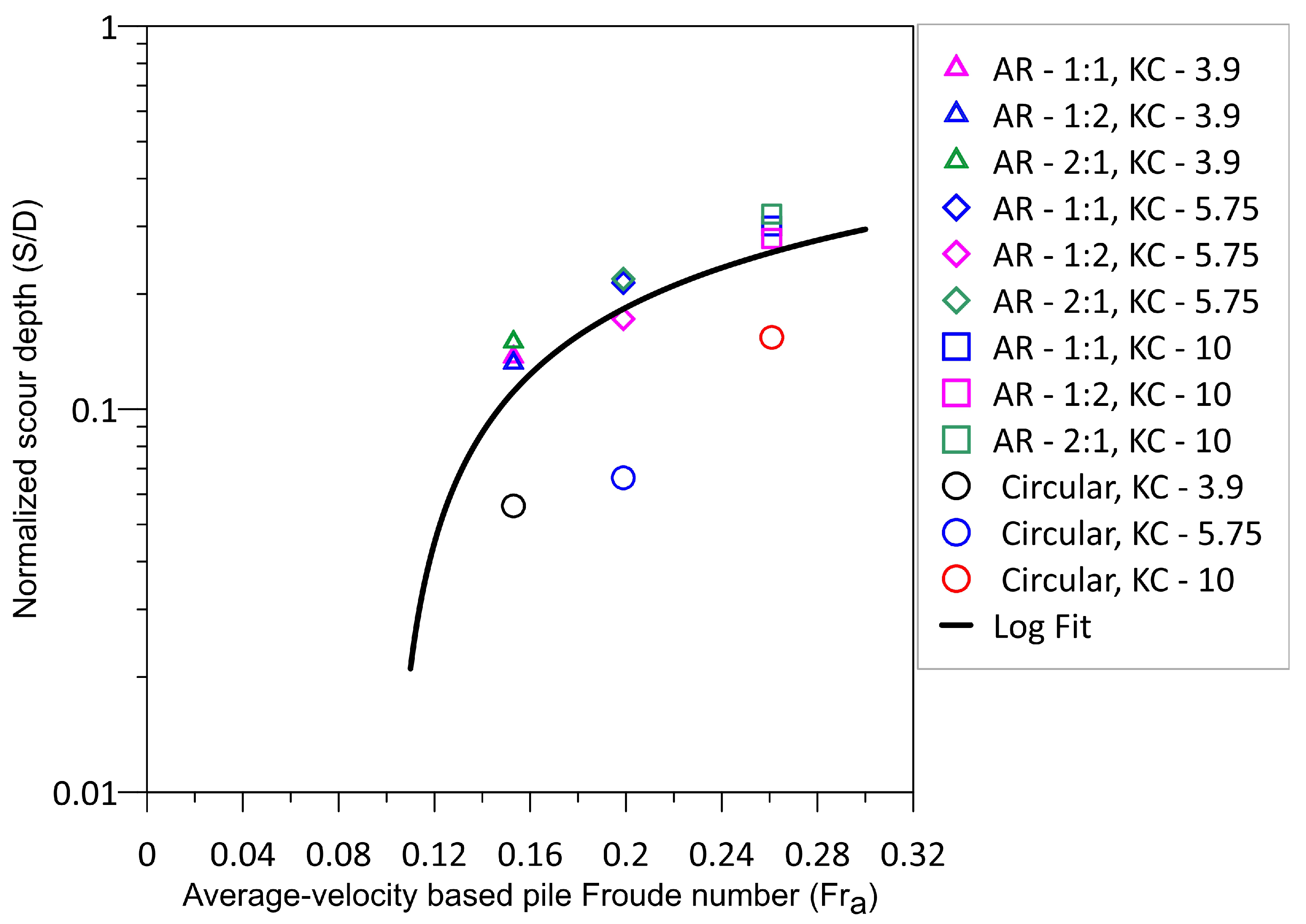
| Analysis | W-C scour (Figure 6a) | 4.5 | 0.156 | 0.104 | 0.4 | 3.9 | 0.138 |
| W-C scour (Figure 6b) | 4.5 | 0.156 | 0.104 | 0.4 | 3.9 | 0.132 | |
| W-C scour (Figure 6c) | 4.5 | 0.156 | 0.104 | 0.4 | 3.9 | 0.151 | |
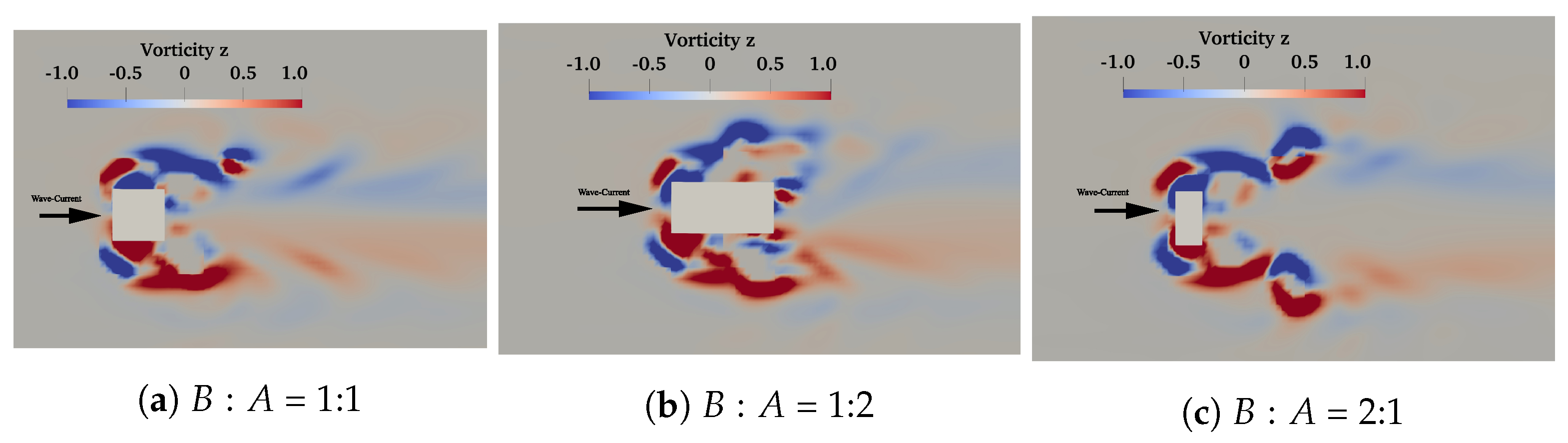
| W-C scour (Figure 8) | 4.5 | 0.179 | 0.119 | 0.4 | 5.75 | 0.214 | |
| W-C scour (Figure 8b) | 4.5 | 0.179 | 0.119 | 0.4 | 5.75 | 0.172 | |
| W-C scour (Figure 8c) | 4.5 | 0.179 | 0.104 | 0.4 | 5.75 | 0.218 | |
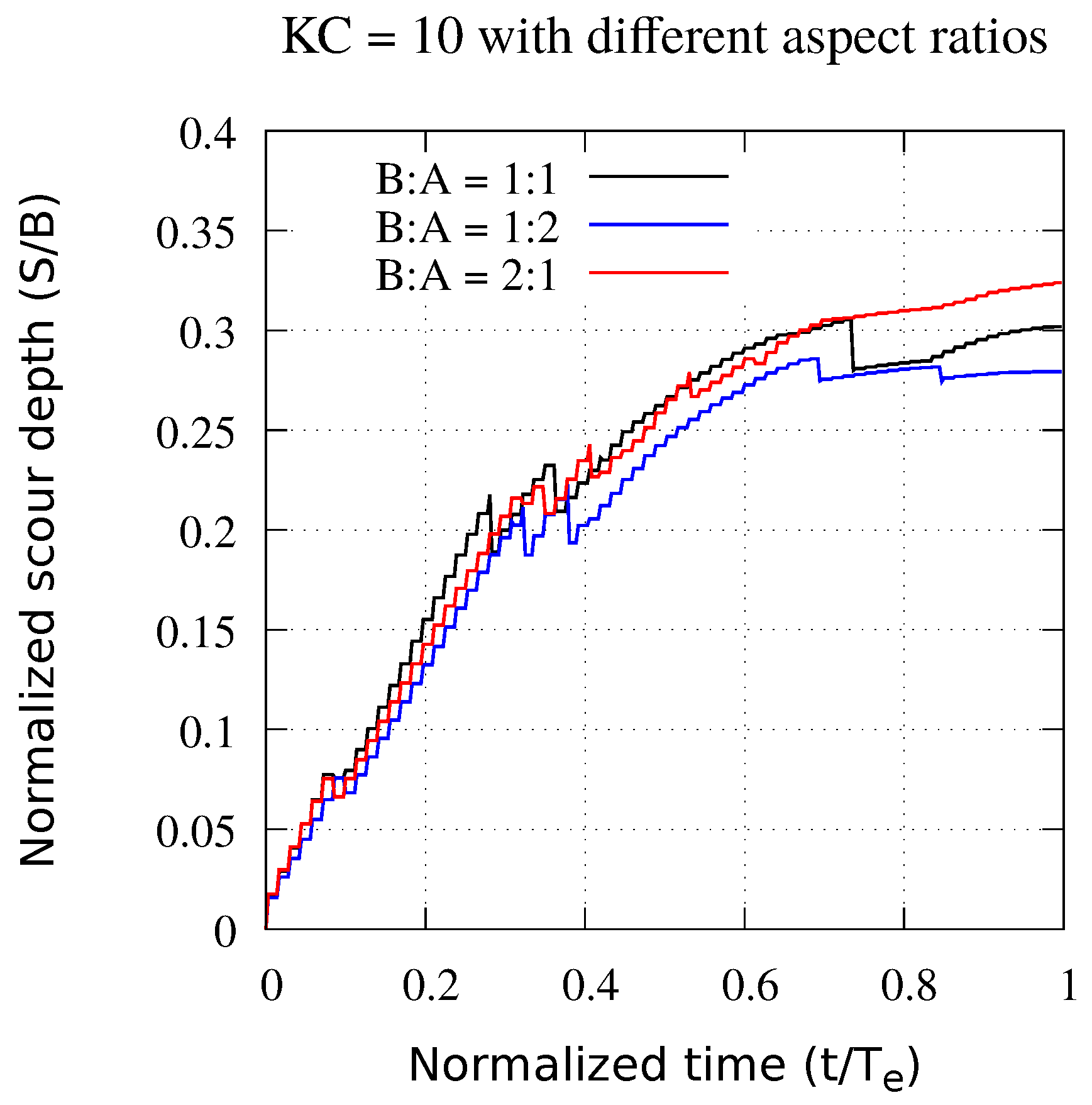
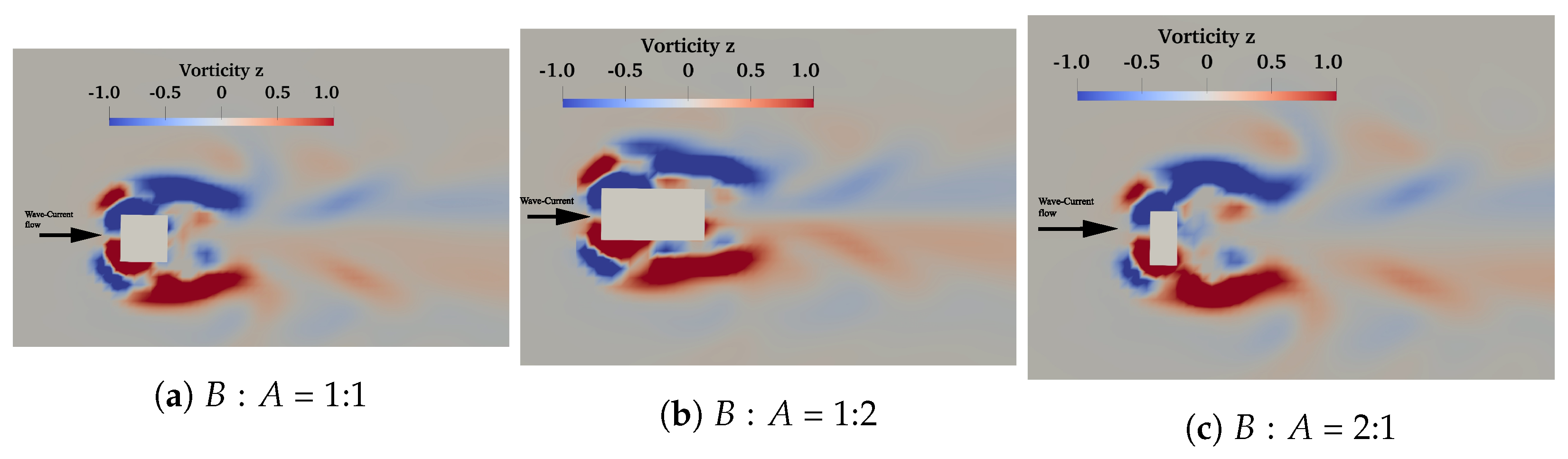
| W-C scour (Figure 10a) | 4.5 | 0.178 | 0.118 | 0.4 | 10 | 0.301 | |
| W-C scour (Figure 10b) | 4.5 | 0.178 | 0.118 | 0.4 | 10 | 0.279 | |
| W-C scour (Figure 10c) | 4.5 | 0.178 | 0.118 | 0.4 | 10 | 0.323 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutta, D.; Afzal, M.S.; Alhaddad, S. 3D CFD Study of Scour in Combined Wave–Current Flows around Rectangular Piles with Varying Aspect Ratios. Water 2023, 15, 1541. https://doi.org/10.3390/w15081541
Dutta D, Afzal MS, Alhaddad S. 3D CFD Study of Scour in Combined Wave–Current Flows around Rectangular Piles with Varying Aspect Ratios. Water. 2023; 15(8):1541. https://doi.org/10.3390/w15081541
Chicago/Turabian StyleDutta, Debasish, Mohammad Saud Afzal, and Said Alhaddad. 2023. "3D CFD Study of Scour in Combined Wave–Current Flows around Rectangular Piles with Varying Aspect Ratios" Water 15, no. 8: 1541. https://doi.org/10.3390/w15081541






