Numerical Evaluation of the Hydrothermal Process in a Water-Surrounded Heater of Natural Gas Pressure Reduction Plants
Abstract
:1. Introduction
2. Materials and Methods
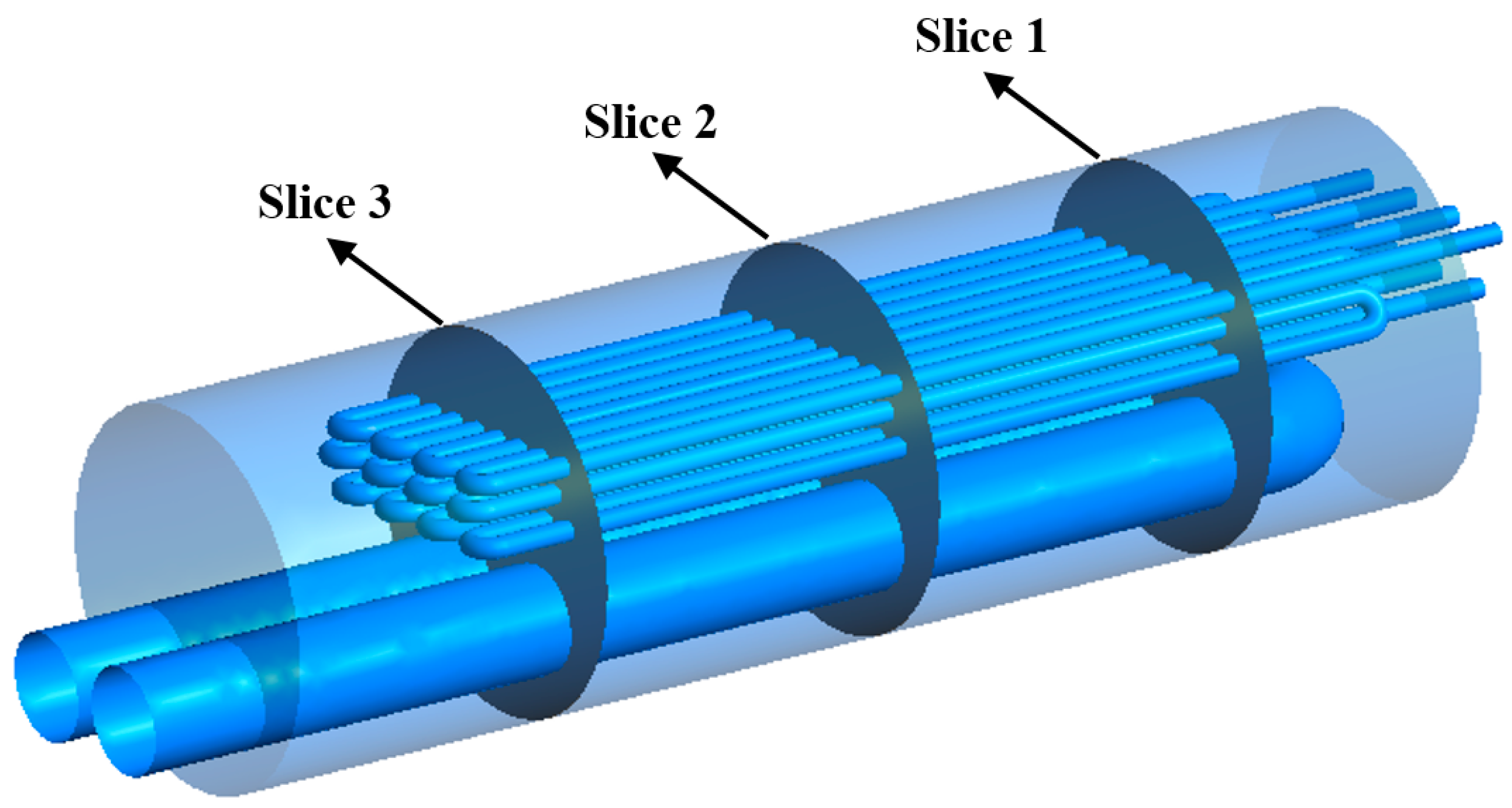
2.1. Geometrical Parameters
2.2. Governing Equations and Parameters
2.3. Boundary Conditions
3. Results and Discussion
3.1. The Mesh-Independent and Validation Analyses
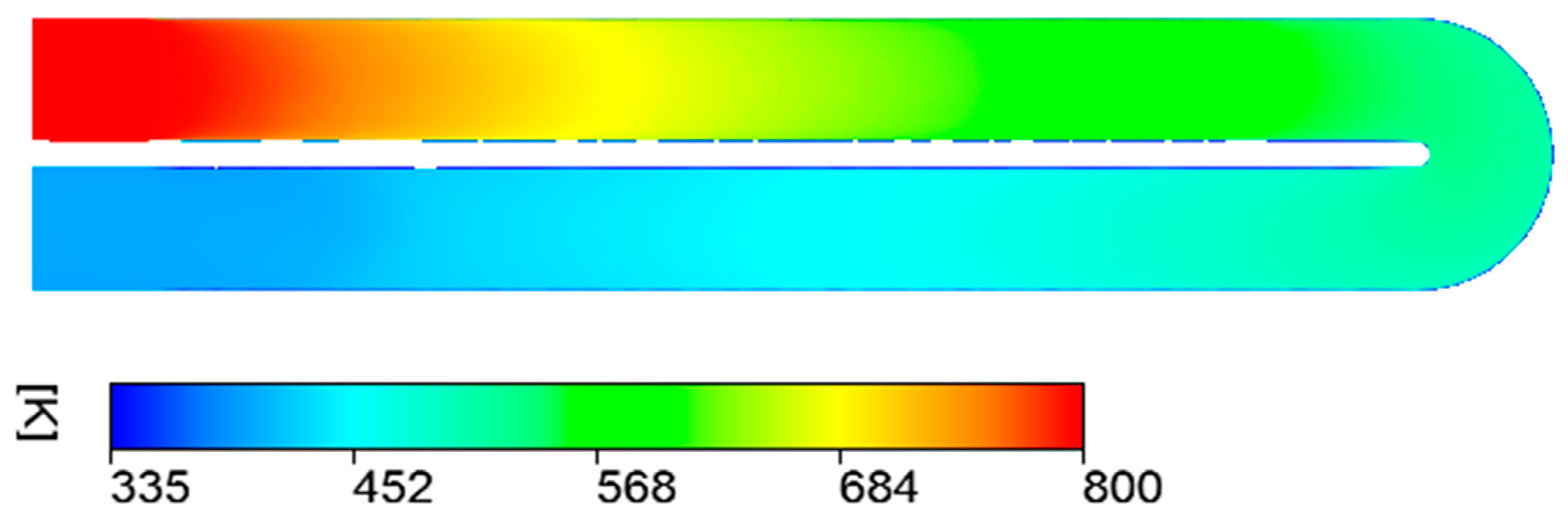
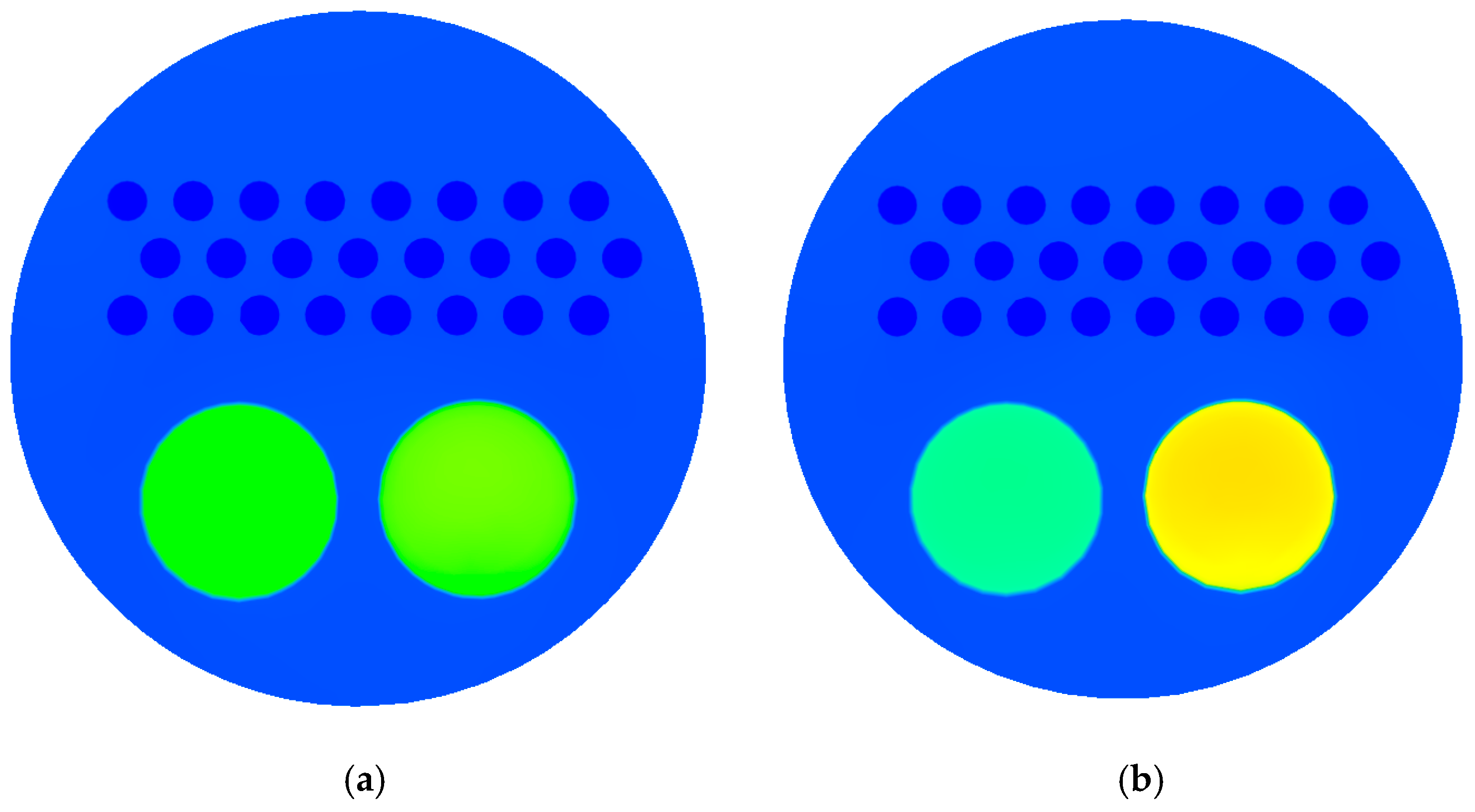
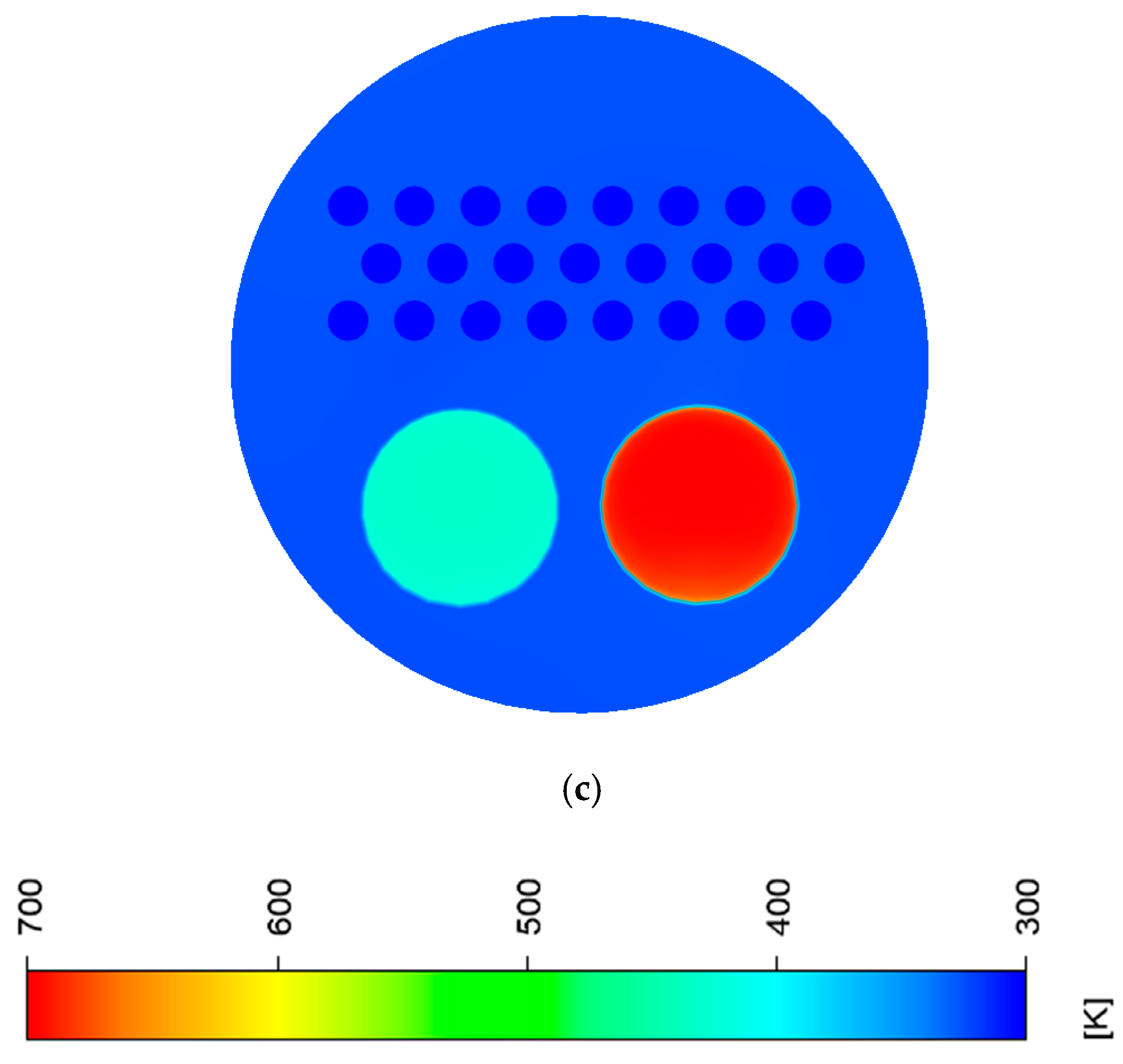
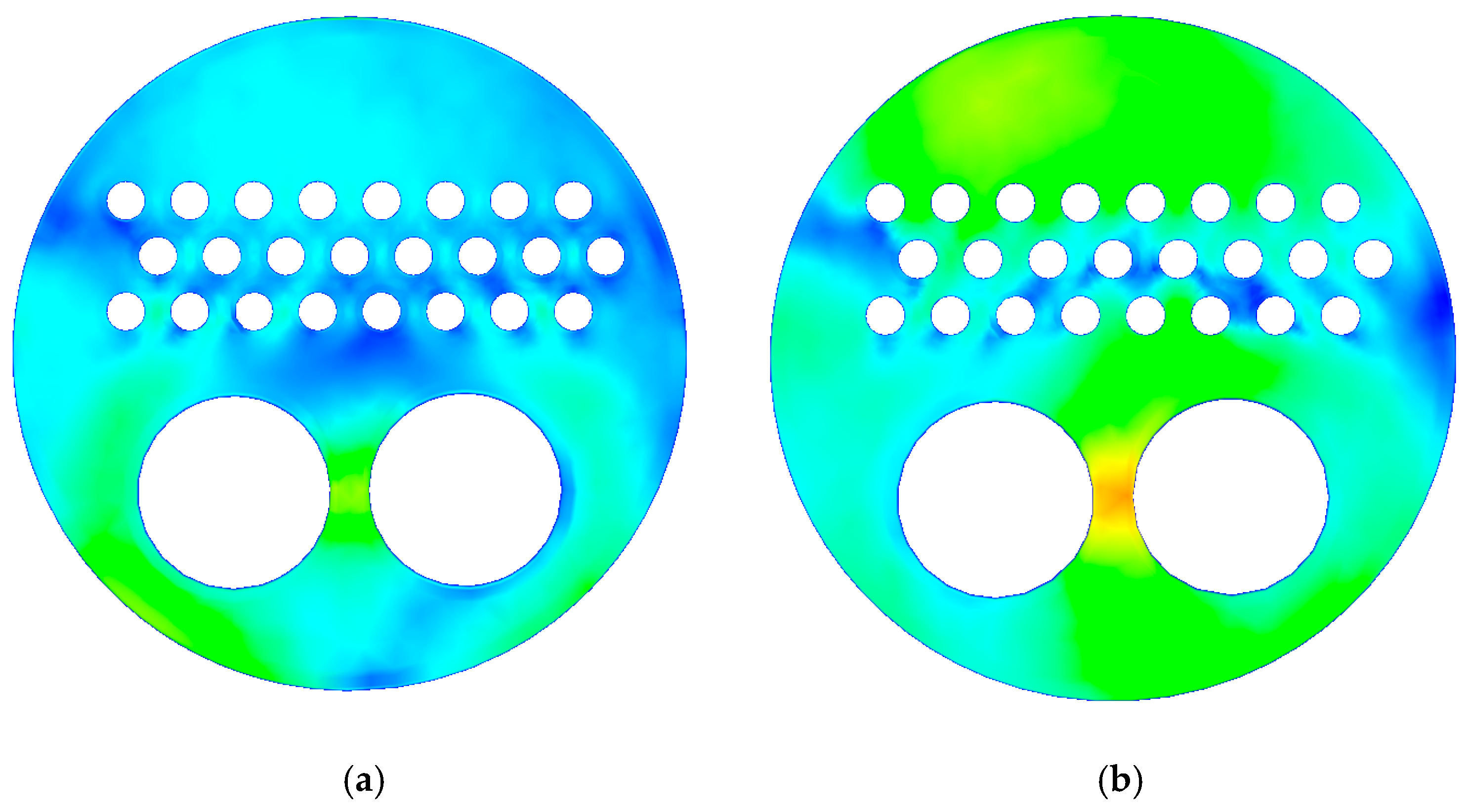
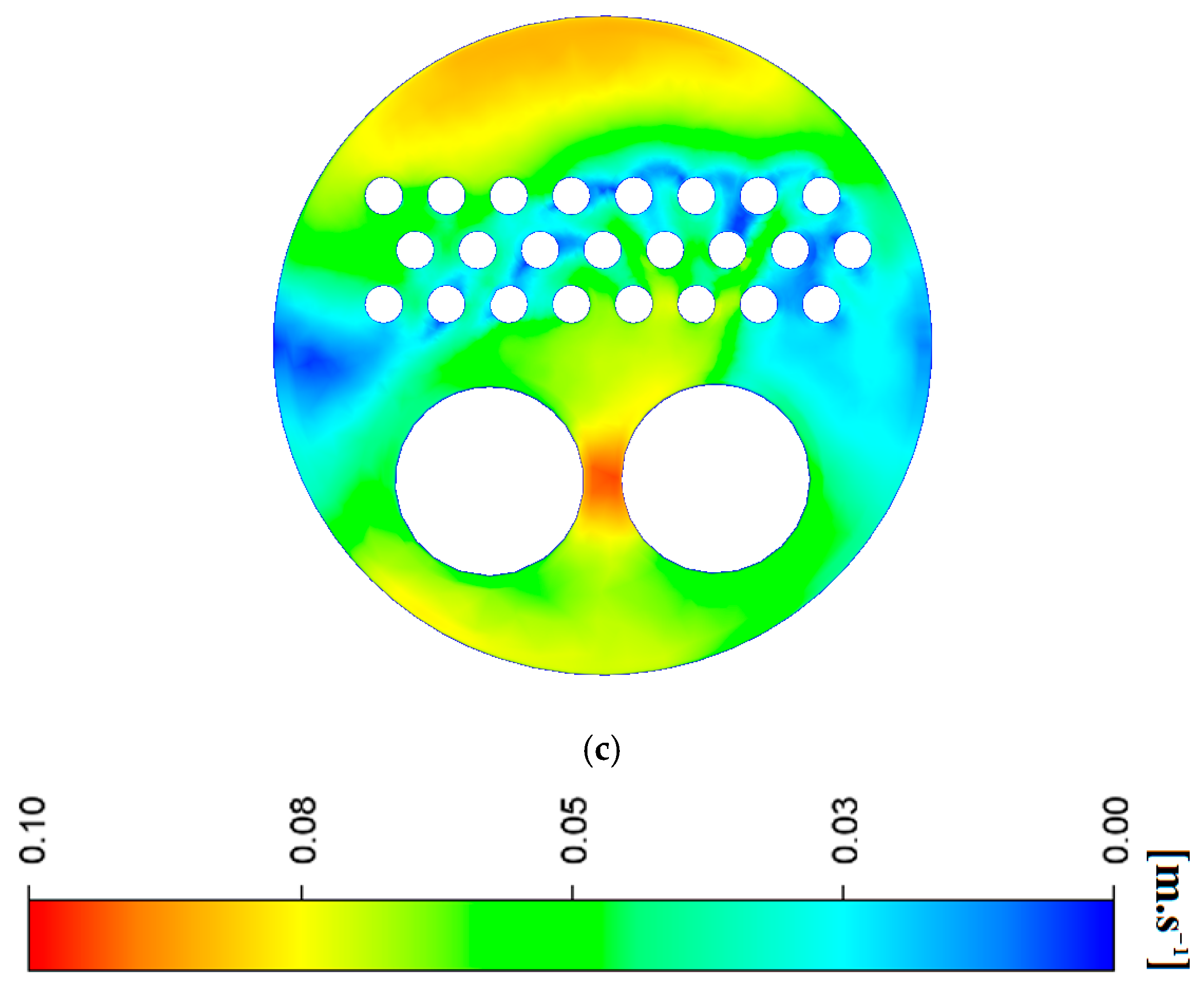
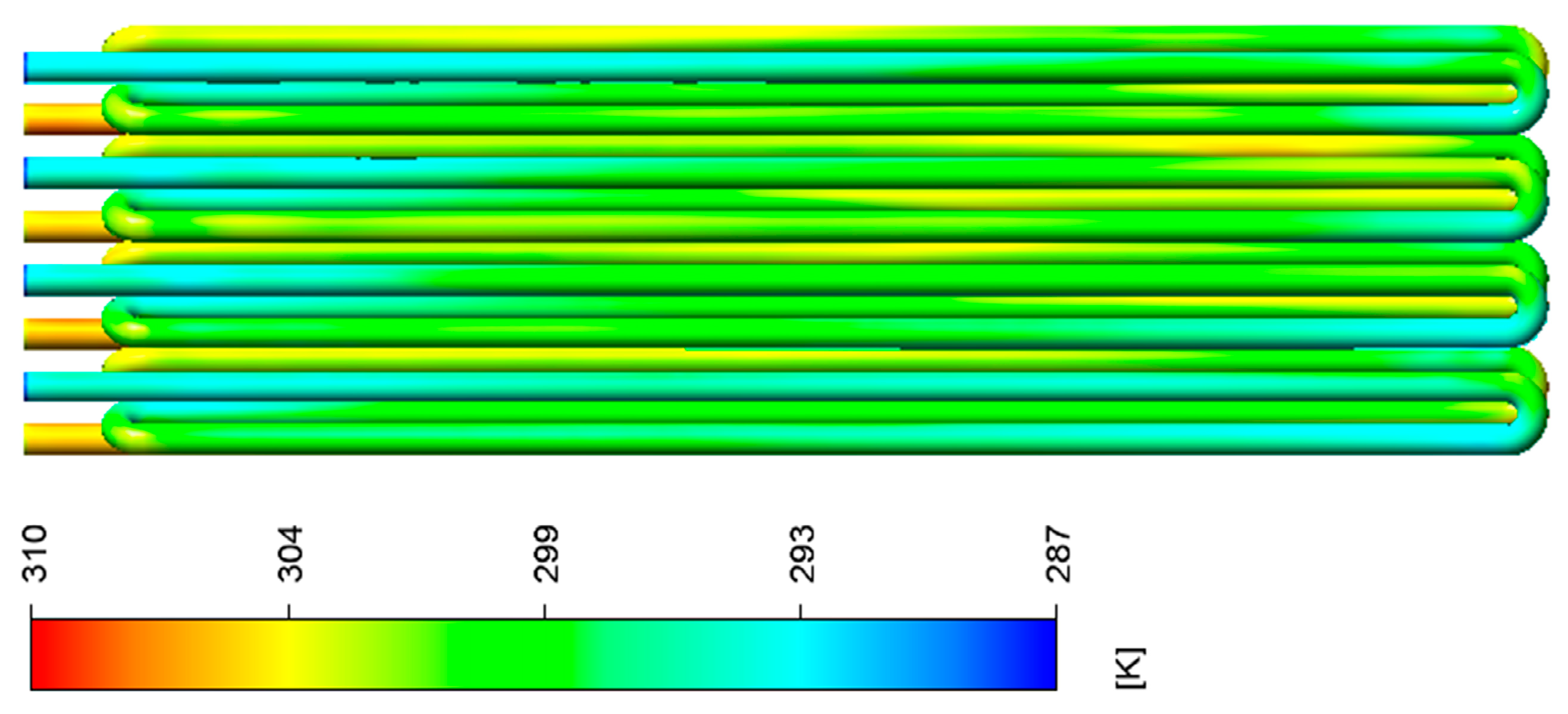
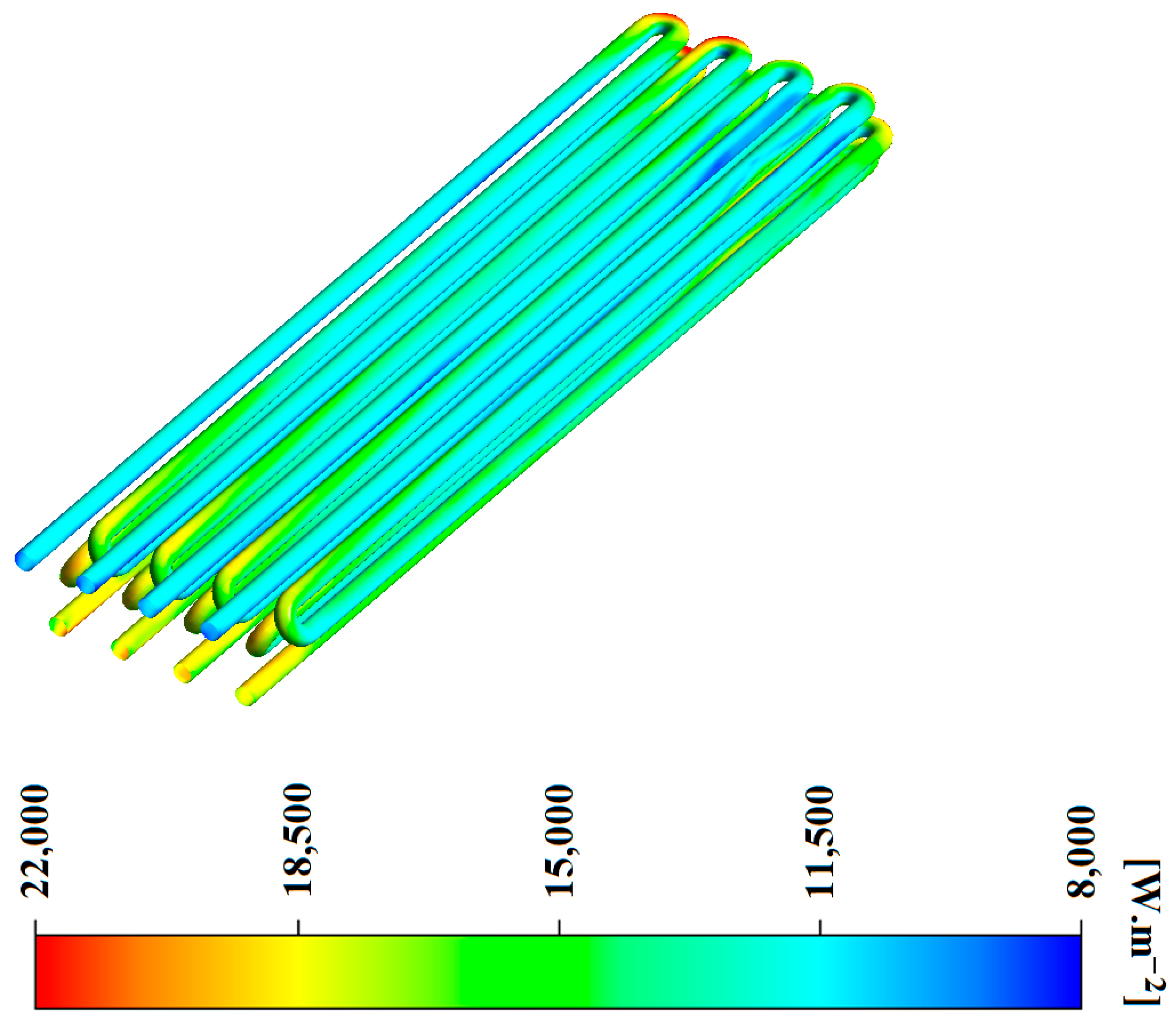
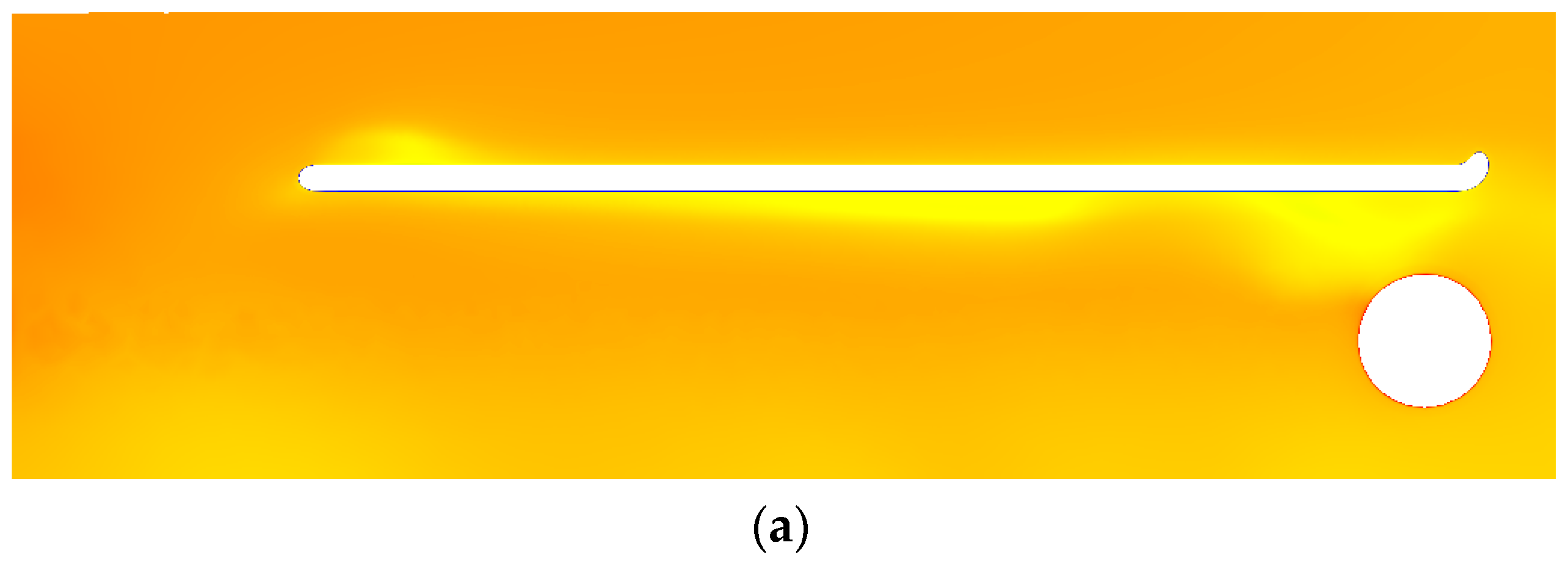
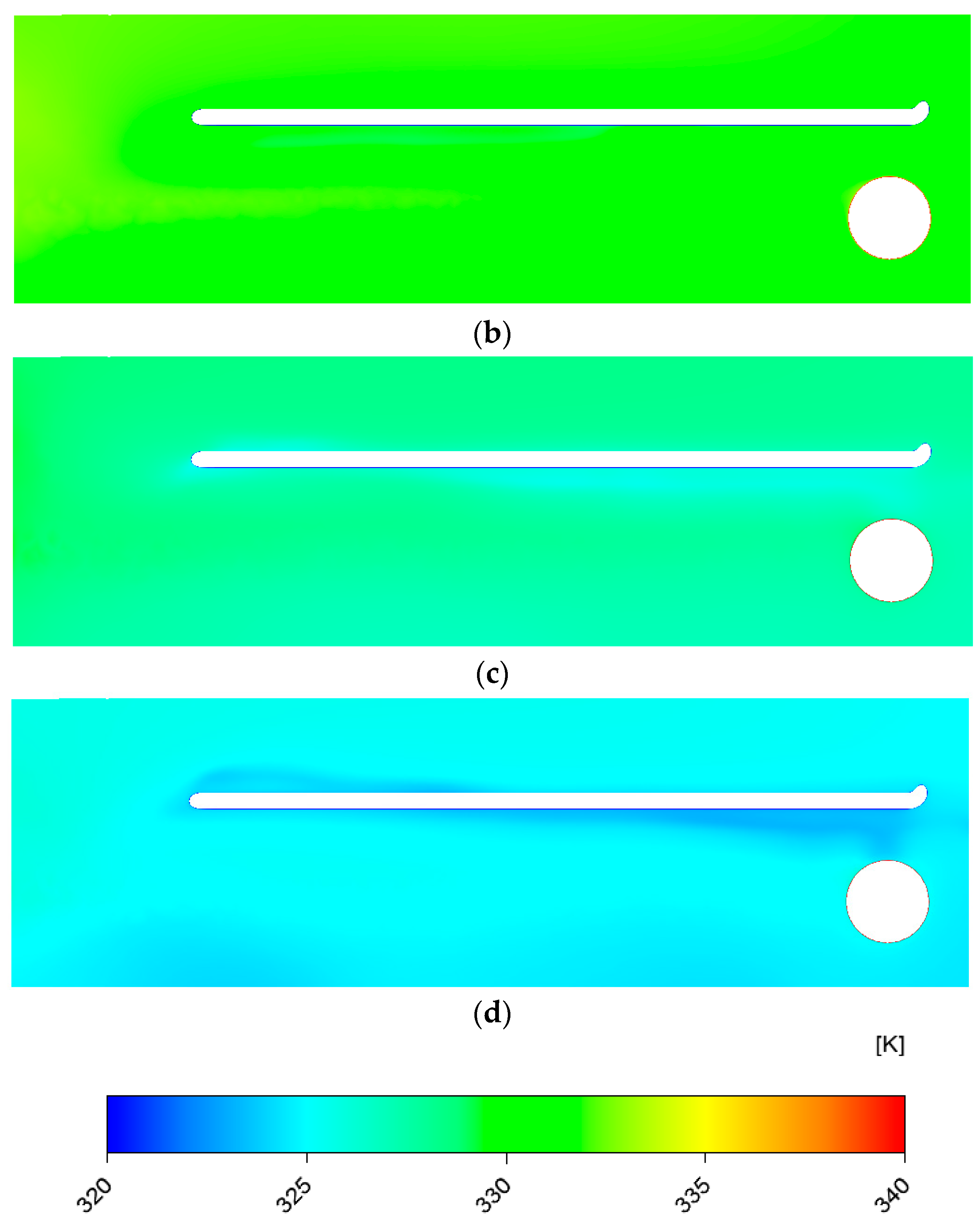
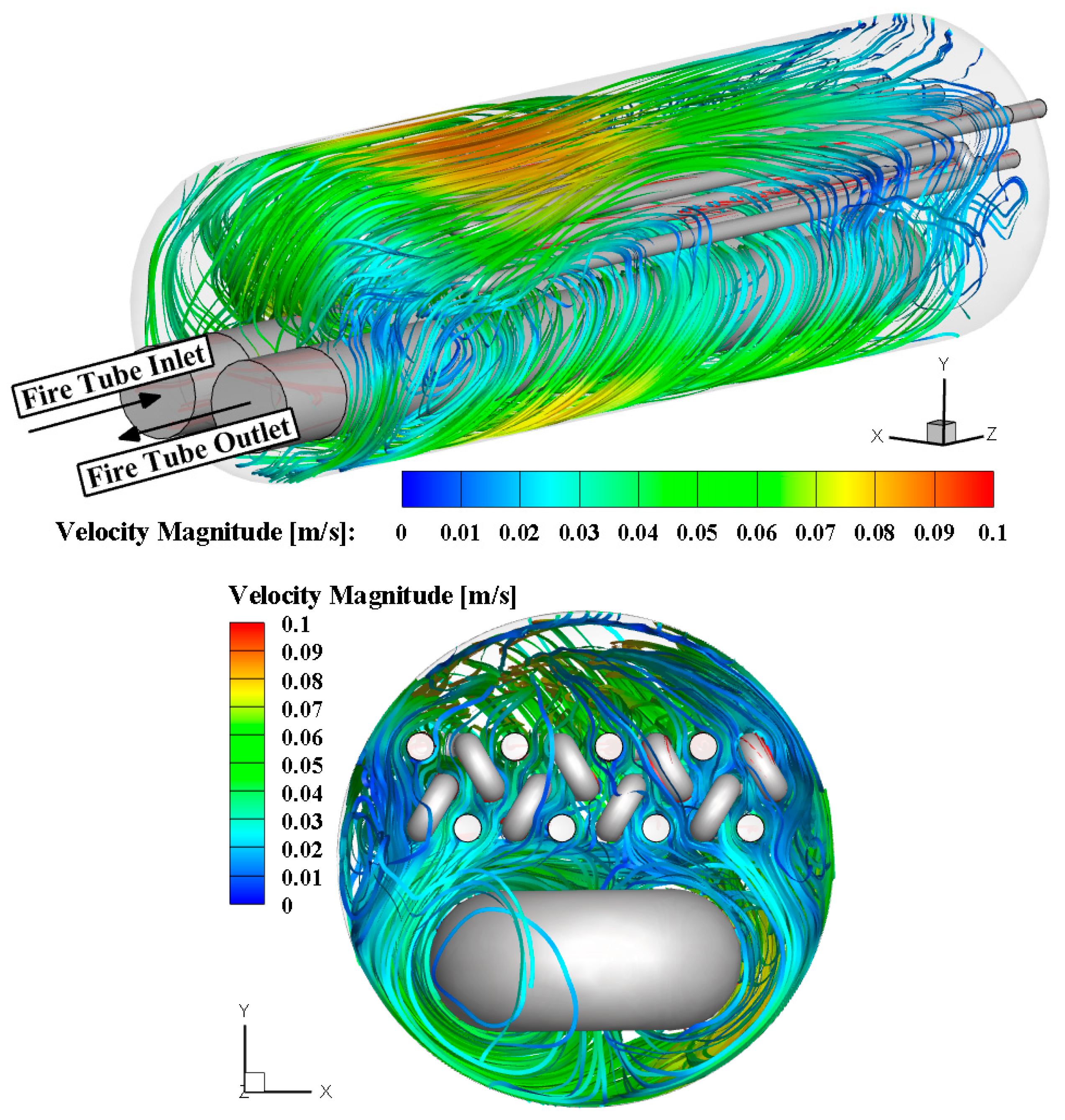
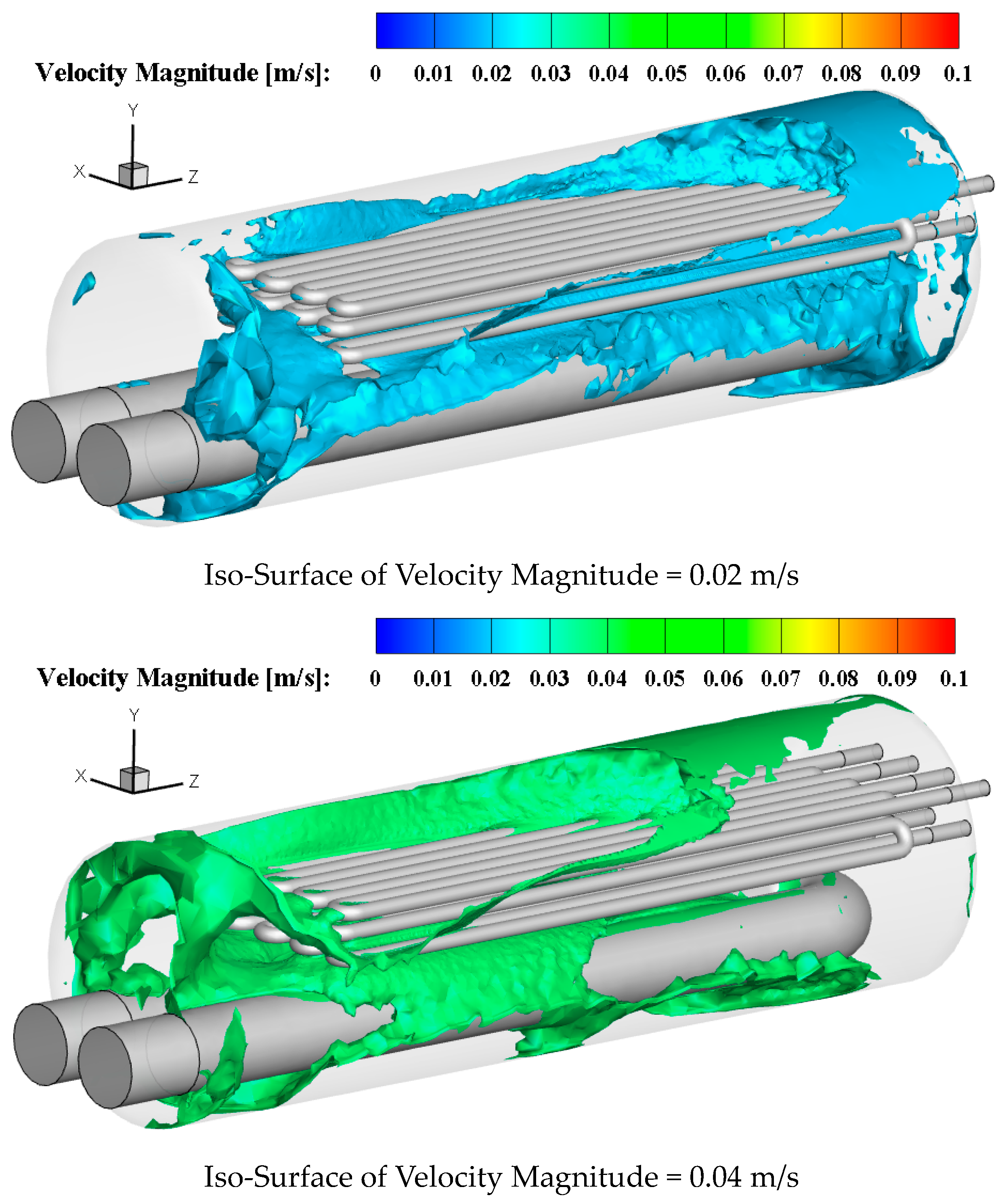
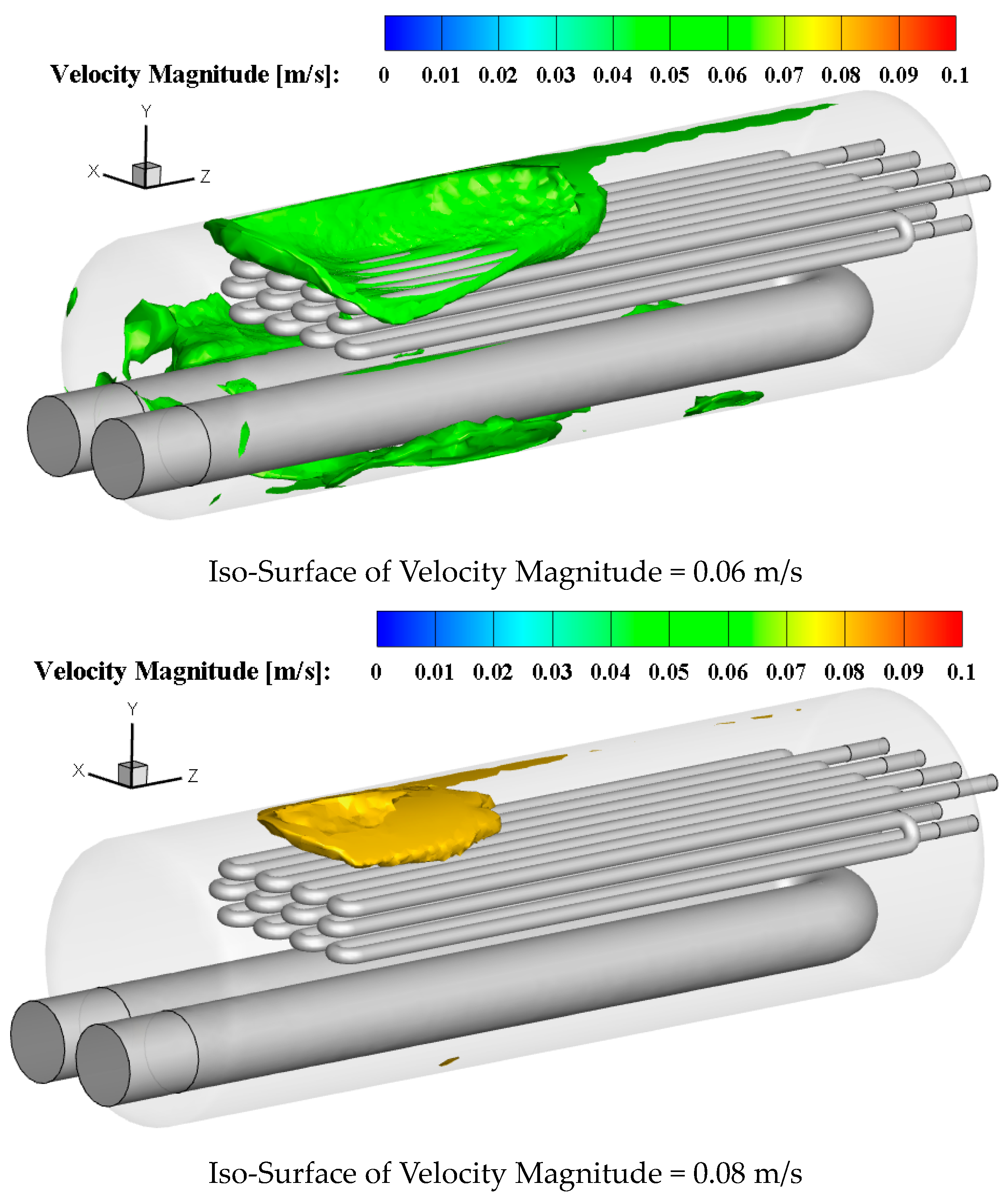
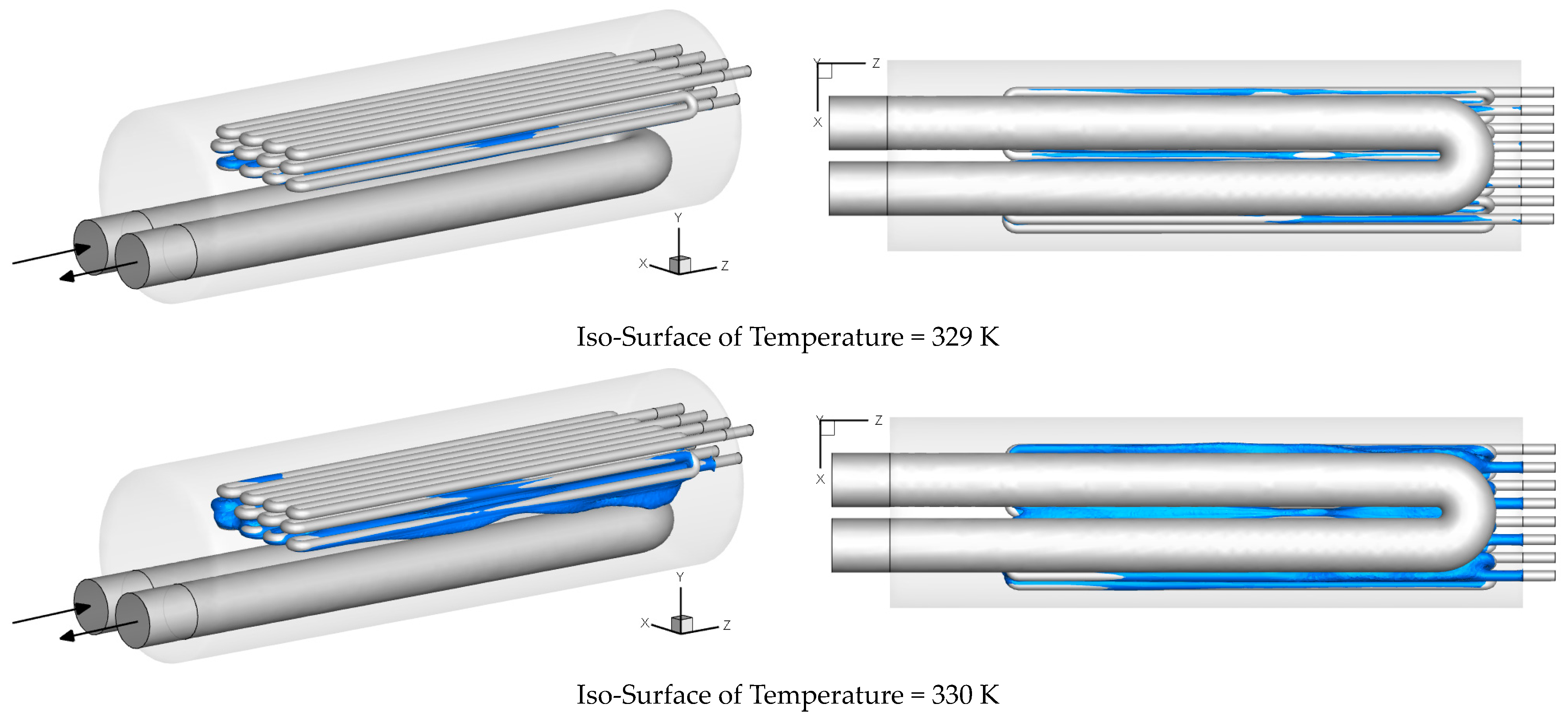
3.2. Investigating the Performance of the Gas Heater at 120,000 SCMH
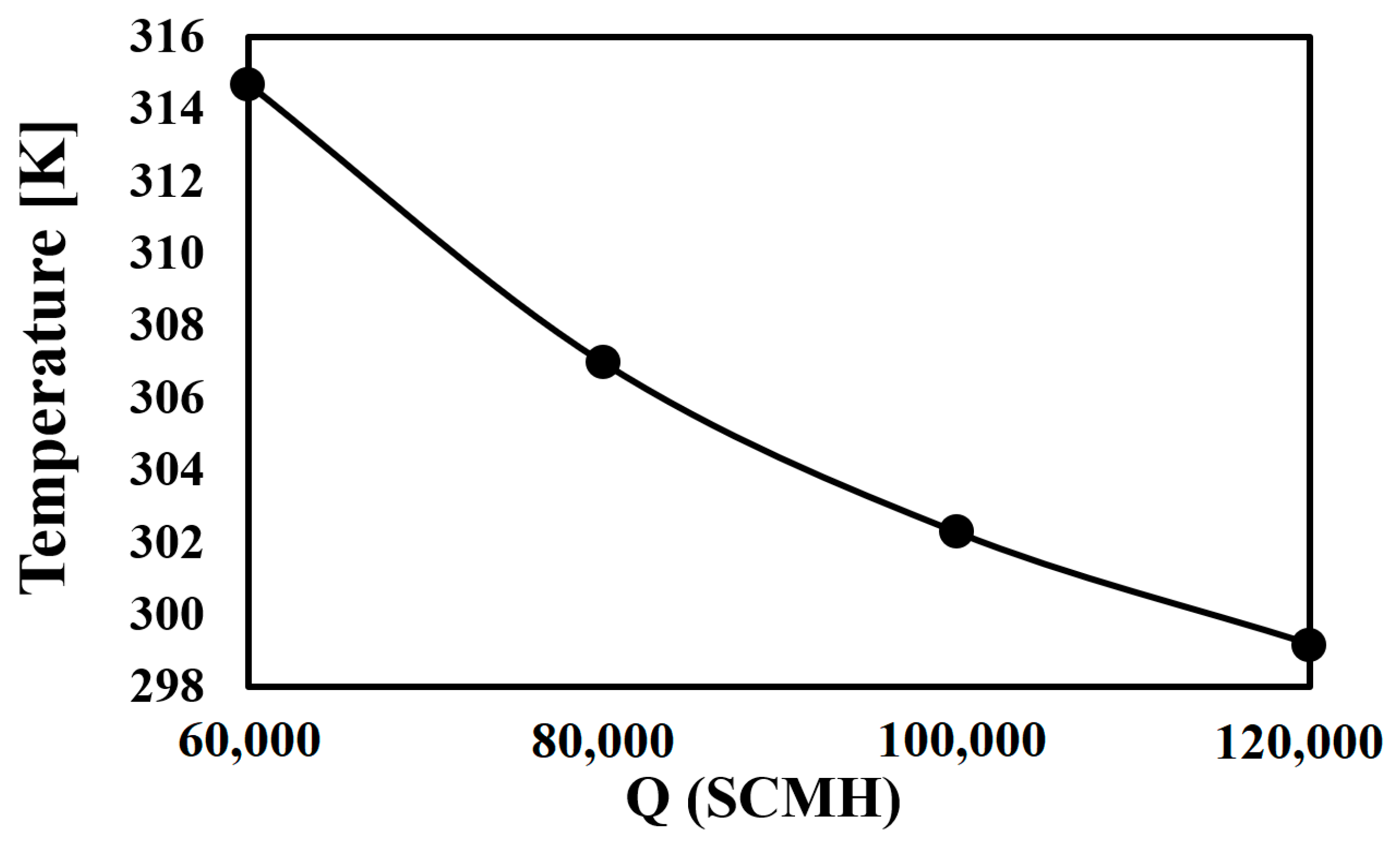
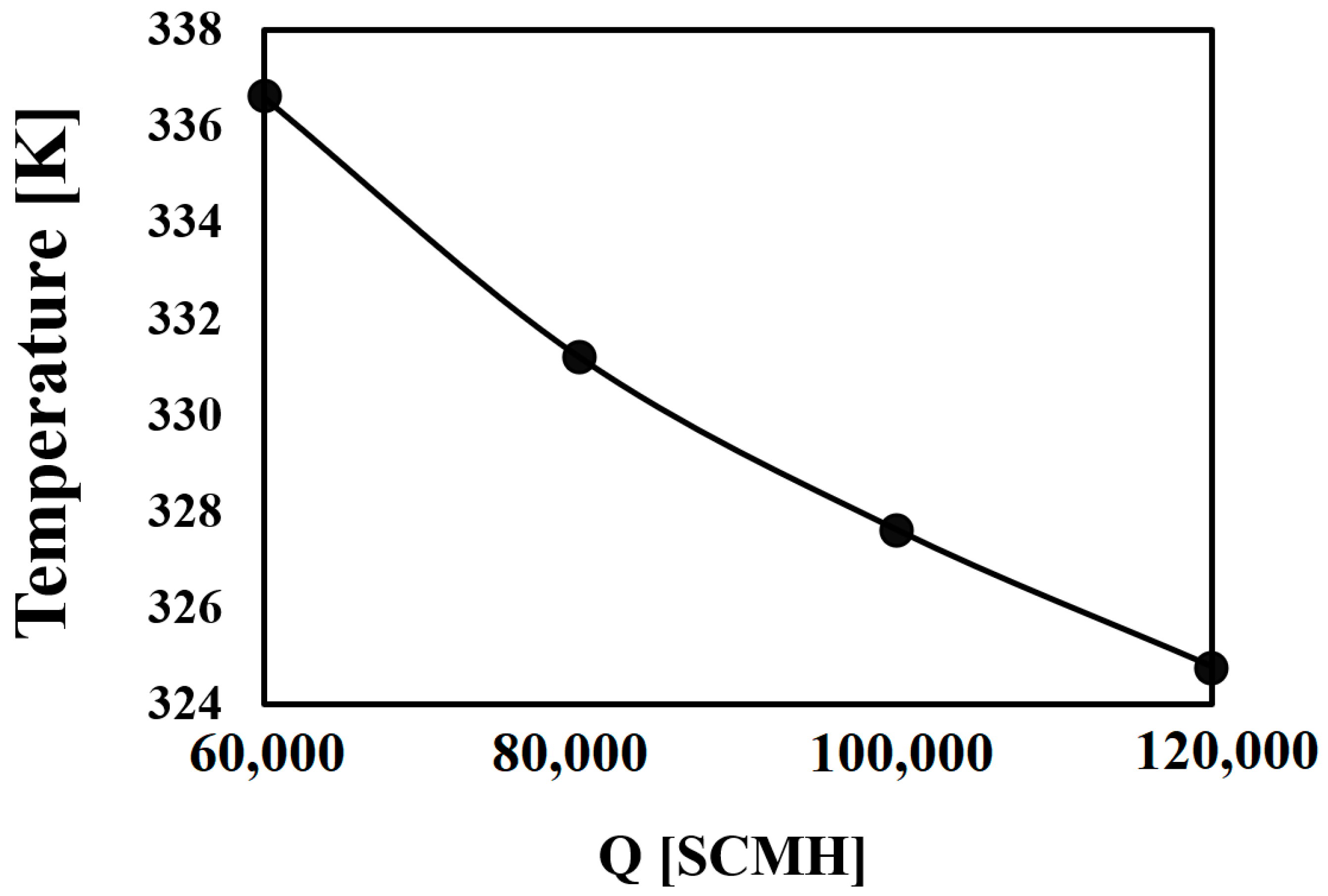
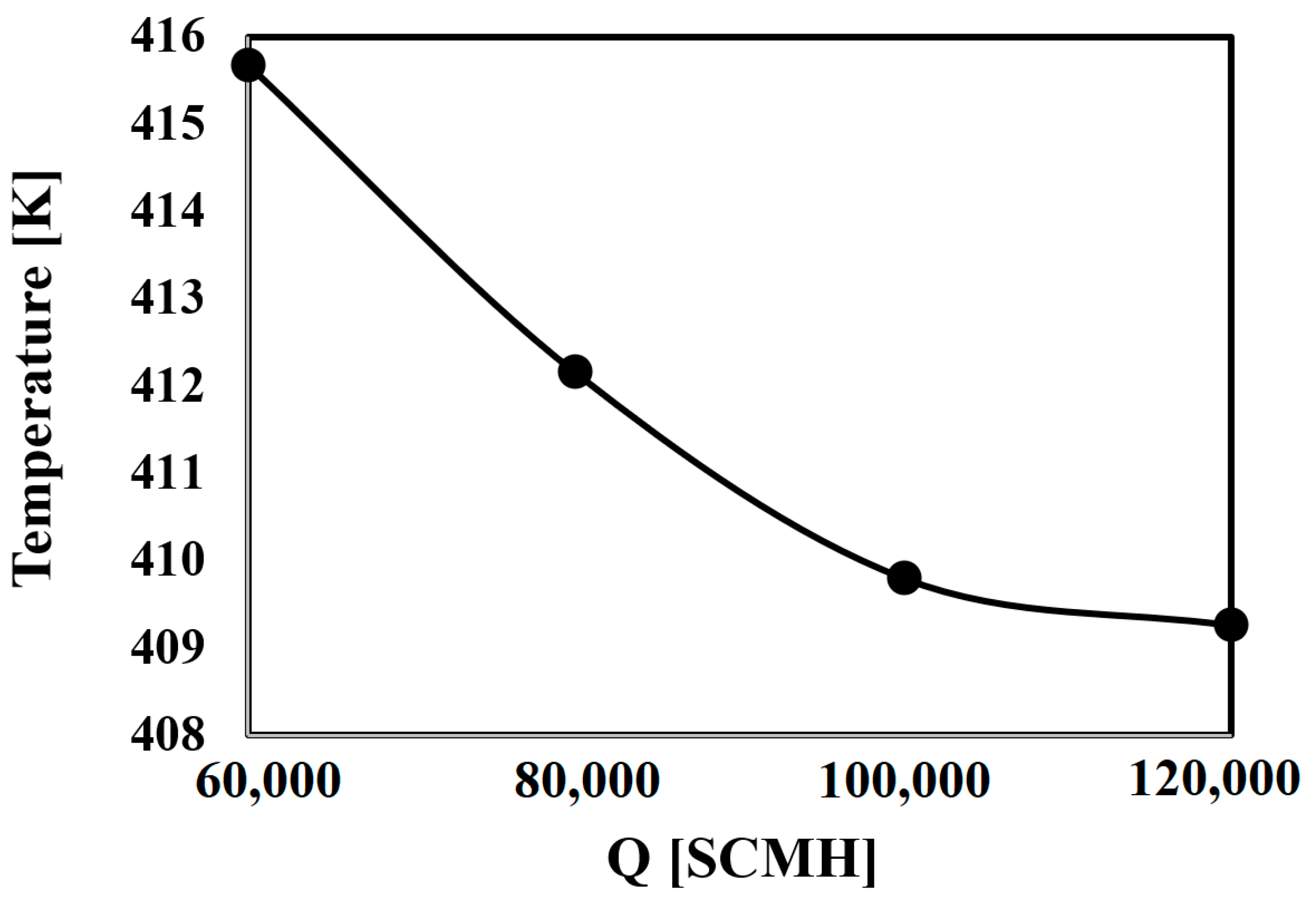
3.3. Investigating the Impact of Gas Mass Flow Rate
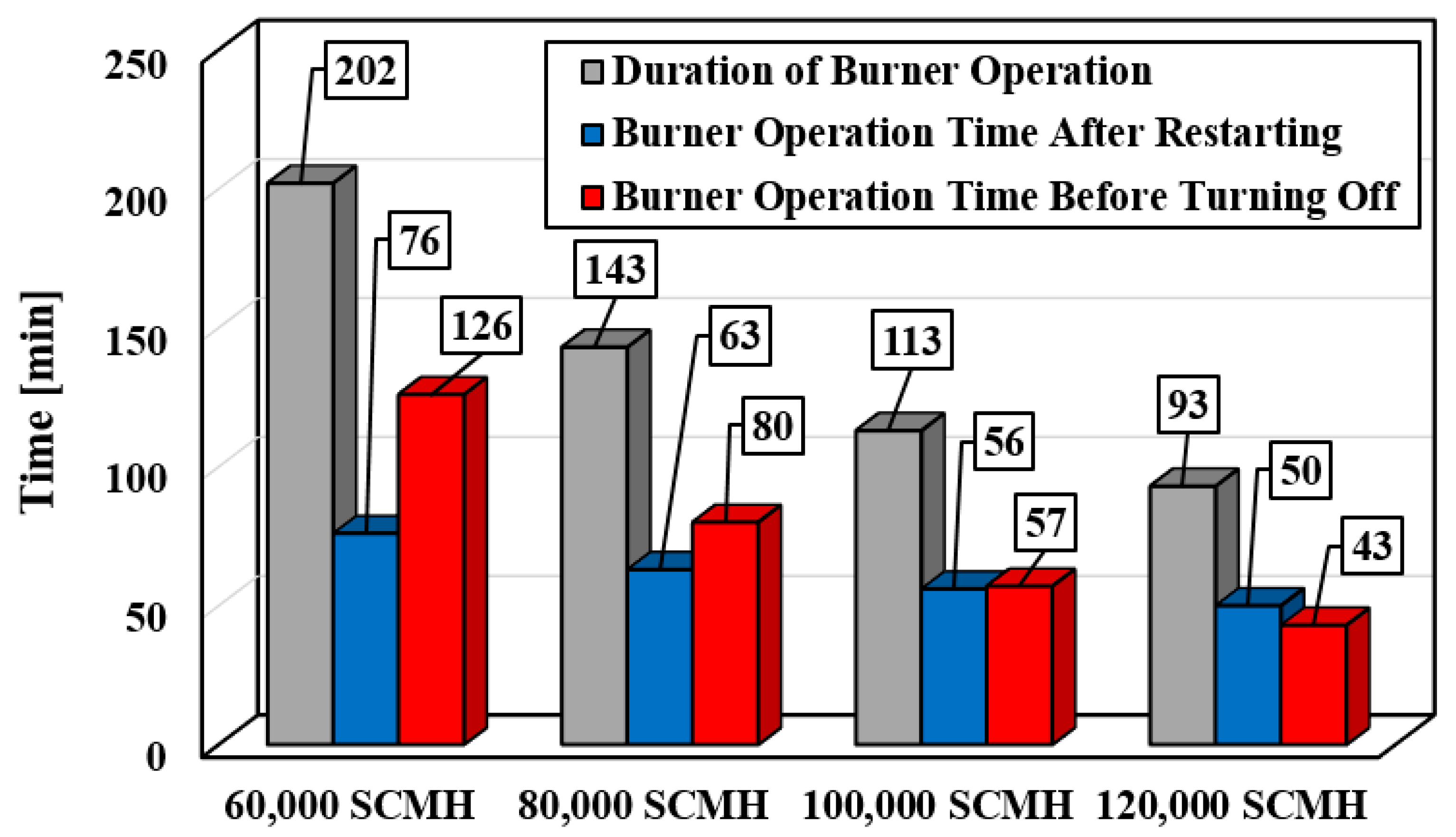
3.4. Investigating the Fuel Consumption Reduction Using the Considered Heater
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shokouhmand, H.; Rezaei Barmi, M.; Tavakoli, B. Gas Heater Availability Analysis and Consideration of Replacement Gas Heaters by Inline Heaters in the Pressure Reducing Stations of Natural Gas. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Seattle, DC, USA, 11–15 November 2007; Volume 43025, pp. 1231–1240. [Google Scholar]
- Hedman, B.A. Waste Energy Recovery Opportunities for Interstate Natural Gas Pipelines; Interstate Natural Gas Association of America: Washington, DC, USA, 2008. [Google Scholar]
- Farzaneh-Gord, M.; Arabkoohsar, A.; Rezaei, M.; Deymi-Dashtebayaz, M.; Rahbari, H.R. Feasibility of employing solar energy in natural gas pressure drop stations. J. Energy Inst. 2011, 84, 165–173. [Google Scholar] [CrossRef]
- Clay, A.; Tansley, G.D. Exploration of a simple, low cost, micro gas turbine recuperator solution for a domestic combined heat and power unit. Appl. Therm. Eng. 2011, 31, 2676–2684. [Google Scholar] [CrossRef] [Green Version]
- Howard, C.; Oosthuizen, P.; Peppley, B. An investigation of the performance of a hybrid turboexpander-fuel cell system for power recovery at natural gas pressure reduction stations. Appl. Therm. Eng. 2011, 31, 2165–2170. [Google Scholar] [CrossRef] [Green Version]
- Andrei, I.; Valentin, T.; Cristina, T.; Niculae, T. Recovery of wasted mechanical energy from the reduction of natural gas pressure. Procedia Eng. 2014, 69, 986–990. [Google Scholar] [CrossRef] [Green Version]
- Ashouri, E.; Veysi, F.; Shojaeizadeh, E.; Asadi, M. The minimum gas temperature at the inlet of regulators in natural gas pressure reduction stations (CGS) for energy saving in water bath heaters. J. Nat. Gas Sci. Eng. 2014, 21, 230–240. [Google Scholar] [CrossRef]
- Farzaneh-Gord, M.; Ghezelbash, R.; Arabkoohsar, A.; Pilevari, L.; Machado, L.; Koury, R.N.N. Employing geothermal heat exchanger in natural gas pressure drop station in order to decrease fuel consumption. Energy 2015, 83, 164–176. [Google Scholar] [CrossRef]
- Ghezelbash, R.; Farzaneh-Gord, M.; Sadi, M. Performance assessment of vortex tube and vertical ground heat exchanger in reducing fuel consumption of conventional pressure drop stations. Appl. Therm. Eng. 2016, 102, 213–226. [Google Scholar] [CrossRef]
- Salari, S.; Goudarzi, K. Heat transfer enhancement and fuel consumption reduction in heaters of CGS gas stations. Case Stud. Therm. Eng. 2017, 10, 641–649. [Google Scholar] [CrossRef]
- Olfati, M.; Bahiraei, M.; Heidari, S.; Veysi, F. A comprehensive analysis of energy and exergy characteristics for a natural gas city gate station considering seasonal variations. Energy 2018, 155, 721–733. [Google Scholar] [CrossRef]
- Naderi, M.; Ahmadi, G.; Zarringhalam, M.; Akbari, O.; Khalili, E. Application of water reheating system for waste heat recovery in NG pressure reduction stations, with experimental verification. Energy 2018, 162, 1183–1192. [Google Scholar] [CrossRef]
- Rahmatpour, A.; Shaibani, M.J. Techno-economic assessment of gas pressure-based electricity generation (A case study of Iran). Energy Sources Part A Recovery Util. Environ. Eff. 2018, 40, 2236–2247. [Google Scholar] [CrossRef]
- Khosravi, M.; Arabkoohsar, A.; Alsagri, A.S.; Sheikholeslami, M. Improving thermal performance of water bath heaters in natural gas pressure drop stations. Appl. Therm. Eng. 2019, 159, 113829. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Ghasemi, G.; Kowsary, F.; Roumi, S.; Jalilinasrabady, S. Modelling of heat supply for natural gas pressure reduction station using geothermal energy. Int. J. Sustain. Energy 2019, 38, 773–793. [Google Scholar] [CrossRef]
- Foo, K.; Liang, Y.Y.; Goh, P.S.; Fletcher, D.F. Computational fluid dynamics simulations of membrane gas separation: Overview, challenges and future perspectives. Chem. Eng. Res. Des. 2023, 191, 127–140. [Google Scholar] [CrossRef]
- Li, W.L.; Ouyang, Y.; Gao, X.Y.; Wang, C.Y.; Shao, L.; Xiang, Y. CFD analysis of gas–liquid flow characteristics in a microporous tube-in-tube microchannel reactor. Comput. Fluids 2018, 170, 13–23. [Google Scholar] [CrossRef]
- Siavash Amoli, B.; Mousavi Ajarostaghi, S.S.; Sedighi, K.; Aghajani Delavar, M. Evaporative pre-cooling of a condenser airflow: Investigation of nozzle cone angle, spray inclination angle and nozzle location. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 8040–8059. [Google Scholar] [CrossRef]
- Salhi, J.E.; Mousavi Ajarostaghi, S.S.; Zarrouk, T.; Saffari Pour, M.; Salhi, N.; Salhi, M. Turbulence and thermo-flow behavior of air in a rectangular channel with partially inclined baffles. Energy Sci. Eng. 2022, 10, 3540–3558. [Google Scholar] [CrossRef]
- Mohammadi, S.; Mousavi Ajarostaghi, S.S.; Pourfallah, M. The latent heat recovery from boiler exhaust flue gas using shell and corrugated tube heat exchanger: A numerical study. Heat Transfer 2020, 49, 3797–3815. [Google Scholar] [CrossRef]
- Nouri Kadijani, O.; Kazemi Moghadam, H.; Mousavi Ajarostaghi, S.S.; Asadi, A.; Saffari Pour, M. Hydrothermal performance of humid air flow in a rectangular solar air heater equipped with V-shaped ribs. Energy Sci. Eng. 2022, 10, 2276–2289. [Google Scholar] [CrossRef]
- Masoumpour-Samakoush, M.; Miansari, M.; Ajarostaghi, S.S.M.; Arıcı, M. Impact of innovative fin combination of triangular and rectangular fins on melting process of phase change material in a cavity. J. Energy Storage 2022, 45, 103545. [Google Scholar] [CrossRef]
- Pakzad, K.; Mousavi Ajarostaghi, S.S.; Sedighi, K. Numerical simulation of solidification process in an ice-on-coil ice storage system with serpentine tubes. SN Appl. Sci. 2019, 1, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Riahi, M.; Yazdirad, B.; Jadidi, M.; Berenjkar, F.; Khoshnevisan, S.; Jamali, M.; Safary, M. Optimization of combustion Efficiency in indirect water bath heaters of Ardabil city gate stations. In Proceedings of the Seventh Mediterranean Combustion Symposium (MCS-7), Cagliari, Italy, 11–15 September 2011; pp. 11–15. [Google Scholar]
- Naderi, M.; Zargar, G.; Khalili, E. A numerical study on using air cooler heat exchanger for low grade energy recovery from exhaust flue gas in natural gas pressure reduction stations. Iran. J. Oil Gas Sci. Technol. 2018, 7, 93–109. [Google Scholar]
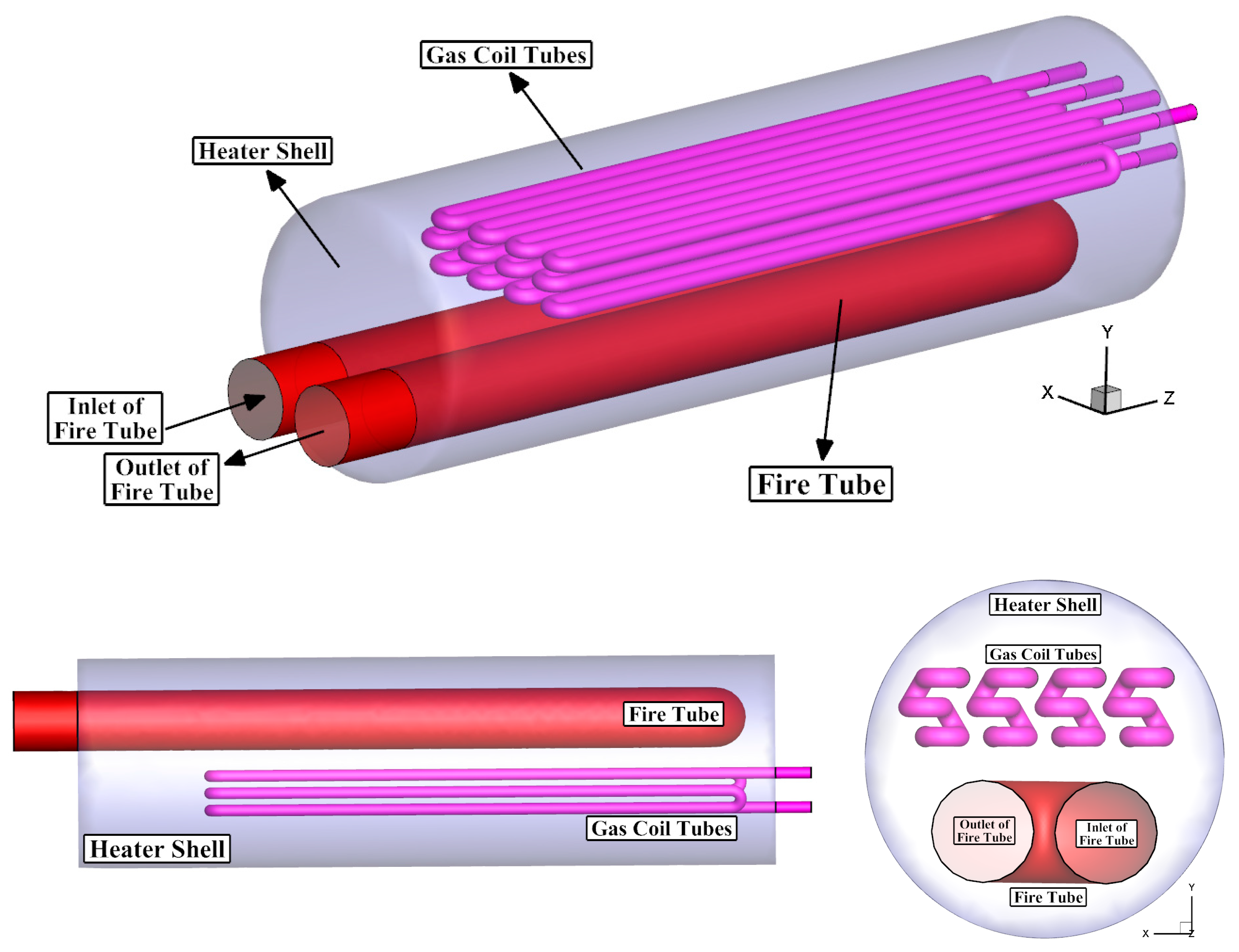
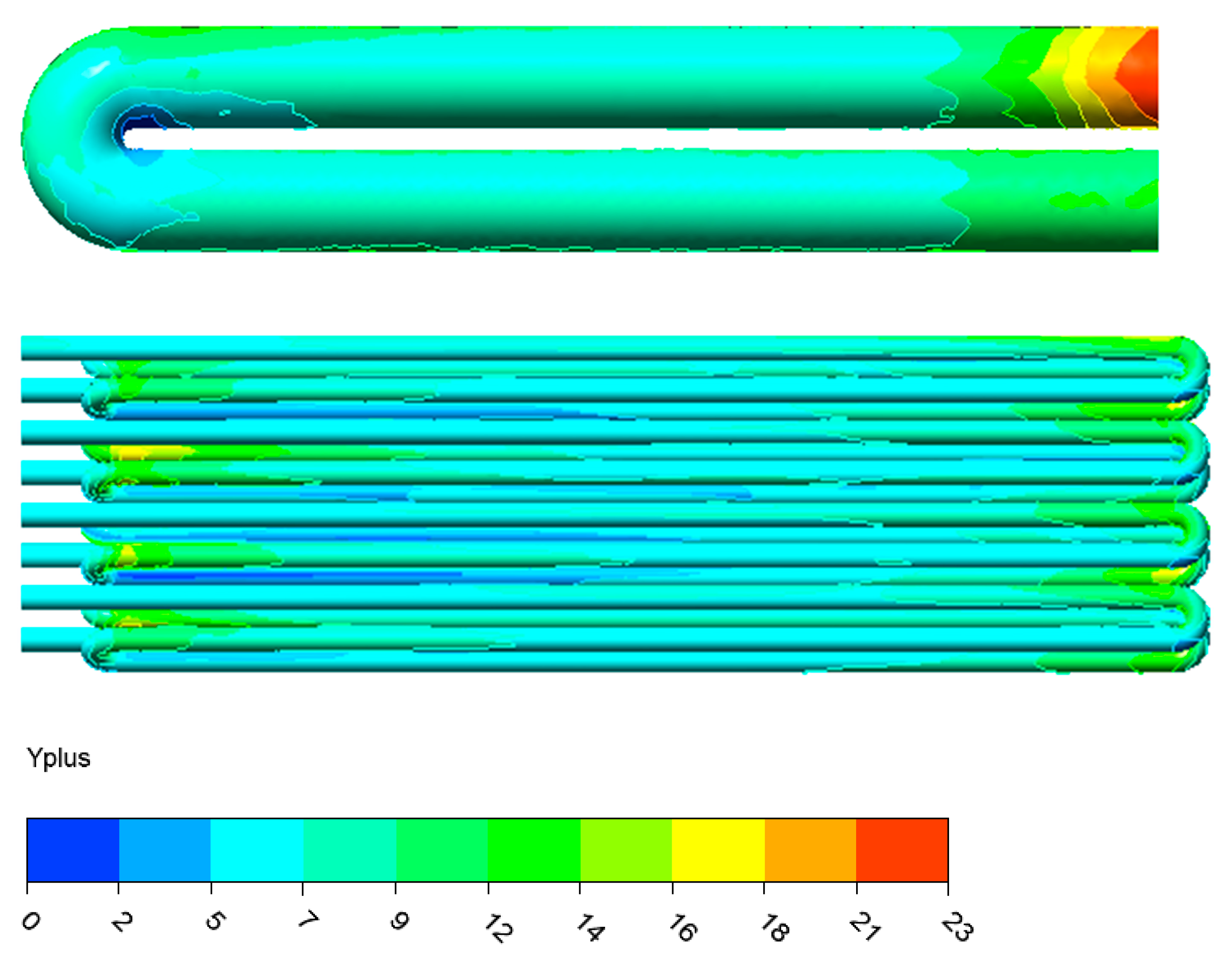

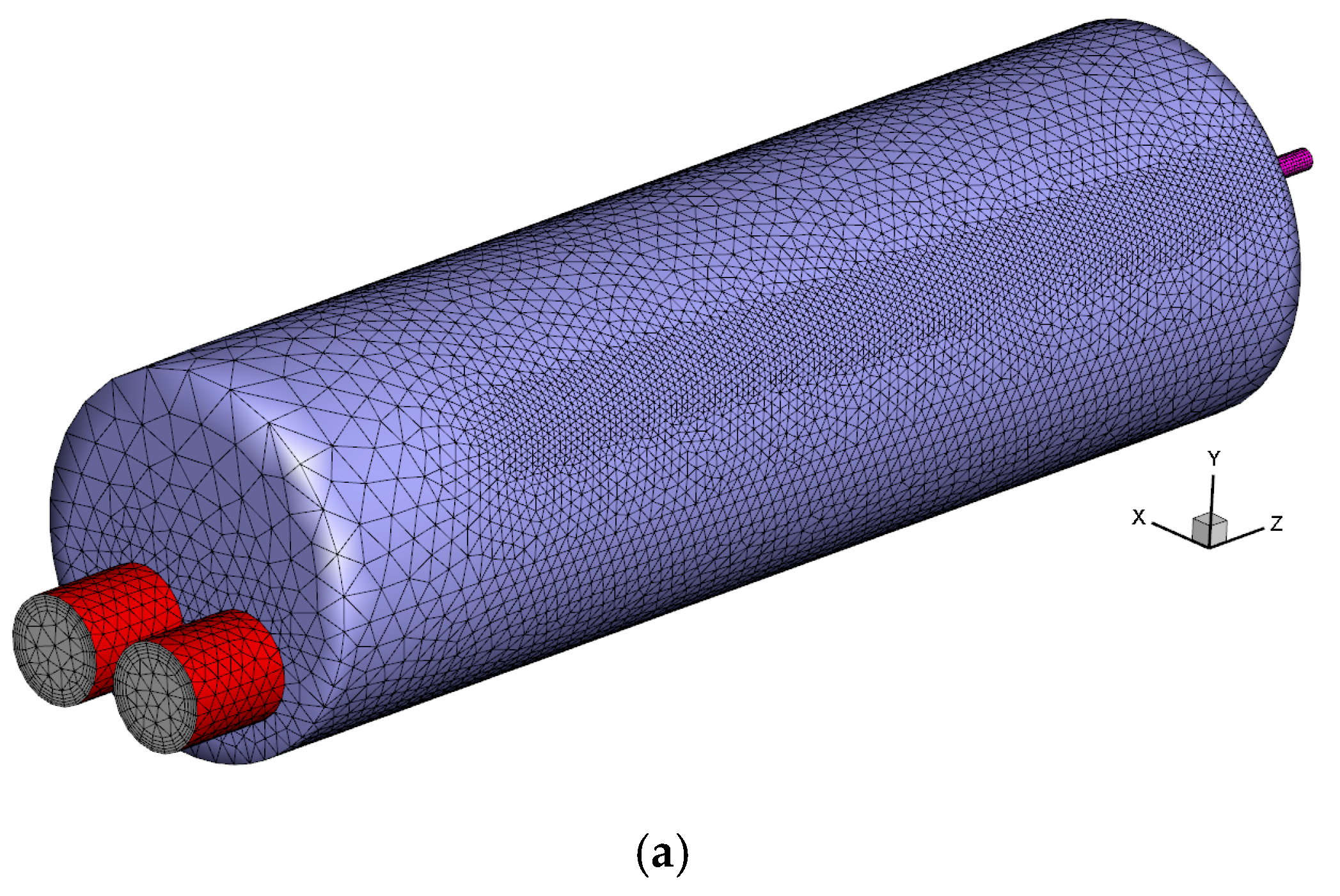
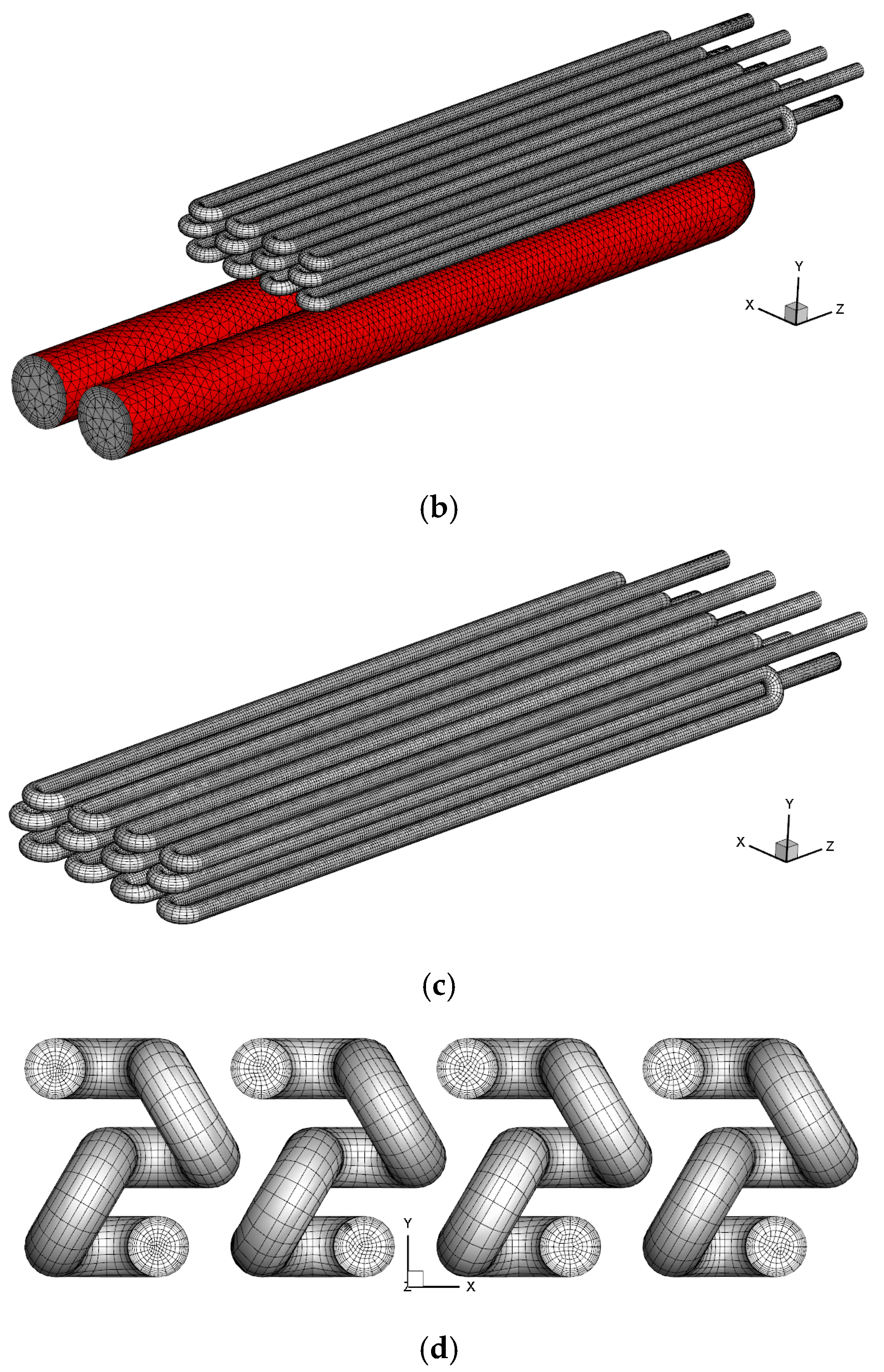






| Name | Chemical Formula | Volume Percentage | ||
|---|---|---|---|---|
| Gas Analysis | Lower Limit | Higher Limit | ||
| Methane | CH4 | 88.332 | 85 | 95 |
| Ethan | C2H6 | 4.672 | 2 | 9 |
| Propane | C3H8 | 4.137 | 0.5 | 3 |
| Isobutene | C4H10 | 0.484 | 0.2 | 0.3 |
| Normal Butane | C4H10 | 0.484 | 0.25 | 0.5 |
| Isopentane | C5H12 | 0.181 | 0.1 | 0.15 |
| Normal Pentane | C5H12 | 0.181 | 0.06 | 0.1 |
| Carbon Dioxide | CO2 | 0.694 | 0.1 | 0.4 |
| Nitrogen | N2 | 4.5 | 2 | 5.7 |
| Sulfide | H2S | 0.849 ppm | 1.25 | 6.25 |
| Heavy/compound | - | 0 | 0.02 | 0.2 |
| Property | Value | |
|---|---|---|
| Density (kg.m−3) | 34.76 | |
| Specific Heat Capacity (kJ/(kg.K)) | CP | 2.57 |
| Dynamic Viscosity (Pa.s) | μ | 11.96 × 10−6 |
| Static Viscosity (m2/s) | υ | 0.344 × 10−6 |
| Fuel Flow Rate (m3/hr) | Carbon Monoxide (ppm) | Carbon Dioxide (ppm) | Nitrogen Oxides (ppm) | Oxygen (%) | Stack Temperature at Input Gate (°C) | Ambient Temperature (°C) | Combustion Efficiency (%) |
|---|---|---|---|---|---|---|---|
| 102 | 81 | 4.14 | 22 | 13.69 | 274 | 8.4 | 73.35 |
| 111 | 284 | 5.63 | 25 | 11.60 | 314 | 9.7 | 76.55 |
| 180 | 202 | 7.92 | 39 | 7.20 | 412 | 9.7 | 76.54 |
| 186 | 301 | 8.14 | 37 | 6.64 | 407 | 9.7 | 77.33 |
| 192 | 159 | 7.52 | 33 | 7.73 | 427 | 9.5 | 74.56 |
| 204 | 111 | 8.41 | 42 | 6.16 | 437 | 1.1 | 76.31 |
| 228 | 44 | 8.36 | 47 | 6.25 | 455 | 0.8 | 75.11 |
| 252 | 32 | 8.89 | 57 | 5.31 | 488 | 9.8 | 74.61 |
| Number | Grid Cell | The Outlet Temperature of the Methane (K) | Error (%) |
|---|---|---|---|
| 1 | 3,708,213 | 313.2 | 0.45 |
| 2 | 4,777,825 | 314.68 | 0.022 |
| 3 | 6,210,401 | 314.61 | - |
| Number | Mass Flow Rate (SCMH (m3/s)) | Experimental Heater Outlet Temperature (°C) | Numerical Heater Outlet Temperature (°C) | Error (%) |
|---|---|---|---|---|
| 1 | 80,000 (22.22) | 34.5 | 33.85 | 1.88 |
| 2 | 100,000 (27.78) | 30.1 | 29.15 | 3.15 |
| 3 | 120,000 (33.33) | 27 | 26.05 | 3.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemi Moghadam, H.; Mousavi Ajarostaghi, S.S.; Saffari Pour, M.; Akbary, M. Numerical Evaluation of the Hydrothermal Process in a Water-Surrounded Heater of Natural Gas Pressure Reduction Plants. Water 2023, 15, 1469. https://doi.org/10.3390/w15081469
Kazemi Moghadam H, Mousavi Ajarostaghi SS, Saffari Pour M, Akbary M. Numerical Evaluation of the Hydrothermal Process in a Water-Surrounded Heater of Natural Gas Pressure Reduction Plants. Water. 2023; 15(8):1469. https://doi.org/10.3390/w15081469
Chicago/Turabian StyleKazemi Moghadam, Hamid, Seyed Soheil Mousavi Ajarostaghi, Mohsen Saffari Pour, and Mohsen Akbary. 2023. "Numerical Evaluation of the Hydrothermal Process in a Water-Surrounded Heater of Natural Gas Pressure Reduction Plants" Water 15, no. 8: 1469. https://doi.org/10.3390/w15081469
APA StyleKazemi Moghadam, H., Mousavi Ajarostaghi, S. S., Saffari Pour, M., & Akbary, M. (2023). Numerical Evaluation of the Hydrothermal Process in a Water-Surrounded Heater of Natural Gas Pressure Reduction Plants. Water, 15(8), 1469. https://doi.org/10.3390/w15081469









