Research on the Application of CEEMD-LSTM-LSSVM Coupled Model in Regional Precipitation Prediction
Abstract
:1. Introduction
2. Research Methodology
2.1. Complementary Ensemble Empirical Modal Decomposition (CEEMD)
- A pair of white noises with opposite signs and zero mean is randomly added to the original time series Xt to obtain two new series M1 and M2, one of which is denoted by ωt.
- 2.
- The EMD algorithm is used to decompose M1 and M2 to obtain two sets of IMF components and residual terms.
- 3.
- Repeat the above steps N times, N = 0, 1, 2,…, and the eigenmodal components of the CEEMD decomposition can be obtained by taking the mean value of the overall 2N modal components generated.
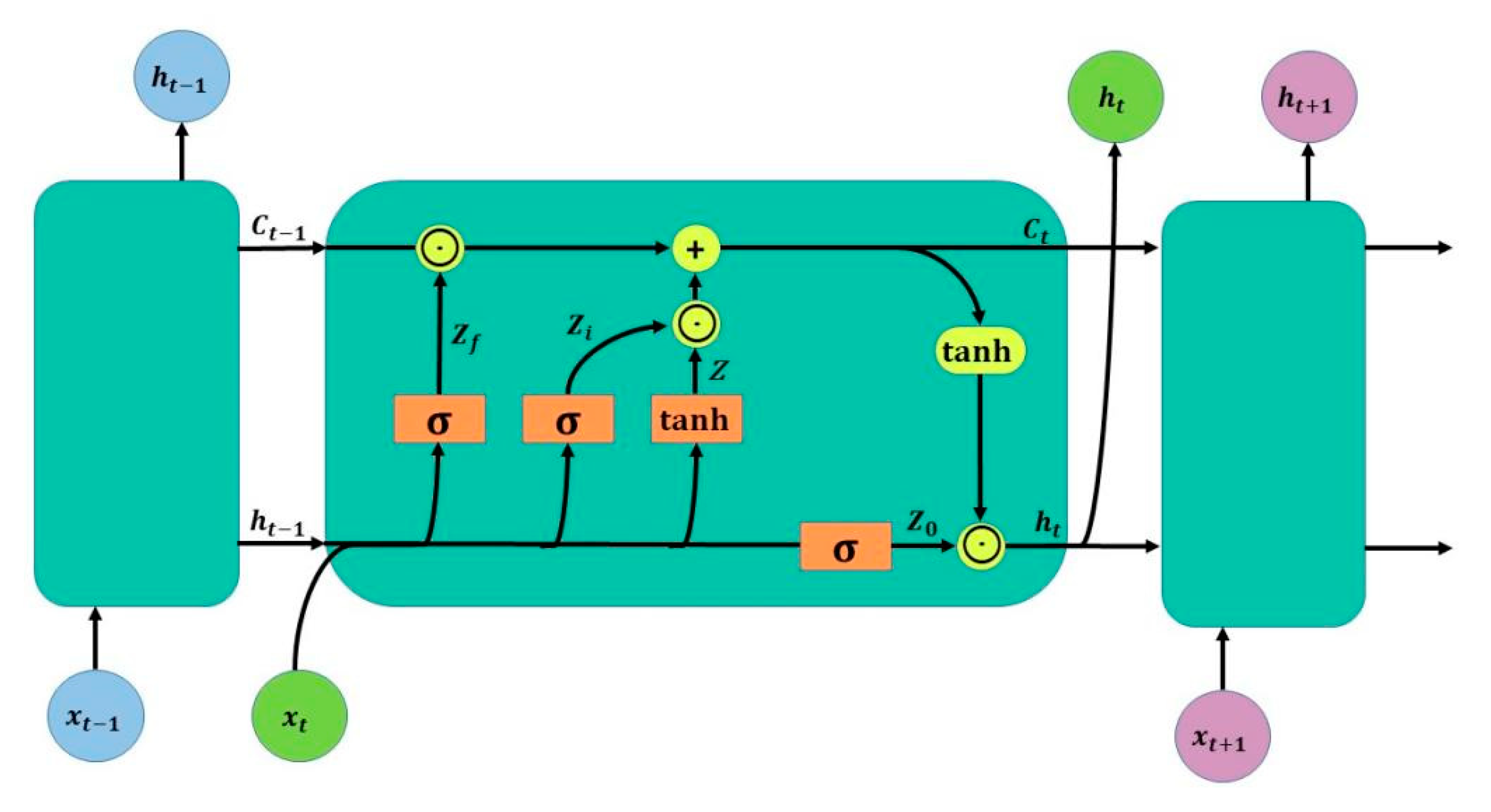
2.2. Long Short-Term Memory Neural Network (LSTM)
2.3. Least Squares Support Vector Machine (LSSVM)
2.4. Mann–Kendall Test
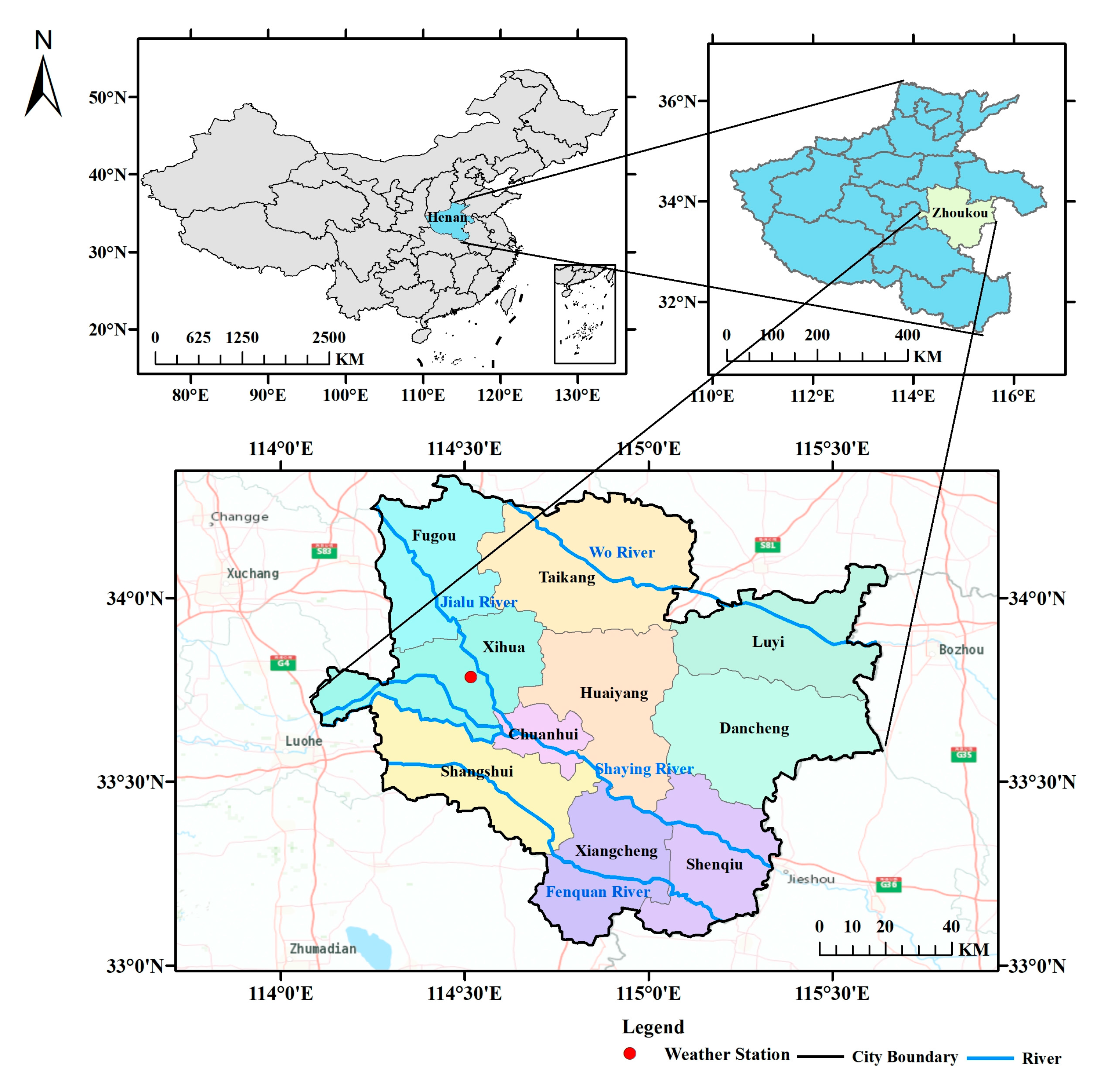
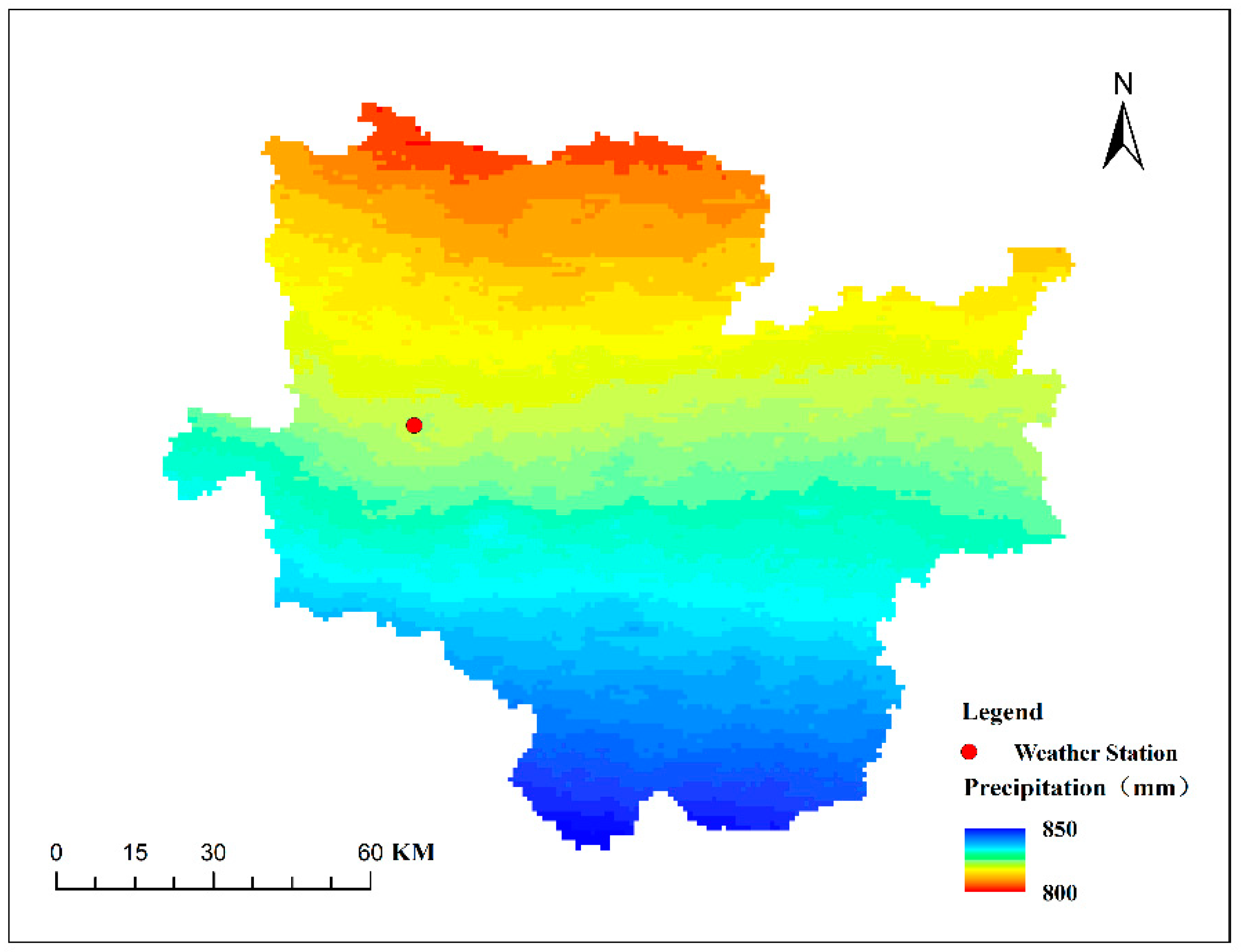
3. Overview of the Study Area
4. Model Building
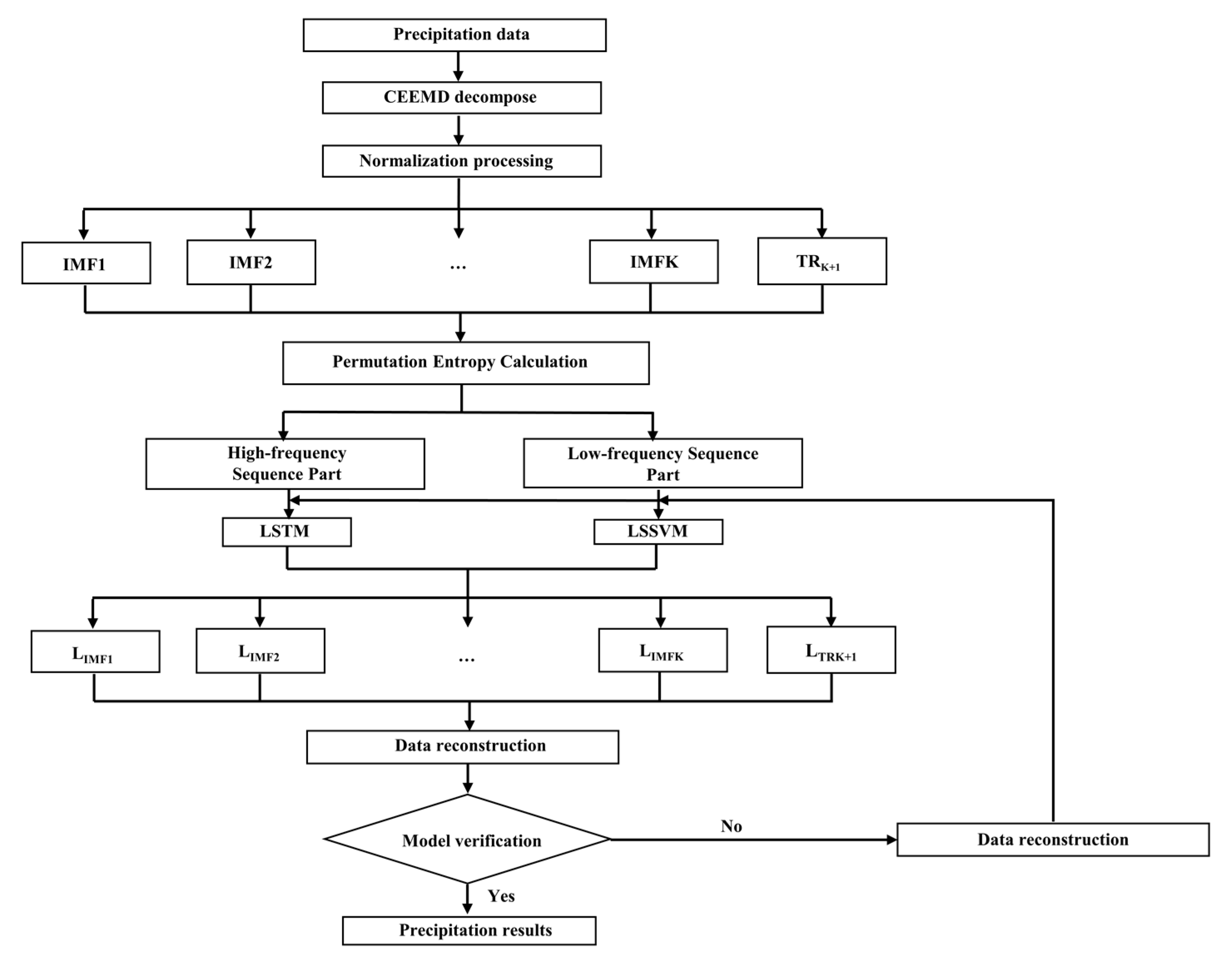
4.1. Modeling Process
- CEEMD decomposition: The rainfall time series are decomposed by CEEMD to obtain K eigenmodal components and one residual term (trend term).
- Data pre-processing: If the decomposed data are used directly as the input term of the prediction, it will generate large errors, so the entire sample data needs to be normalized.
- To determine the training and prediction sets, the monthly precipitation data of Zhoukou City from 1978–2017 are used as the training data set of the prediction model after decomposition by the CEEMD method; similarly, the monthly precipitation data from 2017–2022 are used as the prediction data set of the forecast after decomposition by CEEMD. Then the Permutation Entropy of the IMF component is calculated, dividing the high and low frequencies.
- Model training: Each set of training input data and prediction data is put into the model for training, and the model input parameters are continuously adjusted so that the model is fully trained on the training data set to ensure that the error is at a low level and to improve the prediction accuracy.
- Model prediction: The prediction is performed using the coupled model, and then the results are inverse normalized and reconstructed, and the final prediction is obtained by superimposing the data according to the principle of superimposing the data at the same moment.
- Accuracy evaluation: The evaluation indicators of the model are calculated and compared with other selected models.
4.2. Model Evaluation Indicators
4.3. Model Input
4.4. Model Training
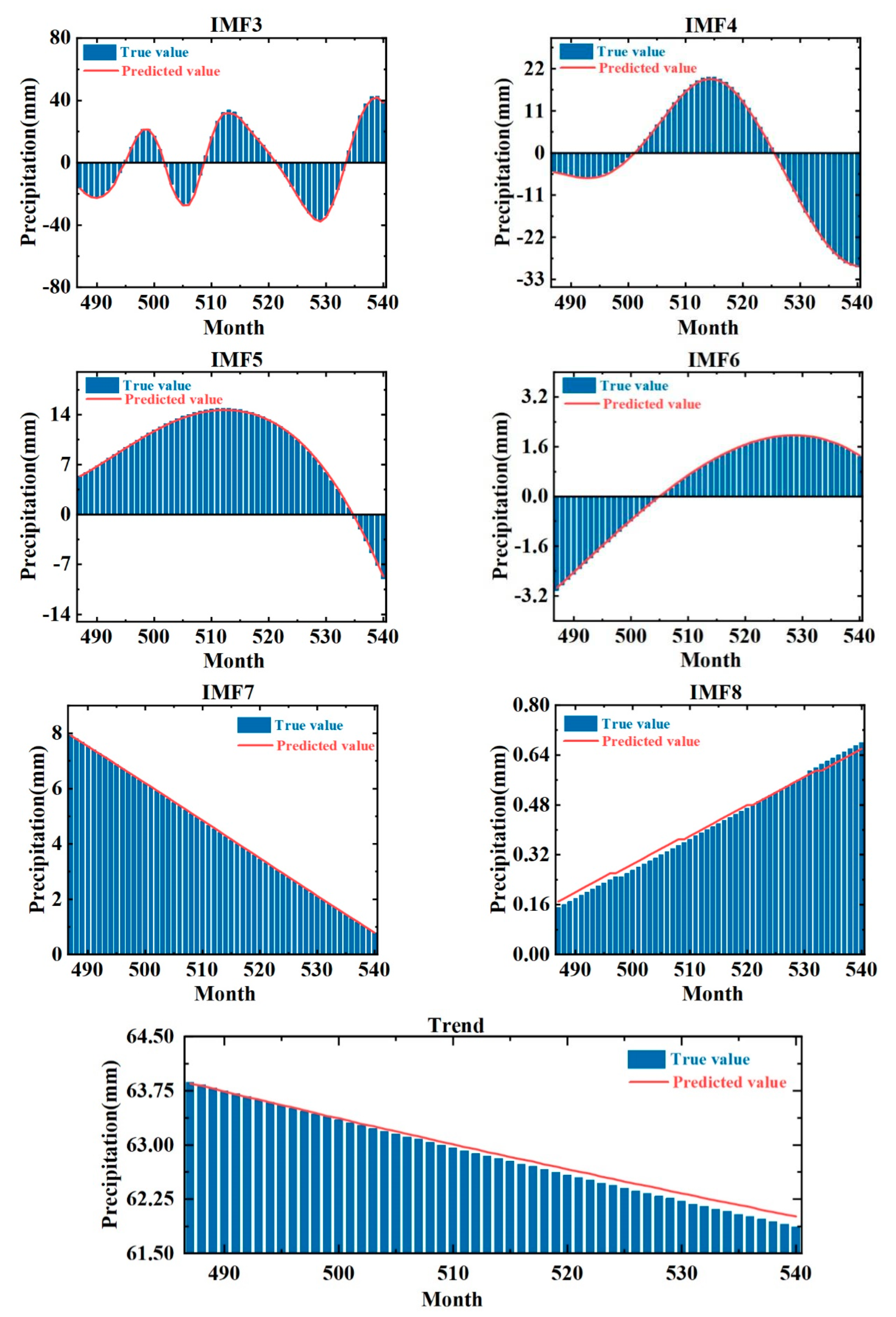
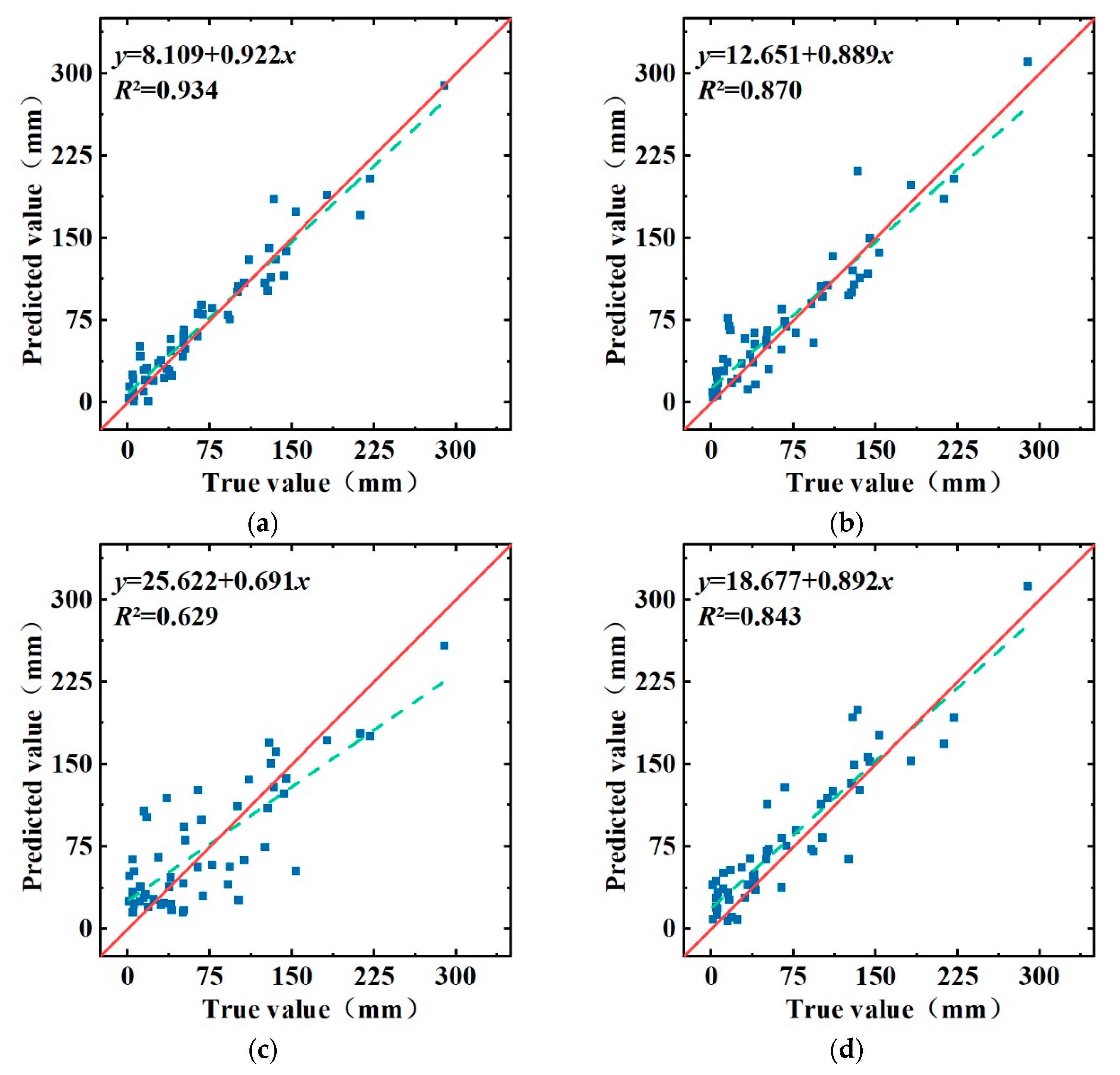
5. Analysis and Discussion
6. Monthly Precipitation Forecasts
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IPCC. Impacts of 1.5 °C of Global Warming on Natural and Human Systems; IPCC: Geneva, Switzerland, 2018; Volume 187. [Google Scholar]
- Chen, J.L.; Huang, R.H. Interannual interdecadal variability of water vapor transport in Asian summer winds in relation to droughts and floods in China. J. Geophys. 2008, 2, 352–359. [Google Scholar]
- Zhou, T.J.; Yu, R.C. Atmospheric water vapor transport associated with typical anomalous summer rainfall patterns in China. J. Geophys. Res. 2005, 110, D08104. [Google Scholar] [CrossRef] [Green Version]
- Hossain, I.; Rasel, H.M.; Imteaz, M.A.; Mekanik, F. Long-term seasonal rainfall forecasting: Efficiency of linear modelling technique. Environ. Earth Sci. 2018, 77, 280. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, R.Y.; Chen, P.; Zhang, Z.W. Objective prediction method of summer precipitation in Jiangsu using deep neural network and precursor signal. J. Meteorol. 2021, 79, 1035–1048. [Google Scholar]
- Han, Y.; Guan, J.; Cao, Y.C.; Luo, J. Application of LSTM-WBLS model in daily precipitation prediction. J. Nanjing Univ. Inf. Eng. 2023, 1–10. Available online: https://kns.cnki.net/kcms/detail/32.1801.N.20221111.1728.004.html (accessed on 20 November 2022).
- Narayanan, P.; Basistha, A.; Sarkar, S.; Sachdeva, K. Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India. Comptes Rendus-Géoscience 2013, 345, 22–27. [Google Scholar] [CrossRef]
- Zhao, Y. Application analysis of gray prediction model for rainfall in Shenwo Reservoir. China Water Energy Electrif. 2016, 12, 68–70. [Google Scholar]
- Gou, Z.J.; Ren, J.L.; Xu, M.; Wang, M. Application of Hadoop-based GA-BP algorithm in precipitation prediction. Comput. Syst. Appl. 2019, 28, 140–146. [Google Scholar]
- Shen, H.J.; Luo, Y.; Zhao, Z.C.; Wang, H.J. Research on summer precipitation prediction in China based on LSTM network. Adv. Clim. Chang. Res. 2020, 16, 263–275. [Google Scholar]
- Wang, R. Research on spatial distribution of rainfall in Handan City based on GIS and support vector machine model. Water Sci. Eng. Technol. 2020, 2, 1–4. [Google Scholar]
- Sha, S.K. Precipitation prediction model based on random forest algorithm in Chengaai irrigation area. Water Resour. Technol. Superv. 2020, 5, 134–137. [Google Scholar]
- Du, K.J. Improved Recurrent Neural Network Method and Its Application Research. Master’s Thesis, Northeastern Electric Power University, Jilin, China, 2021. [Google Scholar]
- Xu, N.N. Research on LSTM-Based ERA5 Day-Scale Precipitation Prediction Method for Mainland China. Master’s Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2021. [Google Scholar]
- Wang, W.C.; Yang, J.X.; Zang, H.F. Monthly precipitation prediction based on WD-COA-LSTM model. J. Water Resour. Water Eng. 2022, 33, 8–13+23. [Google Scholar]
- Yu, Y.H.; Zhang, H.B.; Singh, V.P. Forward Prediction of Runoff Data in Data-Scarce Basins with an Improved Ensemble Empirical Mode Decomposition (EEMD) Model. Water 2018, 10, 388. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Li, D.; Xue, H.F.; Zhang, Y. A combined precipitation prediction model based on empirical modal decomposition. Comput. Simul. 2019, 36, 458–463. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Roushangar, K.; Alizadeh, F. Scenario-based prediction of short-term river stage–discharge process using wavelet-EEMD-based relevance vector machine. J. Hydroinformatics 2019, 21, 56–76. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; John Wiley, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Huang, H.Y.; Li, E.J.; An, J.; Huang, G.; Bai, Z.N.; Li, D.W. Comparative analysis of precipitation mutation test by Kramer method and Mann-Kendall method. Mod. Agric. Sci. Technol. 2018, 8, 2. [Google Scholar]
- He, H.Y.; Guo, Z.H.; Xiao, W.F. Estimation of monthly precipitation on the Tibetan Plateau using GIS and multivariate analysis. J. Ecol. 2005, 11, 141–146. [Google Scholar]
- Graves, A. Supervised sequence labelling with recurrent neural networks. Stud. Comput. Intell. 2012, 2, 42–45. [Google Scholar]
- Luo, S.X.; Zhang, M.L.; Nie, Y.M.; Jia, X.N.; Cao, R.H.; Zhu, M.T.; Li, X.J. Monthly precipitation prediction in Zhengzhou City based on CEEMDAN-LSTM model. Water Resour. Plan. Des. 2022, 2, 45–50. [Google Scholar]

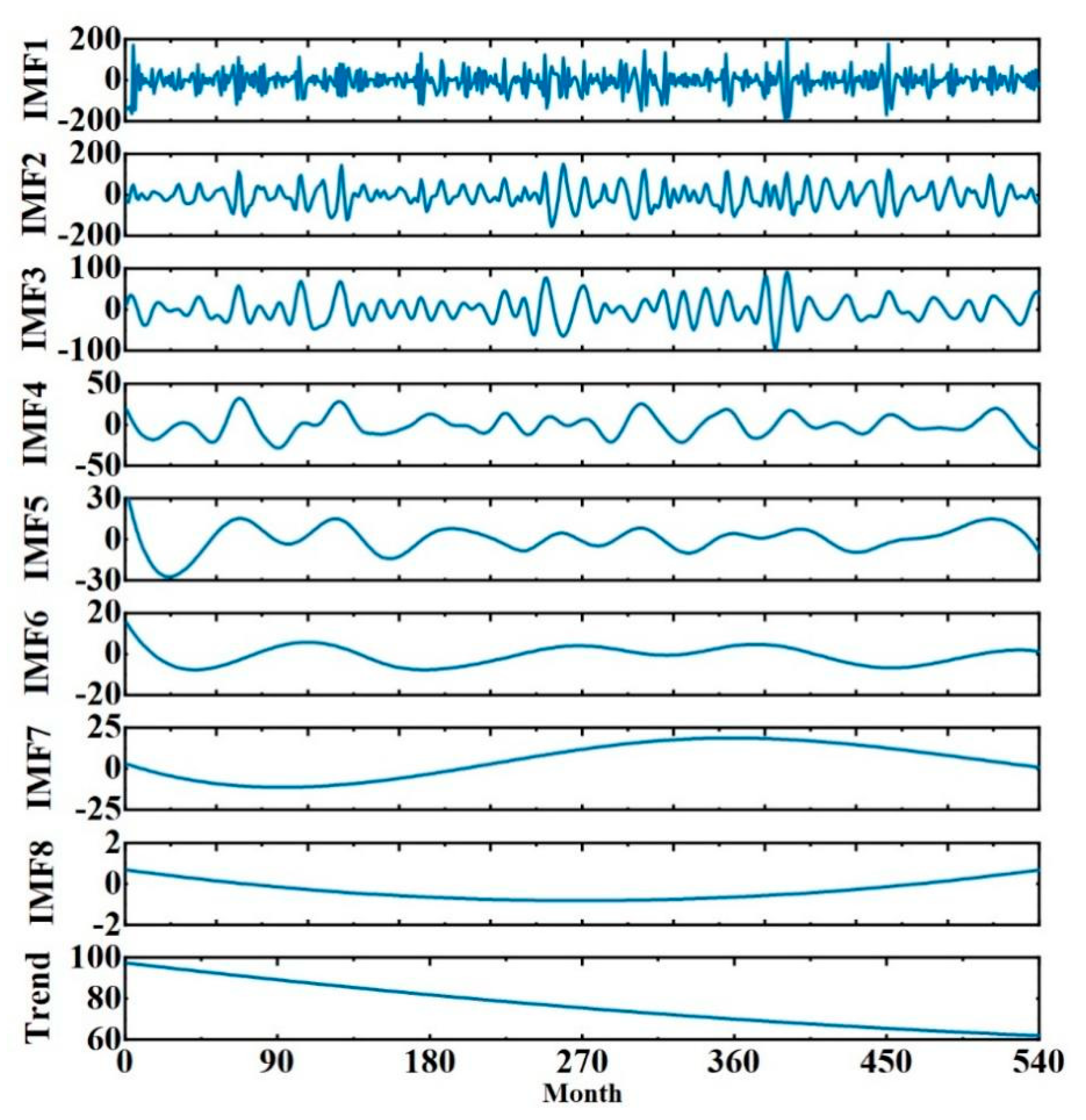
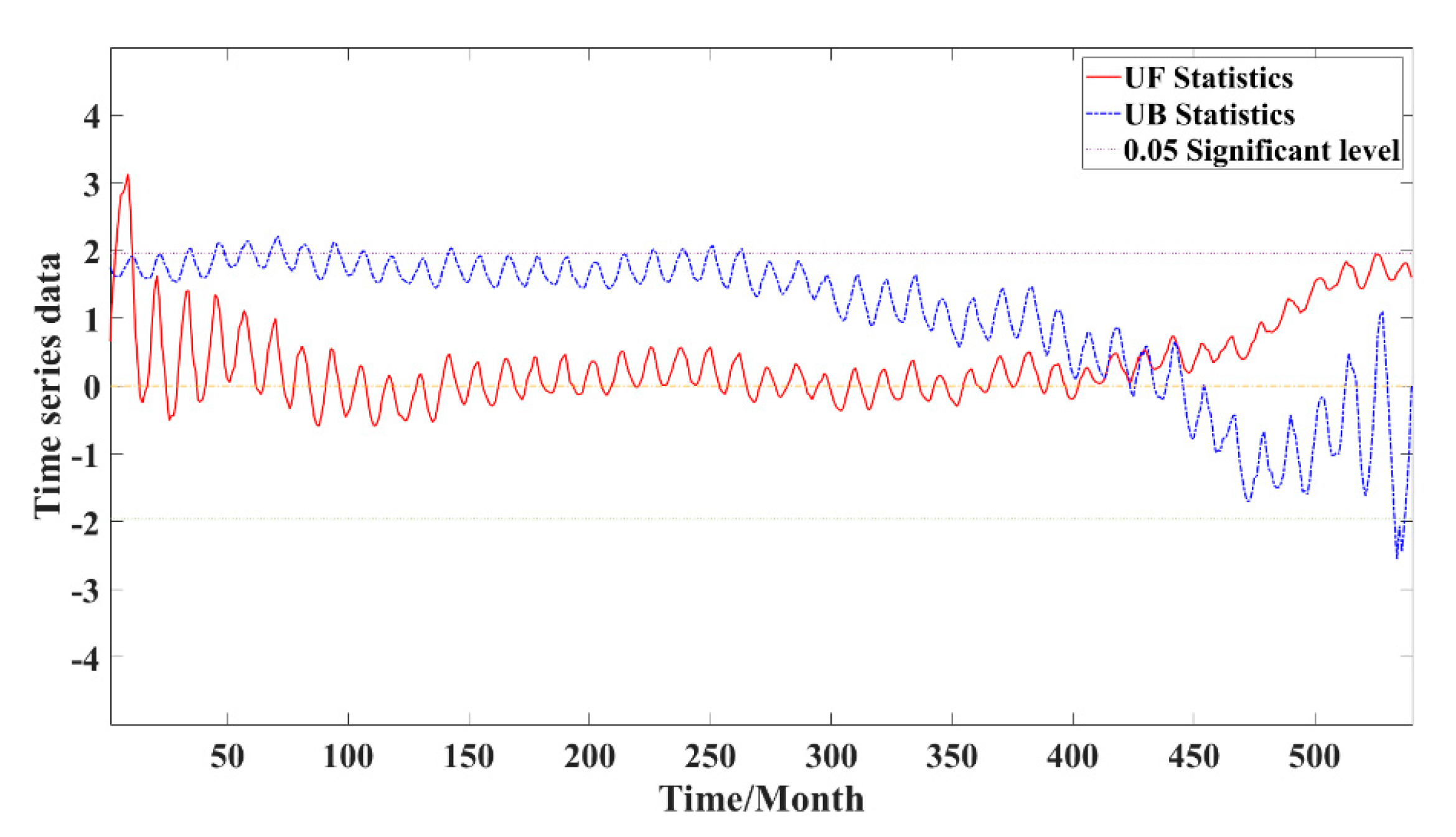
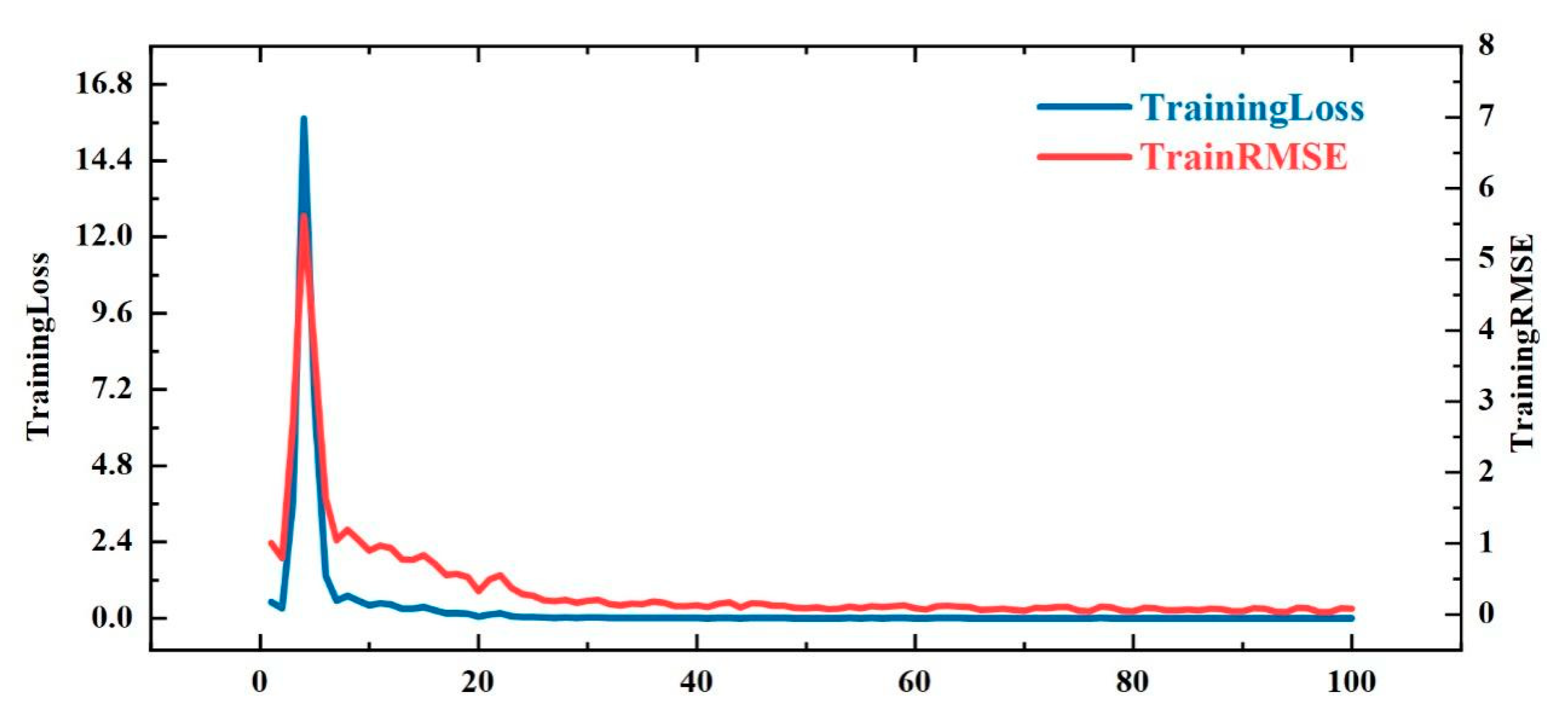
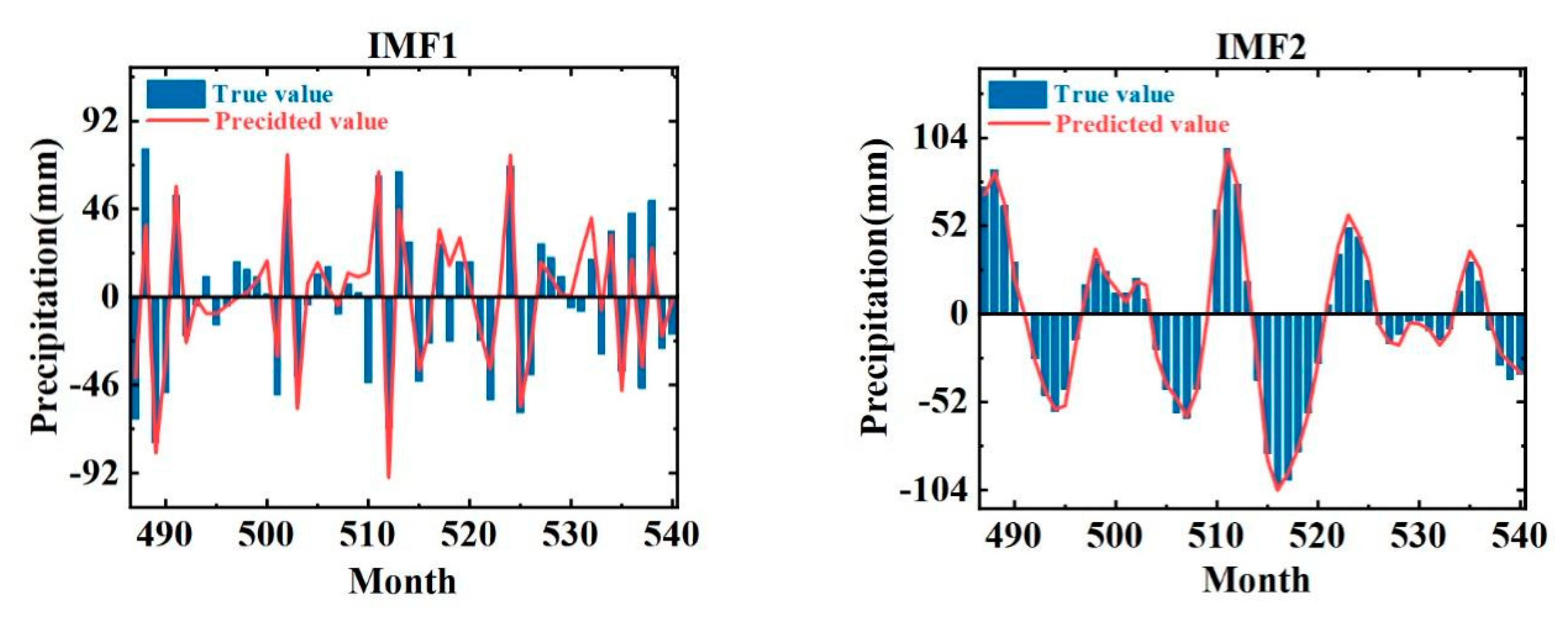

| Rainfall Sequence | Min Value (mm) | Max Value (mm) | Average Value (mm) | Standard Deviation (mm) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Original sequence | 0.00 | 512.06 | 69.46 | 79.13 | 5.66 | 2.16 |
| IMF1 | −194.27 | 201.66 | −5.62 | 52.25 | 1.51 | −0.12 |
| IMF2 | −154.73 | 150.99 | −5.62 | 50.29 | 0.04 | 0.14 |
| IMF3 | −96.53 | 92.15 | 0.21 | 28.46 | 0.36 | 0.25 |
| IMF4 | −29.78 | 32.25 | −0.61 | 12.43 | −0.23 | 0.16 |
| IMF5 | −27.40 | 35.63 | 0.47 | 9.21 | 1.10 | −0.51 |
| IMF6 | −7.70 | 15.21 | −0.71 | 4.34 | −0.56 | 0.07 |
| IMF7 | −11.31 | 18.74 | 4.85 | 10.38 | −1.41 | −0.18 |
| IMF8 | −0.82 | 0.68 | −0.32 | 0.45 | −0.85 | 0.64 |
| Trend | 61.87 | 97.31 | 76.81 | 10.33 | −1.11 | 0.32 |
| Rainfall Sequence | Displacement Entropy | Rainfall Sequence | Displacement Entropy | Displacement Entropy | Displacement Entropy |
|---|---|---|---|---|---|
| IMF1 | 1.8 | IMF4 | 0.85 | IMF7 | 0.68 |
| IMF2 | 1.35 | IMF5 | 0.78 | IMF8 | 0.62 |
| IMF3 | 1.08 | IMF6 | 0.72 | Trend | 0 |
| Rainfall Sequence | Number of Nodes in the Hidden Layer | Number of Training Sessions | Learning Rate |
|---|---|---|---|
| IMF1 | 200 | 230 | 0.01 |
| IMF2 | 200 | 200 | 0.01 |
| IMF3 | 150 | 150 | 0.01 |
| IMF4 | 150 | 110 | 0.008 |
| IMF5 | 130 | 100 | 0.008 |
| IMF6 | 130 | 60 | 0.006 |
| IMF7 | 100 | 50 | 0.005 |
| IMF8 | 100 | 35 | 0.005 |
| Trend | 60 | 25 | 0.005 |
| Portion Size | Average Relative Error (%) | Portion Size | Average Relative Error (%) | Portion Size | Average Relative Error (%) |
|---|---|---|---|---|---|
| IMF1 | 94.59 | IMF4 | 5.4 | IMF7 | 2.85 |
| IMF2 | 25.95 | IMF5 | 5.52 | IMF8 | 0.49 |
| IMF3 | 6.74 | IMF6 | 4.27 | Trend | 0.1 |
| Models | RSME (mm) | MAE (mm) | R2 |
|---|---|---|---|
| CEEMD-LSTM-LSSVM | 16.77 | 13.07 | 0.932 |
| CEEMD-LSTM | 23.66 | 17.86 | 0.864 |
| LSTM | 27.77 | 22.46 | 0.813 |
| LSSVM | 38.92 | 31.06 | 0.633 |
| Year | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2023 | 16.26 | 29.38 | 43.30 | 54.81 | 64.20 | 93.66 | 216.10 | 181.49 | 89.77 | 68.21 | 27.18 | 12.29 |
| 2024 | 15.80 | 27.69 | 41.25 | 53.09 | 65.96 | 115.81 | 270.31 | 134.74 | 89.82 | 57.40 | 24.52 | 14.48 |
| 2025 | 19.76 | 31.65 | 44.89 | 56.92 | 71.65 | 126.32 | 266.02 | 117.23 | 88.56 | 52.17 | 23.12 | 15.36 |
| HistAvg | 16.05 | 20.37 | 34.34 | 50.21 | 88.21 | 87.01 | 197.68 | 146.43 | 83.92 | 56.85 | 33.33 | 19.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Guo, Z.; Zhang, C.; Tian, Y.; Li, Y. Research on the Application of CEEMD-LSTM-LSSVM Coupled Model in Regional Precipitation Prediction. Water 2023, 15, 1465. https://doi.org/10.3390/w15081465
Chen J, Guo Z, Zhang C, Tian Y, Li Y. Research on the Application of CEEMD-LSTM-LSSVM Coupled Model in Regional Precipitation Prediction. Water. 2023; 15(8):1465. https://doi.org/10.3390/w15081465
Chicago/Turabian StyleChen, Jian, Zhikai Guo, Changhui Zhang, Yangyang Tian, and Yaowei Li. 2023. "Research on the Application of CEEMD-LSTM-LSSVM Coupled Model in Regional Precipitation Prediction" Water 15, no. 8: 1465. https://doi.org/10.3390/w15081465
APA StyleChen, J., Guo, Z., Zhang, C., Tian, Y., & Li, Y. (2023). Research on the Application of CEEMD-LSTM-LSSVM Coupled Model in Regional Precipitation Prediction. Water, 15(8), 1465. https://doi.org/10.3390/w15081465








