1. Introduction
Normal precipitation can contribute to the regional water cycle as a positive feedback process. However, global warming due to greenhouse gas emissions is profoundly affecting regional precipitation patterns, with the IPCC Assessment Report 6 indicating that anthropogenic warming reached about 1 °C (±0.2 °C) in 2017, and that average precipitation in the high northern hemisphere will increase significantly when global warming is 1.5 °C or 2 °C compared to pre-industrial conditions [
1]. For example, Chen, J.L. et al. [
2] showed that water vapor transport from the Indian monsoon region and the South China Sea in the context of global change becomes an important condition for strong summer precipitation in southern and eastern China; Zhou, T.J. et al. [
3] also demonstrated that the alteration of water vapor transport channels in the western Pacific Ocean in the context of global change has a more significant effect on summer precipitation anomalies in China. The increase in precipitation events will inevitably lead to a series of serious consequences, so it is necessary to make accurate predictions of future rainfall trends based on available rainfall data to provide technical support for the sustainable use of regional water resources and disaster prevention and mitigation [
4].
Meteorological processes are variable, stochastic, and complex, making precipitation sequences also significantly stochastic, uncertain, and nonlinear [
5], increasing the degree of difficulty in accurately predicting precipitation. In recent years, many scholars have conducted extensive research in precipitation prediction, and the methods they use can be broadly classified into two categories: process-based methods and data-driven methods [
6]. The purpose of process-based precipitation prediction is to explore the physical processes of precipitation and to identify the various factors that influence the precipitation process. However, the interaction laws among the factors in the precipitation process are very complex, and it is often very difficult to solve and build physical models. The data-driven approach refers to the construction of models based on historical precipitation samples or real-time observation data, and the use of models to dig information, avoiding the analysis of the physical process of precipitation.
The data-driven models that have been widely used include the autoregressive sliding average model, gray model, neural network model, support vector machine model, and random forest. These models have achieved good results in solving complex nonlinearities of precipitation series. For example, Narayana et al. [
7] applied the AIRMA model to predict monsoon rainfall in India and concluded that there is an increasing trend of monsoon rainfall; Zhao, Y. [
8] used a gray metabolic prediction model to predict future rainfall, which improved the accuracy and precision of traditional gray model prediction results; Gou, Z.J. et al. [
9] used a BP neural network to establish a genetic neural network, in which the prediction accuracy of the neural network algorithm for precipitation levels was optimized; Shen, H.J. et al. [
10] used a long short-term memory neural network to predict summer precipitation in China in 2014 and 2015, and explored the influence of the starting month data on the seasonal prediction of precipitation. Wang, R. [
11] used GIS data as predictors to construct a support vector machine model based on the spatial distribution model of annual rainfall in Handan city, and derived the characteristics of circular aggregation distribution of rainfall in Handan city and the distribution of high and low values of rainfall in the urban area; Sha, S.K. [
12] fully combined the unique advantages of the random forest algorithm and established a rainfall prediction model based on the random forest algorithm for the Chengai irrigation area, which improved the accuracy and generalization of the rainfall prediction model.
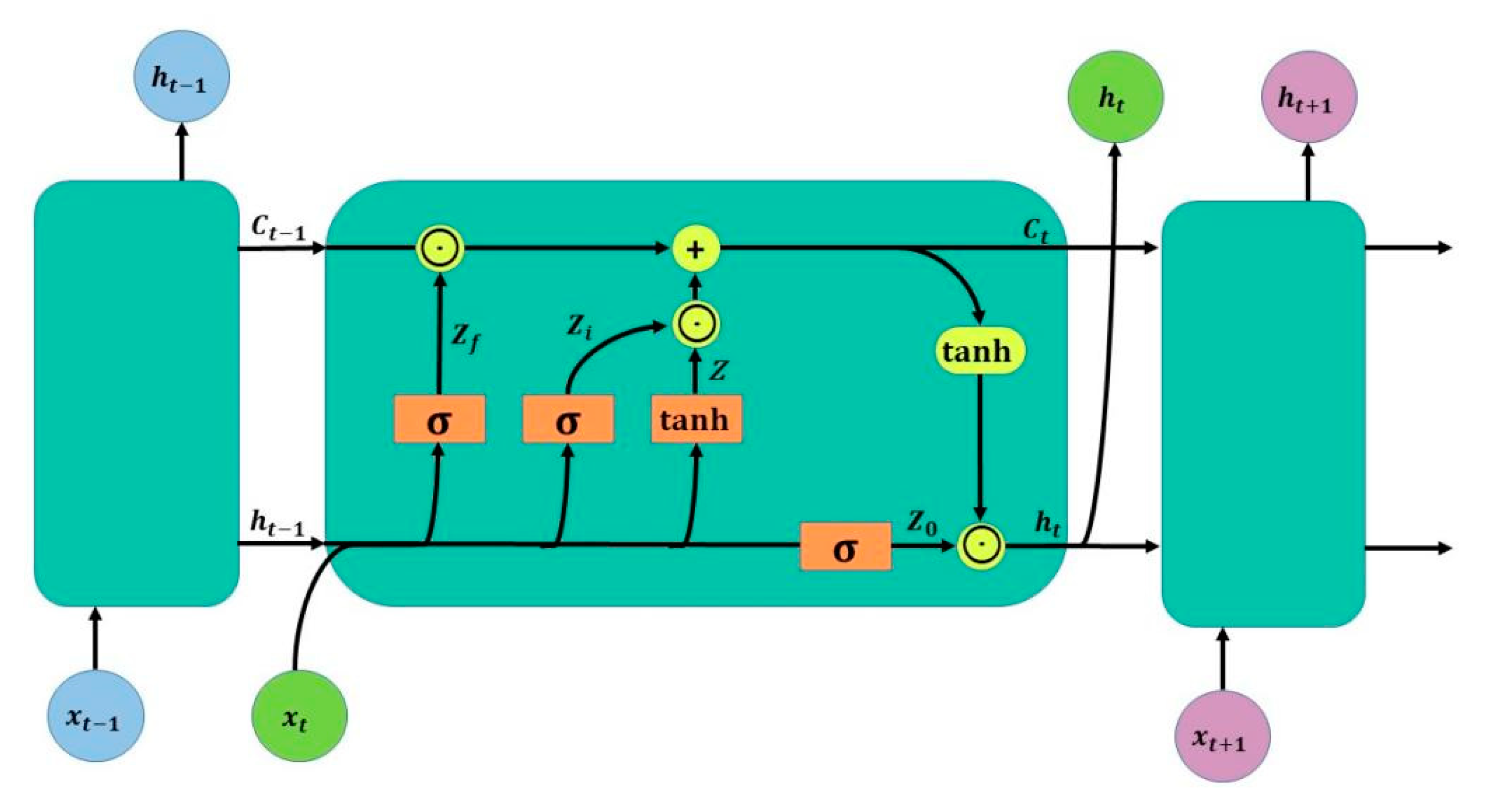
In the classification of neural network models, the recurrent neural network (RNN) can use state variables to store historical information and be combined with current inputs to jointly determine the output compared to other neural networks [
13]. Therefore, it can identify long-term dependencies between precipitation data more effectively, but for long sequences, RNNs suffer from gradient disappearance and excessive gradients during training. Long short-term memory (LSTM) [
14] is a special kind of RNN that controls the information transfer by adding unit states and gate structures, solving the gradient disappearance and gradient explosion problems during the training process of long sequences. However, there is still room for optimization of LSTM for precipitation prediction. Wang, W.C. et al. [
15] used wavelet decomposition and the coyote optimization algorithm to optimize the accuracy of LSTM model prediction. However, it is difficult for a single LSTM model to accurately predict the actual occurrence of extreme precipitation data in some months, so data denoising methods can be incorporated to improve the prediction accuracy [
16].
Empirical modal decomposition (EMD) [
17] is one of the most used data denoising methods, and can decompose complex time series data into several intrinsic modal functions (IMFs) and a residual term R, to achieve the exploitation of the frequency domain features of time series. Compared with the original time series data, the analysis and prediction of IMFs and residuals are simpler. However, EMD suffers from modal confounding [
18], and the ensemble empirical modal decomposition (EEMD) [
19] mitigates the degree of modal confounding in EMD by adding Gaussian white noise to the original sequence and then summing and averaging. Complementary ensemble empirical modal decomposition (CEEMD) [
20] adds a pair of positive and negative white noises with opposite numbers to the original time series as auxiliary noise to eliminate the residual white noise in the reconstructed signal after the decomposition of the original EEMD method, and to reduce the number of iterations required for the decomposition and the computational cost.
When decomposing precipitation series using EMD-like methods, the resulting subseries can contain both high-frequency and low-frequency components. To address this issue, the present study proposes a method of dividing the subseries obtained from the EMD-like decomposition into high-frequency and low-frequency subseries for use in building precipitation prediction models. This approach compensates for the limitations of a single algorithm in dealing with different frequency subseries and enables the classification of subseries to facilitate the construction of prediction models.
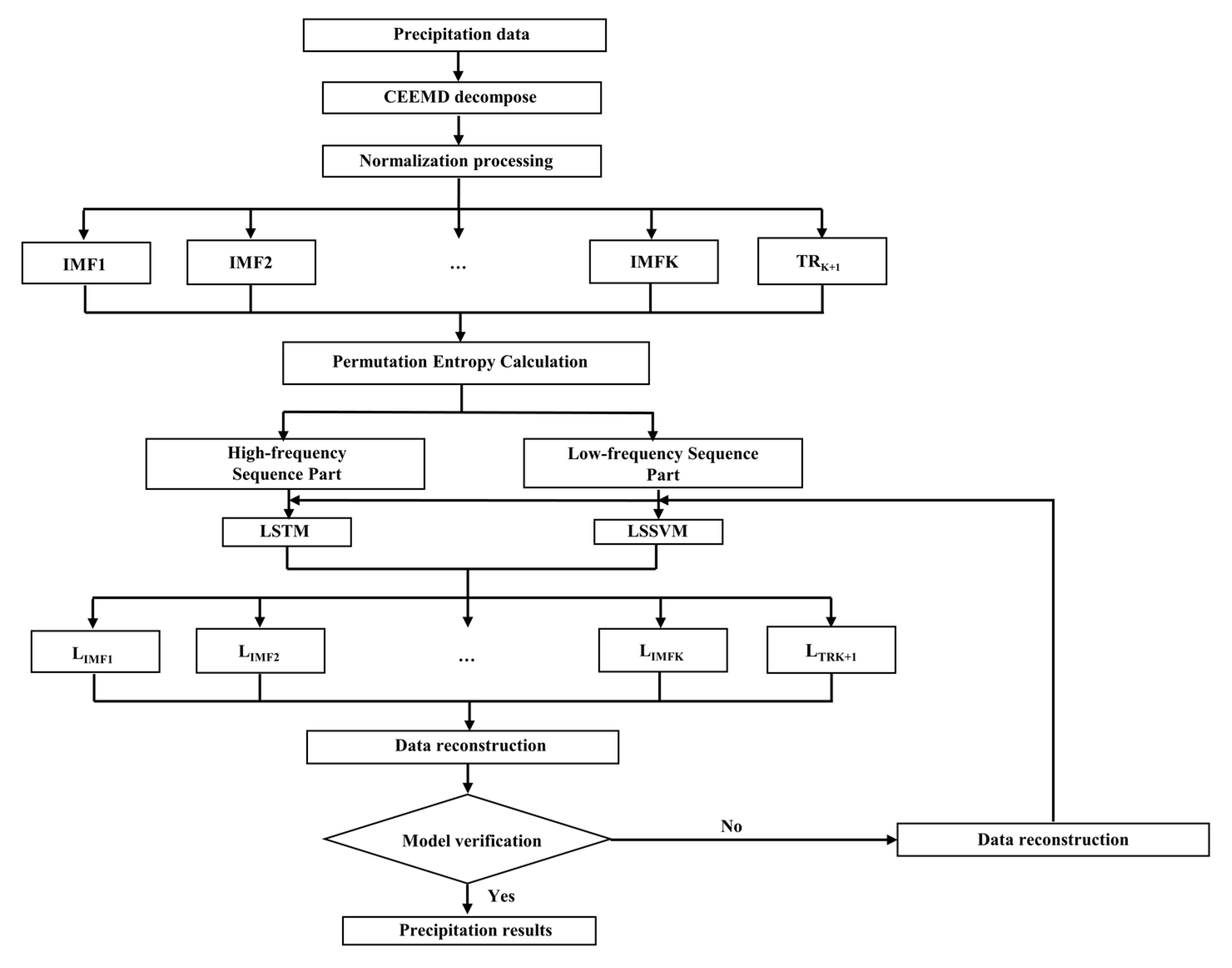
This paper proposes a method for partitioning high- and low-frequency components in each series obtained from the complete ensemble empirical mode decomposition (CEEMD). The high-frequency subseries are then utilized to construct a prediction model based on the long short-term memory (LSTM) algorithm, whereas the low-frequency sub-series are employed to build a prediction model using the least squares support vector machine (LSSVM) algorithm. The resultant coupled CEEMD-LSTM-LSSVM precipitation prediction model is evaluated using historical precipitation data from Zhoukou city, and the simulation prediction results are compared with those of several other models and real data to assess the efficacy of the model. The final model is used to forecast monthly precipitation in the study area for the next three years. This model provides a novel reference for improving the precision of precipitation prediction in the area, and can support disaster prevention and mitigation efforts in the region by providing valuable data.
3. Overview of the Study Area
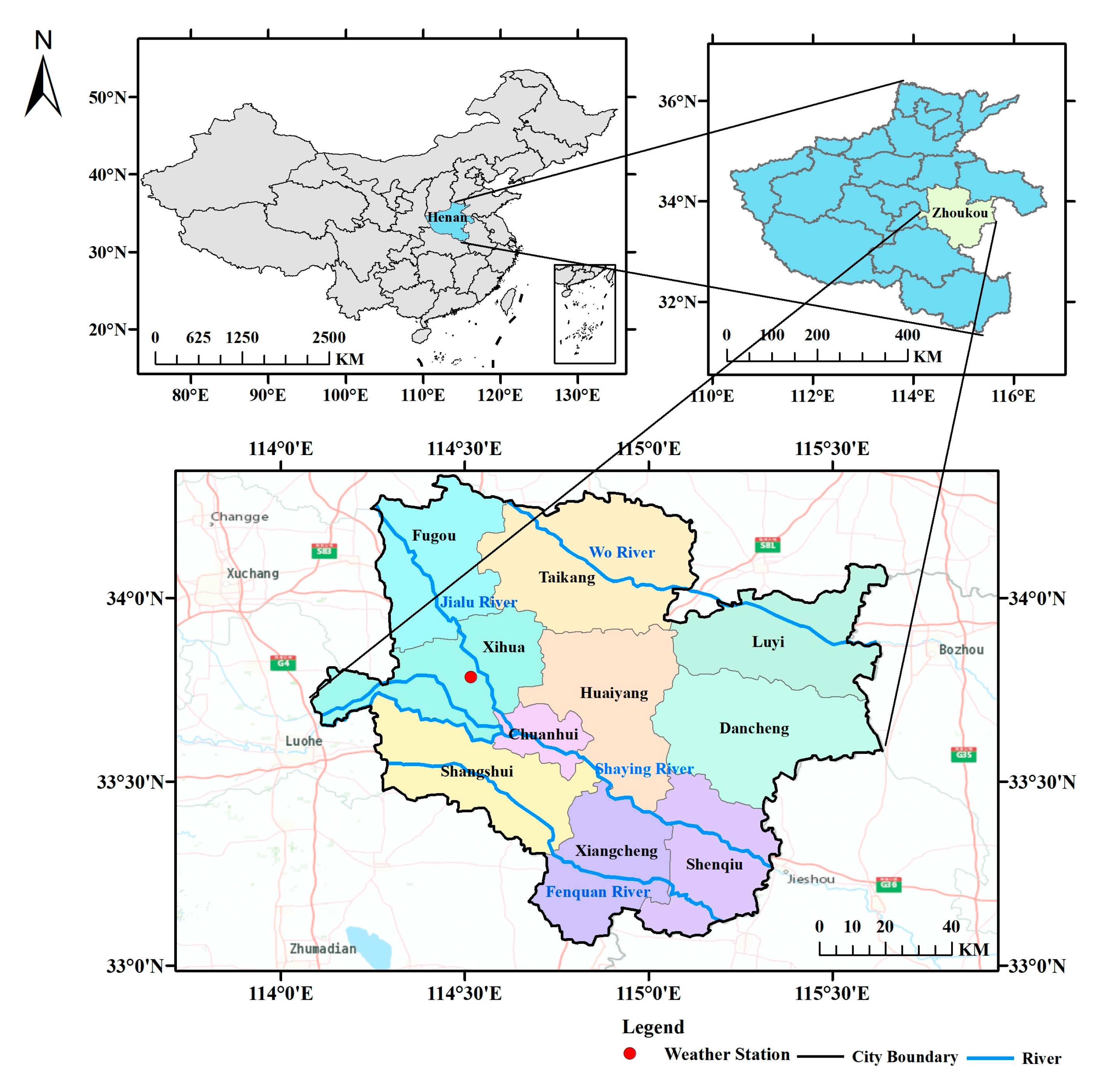
Zhoukou City is located in the central-eastern part of Henan Province, with an area of about 12,000 square kilometers. It is in the middle latitude between the Yellow River and the Huai River, with a flat topography and an elevation between 35.5 and 64.3 m, and belongs to the warm temperate semi-humid semi-arid continental monsoon climate. It is characterized by cold winters and hot summers, rain, and heat in the same period, with an annual average temperature of about 13–22 °C. Daily historical precipitation data were obtained from the National Centers for Environmental Information (
https://ngdc.noaa.gov/ (accessed on 20 November 2022)). Longitude and latitude coordinates of weather stations were downloaded from the website, imported into ArcGIS software, and then correlated with the study area to determine the locations of weather stations situated within the study area. The location of the weather station in the study area is illustrated in
Figure 2.
Zhoukou is influenced by the alternating effect of the cold Mongolian high and the Pacific sub-high atmospheric flow in winter and summer, respectively, and the intra-year distribution of precipitation in the city is extremely unbalanced. The obtained daily historical precipitation data from the National Centers for Environmental Information (
https://ngdc.noaa.gov/ (accessed on 20 November 2022)) website were initially checked and controlled by the article authors. Data with erroneous values, such as single-day precipitation readings of 99.99, were removed. Subsequently, an analysis and collation of the data enabled the calculation of the multi-year average rainfall data for Zhoukou City between 1978 and 2022. Additionally, the multi-year average annual precipitation for each region in China was downloaded from the China Meteorological Data Network (
https://data.cma.cn/ (accessed on 20 November 2022)), and annual precipitation raster data for China were obtained via ArcGIS software and the kriging interpolation method [
25].
The study utilized the two data products to calculate and validate the annual aver-age rainfall data for Zhoukou City. Through this process, a multi-year average rainfall of 833.47 mm was determined for Zhoukou City. The seasonal average rainfall was also calculated, with the following values obtained: 172.76 mm in spring (March to May), 431.12 mm in summer (June to August), 174.1 mm in autumn (September to November), and 55.49 mm in winter (December to February).
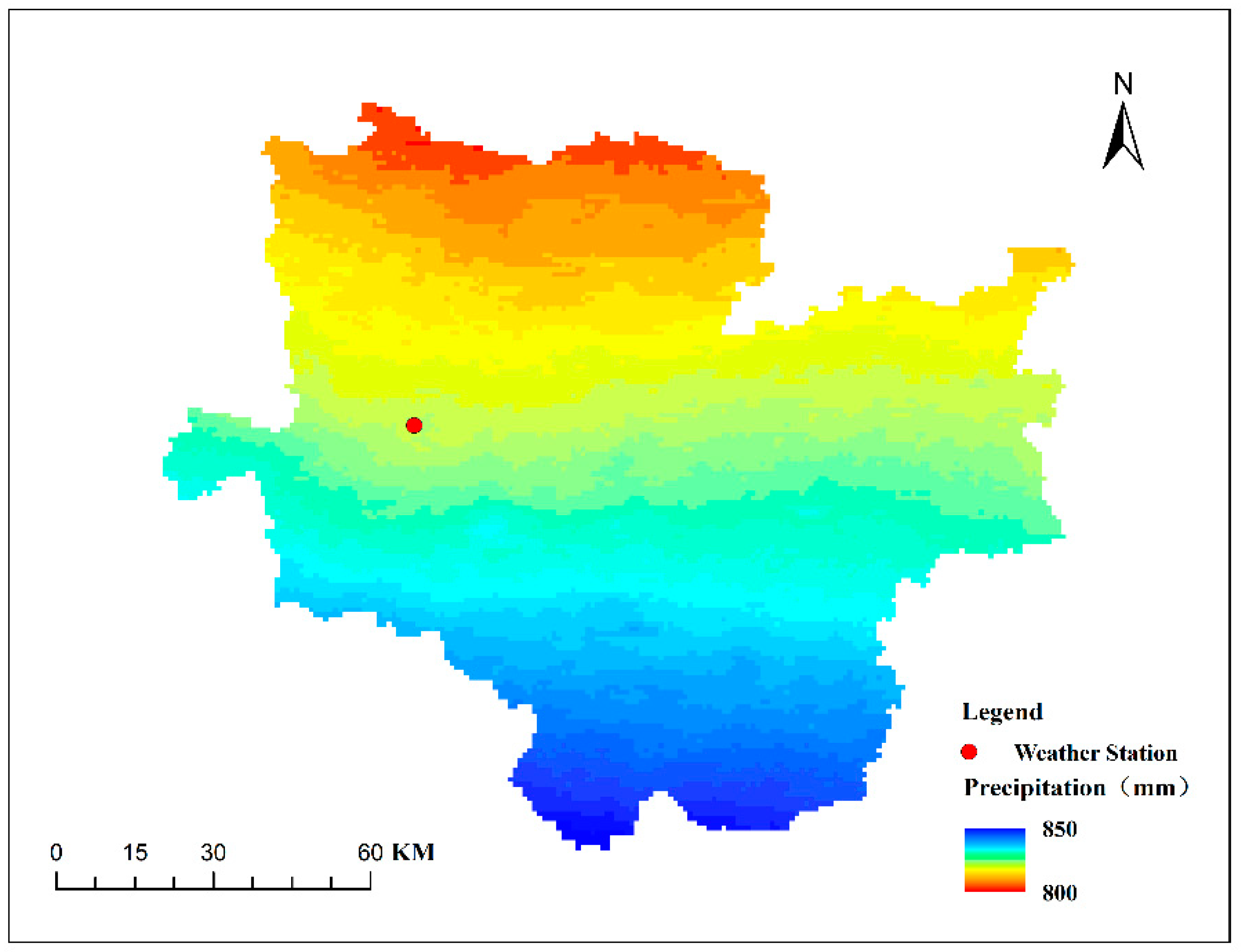
Figure 3 illustrates the multi-year average precipitation distribution in the study area, generated via the “Extract by mask” tool in the Spatial Analyst of ArcGIS software after obtaining the annual precipitation raster data for China.
5. Analysis and Discussion
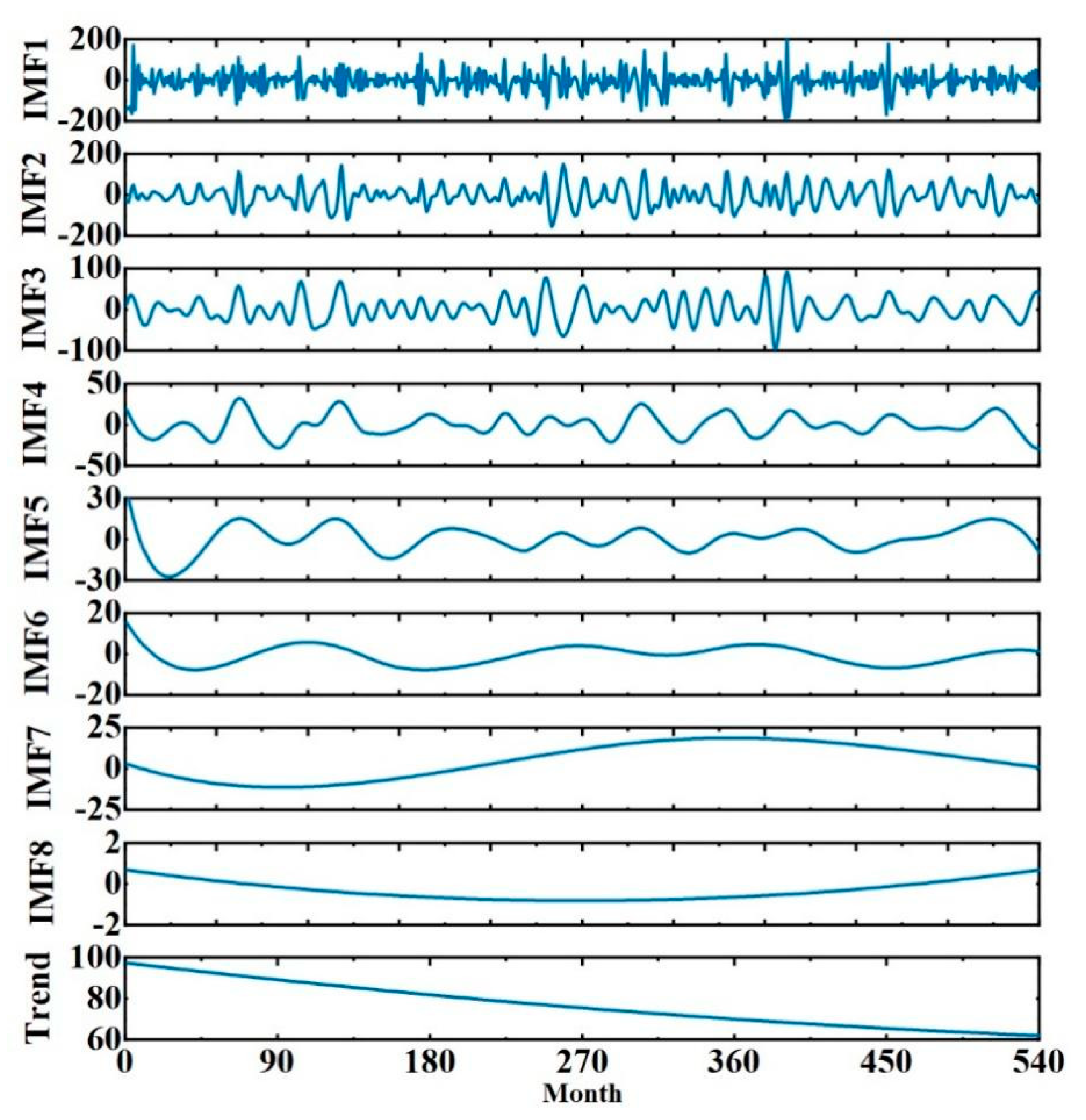
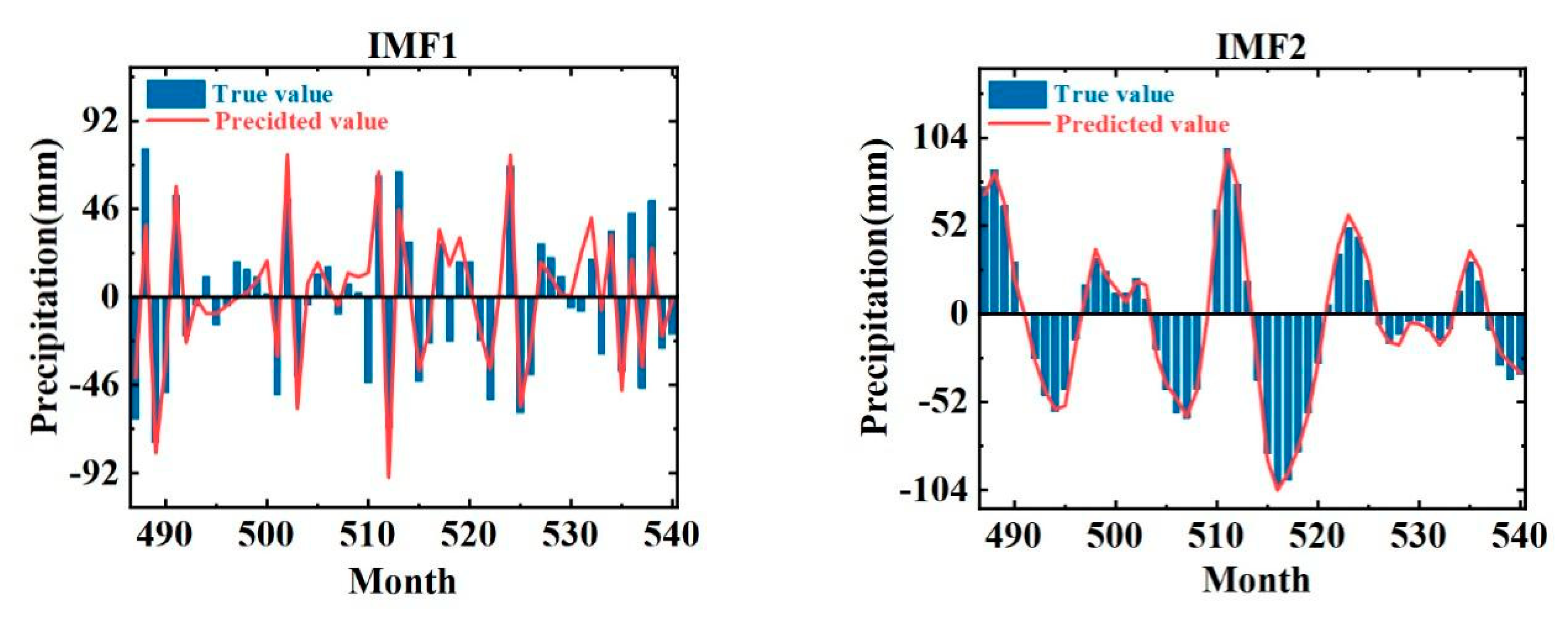
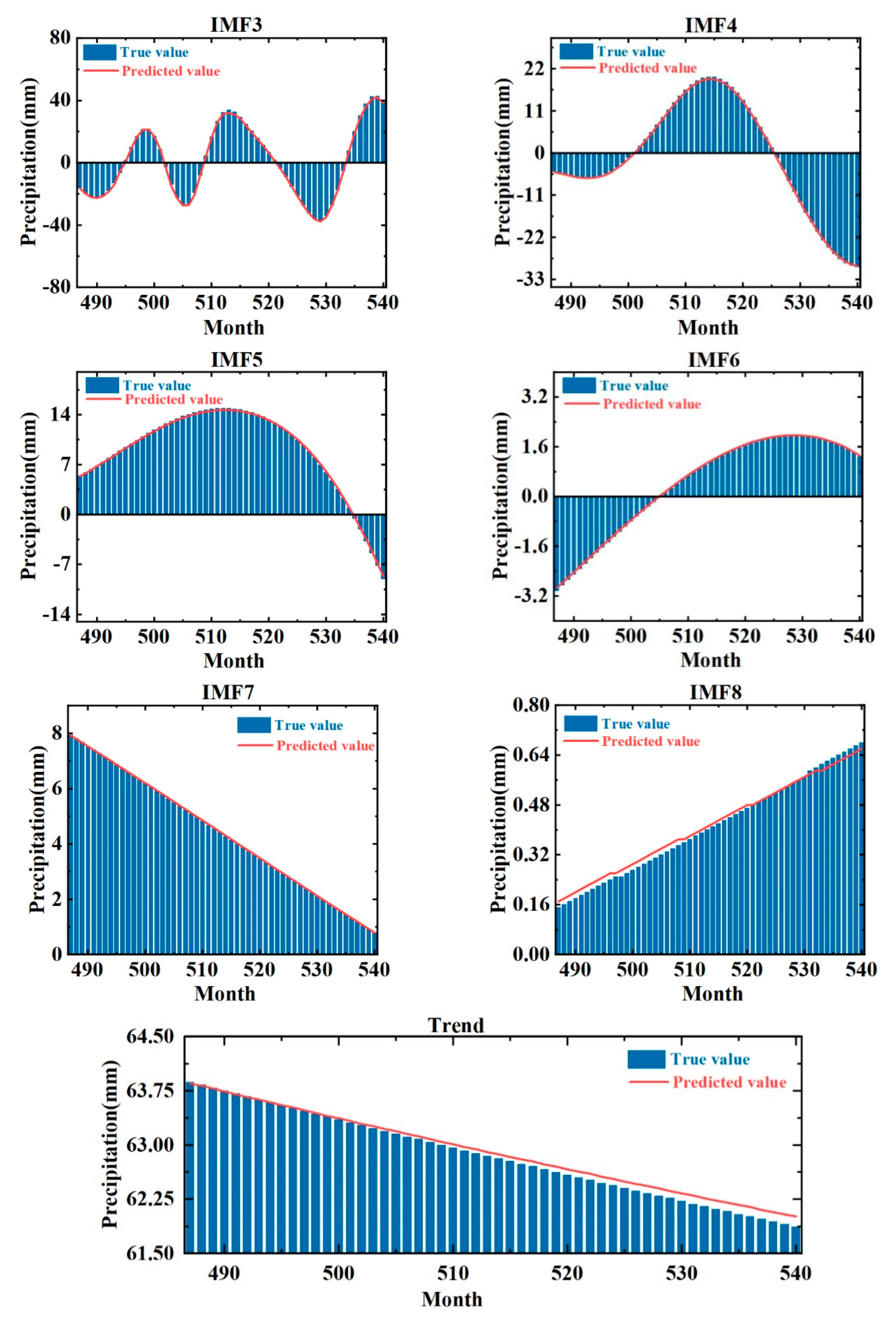
After the prediction of the constructed CEEMD-LSTM-LSSVM coupled model, the data need to be inverse normalized to obtain the component prediction values, and
Figure 9 shows the comparison of each component series with the observed values after inverse normalization. After calculation, the average relative errors of IMF1–8 are shown in
Table 4.
Among them, the average relative errors of IMF1 and 2 are larger, which is due to their larger frequencies. The average relative error from IMF1 to the trend term gradually decreases, and combined with
Figure 9, it can be seen that the predicted values of each component basically match with the true values. Therefore, after CEEMD preprocessing, the LSTM model is better for IMF1-IMF8 prediction and the LSSVM model is better for trend terms.
The predicted values of all components and trend terms were summed to obtain the predicted values of monthly precipitation in Zhoukou City, and the prediction results of LSTM, LSSVM, and CEEMD-LSTM models were selected to compare with this model to verify the prediction effect of the CEEMD-LSTM-LSSVM model. The comparison of the prediction results of different models is shown in
Figure 10a–c, and the prediction accuracy statistics of different models are shown in
Table 5.
As can be seen in
Figure 10, all four models provide an overall picture of the general trend of precipitation over the month, but the single LSSVM model does not provide enough detail compared to the measured results, e.g., the prediction error increases rapidly for some months with high precipitation because the strong randomness of the precipitation series interferes with the model prediction accuracy. However, due to the special nature of precipitation prediction, the focus is more on the extreme precipitation events which are more hazardous. The prediction results of the LSTM model are not only closer to the measured results for the months with more precipitation than the LSSVM model, but also have more details for the rest of the months, because the LSTM model can better handle the gradient disappearance and gradient explosion during the long series training process and thus has better performance [
26]. The CEEMD-LSTM model also has better prediction results than LSTM and is closer to the measured values in the months with more precipitation, indicating that the decomposition of the precipitation series can improve the accuracy of the model. CEEMD-LSTM-LSSVM has the best prediction results, even in months with high precipitation, because CEEMD completely separates the different fluctuation features in the precipitation series and decomposes the added noise to reduce the reconstruction error [
27]. The PE algorithm is then used to divide the high- and low-frequency sequences, and the LSTM model is used to calculate the high-frequency data and the LSSVM model is used to calculate the low-frequency sequences. This allows the model to better capture the variation characteristics of each component, avoiding the situation that a single model produces large errors on inapplicable sequences, and effectively improving the prediction accuracy.
As can be seen from
Table 5, the RMSE of the coupled CEEMD-LSTM-LSSVM model is 16.77 mm, the MAE is 13.07 mm, and the R
2 is 0.932. The smaller values of these two performance indicators, RSME and MAE, indicate that the predicted value is closer to the actual value and the error of prediction is smaller; the closer R
2 to 1, the better the fit of the prediction model. Therefore, the coupled model developed in the article has the highest accuracy compared to the selected comparison model and can be used for the prediction of actual precipitation in the study area.
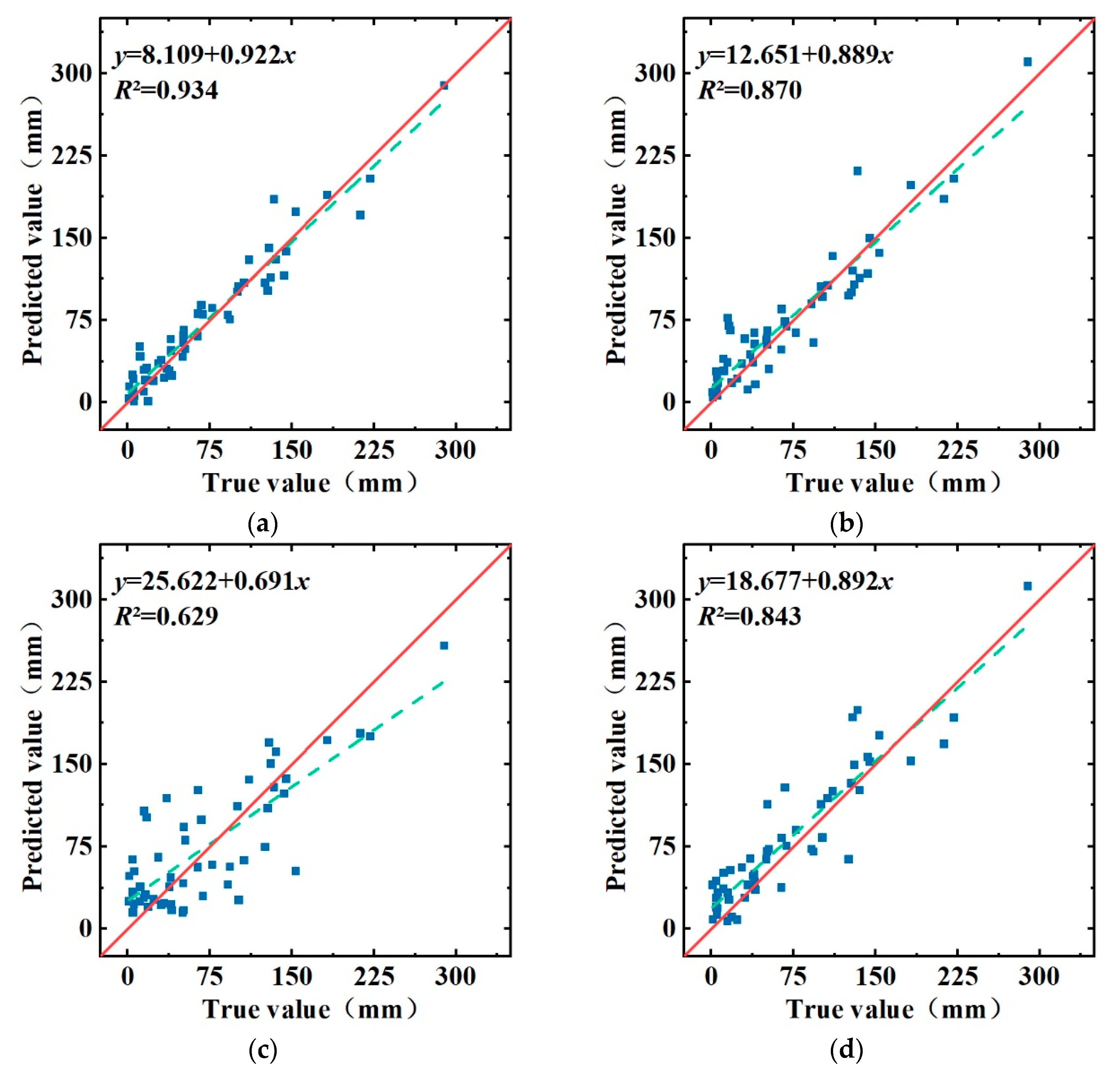
In addition, the scatter plot of the observed and predicted precipitation values can show the distribution of the prediction results of different models and the observed precipitation values more clearly and intuitively. The solid line in
Figure 11 is the diagonal line, and the dashed line is the linear fit of the predicted and observed precipitation values of the model. From the distribution of data points in
Figure 11, we can find that the data points of the LSSVM model are scattered, indicating that the strong randomness of the precipitation series interferes with the model prediction accuracy. The CEEMD-LSTM model has a better overall prediction accuracy for precipitation, but there are some deviations in the prediction of normal precipitation. The LSTM model has higher prediction accuracy for normal precipitation, but it has a skewed prediction value for rainfall in months with little rainfall. The data points of the CEEMD-LSTM-LSSVM model are almost all distributed on the diagonal, indicating that the model is more accurate in predicting precipitation. The linear fit of the model predictions to the observed precipitation values shows that the R
2 of the CEEMD-LSTM-LSSVM model is closest to 1, which indicates that the model predictions are more consistent with the observed precipitation values.
6. Monthly Precipitation Forecasts
The coupled model was used to forecast the rainfall data of Zhoukou City from 2023 to 2025, and the data are shown in
Table 6. The historical average precipitation data in the table were obtained by accumulating and then averaging the corresponding months of the collected precipitation data of Zhoukou City from 1978 to 2022, which has some practical significance for evaluating the forecast data.
Among the predicted monthly precipitation data in Zhoukou City, three months in 2023 are lower than the historical average monthly precipitation and nine months are higher than the historical average monthly precipitation; five months in 2024 are lower than the historical average monthly precipitation and seven months are higher than the historical average monthly precipitation; and four months in 2025 are lower than the historical average monthly precipitation and eight months are higher than the historical average monthly precipitation. In addition, the predicted precipitation in July 2024 is the maximum of the past three years, reaching 270.31 mm, which is in line with the precipitation pattern of Zhoukou City in the same period of rain and heat. In addition, combined with the analysis of historical monthly precipitation, precipitation in Zhoukou City is often high in the summer, while in winter the precipitation is low. This pattern is in line with Zhoukou City winter and summer seasons, respectively. Because of the Mongolian cold high and the Pacific paramount atmospheric alternation, the city precipitation distribution within the year is extremely unbalanced.
The study’s results indicate a tendency for the cumulative value of rainfall to increase from 2023 to 2025. This increase in rainfall poses a particular threat to the safety of Zhoukou City during periods of extreme precipitation, such as in July and August. Therefore, Zhoukou City should take corresponding preventive measures against extreme precipitation to improve its flood warning level and risk emergency management. Additionally, urban municipal infrastructure should be strengthened to prevent river flooding and urban flooding caused by heavy rainfall. It is also essential to pay attention to possible drought disasters during the winter season due to low precipitation, which may threaten agriculture and the ecological environment, as well as increase the risk of forest fires.
7. Conclusions
Because of the advantage that the signal decomposition method of the EMD class can directly start decomposition for a period of unknown signals without performing pre-analysis and research, this study performed CEEMD decomposition for the monthly precipitation series of Zhoukou city from 1978 to 2022. This effectively overcame the problems of modal confusion caused by EMD decomposition and large reconstruction errors caused by adding a single white noise to EEMD decomposition. By analyzing the skewness and kurtosis of the decomposition results, this study also proved that the components are more stable and regular compared with the original series, thereby providing a good basis for subsequent prediction. Meanwhile, the PE algorithm was used to divide each modal component into a high-frequency sequence part and a low-frequency sequence part, and the LSTM and LSSVM models were used to predict the two parts, respectively. This reduced the error of each component’s prediction and improved the overall prediction accuracy. The coupled model can thus be used for the prediction of long-term precipitation sequences.
In addition, a coupled CEEMD-LSTM-LSSVM model was developed and applied to month-by-month precipitation forecasting in Zhoukou City. The results show that the coupled model has advantages over the single LSTM neural network model for long series forecasting; the coupled model can portray the actual changes of precipitation series in more detail, and it can also better simulate months in which there are sudden changes in precipitation. Compared with the CEEMD-LSTM, LSTM, and LSSVM models, the RMSE of the predicted data set was reduced by 29.12%, 39.61%, and 59.61%, MAE was reduced by 26.81%, 41.81%, and 57.92%, and the coefficient of determination R2 was increased by 0.08, 0.14, and 0.47, respectively. This indicates that the coupled model proposed in this paper is applicable to monthly precipitation prediction, improves the accuracy of prediction, and can be applied to data analysis and prediction in related fields as a time-frequency domain analysis method.
The overall prediction accuracy of the coupled model proposed in this paper is high. However, the prediction model does not consider the physical conditions that have a large impact on the actual precipitation. In future research, we can try to include meteorological variables such as temperature, air pressure, relative humidity, and wind speed in the model to further improve the prediction accuracy.