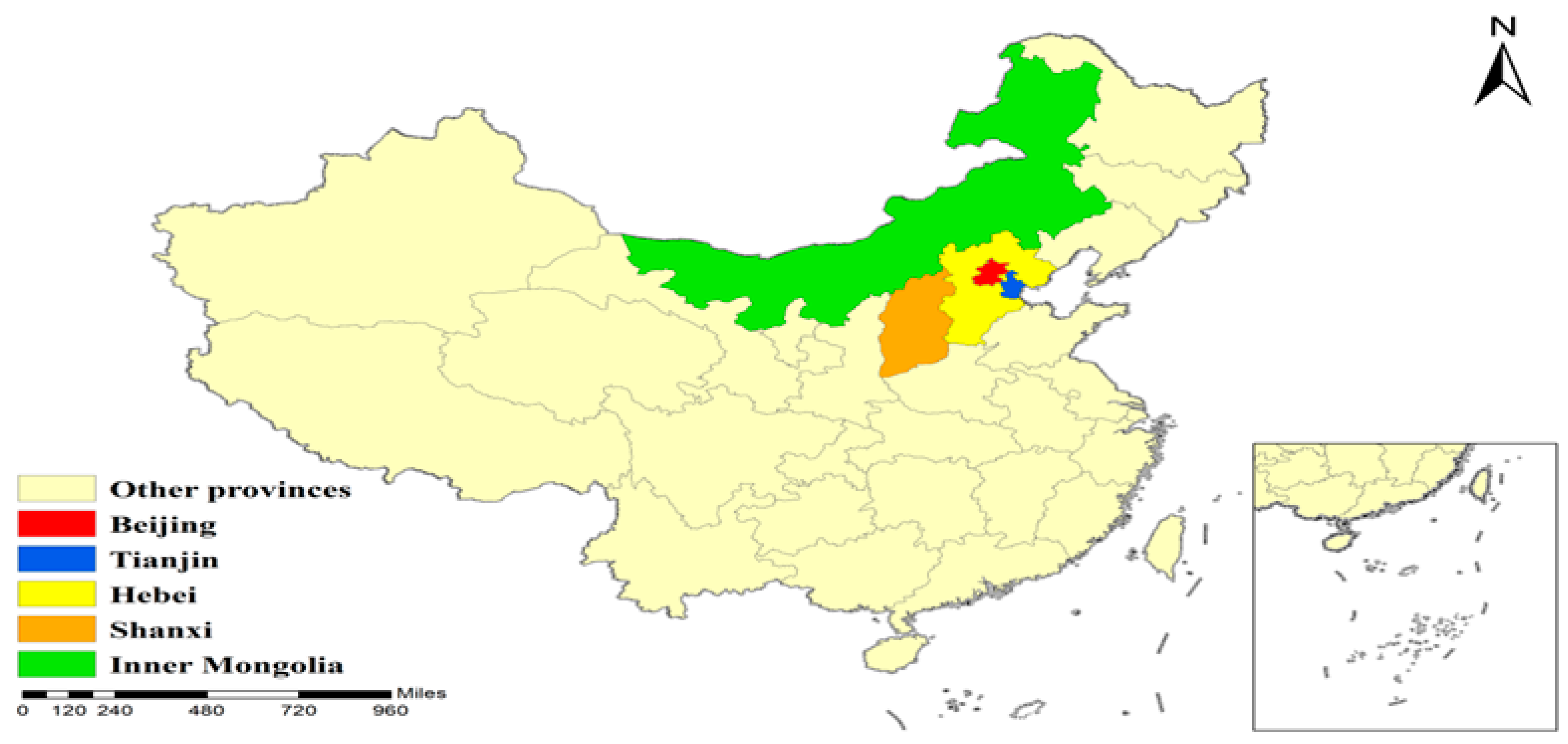
Figure 1.
Geographical location of the research area.
Figure 1.
Geographical location of the research area.
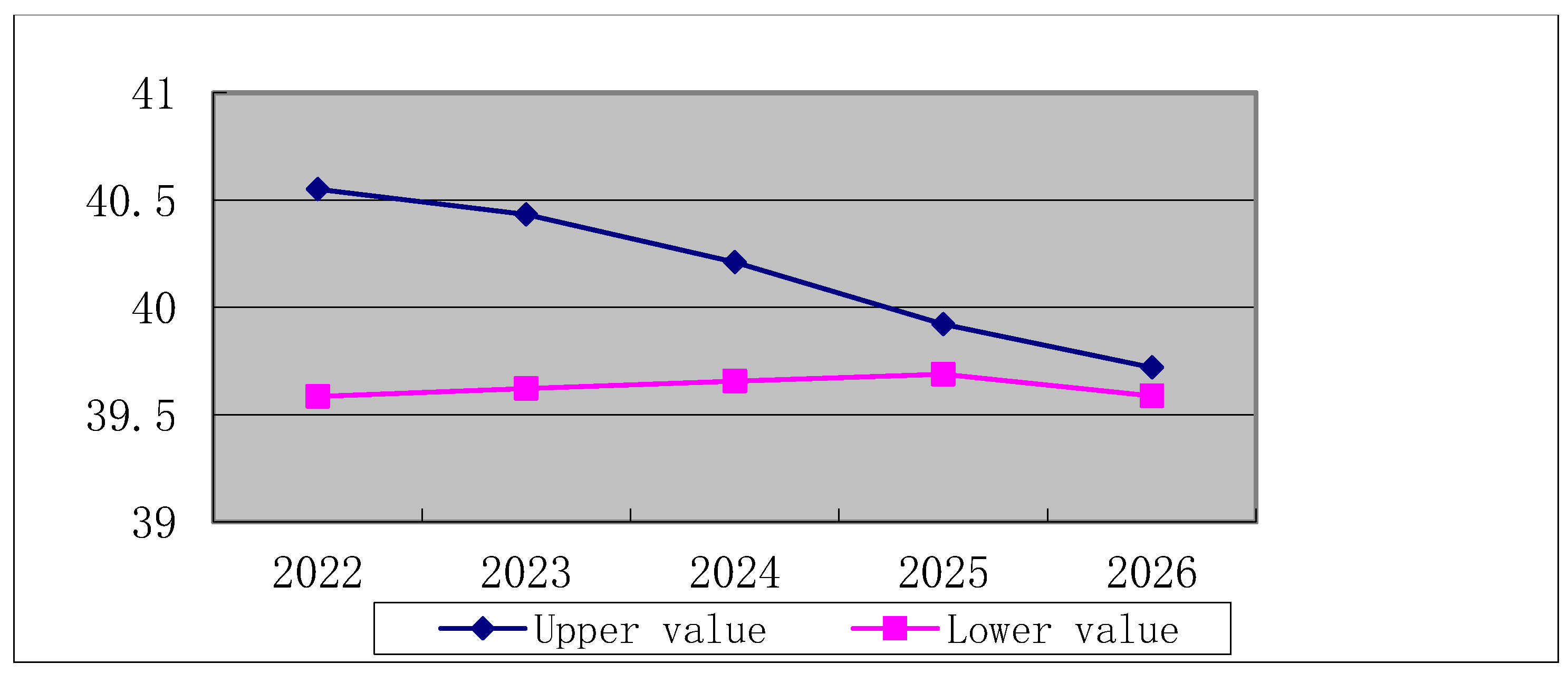
Figure 2.
The variation interval of water requirement with the influence of primary industry in Beijing.
Figure 2.
The variation interval of water requirement with the influence of primary industry in Beijing.
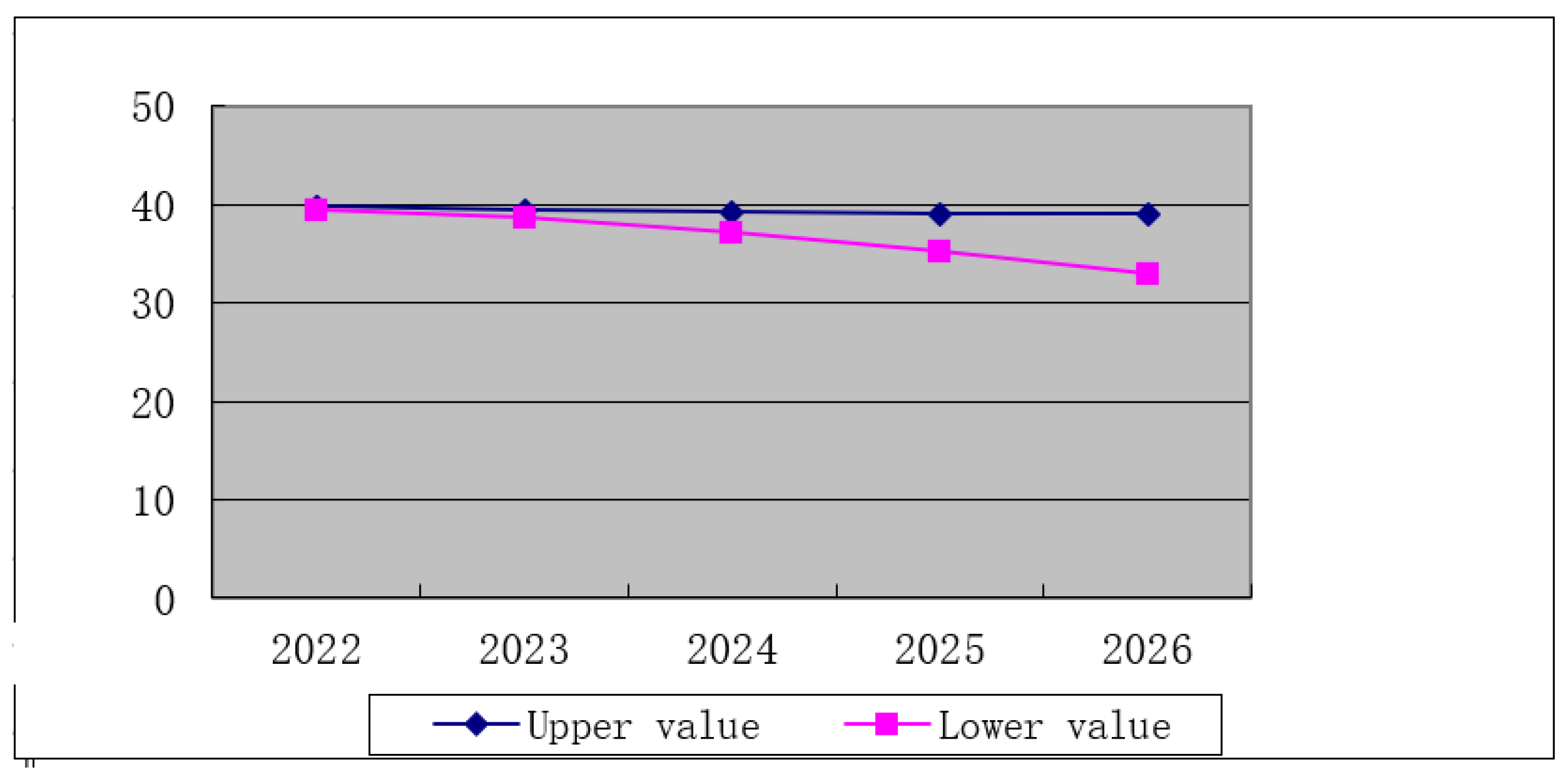
Figure 3.
The variation interval of water requirement with the influence of secondary industry in Beijing.
Figure 3.
The variation interval of water requirement with the influence of secondary industry in Beijing.
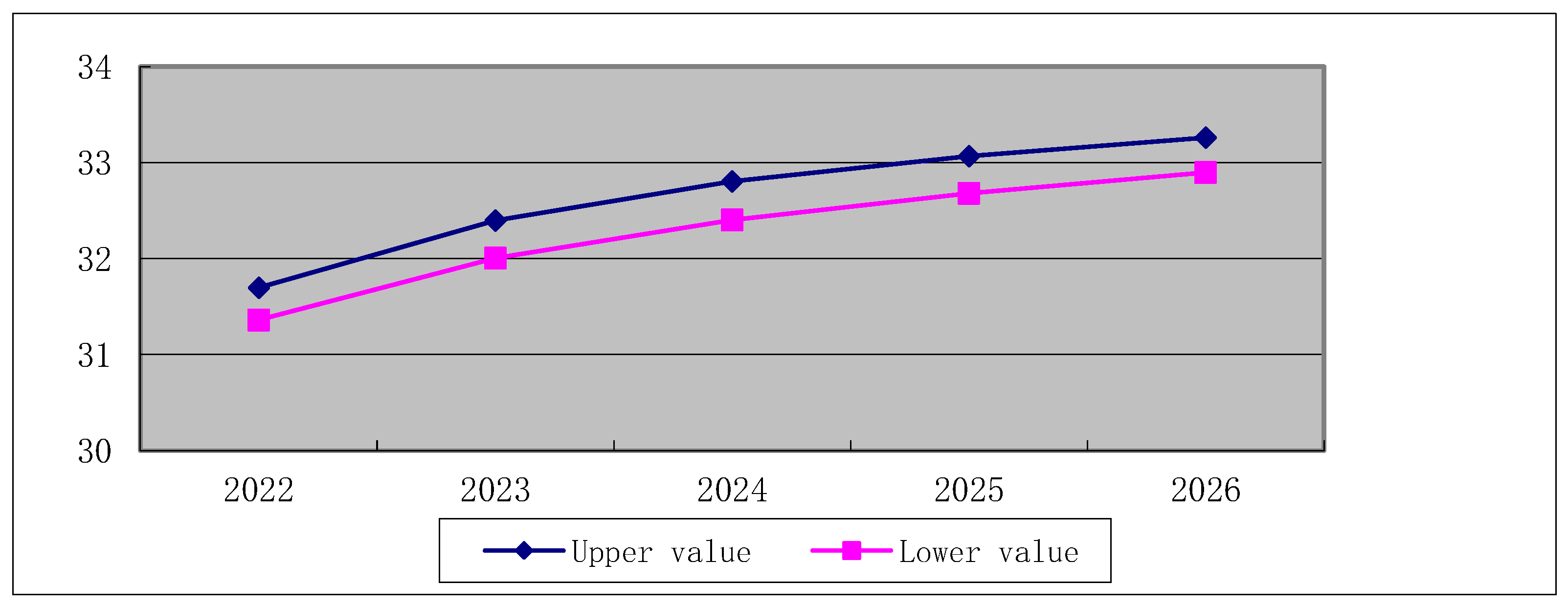
Figure 4.
The variation interval of water requirement with the influence of tertiary industry in Beijing.
Figure 4.
The variation interval of water requirement with the influence of tertiary industry in Beijing.
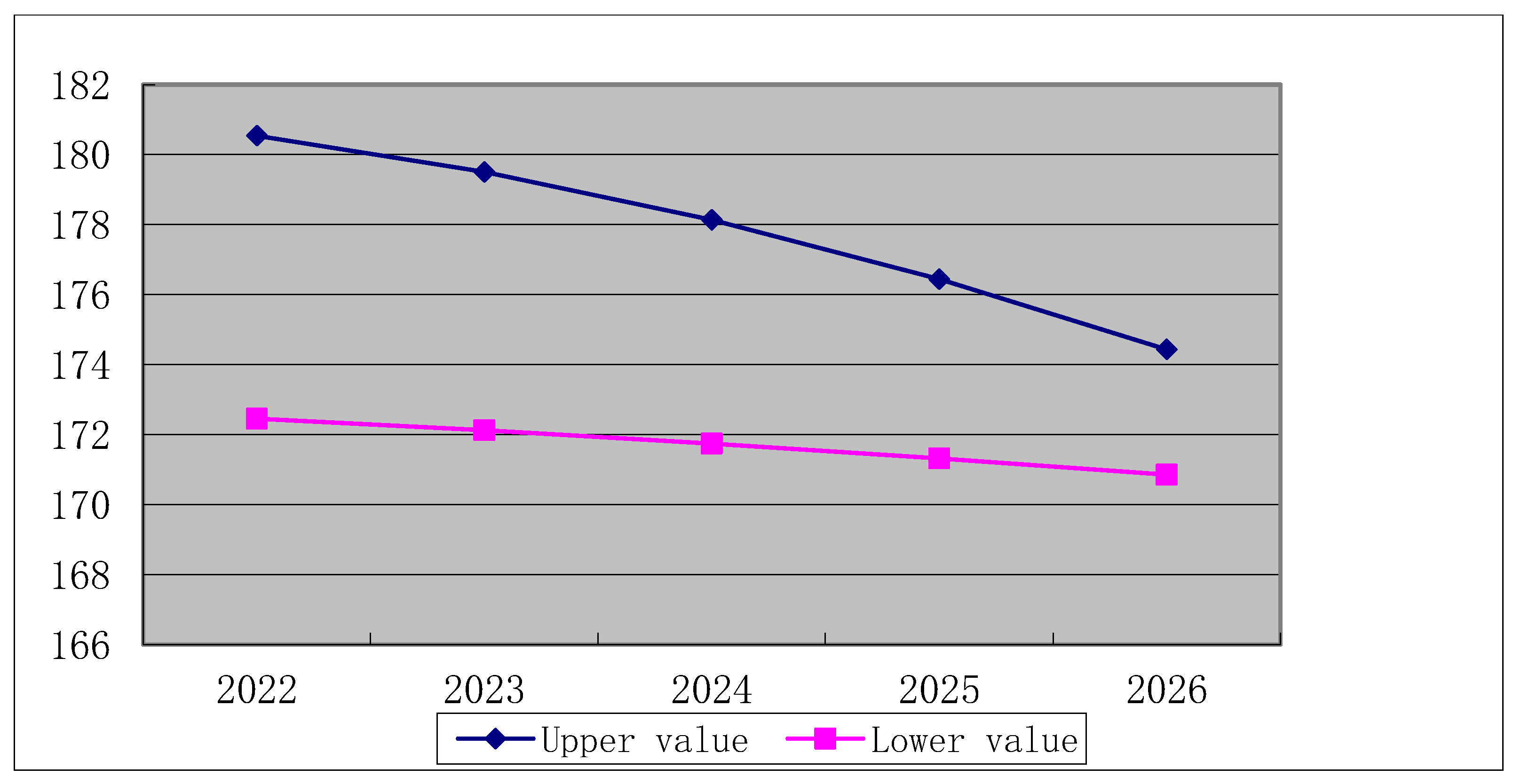
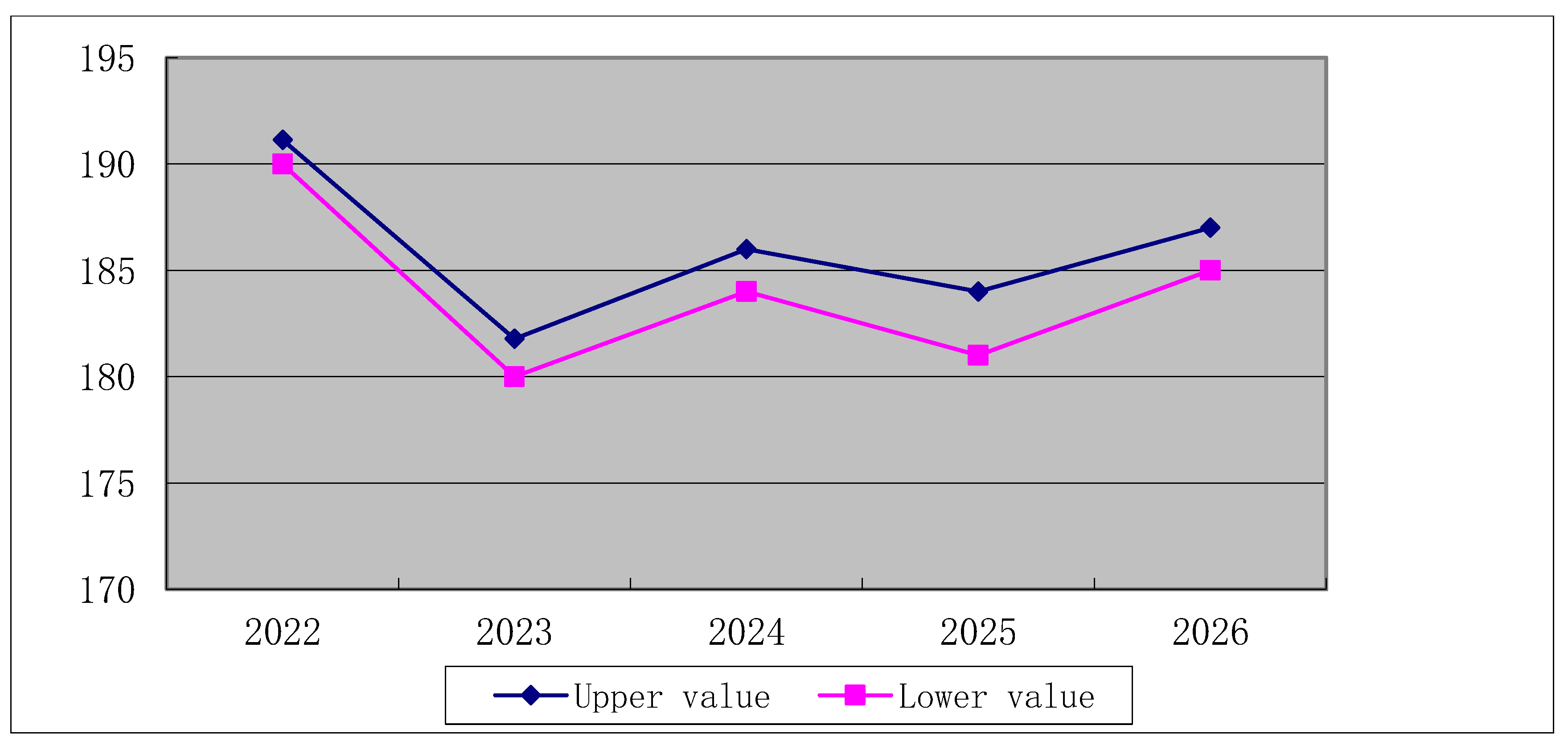
Figure 5.
The variation interval of water requirement with the influence of population in Beijing.
Figure 5.
The variation interval of water requirement with the influence of population in Beijing.
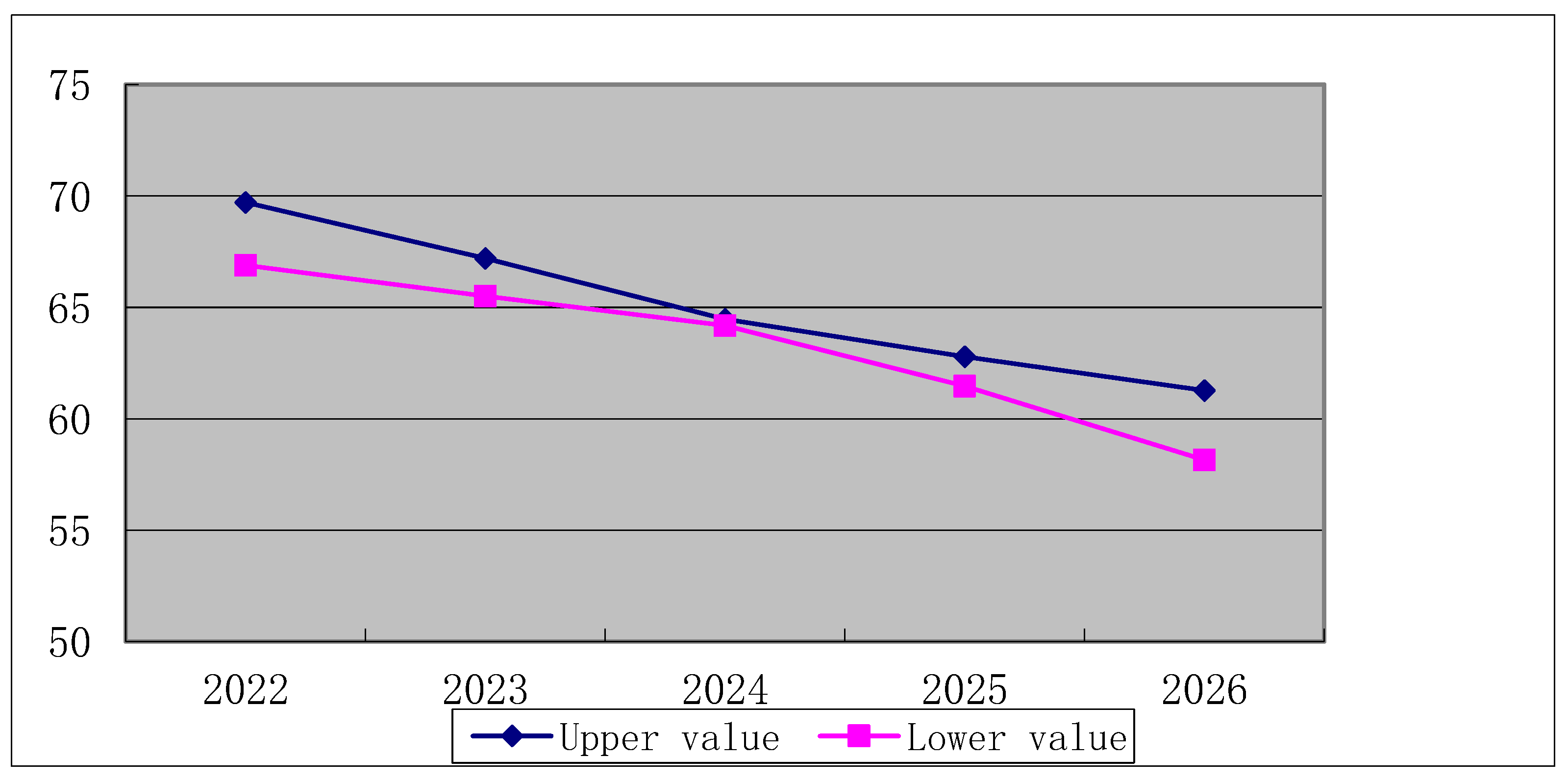
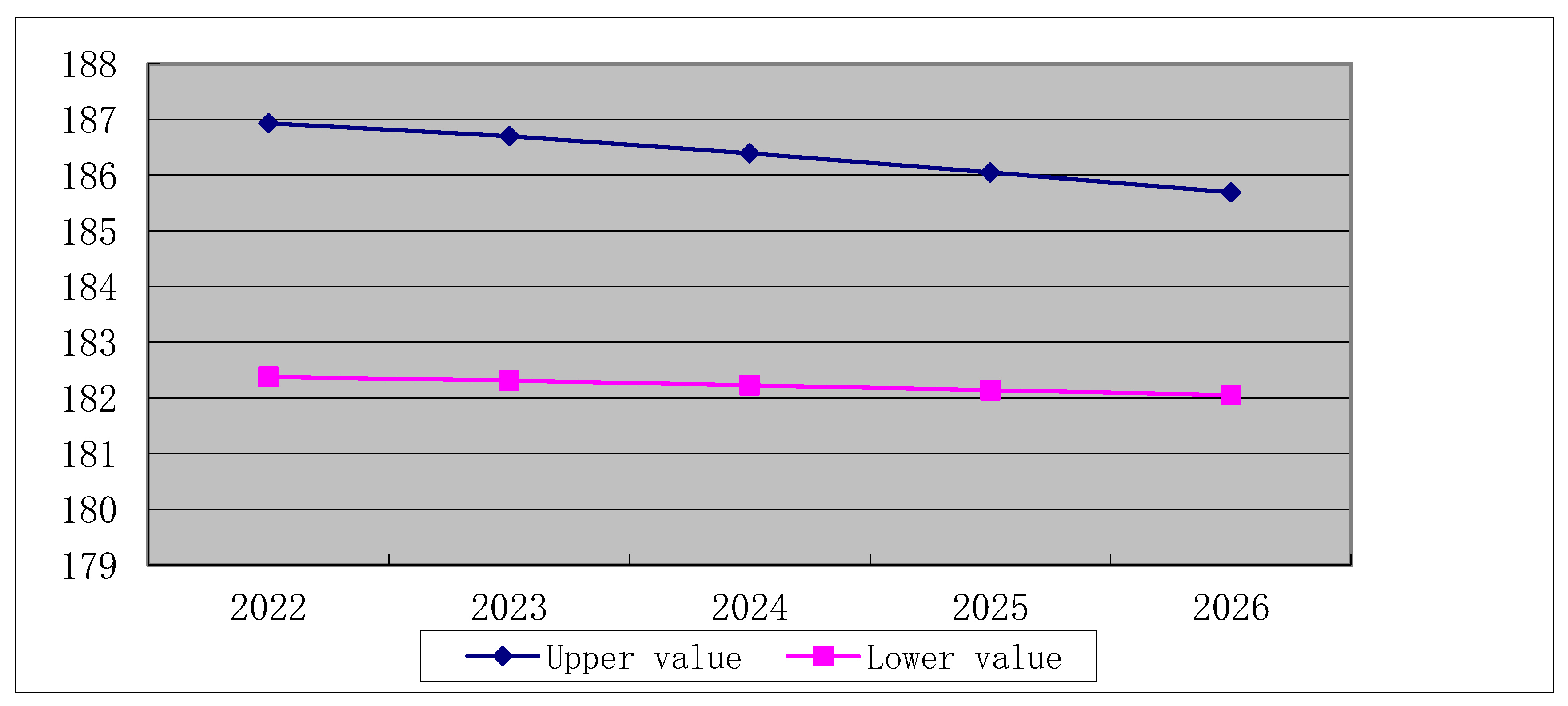
Figure 6.
The variation interval of water requirement with the influence of primary industry in Tianjin.
Figure 6.
The variation interval of water requirement with the influence of primary industry in Tianjin.
Figure 7.
The variation interval of water requirement with the influence of the secondary industry in Tianjin.
Figure 7.
The variation interval of water requirement with the influence of the secondary industry in Tianjin.
Figure 8.
The variation interval of water requirement with the influence of the tertiary industry in Tianjin.
Figure 8.
The variation interval of water requirement with the influence of the tertiary industry in Tianjin.
Figure 9.
The variation interval of water requirement with the influence of the population in Tianjin.
Figure 9.
The variation interval of water requirement with the influence of the population in Tianjin.
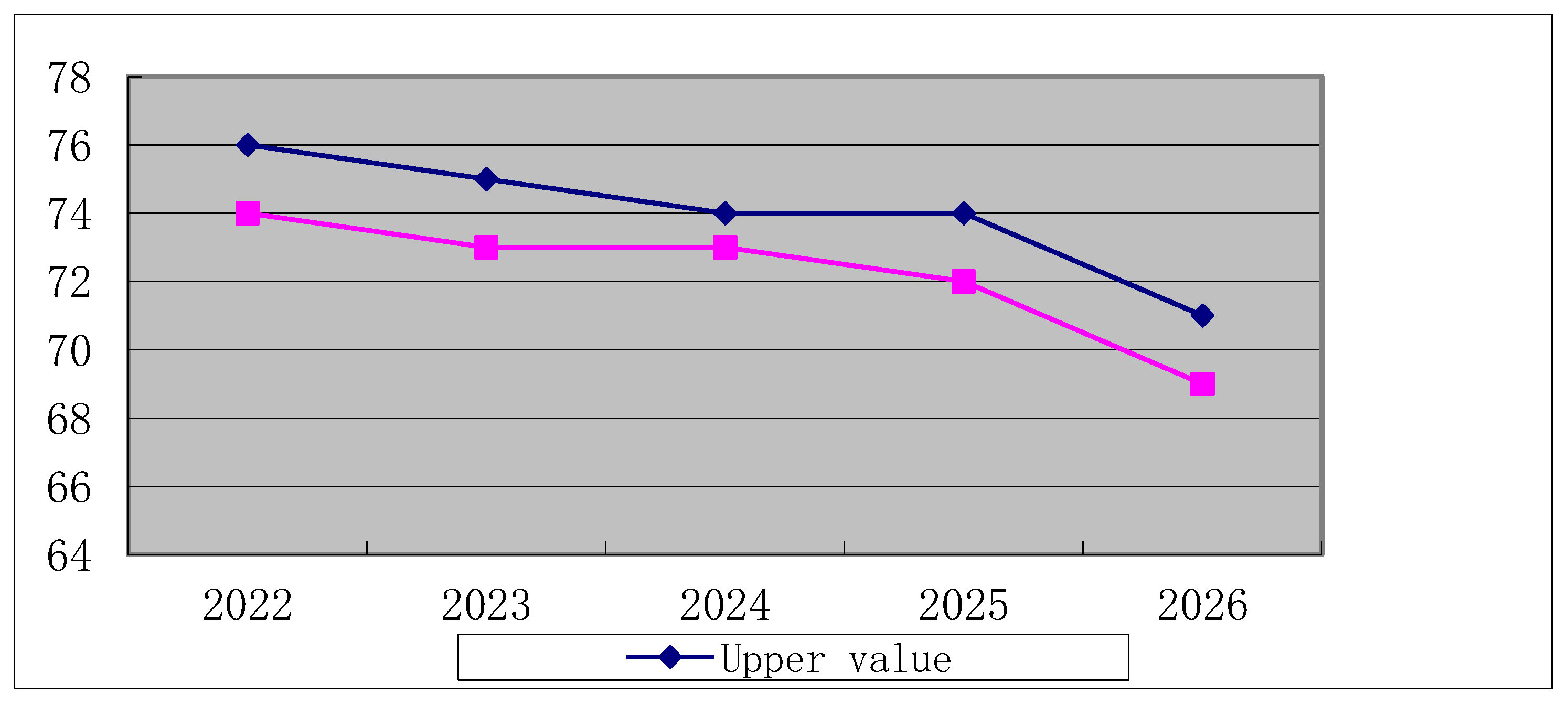
Figure 10.
The variation interval of water requirement with the influence of primary industry in Hebei.
Figure 10.
The variation interval of water requirement with the influence of primary industry in Hebei.
Figure 11.
The variation interval of water requirement with the influence of the secondary industry in Hebei.
Figure 11.
The variation interval of water requirement with the influence of the secondary industry in Hebei.
Figure 12.
The variation interval of water requirement with the influence of the tertiary industry in Hebei.
Figure 12.
The variation interval of water requirement with the influence of the tertiary industry in Hebei.
Figure 13.
The variation interval of water requirement with the influence of population in Hebei Province.
Figure 13.
The variation interval of water requirement with the influence of population in Hebei Province.
Figure 14.
The variation interval of water requirement with the influence of primary industry in Shanxi Province.
Figure 14.
The variation interval of water requirement with the influence of primary industry in Shanxi Province.
Figure 15.
The variation interval of water requirement with the influence of secondary industry in Shanxi Province.
Figure 15.
The variation interval of water requirement with the influence of secondary industry in Shanxi Province.
Figure 16.
The variation interval of water requirement with the influence of the tertiary industry in Shanxi Province.
Figure 16.
The variation interval of water requirement with the influence of the tertiary industry in Shanxi Province.
Figure 17.
The variation interval of water requirement with the influence of population in Shanxi Province.
Figure 17.
The variation interval of water requirement with the influence of population in Shanxi Province.
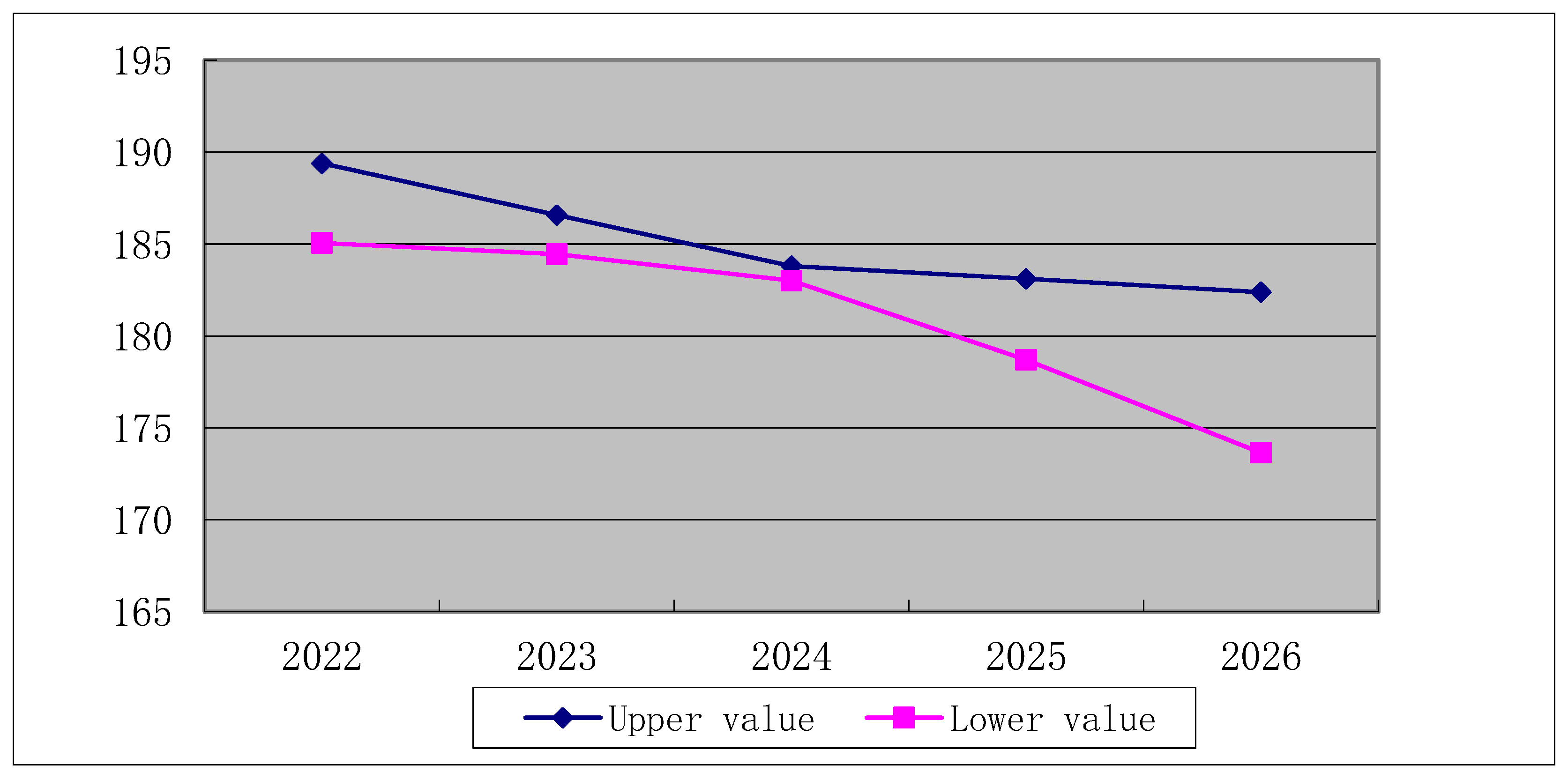
Figure 18.
The variation interval of water requirement with the influence of the primary industry in Inner Mongolia.
Figure 18.
The variation interval of water requirement with the influence of the primary industry in Inner Mongolia.
Figure 19.
The variation interval of water requirement with the influence of the secondary industry in Inner Mongolia.
Figure 19.
The variation interval of water requirement with the influence of the secondary industry in Inner Mongolia.
Figure 20.
The variation interval of water requirement with the influence of the tertiary industry in Inner Mongolia.
Figure 20.
The variation interval of water requirement with the influence of the tertiary industry in Inner Mongolia.
Figure 21.
The variation interval of water requirement with the influence of population in Inner Mongolia.
Figure 21.
The variation interval of water requirement with the influence of population in Inner Mongolia.
Table 1.
Social and economic index.
Table 1.
Social and economic index.
| Index | Unit |
|---|
| AVPI | 100 million Yuan |
| AVSI | 100 million Yuan |
| AVTI | 100 million Yuan |
| YEP | 10,000 people |
| Water requirement | 100 million m3 |
Table 2.
The related data in Beijing.
Table 2.
The related data in Beijing.
| Year | AVPI | AVSI | AVTI | YEP | Water Requirement |
|---|
| 2016 | 129.79 | 4944.44 | 20,594.9 | 2195 | 38.8 |
| 2017 | 120.42 | 5326.76 | 22,567.76 | 2194 | 39.5 |
| 2018 | 118.69 | 5647.65 | 24,553.64 | 2192 | 39.3 |
| 2019 | 113.69 | 5715.06 | 29,542.53 | 2190 | 41.7 |
| 2020 | 107.61 | 5716.37 | 30,278.57 | 2189 | 40.6 |
| 2021 | 111.34 | 7268.60 | 32,889.61 | 2189 | 40.8 |
Table 3.
The related data in Tianjin.
Table 3.
The related data in Tianjin.
| Year | AVPI | AVSI | AVTI | YEP | Water Requirement |
|---|
| 2016 | 220.22 | 7571.35 | 10,093.82 | 1443 | 27.2 |
| 2017 | 168.96 | 7593.59 | 10,786.64 | 1410 | 27.5 |
| 2018 | 172.71 | 7609.81 | 11,027.12 | 1383 | 28.4 |
| 2019 | 185.23 | 4969.18 | 8949.87 | 1385 | 28.4 |
| 2020 | 210.18 | 4804.08 | 9069.47 | 1387 | 27.8 |
| 2021 | 225.41 | 5854.27 | 9615.37 | 1373 | 32.3 |
Table 4.
Related data in Hebei Province.
Table 4.
Related data in Hebei Province.
| Year | AVPI | AVSI | AVTI | YEP | Water Requirement |
|---|
| 2016 | 3492.81 | 15,256.93 | 13,320.71 | 7375 | 182.6 |
| 2017 | 3129.98 | 15,846.21 | 15,040.13 | 7409 | 181.6 |
| 2018 | 3338 | 16,040.06 | 16,632.21 | 7426 | 182.4 |
| 2019 | 3518.44 | 13,597.26 | 17,988.82 | 7447 | 182.3 |
| 2020 | 3880.14 | 13,597.2 | 18,729.54 | 7464 | 182.8 |
| 2021 | 4030.3 | 16,364.2 | 19,996.7 | 7448 | 181.9 |
Table 5.
The related data in Shanxi Province.
Table 5.
The related data in Shanxi Province.
| Year | AVPI | AVSI | AVTI | YEP | Water Requirement |
|---|
| 2016 | 784.78 | 5028.99 | 7236.64 | 3514 | 75.5 |
| 2017 | 719.16 | 6778.89 | 8030.37 | 3510 | 74.9 |
| 2018 | 760.64 | 7089.19 | 8988.28 | 3502 | 74.3 |
| 2019 | 824.72 | 7453.09 | 8748.87 | 3497 | 76.0 |
| 2020 | 946.68 | 7675.44 | 9029.81 | 3490 | 72.8 |
| 2021 | 1286.9 | 11,213.1 | 10,090.2 | 3480 | 72.6 |
Table 6.
The related data in Inner Mongolia autonomous region.
Table 6.
The related data in Inner Mongolia autonomous region.
| Year | AVPI | AVSI | AVTI | YEP | Water Requirement |
|---|
| 2016 | 1637.39 | 5579.77 | 7937.08 | 2436 | 190.3 |
| 2017 | 1649.77 | 5874.25 | 8046.76 | 2433 | 188.0 |
| 2018 | 1753.82 | 6335.38 | 8728.10 | 2422 | 192.1 |
| 2019 | 1863.19 | 6763.14 | 8728.1 | 2415 | 190.9 |
| 2020 | 2025.12 | 6908.17 | 8466.66 | 2403 | 194.4 |
| 2021 | 2225.2 | 9374.19 | 8914.8 | 2400 | 191.7 |
Table 7.
The fitted value and the real value of water requirement.
Table 7.
The fitted value and the real value of water requirement.
| Year | The Real Value | The Fitted Value |
|---|
| 2016 | 38.8 | 38.8 |
| 2017 | 39.5 | 39.1 |
| 2018 | 39.3 | 40.0 |
| 2019 | 41.7 | 40.7 |
| 2020 | 40.6 | 41.5 |
| MAPE | 1.5% |
| 2021 | 40.8 | 42.3 |
| MAPE | 3.7% |
Table 8.
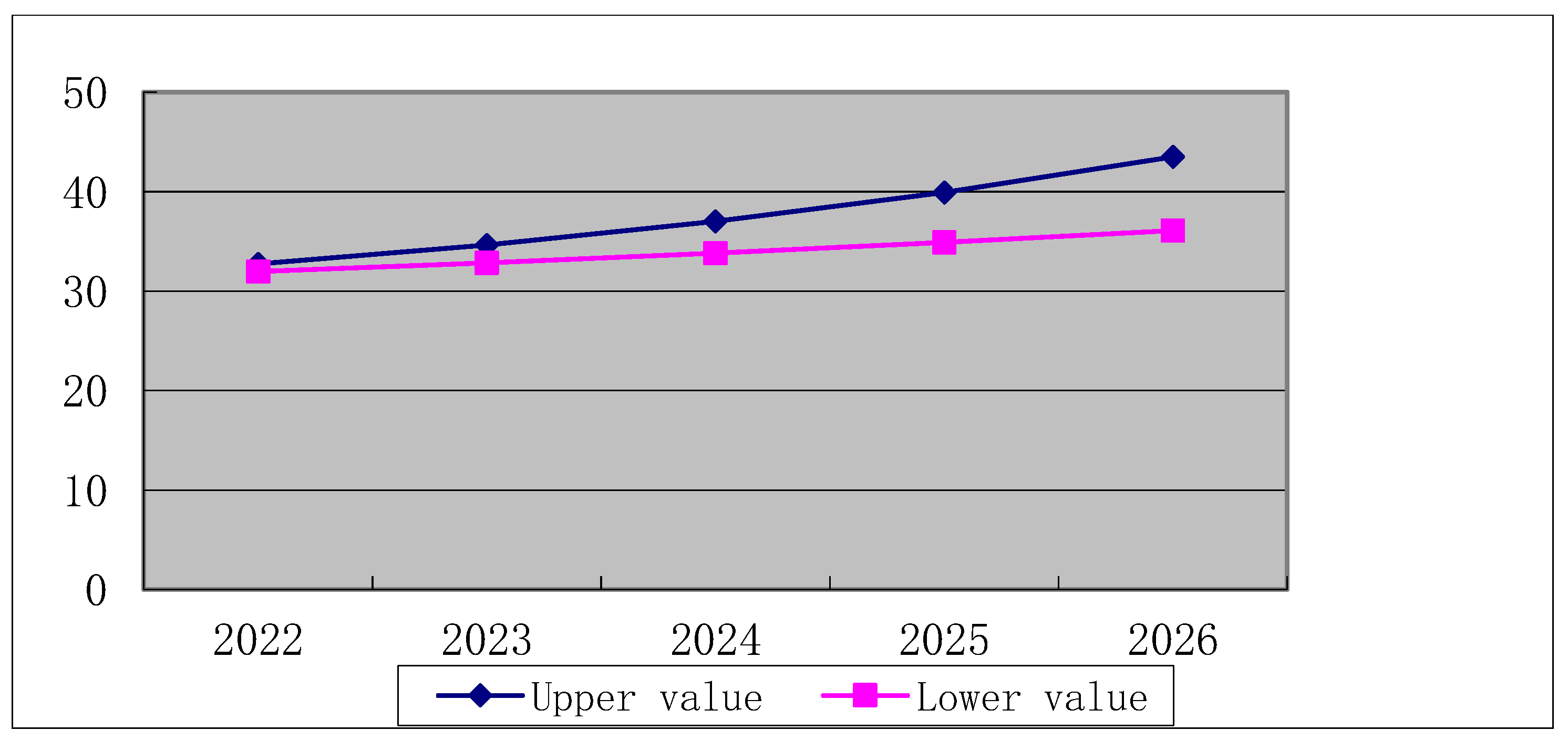
Prediction results of water requirement with different growth rates of AVPI in Beijing.
Table 8.
Prediction results of water requirement with different growth rates of AVPI in Beijing.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −2% | 40.47 | 40.10 | 39.39 | 38.30 | 36.77 |
| 1% | 40.97 | 41.27 | 41.70 | 42.25 | 42.94 |
Table 9.
Prediction results of water requirement with different growth rates of AVSI in Beijing.
Table 9.
Prediction results of water requirement with different growth rates of AVSI in Beijing.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 40.14 | 39.63 | 39.24 | 38.96 | 38.76 |
| 3% | 41.07 | 41.26 | 41.41 | 41.54 | 41.64 |
Table 10.
Prediction results of water requirement with different growth rates of AVTI in Beijing.
Table 10.
Prediction results of water requirement with different growth rates of AVTI in Beijing.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 40.23 | 39.84 | 39.46 | 39.06 | 38.66 |
| 9% | 38.94 | 39.11 | 39.30 | 39.50 | 39.73 |
Table 11.
Prediction results of water requirement with different growth rates of YEP in Beijing.
Table 11.
Prediction results of water requirement with different growth rates of YEP in Beijing.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 40.47 | 40.20 | 39.74 | 39.17 | 38.53 |
| 1% | 40.71 | 41.08 | 41.52 | 42.01 | 42.52 |
Table 12.
Prediction result of water requirement with different growth rates of AVPI in Tianjin.
Table 12.
Prediction result of water requirement with different growth rates of AVPI in Tianjin.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| 1% | 30.13 | 30.53 | 30.77 | 30.97 | 31.16 |
| 2% | 30.82 | 31.47 | 31.96 | 32.40 | 32.82 |
Table 13.
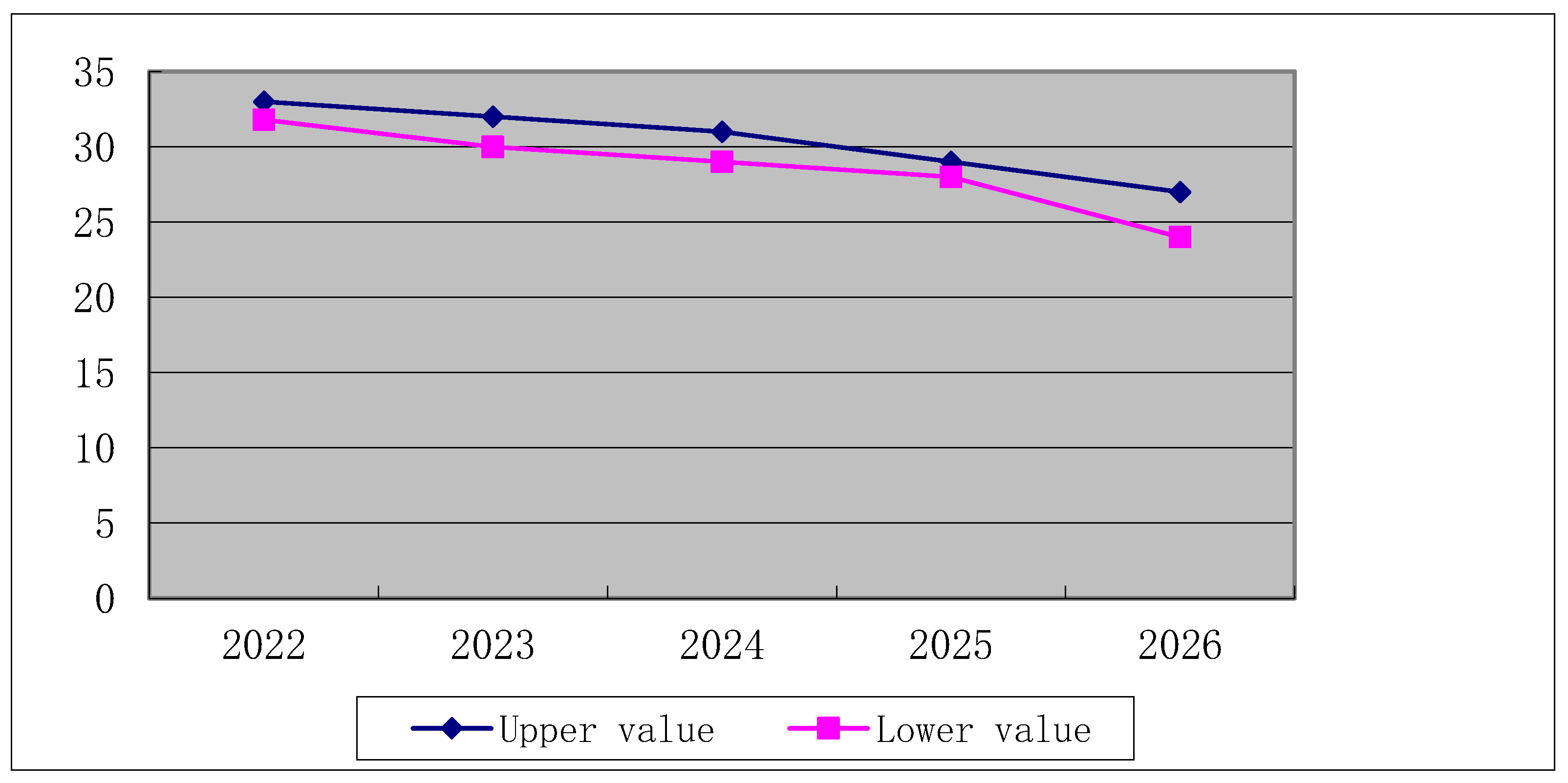
Prediction result of water requirement with different growth rates of AVSI in Tianjin.
Table 13.
Prediction result of water requirement with different growth rates of AVSI in Tianjin.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −6% | 24.43 | 23.60 | 22.45 | 20.78 | 18.26 |
| −4% | 24.99 | 24.43 | 23.66 | 22.55 | 20.90 |
Table 14.
Prediction result of water requirement with different growth rates of AVTI in Tianjin.
Table 14.
Prediction result of water requirement with different growth rates of AVTI in Tianjin.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −2% | 25.15 | 24.75 | 24.30 | 23.74 | 23.02 |
| 1% | 31.87 | 32.34 | 32.63 | 32.77 | 32.78 |
Table 15.
Prediction result of water requirement with different growth rates of YEP in Tianjin.
Table 15.
Prediction result of water requirement with different growth rates of YEP in Tianjin.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 12.13 | 13.14 | 14.14 | 15.13 | 16.11 |
| 1% | 33.40 | 37.63 | 41.09 | 43.13 | 42.58 |
Table 16.
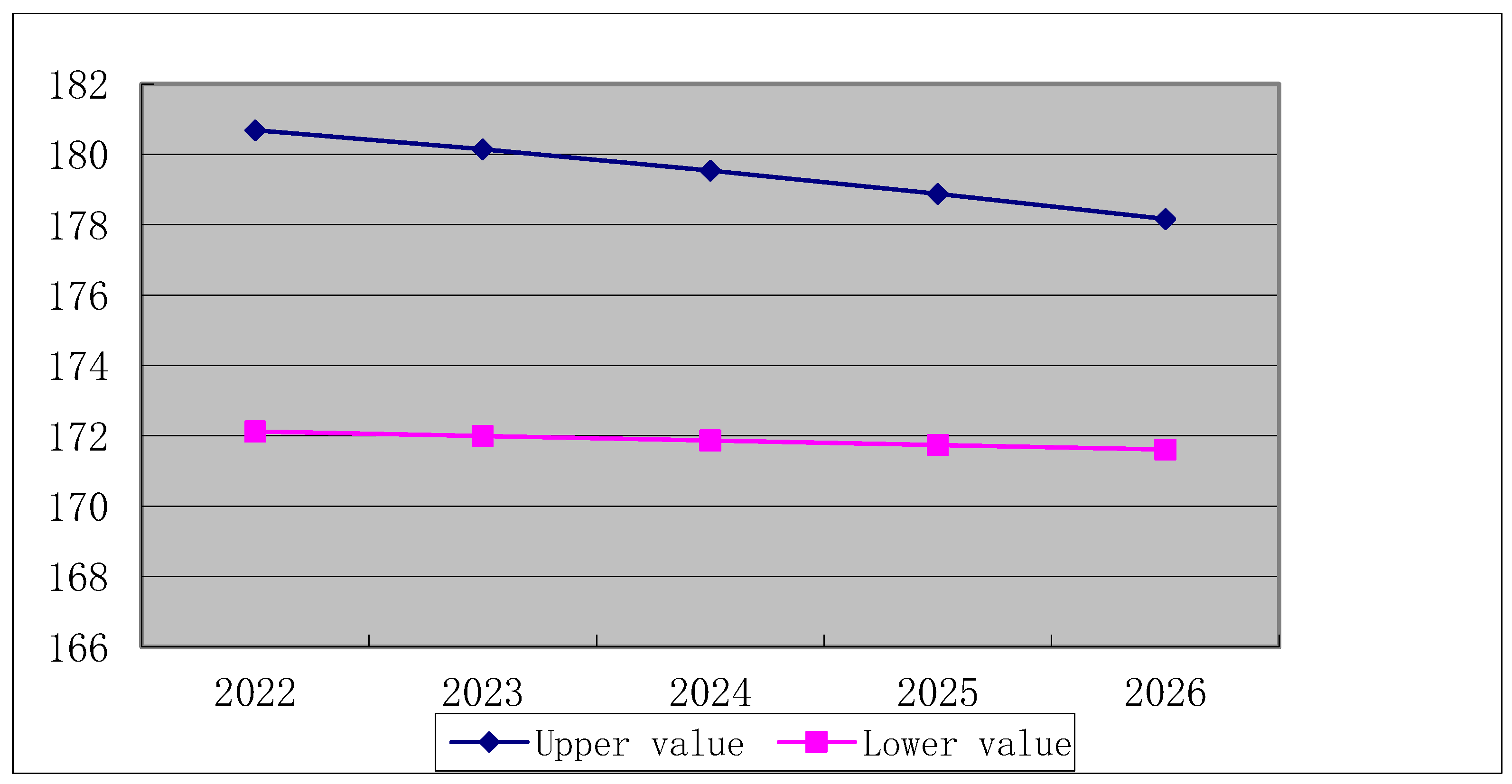
Prediction result of water requirement with different growth rates of AVPI in Hebei Province.
Table 16.
Prediction result of water requirement with different growth rates of AVPI in Hebei Province.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 178.47 | 177.00 | 175.28 | 173.24 | 170.80 |
| 1% | 187.16 | 188.46 | 190.21 | 192.60 | 195.90 |
Table 17.
Prediction result of water requirement with different growth rates of AVSI in Hebei Province.
Table 17.
Prediction result of water requirement with different growth rates of AVSI in Hebei Province.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 177.85 | 176.92 | 175.43 | 173.23 | 170.14 |
| 1% | 182.17 | 182.86 | 183.69 | 184.70 | 185.91 |
Table 18.
Prediction result of water requirement with different growth rates of AVTI in Hebei Province.
Table 18.
Prediction result of water requirement with different growth rates of AVTI in Hebei Province.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| 7% | 199.65 | 207.64 | 219.16 | 236.13 | 261.55 |
| 9% | 204.43 | 215.53 | 231.95 | 256.73 | 294.72 |
Table 19.
Prediction result of water requirement with different growth rates of YEP in Hebei Province.
Table 19.
Prediction result of water requirement with different growth rates of YEP in Hebei Province.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| 1% | 191.82 | 195.23 | 197.67 | 198.40 | 196.12 |
| 2% | 200.20 | 207.13 | 212.64 | 215.33 | 212.63 |
Table 20.
Prediction result of water requirement with different growth rates of AVPI in Shanxi Province.
Table 20.
Prediction result of water requirement with different growth rates of AVPI in Shanxi Province.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 69.67 | 68.74 | 68.27 | 68.06 | 68.00 |
| 5% | 79.19 | 82.75 | 88.68 | 98.53 | 114.86 |
Table 21.
Prediction result of water requirement with different growth rates of AVSI in Shanxi Province.
Table 21.
Prediction result of water requirement with different growth rates of AVSI in Shanxi Province.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 68.93 | 68.05 | 67.71 | 67.62 | 67.66 |
| 10% | 80.77 | 86.16 | 95.51 | 111.65 | 139.36 |
Table 22.
Prediction result of water requirement with different growth rates of AVTI in Shanxi Province.
Table 22.
Prediction result of water requirement with different growth rates of AVTI in Shanxi Province.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 70.33 | 69.36 | 68.88 | 68.71 | 68.75 |
| 5% | 77.53 | 79.90 | 83.87 | 90.43 | 101.19 |
Table 23.
Prediction result of water requirement with different growth rates of YEP in Shanxi Province.
Table 23.
Prediction result of water requirement with different growth rates of YEP in Shanxi Province.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 68.58 | 66.02 | 61.96 | 54.68 | 40.45 |
| 1% | 75.70 | 76.87 | 77.86 | 78.43 | 78.08 |
Table 24.
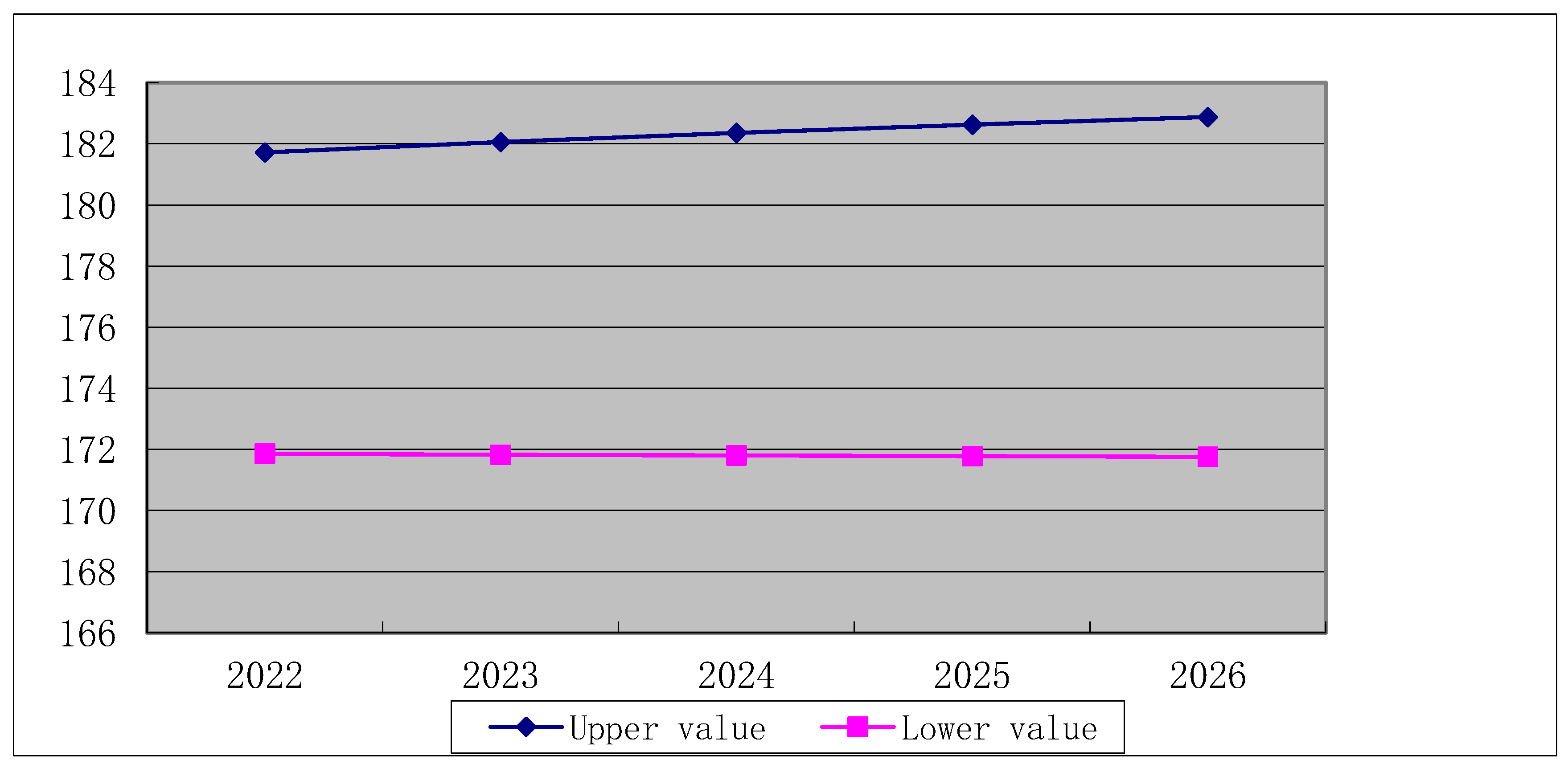
Prediction result of water requirement with different growth rates of AVPI in Inner Mongolia.
Table 24.
Prediction result of water requirement with different growth rates of AVPI in Inner Mongolia.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 190.02 | 188.25 | 186.69 | 185.33 | 184.18 |
| 5% | 210.65 | 214.97 | 219.65 | 224.81 | 230.64 |
Table 25.
Prediction result of water requirement with different growth rates of AVSI in Inner Mongolia.
Table 25.
Prediction result of water requirement with different growth rates of AVSI in Inner Mongolia.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −2% | 185.90 | 180.65 | 175.93 | 171.74 | 168.05 |
| −1% | 187.55 | 183.82 | 180.50 | 177.56 | 174.97 |
Table 26.
Prediction result of water requirement with different growth rates of AVTI in Inner Mongolia.
Table 26.
Prediction result of water requirement with different growth rates of AVTI in Inner Mongolia.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| 1% | 210.85 | 214.40 | 217.97 | 221.53 | 225.09 |
| 3% | 210.47 | 216.93 | 224.74 | 234.65 | 247.80 |
Table 27.
Prediction result of water requirement with different growth rates of YEP in Inner Mongolia.
Table 27.
Prediction result of water requirement with different growth rates of YEP in Inner Mongolia.
| Year | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|
| −1% | 188.33 | 186.84 | 184.83 | 182.55 | 180.13 |
| 1% | 189.73 | 191.43 | 193.70 | 196.29 | 199.09 |