Transport of Thiophanate Methyl in Porous Media in the Presence of Titanium Dioxide Nanoparticles
Abstract
:1. Introduction
2. Materials and Methods
3. Mathematical Modeling
3.1. Governing Partial Differential Equations
3.2. The Fitting Process
3.3. Additional Theoretical Calculations
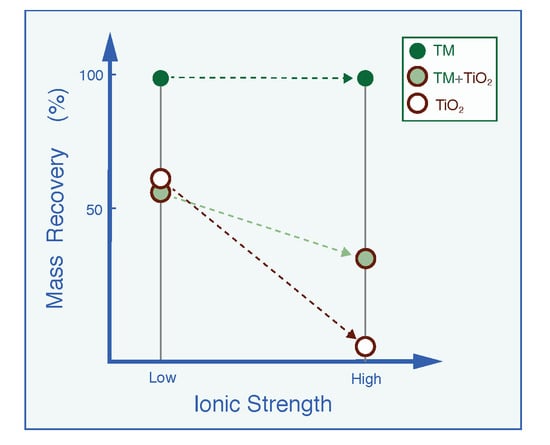
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| aqueous phase concentration, M/L3 | |
| aqueous phase concentration of suspended nanoparticles, Mn/L3. | |
| concentration of nanoparticles attached onto the solid matrix, Mn/Msm. | |
| aqueous phase solute concentration, Ms/L3. | |
| concentration of solutes sorbed onto the solid matrix, Ms/Msm. | |
| concentration of suspended solute-nanoparticle complex, Ms/Mn. | |
| concentration of solute-nanoparticle complex attached onto the solid matrix, Ms/Mn. | |
| concentration of nanoparticles irreversibly attached onto the solid matrix, Mn/Msm. | |
| concentration of nanoparticles reversibly attached onto the solid matrix, Mn/Msm. | |
| initial aqueous phase solute concentration, Ms/L | |
| dH | hydrodynamic diameter, L |
| Di | hydrodynamic dispersion coefficient of species i, L2/t. |
| Fi | general form of the source configuration of species i, Mi/L3t. |
| Gi(t) | mass release function of species i (point source), Mi/t. |
| Is | ionic strength, mM |
| rate of irreversible solute-nanoparticle complex attachment onto the solid matrix, 1/t | |
| L | length, L. |
| m0 | zeroth absolute temporal moment, tM/L3 |
| Mn | mass of nanoparticles, Mn. |
| Msm | mass of the solid matrix, Msm. |
| Ms | mass of solutes, Ms. |
| Mr | ratio of recovered mass, [-] |
| rate of irreversible nanoparticle attachment onto the solid matrix, 1/t. | |
| rate of reversible nanoparticle attachment onto the solid matrix, 1/t. | |
| rate of reversible nanoparticle detachment from the solid matrix, 1/t. | |
| rate of irreversible solute sorption onto the solid matrix, 1/t. | |
| rate of reversible solute sorption onto the solid matrix, 1/t. | |
| rate of reversible solute desorption from the solid matrix, 1/t. | |
| rate of solute sorption onto suspended nanoparticles, L6/Mn2t. | |
| rate of solute desorption from suspended nanoparticles, 1/t. | |
| rate of solute sorption onto nanoparticles already attached onto the solid matrix, L3Msm/Mn2t. | |
| rate of solute-nanoparticle complex attachment onto the solid matrix,1/t. | |
| rate of solute desorption from suspended nanoparticles, 1/t. | |
| rate of solute-nanoparticle complex detachment from the solid matrix, 1/t. | |
| t | time, t. |
| tp | source duration time period, t. |
| U | interstitial velocity, L/t. |
| W | characterizes the source physical geometry (point source), 1/L3. |
| x | Cartesian coordinate, L. |
| Greek Letters | |
| Θ | porosity, (L3 voids)/(L3 solid matrix). |
| ζ | zeta potential, V |
| ρ | bulk density of the solid matrix, Msm/L3 |
References
- Yadav, H.; Kumar, R.; Sankhla, M.S. Residues of pesticides and heavy metals in crops resulting in toxic effects on living organism. J. Seybold Rep. 2020, 15, 1527–1541. [Google Scholar]
- Berg, H.; Tam, N.T. Decreased use of pesticides for increased yields of rice and fish-options for sustainable food production in the Mekong Delta. Sci. Total Environ. 2018, 619–620, 319–327. [Google Scholar] [CrossRef]
- Albaseer, S.S. Factors controlling the fate of pyrethroids residues during post-harvest processing of raw agricultural crops: An overview. Food Chem. 2019, 295, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Malandrakis, A.A.; Kavroulakis, N.; Chrysikopoulos, C.V. Metal nanoparticles against fungicide resistance: Alternatives or partners? Pest Manag. Sci. 2022, 78, 3953–3956. [Google Scholar] [CrossRef]
- Pignati, W.A.; Lima, F.A.N.S.E.; Lara, S.S.; Correa, M.L.M.; Barbosa, J.R.; Leão, L.H.D.C.; Pignatti, M.G. Spatial distribution of pesticide use in Brazil: A strategy for health surveillance. Ciênc. Saúde Coletiva 2017, 22, 3281–3293. [Google Scholar] [CrossRef]
- Jiang, W.; Luo, Y.; Conkle, J.L.; Li, J.; Gan, J. Pesticides on residential outdoor surfaces: Environmental impacts and aquatic toxicity. Pest Manag. Sci. 2016, 72, 1411–1420. [Google Scholar] [CrossRef]
- Nordborg, M.; Davis, J.; Cederberg, C.; Woodhouse, A. Freshwater ecotoxicity impacts from pesticide use in animal and vegetable foods produced in Sweden. Sci. Total Environ. 2017, 581–582, 448–459. [Google Scholar] [CrossRef] [Green Version]
- Anderson, S.E.; Meade, B.J. Potential health effects associated with dermal exposure to occupational chemicals. Environ. Health Insights 2014, 8, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Kapka-Skrzypczak, L.; Cyranka, M.; Skrzypczak, M.; Kruszewski, M. Biomonitoring and biomarkers of organophosphate pesticides exposure—state of the art. Ann. Agric. Environ. Med. 2011, 18, 294–303. [Google Scholar] [PubMed]
- Nowack, B.; Bucheli, T.D. Occurrence, behavior and effects of nanoparticles in the environment. Environ. Pollut. 2007, 150, 5–22. [Google Scholar] [CrossRef]
- Sellers, K.; Mackay, C.; Bergeson, L.L.; Clough, S.R.; Hoyt, M.; Chen, J.; Henry, K.; Hamblen, J. Nanotechnology and the Environment; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Hardman, R. A toxicologic review of quantum dots: Toxicity depends on physicochemical and environmental factors. Environ. Health Perspect. 2005, 114, 165–172. [Google Scholar] [CrossRef]
- Nel, A.; Xia, T.; Mädler, L.; Li, N. Toxic potential of materials at the nano level. Science 2006, 311, 622–627. [Google Scholar] [CrossRef] [Green Version]
- Buzea, C.; Pacheco, I.I.; Robbie, K. Nanomaterials and Nanoparticles: Sources and Toxicity. Biointerphases 2007, 2, MR17–MR71. [Google Scholar] [CrossRef] [Green Version]
- Syngouna, V.I.; Chrysikopoulos, C.V.; Kokkinos, P.; Tselepi, M.A.; Vantarakis, A. Cotransport of human adenoviruses with clay colloids and TiO2 nanoparticles in saturated porous media: Effect of flow velocity. Sci. Total Environ. 2017, 598, 160–167. [Google Scholar] [CrossRef]
- Hendren, C.O.; Mesnard, X.; Droge, J.; Wiesner, M.R. Estimating production data for five engineered nanomaterials as a basis for exposure assessment. Environ. Sci. Technol. 2011, 45, 2562–2569. [Google Scholar] [CrossRef] [PubMed]
- Maurer-Jones, M.A.; Gunsolus, I.L.; Murphy, C.J.; Haynes, C.L. Toxicity of engineered nanoparticles in the environment. Anal. Chem. 2013, 85, 3036–3049. [Google Scholar] [CrossRef] [Green Version]
- Sygouni, V.; Chrysikopoulos, C.V. Characterization of TiO2 nanoparticle suspensions in aqueous solutions and TiO2 nanoparticle retention in water saturated columns packed with glass beads. Chem. Eng. J. 2015, 262, 823–830. [Google Scholar] [CrossRef]
- Musial, J.; Krakowiak, R.; Mlynarczyk, D.T.; Goslinski, T.; Stanisz, B.J. Titanium dioxide nanoparticles in food and personal care products—What do we know about their safety? Nanomaterials 2020, 10, 1110. [Google Scholar] [CrossRef] [PubMed]
- Ye, C.L.; Zhou, Q.X.; Wang, X.M. Determination of thiophanate-methyl and chlorotoluron in water samples by improved single-drop microextraction coupled with high-performance liquid chromatography. Internat. J. Environ. Anal. Chem. 2008, 88, 461–471. [Google Scholar] [CrossRef]
- WHO (World Health Organization). The WHO Recommended Classification of Pesticides by Hazard and Guidelines to Classification; WHO: Geneva, Switzerland, 2009. [Google Scholar]
- De Falco, M.; Sciarrillo, R.; Capaldo, A.; Russo, T.; Gay, F.; Valiante, S.; Varano, L.; Laforgia, V. The effects of the fungicide methyl thiophanate on adrenal gland morphophysiology of the lizard, Podarcis sicula. Arch. Environ. Contam. 2007, 53, 241–248. [Google Scholar] [CrossRef]
- Ibtissem, B.A.; Hajer, B.S.; Ahmed, H.; Awatef, E.; Choumous, K.; Ons, B.; Mounir, Z.K.; Najiba, Z. Oxidative stress and histopathological changes induced by methylthiophanate, a systemic fungicide, in blood, liver and kidney of adult rats. Afr. Health Sci. 2017, 17, 154–163. [Google Scholar] [CrossRef] [Green Version]
- Cosgrove, S.; Jefferson, B.; Jarvis, P. Pesticide removal from drinking water sources by adsorption: A review. Environ. Technol. Rev. 2019, 8, 1–24. [Google Scholar] [CrossRef]
- Mojiri, A.; Kazeroon, R.A.; Gholami, A. Cross-Linked magnetic chitosan/activated biochar for removal of emerging micropollutants from water: Optimization by the artificial neural network. Water 2019, 11, 551. [Google Scholar] [CrossRef] [Green Version]
- Shamsollahi, Z.; Partovinia, A. Recent advances on pollutants removal by rice husk as a bio-based adsorbent: A critical review. J. Environ. Manag. 2019, 246, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Yagub, M.T.; Sen, T.K.; Afroze, S.; Ang, H.M. Dye and its removal from aqueous solution by adsorption: A review. Adv. Colloid Interface Sci. 2014, 209, 172–184. [Google Scholar] [CrossRef] [PubMed]
- Sadon, F.N.; Ibrahem, A.S.; Ismail, K.N. An overview of rice husk applications and modification techniques in wastewater treatment. J. Purity Util. React. Environ. 2012, 1, 308–334. [Google Scholar]
- Firozjaee, T.T.; Mehrdadi, N.; Baghdadi, M.; Bidhendi, G.R.N. Application of nanotechnology in pesticides removal from aqueous solutions—A review. Int. J. Nanosci. Nanotechnol. 2018, 14, 43–56. [Google Scholar]
- Kajitvichyanukul, P.; Nguyen, V.-H.; Boonupara, T.; Phan Thi, L.-A.; Watcharenwong, A.; Sumitsawan, S.; Udomkun, P. Challenges and effectiveness of nanotechnology-based photocatalysis for pesticides-contaminated water: A review. Environ. Res. 2022, 212, 113336. [Google Scholar] [CrossRef] [PubMed]
- Zeshan, M.; Bhatti, I.A.; Mohsin, M.; Iqbal, M.; Amjed, N.; Nisar, J.; AlMasoud, N.; Alomar, T.S. Remediation of pesticides using TiO2 based photocatalytic strategies: A review. Chemosphere 2022, 300, 134525. [Google Scholar] [CrossRef]
- National Center for Biotechnology Information. PubChem Compound Summary for CID 3032791, Thiophanate-methyl. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/3032791#section=2D-Structure&fullscreen=true (accessed on 14 March 2023).
- Chrysikopoulos, C.V.; Aravantinou, A.F. Virus inactivation in the presence of quartz sand under static and dynamic batch conditions at different temperatures. J. Hazard. Mater. 2012, 233–234, 148–157. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Syngouna, V.I.; Vasiliadou, I.A.; Katzourakis, V.E. Transport of Pseudomonas putida in a three-dimensional bench scale experimental aquifer. Transp. Porous Media 2012, 94, 617–642. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Syngouna, V.I. Effect of gravity on colloid transport through water-saturated columns packed with glass beads: Modeling and experiments. Environ. Sci. Technol. 2014, 48, 6805–6813. [Google Scholar] [CrossRef]
- Lewis, J.; Sjöstrom, J. Optimizing the experimental design of soil columns in saturated and unsaturated transport experiments. J. Contam. Hydrol. 2010, 115, 1–13. [Google Scholar] [CrossRef]
- Syngouna, V.I.; Chrysikopoulos, C.V. Transport of biocolloids in water saturated columns packed with sand: Effect of grainsize and pore water velocity. J. Contamin. Hydrol. 2011, 126, 301–314. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Sotirelis, N.P.; Kallithrakas-Kontos, N.G. Cotransport of graphene oxide nanoparticles and kaolinite colloids in porous media. Transp. Porous Media 2017, 119, 181–202. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Modeling dense-colloid and virus cotransport in three-dimensional porous media. J. Contam. Hydrol. 2015, 181, 102–113. [Google Scholar] [CrossRef] [PubMed]
- Sim, Y.; Chrysikopoulos, C.V. Three-dimensional analytical models for virus transport in saturated porous media. Transp. Porous Media 1998, 30, 87–112. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Mathematical modeling of colloid and virus cotransport in porous media: Application to experimental data. Adv. Water Resour. 2014, 68, 62–73. [Google Scholar] [CrossRef]
- Sim, Y.; Chrysikopoulos, C.V. Analytical solutions for solute transport in saturated porous media with semi-infinite or finite thickness. Adv. Water Resour. 1999, 22, 507–519. [Google Scholar] [CrossRef]
- Compere, F.; Porel, G.; Delay, F. Transport and retention of clay particles in saturated porous media. Influence of ionic strength and pore velocity. J. Contam. Hydrol. 2001, 49, 1–21. [Google Scholar] [CrossRef]
- Abdel-Salam, A.; Chrysikopoulos, C.V. Analytical solutions for one-dimensional colloid transport in saturated fractures. Adv. Water Resour. 1994, 17, 283–296. [Google Scholar] [CrossRef]
- Abdel-Salam, A.; Chrysikopoulos, C.V. Modeling of colloid and colloid-facilitated contaminant transport in a two-dimensional fracture with spatially variable aperture. Transp. Porous Media 1995, 20, 197–221. [Google Scholar] [CrossRef]
- Bekhit, H.M.; El-Kordy, M.A.; Hassan, A.E. Contaminant transport in groundwater in the presence of colloids and bacteria: Model development and verification. J. Contam. Hydrol. 2009, 108, 152–167. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Fitting the transport and attachment of dense biocolloids in one-dimensional porous media: ColloidFit. Groundwater 2017, 55, 156–159. [Google Scholar] [CrossRef] [PubMed]
- Doherty, J. PEST: Software for Model-Independent Parameter Estimation; Watermark Numerical Computing: Brisbane, Australia, 2005. [Google Scholar]
- Flores, F.M.; Undabeytia, T.; Jaworski, M.; Morillo, E.; Torres Sánchez, R.M. Organo-montmorillonites as adsorbent materials for thiophanate-methyl removal: Adsorption-desorption studies and technological applications. J. Environ. Chem. Eng. 2020, 8, 103806. [Google Scholar] [CrossRef]
- Wauchope, R.D.; Buttler, T.M.; Hornsby, A.G.; Augustijn-Beckers, P.W.; Burt, J.P. The SCS/ARS/CES pesticide properties database for environmental decision making. Rev. Environ. Contam. Toxicol. 1992, 123, 1–155. [Google Scholar] [PubMed]
- Ter Laak, T.L.; Gebbink, W.A.; Tolls, J. The effect of pH and ionic strength on the sorption of sulfachloropyridazine, tylosin, and oxytetracycline to soil. Environ. Toxicol. Chem. 2006, 25, 904–911. [Google Scholar] [CrossRef]
- Wang, S.; Jin, X.; Bu, Q.; Zhou, X.; Wu, F. Effects of particle size, organic matter and ionic strength on the phosphate sorption in different trophic lake sediments. J. Hazard. Mater. 2006, 128, 95–105. [Google Scholar] [CrossRef]
- Matulova, M.; Urik, M.; Bujdos, M.; Duborska, E.; Cesnek, M.; Miglierini, M.B. Selenite sorption onto goethite: Isotherm and ion-competitive studies, and effect of pH on sorption kinetics. Chem. Pap. 2019, 73, 2975–2985. [Google Scholar] [CrossRef]
- Malandrakis, A.A.; Kavroulakis, N.; Chrysikopoulos, C.V. Zinc nanoparticles: Mode of action and efficacy against boscalid-resistant Alternaria alternata isolates. Sci. Total Environ. 2022, 829, 154638. [Google Scholar] [CrossRef]
- Zheng, M.; Wang, Y.; Wang, C.; Wei, W.; Ma, S.; Sun, X.; He, J. Silver nanoparticlesbased colorimetric array for the detection of Thiophanate-methyl. Spectrochim. Acta–Part A Mol. Biomol. Spectrosc. 2018, 198, 315–321. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Modeling the transport of aggregating nanoparticles in porous media. Water Resour. Res. 2021, 57, e2020WR027946. [Google Scholar] [CrossRef]
- McBride, M.B. A critique of diffuse double layer model applied to colloid and surface chemistry. Clays Clay Miner. 1997, 45, 598–608. [Google Scholar] [CrossRef]
- Anirudhan, T.S.; Ramachandran, M. Surfactant-modified bentonite as adsorbent for the removal of humic acid from wastewaters. Appl. Clay Sci. 2007, 35, 276–281. [Google Scholar] [CrossRef]
- Fang, J.; Xu, M.-J.; Wang, D.; Wen, B. Modeling the transport of TiO2 nanoparticle aggregates in saturated and unsaturated granular media: Effects of ionic strength and pH. Water Res. 2013, 47, 1399–1408. [Google Scholar] [CrossRef] [PubMed]
- Chrysikopoulos, C.V.; Fountouli, T.V. Cotransport of titanium dioxide nanoparticles and formaldehyde in saturated and unsaturated columns packed with quartz sand. Vadose Zone J. 2023, 22, e20175. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Katzourakis, V.E. Colloid particle size-dependent dispersivity. Water Resour. Res. 2015, 51, 4668–4683. [Google Scholar] [CrossRef]





| Experimental Conditions * | TiO2 | ||
|---|---|---|---|
| pH | Ionic Strength (mM) | ζ (mV) | dH (nm) |
| 3 | - | −25.1 | 315.6 |
| 5 | - | −25.7 | 317.0 |
| 7 | - | −28.0 | 326.6 |
| 10 | - | −42.3 | 567.3 |
| 7.5 | 1 | −36.0 | 389.3 |
| 7.5 | 10 | −41.0 | 278.0 |
| 5.4 | 50 | −29.9 | 386.3 |
| 5.1 | 100 | −27.0 | 1004.4 |
| Experimental Conditions | pH | Ionic Strength (mM) | ||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | 1 | 10 | 50 | 100 | |
| Transport parameter values for TM | ||||||||
| Mr (%) | 99.0 | 100 | 100 | 100 | 97.2 | 95.3 | 99.5 | 99.3 |
| U (cm/min) | 0.53 | 0.54 | 0.54 | 0.54 | 0.53 | 0.54 | 0.55 | 0.54 |
| tp (min) | 240 | 242 | 242 | 234 | 231 | 237 | 239 | 234 |
| θ (-) | 0.38 | 0.38 | 0.39 | 0.38 | 0.38 | 0.37 | 0.37 | 0.38 |
| Ds (cm/min) | 0.26 | 0.24 | 0.29 | 0.30 | 0.22 | 0.23 | 0.27 | 0.29 |
| (1/min) | 0.0055 | 0.0032 | 0.0022 | 0.0019 | 0.0036 | 0.0038 | 0.0058 | 0.0060 |
| (1/min) | 0.0204 | 0.0182 | 0.0136 | 0.0060 | 0.0117 | 0.0136 | 0.0165 | 0.0171 |
| (1/min) | 0.00086 | 0 | 0 | 0 | 0.00037 | 0.00072 | 0.00090 | 0.00094 |
| Cotransport parameter values for TM | ||||||||
| Mr (%) | 92.9 | 95.2 | 98.6 | 90.9 | 57.9 | 54.3 | 34.3 | 31.5 |
| U (cm/min) | 0.54 | 0.53 | 0.54 | 0.54 | 0.54 | 0.55 | 0.54 | 0.53 |
| tp (min) | 231 | 229 | 232 | 237 | 235 | 228 | 222 | 224 |
| θ (-) | 0.37 | 0.38 | 0.38 | 0.38 | 0.38 | 0.37 | 0.38 | 0.38 |
| Ds (cm/min) | 0.26 | 0.24 | 0.29 | 0.30 | 0.22 | 0.23 | 0.27 | 0.29 |
| (L6/Mn2t) | 0.00064 | 0.0020 | 0.0023 | 0.0071 | 0.9000 | 0.2870 | - | - |
| (1/min) | 0.0102 | 0.0296 | 0.0585 | 0.0654 | 0.7300 | 0.1780 | - | - |
| (1/min) | 0.0085 | 0.0004 | 0.0786 | 0.0834 | 0.2820 | 0.0003 | - | - |
| Cotransport parameter values for TiO2 nanoparticles | ||||||||
| Mr (%) | 92.8 | 94.6 | 100 | 100 | 61.5 | 53.3 | 3.29 | 2.81 |
| U (cm/min) | 0.54 | 0.53 | 0.54 | 0.54 | 0.54 | 0.55 | 0.54 | 0.53 |
| tp (min) | 231 | 229 | 232 | 237 | 235 | 228 | 222 | 224 |
| θ (-) | 0.37 | 0.38 | 0.38 | 0.38 | 0.38 | 0.37 | 0.38 | 0.38 |
| Dn (cm/min) | 0.26 | 0.23 | 0.29 | 0.30 | 0.22 | 0.5 | - | - |
| (1/min) | 0.001 | 0.0008 | 0.0004 | 0.0007 | 0.0015 | 0.0044 | - | - |
| (1/min) | 0.0185 | 0.0205 | 0.0111 | 0.0053 | 0.0127 | 0.0257 | - | - |
| (1/min) | 0.0014 | 0.0009 | - | 0.0009 | 0.0089 | 0.0110 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefanarou, A.S.; Katzourakis, V.E.; Fu, F.; Malandrakis, A.A.; Chrysikopoulos, C.V. Transport of Thiophanate Methyl in Porous Media in the Presence of Titanium Dioxide Nanoparticles. Water 2023, 15, 1415. https://doi.org/10.3390/w15071415
Stefanarou AS, Katzourakis VE, Fu F, Malandrakis AA, Chrysikopoulos CV. Transport of Thiophanate Methyl in Porous Media in the Presence of Titanium Dioxide Nanoparticles. Water. 2023; 15(7):1415. https://doi.org/10.3390/w15071415
Chicago/Turabian StyleStefanarou, Anthi S., Vasileios E. Katzourakis, Fenglian Fu, Anastasios A. Malandrakis, and Constantinos V. Chrysikopoulos. 2023. "Transport of Thiophanate Methyl in Porous Media in the Presence of Titanium Dioxide Nanoparticles" Water 15, no. 7: 1415. https://doi.org/10.3390/w15071415