Groundwater Contamination Site Identification Based on Machine Learning: A Case Study of Gas Stations in China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methodology
2.2. Data
2.3. Machine Learning Approach
2.3.1. Models
2.3.2. Input Setting and Feature Importance Analysis
2.3.3. Model Evaluation
3. Results and Discussion
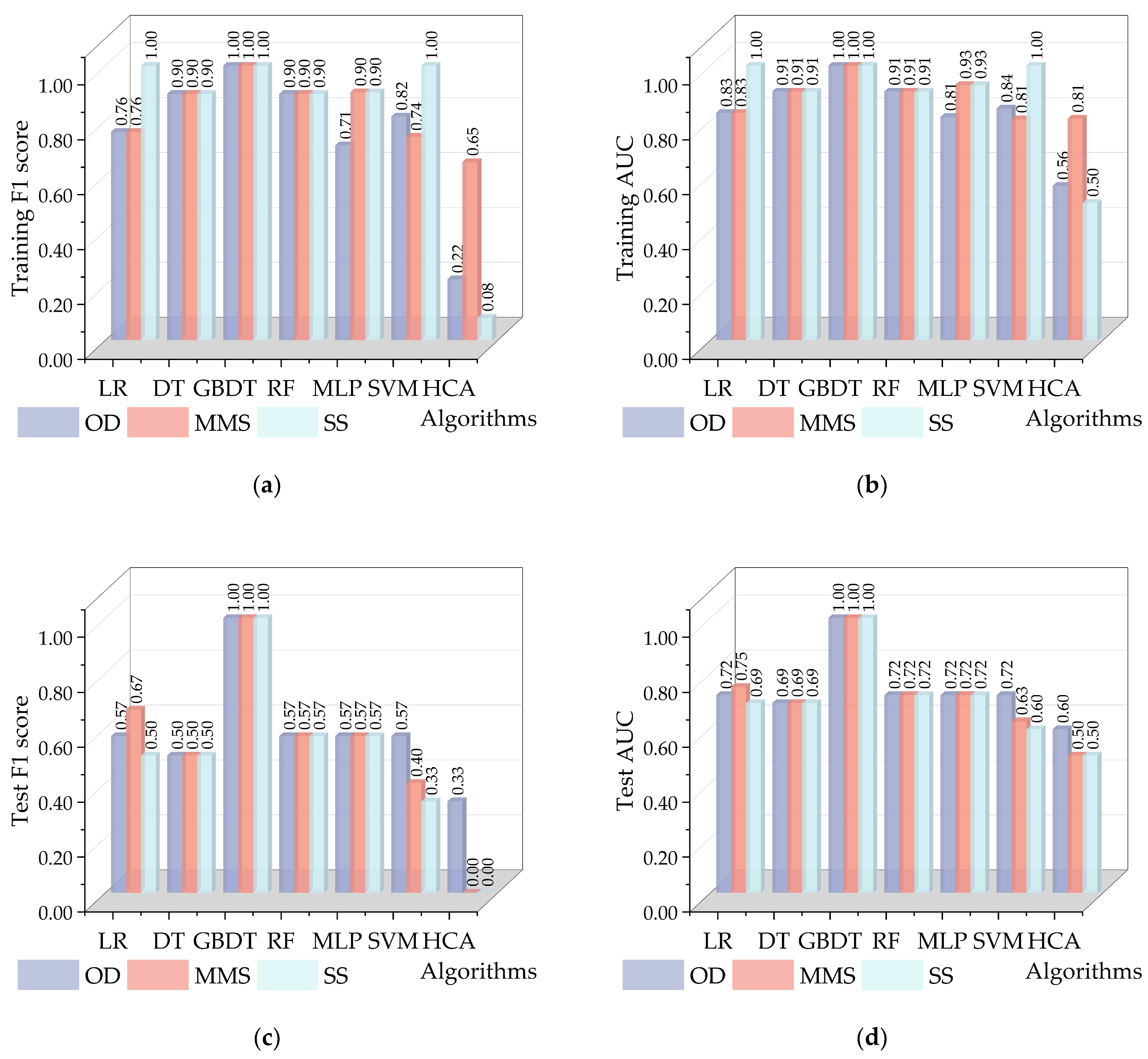
3.1. Performance of Machine Learning Models
3.2. Model Optimization
- Black box function: the cross-validation score of the GBDT algorithm, and the metrics are F1 score and AUC.
- Random search step: 5.
- The number of iterations: 100.
- Range of hyperparameters: see Table 5. The input of hyperparameters to BO can only be float instead of string and integer. Therefore, the criterion of GBDT is set to friedman_mse, which is also the default value of the model.
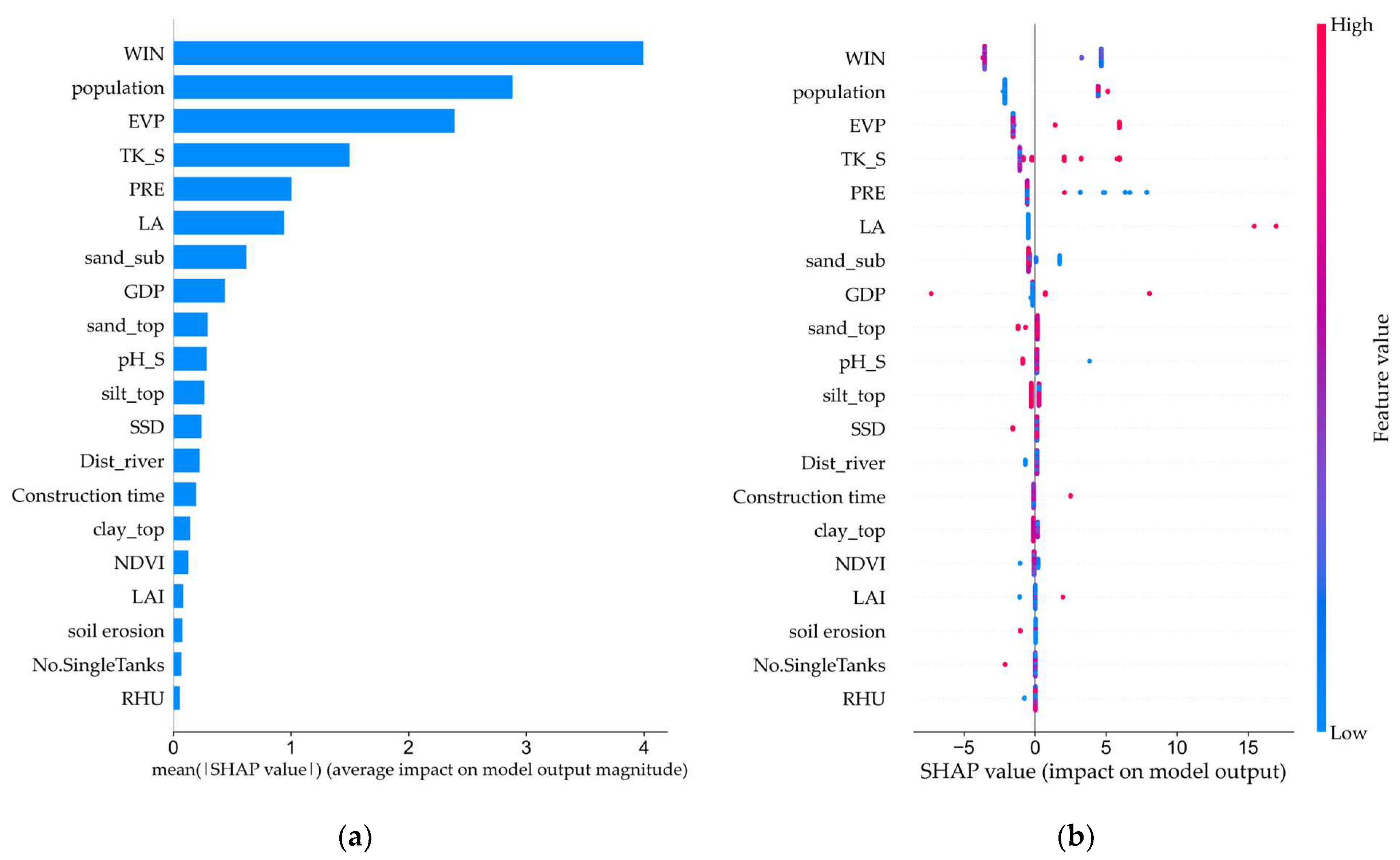
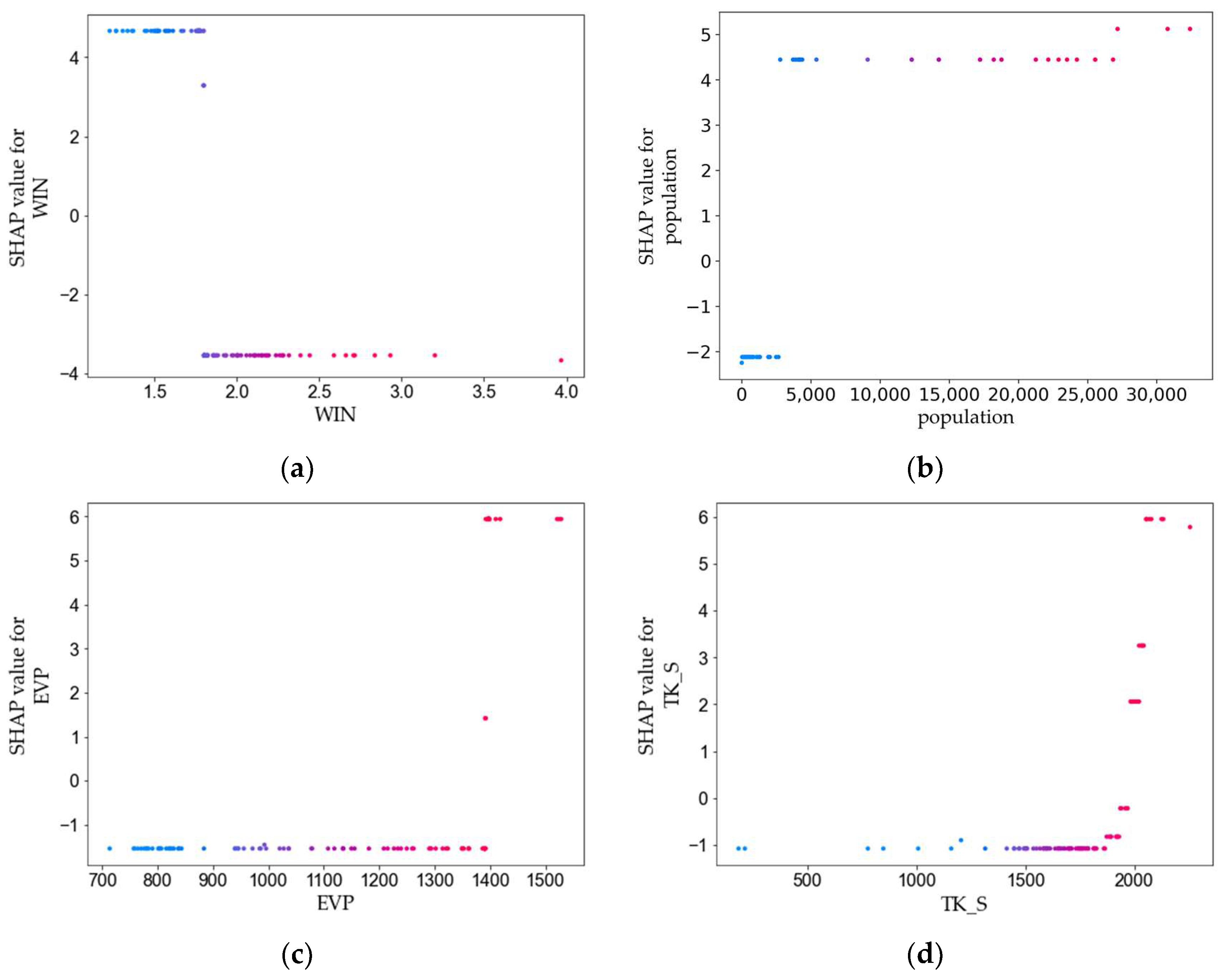
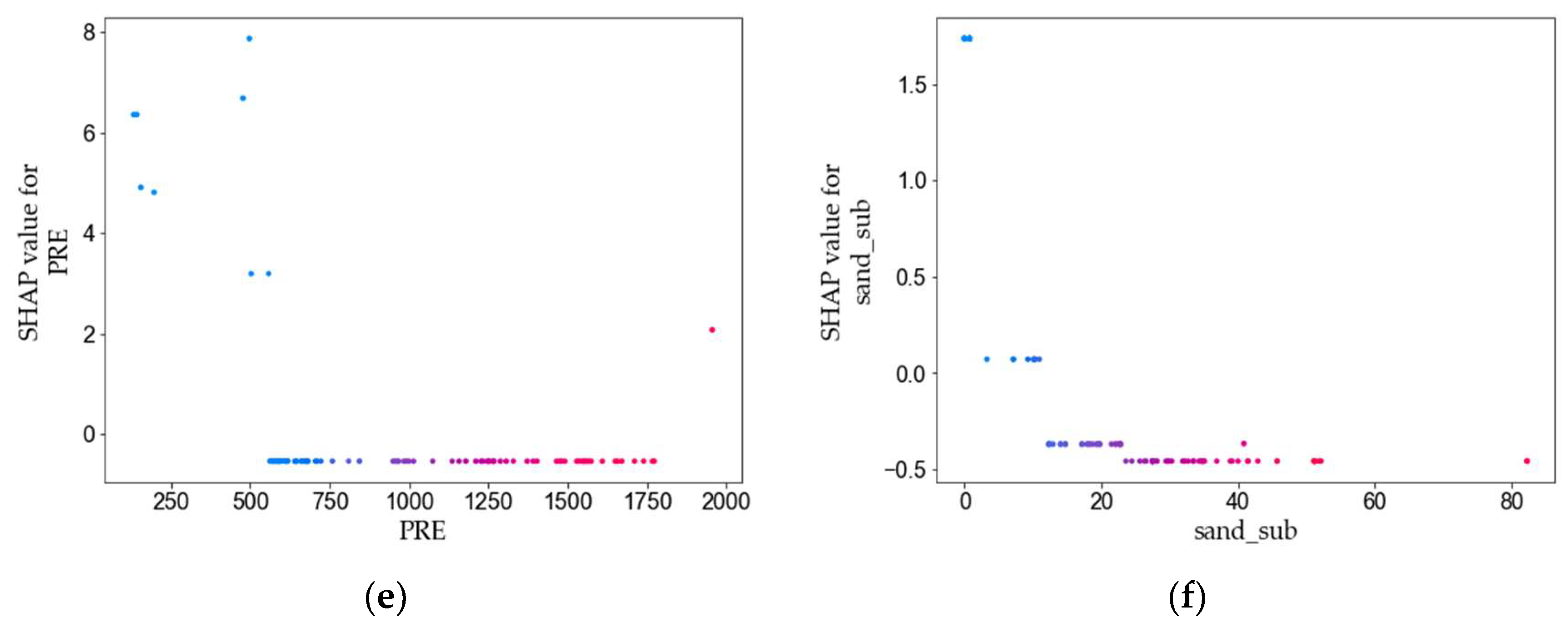
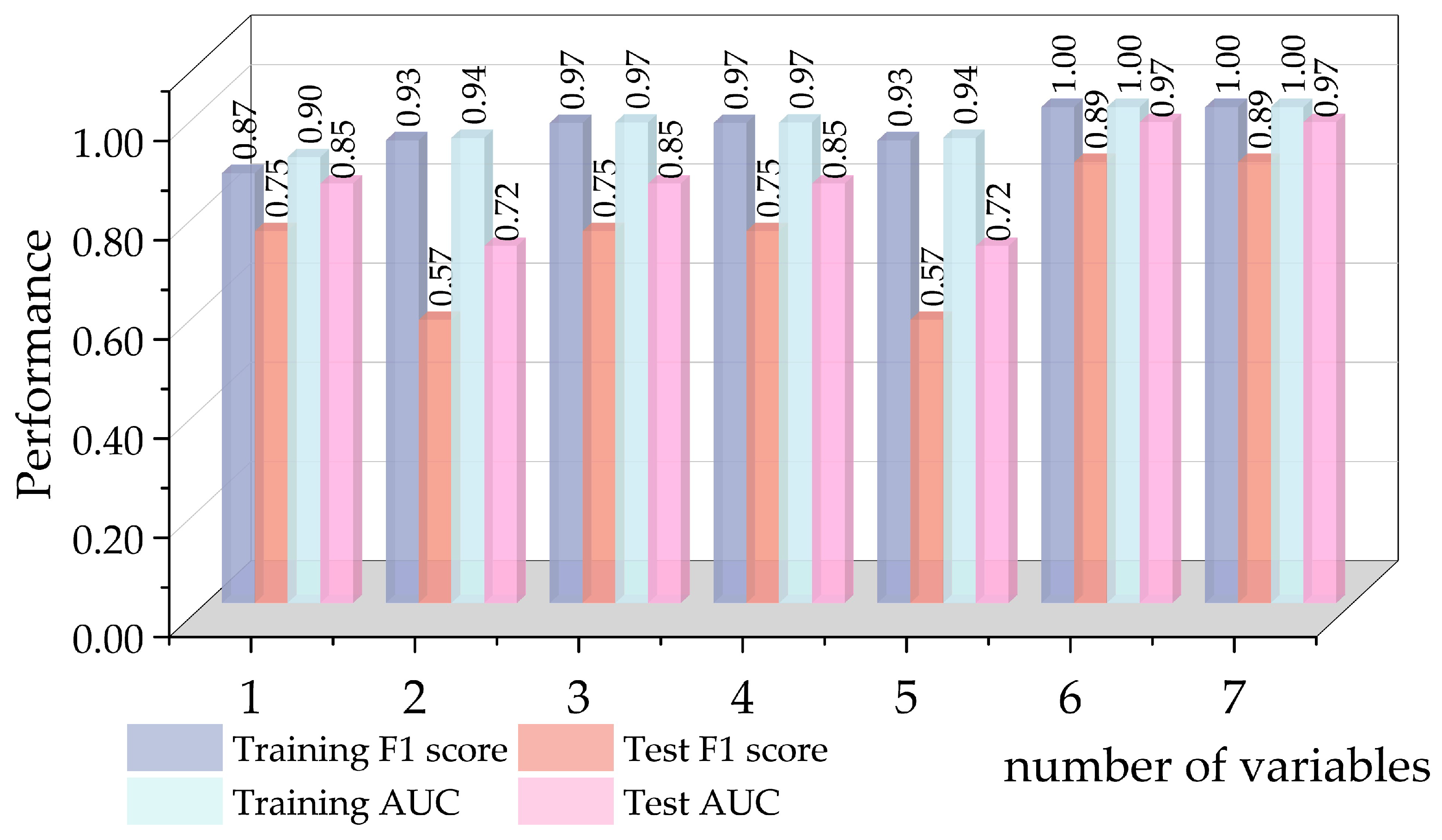
3.3. Feature Variables Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, Y.; Huang, M.; Chen, X.; Wang, Z.; Xiao, L.; Xu, K.; Zhang, S.; Wang, M.; Xu, Z.; Shi, Z. Identification and risk prediction of potentially contaminated sites in the Yangtze River Delta. Sci. Total Environ. 2022, 815, 151982. [Google Scholar] [CrossRef] [PubMed]
- Hou, D. Ten grand challenges for groundwater pollution prevention and remediation at contaminated sites in China. Res. Environ. Sci. 2022, 35, 2015–2025. [Google Scholar]
- Li, H.; Gu, J.; Hanif, A.; Dhanasekar, A.; Carlson, K. Quantitative decision making for a groundwater monitoring and subsurface contamination early warning network. Sci. Total Environ. 2019, 683, 498–507. [Google Scholar] [CrossRef]
- Van Liedekerke, M.; Prokop, G.; Rabl-Berger, S.; Kibblewhite, M.; Louwagie, G. Progress in the Management of Contaminated Sites in Europe; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- Jiang, Y.; Wang, H.; Lei, M.; Hou, D.; Chen, S.; Hu, B.; Huang, M.; Song, W.; Shi, Z. An integrated assessment methodology for management of potentially contaminated sites based on public data. Sci. Total Environ. 2021, 783, 146913. [Google Scholar] [CrossRef] [PubMed]
- Rampanelli, G.B.; Braun, A.B.; Visentin, C.; Trentin, A.W.d.S.; da Cruz, R.; Thomé, A. The process of selecting a method for identifying potentially contaminated sites—A case study in a municipality in southern Brazil. Water Air Soil Pollut. 2021, 232, 26. [Google Scholar] [CrossRef]
- Pitsaki, K.; Boura, F.; Pantazidou, M.; Katsiri, A. Methodologies for compiling national inventories of contaminated sites and conducting preliminary site screening. Glob. Nest J. 2014, 16, 24–35. [Google Scholar] [CrossRef]
- Rouillon, M.; Taylor, M.P.; Dong, C.Y. Reducing risk and increasing confidence of decision making at a lower cost: In-situ pXRF assessment of metal-contaminated sites. Environ. Pollut. 2017, 229, 780–789. [Google Scholar] [CrossRef]
- Wiséen, T.; Wester-Herber, M. Dirty soil and clean consciences: Examining communication of contaminated soil. Water Air Soil Pollut. 2007, 181, 173–182. [Google Scholar] [CrossRef]
- Sjöberg, L. The allegedly simple structure of experts’ risk perception: An urban legend in risk research. Sci. Technol. Hum. Values 2002, 27, 443–459. [Google Scholar] [CrossRef]
- Wester-Herber, M.; Warg, L.-E. Did they get it? Examining the goals of risk communication within the Seveso II Directive in a Swedish context. J. Risk Res. 2004, 7, 495–506. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Rizeei, H.M.; Azeez, O.S.; Pradhan, B.; Khamees, H.H. Assessment of groundwater nitrate contamination hazard in a semi-arid region by using integrated parametric IPNOA and data-driven logistic regression models. Environ. Monit. Assess. 2018, 190, 633. [Google Scholar] [CrossRef] [PubMed]
- Saghebian, S.M.; Sattari, M.T.; Mirabbasi, R.; Pal, M. Ground water quality classification by decision tree method in Ardebil region, Iran. Arab. J. Geosci. 2013, 7, 4767–4777. [Google Scholar] [CrossRef]
- Erickson, M.L.; Elliott, S.M.; Brown, C.J.; Stackelberg, P.E.; Ransom, K.M.; Reddy, J.E.; Cravotta, C.A., III. Machine-Learning predictions of high arsenic and high manganese at drinking water depths of the glacial aquifer system, northern continental United States. Environ. Sci. Technol. 2021, 55, 5791–5805. [Google Scholar] [CrossRef] [PubMed]
- Nafouanti, M.B.; Li, J.; Mustapha, N.A.; Uwamungu, P.; Al-Alimi, D. Prediction on the fluoride contamination in groundwater at the Datong Basin, Northern China: Comparison of random forest, logistic regression and artificial neural network. Appl. Geochem. 2021, 132, 105054. [Google Scholar] [CrossRef]
- Jafari, R.; Torabian, A.; Ghorbani, M.A.; Mirbagheri, S.A.; Hassani, A.H. Prediction of groundwater quality parameter in the Tabriz plain, Iran using soft computing methods. J. Water Supply Res. Technol.-Aqua 2019, 68, 573–584. [Google Scholar] [CrossRef]
- Mao, H.R.; Wang, C.Y.; Qu, S.; Liao, F.; Wang, G.C.; Shi, Z.M. Source and evolution of sulfate in the multi-layer groundwater system in an abandoned mine-Insight from stable isotopes and Bayesian isotope mixing model. Sci. Total Environ. 2023, 859, 12. [Google Scholar] [CrossRef]
- An, Y.; Zhang, Y.; Yan, X. An integrated Bayesian and machine learning approach application to identification of groundwater contamination source parameters. Water 2022, 14, 2447. [Google Scholar] [CrossRef]
- Li, J.; Lu, W.; Luo, J. Groundwater contamination sources identification based on the Long-Short Term Memory network. J. Hydrol. 2021, 601, 126670. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, X.; Zhang, Q. Current situation and control measures of groundwater pollution in gas station. In Proceedings of the 2017 3rd International Conference on Energy, Environment and Materials Science (EEMS), Northwestern Polytechnical University, Singapore, 28–30 July 2017. [Google Scholar]
- Rosales, R.M.; Martínez-Pagán, P.; Faz, A.; Bech, J. Study of subsoil in former petrol stations in SE of Spain: Physicochemical characterization and hydrocarbon contamination assessment. J. Geochem. Explor. 2014, 147, 306–320. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, X.; Sun, C.; Kang, L.; Zhao, Z.; Chen, M. Spatial distribution of typical pollutants of gas stations in shallow water-table areas. Chin. J. Environ. Eng. 2014, 8, 98–103. [Google Scholar]
- Tiburtius, E.R.L.; Peralta-Zamora, P.; Emmel, A. Treatment of gasoline-contaminated waters by advanced oxidation processes. J. Hazard. Mater. 2005, 126, 86–90. [Google Scholar] [CrossRef]
- Zhao, L.; Deng, Y.; Huang, X.; Sun, Q. Problems and countermeasures of soil and groundwater environmental management in gas station. Adm. Tech. Environ. Monit. 2019, 31, 4–7. [Google Scholar]
- Lesage, S.; Xu, H.; Novakowski, K.S. Distinguishing natural hydrocarbons from anthropogenic contamination in ground water. Groundwater 1997, 35, 149–160. [Google Scholar] [CrossRef]
- GB 5749-2006; Standards for Drinking Water Quality. Ministry of Health of the People’s Republic of China; Standardization Administration of China: Beijing, China, 2006.
- HJ 164-2004; Technical Specification for Environmental Monitoring of Groundwater. State Environmental Protection Administration of the People’s Republic of China: Beijing, China, 2004.
- HJ 894-2017; Water Quality-Determination of Extractable Petroleum Hydro-Carbons (C10-C40)-Gas Chro-Matography. Ministry of Environmental Protection of the People’s Republic of China: Beijing, China, 2017.
- Mojaddadi, H.; Pradhan, B.; Nampak, H.; Ahmad, N.; Ghazali, A.H.b. Ensemble machine-learning-based geospatial approach for flood risk assessment using multi-sensor remote-sensing data and GIS. Geomat. Nat. Hazards Risk 2017, 8, 1080–1102. [Google Scholar] [CrossRef] [Green Version]
- McManus, S.L.; Richards, K.G.; Grant, J.; Mannix, A.; Coxon, C.E. Pesticide occurrence in groundwater and the physical characteristics in association with these detections in Ireland. Environ. Monit. Assess. 2014, 186, 7819–7836. [Google Scholar] [CrossRef]
- Wu, R.; Podgorski, J.; Berg, M.; Polya, D.A. Geostatistical model of the spatial distribution of arsenic in groundwaters in Gujarat State, India. Environ. Geochem. Health 2021, 43, 2649–2664. [Google Scholar] [CrossRef] [PubMed]
- Hinkle, S.R.; Tesoriero, A.J. Nitrogen speciation and trends, and prediction of denitrification extent, in shallow US groundwater. J. Hydrol. 2014, 509, 343–353. [Google Scholar] [CrossRef]
- Barad, S.; Mishra, P.; Sahu, P.C.; Sarkar, T.; Amin, M.F.M.; Choudhury, T.; Edinur, H.A.; Kari, Z.A.; Nandi, D.; Pati, S. Comparative approach of decision tree and CWQI analysis for classification of groundwater with a special reference to fluoride ion in drought-prone Boudh district of Odisha, India. Sustain. Water Resour. Manag. 2021, 7, 94. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Liu, Q.; Xing, Y.; Yang, H.; Cao, V.; Sauter, M.; Butscher, C. Predicting methane solubility in water and seawater by machine learning algorithms: Application to methane transport modeling. J. Contam. Hydrol. 2021, 242, 103844. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef] [PubMed]
- Band, S.S.; Janizadeh, S.; Pal, S.C.; Chowdhuri, I.; Siabi, Z.; Norouzi, A.; Melesse, A.M.; Shokri, M.; Mosavi, A. Comparative analysis of artificial intelligence models for accurate estimation of groundwater nitrate concentration. Sensors 2020, 20, 5763. [Google Scholar] [CrossRef] [PubMed]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- Ali, E.B.; Abdeslam, T.; Youssef, B. Groundwater quality forecasting using machine learning algorithms for irrigation purposes. Agric. Water Manag. 2021, 245, 106625. [Google Scholar] [CrossRef]
- Mosavi, A.; Sajedi Hosseini, F.; Choubin, B.; Taromideh, F.; Ghodsi, M.; Nazari, B.; Dineva, A.A. Susceptibility mapping of groundwater salinity using machine learning models. Environ. Sci. Pollut. Res. Int. 2020, 28, 10804–10817. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, C. Deep learning and machine learning with Grid search to predict later occurrence of breast cancer metastasis using clinical data. J. Clin. Med. 2022, 11, 5772. [Google Scholar] [CrossRef]
- Shamsuddin, I.I.S.; Othman, Z.; Sani, N.S. Water quality index classification based on machine learning: A case from the Langat River Basin model. Water 2022, 14, 2939. [Google Scholar] [CrossRef]
- Im, G.; Lee, D.; Lee, S.; Lee, J.; Lee, S.; Park, J.; Heo, T.-Y. Estimating chlorophyll-a concentration from hyperspectral data using various machine learning techniques: A case study at Paldang Dam, South Korea. Water 2022, 14, 4080. [Google Scholar] [CrossRef]
- Wong, J.; Manderson, T.; Abrahamowicz, M.; Buckeridge, D.L.; Tamblyn, R. Can hyperparameter tuning improve the performance of a super learner?: A case study. Epidemiology 2019, 30, 521–531. [Google Scholar] [CrossRef]
- Pannakkong, W.; Harncharnchai, T.; Buddhakulsomsiri, J. Forecasting daily electricity consumption in Thailand using regression, artificial neural network, support vector machine, and hybrid Models. Energies 2022, 15, 3105. [Google Scholar] [CrossRef]
- Garrido-Merchán, E.C.; Hernández-Lobato, D. Dealing with categorical and integer-valued variables in Bayesian Optimization with Gaussian processes. Neurocomputing 2020, 380, 20–35. [Google Scholar] [CrossRef] [Green Version]
- Yan, M.; Shen, Y. Traffic accident severity prediction based on random forest. Sustainability 2022, 14, 1729. [Google Scholar] [CrossRef]
- Wang, Y.; Kandeal, A.W.; Swidan, A.; Sharshir, S.W.; Abdelaziz, G.B.; Halim, M.A.; Kabeel, A.E.; Yang, N. Prediction of tubular solar still performance by machine learning integrated with Bayesian optimization algorithm. Appl. Therm. Eng. 2021, 184, 116233. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Vega García, M.; Aznarte, J.L. Shapley additive explanations for NO2 forecasting. Ecol. Inform. 2020, 56, 101039. [Google Scholar] [CrossRef]
- Fryer, D.; Strümke, I.; Nguyen, H. Shapley values for feature selection: The good, the bad, and the axioms. IEEE Access 2021, 9, 144352–144360. [Google Scholar] [CrossRef]
- Shen, Z.; Yong, B. Downscaling the GPM-based satellite precipitation retrievals using gradient boosting decision tree approach over Mainland China. J. Hydrol. 2021, 602, 126803. [Google Scholar] [CrossRef]
- Song, Y.; Niu, R.; Xu, S.; Ye, R.; Peng, L.; Guo, T.; Li, S.; Chen, T. Landslide susceptibility mapping based on weighted gradient boosting decision tree in Wanzhou section of the Three Gorges Reservoir area (China). ISPRS Int. J. Geo-Inf. 2019, 8, 4. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.; Ligaray, M.; Kim, Y.M.; Kim, J.H.; Cho, K.H.; Sthiannopkao, S. Development of enhanced groundwater arsenic prediction model using machine learning approaches in Southeast Asian countries. Desalination Water Treat. 2015, 57, 12227–12236. [Google Scholar] [CrossRef]
- Purkait, B. Application of artificial neural network model to study arsenic contamination in groundwater of Malda District, eastern India. J. Environ. Inform. 2008, 12, 140–149. [Google Scholar] [CrossRef] [Green Version]
- Bi, P.; Pei, L.; Huang, G.; Han, D.; Song, J. Identification of groundwater contamination in a rapidly urbanized area on a regional scale: A new approach of multi-hydrochemical evidences. Int. J. Environ. Res. Public Health 2021, 18, 12143. [Google Scholar] [CrossRef]
- Han, H.; Jiang, X. Overcome support vector machine diagnosis overfitting. Cancer Inform. 2014, 13, 145–158. [Google Scholar] [CrossRef] [PubMed]
- Krzywinski, M.; Altman, N. Classification and regression trees. Nat. Methods 2017, 14, 757–758. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Rong, G.; Alu, S.; Li, K.; Su, Y.; Zhang, J.; Zhang, Y.; Li, T. Rainfall induced landslide susceptibility mapping based on Bayesian optimized random forest and gradient boosting decision tree models—A case study of Shuicheng County, China. Water 2020, 12, 3066. [Google Scholar] [CrossRef]
- Halmemies, S.; Gröndahl, S.; Nenonen, K.; Tuhkanen, T. Estimation of the time periods and processes for penetration of selected spilled oils and fuels in different soils in the laboratory. Spill Sci. Technol. Bull. 2003, 8, 451–465. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Chow, F.K.; Kollet, S.J. The groundwater–land-surface–atmosphere connection: Soil moisture effects on the atmospheric boundary layer in fully-coupled simulations. Adv. Water Resour. 2007, 30, 2447–2466. [Google Scholar] [CrossRef] [Green Version]
- Vandana; Priyadarshanee, M.; Mahto, U.; Das, S. Chapter 2-Mechanism of toxicity and adverse health effects of environmental pollutants. In Microbial Biodegradation and Bioremediation, 2nd ed.; Das, S., Dash, H.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 33–53. [Google Scholar]
- Sun, H.; Yang, X.; Xie, J.; Li, X.; Zhao, Y. Remediation of diesel-contaminated aquifers using thermal conductive heating coupled with thermally activated persulfate. Water Air Soil Pollut. 2021, 232, 293. [Google Scholar] [CrossRef]
- Falciglia, P.P.; Maddalena, R.; Mancuso, G.; Messina, V.; Vagliasindi, F.G.A. Lab-scale investigation on remediation of diesel-contaminated aquifer using microwave energy. J. Environ. Manag. 2016, 167, 196–205. [Google Scholar] [CrossRef] [Green Version]
- McAlexander, B.; Sihota, N. Influence of ambient temperature, precipitation, and groundwater level on natural source zone depletion rates at a large semiarid LNAPL site. Groundw. Monit. Remediat. 2019, 39, 54–65. [Google Scholar] [CrossRef] [Green Version]
- Ma, J. The influence of rainstorm on soil components and properties:a case study of Biyang rainstorm area, Henan province. Geogr. Res. 2004, 23, 55–62. [Google Scholar]
- Zhang, S.; Su, X.; Lin, X.; Zhang, Y.; Zhang, Y. Experimental study on the multi-media PRB reactor for the remediation of petroleum-contaminated groundwater. Environ. Earth Sci. 2015, 73, 5611–5618. [Google Scholar] [CrossRef]
- Isazadeh, M.; Biazar, S.M.; Ashrafzadeh, A. Support vector machines and feed-forward neural networks for spatial modeling of groundwater qualitative parameters. Environ. Earth Sci. 2017, 76, 610. [Google Scholar] [CrossRef]


| Category | Variable | Description | Type |
|---|---|---|---|
| Management variables | KIL | Key investigation list. Whether the station is on the key investigation list or not | categorical |
| OC | Operating condition. Whether the station is open for business | categorical | |
| Owner | The owner of the gas station | categorical | |
| LA | Leakage accident. Whether the station has ever had oil leakage accidents | categorical | |
| GWPA | Groundwater protection area. Whether the station is located in a groundwater protection area | categorical | |
| Gas station variables | Construction Time | The length of time since the station was constructed | discrete |
| No.Tanks | Total number of tanks at the gas station | discrete | |
| No.SingleTanks | Total number of single-layer tanks at the gas station | discrete | |
| Impermeable ponds | Whether the gas station has built impermeable ponds | categorical | |
| Pipeline | Type of pipeline at the station | categorical | |
| Geography and remote sensing variables | Dist_lake | The distance from the nearest lake | continuous |
| Dist_river | The distance from the nearest river | continuous | |
| Elevation | The elevation where the gas station is located | continuous | |
| NPP | Net primary productivity at the location of the gas station | continuous | |
| LAI | Leaf area index. The leaf area index of the location of the gas station | continuous | |
| Landuse | Land use types around gas stations | categorical | |
| NDVI | Normalized vegetation index of the gas station location | continuous | |
| Social economy variables | NLI | Night light index. The night light index of the gas station location | continuous |
| population | The population of the town where the gas station is located | continuous | |
| GDP | Total GDP of the cell grid where the gas station is located | continuous | |
| Meteorological variables | Permafrost type | The type of frozen soil | categorical |
| EVP | Annual mean evaporation | continuous | |
| GST | Annual mean ground surface temperature | continuous | |
| PRE | Annual precipitation | continuous | |
| PRS | Annual mean pressure | continuous | |
| RHU | Annual mean relative humidity | continuous | |
| SSD | Annual sunshine | continuous | |
| TEM | Annual mean temperature | continuous | |
| WIN | Annual mean wind speed | continuous | |
| Soil variables | Soil erosion | Types and properties of external forces of soil erosion | categorical |
| clay_top | The proportion of clay in the topsoil (0–30 cm) | continuous | |
| sand_top | The proportion of sand in the topsoil | continuous | |
| silt_top | The proportion of silt in the topsoil | continuous | |
| soil moisture | The moisture of the topsoil | continuous | |
| clay_sub | The content of clay in the subsoil (30–100 cm) | continuous | |
| sand_sub | The content of sand in the subsoil | continuous | |
| CEC_S | Soil cation exchange capacity in 100–200 cm | continuous | |
| TK_S | Total potassium in soil from 15 to 30 cm | continuous | |
| gravel_S | Gravel content in soil from 30 to 60 cm | continuous | |
| pH_S | Soil pH in the range of 30–60 cm | continuous |
| Algorithm | Hyperparameter | Description | Range |
|---|---|---|---|
| LR | C | Regularization parameter. A smaller C means that the model may have better generalization, but it is also more likely to underfit | [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10,000] |
| DT | criterion | Selects the criteria by which attributes will be selected for separation | [gini, entropy, log_loss] |
| min_samples_leaf | The minimum number of samples required at a leaf node | [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] | |
| max_depth | The maximum depth of the tree | [3, 4, 5, 6] | |
| min_samples_split | The minimum number of samples required to split internal nodes | [0.1, 0.2, 0.3, 0.4, 0.6, 0.8, 1.2] | |
| GBDT | criterion | Selects the criteria by which attributes will be selected for separation | [friedman_mse, squared_error] |
| n_estimators | The number of boosting stages to perform. It is represented in GBDT as the number of decision trees | [10, 25, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 500, 1000, 1500, 2000] | |
| DT hyperparameters | min_samples_leaf, max_depth, and min_samples_split | Same as DT | |
| RF | n_estimators | The number of trees in the random forest | Same as GBDT |
| DT hyperparameters | Criterion, min_samples_leaf, max_depth, and min_samples_split | Same as DT | |
| MLP | hidden_layer_sizes | The number of hidden layers in the neural network and the number of neurons in each hidden layer | [‘layer1’: 1 to 20 (n), ‘layer2’: 0 to n] |
| activation | Activation function for the hidden layer | [identity, logistic, tanh, relu] | |
| max_iter | The maximum number of iterations of the solver | [100, 280, 460, 640, 820, 1000] | |
| learning_rate_init | The initial learning rate used. It controls the step size when the weight is updated | [0.001, 0.0108, 0.0206, 0.0304, 0.0402, 0.05] | |
| momentum | Momentum for gradient descent update | [0.5, 0.58, 0.66, 0.74, 0.82, 0.9] | |
| SVM | C | Regularization parameter | [0.001, 0.01, 0.1, 1, 10, 100, 3300, 1000] |
| kernel | Specifies the kernel type used in the algorithm | [linear, rbf, poly, sigmoid] |
| Algorithm | Pre-Processing | Hyperparameter | Parameter Optimum |
|---|---|---|---|
| GBDT | OD | criterion | friedman_mse |
| n_estimators | 25 | ||
| min_samples_leaf | 3 | ||
| max_depth | 3 | ||
| min_samples_split | 0.1 |
| Algorithm | Pre-Processing | Number of Parameter Groups | Total Time (s) | Single Attempt Time (s) |
|---|---|---|---|---|
| LR | OD | 9 | 53.10 | 5.90 |
| MMS | 9 | 13.10 | 1.46 | |
| SS | 9 | 7.75 | 0.86 | |
| DT | OD | 840 | 60.57 | 0.07 |
| MMS | 840 | 60.07 | 0.07 | |
| SS | 840 | 70.70 | 0.08 | |
| GBDT | OD | 12,320 | 19,125 | 1.55 |
| MMS | 12,320 | 18,665 | 1.52 | |
| SS | 12,320 | 18,961 | 1.54 | |
| RF | OD | 18,480 | 67,283 | 3.64 |
| MMS | 18,480 | 66,574 | 3.60 | |
| SS | 18,480 | 65,326 | 3.53 | |
| MLP | OD | 198,720 | 253,500 | 1.28 |
| MMS | 198,720 | 248,400 | 1.25 | |
| SS | 198,720 | 240,780 | 1.21 | |
| SVM | OD | 32 | 2.24 | 0.07 |
| MMS | 32 | 3.95 | 0.12 | |
| SS | 32 | 3.02 | 0.09 |
| Hyperparameter | Range |
|---|---|
| n_estimators | (1, 2000) |
| min_samples_leaf | (1, 10) |
| max_depth | (3, 6) |
| min_samples_split | (0.1, 1) |
| Hyperparameter | Hyperparameter Optimum | Performance | Training Time |
|---|---|---|---|
| n_estimators | 978 | Training: F1 score = 1, AUC = 1 Test: F1 score = 1, AUC = 1 | 513 s |
| min_samples_leaf | 1 | ||
| max_depth | 3 | ||
| min_samples_split | 0.9745 |
| Number of Variables | Input Variables |
|---|---|
| 1 | WIN |
| 2 | WIN, population |
| 3 | WIN, population, EVP |
| 4 | WIN, population, EVP, TK_S |
| 5 | WIN, population, EVP, TK_S, PRE |
| 6 | WIN, population, EVP, TK_S, PRE, LA |
| 7 | WIN, population, EVP, TK_S, PRE, LA, sand_sub |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Ding, L.; Liu, W.; Niu, H.; Yang, M.; Lyu, G.; Lin, S.; Hu, Q. Groundwater Contamination Site Identification Based on Machine Learning: A Case Study of Gas Stations in China. Water 2023, 15, 1326. https://doi.org/10.3390/w15071326
Huang Y, Ding L, Liu W, Niu H, Yang M, Lyu G, Lin S, Hu Q. Groundwater Contamination Site Identification Based on Machine Learning: A Case Study of Gas Stations in China. Water. 2023; 15(7):1326. https://doi.org/10.3390/w15071326
Chicago/Turabian StyleHuang, Yanpeng, Longzhen Ding, Weijiang Liu, Haobo Niu, Mengxi Yang, Guangfeng Lyu, Sijie Lin, and Qing Hu. 2023. "Groundwater Contamination Site Identification Based on Machine Learning: A Case Study of Gas Stations in China" Water 15, no. 7: 1326. https://doi.org/10.3390/w15071326





