Calculation Model of Multi-Well Siphoning and Its Feasibility Analysis of Discharging the Groundwater in Soft Soil
Abstract
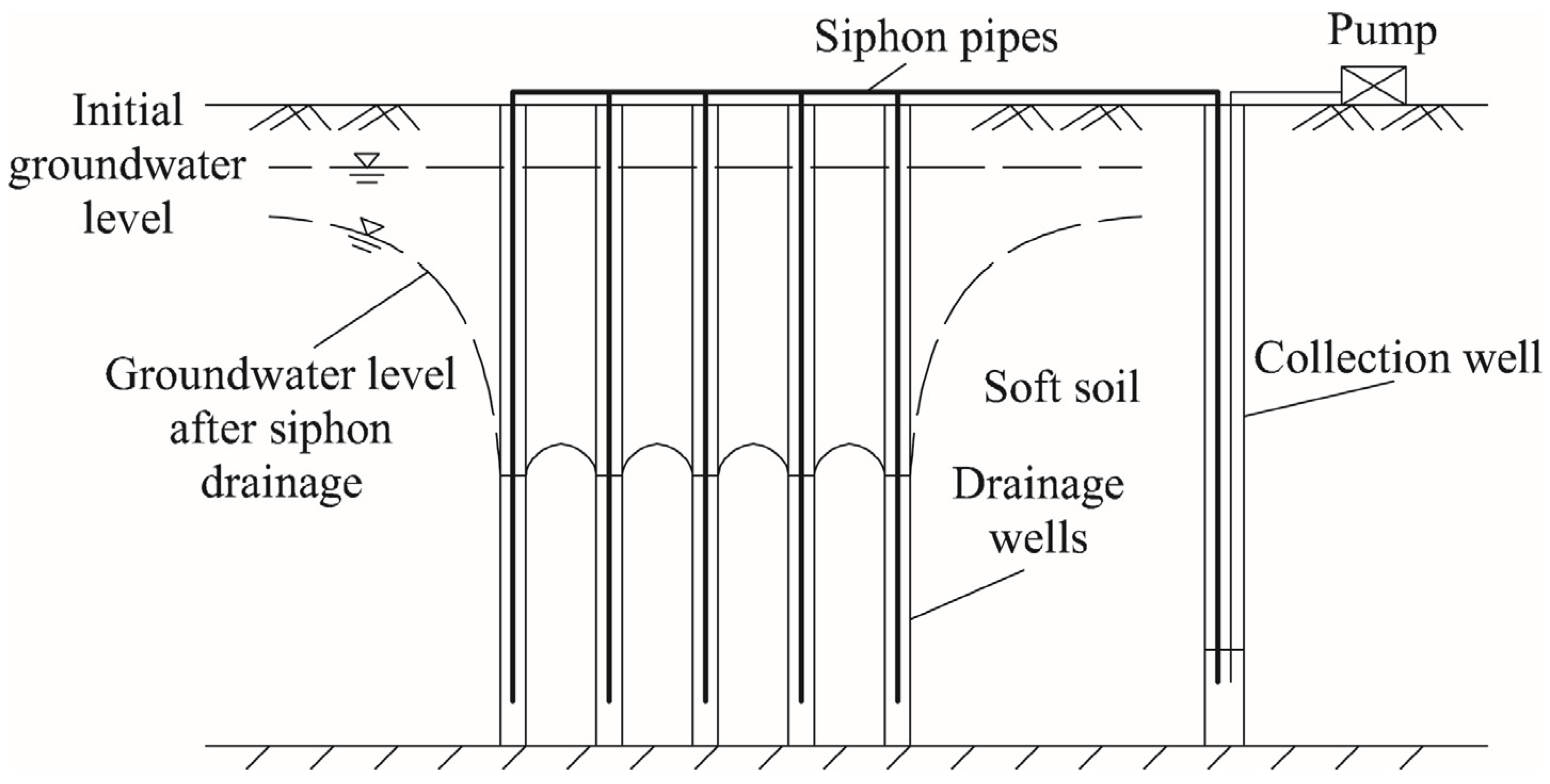
:1. Introduction
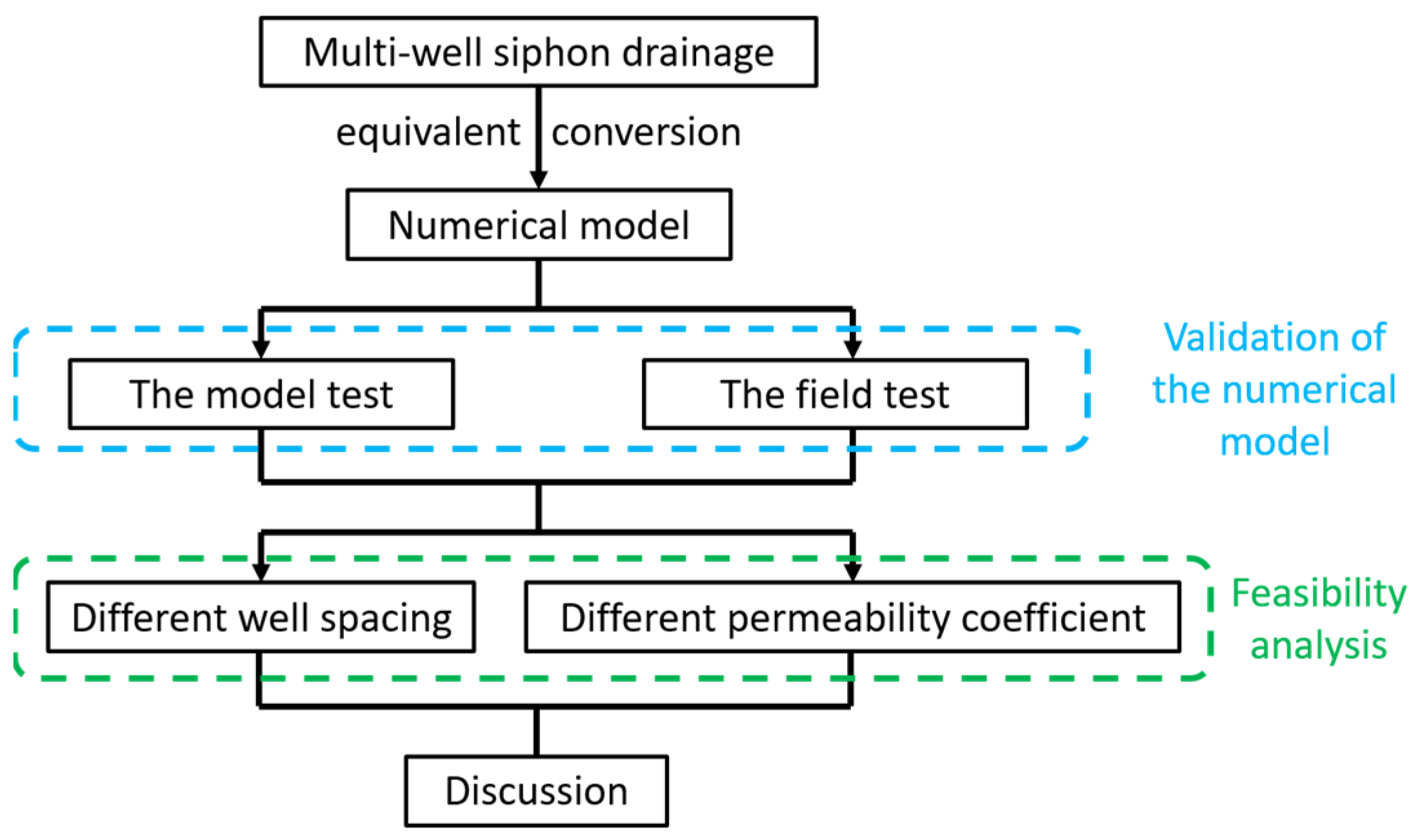
2. Method
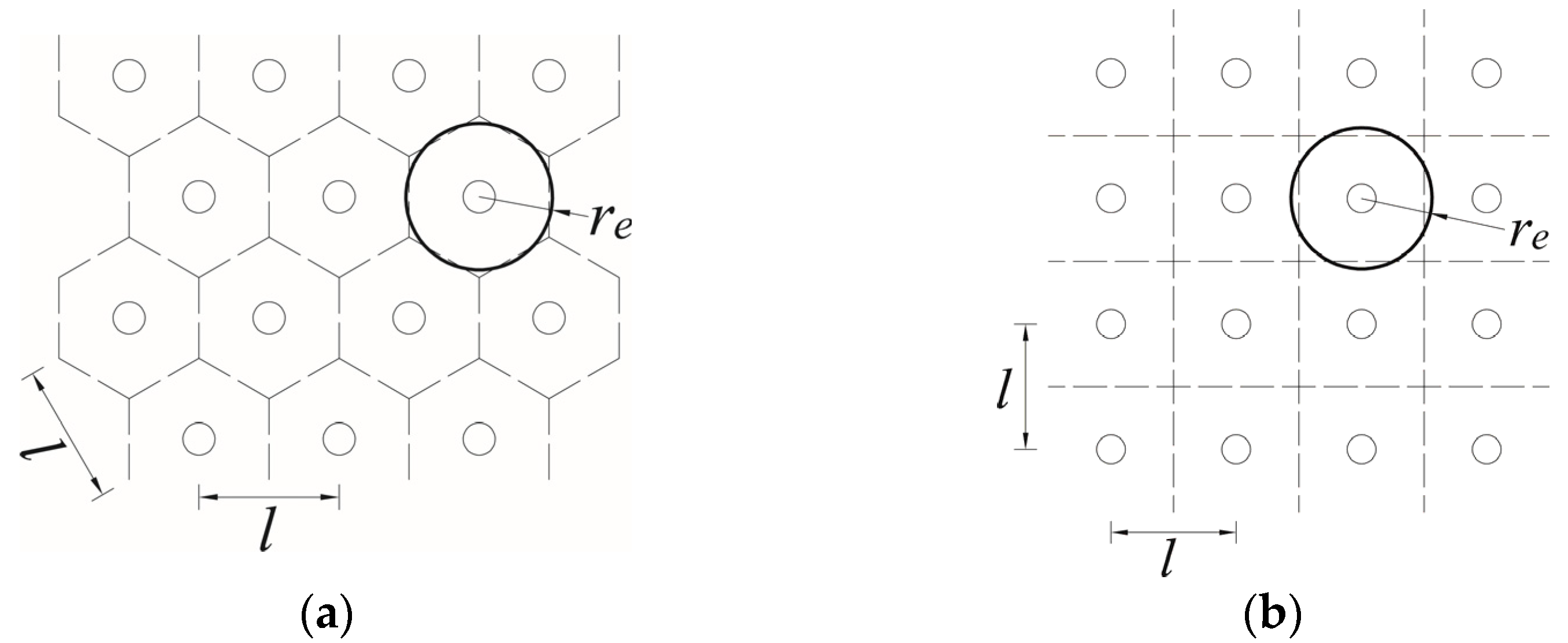
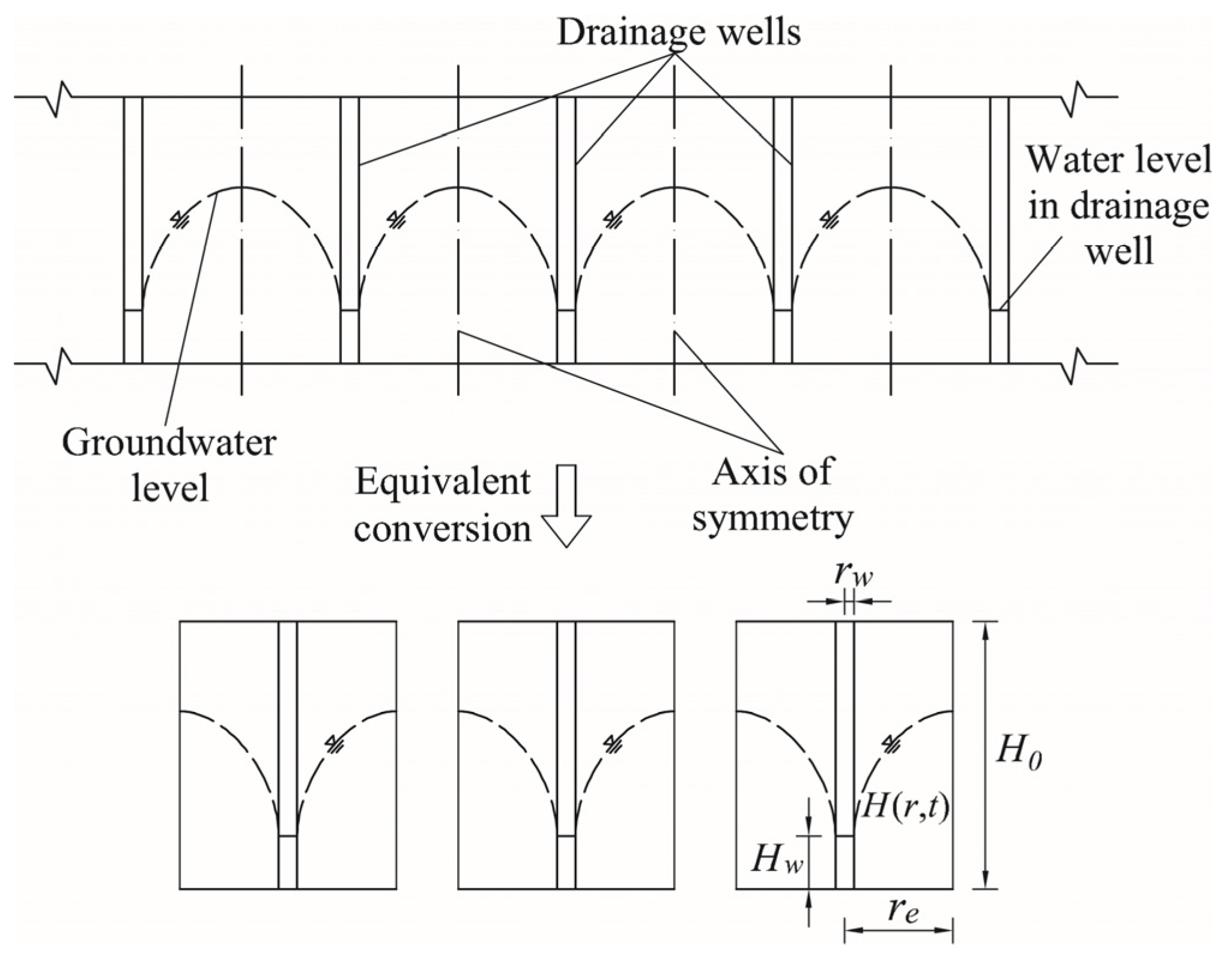
2.1. Equivalent Conversion
2.2. Solution of the Numerical Model
3. Validation of the Numerical Model
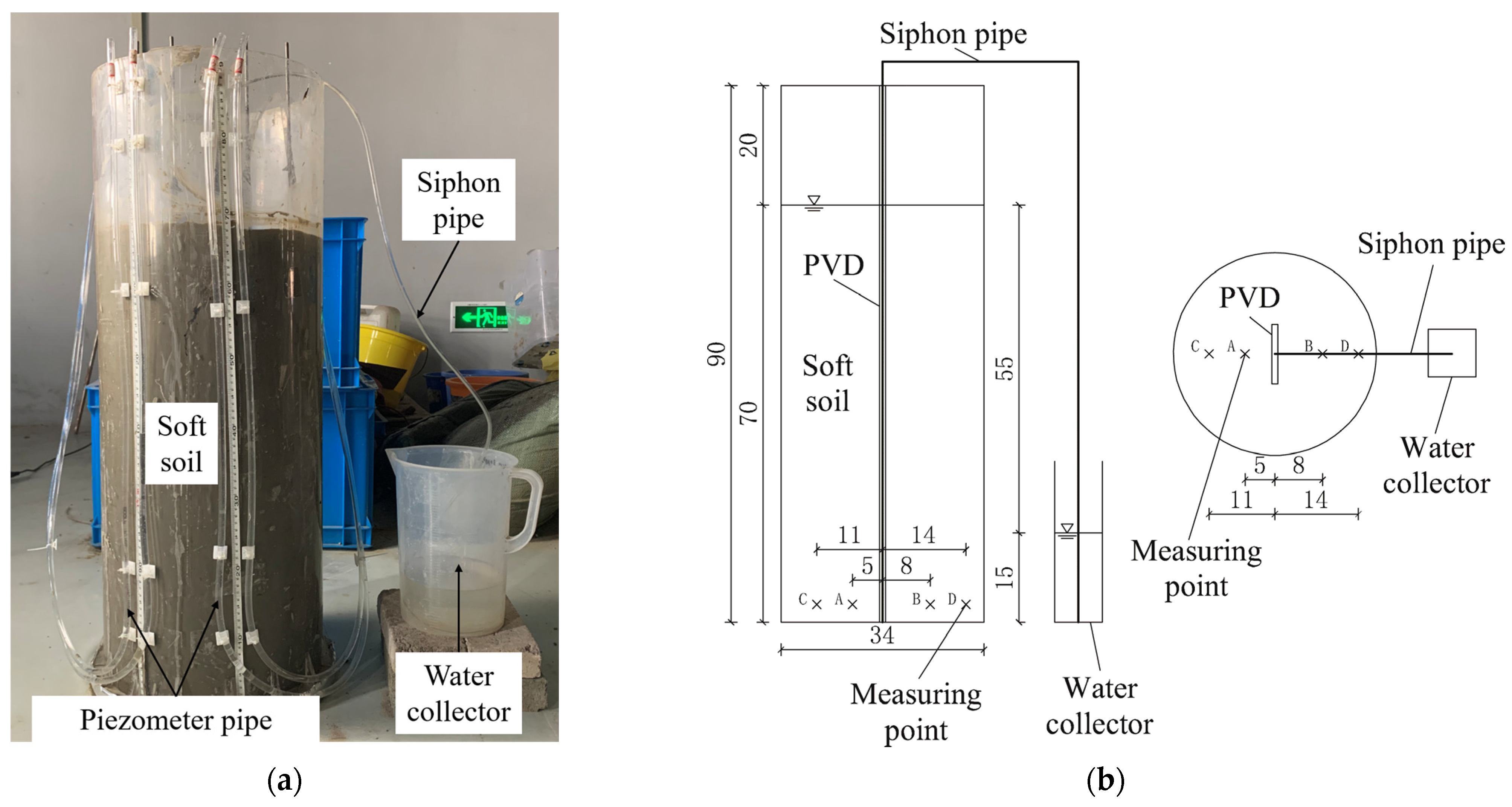
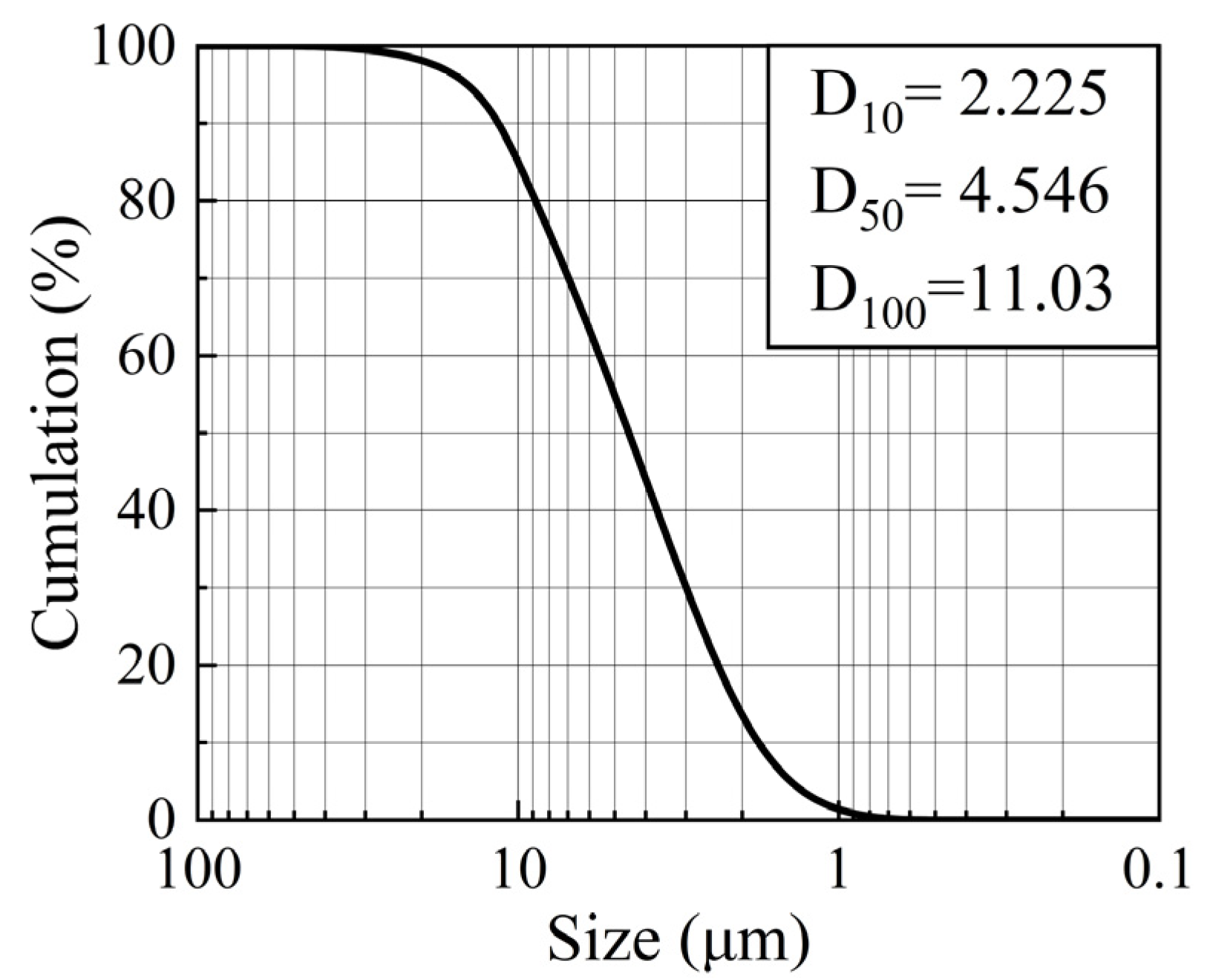
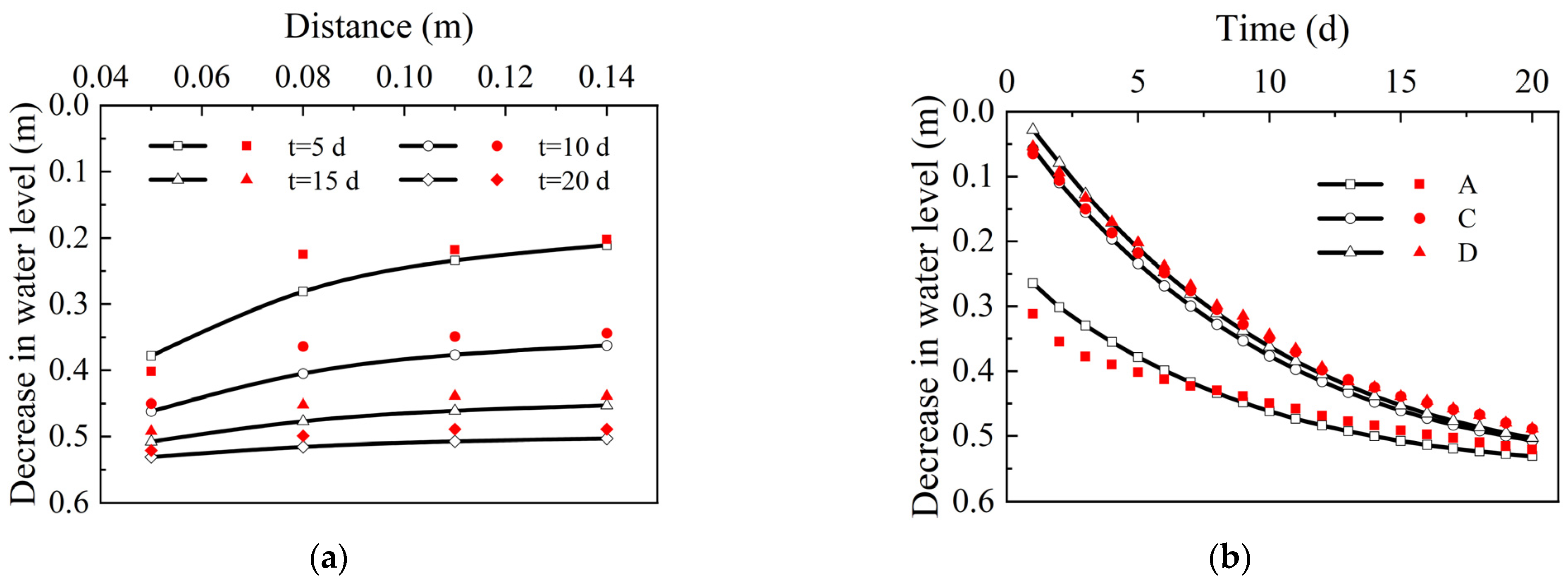
3.1. The Model Test
3.2. The Field Test
4. Feasibility Analysis
5. Discussion
6. Conclusions
- (1)
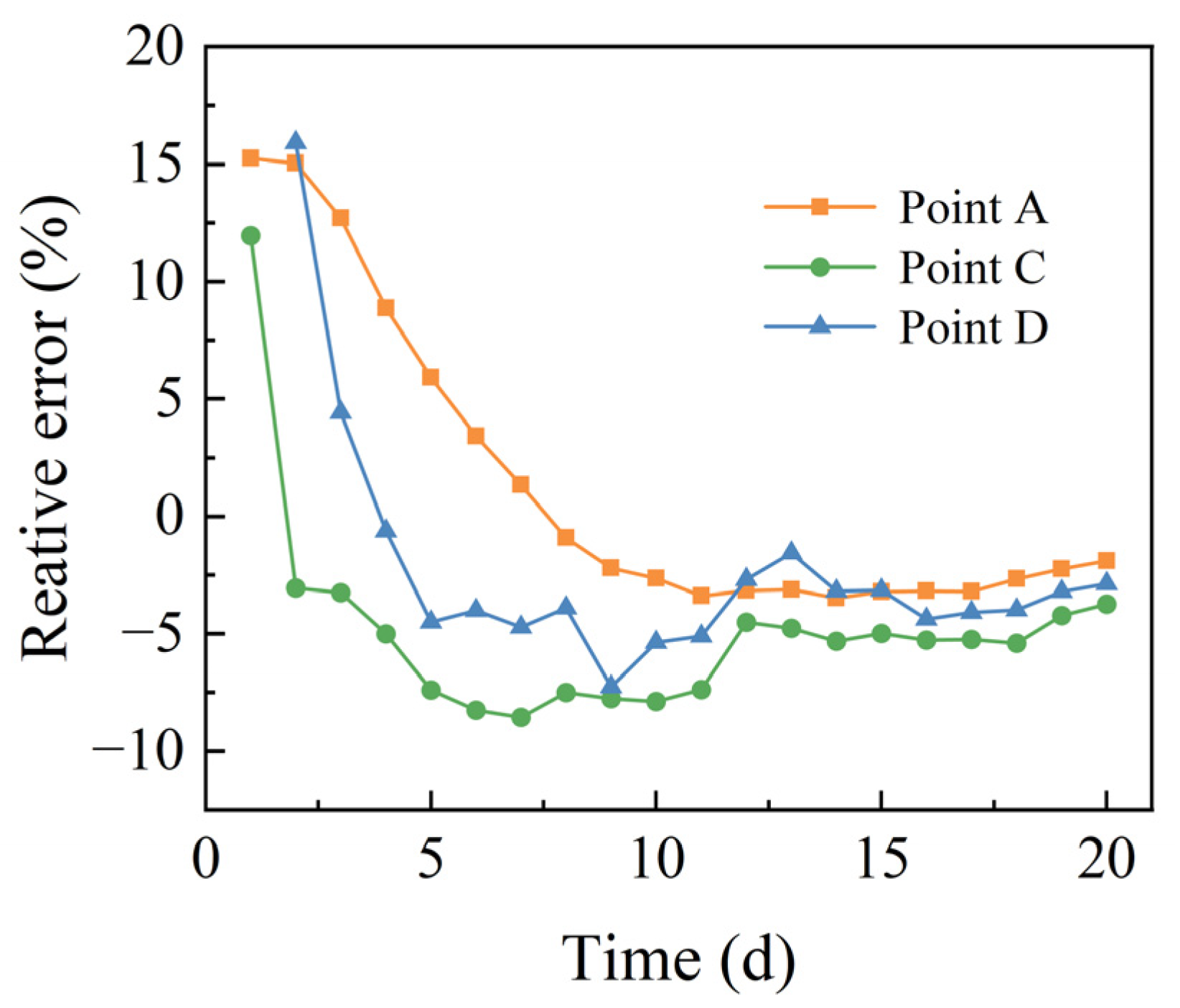
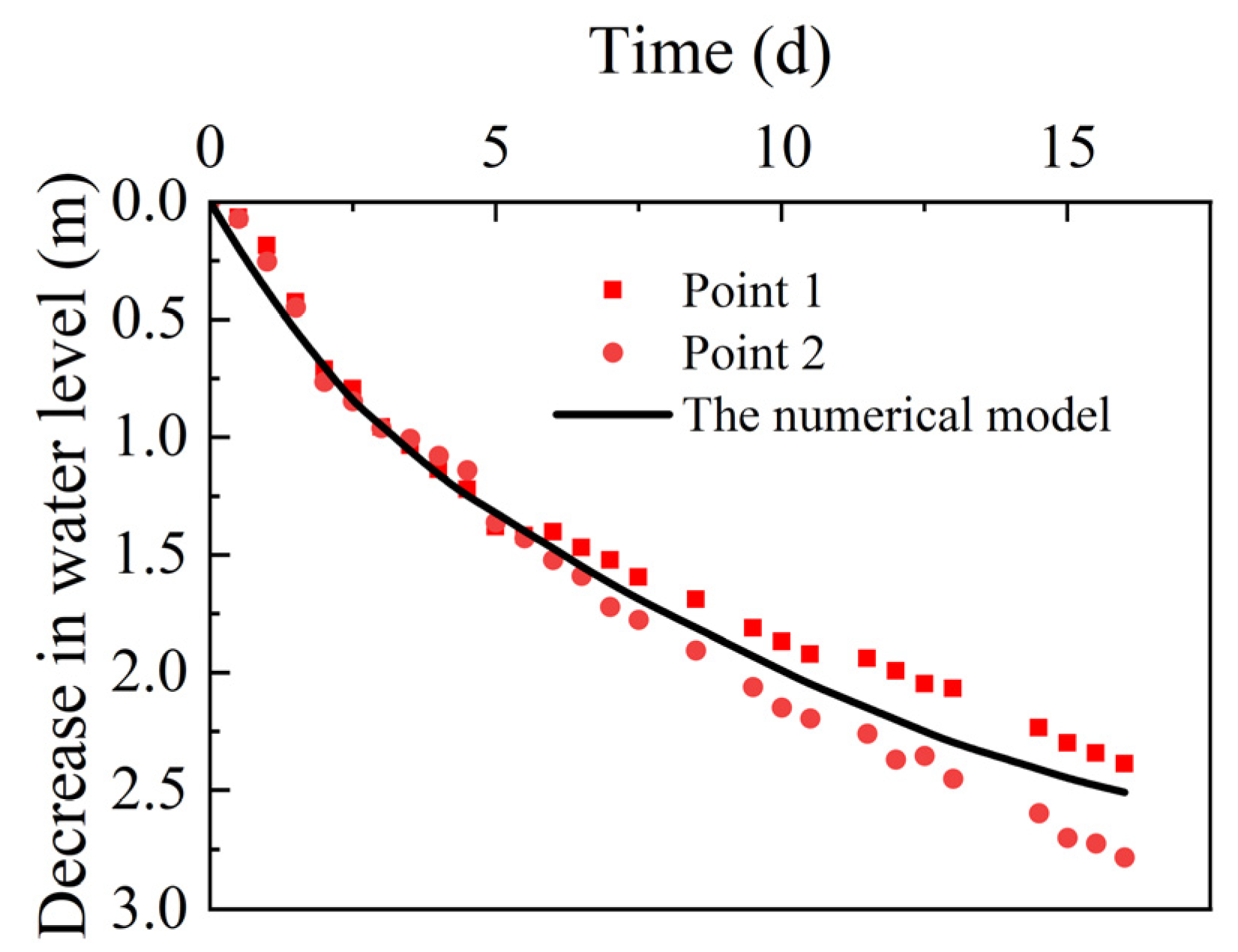
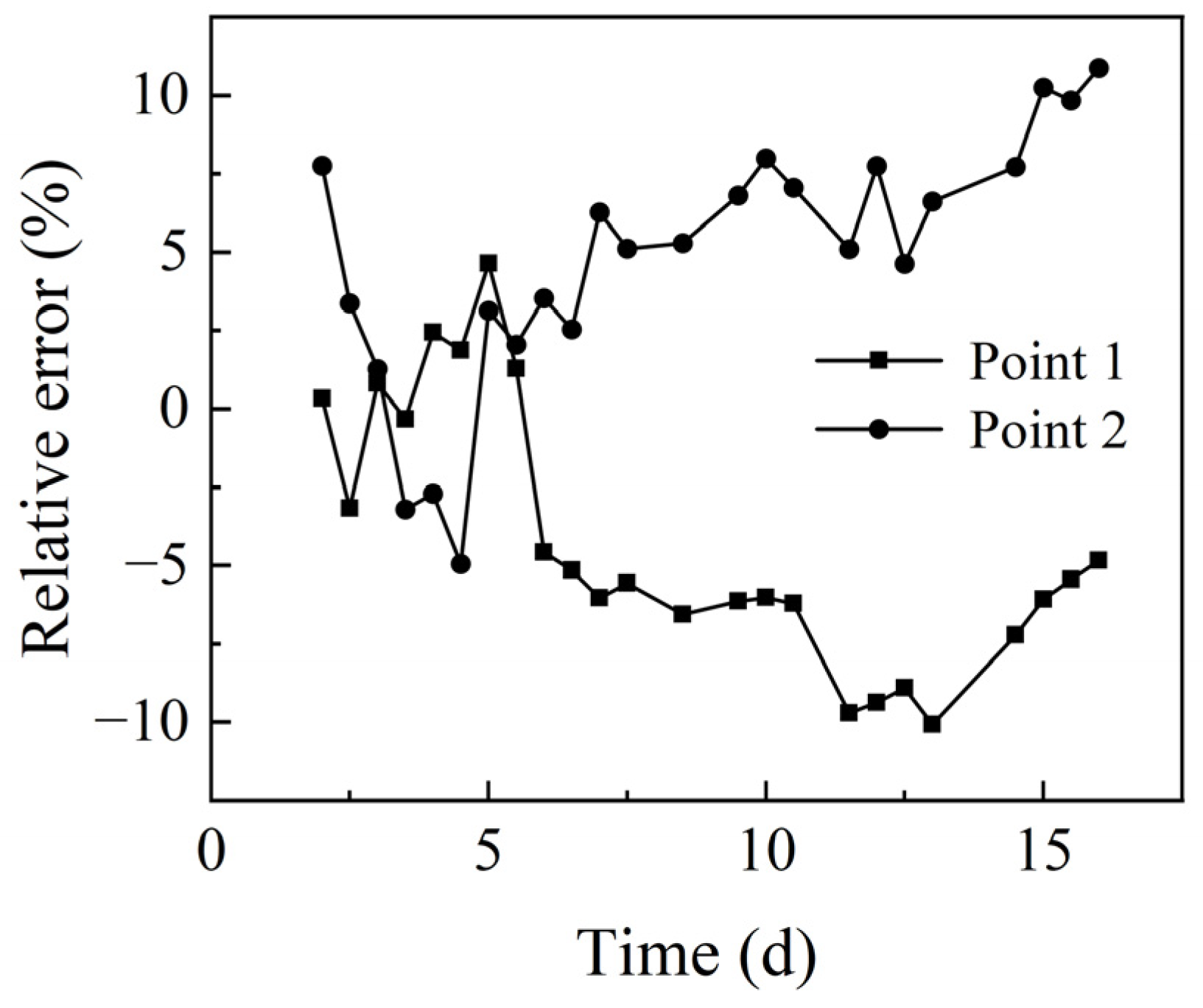
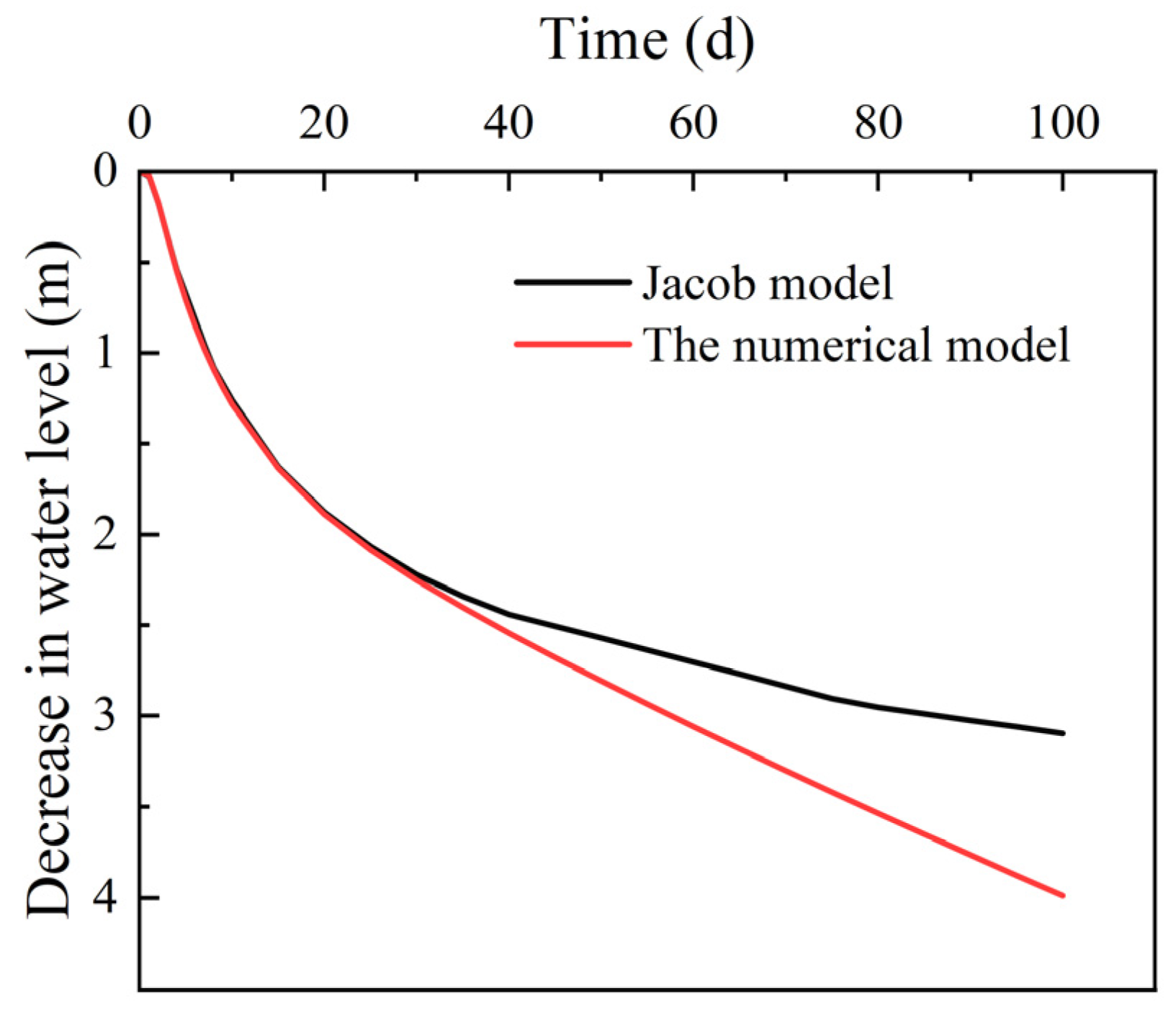
- When the soil is homogeneous and isotropic, the seepage field between the two drainage wells is distributed symmetrically. The wells can be divided into identical single wells so that the water level change in multi-well siphoning can be calculated. Comparing the numerical model with the model test and the field test, the relative error was within 10%.
- (2)
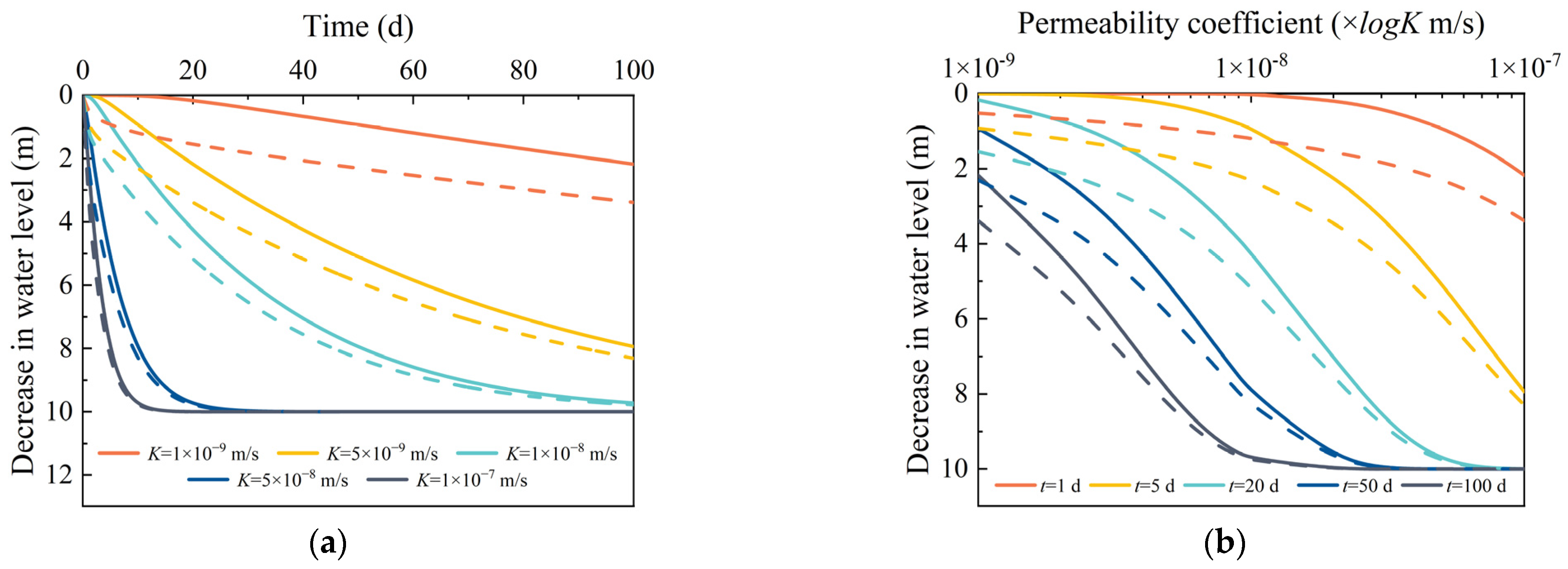
- It is feasible to apply siphon drainage technology to discharge the groundwater in soft soil. The decrease in the water level increases as the well spacing decreases or the permeability coefficient increases. When the soft soil permeability coefficient is 1 × 10−8 m/s and the well spacing is 2 m, the decrease in the water level can reach 9.72 m after 100 days of drainage.
- (3)
- Both Jacob’s model and the numerical model in this paper assume that the water level in the drainage well is fixed. However, the Jacob model considers single-well drainage, and the numerical model in this paper considers multi-well drainage. The two models basically are identical at the initial stage of drainage, after which the deviation begins to appear. The difference increases gradually with time.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-bared, M.; Marto, A. A review on the geotechnical and engineering characteristics of marine clay and the modern methods of improvements. Malays. J. Fundam. Appl. Sci. 2017, 13, 825–831. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Zhang, B.; Yu, W.; Lu, L.; Zhang, C.; Niu, T. Rheological Behaviors of Structural Soft Soil in Dongting Lake Area. Geotech. Geol. Eng. 2020, 38, 4995–5003. [Google Scholar] [CrossRef]
- Jun, S.H.; Kwon, H.J. Constitutive Relationship Proposition of Marine Soft Soil in Korea Using Finite Strain Consolidation Theory. J. Mar. Sci. Eng. 2020, 8, 429. [Google Scholar] [CrossRef]
- Kim, Y.T.; Nguyen, B.P.; Yun, D.H. Analysis of consolidation behavior of PVD-improved ground considering a varied discharge capacity. Eng. Comput. 2018, 35, 1183–1202. [Google Scholar] [CrossRef]
- Sang, Q.; Xiong, Y.; Liu, G.; Zheng, R. Experimental study on the effect of temperature on marine clay consolidation with vertical sand drains. Mar. Georesour. Geotechnol. 2020, 39, 1387–1395. [Google Scholar] [CrossRef]
- Wang, J.; Zhuang, H.; Guo, L.; Cai, Y.; Li, M.; Shi, L. Secondary compression behavior of over-consolidated soft clay after surcharge preloading. Acta Geotech. 2022, 17, 1009–1016. [Google Scholar] [CrossRef]
- Bhosle, S.; Deshmukh, V. Experimental studies on soft marine clay under combined vacuum and surcharge preloading with PVD. Int. J. Geotech. Eng. 2021, 15, 461–470. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Lei, H.; Zheng, J.; Jin, Y. Ground improvement of dredged fills with two improved vacuum preloading methods: Case study. J. Geotech. Geoenviron. Eng. 2022, 148, 05022008. [Google Scholar] [CrossRef]
- Bo, M.W.; Arulrajah, A.; Horpibulsuk, S.; Chinkulkijniwat, A.; Leong, M. Laboratory measurements of factors affecting discharge capacity of prefabricated vertical drain materials. Soils Found. 2016, 56, 129–137. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Qiao, H.; Wang, J.; Geng, X.; Wang, P.; Cai, Y. Experimental tests on effect of deformed prefabricated vertical drains in dredged soil on consolidation via vacuum preloading. Eng. Geol. 2017, 222, 10–19. [Google Scholar] [CrossRef]
- Cai, Y.; Sun, H.; Shang, Y.; Xiong, X. An investigation of flow characteristics in slope siphon drains. J. Zhejiang Univ.—Sci. A (Appl. Phys. Eng.) 2014, 15, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Sedlar, M.; Prochazka, P.; Komarek, M.; Uruba, V.; Skala, V. ProExperimental Research and Numerical Analysis of Flow Phenomena in Discharge Object with Siphon. Water 2021, 12, 3330. [Google Scholar] [CrossRef]
- Zheng, J.; Guo, J.; Wang, J.; Zhang, Y.; Lv, Q.; Sun, H. Calculation of the flow velocity of a siphon. Phys. Fluids 2021, 33, 017105. [Google Scholar] [CrossRef]
- Yu, Y.; Lv, C.; Wang, D.; Ge, Q.; Sun, H.; Shang, Y. A siphon drainage method for stabilizing bank slopes under water drawdown condition. Nat. Hazards 2020, 105, 2263–2282. [Google Scholar] [CrossRef]
- Tohari, A.; Wibawa, S.; Koizumi, K.; Oda, K.; Komatsu, M. Effectiveness of Siphon Drainage Method for Landslide Stabilization in a Tropical Volcanic Hillslope: A Case Study of Cibitung Landslide, West Java, Indonesia. Bull. Eng. Geol. Environ. 2021, 80, 2101–2116. [Google Scholar] [CrossRef]
- Sun, H.; Shuai, F.; Wang, D.; Lv, C.; Shang, Y. Vacuum formation and negative pressure transmission under a self-starting drainage process. Q. J. Eng. Geol. Hydrogeol. 2021, 54, qjegh2019-129. [Google Scholar] [CrossRef]
- Sun, H.; Wu, G.; Liang, X.; Yan, X.; Wang, D.; Wei, Z. Laboratory modeling of siphon drainage combined with surcharge loading consolidation for soft ground treatment. Mar. Georesources Geotechnol. 2018, 36, 940–949. [Google Scholar] [CrossRef]
- Wu, G.; Xie, W.; Sun, H.; Yan, X.; Tang, B. Consolidation behaviour with and without siphon drainage. Proceeding Inst. Civ. Eng.-Geotech. Eng. 2018, 171, 377–378. [Google Scholar] [CrossRef]
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage. Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Hantush, M.S.; Jacob, C.E. Non-steady radial flow in an in finite leaky aquifer. Trans. Am. Geophys. Union 1955, 36, 95–100. [Google Scholar] [CrossRef]
- Neuman, S.P. Theory of flow in unconfined aquifers considering delayed response of the water table. Water Resour. Res. 1972, 8, 1031–1045. [Google Scholar] [CrossRef]
- Sen, Z. Type curves for large-diameter wells near barriers. Ground Water 1982, 20, 274–277. [Google Scholar] [CrossRef]
- Cohen, R.M.; Rabold, R.R. Simulation of sampling and hydraulic tests to assess a hybrid monitoring well design. Ground Water Monit. Remediat. 1988, 8, 51–59. [Google Scholar] [CrossRef]
- Feng, Q.; Zhan, H. On the aquitard–aquifer interface flow and the drawdown sensitivity with a partially penetrating pumping well in an anisotropic leaky confined aquifer. J. Hydrol. 2015, 521, 74–83. [Google Scholar] [CrossRef]
- Parker, A.H.; West, L.J.; Odling, N.E. Well flow and dilution measurements for characterization of vertical hydraulic conductivity structure of a carbonate aquifer. Q. J. Eng. Geol. Hydrogeol. 2019, 52, 74–82. [Google Scholar] [CrossRef]
- Nguyen, B.P.; Nguyen, T.T.; Le, T.T.; Mridakh, A.H. Consolidation and Load Transfer Characteristics of Soft Ground Improved by Combined PVD-SC Column Method Considering Finite Discharge Capacity of PVDs. Indian Geotech. J. 2022, 53, 127–138. [Google Scholar] [CrossRef]
- Nguyen, B.P. Nonlinear Analytical Modeling of Vertical Drain-Installed Soft Soil Considering a Varied Discharge Capacity. Geotech. Geol. Eng. 2021, 39, 119–134. [Google Scholar] [CrossRef]
- Mangarengi, N.A.P.; Abdullah, N.O.; Fisu, A.F. Application of Cation Resin Regeneration for Ferrous (Fe) and Manganese (Mn) Removal from Shallow Groundwater using Packed-Bed Column with Thomas Model. IOP Conf. Ser. Earth Environ. Sci. 2022, 1117, 012046. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, J.; Shu, J.; Shang, Y.; Sun, H. Analysis of the influence of siphon hole spacing on soft-soil drainage effect. Proceeding Inst. Civ. Eng.-Geotech. Eng. 2023. ahead of print. [Google Scholar] [CrossRef]
- Jacob, C.E. Radial flow in a leaky artesian aquifer. Trans. Am. Geophys. Union 1946, 27, 198–208. [Google Scholar] [CrossRef]

| re | rw | H0 | Hw | K | μ | a | dr | dt |
|---|---|---|---|---|---|---|---|---|
| 0.16 m | 0.033 m | 0.7 m | 0.15 m | 7.93 × 10−4 m/d | 0.2 | 2.8 × 10−3 m2/d | 0.01 m | 1 × 10−3 d |
| Layers | Dredger Soil | Mucky Clay | Mucky Clay |
|---|---|---|---|
| Thickness | 10.2 m | 6.1 m | 9.4 m |
| Water content | 47.2% | 35.8% | 42.4% |
| Specific gravity | 2.74 | 2.72 | 2.74 |
| Void ratio | 1.318 | 1.052 | 1.204 |
| Liquid limit | 40.2% | 34.5% | 40.2% |
| Plastic limit | 22.2% | 20.6% | 22.2% |
| Horizontal permeability coefficient | 5.32 × 10−9 m/s | 6.24 × 10−9 m/s | 3.97 × 10−9 m/s |
| Vertical permeability coefficient | 6.95 × 10−9 m/s | 8.12 × 10−9 m/s | 5.10 × 10−9 m/s |
| Compressive modulus | 2.89 MPa | 2.57 MPa | 2.42 MPa |
| re | rw | H0 | Hw | K | μ | a | dr | dt |
|---|---|---|---|---|---|---|---|---|
| 0.51 m | 0.04 m | 18 m | 8 m | 5.31 × 10−3 m/d | 0.2 | 4.78 × 10−2 m2/d | 0.01 m | 1 × 10−4 d |
| rw | H0 | Hw | K | μ | a |
|---|---|---|---|---|---|
| 0.05 m | 15 m | 5 m | 8.64 × 10−4 m/d | 0.2 | 6.48 × 10−3 m2/d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Q.; Wu, C.; Wang, J.; Yuan, S.; Shang, Y.; Sun, H. Calculation Model of Multi-Well Siphoning and Its Feasibility Analysis of Discharging the Groundwater in Soft Soil. Water 2023, 15, 1319. https://doi.org/10.3390/w15071319
Shen Q, Wu C, Wang J, Yuan S, Shang Y, Sun H. Calculation Model of Multi-Well Siphoning and Its Feasibility Analysis of Discharging the Groundwater in Soft Soil. Water. 2023; 15(7):1319. https://doi.org/10.3390/w15071319
Chicago/Turabian StyleShen, Qingsong, Chaofeng Wu, Jun Wang, Shuai Yuan, Yuequan Shang, and Hongyue Sun. 2023. "Calculation Model of Multi-Well Siphoning and Its Feasibility Analysis of Discharging the Groundwater in Soft Soil" Water 15, no. 7: 1319. https://doi.org/10.3390/w15071319




