Simulation of Soil Water Movement and Root Uptake under Mulched Drip Irrigation of Greenhouse Tomatoes
Abstract
:1. Introduction
2. Materials and Methods
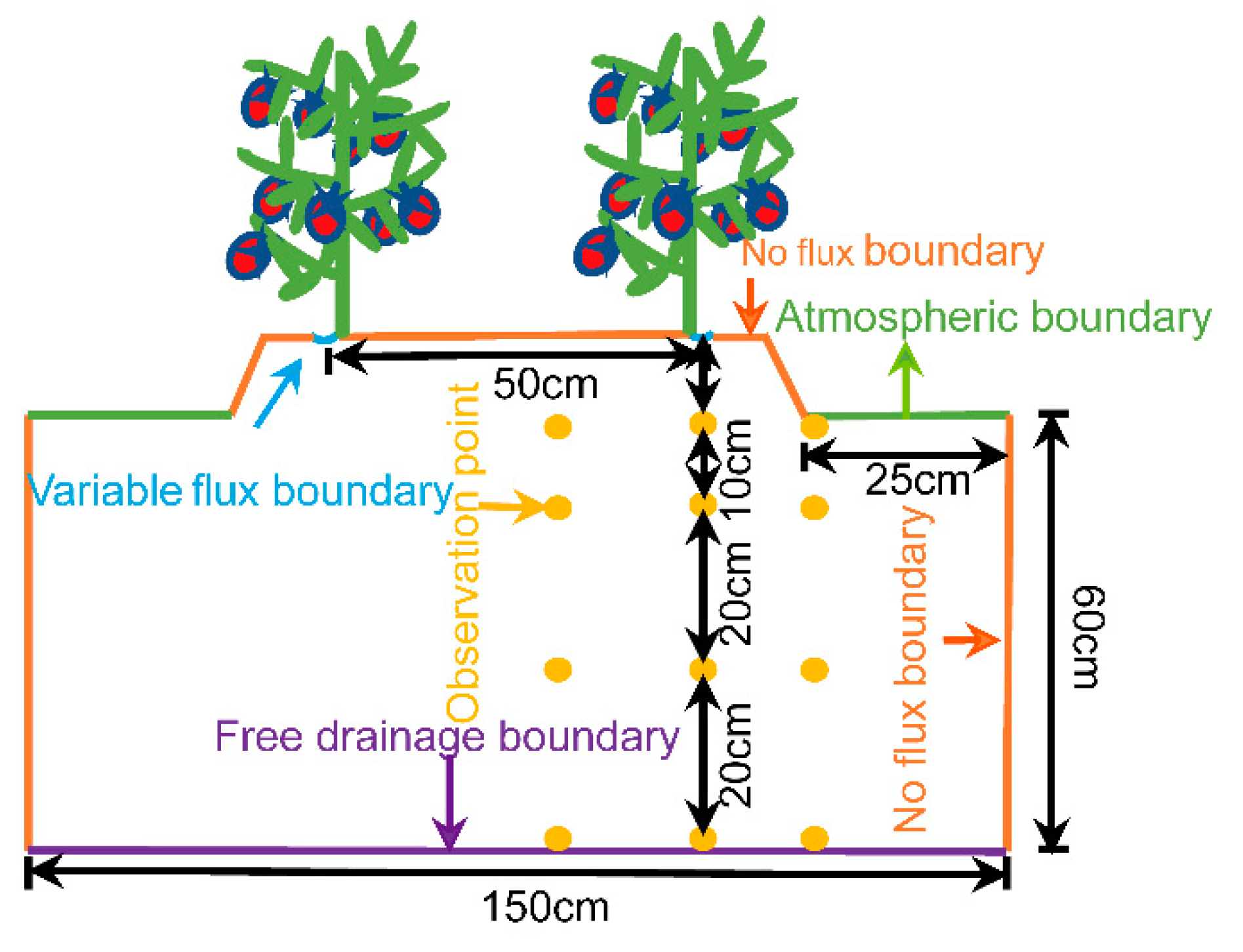
2.1. Overview of the Test Area
2.2. Experimental Design
2.3. HYDRUS-2D Model
2.3.1. Initial Conditions and Boundary Conditions
2.3.2. Root Water Uptake
2.3.3. Transpiration and Evaporation of Greenhouse Tomatoes
2.4. Susceptivity Analysis
2.5. Calibration and Validation of HYDRUS-2D Model
3. Results
3.1. Parameter Determination and Validation of Soil Water Movement Model
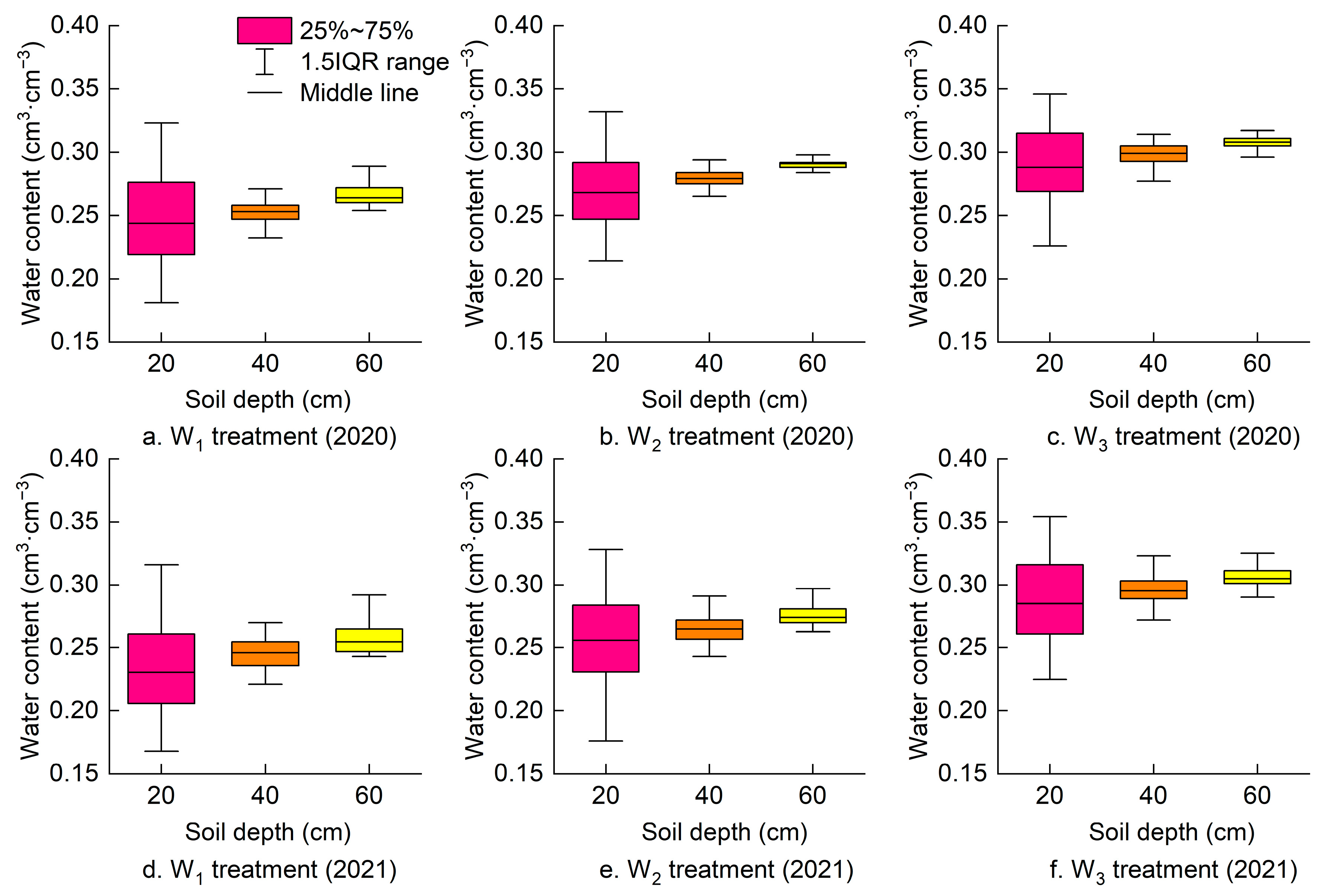
3.2. Simulation of Soil Water Movement
3.3. Simulation of Root Water Uptake
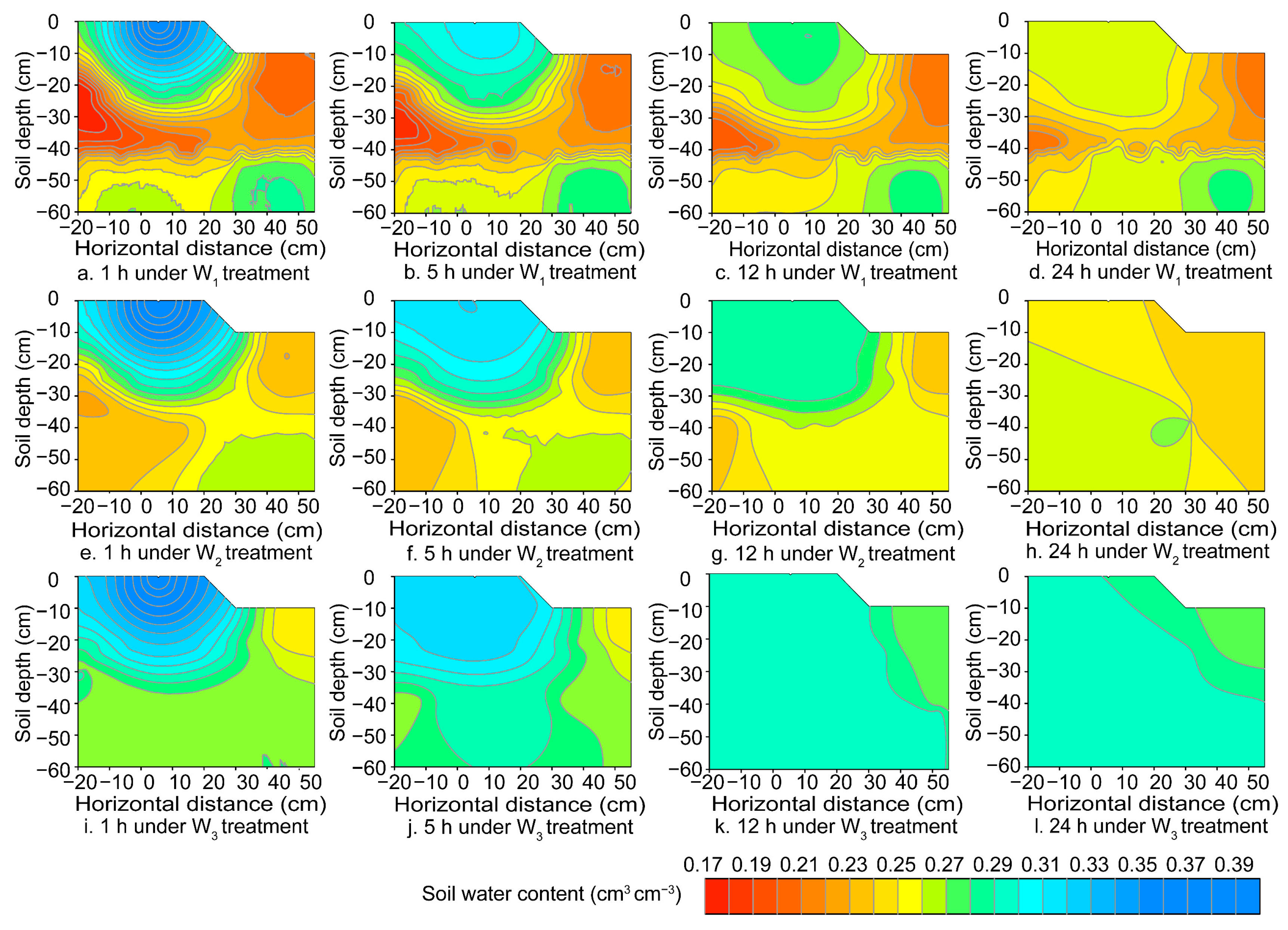
3.4. Two-Dimensional Distribution of Soil Water Content
3.5. Sensitivity of Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.M.; Lv, H.F.; Qasim, W.; Wan, L.; Wang, Y.F.; Lian, X.J.; Liu, Y.N.; Hu, J.; Wang, Z.X.; Li, G.Y.; et al. Drip fertigation with straw incorporation significantly reduces N2O emission and N leaching while maintaining high vegetable yields in solar greenhouse production. Environ. Pollut. 2021, 273, 116521. [Google Scholar] [CrossRef] [PubMed]
- Hong, M.; Zhang, Z.Y.; Fu, Q.P.; Liu, Y.P. Water Requirement of Solar Greenhouse Tomatoes with Drip Irrigation under Mulch in the Southwest of the Taklimakan Desert. Water 2022, 14, 3050. [Google Scholar] [CrossRef]
- Liu, H.J.; Yuan, B.Z.; Hu, X.D.; Yin, C.Y. Drip irrigation enhances water use efficiency without losses in cucumber yield and economic benefits in greenhouses in North China. Irrig. Sci. 2022, 40, 135–149. [Google Scholar] [CrossRef]
- Maureira, F.; Rajagopalan, K.; Stockle, C.O. Evaluating tomato production in open-field and high-tech greenhouse systems. J. Clean. Prod. 2022, 337, 130459. [Google Scholar] [CrossRef]
- Zapata-Sierra, A.J.; Moreno-Perez, M.F.; Reyes-Requena, R.; Manzano-Agugliaro, F. Root distribution with the use of drip irrigation on layered soils at greenhouses crops. Sci. Total Environ. 2021, 768, 144944. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Kang, S.Z.; Du, T.S.; Qiu, R.J.; Guo, P.; Chen, R.Q. Quantitative response of greenhouse tomato yield and quality to water deficit at different growth stages. Agric. Water Manag. 2013, 129, 152–162. [Google Scholar] [CrossRef]
- Testa, R.; di Trapani, A.M.; Sgroi, F.; Tudisca, S. Economic Sustainability of Italian Greenhouse Cherry Tomato. Sustainability 2014, 6, 7967–7981. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Shukla, M.K.; Du, T.S. Combined environmental stresses induced by drip irrigation positively affect most solar greenhouse grown tomato fruit quality. Sci. Hortic. 2021, 288, 110334. [Google Scholar] [CrossRef]
- Wu, Y.; Yan, S.C.; Fan, J.L.; Zhang, F.C.; Zhao, W.J.; Zheng, J.; Guo, J.J.; Xiang, Y.Z.; Wu, L.F. Combined effects of irrigation level and fertilization practice on yield, economic benefit and water-nitrogen use efficiency of drip-irrigated greenhouse tomato. Agric. Water Manag. 2022, 262, 107401. [Google Scholar] [CrossRef]
- Gercek, S.; Demirkaya, M.; Isik, D. Water pillow irrigation versus drip irrigation with regard to growth and yield of tomato grown under greenhouse conditions in a semi-arid region. Agric. Water Manag. 2017, 180, 172–177. [Google Scholar] [CrossRef]
- Gercek, S.; Demirkaya, M. Impact of colored water pillows on yield and water productivity of pepper under greenhouse conditions. Agric. Water Manag. 2021, 250, 106835. [Google Scholar] [CrossRef]
- Li, Y.K.; Xue, X.Z.; Xu, F.; Guo, W.Z.; Duan, M.J.; Lin, S.; Li, Y.L.; Wang, Z. Negative-pressure irrigation improves water and fertilizer use efficiencies and fruit yield of greenhouse tomato on the North China Plain*. Irrig. Drain. 2021, 70, 1027–1038. [Google Scholar] [CrossRef]
- Zotarelli, L.; Scholberg, J.M.; Dukes, M.D.; Munoz-Carpena, R.; Icerman, J. Tomato yield, biomass accumulation, root distribution and irrigation water use efficiency on a sandy soil, as affected by nitrogen rate and irrigation scheduling. Agric. Water Manag. 2009, 96, 23–34. [Google Scholar] [CrossRef]
- Ge, J.K.; Zhao, L.F.; Gong, X.W.; Lai, Z.Q.; Traore, S.; Li, Y.B.; Long, H.; Zhang, L. Combined Effects of Ventilation and Irrigation on Temperature, Humidity, Tomato Yield, and Quality in the Greenhouse. Hortscience 2021, 56, 1080–1088. [Google Scholar] [CrossRef]
- Bandte, M.; Rodriguez, M.H.; Schuch, I.; Schmidt, U.; Buettner, C. Plant viruses in irrigation water: Reduced dispersal of viruses using sensor-based disinfection. Irrig. Sci. 2016, 34, 221–229. [Google Scholar] [CrossRef]
- Vanderborght, J.; Couvreur, V.; Meunier, F.; Schnepf, A.; Vereecken, H.; Bouda, M.; Javaux, M. From hydraulic root architecture models to macroscopic representations of root hydraulics in soil water flow and land surface models. Hydrol. Earth Syst. Sci. 2021, 25, 4835–4860. [Google Scholar] [CrossRef]
- Besharat, S.; Nazemi, A.H.; Sadraddini, A.A. Parametric modeling of root length density and root water uptake in unsaturated soil. Turk. J. Agric. For. 2010, 34, 439–449. [Google Scholar] [CrossRef]
- Thomas, A.; Yadav, B.K.; Simunek, J. Root water uptake under heterogeneous soil moisture conditions: An experimental study for unraveling compensatory root water uptake and hydraulic redistribution. Plant Soil 2020, 457, 421–435. [Google Scholar] [CrossRef]
- Angaleeswari, M.; Ravikumar, V. Estimating evapotranspiration parameters by inverse modelling and non-linear optimization. Agric. Water Manag. 2019, 223, 105681. [Google Scholar] [CrossRef]
- Maharjan, G.R.; Prescher, A.K.; Nendel, C.; Ewert, F.; Mboh, C.M.; Gaiser, T.; Seidel, S.J. Approaches to model the impact of tillage implements on soil physical and nutrient properties in different agro-ecosystem models. Soil Tillage Res. 2018, 180, 210–221. [Google Scholar] [CrossRef]
- Tenreiro, T.R.; Garcia-Vila, M.; Gomez, J.A.; Jimenez-Berni, J.A.; Fereres, E. Water modelling approaches and opportunities to simulate spatial water variations at crop field level. Agric. Water Manag. 2020, 240, 106254. [Google Scholar] [CrossRef]
- Nazari, E.; Besharat, S.; Zeinalzadeh, K.; Mohammadi, A. Measurement and simulation of the water flow and root uptake in soil under subsurface drip irrigation of apple tree. Agric. Water Manag. 2021, 255, 106972. [Google Scholar] [CrossRef]
- Geng, L.; Li, L.; Li, W.; Yang, C.F.; Meng, F.J. HYDRUS-2D simulations of water movement in a drip irrigation system under soilless substrate. Int. J. Agric. Biol. Eng. 2022, 15, 210–216. [Google Scholar] [CrossRef]
- Karandish, F.; Simunek, J. A field-modeling study for assessing temporal variations of soil-water-crop interactions under water-saving irrigation strategies. Agric. Water Manag. 2016, 178, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Li, X.Y.; Shi, H.B.; Simunek, J.; Gong, X.W.; Peng, Z.Y. Modeling soil water dynamics in a drip-irrigated intercropping field under plastic mulch. Irrig. Sci. 2015, 33, 289–302. [Google Scholar] [CrossRef] [Green Version]
- Bufon, V.B.; Lascano, R.J.; Bednarz, C.; Booker, J.D.; Gitz, D.C. Soil water content on drip irrigated cotton: Comparison of measured and simulated values obtained with the Hydrus 2-D model. Irrig. Sci. 2012, 30, 259–273. [Google Scholar] [CrossRef]
- He, Q.; Li, S.; Kang, S.; Yang, H.; Qin, S. Simulation of water balance in a maize field under film-mulching drip irrigation. Agric. Water Manag. 2018, 210, 252–260. [Google Scholar] [CrossRef]
- Li, Y.; Simunek, J.; Jing, L.; Zhang, Z.; Ni, L. Evaluation of water movement and water losses in a direct-seeded-rice field experiment using Hydrus-1D. Agric. Water Manag. 2014, 142, 38–46. [Google Scholar] [CrossRef] [Green Version]
- Tafteh, A.; Sepaskhah, A.R. Application of HYDRUS-1D model for simulating water and nitrate leaching from continuous and alternate furrow irrigated rapeseed and maize fields. Agric. Water Manag. 2022, 272, 107879. [Google Scholar] [CrossRef]
- Simunek, J.; van Genuchten, M.T.; Sejna, M. Recent Developments and Applications of the HYDRUS Computer Software Packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef] [Green Version]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Han, M.; Zhao, C.; Feng, G.; Yan, Y.; Sheng, Y. Evaluating the Effects of Mulch and Irrigation Amount on Soil Water Distribution and Root Zone Water Balance Using HYDRUS-2D. Water 2015, 7, 2622–2640. [Google Scholar] [CrossRef] [Green Version]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Wiley & Sons: New York, NY, USA, 1978; Available online: https://lib.ugent.be/catalog/rug01:000032129 (accessed on 5 July 2021).
- Wesseling, J.G.; Brandyk, T. Introduction of the Occurrence of High Groundwater Levels and Surface Water Storage in Computer Program SWATRE; Institute for Land and Water Management Research (ICW): Wageningen, UK, 1985; 46p, Available online: https://edepot.wur.nl/214032 (accessed on 12 July 2021).
- Gong, X.W.; Liu, H.; Sun, J.S.; Gao, Y.; Zhang, H. Comparison of Shuttleworth-Wallace model and dual crop coefficient method for estimating evapotranspiration of tomato cultivated in a solar greenhouse. Agric. Water Manag. 2019, 217, 141–153. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration–Guidelines for Computing Crop Water Requirements–FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Available online: https://www.fao.org/3/X0490E/x0490e00.htm (accessed on 25 May 2021).
- Muller, T.; Bouleau, C.R.; Perona, P. Optimizing drip irrigation for eggplant crops in semi-arid zones using evolving thresholds. Agric. Water Manag. 2016, 177, 54–65. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.W.; Du, Y.D.; Niu, W.Q.; Han, J.X.; Li, Y.; Yang, P.G. Drip irrigation mode affects tomato yield by regulating root-soil-microbe interactions. Agric. Water Manag. 2022, 260, 107188. [Google Scholar] [CrossRef]
- Li, X.Y.; Simunek, J.; Shi, H.B.; Yan, J.W.; Peng, Z.Y.; Gong, X.W. Spatial distribution of soil water, soil temperature, and plant roots in a drip-irrigated intercropping field with plastic mulch. Eur. J. Agron. 2017, 83, 47–56. [Google Scholar] [CrossRef] [Green Version]
- Shan, G.L.; Sun, Y.R.; Zhou, H.Y.; Lammers, P.S.; Grantz, D.A.; Xue, X.Z.; Wang, Z.Y. A horizontal mobile dielectric sensor to assess dynamic soil water content and flows: Direct measurements under drip irrigation compared with HYDRUS-2D model simulation. Biosyst. Eng. 2019, 179, 13–21. [Google Scholar] [CrossRef]
- Peddinti, S.R.; Kambhammettu, B.; Lad, R.S.; Simunek, J.; Gade, R.M.; Adinarayana, J. A macroscopic soil-water transport model to simulate root water uptake in the presence of water and disease stress. J. Hydrol. 2020, 587, 124940. [Google Scholar] [CrossRef]
- Ge, J.K.; Gong, X.W.; Liu, Y.F.; Chen, H.R.; Sun, H.W.; Traore, S.; Zhang, L. The potential effects of drip irrigation on soil environment, root distribution and yield of greenhouse tomato. Eur. J. Hortic. Sci. 2022, 87, 11. [Google Scholar] [CrossRef]
- Shabbir, A.; Mao, H.P.; Ullah, I.; Buttar, N.A.; Ajmal, M.; Solangi, K.A. Improving Water Use Efficiency by Optimizing the Root Distribution Patterns under Varying Drip Emitter Density and Drought Stress for Cherry Tomato. Agronomy 2021, 11, 3. [Google Scholar] [CrossRef]
- Li, Z.Y.; Zong, R.; Wang, T.Y.; Wang, Z.H.; Zhang, J.Z. Adapting Root Distribution and Improving Water Use Efficiency via Drip Irrigation in a Jujube (Zizyphus jujube Mill.) Orchard after Long-Term Flood Irrigation. Agriculture 2021, 11, 1184. [Google Scholar] [CrossRef]
- Deb, S.K.; Shukla, M.K.; Mexal, J.G. Numerical Modeling of Water Fluxes in the Root Zone of a Mature Pecan Orchard. Soil Sci. Soc. Am. J. 2011, 75, 1667–1680. [Google Scholar] [CrossRef]
- Malash, N.M.; Flowers, T.J.; Ragab, R. Plant Water Relations Growth and Productivity of Tomato Irrigated by Different Methods with Saline and Non-Saline Water. Irrig. Drain. 2011, 60, 446–453. [Google Scholar] [CrossRef]
- Cheviron, B.; Coquet, Y. Sensitivity Analysis of Transient-MIM HYDRUS-1D: Case Study Related to Pesticide Fate in Soils. Vadose Zone J. 2009, 8, 1064–1079. [Google Scholar] [CrossRef]

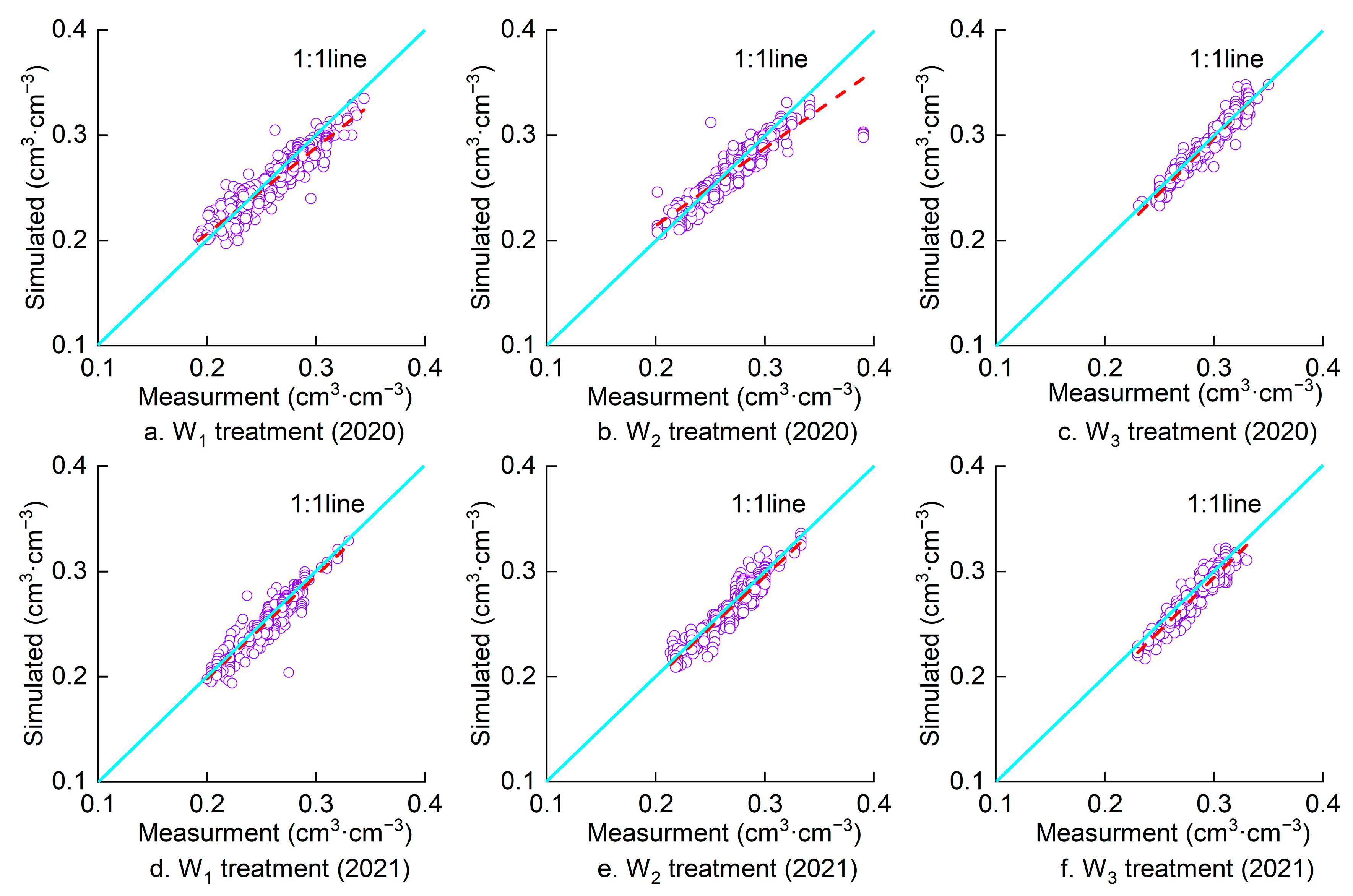

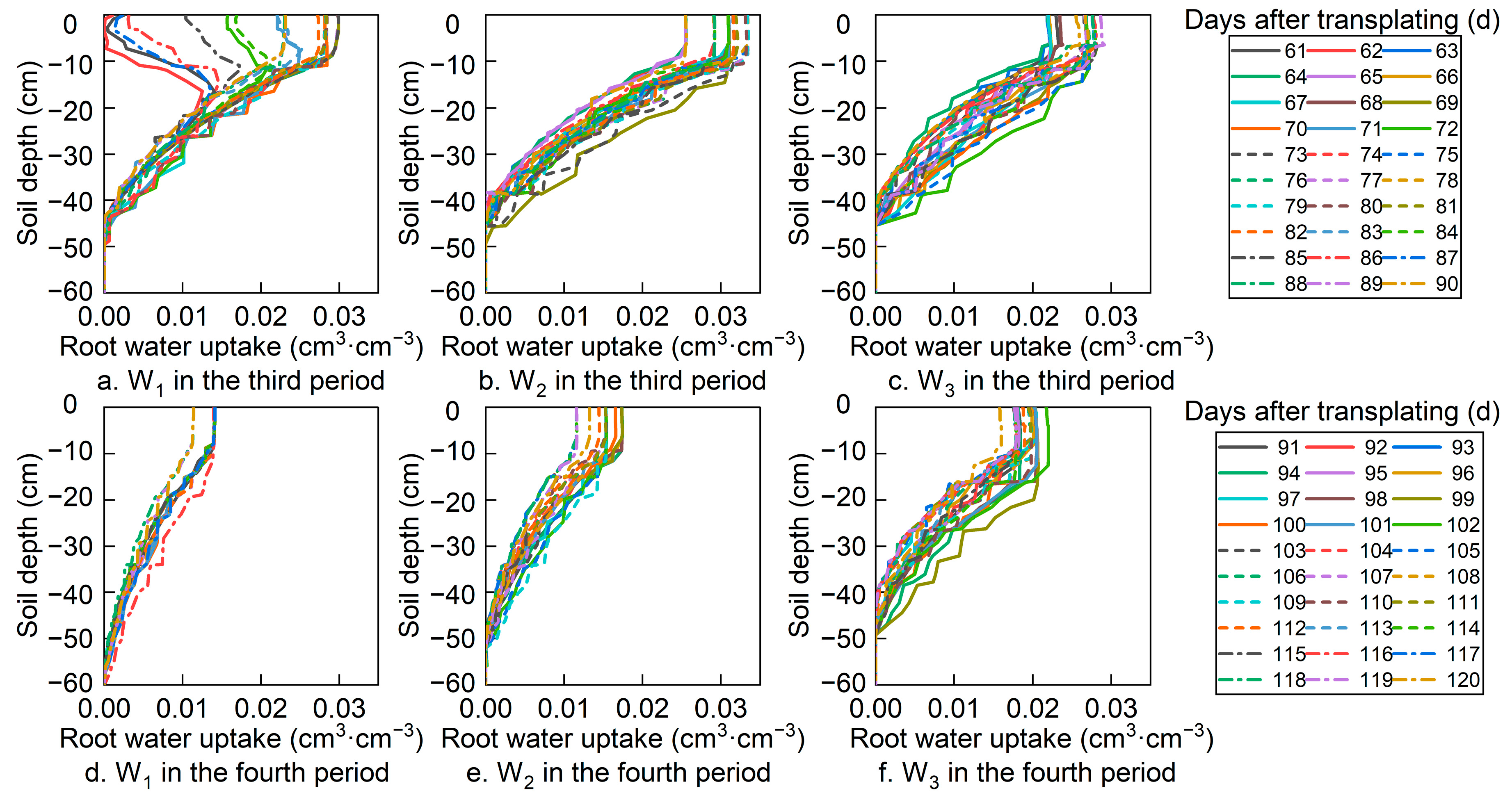
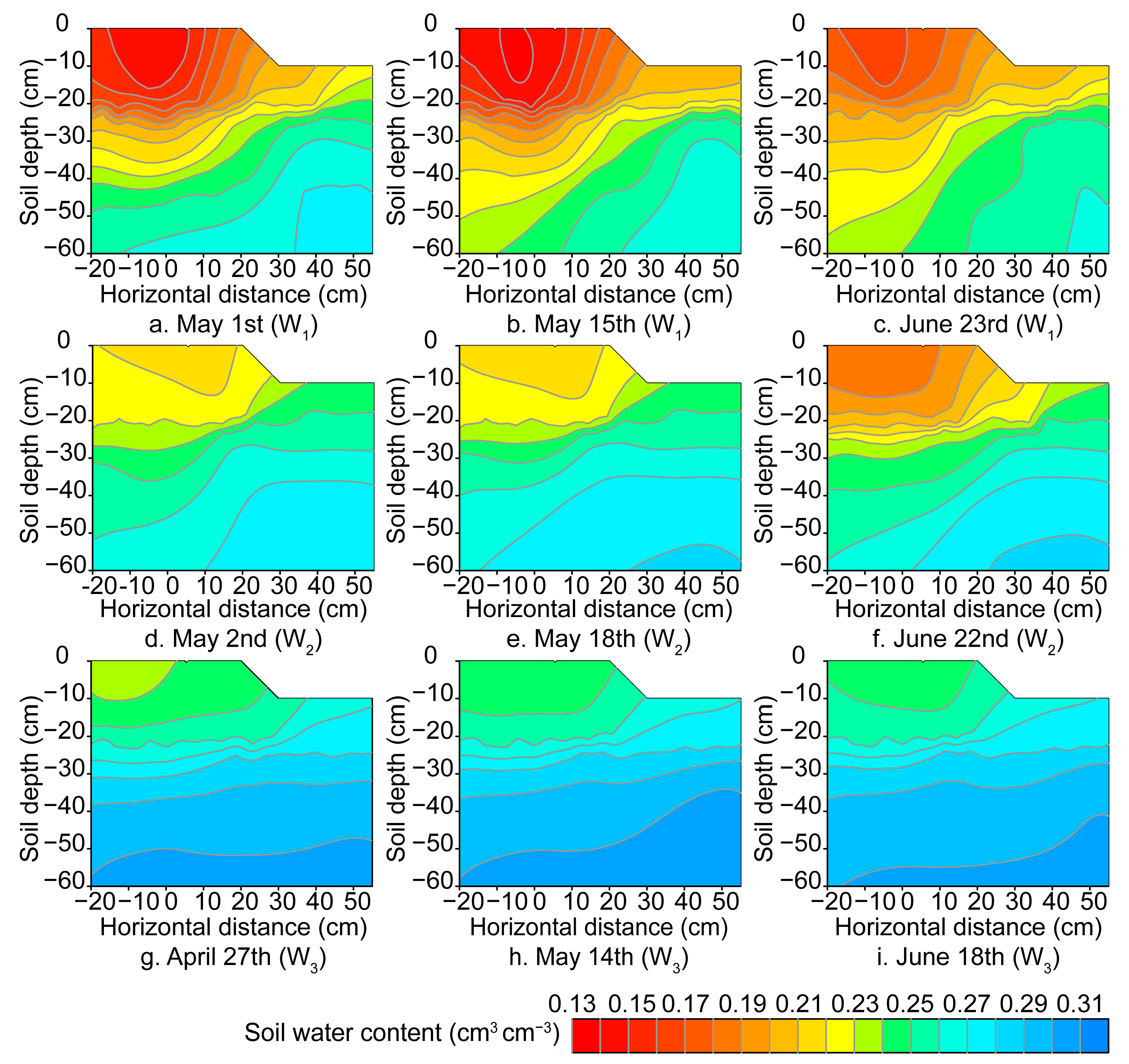
| Year | Moisture Treatment | R2 | MRE (cm3·cm−3) | RMSE (cm3·cm−3) |
|---|---|---|---|---|
| 2020 | W1 | 0.86 | 0.1260 | 0.0230 |
| W2 | 0.79 | 0.1040 | 0.0270 | |
| W3 | 0.89 | 0.0620 | 0.0140 | |
| 2021 | W1 | 0.87 | 0.0840 | 0.0170 |
| W2 | 0.89 | 0.0790 | 0.0160 | |
| W3 | 0.92 | 0.0820 | 0.0160 |
| Index | Soil Layer (cm) | ||
|---|---|---|---|
| 0–20 | 20–40 | 40–60 | |
| Residual soil moisture (cm3·cm−3) | 0.09 | 0.08 | 0.07 |
| Saturated soil moisture (cm3·cm−3) | 0.42 | 0.40 | 0.38 |
| Shape parameter (cm−1) | 0.0070 | 0.0070 | 0.0050 |
| Parameter n | 1.68 | 1.48 | 1.48 |
| Saturated hydraulic conductivity (cm·d−1) | 10.45 | 1.43 | 1.20 |
| l | 0.50 | 0.50 | 0.50 |
| Level | The Range of Ai Value | Sensitivity Characterization |
|---|---|---|
| Ⅰ | ≥1 | Highly sensitive |
| II | [0.2, 1) | Sensitive |
| III | [0.05, 0.2) | Moderate sensitivity |
| IV | [0, 0.05) | Insensitive |
| Independent Variable | Sensitivity Coefficient | ||
|---|---|---|---|
| 20cm | 40cm | 60cm | |
| α1 | −0.098 | 0.041 | 0.058 |
| n1 | −0.918 * | 0.128 | 0.233 * |
| KS1 | −0.033 | −0.043 | 0.022 |
| α2 | 0.114 | −0.255 * | −0.058 |
| n2 | 0.098 | −1.404 * | 0.291 * |
| KS2 | −0.033 | −0.043 | 0.012 |
| α3 | 0.066 | 0.128 | −0.116 |
| n3 | 0.033 | 0.128 | −1.279 * |
| KS3 | −0.033 | −0.085 | −0.116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Li, B.; Yao, M.; Mao, L.; Zhao, M.; Niu, H.; Xu, Z.; Wang, T.; Wang, J. Simulation of Soil Water Movement and Root Uptake under Mulched Drip Irrigation of Greenhouse Tomatoes. Water 2023, 15, 1282. https://doi.org/10.3390/w15071282
Sun L, Li B, Yao M, Mao L, Zhao M, Niu H, Xu Z, Wang T, Wang J. Simulation of Soil Water Movement and Root Uptake under Mulched Drip Irrigation of Greenhouse Tomatoes. Water. 2023; 15(7):1282. https://doi.org/10.3390/w15071282
Chicago/Turabian StyleSun, Lei, Bo Li, Mingze Yao, Lizhen Mao, Mingyu Zhao, Hongfei Niu, Zhanyang Xu, Tieliang Wang, and Jingkuan Wang. 2023. "Simulation of Soil Water Movement and Root Uptake under Mulched Drip Irrigation of Greenhouse Tomatoes" Water 15, no. 7: 1282. https://doi.org/10.3390/w15071282
APA StyleSun, L., Li, B., Yao, M., Mao, L., Zhao, M., Niu, H., Xu, Z., Wang, T., & Wang, J. (2023). Simulation of Soil Water Movement and Root Uptake under Mulched Drip Irrigation of Greenhouse Tomatoes. Water, 15(7), 1282. https://doi.org/10.3390/w15071282






