Impacts of Land Cover Change on the Spatial Distribution of Nonpoint Source Pollution Based on SWAT Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Watershed Description, Software, and Data Availability
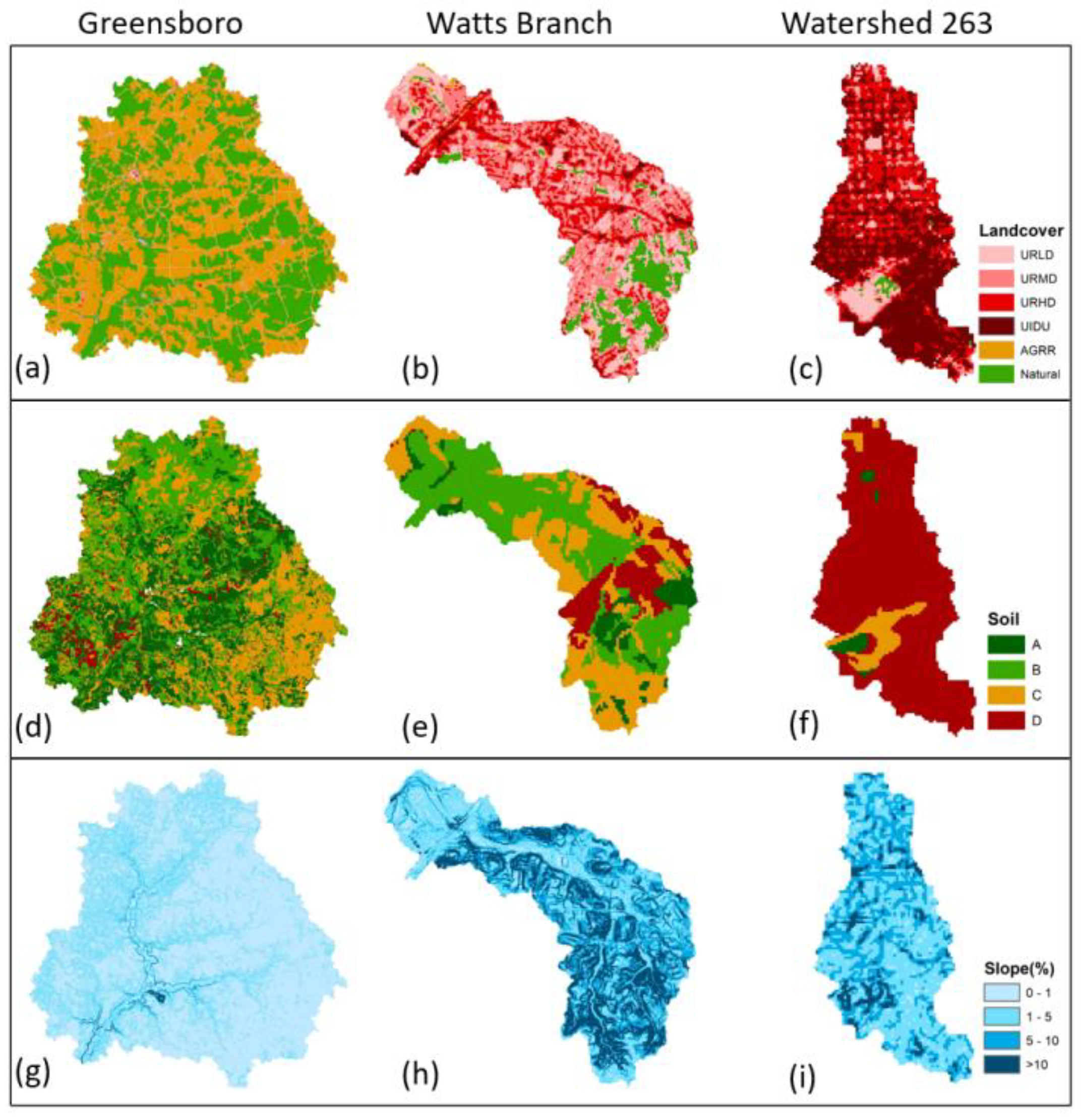
2.2. SWAT Model Parameter Development in Three Watersheds
- —observed values at time step i;
- —average observed value;
- —simulated value at time step i;
- —average simulated value.
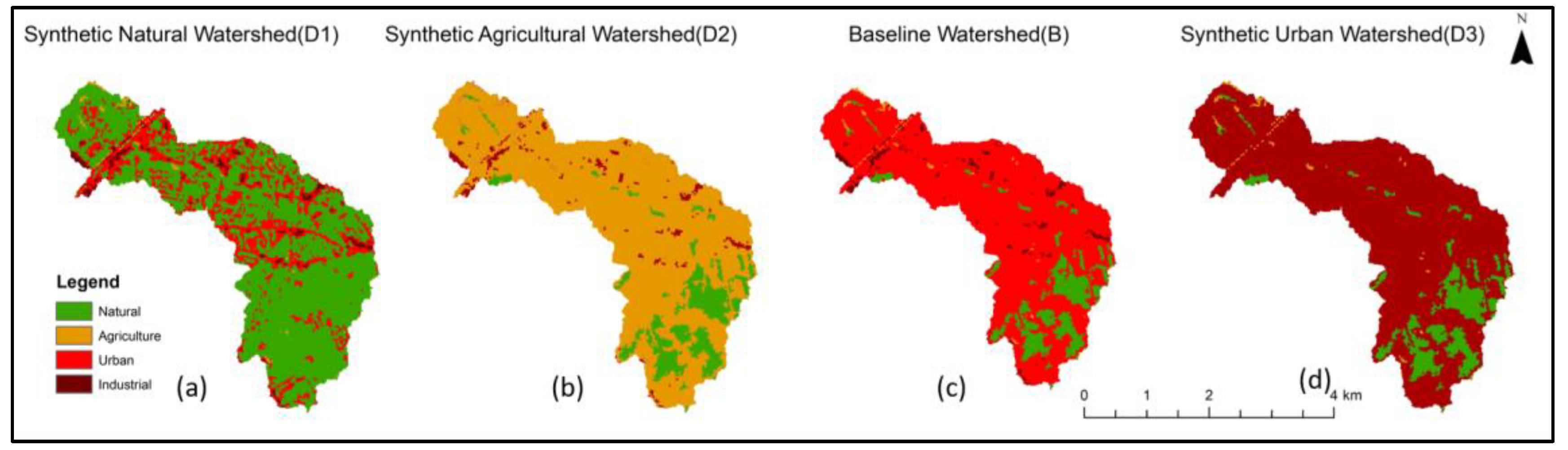
2.3. Synthetic Watershed Model Development
3. Results and Discussions
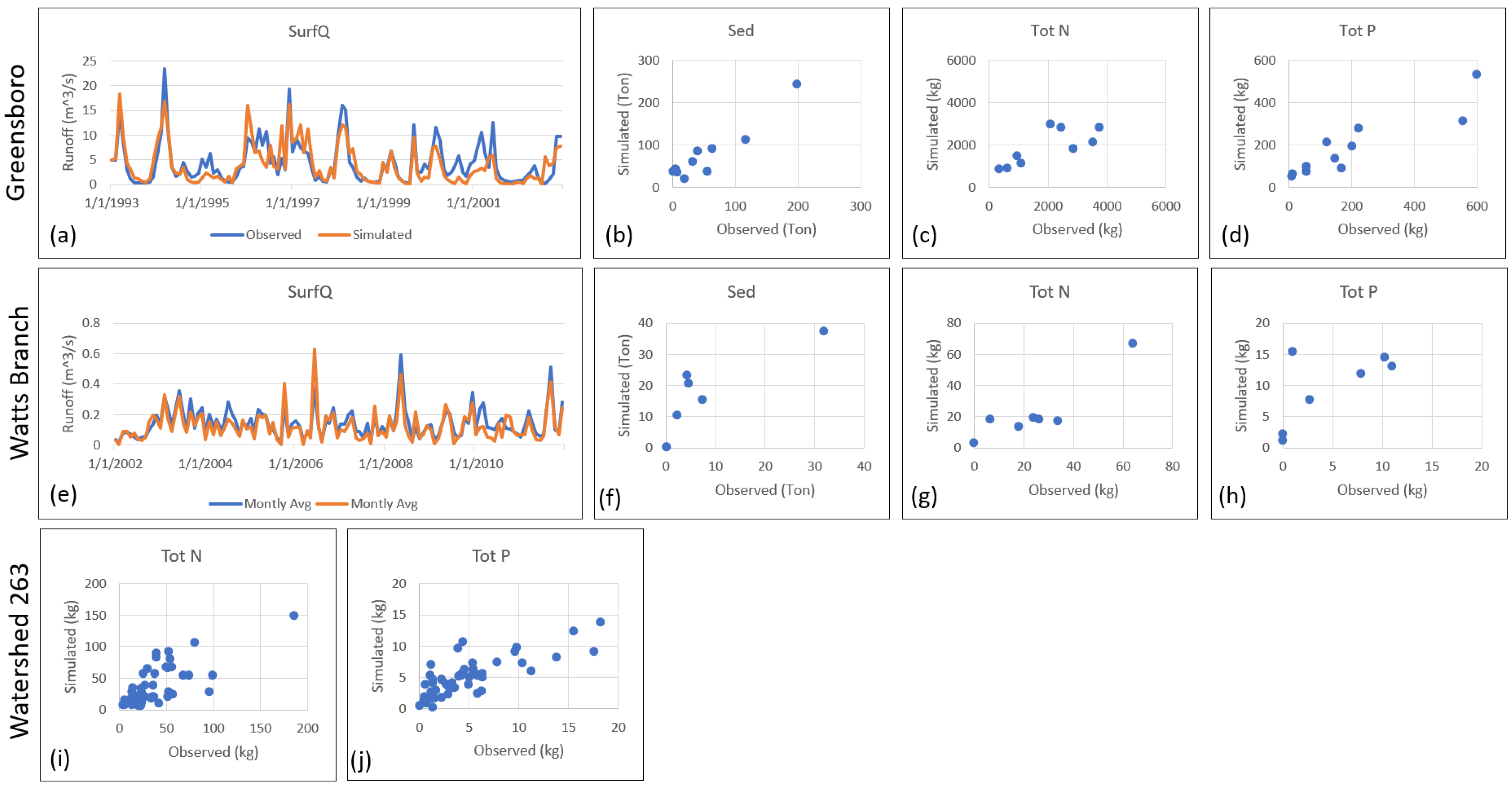
3.1. SWAT Model Performances
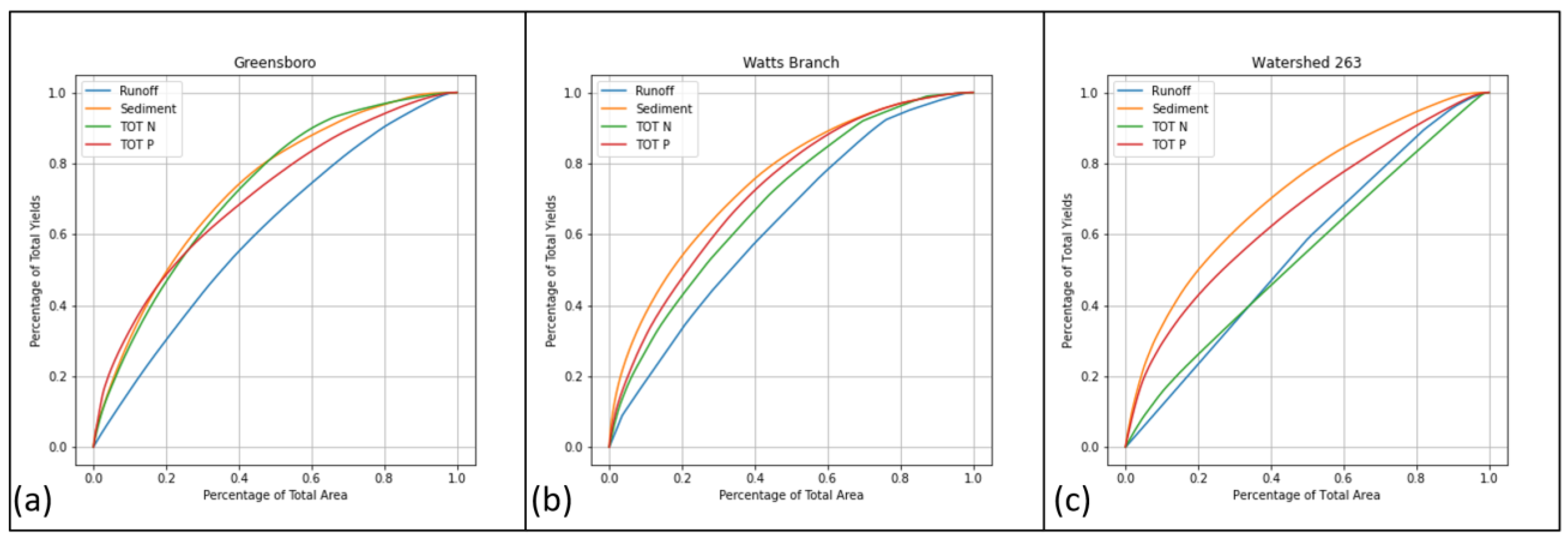
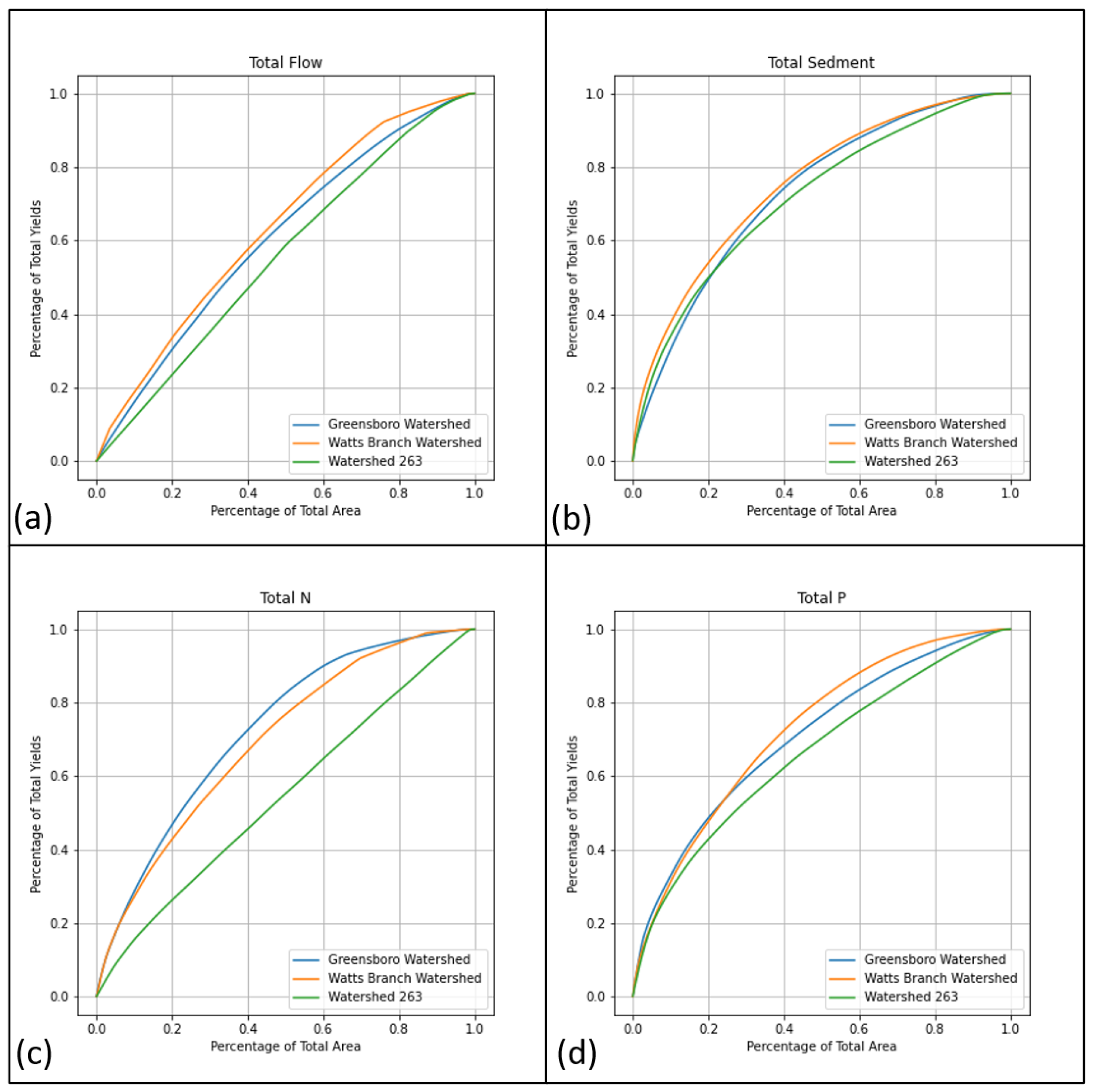
3.2. Spatial Distribution of NPS Constituents in the Three Study Watersheds
3.2.1. Mass-Area Ratio for Three Watersheds
3.2.2. Comparison of the Same Pollutant among Different Watersheds
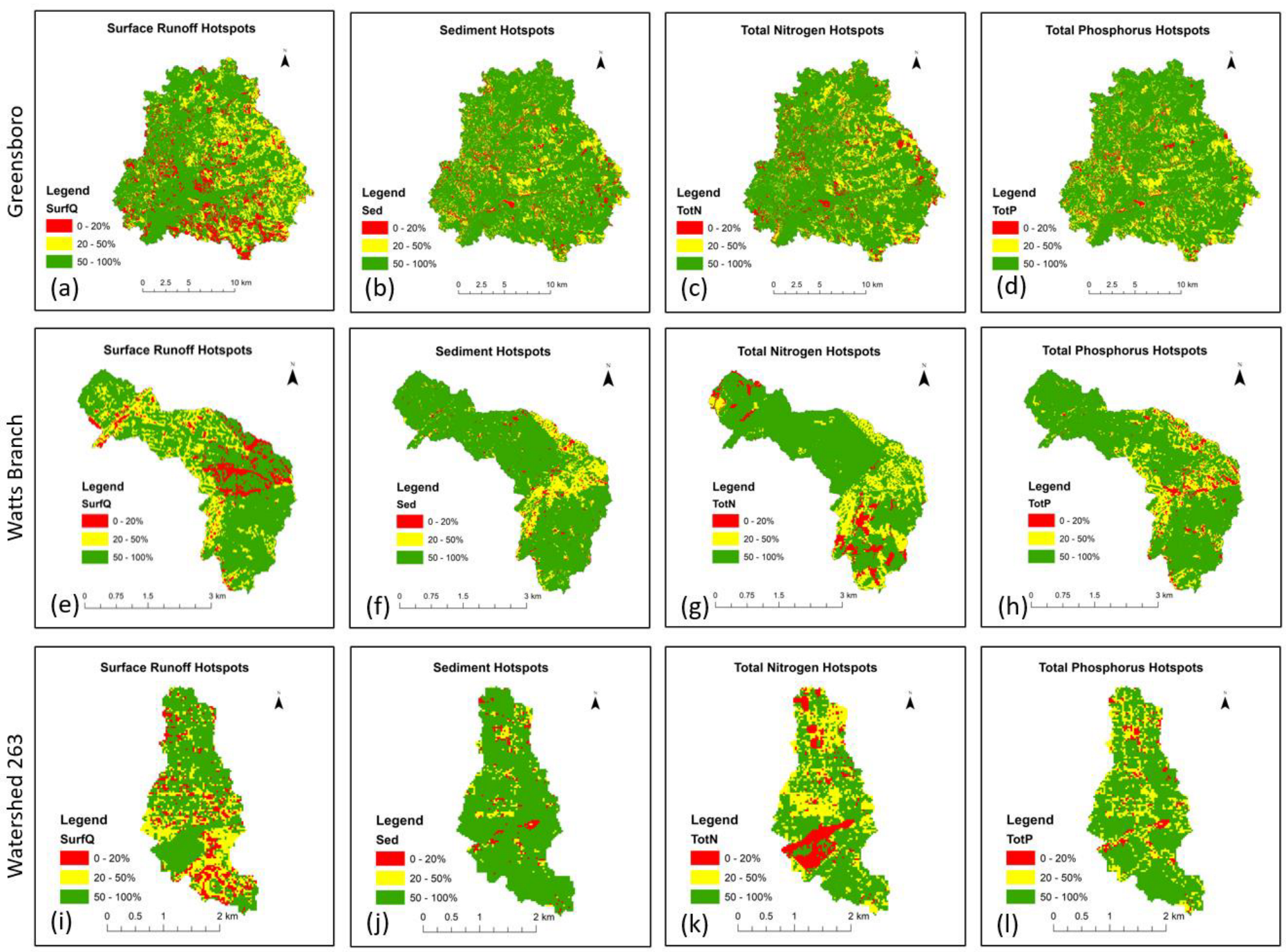
3.2.3. Hotspots’ Spatial Distribution
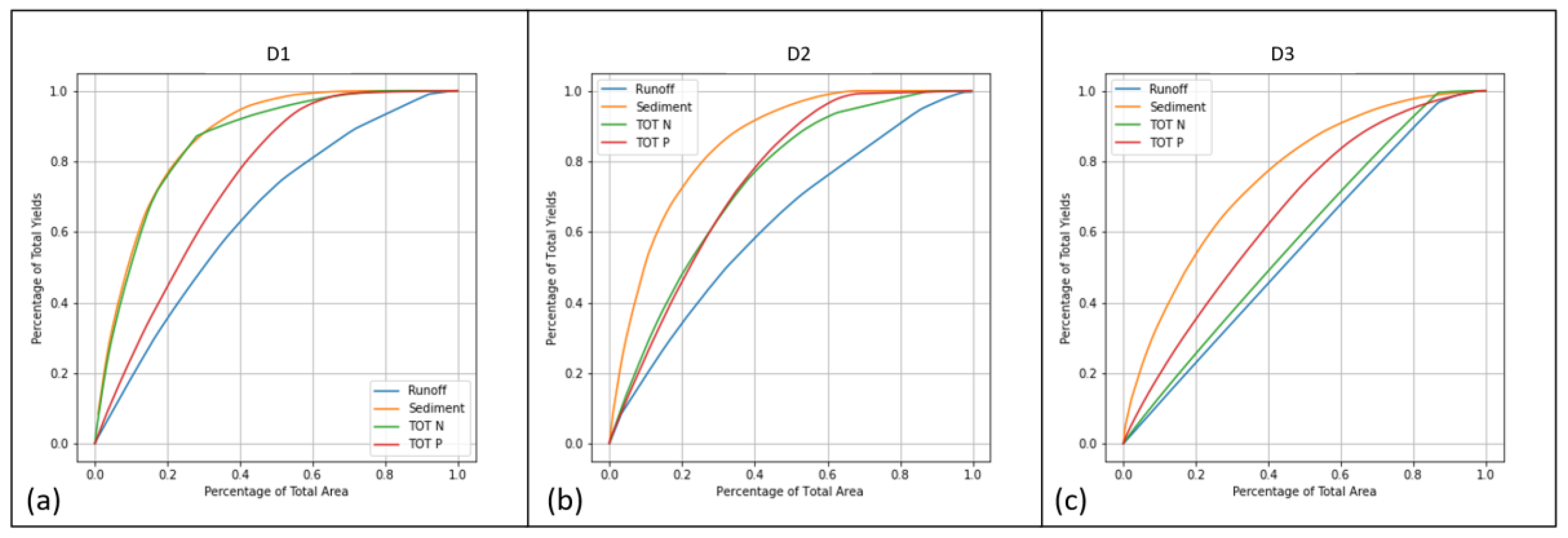
3.3. Confirming Distribution Pattern in Synthetic Watersheds
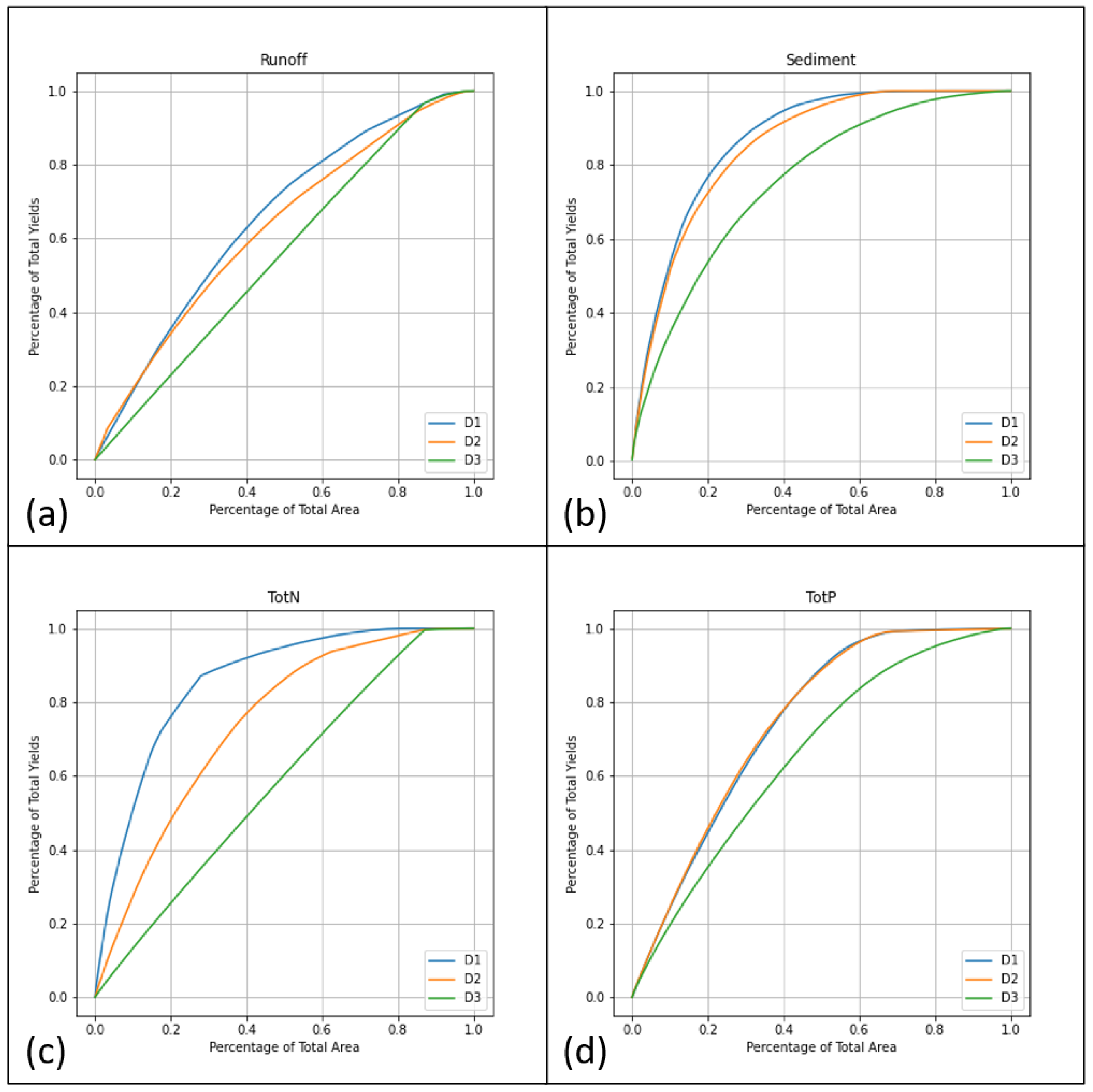
3.3.1. Mass-Area Ratio in Three Synthetic Watersheds
3.3.2. Comparison of NPS Pollutants among Synthetic Watersheds
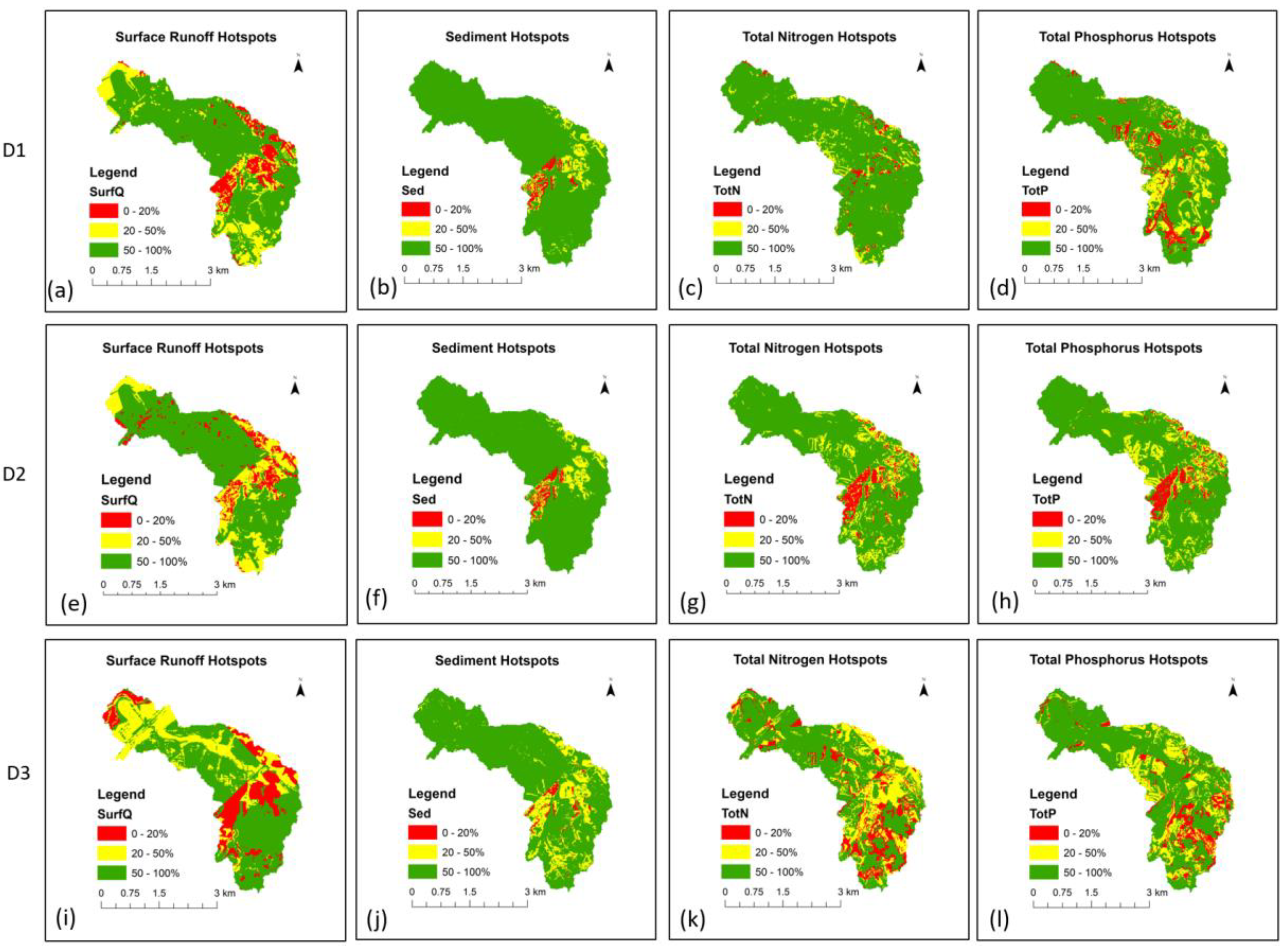
3.3.3. Spatial Distribution of Hotspots in Synthetic Watersheds
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- USEPA. National Water Quality Inventory: Report to Congress; USEPA, Office of Water: Washington, DC, USA, 2017. [Google Scholar]
- Schlimm, H. Chesapeake Bay Policy: 34 Years and Counting. Stream Conscious. 2018, 49, 7–9. [Google Scholar]
- Kemp, W.M.; Boynton, W.R.; Adolf, J.E.; Boesch, D.F.; Boicourt, W.C.; Brush, G.; Cornwell, J.C.; Fisher, T.R.; Glibert, P.M.; Hagy, J.D. Eutrophication of Chesapeake Bay: Historical trends and ecological interactions. Mar. Ecol. Prog. Ser. 2005, 303, 1–29. [Google Scholar] [CrossRef] [Green Version]
- USEPA. Guidance for Federal Land Management in the Chesapeake Bay Watershed; USEPA: Washington, DC, USA, 2010. [Google Scholar]
- Beegle, D. Nutrient management and the Chesapeake Bay. J. Contemp. Water Res. Educ. 2013, 151, 3–8. [Google Scholar] [CrossRef]
- Murphy, R.R.; Kemp, W.M.; Ball, W.P. Long-term trends in Chesapeake Bay seasonal hypoxia, stratification, and nutrient loading. Estuaries Coasts 2011, 34, 1293–1309. [Google Scholar] [CrossRef]
- Land, L.S. Chesapeake Bay nutrient pollution: Contribution from the land application of sewage sludge in Virginia. Mar. Pollut. Bull. 2012, 64, 2305–2308. [Google Scholar] [CrossRef]
- Ribaudo, M.; Savage, J.; Aillery, M. An Economic Assessment of Policy Options to Reduce Agricultural Pollutants in the Chesapeake Bay; USDA-ERS Economic Research Report; USDA: Washington, DC, USA, 2014. [Google Scholar]
- Ice, G. History of innovative best management practice development and its role in addressing water quality limited waterbodies. J. Environ. Eng. 2004, 130, 684–689. [Google Scholar] [CrossRef]
- Gao, Y.; Babin, N.; Turner, A.J.; Hoffa, C.R.; Peel, S.; Prokopy, L.S. Understanding urban-suburban adoption and maintenance of rain barrels. Landsc. Urban Plan. 2016, 153, 99–110. [Google Scholar] [CrossRef]
- Niraula, R.; Kalin, L.; Srivastava, P.; Anderson, C.J. Identifying critical source areas of nonpoint source pollution with SWAT and GWLF. Ecol. Model. 2013, 268, 123–133. [Google Scholar] [CrossRef]
- Shore, M.; Jordan, P.; Mellander, P.-E.; Kelly-Quinn, M.; Wall, D.; Murphy, P.; Melland, A. Evaluating the critical source area concept of phosphorus loss from soils to water-bodies in agricultural catchments. Sci. Total Environ. 2014, 490, 405–415. [Google Scholar] [CrossRef]
- Shang, X.; Wang, X.; Zhang, D.; Chen, W.; Chen, X.; Kong, H. An improved SWAT-based computational framework for identifying critical source areas for agricultural pollution at the lake basin scale. Ecol. Model. 2012, 226, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Montas, H.J.; Brubaker, K.L.; Leisnham, P.T.; Shirmohammadi, A.; Chanse, V.; Rockler, A.K. Impact of spatial discretization of hydrologic models on spatial distribution of nonpoint source pollution hotspots. J. Hydrol. Eng. 2016, 21, 04016047. [Google Scholar] [CrossRef] [Green Version]
- Xiang, C.; Wang, Y.; Liu, H. A scientometrics review on nonpoint source pollution research. Ecol. Eng. 2017, 99, 400–408. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic modeling: Progress and future directions. Geosci. Lett. 2018, 5, 15–33. [Google Scholar] [CrossRef]
- Knisel, W.G. CREAMS: A Field Scale Model for Chemicals, Runoff, and Erosion from Agricultural Management Systems; Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1980. [Google Scholar]
- Carter, H.; Eslinger, D. Nonpoint Source Pollution and Erosion Comparison Tool (N-SPECT) Technical Guide; National Oceanic and Atmospheric Administration: Washington, DC, USA, 2004. [Google Scholar]
- Tetra Tech; Sam Nunn Atlanta Federal Center. Loading Simulation Program in C++ (LSPC) Version 3.1 User’s Manual; Tetra Tech: Fairfax, VA, USA, 2009. [Google Scholar]
- Srinivasan, R.; Zhang, X.; Arnold, J. SWAT ungauged: Hydrological budget and crop yield predictions in the Upper Mississippi River Basin. Trans. ASABE 2010, 53, 1533–1546. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef] [Green Version]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Griensven, A.v.; Liew, M.W.V.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Huber, W.C.; Rossman, L.A.; Dickinson, R.E. EPA storm water management model, SWMM5. Watershed Model. 2005, 338, 359. [Google Scholar]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Arabi, M.; Frankenberger, J.R.; Engel, B.A.; Arnold, J.G. Representation of agricultural conservation practices with SWAT. Hydrol. Process. Int. J. 2008, 22, 3042–3055. [Google Scholar] [CrossRef]
- Krysanova, V.; Arnold, J.G. Advances in ecohydrological modelling with SWAT—A review. Hydrol. Sci. J. 2009, 53, 939–947. [Google Scholar] [CrossRef]
- Laurent, F.; Ruelland, D. Assessing impacts of alternative land use and agricultural practices on nitrate pollution at the catchment scale. J. Hydrol. 2011, 409, 440–450. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, S.; Liu, L.; Guo, X.; Wang, Z.; Qin, C.; Hao, R.; Lu, J.; Gao, J. Assessing the effects of land use changes on non-point source pollution reduction for the Three Gorges Watershed using the SWAT model. J. Environ. Inform. 2013, 22, 13–26. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, L. Hydrological and Water Quality Assessment in a Suburban Watershed with Mixed Land Uses Using the SWAT Model. J. Hydrol. Eng. 2014, 19, 816–827. [Google Scholar] [CrossRef]
- Shen, Z.; Qiu, J.; Hong, Q.; Chen, L. Simulation of spatial and temporal distributions of non-point source pollution load in the Three Gorges Reservoir Region. Sci. Total Environ. 2014, 493, 138–146. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Yang, X.; Haywood, J. A review of SWAT applications, performance and future needs for simulation of hydro-climatic extremes. Adv. Water Resour. 2020, 143, 103662. [Google Scholar] [CrossRef]
- Nicks, A.; Harp, J. Stochastic generation of temperature and solar radiation data. J. Hydrol. 1980, 48, 1–17. [Google Scholar] [CrossRef]
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnold, J. ArcSWAT Interface for SWAT 2009; User’s Guide; Blackland Research Center, Texas Agricultural Experiment Station: Temple, TX, USA, 2010. [Google Scholar]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Program—A User Manual; Eawag: Dübendorf, Switzerland, 2015. [Google Scholar]
- Arnold, J.; Kiniry, J.; Srinivasan, R.; Williams, J.; Haney, E.; Neitsch, S. SWAT 2012 Input/Output Documentation; Texas Water Resources Institute: College Station, TX, USA, 2013. [Google Scholar]
- Renkenberger, J.; Montas, H.; Leisnham, P.T.; Chanse, V.; Shirmohammadi, A.; Sadeghi, A.; Brubaker, K.; Rockler, A.; Hutson, T.; Lansing, D. Climate change impact on critical source area identification in a Maryland watershed. Trans. ASABE 2016, 59, 1803–1819. [Google Scholar]
- Renkenberger, J.; Montas, H.; Leisnham, P.T.; Chanse, V.; Shirmohammadi, A.; Sadeghi, A.; Brubaker, K.; Rockler, A.; Hutson, T.; Lansing, D. Effectiveness of best management practices with changing climate in a Maryland watershed. Trans. ASABE 2017, 60, 769. [Google Scholar] [CrossRef]
- Wang, Y. A Diagnostic Decision Support System for Selecting Best Management Practices in Urban/Suburban Watersheds; University of Maryland: College Park, MD, USA, 2015. [Google Scholar]
- Khalid, K.; Ali, M.; Abd Rahman, N.; Mispan, M. Application on one-at-a-time sensitivity analysis of semi-distributed hydrological model in tropical watershed. Int. J. Eng. Technol. 2016, 8, 132–136. [Google Scholar] [CrossRef] [Green Version]
- Cho, J.; Her, Y.; Bosch, D. Sensitivity of simulated conservation practice effectiveness to representation of field and in-stream processes in the Little River Watershed. Environ. Model. Assess. 2017, 22, 159–173. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Vaghefi, S.A.; Srinivasan, R. A guideline for successful calibration and uncertainty analysis for soil and water assessment: A review of papers from the 2016 international SWAT conference. Water 2018, 10, 6. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wilson, C.; Weng, Q. Assessing surface water quality and its relation with urban land cover changes in the Lake Calumet Area, Greater Chicago. Environ. Manag. 2010, 45, 1096–1111. [Google Scholar] [CrossRef]
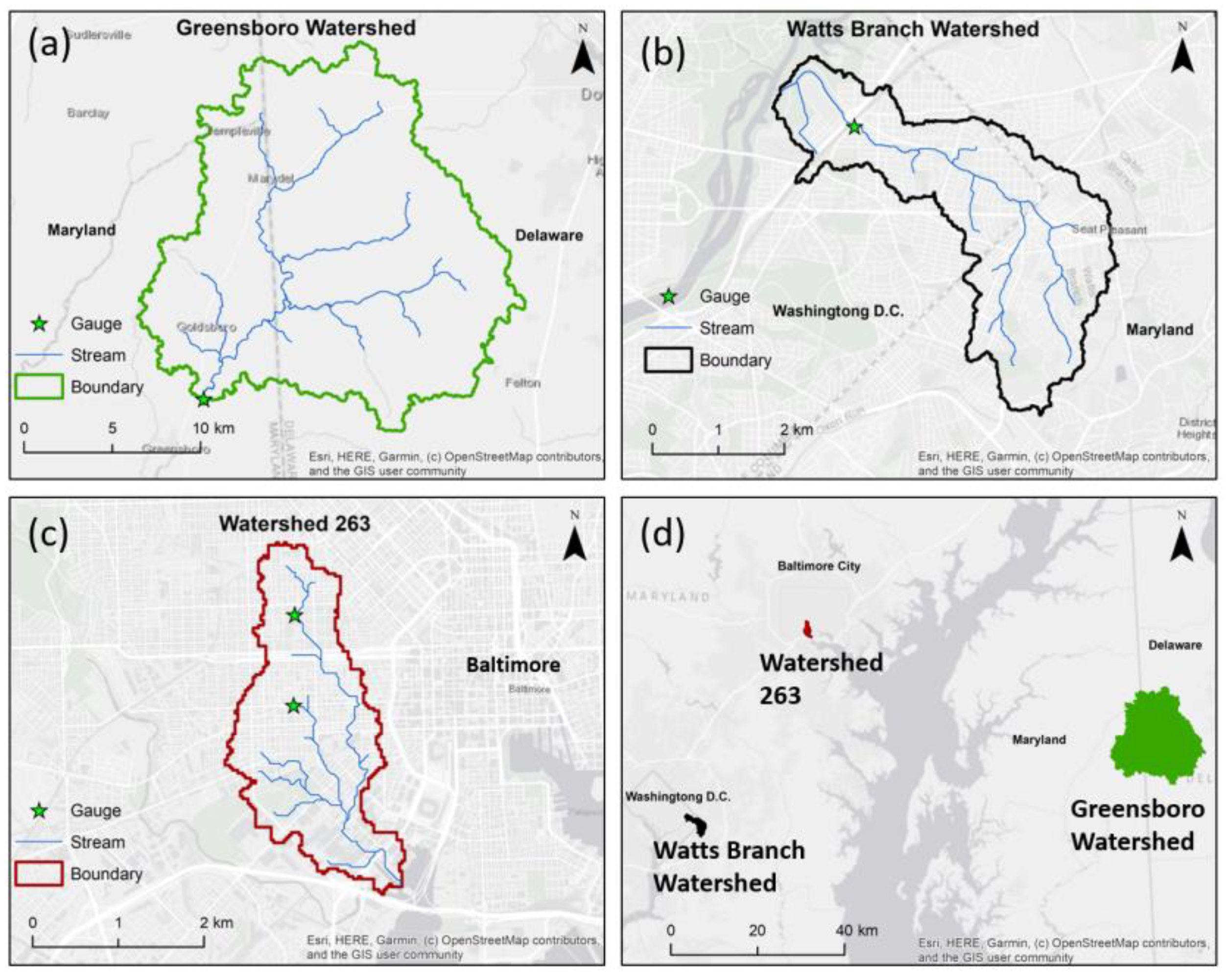
| Greensboro | Watts Branch | Watershed 263 | |
|---|---|---|---|
| Software | |||
| Model Development | ArcSWAT | ArcSWAT | ArcSWAT |
| Spatial Analysis | ArcGIS | ArcGIS | ArcGIS |
| Model Calibration | SWAT-CUP | SWAT-CUP | SWAT-CUP |
| Spatial Data | |||
| Topography | USGS NED 2006 30 m DEM | USGS NED 2006 30 m DEM | USGS NED 2006 30 m DEM |
| Land Use/Land Cover | NLCD 2006 30 m shapefile | NLCD 2006 30 m Shapefile | NLCD 2006 30 m Shapefile |
| Soils | SSRUGO 2012 1:24,000 shapefile | SSURGO 2012 1:24,000 Shapefile | SSURGO 2012 1:24,000 Shapefile |
| Time-series Data | |||
| Discharge (SurfQ) | USGS NO. 1,491,000, Points: 3651 | USGS N0. 1,651,800, Points: 3651 | NA |
| Total Sediment (Sed) | USGS NO. 1,491,000, Points: 197 | Points: 8 daily grab samples | NA |
| Total Nitrogen (Tot N) | USGS NO. 1,491,000, Points: 224 | Points: 8 daily grab samples | Points: 120 daily grab samples |
| Total Phosphorus (Tot P) | USGS NO. 1,491,000, Points: 217 | Points: 8 daily grab samples | Points: 120 daily grab samples |
| Weather Data | TAMU NOAA NCDC Stations: Precipitation, temperature, relative humidity, solar radiation, wind speed | Washington National Airport, VA, USW00013743, precipitation, temperature | Maryland Science Center, MD, USW00093784, precipitation, temperature |
| Synthetic Natural Watershed (D1) | Synthetic Agricultural Watershed (D2) | Baseline Watershed (B) | Synthetic Urban Watershed (D3) | |||||
|---|---|---|---|---|---|---|---|---|
| Area (ha) | Percentage (%) | Area (ha) | Percentage (%) | Area (ha) | Percentage (%) | Area (ha) | Percentage (%) | |
| Natural | 751.35 | 72.15 | 134.26 | 12.90 | 134.26 | 12.90 | 134.26 | 12.90 |
| Agriculture | 3.66 | 0.35 | 871.98 | 83.77 | 3.66 | 0.35 | 3.66 | 0.35 |
| Urban Residential | 286.25 | 27.5 | 0 | 0 | 868.32 | 83.42 | 0 | 0 |
| Industrial | 0 | 0 | 34.66 | 3.33 | 34.66 | 3.33 | 902.98 | 86.85 |
| Greensboro Watershed (Annual) | Watts Branch Watershed (Daily) | Watershed 263 (Annual) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | NSE | PBIAS (%) | R2 | NSE | PBIAS (%) | R2 | NSE | PBIAS (%) | |
| SurfQ | 0.64 | 0.51 | −10.17 | 0.76 | 0.73 | 17.4 | NON | ||
| Sed | 0.85 | 0.57 | 50.12 | 0.75 | 0.57 | 57 | |||
| Tot N | 0.60 | 0.47 | −13.2 | 0.77 | 0.79 | −9.2 | 0.67 | 0.50 | 5.2 |
| Tot P | 0.83 | 0.79 | −5.83 | 0.92 | 0.45 | 58.2 | 0.66 | 0.50 | 5.3 |
| SurfQ (mm) | Sed (t/ha) | Tot N (kg/ha) | Tot P (kg/ha) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Output (%) | 20 | 50 | 20 | 50 | 20 | 50 | 20 | 50 | |
| Greensboro watershed | area (%) | 12.63 | 33.48 | 5.7 | 20.35 | 6.2 | 22.08 | 4.08 | 21.13 |
| Threshold | 345.63 | 273.84 | 4.146 | 1.54 | 13.02 | 10.79 | 5. 60 | 2.58 | |
| Watts Branch | area (%) | 10.91 | 33.29 | 3.09 | 17.19 | 6.2 | 25.45 | 5.11 | 21.7 |
| Threshold | 358.01 | 241.14 | 7.70 | 4.99 | 23.51 | 21.63 | 6.81 | 4.40 | |
| Watershed 263 | area (%) | 17.1 | 42.65 | 4.31 | 20.09 | 14.05 | 44.66 | 5.21 | 26.72 |
| Threshold | 811.51 | 811.14 | 8.44 | 3.53 | 19.11 | 17.98 | 6.49 | 3.49 | |
| SurfQ (mm) | Sed (t/ha) | Tot N (kg/ha) | Tot P (kg/ha) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Output (%) | 20 | 50 | 20 | 50 | 20 | 50 | 20 | 50 | |
| D1 | Area (%) | 10.81 | 29.83 | 2.71 | 9.05 | 2.84 | 9.78 | 8.12 | 22.83 |
| Threshold | 307.70 | 242.42 | 2.636 | 1.404 | 8.21 | 4.93 | 5.90 | 4.84 | |
| D2 | Area (%) | 10.65 | 32.48 | 2.74 | 9.47 | 6.98 | 21.19 | 7.96 | 22.40 |
| Threshold | 420.68 | 307.99 | 6.273 | 3.778 | 25.77 | 16.97 | 10.31 | 8.34 | |
| D3 | Area (%) | 17.29 | 44.09 | 4.45 | 18.03 | 15.46 | 41.00 | 9.87 | 30.67 |
| Threshold | 688.60 | 683.26 | 9.513 | 5.140 | 11.94 | 11.24 | 11.09 | 8.78 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Montas, H.; Shirmohammadi, A.; Leisnham, P.T.; Negahban-Azar, M. Impacts of Land Cover Change on the Spatial Distribution of Nonpoint Source Pollution Based on SWAT Model. Water 2023, 15, 1174. https://doi.org/10.3390/w15061174
Zhang Z, Montas H, Shirmohammadi A, Leisnham PT, Negahban-Azar M. Impacts of Land Cover Change on the Spatial Distribution of Nonpoint Source Pollution Based on SWAT Model. Water. 2023; 15(6):1174. https://doi.org/10.3390/w15061174
Chicago/Turabian StyleZhang, Zeshu, Hubert Montas, Adel Shirmohammadi, Paul T. Leisnham, and Masoud Negahban-Azar. 2023. "Impacts of Land Cover Change on the Spatial Distribution of Nonpoint Source Pollution Based on SWAT Model" Water 15, no. 6: 1174. https://doi.org/10.3390/w15061174







