On a Problem of Marine Current Velocity Estimation from Microwave Radar Data
Abstract
:1. Introduction
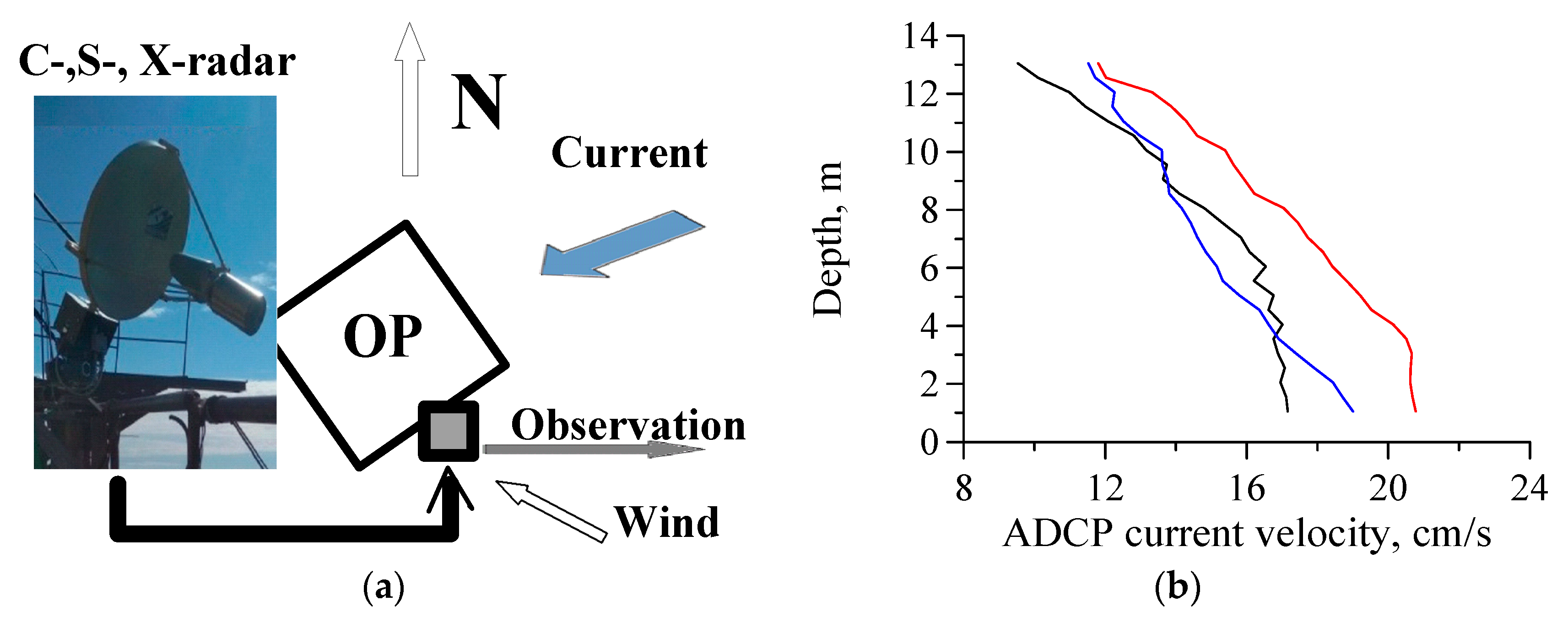
2. Apparatus and Experiment
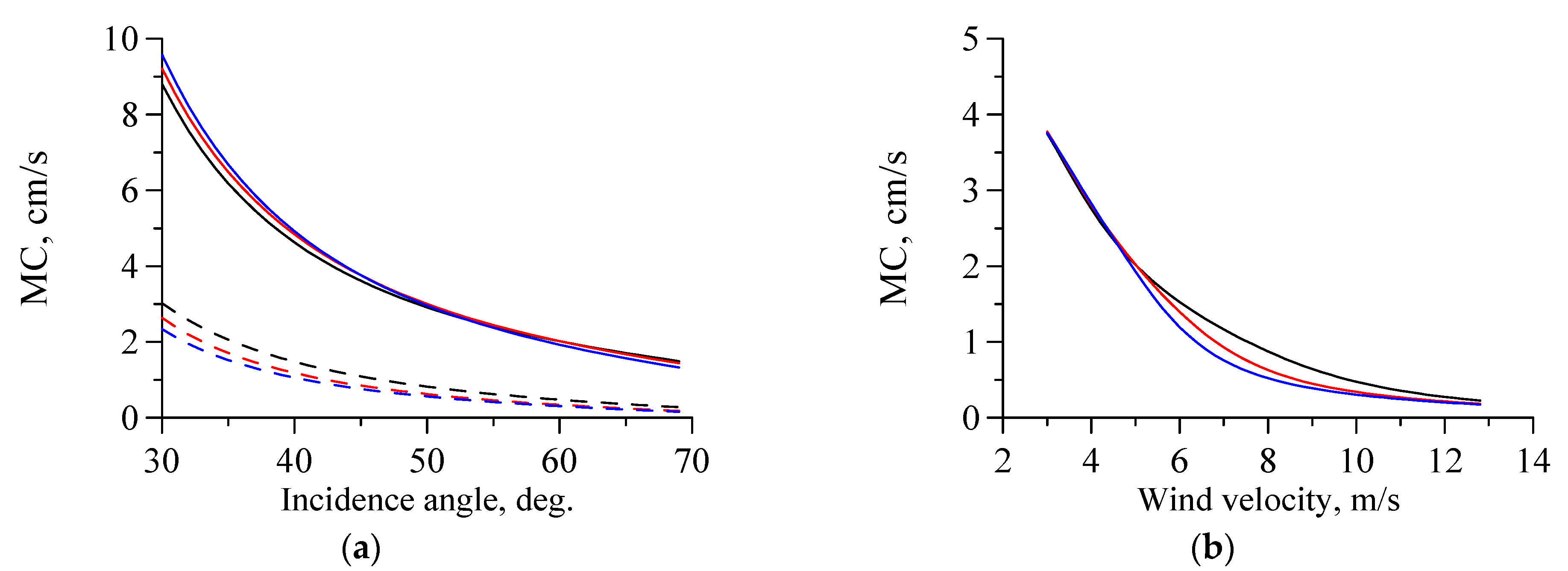
3. Theoretical Background and Data Processing
4. Results
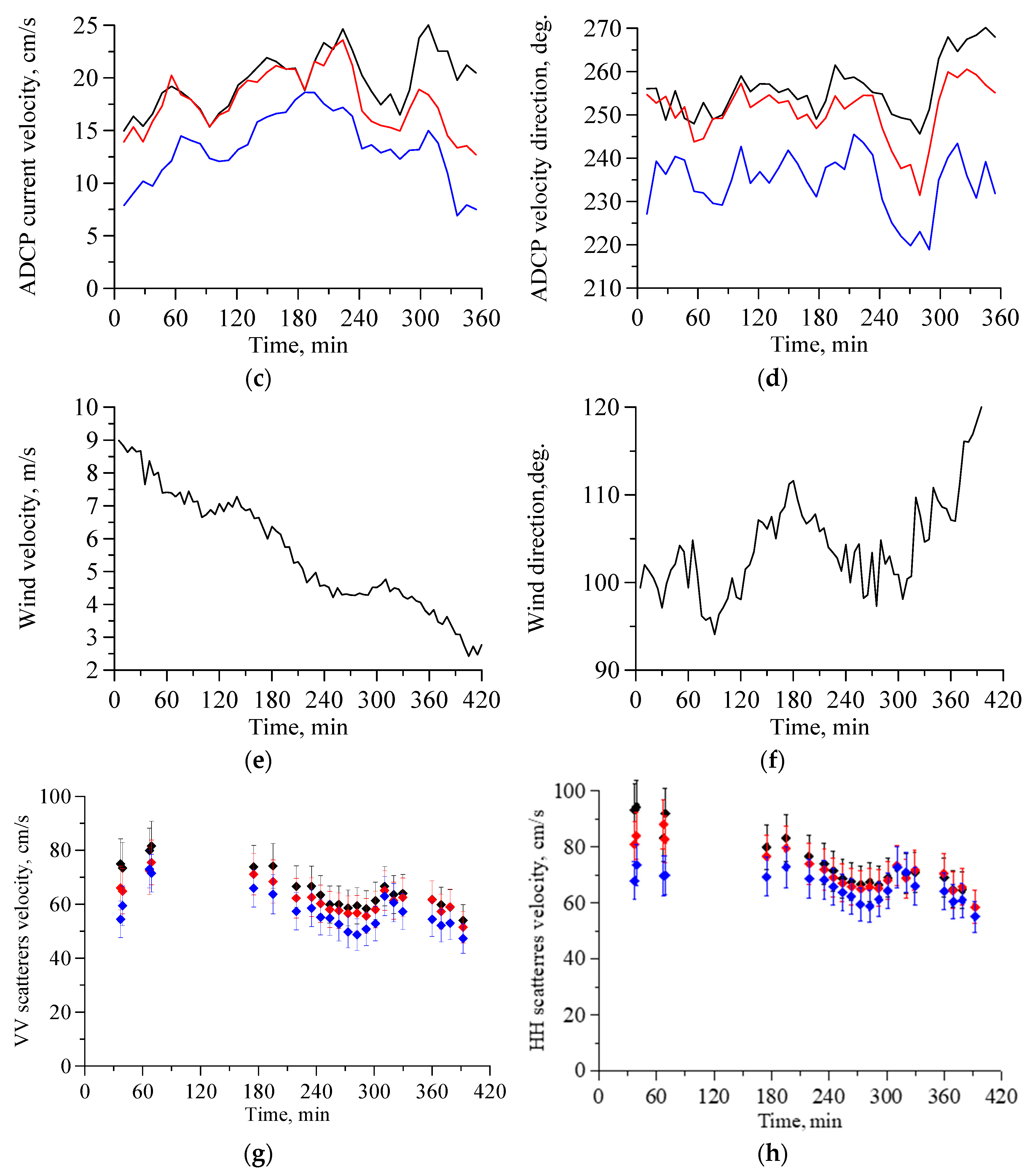
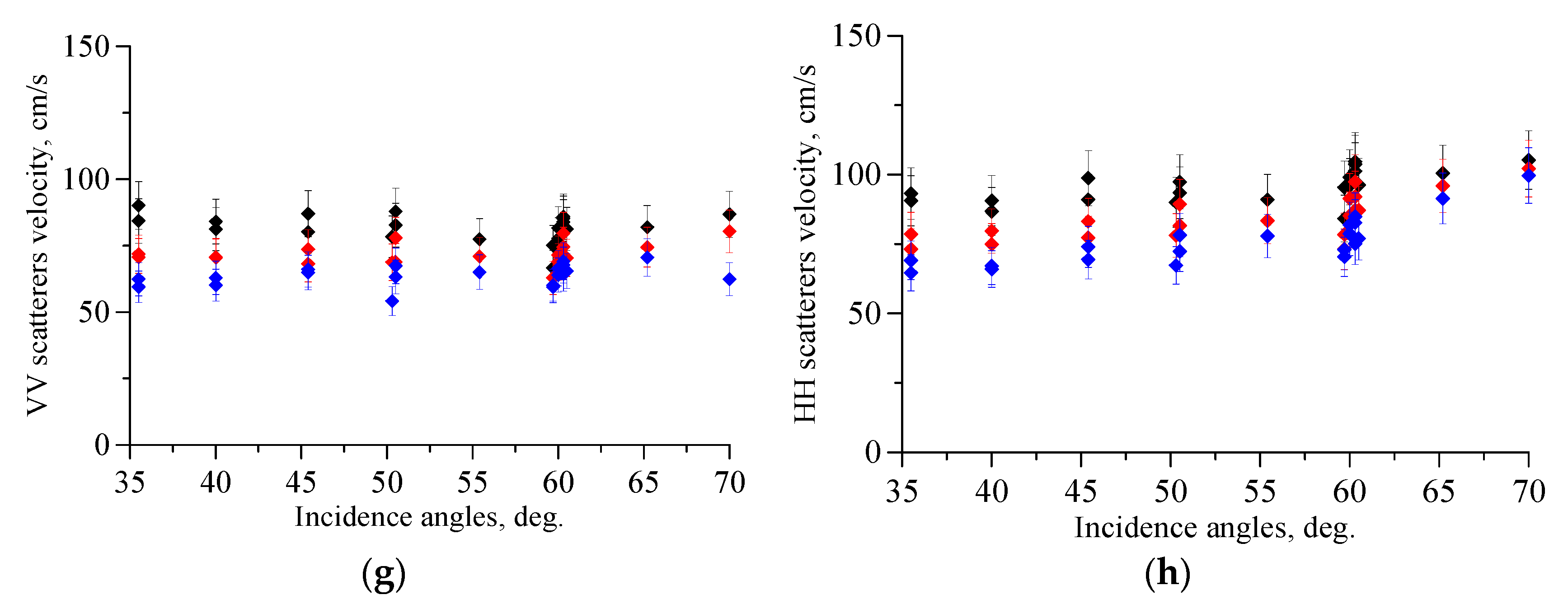
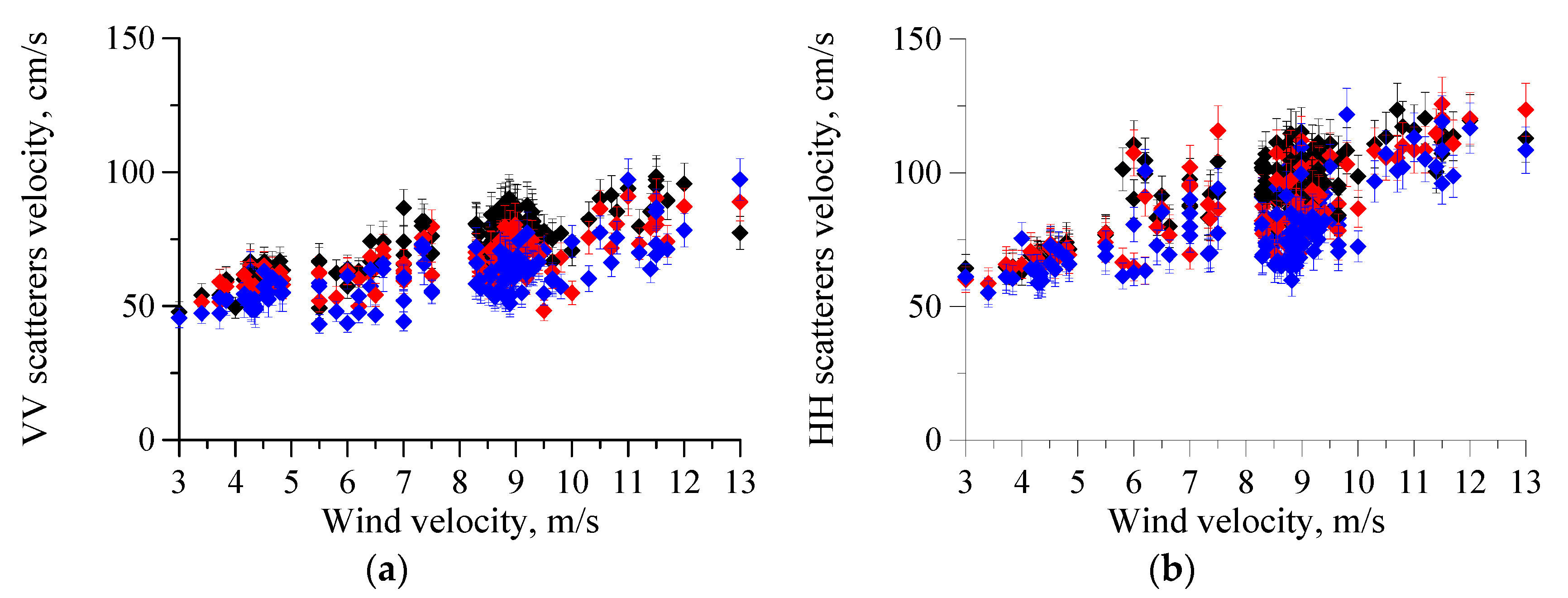
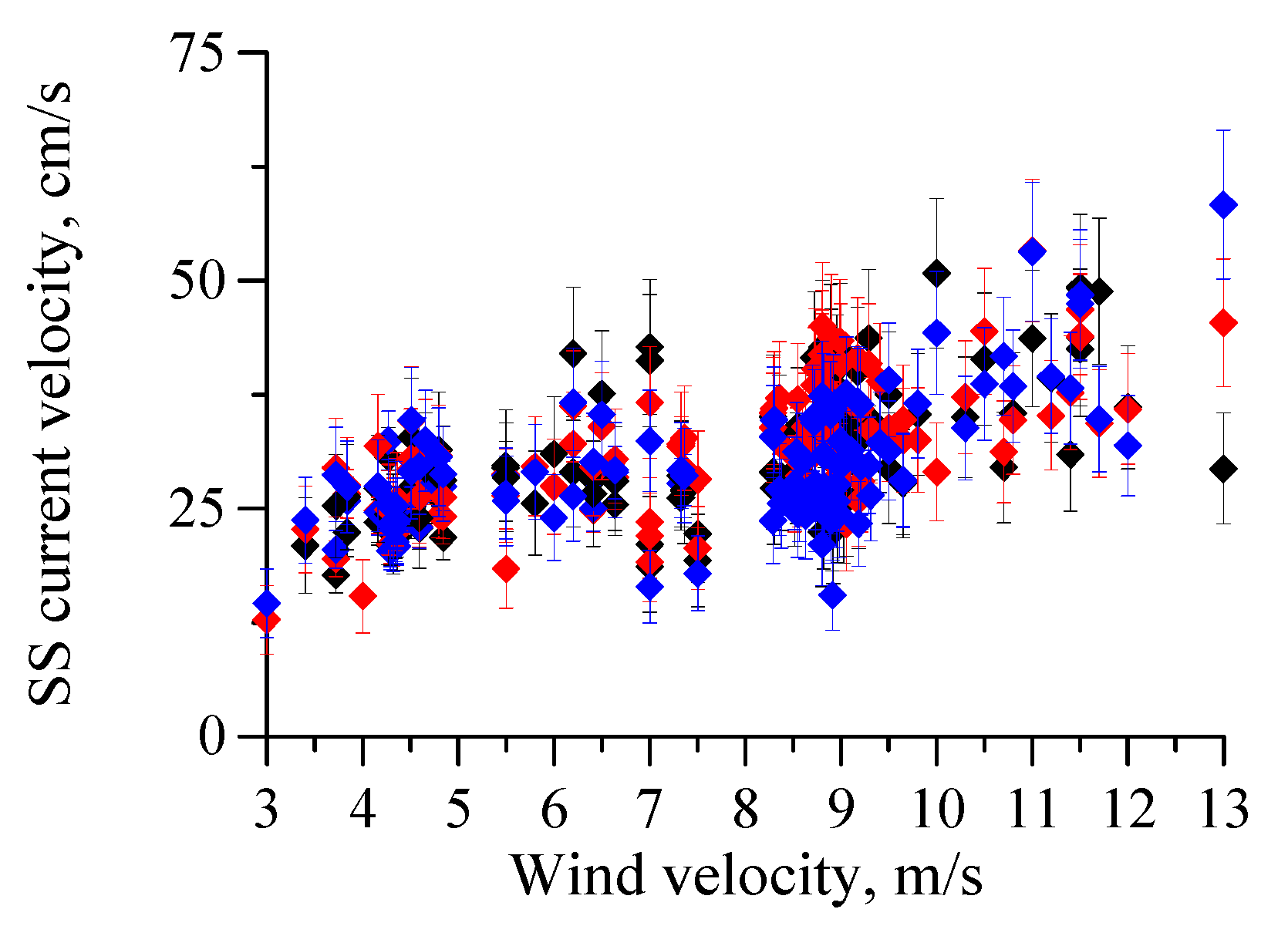
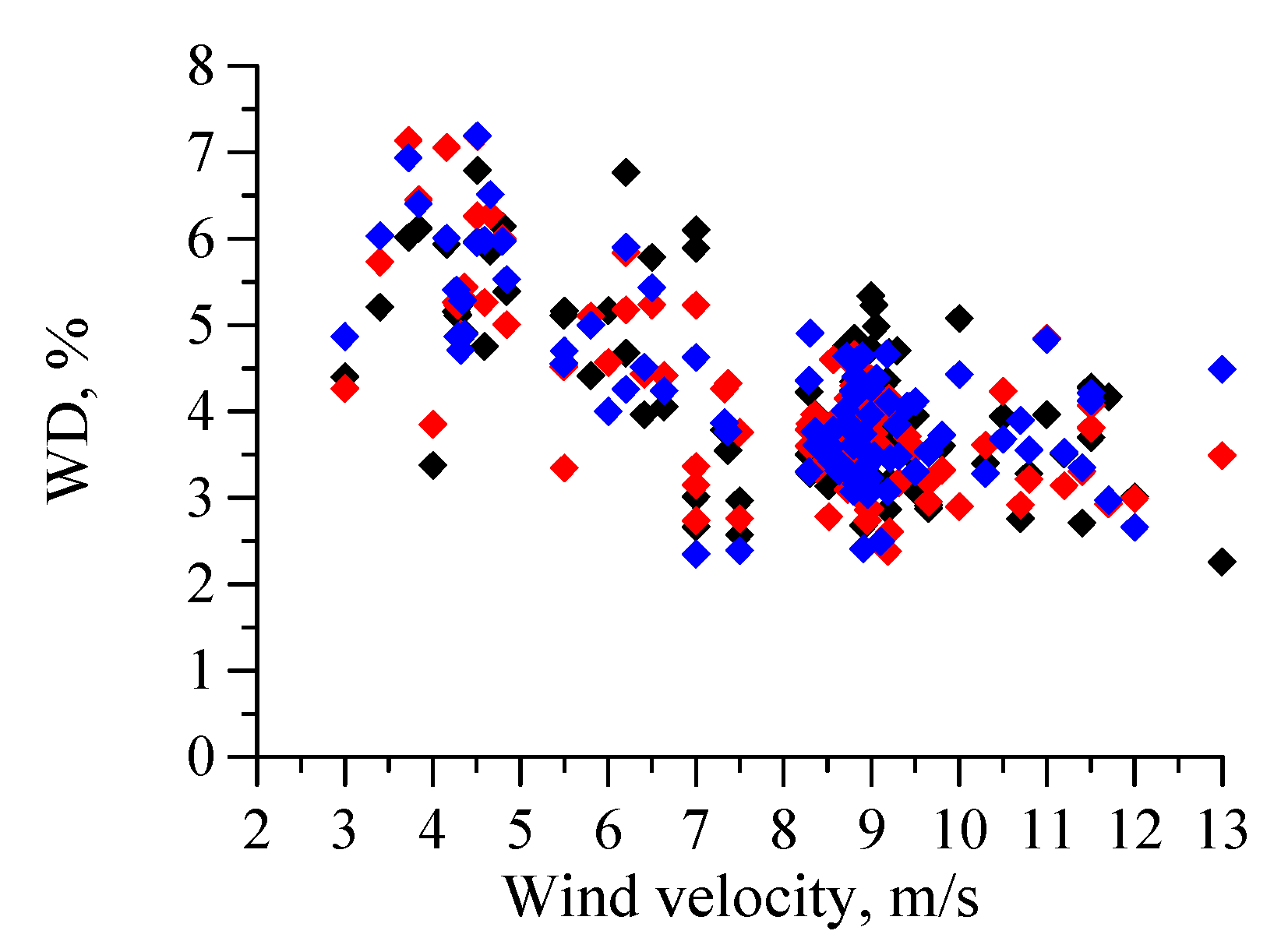
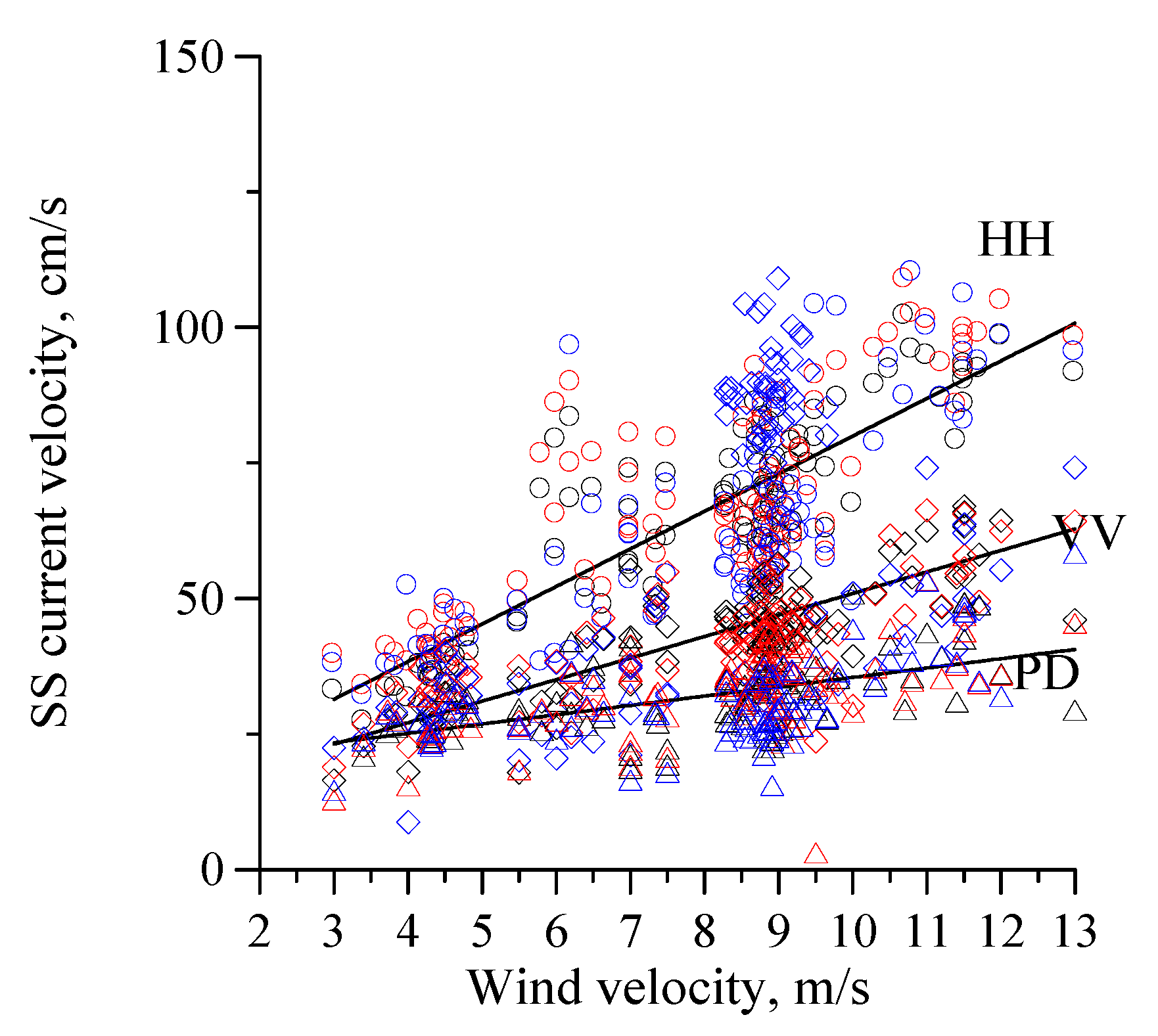
4.1. Scatterer’ Velocities with a Falling Wind
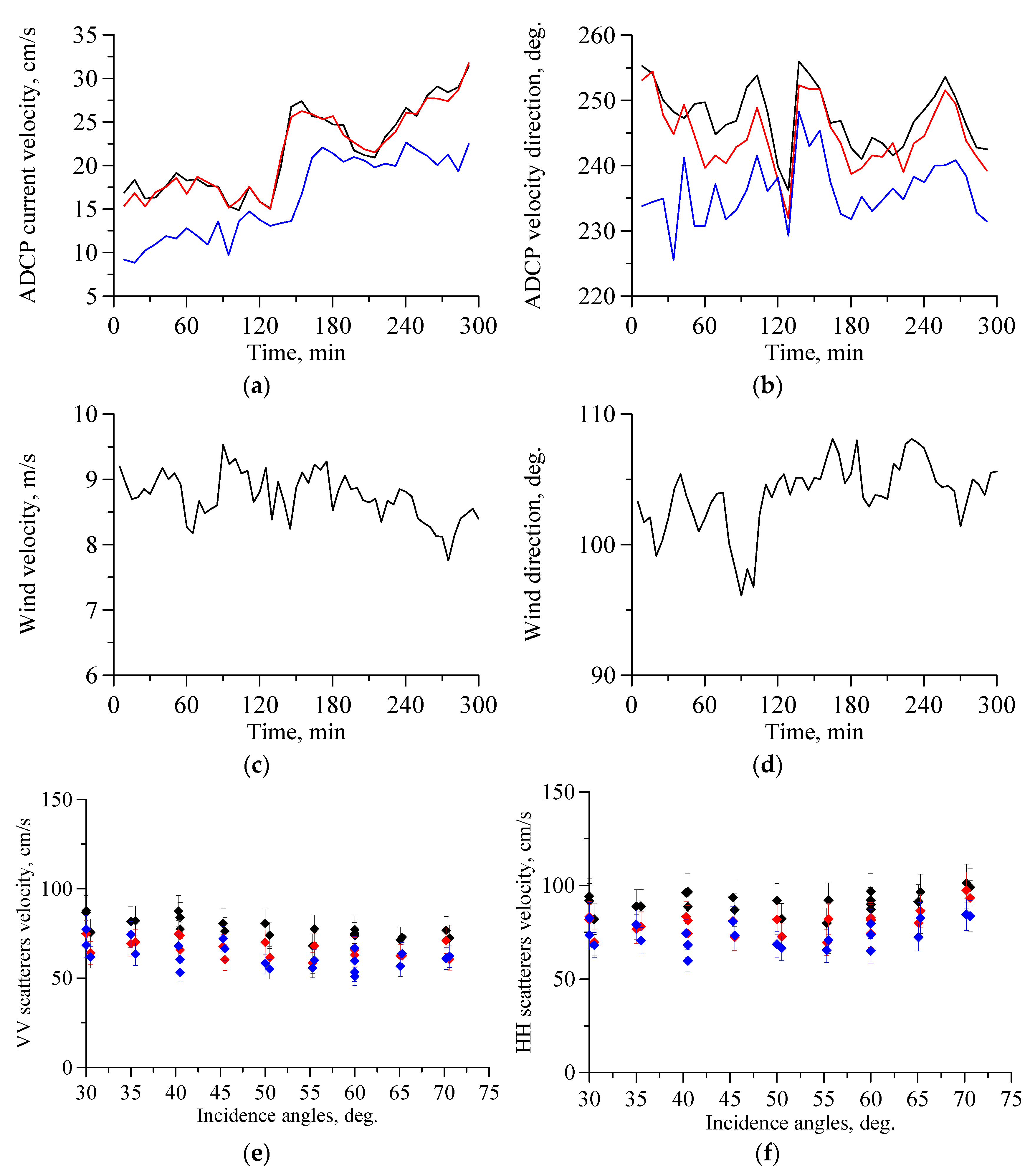
4.2. Scatterer’s Velocities with a Constant Wind
5. Discussion
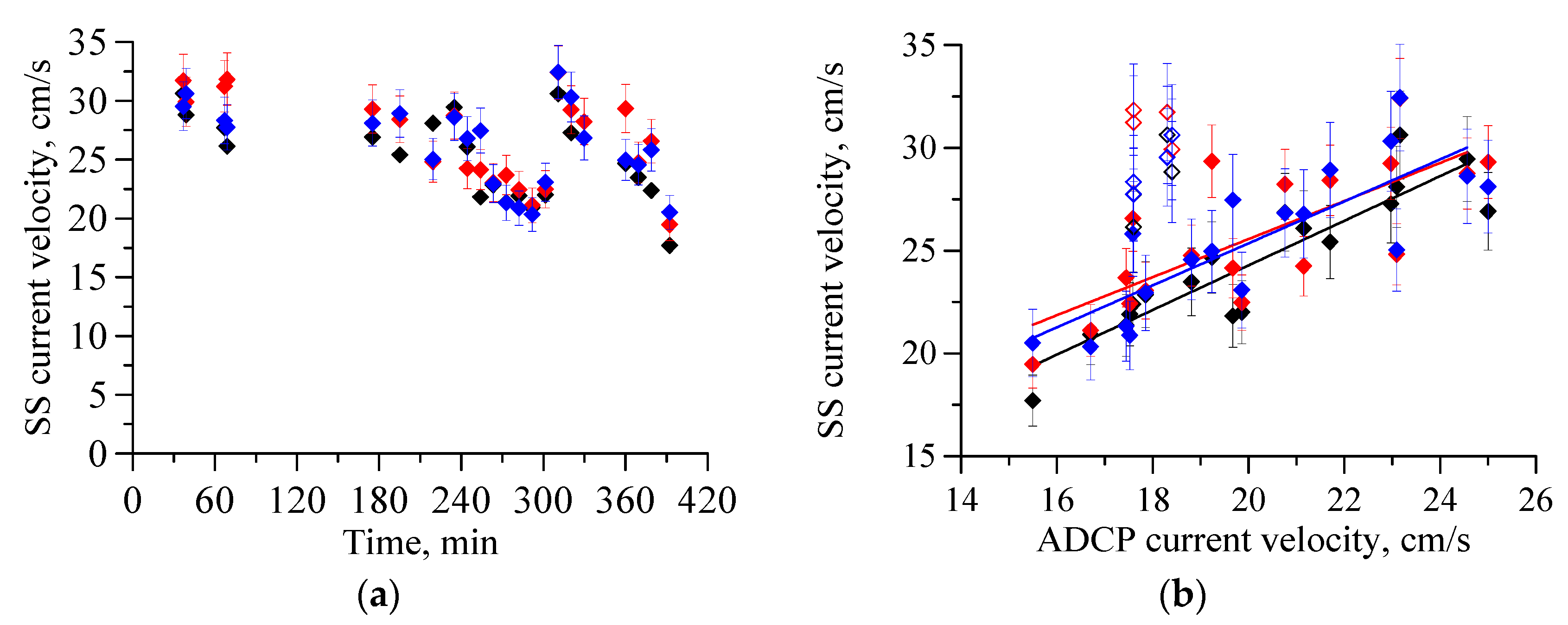
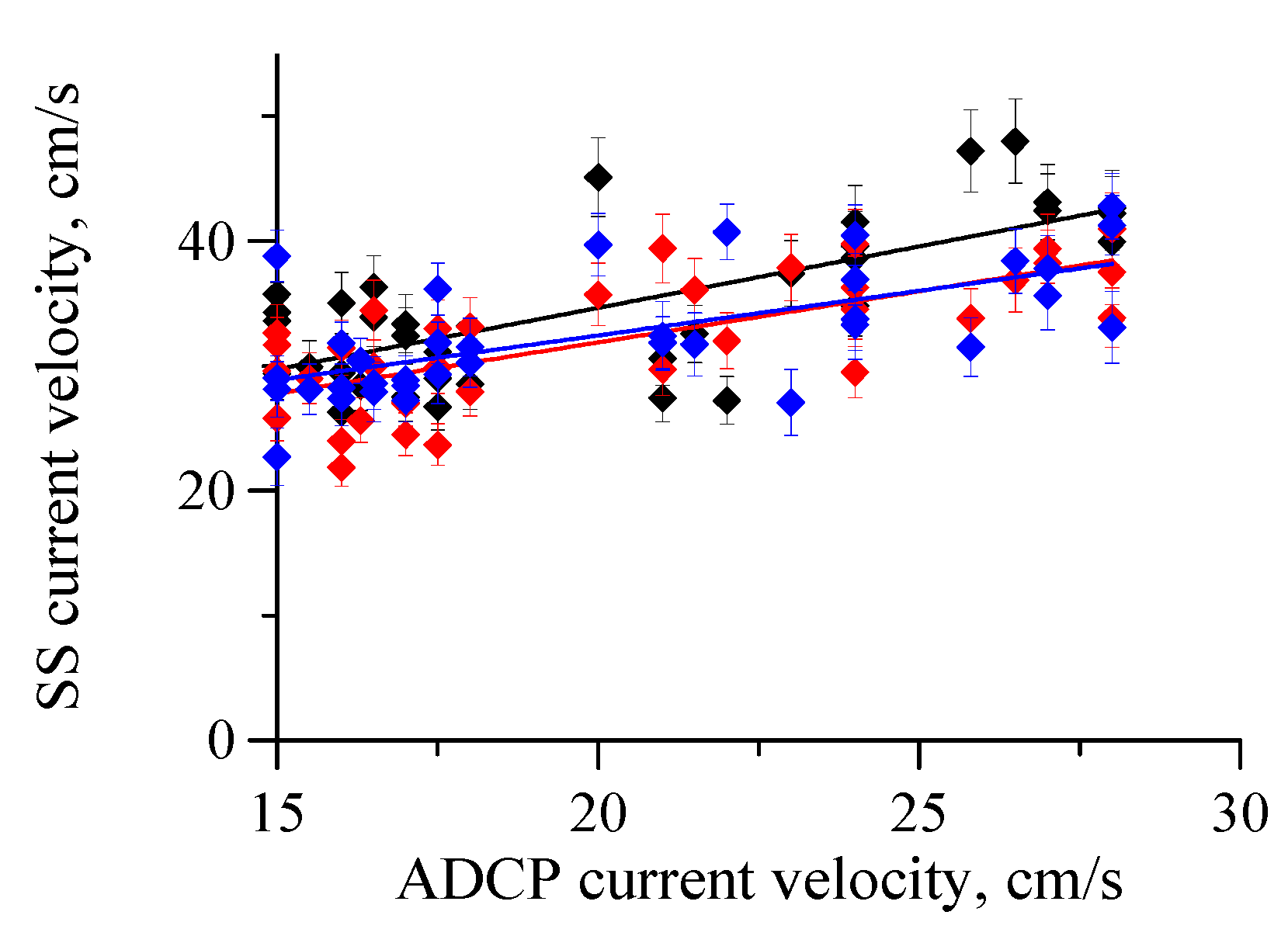
5.1. Relation between Changes in ADCP Current Velocity and Subsurface Current Velocity Retrieved from the Polarization Difference
5.2. A Problem of Estimating the Marine Current Speed from the Subsurface Current Velocity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klemas, V. Remote sensing of coastal and ocean currents: An overview. J. Coast. Res. 2012, 28, 576–586. [Google Scholar] [CrossRef]
- Elyouncha, A.; Eriksson, L.E.B.; Romeiser, R.; Ulander, L.M.H. Empirical Relationship between the Doppler Centroid Derived from X-Band Spaceborne InSAR Data and Wind Vectors. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4201120. [Google Scholar] [CrossRef]
- Martin, A.C.H.; Gommenginger, C.P.; Jacob, B.; Staneva, J. First multi-year assessment of Sentinel-1 radial velocity products using HF radar currents in a coastal environment. Remote Sens. Environ. 2022, 268, 112758. [Google Scholar] [CrossRef]
- Wang, L.; Shi, B.; Zhou, Y.; Sheng, H.; Gao, Y.; Fan, L.; Yang, Z. Radial velocity of ocean surface current estimated from SAR Doppler frequency measurements—A case study of Kuroshio in the East China Sea. Acta Oceanol. Sin. 2021, 40, 135–147. [Google Scholar] [CrossRef]
- Moiseev, A.; Johnsen, H.; Johannessen, J.A. Retrieving Ocean Surface Currents from the Sentinel-1 Doppler Shift Observations: A Case Study of the Norwegian Coastal Current. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5670–5673. [Google Scholar] [CrossRef]
- Moiseev, A.; Johnsen, H.; Hansen, M.W.; Johannessen, J.A. Evaluation of radial ocean surface currents derived from Sentinel-1 IW Doppler shift using coastal radar and Lagrangian surface drifter observations. J. Geophys. Res. Oceans 2020, 125, e2019JC015743. [Google Scholar] [CrossRef]
- Mouche, A.A.; Collard, F.; Chapron, B.; Dagestad, K.-F.; Guitton, G.; Johannessen, J.A.; Kerbaol, V.; Hansen, M.W. On the Use of Doppler Shift for Sea Surface Wind Retrieval from SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2901–2909. [Google Scholar] [CrossRef]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. 2005, 110, C07008. [Google Scholar] [CrossRef]
- Bass, F.G.; Fuks, M. Wave Scattering from Statistically Rough Surfaces; Pergamon: Oxford, UK, 1979; p. 540. ISBN 9781483187754. [Google Scholar]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound. Layer Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Voronovich, A.G.; Zavorotny, V.U. A numerical model of radar scattering from steep and breaking waves. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006; pp. 469–472. [Google Scholar] [CrossRef]
- Fois, F.; Hoogeboom, P.; Le Chevalier, F.; Stoffelen, A. An analytical model for the description of the full polarimetric sea surface Doppler signature. J. Geophys. Res. Oceans 2015, 120, 988–1015. [Google Scholar] [CrossRef] [Green Version]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semi-empirical model of the normalized radar cross section of the sea surface. 1. Background model. J. Geophys. Res. 2003, 108, 8054. [Google Scholar] [CrossRef] [Green Version]
- Ermakov, S.A.; Sergievskaya, I.A.; da Silva, J.C.B.; Kapustin, I.A.; Shomina, O.V.; Kupaev, A.V.; Molkov, A.A. Remote Sensing of Organic Films on the Water Surface Using Dual Co-Polarized Ship-Based X-/C-/S-Band Radar and TerraSAR-X. Remote Sens. 2018, 10, 1097. [Google Scholar] [CrossRef] [Green Version]
- Sergievskaya, I.A.; Ermakov, S.A.; Ermoshkin, A.V.; Kapustin, I.A.; Molkov, A.A.; Danilicheva, O.A.; Shomina, O.V. Modulation of Dual-Polarized X-Band Radar Backscatter due to Long Wind Waves. Remote Sens. 2019, 11, 423. [Google Scholar] [CrossRef] [Green Version]
- Sergievskaya, I.A.; Ermakov, S.A.; Ermoshkin, A.V.; Kapustin, I.A.; Shomina, O.V.; Kupaev, A.V. The Role of Micro Breaking of Small-Scale Wind Waves in Radar Backscattering from Sea Surface. Remote Sens. 2020, 12, 4159. [Google Scholar] [CrossRef]
- Martin, A.C.H.; Gommenginger, C.; Marquez, J.; Doody, S.; Navarro, V.; Buck, C. Wind-wave-induced velocity in ATI SAR ocean surface currents: First experimental evidence from an airborne campaign. J. Geophys. Res. Oceans 2016, 121, 1640–1653. [Google Scholar] [CrossRef] [Green Version]
- Nouguier, F.; Chapron, B.; Collard, F.; Mouche, A.A.; Rascle, N.; Ardhuin, F.; Wu, X. Sea Surface Kinematics from Near-Nadir Radar Measurement. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6169–6179. [Google Scholar] [CrossRef]
- Ermakov, S.A.; Sergievskaya, I.A.; Zuikova, E.M.; Shchegol’kov, Y.B. Modulation of Radar Backscatter by Long Waves on the Sea Surface Covered with a Surfactant Film. Izv. Atmos. Ocean. Phys. 2004, 4, 91–98. [Google Scholar]
- Kapustin, I.A.; Shomina, O.V.; Ermoshkin, A.V.; Bogatov, N.A.; Kupaev, A.V.; Molkov, A.A.; Ermakov, S.A. On Capabilities of Tracking Marine Surface Currents Using Artificial Film Slicks. Remote Sens. 2019, 11, 840. [Google Scholar] [CrossRef] [Green Version]
- Wu, J. Wind-induced drift currents. J. Fluid Mech. 1975, 68, 49–70. [Google Scholar] [CrossRef]
- Wu, J. Sea-surface drift currents induced by wind and waves. J. Geophys. Res. 1983, 13, 1441–1451. [Google Scholar] [CrossRef]
- Van der Mheen, M.; Pattiaratchi, C.; Cosoli, S.; Wandres, M. Depth-Dependent Correction for Wind-Driven Drift Current in Particle Tracking Applications. Front. Mar. Sci. 2020, 7, 305. [Google Scholar] [CrossRef]
- Leibovich, S. On the evolution of the system of wind drift currents and Langmuir circulations in the ocean. Part 1. Theory and averaged current. J. Fluid Mech. 1977, 79, 715–743. [Google Scholar] [CrossRef]
- Phillips, O.M. Radar returns from the sea surface—Bragg scattering and breaking waves. J. Phys. Oceanogr. 1988, 18, 1065–1074. [Google Scholar] [CrossRef]
- Troitskaya, Y.I. Modulation of the growth rate of short, surface capillary-gravity wind waves by a long wave. J. Fluid Mech. 1994, 273, 169–187. [Google Scholar] [CrossRef]
- Hara, T.; Plant, W.J. Hydrodynamic modulation of short wind-wave spectra by long waves and its measurement using microwave backscatter. J. Geophys. Res. 1994, 99, 9767–9783. [Google Scholar] [CrossRef]
- Plant, W.J. The Modulation Transfer Function: Concept and Applications. In Radar Scattering from Modulated Wind Waves, 1st ed.; Komen, G.J., Oost, W.A., Eds.; Springer: Dordrecht, The Netherlands, 1989; pp. 155–172. [Google Scholar] [CrossRef]
- Sergievskaya, I.A.; Ermakov, S.A.; Plotnikov, L.M.; Kapustin, I.A.; Ermoshkin, A.V. On the estimation of surface current velocities from microwave sea surface measurements at moderate incidence angles. Sovr. Probl. DZZ Kosm. 2022, 19, 212–222. [Google Scholar] [CrossRef]
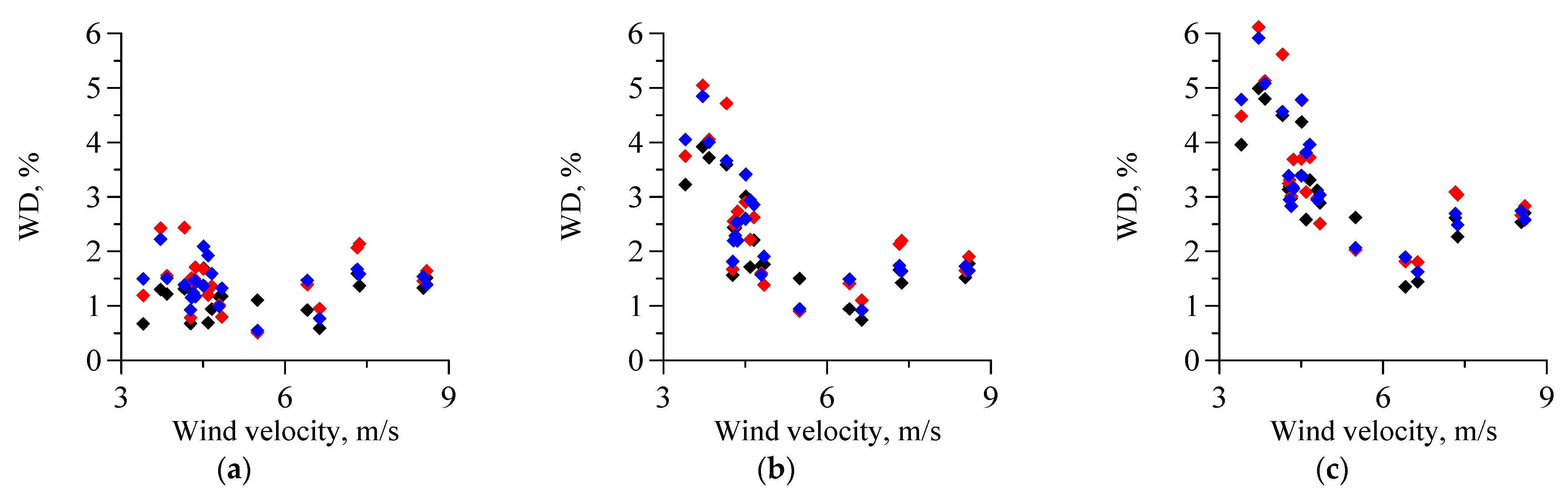

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sergievskaya, I.; Ermakov, S.; Plotnikov, L.; Kapustin, I.; Kupaev, A. On a Problem of Marine Current Velocity Estimation from Microwave Radar Data. Water 2023, 15, 1153. https://doi.org/10.3390/w15061153
Sergievskaya I, Ermakov S, Plotnikov L, Kapustin I, Kupaev A. On a Problem of Marine Current Velocity Estimation from Microwave Radar Data. Water. 2023; 15(6):1153. https://doi.org/10.3390/w15061153
Chicago/Turabian StyleSergievskaya, Irina, Stanislav Ermakov, Leonid Plotnikov, Ivan Kapustin, and Alexander Kupaev. 2023. "On a Problem of Marine Current Velocity Estimation from Microwave Radar Data" Water 15, no. 6: 1153. https://doi.org/10.3390/w15061153




