Online Control of the Raw Water System of a High-Sediment River Based on Deep Reinforcement Learning
Abstract
1. Introduction
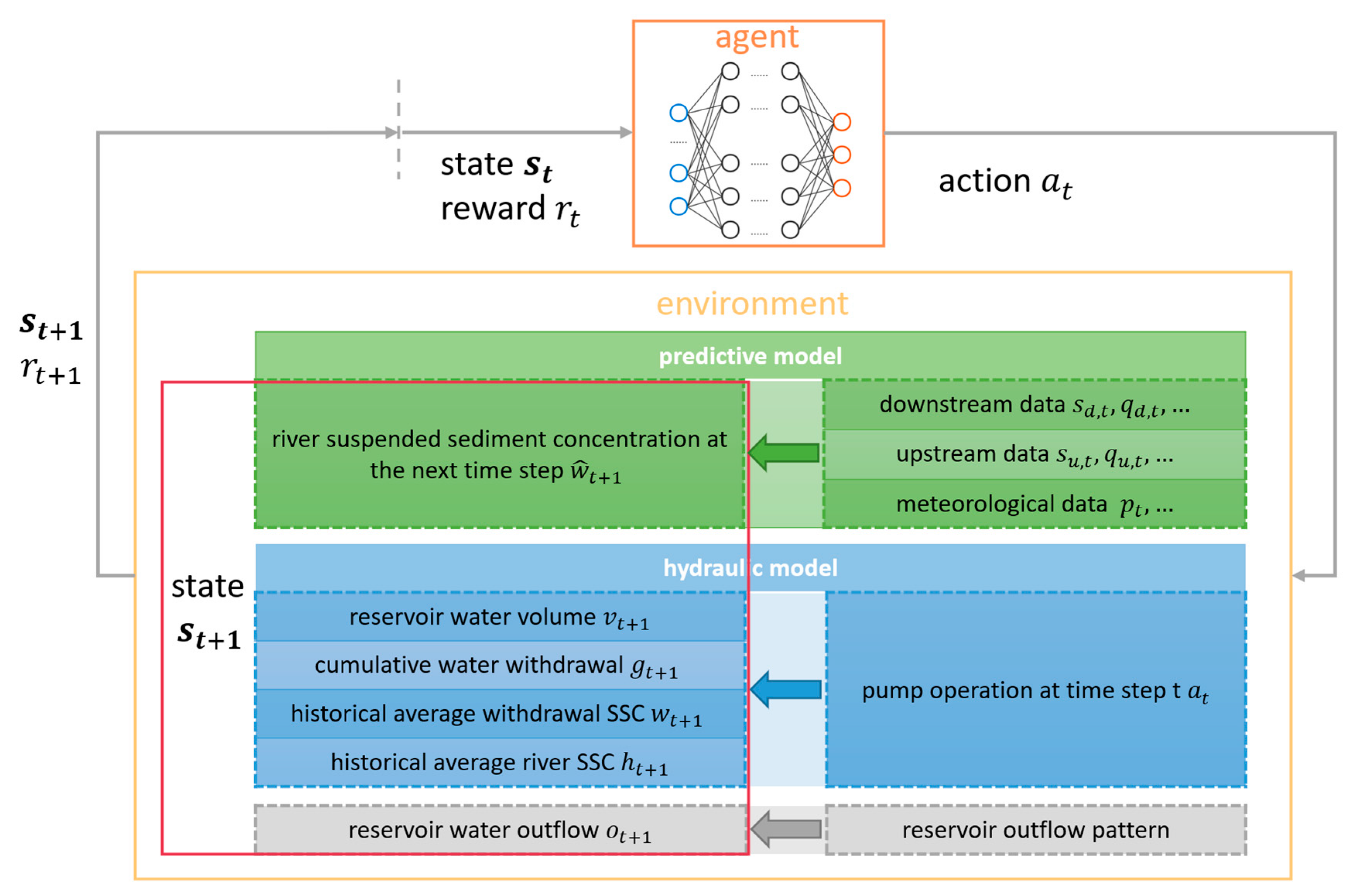
2. Methods
- Manual strategy: the actual pumping station control strategy developed through the experience of human operators.
- Predictive control strategy: with a predicted river SSC, the strategy generated by the DRL-based predictive online control model framework.
- Perfect predictive control strategy: the strategy generated by training with the real-world river SSC. The robustness of the reinforcement learning framework to uncertain data is verified by comparing the test performance of the two strategies (predictive control strategy and perfect predictive control strategy). Perfect predictive control strategy is impractical because it is impossible to make unbiased predictions of the river’s SSC, and it is precisely the future river SSC that influences the choice of control action.
2.1. Hydraulic Model
2.2. SSC Predictive Model
2.3. DRL Agent
2.3.1. Action Space
2.3.2. State Space
2.3.3. Reward Function
2.3.4. Training Method and Process
- Initialize the simulation environment and return the initial state (randomly select a year from the training dataset as the hydrological year of this episode; randomly select a year from the training dataset as the water consumption year of this episode; randomly sample a reservoir water volume as the annual initial reservoir volume ).
- For each time step:
- (a)
- Sample of actions from the control strategy according to the state at the current time step;
- (b)
- Apply action to the simulated environment, and this action will affect the state at the next step. Part of the state changed by the action is calculated using the hydraulic model; the rest of the state not related to the action is updated using the prediction model;
- (c)
- Calculate the reward ;
- (d)
- Store the data sample [, , , ] into the training dataset.
- Update the parameters of the DRL agent using the PPO algorithm.
3. Case Study
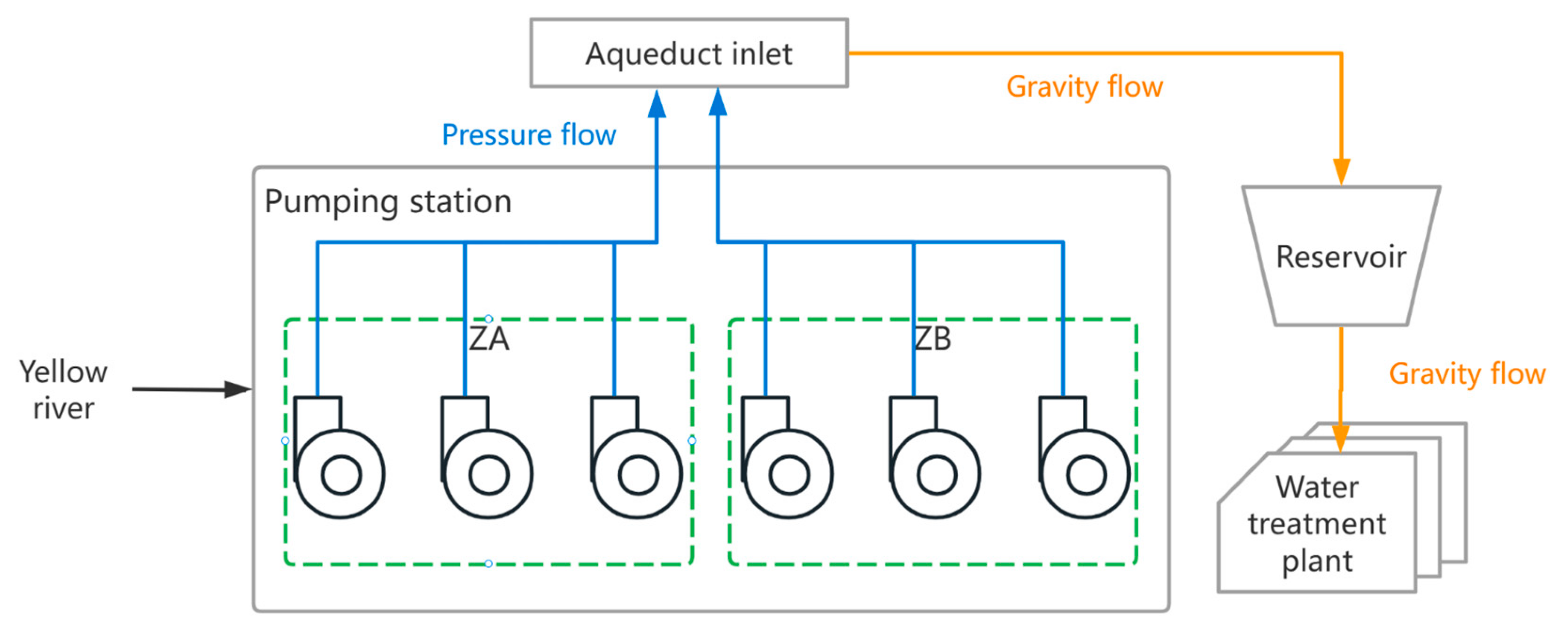
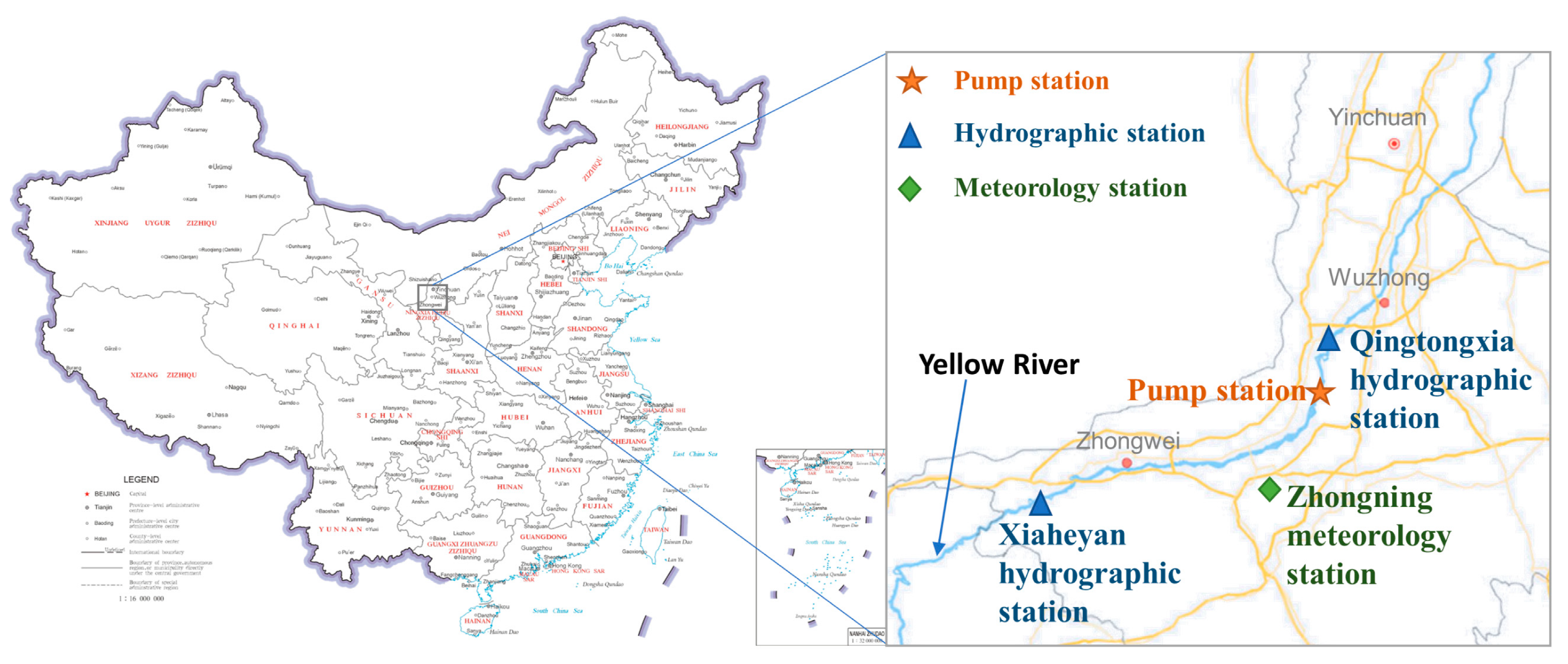
3.1. Raw Water System of the Study Area
3.2. Modeling
3.2.1. Simplify the Action Space
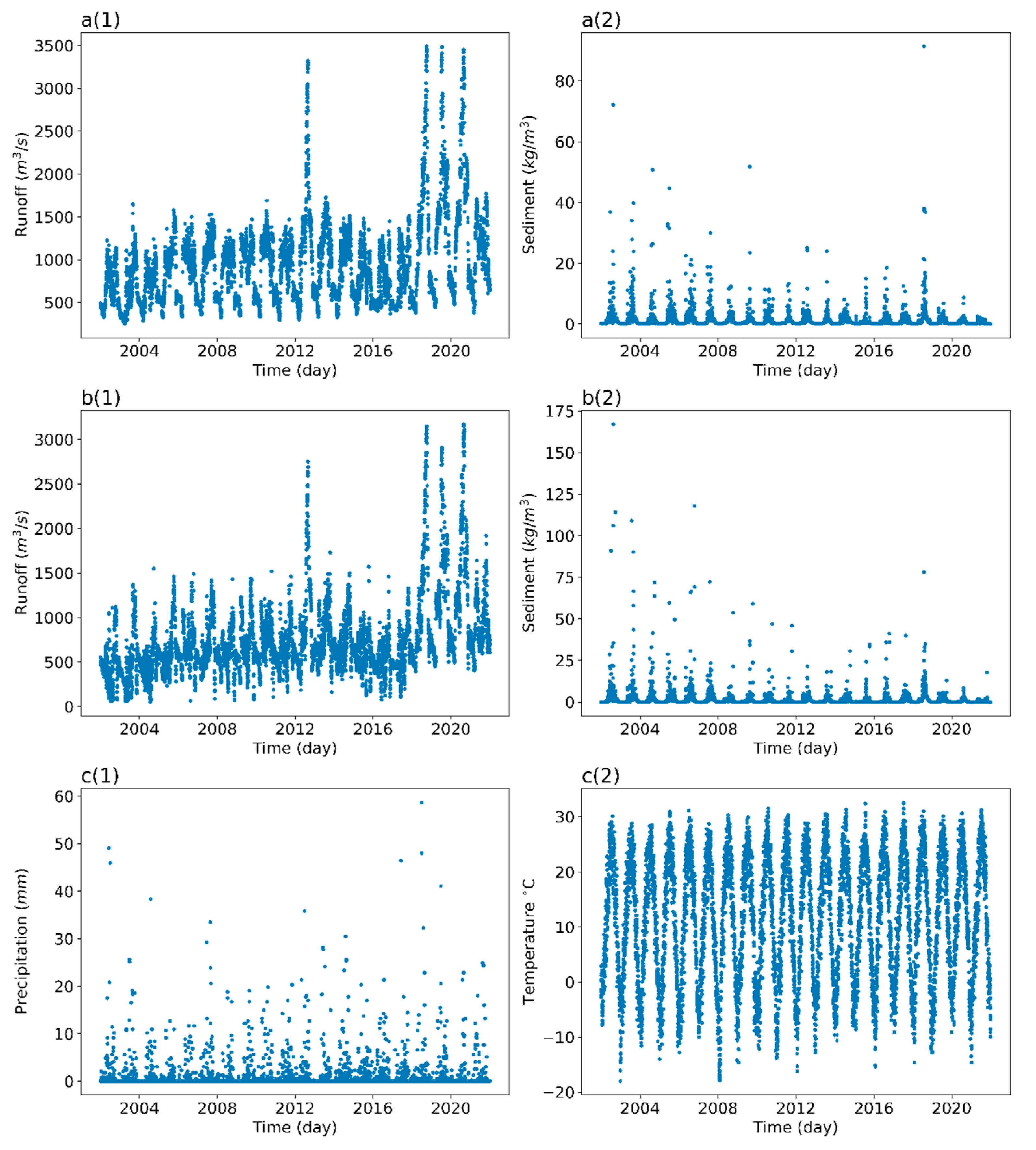
3.2.2. Water Consumption Data
3.2.3. SSC Forecasting
3.2.4. DRL Configuration
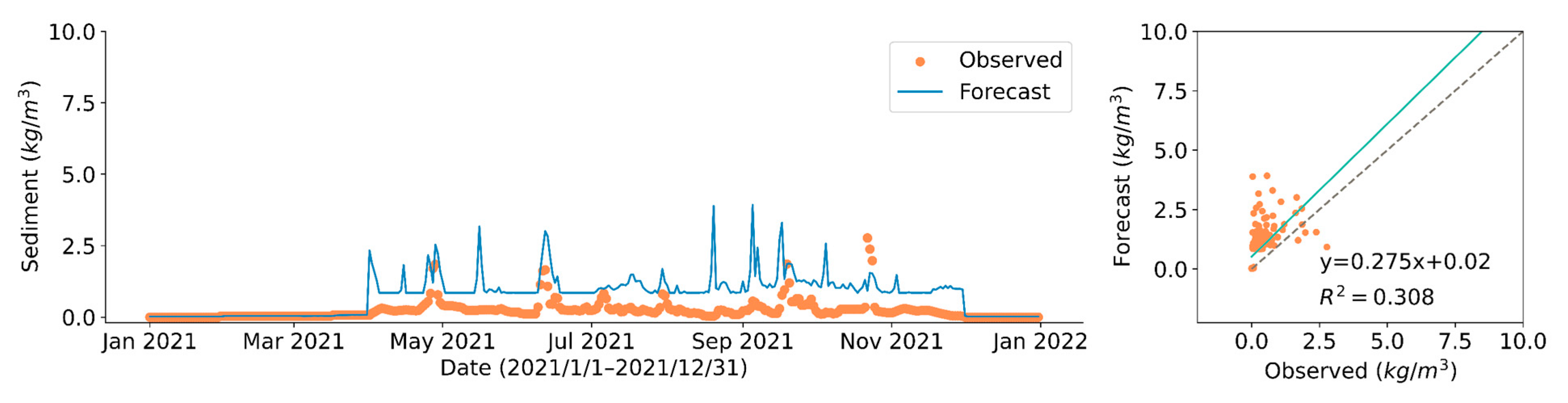
3.3. Predict Model Performance
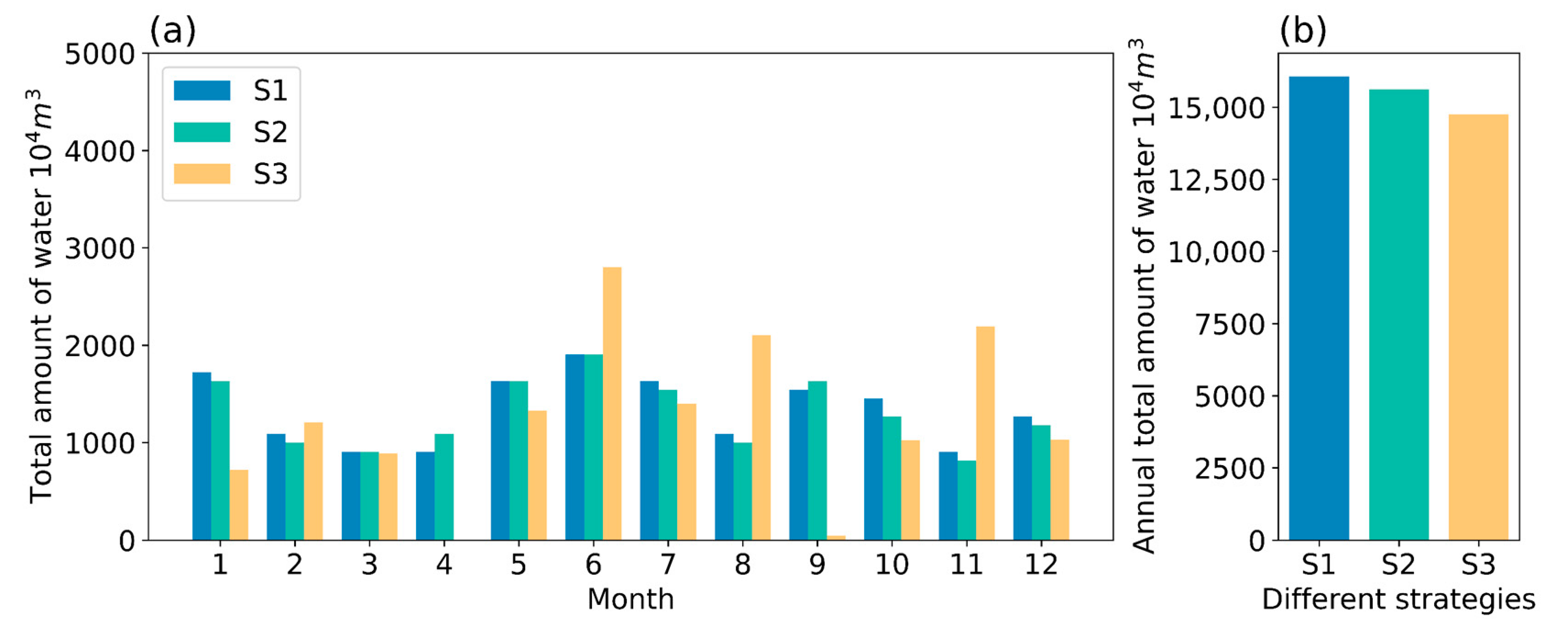
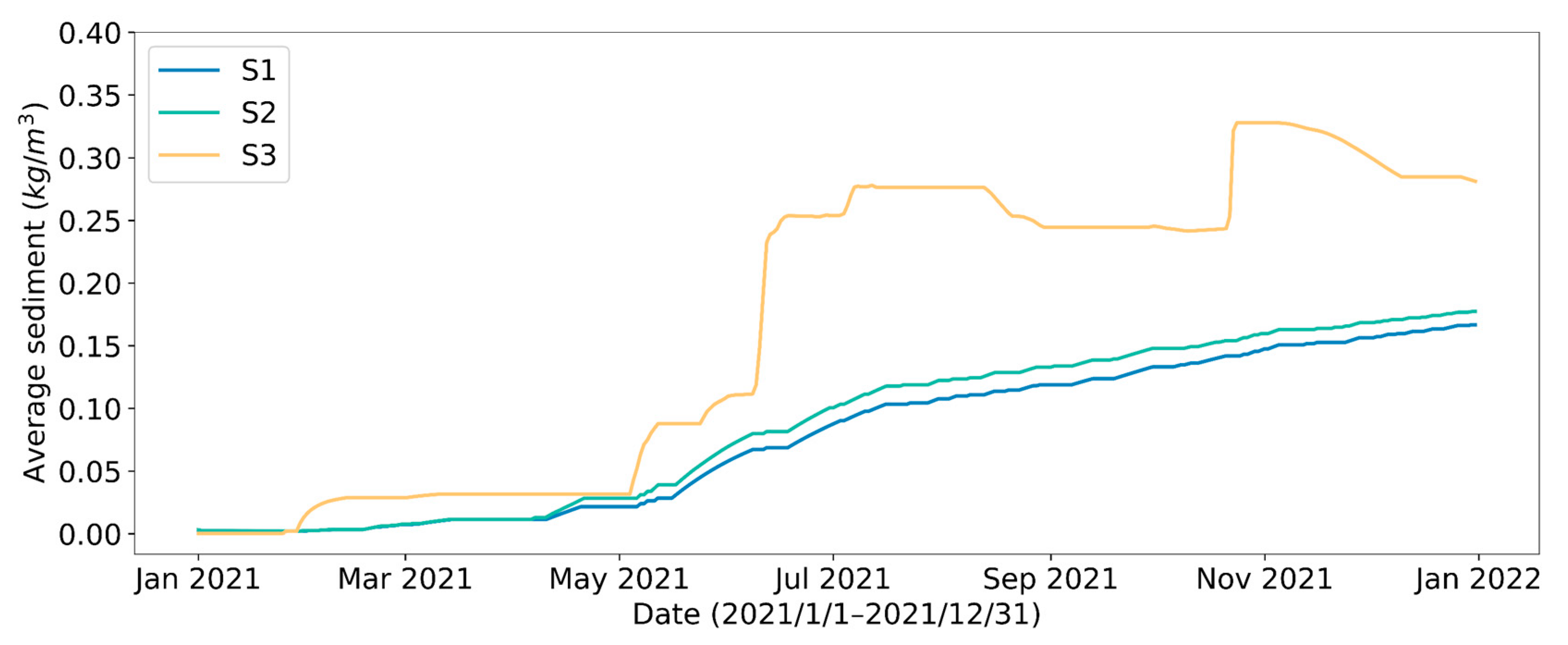
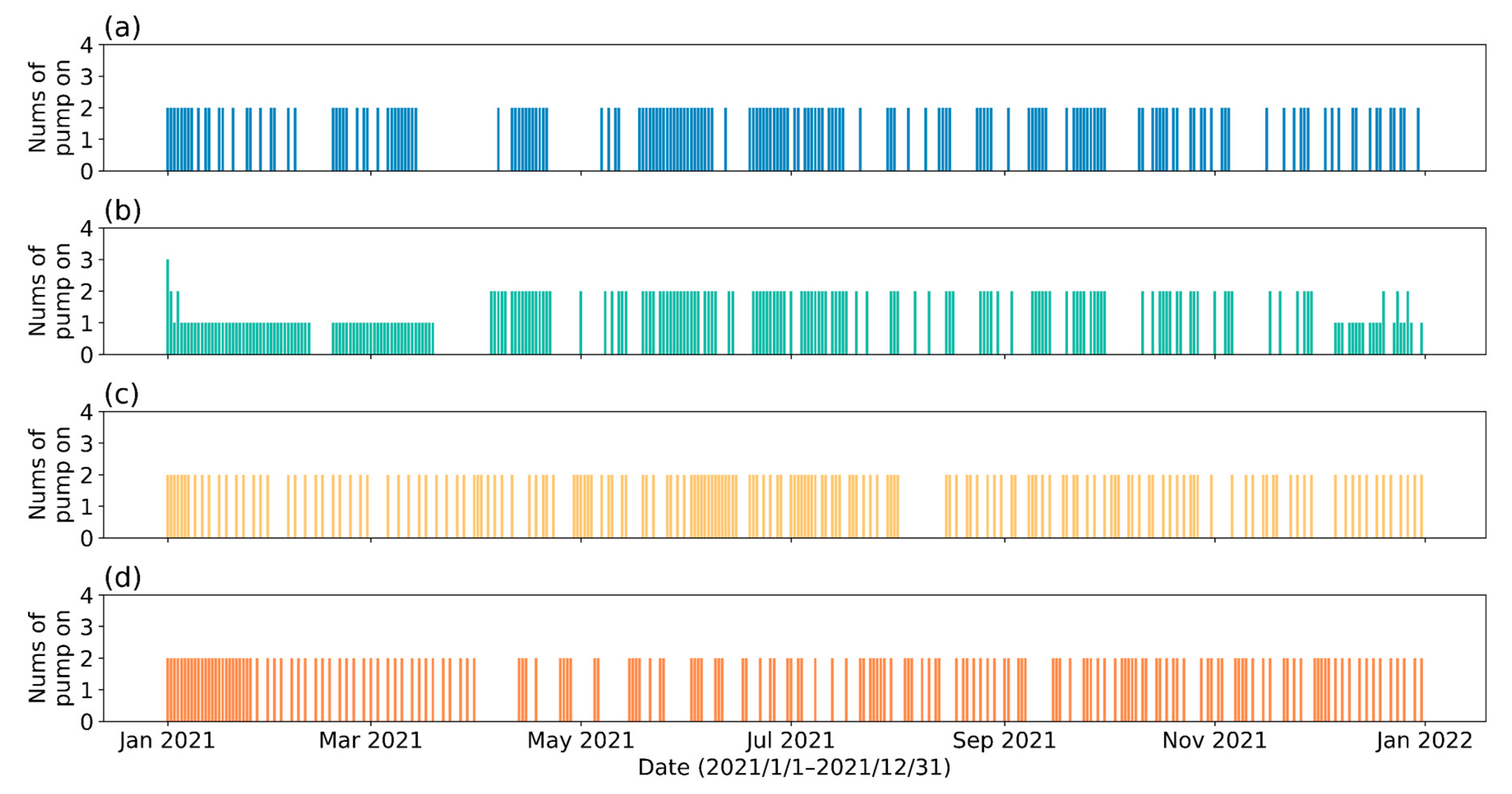
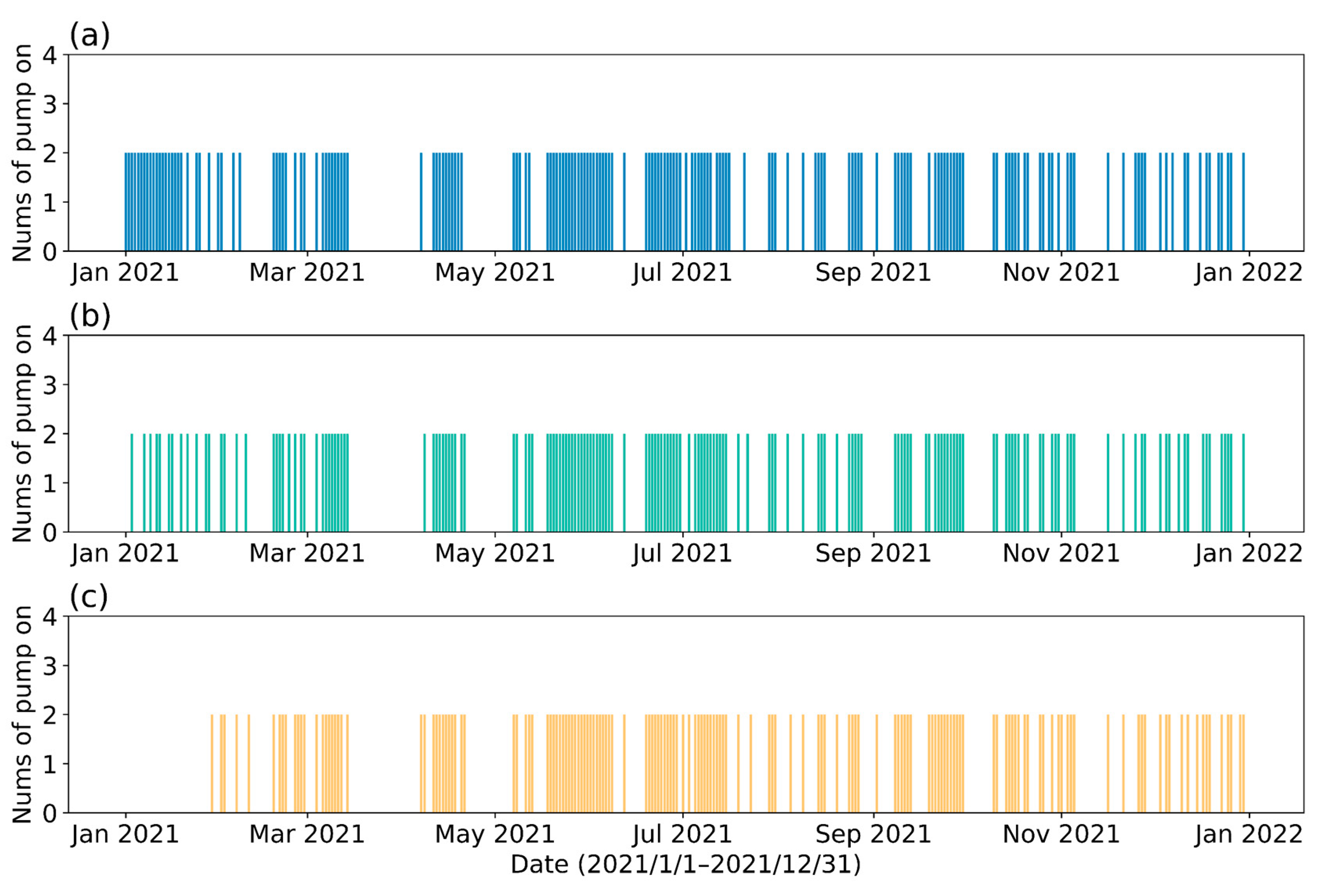
3.4. Results of the DRL
4. Results and Discussion
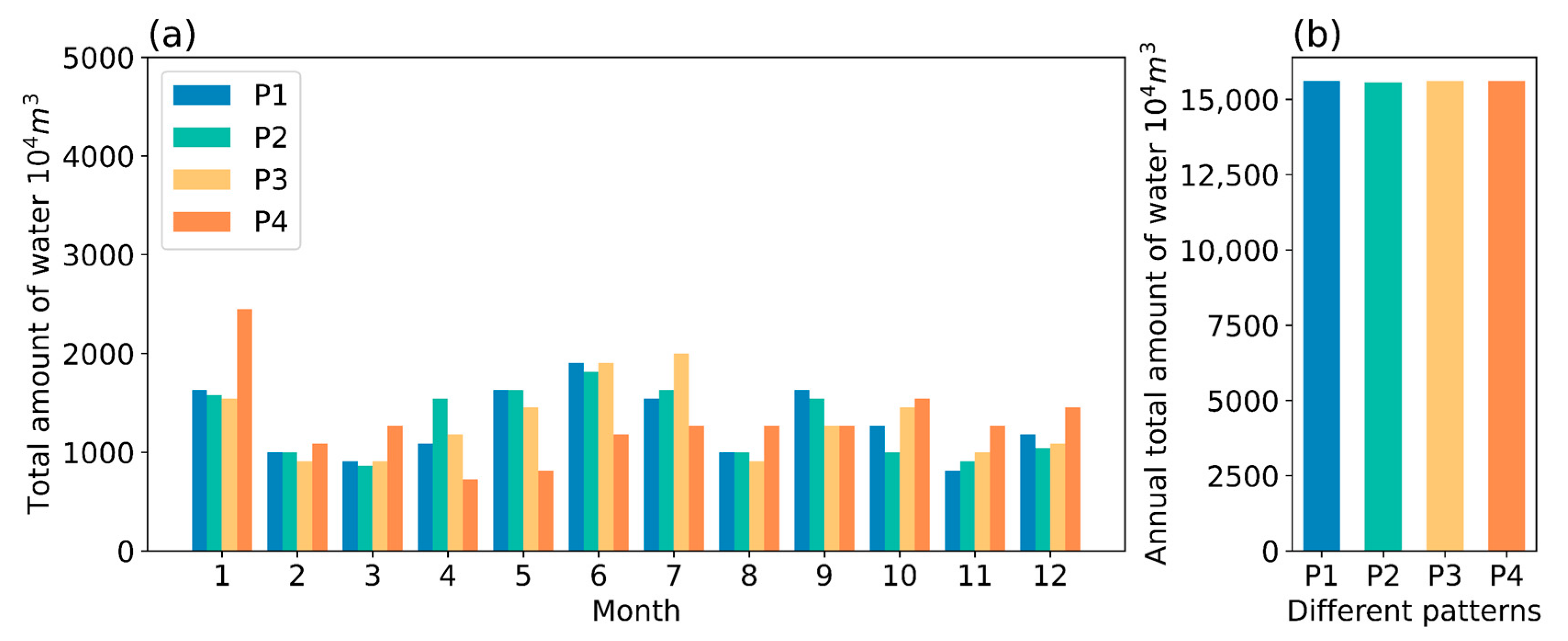
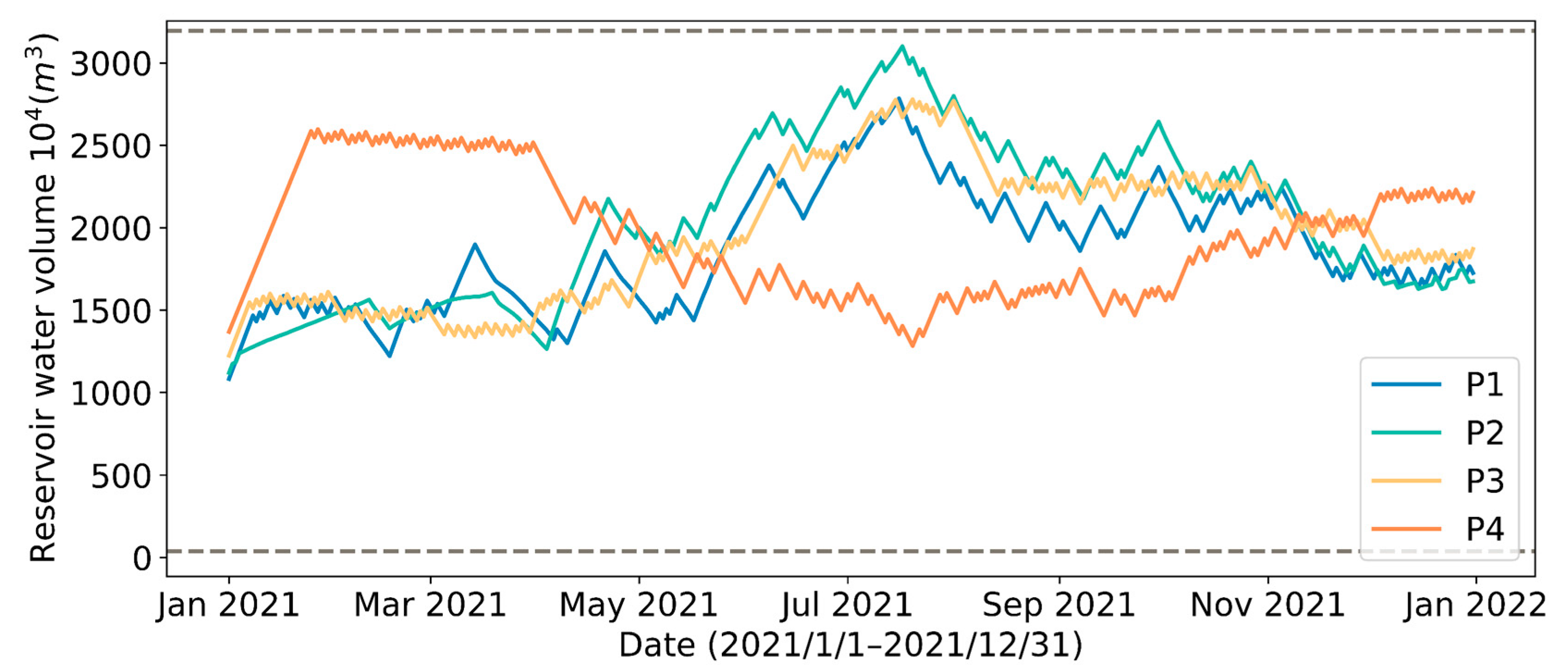
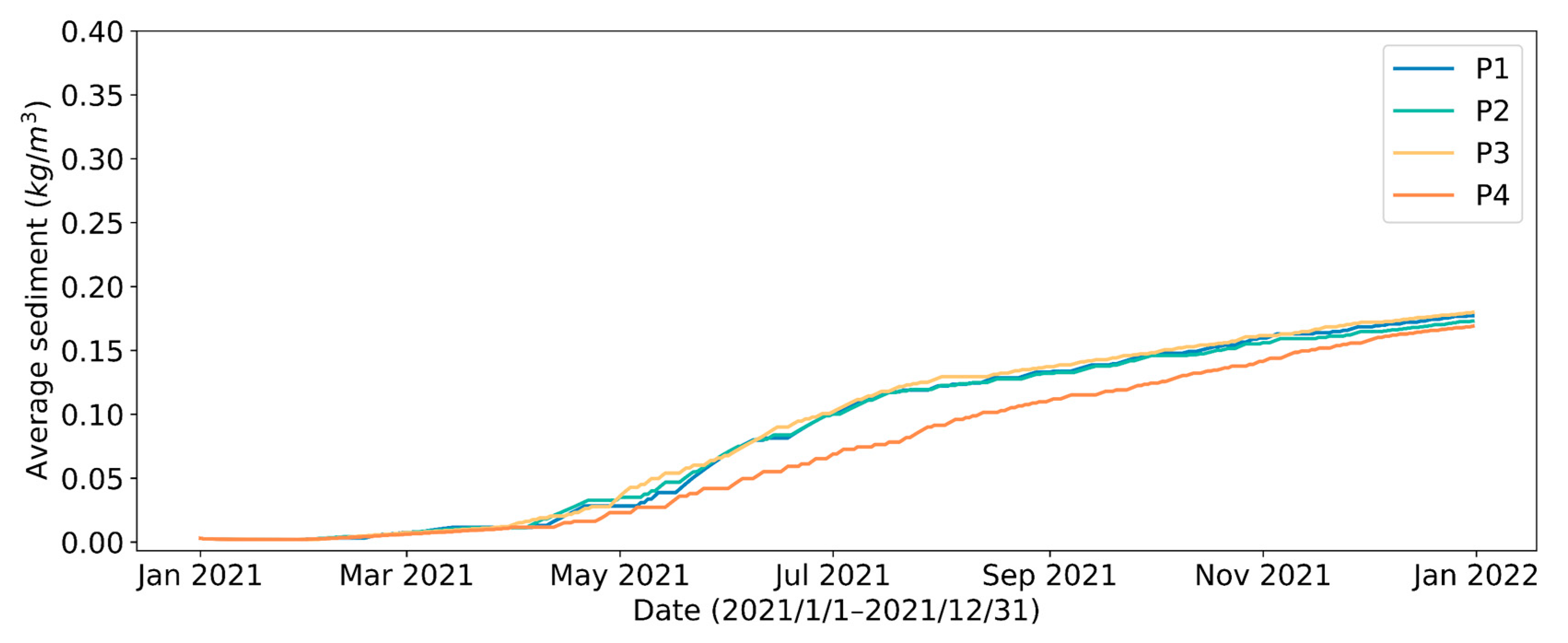
4.1. Effect of Different Reservoir Water Outflow Patterns
4.2. Effect of Different Initial Reservoir Water Volumes
4.3. Limitation and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wee, W.J.; Zaini, N.B.; Ahmed, A.N.; El-Shafie, A. A review of models for water level forecasting based on machine learning. Earth Sci. Inform. 2021, 14, 1707–1728. [Google Scholar] [CrossRef]
- Giuliani, M.; Herman, J.D.; Castelletti, A.; Reed, P. Many-objective reservoir policy identification and refinement to reduce policy inertia and myopia in water management. Water Resour. Res. 2014, 50, 3355–3377. [Google Scholar] [CrossRef]
- Şen, Z. Reservoirs for Water Supply Under Climate Change Impact—A Review. Water Resour. Manag. 2021, 35, 3827–3843. [Google Scholar] [CrossRef]
- Annandale, G.W.; Morris, G.L.; Karki, P. Extending the Life of Reservoirs: Sustainable Sediment Management for Dams and Run-of-River Hydropower; Directions in Development—Energy and Mining; World Bank: Washington, DC, USA, 2016; Available online: https://openknowledge.worldbank.org/handle/10986/25085 (accessed on 8 March 2023).
- Schleiss, A.J.; Franca, M.J.; Juez, C.; De Cesare, G. Reservoir sedimentation. J. Hydraul. Res. 2016, 54, 595–614. [Google Scholar] [CrossRef]
- Annandale, G.W. Quenching the Thirst: Sustainable Water Supply and Climate Change; Create Space Independent Publishing Platform: North Charleston, SC, USA, 2013; p. 250. [Google Scholar]
- Morris, G.L. Classification of Management Alternatives to Combat Reservoir Sedimentation. Water 2020, 12, 861. [Google Scholar] [CrossRef]
- Bohorquez, J.; Saldarriaga, J.; Vallejo, D. Pumping pattern optimization in order to reduce WDS operation costs. In Proceedings of the Computing and Control for the Water Industry (CCWI2015)—Sharing the Best Practice in Water Management, Leicester, UK, 2–4 September 2015; pp. 1069–1077. [Google Scholar]
- Bagloee, S.A.; Asadi, M.; Patriksson, M. Minimization of water pumps’ electricity usage: A hybrid approach of regression models with optimization. Expert Syst. Appl. 2018, 107, 222–242. [Google Scholar] [CrossRef]
- Galindo, J.; Torok, S.; Salguero, F.; de Campos, S.; Romera, J.; Puig, V. Optimal Management of Water and Energy in Irrigation Systems: Application to the Bardenas Canal. In Proceedings of the 20th World Congress of the International-Federation-of-Automatic-Control (IFAC), Toulouse, France, 9–14 July 2017; pp. 6613–6618. [Google Scholar]
- Chen, W.; Tao, T.; Zhou, A.; Zhang, L.; Liao, L.; Wu, X.; Yang, K.; Li, C.; Zhang, T.C.; Li, Z. Genetic optimization toward operation of water intake-supply pump stations system. J. Clean. Prod. 2021, 279, 123573. [Google Scholar] [CrossRef]
- Vakilifard, N.; Anda, M.; Bahri, P.A.; Ho, G. The role of water-energy nexus in optimising water supply systems—Review of techniques and approaches. Renew. Sustain. Energy Rev. 2018, 82, 1424–1432. [Google Scholar] [CrossRef]
- Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir Optimization in Water Resources: A Review. Water Resour. Manag. 2014, 28, 3391–3405. [Google Scholar] [CrossRef]
- Macian-Sorribes, H.; Pulido-Velazquez, M. Inferring efficient operating rules in multireservoir water resource systems: A review. Wiley Interdiscip. Rev. Water 2020, 7, e1400. [Google Scholar] [CrossRef]
- Jahandideh-Tehrani, M.; Bozorg-Haddad, O.; Loaiciga, H.A. A review of applications of animal-inspired evolutionary algorithms in reservoir operation modelling. Water Environ. J. 2021, 35, 628–646. [Google Scholar] [CrossRef]
- Lai, V.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. A Review of Reservoir Operation Optimisations: From Traditional Models to Metaheuristic Algorithms. Arch. Comput. Methods Eng. 2022, 29, 3435–3457. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Wang, H.; Rao, J.; Wang, J. Zone scheduling optimization of pumps in water distribution networks with deep reinforcement learning and knowledge-assisted learning. Soft Comput. 2021, 25, 14757–14767. [Google Scholar] [CrossRef]
- Sarbu, I. Optimization of Urban Water Distribution Networks Using Deterministic and Heuristic Techniques: Comprehensive Review. J. Pipeline Syst. Eng. Pract. 2021, 12, 03121001. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef]
- Jean, M.-È.; Morin, C.; Duchesne, S.; Pelletier, G.; Pleau, M. Real-time model predictive and rule-based control with green infrastructures to reduce combined sewer overflows. Water Res. 2022, 221, 118753. [Google Scholar] [CrossRef] [PubMed]
- García, L.; Barreiro-Gomez, J.; Escobar, E.; Téllez, D.; Quijano, N.; Ocampo-Martinez, C. Modeling and real-time control of urban drainage systems: A review. Adv. Water Resour. 2015, 85, 120–132. [Google Scholar] [CrossRef]
- Mollerup, A.L.; Thornberg, D.; Mikkelsen, P.S.; Johansen, N.B.; Sin, G. 16 Years of Experience with Rule Based Control of Copenhagen’s Sewer System. In Proceedings of the 11th IWA conference on instrumentation control and automation, Narbonne, France, 18–20 September 2013. [Google Scholar]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Dong, W.; Yang, Q. Data-Driven Solution for Optimal Pumping Units Scheduling of Smart Water Conservancy. IEEE Internet Things J. 2020, 7, 1919–1926. [Google Scholar] [CrossRef]
- Salehi, M.J.; Shourian, M. Comparative Application of Model Predictive Control and Particle Swarm Optimization in Optimum Operation of a Large-Scale Water Transfer System. Water Resour. Manag. 2021, 35, 707–727. [Google Scholar] [CrossRef]
- Wang, Y.; Yok, K.T.; Wu, W.; Simpson, A.R.; Weyer, E.; Manzie, C. Minimizing Pumping Energy Cost in Real-Time Operations of Water Distribution Systems Using Economic Model Predictive Control. J. Water Resour. Plan. Manag. 2021, 147, 04021042. [Google Scholar] [CrossRef]
- Mesbah, A. Stochastic Model Predictive Control: An Overview and Perspectives for Future Research. IEEE Control. Syst. Mag. 2016, 36, 30–44. [Google Scholar] [CrossRef]
- Xie, L.; Xie, L.; Su, H. A Comparative Study on Algorithms of Robust and Stochastic MPC for Uncertain Systems. Acta Autom. Sin. 2017, 43, 969–992. [Google Scholar]
- Lee, J.H.; Wong, W. Approximate dynamic programming approach for process control. J. Process Control 2010, 20, 1038–1048. [Google Scholar] [CrossRef]
- Lund, N.S.V.; Falk, A.K.V.; Borup, M.; Madsen, H.; Mikkelsen, P.S. Model predictive control of urban drainage systems: A review and perspective towards smart real-time water management. Crit. Rev. Environ. Sci. Technol. 2018, 48, 279–339. [Google Scholar] [CrossRef]
- Shin, J.; Badgwell, T.A.; Liu, K.-H.; Lee, J.H. Reinforcement Learning—Overview of recent progress and implications for process control. Comput. Chem. Eng. 2019, 127, 282–294. [Google Scholar] [CrossRef]
- Prag, K.; Woolway, M.; Celik, T. Toward Data-Driven Optimal Control: A Systematic Review of the Landscape. IEEE Access 2022, 10, 32190–32212. [Google Scholar] [CrossRef]
- Yin, L.; Li, S.; Liu, H. Lazy reinforcement learning for real-time generation control of parallel cyber-physical-social energy systems. Eng. Appl. Artif. Intell. 2020, 88, 103380. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q. Reinforcement learning-based real-time power management for hybrid energy storage system in the plug-in hybrid electric vehicle. Appl. Energy 2018, 211, 538–548. [Google Scholar] [CrossRef]
- Yang, J.; You, X.; Wu, G.; Hassan, M.M.; Almogren, A.; Guna, J. Application of reinforcement learning in UAV cluster task scheduling. Future Gener. Comput. Syst. 2019, 95, 140–148. [Google Scholar] [CrossRef]
- Wei, H.; Zheng, G.; Yao, H.; Li, Z.; Acm. IntelliLight: A Reinforcement Learning Approach for Intelligent Traffic Light Control. In Proceedings of the 24th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), London, UK, 19–23 2018; pp. 2496–2505. [Google Scholar]
- Chu, K.-F.; Lam, A.Y.S.; Li, V.O.K. Traffic Signal Control Using End-to-End Off-Policy Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7184–7195. [Google Scholar] [CrossRef]
- Abdulhai, B.; Pringle, R.; Karakoulas, G.J. Reinforcement learning for True Adaptive traffic signal control. J. Transp. Eng. 2003, 129, 278–285. [Google Scholar] [CrossRef]
- Powell, W.B. Approximate Dynamic Programming: Solving the Curses of Dimensionality; John Wiley & Sons: New York, NY, USA, 2007; pp. 1–469. [Google Scholar]
- Bowes, B.D.; Tavakoli, A.; Wang, C.; Heydarian, A.; Behl, M.; Beling, P.A.; Goodall, J.L. Flood mitigation in coastal urban catchments using real-time stormwater infrastructure control and reinforcement learning. J. Hydroinformatics 2021, 23, 529–547. [Google Scholar] [CrossRef]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-Line Building Energy Optimization Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 10, 3698–3708. [Google Scholar] [CrossRef]
- Hajgató, G.; Paál, G.; Gyires-Tóth, B. Deep Reinforcement Learning for Real-Time Optimization of Pumps in Water Distribution Systems. J. Water Resour. Plan. Manag. 2020, 146I, 04020079. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Lobbrecht, A.H.; Solomatine, D.P. Neural networks and reinforcement learning in control of water systems. J. Water Resour. Plan. Manag. 2003, 129, 458–465. [Google Scholar] [CrossRef]
- Tian, W.; Liao, Z.; Zhi, G.; Zhang, Z.; Wang, X. Combined Sewer Overflow and Flooding Mitigation Through a Reliable Real-Time Control Based on Multi-Reinforcement Learning and Model Predictive Control. Water Resour. Res. 2022, 58, e2021WR030703. [Google Scholar] [CrossRef]
- Mullapudi, A.; Lewis, M.J.; Gruden, C.L.; Kerkez, B. Deep reinforcement learning for the real time control of stormwater systems. Adv. Water Resour. 2020, 140, 103600. [Google Scholar] [CrossRef]
- Tian, W.; Liao, Z.; Zhang, Z.; Wu, H.; Xin, K. Flooding and Overflow Mitigation Using Deep Reinforcement Learning Based on Koopman Operator of Urban Drainage Systems. Water Resour. Res. 2022, 58, e2021WR030939. [Google Scholar] [CrossRef]
- Liao, Z.; Zhang, Z.; Tian, W.; Gu, X.; Xie, J. Comparison of Real-time Control Methods for CSO Reduction with Two Evaluation Indices: Computing Load Rate and Double Baseline Normalized Distance. Water Resour. Manag. 2022, 36, 4469–4484. [Google Scholar] [CrossRef]
- Bowes, B.D.; Wang, C.; Ercan, M.B.; Culver, T.B.; Beling, P.A.; Goodall, J.L. Reinforcement learning-based real-time control of coastal urban stormwater systems to mitigate flooding and improve water quality. Environ. Sci. Water Res. Technol. 2022, 8, 2065–2086. [Google Scholar] [CrossRef]
- Filipe, J.; Bessa, R.J.; Reis, M.; Alves, R.; Póvoa, P. Data-driven predictive energy optimization in a wastewater pumping station. Appl. Energy 2019, 252, 113423. [Google Scholar] [CrossRef]
- Seo, G.; Yoon, S.; Kim, M.; Mun, C.; Hwang, E. Deep Reinforcement Learning-Based Smart Joint Control Scheme for On/Off Pumping Systems in Wastewater Treatment Plants. IEEE Access 2021, 9, 95360–95371. [Google Scholar] [CrossRef]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: New York, NY, USA, 2001; Volume 36, pp. i–xxiii. [Google Scholar]
- Kaveh, K.; Bui, M.D.; Rutschmann, P. A comparative study of three different learning algorithms applied to ANFIS for predicting daily suspended sediment concentration. Int. J. Sediment Res. 2017, 32, 340–350. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.I.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Hui, L. Study on Prediction of Runoff and Sedimentation and Multi-Objective Optimal Operation of Reservoir. Ph.D. Thesis, Tianjin University, Tianjin, China, 2008. [Google Scholar]






| Number of Pumps On | Possible Pump Combinations | Energy Consumption per Unit of Water Intake | Average Pump Efficiency | Pump Combination after Simplifying the Action Space |
|---|---|---|---|---|
| 0 | No pump on | 0 | - | No pump on |
| 1 | 99.7 | 89.74 | ||
| 2 | 113.8 | 90.04 | ||
| 99.7 | 89.04 | |||
| 3 | 129.9 | 86.97 | ||
| 108.7 | 89.71 | |||
| 4 | 120.8 | 87.66 | Z | |
| 113.8 | 90.04 |
| Model | Input Variables | Number of Input Layer Neurons | Number of Hidden Layer Neurons |
|---|---|---|---|
| non-freezing period model | 8 | 12 | |
| freezing period model | 6 | 10 |
| Variable | Value |
|---|---|
| Num iterations | 300 k |
| Timesteps per update | 840 |
| Batch size | 420 |
| Adam step size | |
| Clipping parameter () | 0.2 |
| Discount () | 0.99 |
| GAE parameter () | 0.95 |
| Model | Training Set | Validation Set | Test Set | |
|---|---|---|---|---|
| non-freezing period | 4.317 | 2.942 | 0.948 | |
| freezing period | 0.023 | 0.024 | 0.016 | |
| non-freezing period | 1.140 | 1.007 | 0.837 | |
| freezing period | 0.008 | 0.009 | 0.013 |
| Strategy | Energy Consumption per Unit of Water Intake | ||||
|---|---|---|---|---|---|
| Perfect prediction control | 15,980 | 15,931 | 99.7(−8.33%) | 2679(−35.40%) | 0.167(−40.57%) |
| Predictive control | 15,617 | 15,569 | 99.7(−8.33%) | 2768(−33.25%) | 0.177(−37.01%) |
| Manual control | 14,747 | 15,970 | 108 | 4147 | 0.281 |
| Water Outflow Type | Energy Consumption per Unit of Water Intake | ||||
|---|---|---|---|---|---|
| P1 | 15,617 | 15,569 | 99.7 | 2768 | 0.177 |
| P2 | 15,561 | 15,524 | 99.8 | 2691 | 0.173 |
| P3 | 15,617 | 15,569 | 99.7 | 2808 | 0.180 |
| P4 | 15,616 | 15,568 | 99.7 | 2639 | 0.169 |
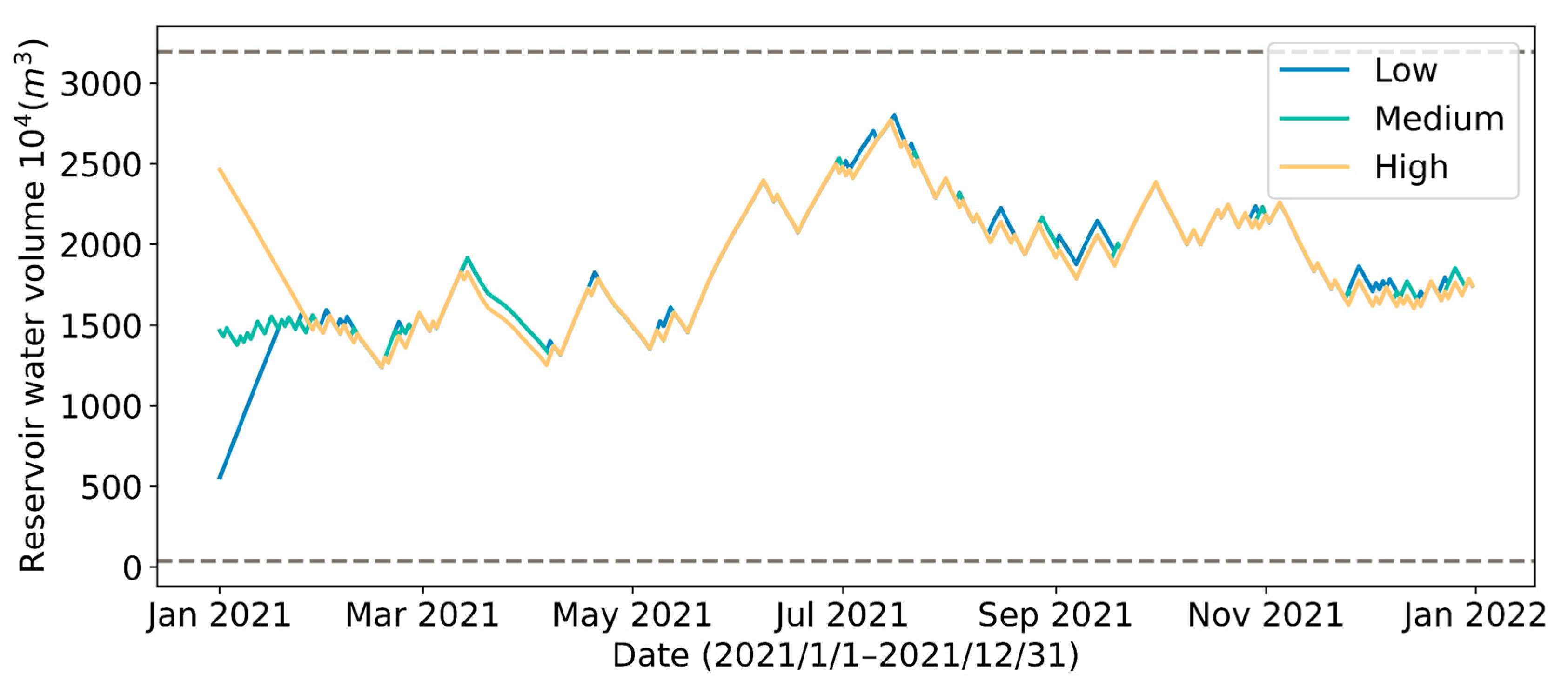
| Initial Reservoir Volume | Energy Consumption per Unit of Water Intake | ||||
|---|---|---|---|---|---|
| Low | 16,161 | 16,112 | 99.7 | 2777 | 0.172 |
| Medium | 15,163 | 15,116 | 99.7 | 2776 | 0.183 |
| High | 14,164 | 14,120 | 99.7 | 2779 | 0.196 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Bai, L.; Tian, W.; Yan, H.; Hu, W.; Xin, K.; Tao, T. Online Control of the Raw Water System of a High-Sediment River Based on Deep Reinforcement Learning. Water 2023, 15, 1131. https://doi.org/10.3390/w15061131
Li Z, Bai L, Tian W, Yan H, Hu W, Xin K, Tao T. Online Control of the Raw Water System of a High-Sediment River Based on Deep Reinforcement Learning. Water. 2023; 15(6):1131. https://doi.org/10.3390/w15061131
Chicago/Turabian StyleLi, Zhaomin, Lu Bai, Wenchong Tian, Hexiang Yan, Wanting Hu, Kunlun Xin, and Tao Tao. 2023. "Online Control of the Raw Water System of a High-Sediment River Based on Deep Reinforcement Learning" Water 15, no. 6: 1131. https://doi.org/10.3390/w15061131
APA StyleLi, Z., Bai, L., Tian, W., Yan, H., Hu, W., Xin, K., & Tao, T. (2023). Online Control of the Raw Water System of a High-Sediment River Based on Deep Reinforcement Learning. Water, 15(6), 1131. https://doi.org/10.3390/w15061131





