1. Introduction
In Latin America, access to clean water is still an everyday problem for millions of people [
1]. In terms of water availability, Brazil ranks among the biggest countries globally; however, when economic and demographic factors are considered, water scarcity is also a reality in some areas [
2]. Ghisi [
3] points out that, as of 2050, the northeast and southeast regions of Brazil will have water availability of less than 2000 m
3 per capita per year, which is classified as very low by the UNEP [
4]. However, if the widespread implementation of residential rainwater harvesting (RWH) is considered in these regions, water availability will remain above the precarious threshold in the following decades.
Traditional approaches to urban water supply prioritise centralised facilities that seek water resources in increasingly distant locations, as potable water demand increases in the city scale [
5]. In this sense, RWH systems aim to reduce potable water demand from centralised distribution systems. Ghisi [
3] estimated the potential for potable water savings to be between 48% and 100%, employing RWH systems in the residential sector of five Brazilian regions. However, high payback often deems most residential RWH systems as financially unfeasible [
6]. In Brazil, payback periods for such systems can be as short as 1.5 years but more often range from 20.1 to 25 years [
7]. Costs of RWH are characterised by high initial outlays, followed by low operational costs throughout their service life [
8]. The high cost of such a solution is still a limiting factor for its implementation, and it is recommended that public authorities provide incentives to encourage the population to adopt it [
5]. In addition, developing more cost-effective design solutions and innovations is also necessary for improving the financial appeal of RWH systems [
6].
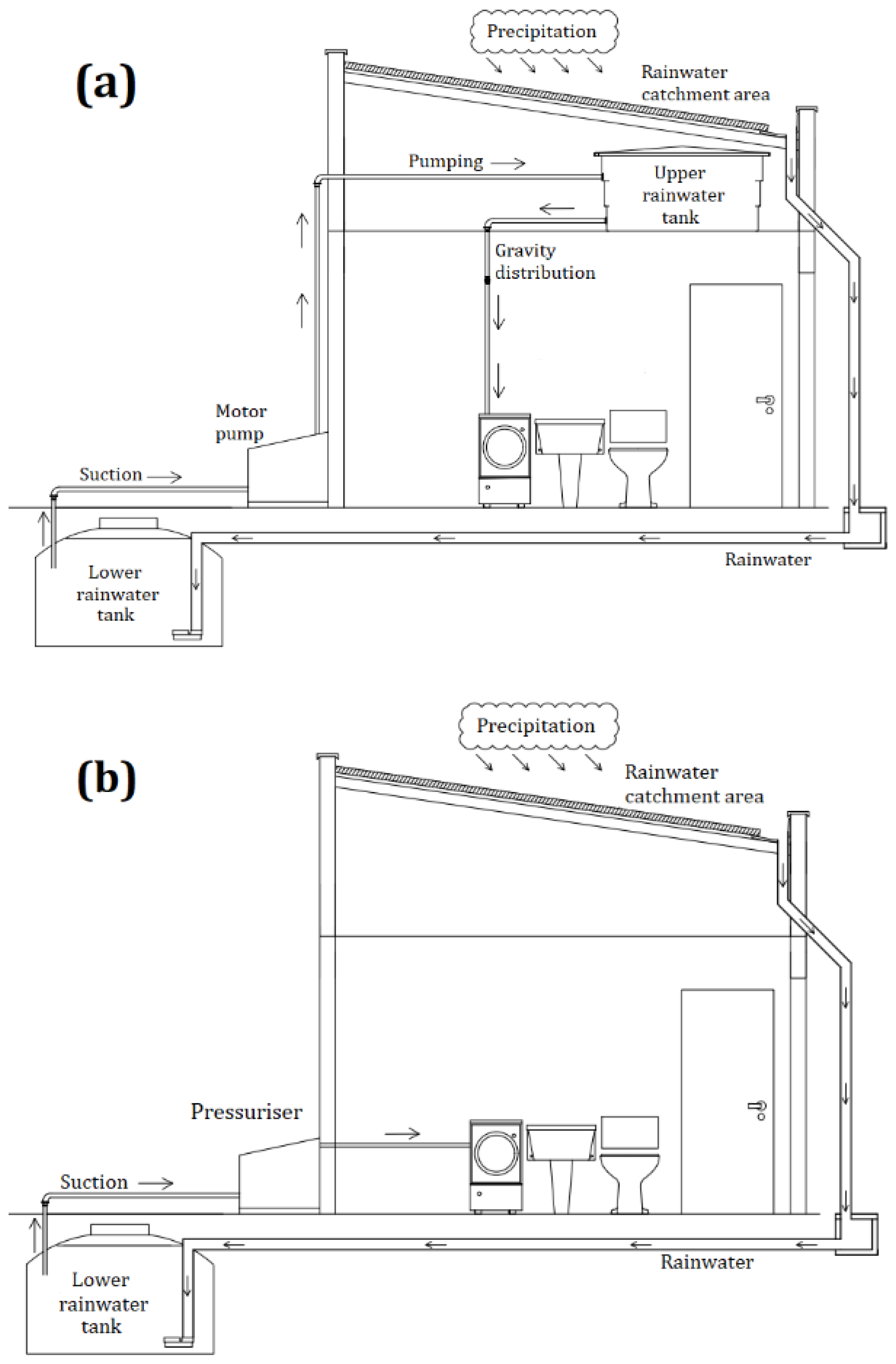
Usually, rainwater distribution to the water appliances can be done directly or indirectly. In systems with indirect distribution, a motor pump pumps rainwater from the primary storage tank at ground level to an upper rainwater tank [
6]. From the upper tank, rainwater is distributed to the water appliances by gravity. As an alternative, rainwater distribution can be done from the lower tank by directly pressurising the distribution system to the water appliances. In this study, systems with both direct and indirect rainwater distribution schemes were evaluated. Direct rainwater distribution tends to be more financially feasible when compared to indirect rainwater distribution in single-family RWH systems [
9]. However, as Vieira et al. [
10] pointed out, the direct configuration consumes more energy than systems with indirect rainwater distribution.
The dissemination of RWH systems depends greatly on their financial feasibility, which is often neglected by residential users [
11]. This study determines the costs and benefits of residential RWH systems in eight Brazilian cities with different rainfall patterns, aiming to demonstrate the conditions for financial return. The net present value, internal rate of return and payback were used as feasibility indicators, as this is a common practice in the literature [
12,
13].
Comparison of results from studies that investigate the financial feasibility of RWH systems is generally difficult. As Amos et al. [
13] point out, this is because such studies usually employ significantly different building and design conventions for determining initial outlays. In this sense, Teston et al. [
7] indicate that the tank sizing method commonly differs among studies and directly influences the potential for potable water savings and the financial feasibility of RWH systems. Correspondingly, Ward et al. [
14] compared simple design methods with continuous simulation methods for RWH system designs. Methods based on continuous simulation resulted in smaller tank sizes, thus positively impacting the systems’ installation costs and financial feasibility. Furthermore, it was found that RWH systems tend to be more feasible for large commercial buildings than for domestic and more compact systems.
Installation costs of RWH systems can vary greatly, primarily depending on the tank size. Teston et al. [
7] observed a wide range of paybacks (0.5 to more than 25 years) for residential RWH among six Brazilian studies. According to Li et al. [
15], rainwater tanks are the most expensive components of the RWH systems, corresponding to 50–70% of their total cost in domestic settings. Similarly, Gómez and Teixeira [
12] obtained tank cost corresponding to 68% of the total outlay in Belém, northern Brazil. The underground installation of rainwater tanks tends to be more expensive than the installation on the surface [
15]. In this sense, for a city in southern Brazil, Istchuk and Ghisi [
16] observed tank costs corresponding to 23% of the initial outlay of single-family houses. In this case, a thorough item-by-item cost survey procedure was performed.
Several Brazilian studies [
12,
17,
18] found that the rainwater demand directly influences the financial feasibility of single-family RWH systems. Ghisi and Schondermark [
17] observed that the systems are feasible (paybacks between 1.5–10 years) in most cases. Berwanger and Ghisi [
18] observed feasible systems with rainwater demand above 18 m
3/month. Severis et al. [
9] conducted financial analyses on residential RWH systems comparing three different system typologies: direct distribution, indirect distribution and a simpler system with a single rainwater tank. The system with direct rainwater distribution proved to be the most feasible, with an internal rate of return of 6.85% per year.
The potable water tariff schemes practised by local water utilities are also influential for the feasibility of domestic RWH systems. Liang and Van Dijk [
19] observed that, in Beijing, China, the financial feasibility of RWH systems depends largely on potable water tariffs. In this sense, Li et al. [
15] point out that paybacks tend to increase in the future for these systems, given the upward trend in water costs and the current lack of government incentives in the country for RWH. Gómez and Teixeira [
12] studied the financial feasibility of twelve houses in northern Brazil. Similarly, as observed in other works [
18], the tariff scheme of the local water utility makes it unfeasible to use rainwater in homes that pay a fixed rate for consumption up to a certain threshold. This observation reinforces the importance of reviewing the tariff scheme practised in some locations and establishing government incentive policies that encourage implementing RWH systems.
Large-scale implementation of RWH systems could be financially beneficial for water companies. Cureau and Ghisi [
20] evaluated the possible financial impacts of different water-saving strategies on public administration in the city of Joinville, southern Brazil. When considering the extensive implementation of RWH systems in the city, annual savings of up to five million Brazilian reais (BRL) could be achieved by reducing the need to expand centralised supply systems. The study concludes that the utility would not fail to profit and would obtain total financial gains between 13 and 45 million BRL annually by adopting the use of rainwater at the scale of the city.
In Brazil, the technical standard NBR 15527 specifies RWH requirements for non-potable uses [
21]. According to Teston et al. [
7] non-potable uses correspond to about 50% of residential water use nationally. The Brazilian technical standard [
21] states that the RWH systems design must consider several variables, including the local rainfall characteristics, the catchment area and rainwater demand. To assess the influence of these variables on the model outputs, sensitivity analysis methods are practical and widely used tools [
22,
23,
24].
According to Saltelli and Marivoet [
25], sensitivity analysis techniques are fundamental for understanding complex models, especially when they involve many input variables. For instance, Jin et al. [
26] employed a sensitivity analysis to determine the relative importance of uncertain parameters such as inflation and discount rates on financial support programs to promote installation of RWH systems in South Korea. The net present value was deemed as an appropriate indicator to estimate the financial feasibility of RWH systems. Moreover, funding programs and financial support policies were recommended to increase financial feasibility of RWH systems. Conversely, Severis et al. [
9] employed a sensitivity analysis to assess the financial feasibility of RWH systems in Lages, southern Brazil. Systems with direct and indirect rainwater distribution were analysed, and the potable water tariff was pointed out as the variable with the most significant influence on the system’s financial feasibility.
Silva and Ghisi [
24] also used a sensitivity analysis to determine the influence of design variables on RWH systems’ performance in eight Brazilian cities. Rainwater demand was the most important parameter affecting most cities’ potential for potable water savings. Considering the diversity of input variables involved in the design of RWH systems, sensitivity analysis is a valuable tool for designers, customers and decision-makers to make their choices towards implementing this technology more broadly.
Not many studies can be found in the literature on the influence of rainfall characteristics on the performance of RWH systems. Pacheco et al. [
27] evaluated the influence of different rainfall patterns on the financial feasibility of 1000 RWH system design scenarios in the same location in central Brazil. The number of days without precipitation was deemed an essential parameter for the feasibility of RWH systems. Similarly, Geraldi and Ghisi [
28] found that short-term rainfall time series can be used instead of long-term time series for simulating RWH with similar results. The main condition for this is that the average number of dry days per year should be similar for both series, thus pointing to this indicator as an important parameter for RWH design.
Considering the water scarcity perspective due to urbanisation and climate change, the current water and sanitation model must undergo structural changes, aiming toward more decentralised water supply strategies [
29]. In this sense, the broad adoption of RWH systems contributes to the water security of cities, delaying the need to build or expand centralised water treatment units [
30]. In addition, it is also important to highlight other benefits of RWH systems, such as the reduction in energy consumption linked to the treatment and distribution of potable water, reduction in the emission of greenhouse gases and mitigation of urban flooding during intense precipitation events [
6].
For a more complete and realistic analysis of the financial feasibility of RWH systems, it is important to consider their indirect benefits. Despite this, most approaches used in research are simplistic because they do not consider the full benefits of this type of technology [
6]. Considering this, government support through policies and incentives designed to encompass the socio-environmental benefits of RWH systems are essential to disseminate their use on a wider scale [
5,
12,
31,
32].
Reliable information regarding the financial feasibility of RWH systems is imperative for the development of accurate incentive schemes for its promotion. Conversely, most research about the topic employs different approaches, making it difficult to equitably analyse their results. Considering the knowledge gap regarding the financial feasibility of residential RWH systems in the literature [
33] and the great diversity observed in design conventions for RWH systems [
13], this study aims to provide relevant information for potential investors or policymakers through presenting a comparable financial feasibility analysis among cities with different rainfall characteristics. Moreover, the study classifies the initial outlays of RWH systems of varied sizes into relevant categories for RWH design, thus providing a reference for further studies or other locations.
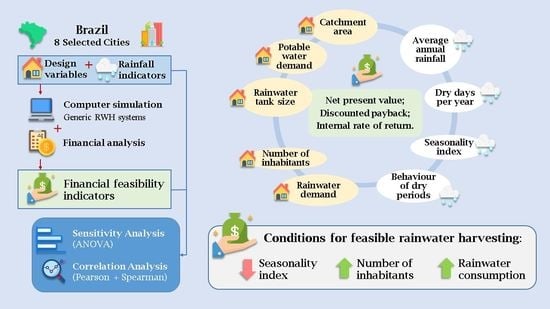
The main output of this study consists in evaluating the influence of rainfall time series indicators (average annual rainfall, average number of dry days per year, seasonality index, average duration, standard deviation, coefficient of variation and maximum duration of dry periods) and design variables (catchment area, rainwater demand, number of inhabitants, potable water demand and rainwater tank size) on the financial feasibility of RWH systems. For this, this study introduces two novel approaches: sensitivity analysis of design variables over the net present value and correlation analysis between rainfall characteristics and the financial feasibility of RWH systems.
3. Results
Based on the cluster analysis method described in the work by Istchuk and Ghisi [
35], the representative cities chosen for this study are Belém, Recife, Campo Grande, Salvador, Brasília, Florianópolis, Belo Horizonte, and São Paulo.
Table 4 shows the rainfall indicators obtained for the cities analysed.
A total of 432 scenarios were simulated (54 for each city) to obtain financial feasibility indicators. All costs correspond to March 2021. Results from other studies were also corrected to March 2021, according to Brazil’s National Index of Civil Construction [
54].
3.1. Initial Outlay
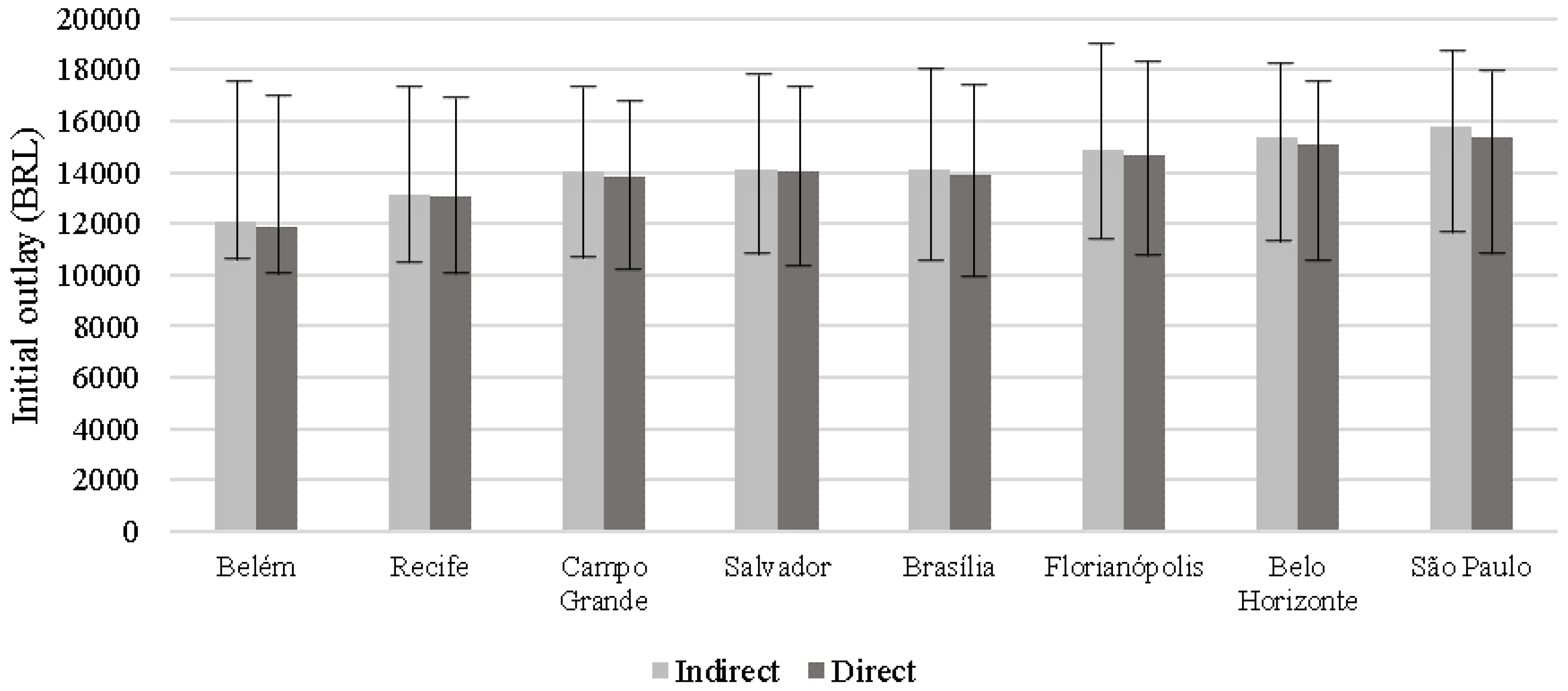
Figure 2 shows the average initial investment values for each city, considering RWH systems with direct and indirect rainwater distribution.
Initial outlays presented slight variations among the cities surveyed. The highest average initial cost among the cities was obtained for the city of São Paulo (BRL 15,785.17 and BRL 15,360.22 for systems with indirect and direct rainwater distribution, respectively). The lowest cost was observed in Belém (similarly, BRL 12,094.61 and BRL 11,904.50). Systems with direct rainwater distribution presented initial outlays between 0.30% (Salvador) and 2.69% (São Paulo), below the outlays of systems with indirect rainwater distribution. RWH systems with direct distribution tend to have lower initial costs due to the absence of an upper rainwater tank. However, higher costs for pressurisation equipment tend to make such savings less significant.
Table 5 shows the average initial outlays among all cities for both rainwater distribution schemes evaluated herein.
Ghisi and Oliveira [
55] evaluated initial outlays of RWH systems with indirect distribution in two single-storey houses in Palhoça, Santa Catarina and obtained costs that correspond from 44.3% to 55.2% of the outlays obtained herein in similar systems in Florianópolis. Similarly, Carvalho [
56] estimated an initial cost of BRL 7199.29, corresponding to 52.9% of the cost taken as a reference in this analysis.
Both in this work and in the literature cited herein, materials and labour were considered in the outlays. However, as Teston et al. [
7] pointed out, the significant difference observed among works is related to different design conventions adopted. Higher initial costs indicate that a more comprehensive list of items has been considered herein when compared to results obtained by Ghisi and Oliveira [
55] and Carvalho [
56].
Severis et al. [
9] evaluated larger systems and indirect rainwater distribution. The authors obtained an initial cost that corresponds to 88.9% of the average cost obtained herein for a similar system. Considering the greater proximity between the costs compared, it can be assumed that the authors considered a similar level of detail in the cost surveys.
Initial outlays were also distributed into categories representing different component groups of RWH systems.
Table 6 shows the average results among all cities. Systems with a catchment area of 200 m
2 were taken as a reference.
As tank size increases, costs relative to tanks and civil works also increase. In this study, most civil works correspond to the underground tank installation. For the other items, the representative cost decreases as the capacity of the tanks increases. Despite having similar outlays, indirect and direct rainwater distribution systems presented different cost distributions. Although systems with direct distribution require less investment for tanks, the costs of electrical installations tend to be higher due to the considerable cost difference observed between the pressurizer and the motor pump.
3.2. Operational Cost
On average, the operating costs obtained for systems with direct rainwater distribution were only 3.08% lower than those obtained for indirect rainwater distribution, mainly due to the lower electricity costs attributed to the pressuriser.
Table 7 shows the average operational costs obtained in each city, considering both rainwater distribution schemes evaluated herein. Average operational costs were obtained per cubic meter of consumed rainwater for both feasible and unfeasible systems.
3.3. Financial Feasibility
Systems with paybacks under 30 years, positive net present values and internal rates of return above 0.50% per month were considered financially feasible.
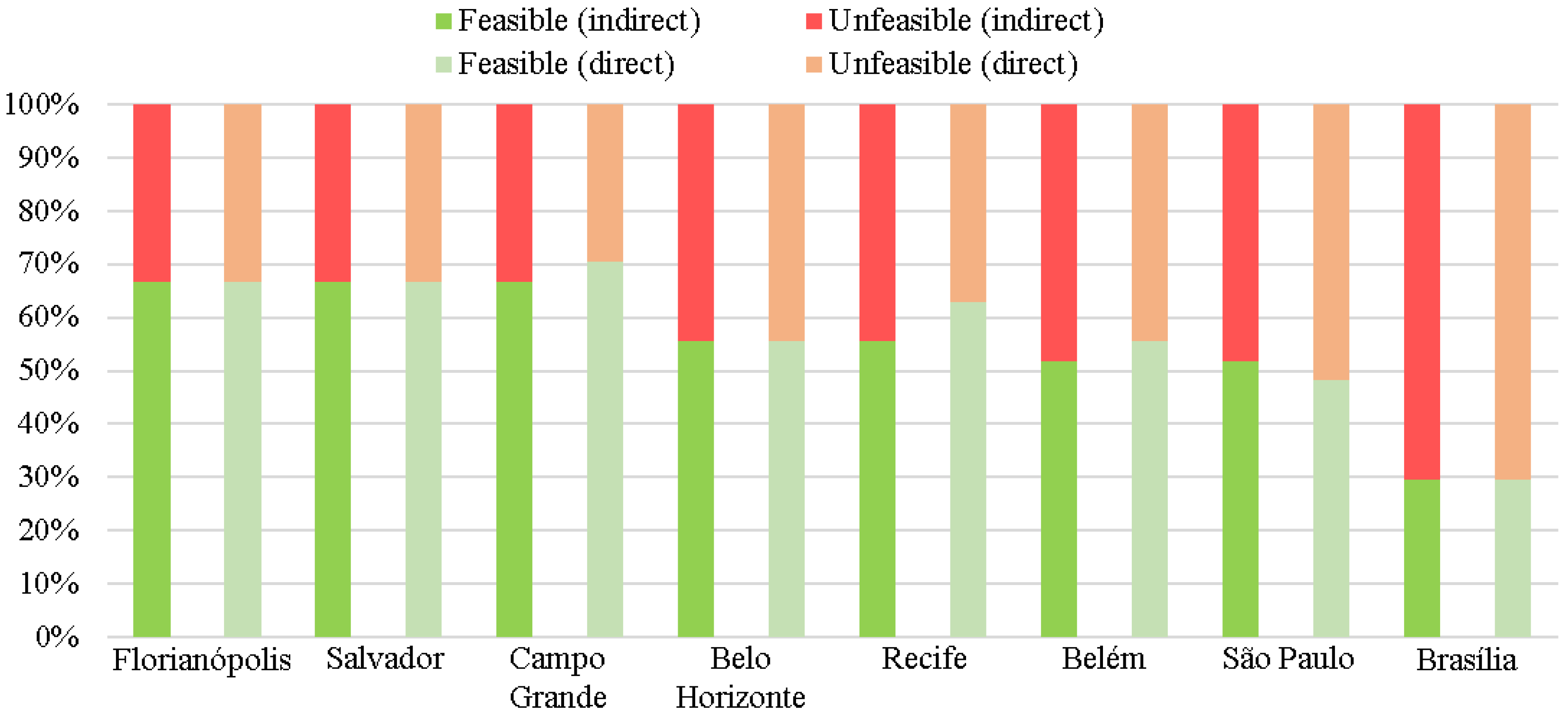
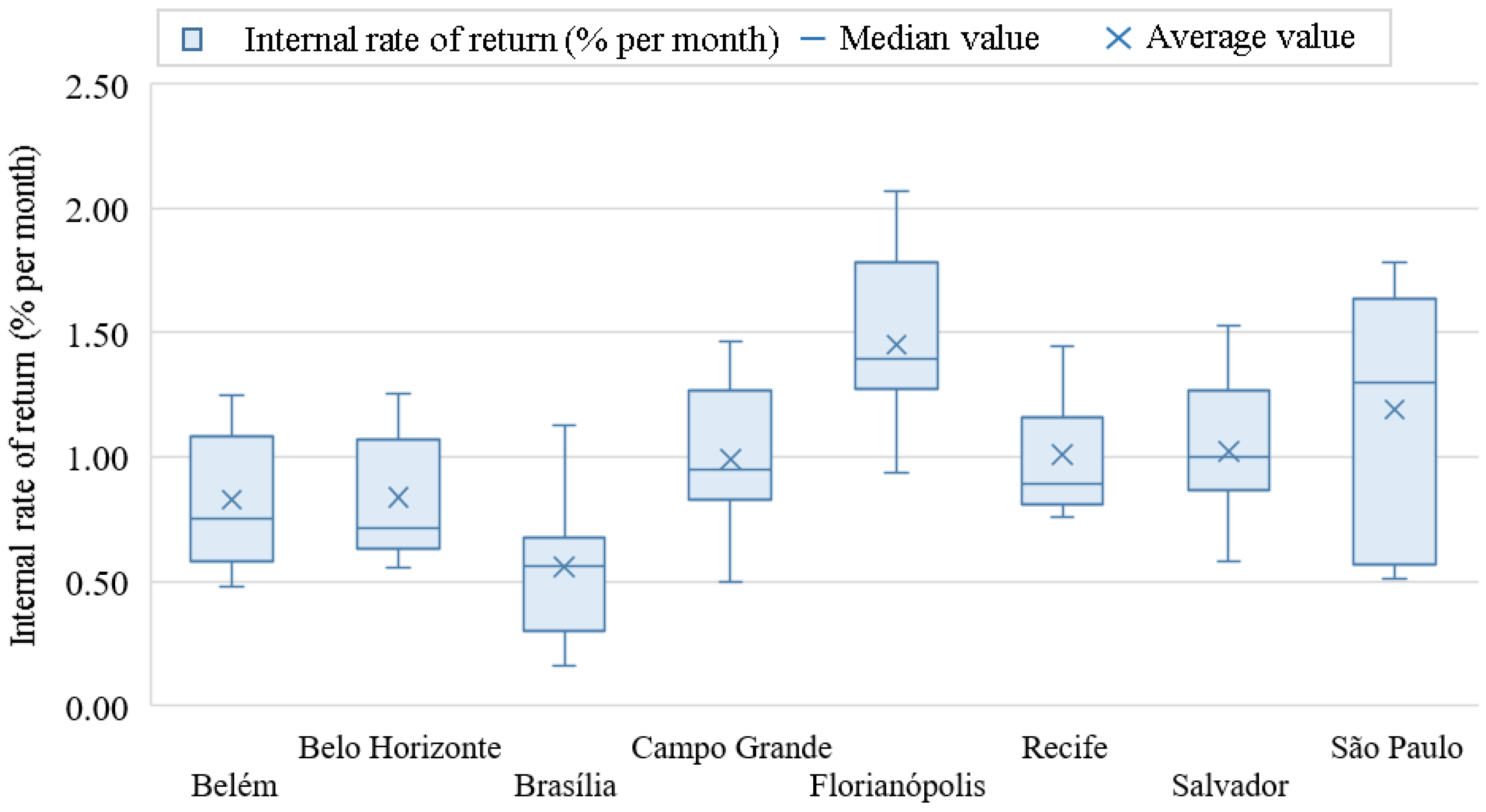
Figure 3 shows the financial feasibility of the eight cities studied herein for RWH systems with direct and indirect rainwater distribution.
Florianópolis, Salvador and Campo Grande performed best in terms of financial feasibility. Despite presenting similar feasibility results, it is interesting to point out the significant differences among their rainfall indicators. Campo Grande, for instance, is much drier (1479 mm/year) than Florianópolis and Salvador (1857 and 1754 mm/year, respectively). Campo Grande and Salvador have similar seasonality indexes (0.47 and 0.48, respectively), while Florianópolis stands out for its excellent rainfall distribution throughout the year (S = 0.22).
Campo Grande, Recife, Belém performed best in terms of feasibility for direct systems when compared to indirect systems. Severis et al. [
9], in this sense, found that systems with direct rainwater distribution tend to be more financially feasible than those with indirect rainwater distribution.
Belo Horizonte stands out for presenting a feasibility percentage of 56%, even with a seasonality index equal to that of Brasília (0.74) and an average of 263 dry days per year, the highest among the cities studied. The different tariff structures practised in the eight cities can explain such a difference.
Figure S1, in the Supplementary Materials, shows the water tariff schemes practised in each city.
Belém stands out as the city with the highest rainfall availability (2998 mm/year) and a seasonality index similar to Campo Grande and Salvador (0.46). With an average of only 98 dry days per year, the feasibility of RWH systems in Belém was compromised by the water pricing scheme practised there.
Water tariffs in Belém, despite being lower than the national average, do not produce significant savings on the water bill from potable water savings. On the other hand, Campo Grande benefited in this sense by implementing a water tariff structure that favours the financial benefit of RWH systems.
Berwanger and Ghisi [
18] evaluated residential RWH systems in the city of Itapiranga, southern Brazil. They pointed out that no financial feasibility is possible in systems with water consumption below 10 m
3/month due to the fixed tariff practised by the local water utility. In this research, the same can be observed in Belém, Recife and São Paulo. Salvador and Belo Horizonte also have fixed tariffs for monthly water consumption lower than a water consumption threshold. Campo Grande, Brasília and Florianópolis do not adopt fixed tariffs.
In this sense, Ghisi and Oliveira [
55] highlight the importance of reviewing Brazilian legislation regarding water tariff schemes to stimulate potable water savings. Based on a case study in Belém, Gómez and Teixeira [
12] also mention the tariff structure practised and suggest adjustments so that more significant financial benefit can be obtained from potable water savings.
Financial feasibility indicators did not vary significantly for RWH systems with direct or indirect rainwater distribution.
Table 8 shows the average results among all simulated scenarios for both rainwater distribution schemes evaluated herein.
Figure 4,
Figure 5 and
Figure 6 show the financial feasibility indicators obtained for systems with indirect rainwater distribution.
Shorter paybacks can be expected as lower seasonality indexes are observed. The best financial feasibility of RWH systems was observed in Florianópolis. Abundant (1857 mm/year) and well-distributed (0.22) rainfall contribute to these results, in addition to water tariffs that benefit financial savings from using rainwater. Recife (2360 mm/year), Salvador (1754 mm/year) and Campo Grande (1479 mm/year) presented intermediate results. Despite being a drier location, Campo Grande obtained better financial feasibility due to the water tariff scheme adopted by the local water utility. Systems simulated in Brasília (1449 mm/year), Belo Horizonte (1486 mm/year) and Belém (2998 mm/year) had low financial feasibility indexes. Despite the high rainfall, the financial feasibility of RWH systems in Belém was hindered by its water tariff scheme. São Paulo (1658 mm/year) presented average results similar to those of Recife, Salvador and Campo Grande.
In every city, the net present value was correlated with the rainwater consumption, and
Figure 7 shows such correlations for systems with indirect rainwater distribution. The graphs also show the minimum and maximum rainwater consumptions that the rainfall regime of each city was capable of supplying according to the design conventions adopted in this study.
The rainfall regime in Belém (2998 mm/year) supplied a maximum rainwater consumption of 14.5 m3/month of rainwater for systems with a catchment area of 100 m2, 18.2 m3/month for systems with a catchment area of 200 m2 and of 19.1 m3/month for systems with 300 m2 according to the design variables used in this simulation. Systems with indirect distribution of rainwater and rainwater consumption below 9 m3/month did not reach financial feasibility. No scenario with two inhabitants in the household was considered financially feasible, while all simulated scenarios with six inhabitants were considered feasible.
Rainfall in Belo Horizonte (1486 mm/year) provided significantly less rainwater than in Belém, with a maximum of 7.4 m3/month for systems with catchment areas of 100 m2, 10.3 m3/month for catchment areas of 200 m2 and 11.2 m3/month for catchment areas of 300 m2. Systems with a catchment area of 100 m2 showed financial feasibility with rainwater consumption above 5.6 m3/month. In systems with a catchment area of 200 m2 and 300 m2, feasibility was achieved with rainwater consumptions above 6.5 m3/month and 6.8 m3/month, respectively. Only systems with four or more inhabitants achieved financial feasibility.
For both rainwater distribution schemes, Brasília presented financial feasibility in only 30% of the scenarios. The low rainfall availability (1499 mm/year) and a water tariff scheme that does not favour financial savings due to the potable water savings contributed to this result. The maximum rainwater consumption in Brasília is similar to that of Belo Horizonte—between 8 m3/month and 12 m3/month in feasible systems, depending on the catchment area and other design variables.
Despite having similar rainfall availability to Brasília (1479 mm/year), the water tariff scheme practised in Campo Grande helped this city to achieve superior financial feasibility results. Conversely, even though the rainfall regime of Florianópolis (1857 mm/year) is not as high as in Belém, this city obtained very similar rainwater consumptions. The excellent annual rainfall uniformity explains this in Florianópolis (0.22).
Recife’s rainfall regime was able to supply a rainwater consumption similar to what was found for Campo Grande. In Recife, rainfall availability is higher (2360 mm/year), the periods without precipitation are shorter (average duration = 2.58 days), but rainfall is less evenly distributed throughout the year (S = 0.56). Like in Campo Grande, RWH systems in Recife were feasible in 67% of the scenarios with indirect rainwater distribution.
Salvador’s rainfall regime supplied rainwater consumption between 5.2 m3/month and 15.3 m3/month, as observed in Campo Grande, Recife and São Paulo. São Paulo and Salvador have relatively similar rainfall regimes based on the indicators used in this research. In this case, the difference in financial feasibility is related to the different potable water tariff schemes between the two cities. São Paulo also has the highest installation costs among the studied locations and operating costs among the highest.
It is interesting to highlight the relationship between the maximum rainwater consumption and the system’s catchment areas. Such a difference between systems with a catchment area of 200 m
2 and 300 m
2 varied only 1.4 m
3/month compared to 3.9 m
3/month obtained between 100 m
2 and 200 m
2. This means that increasing catchment areas from 200 m
2 to 300 m
2 does not imply an increase in rainwater availability in the same proportion as an increase from 100 m
2 to 200 m
2. The average maximum consumption of rainwater observed for all cities was 15.1 m
3/month. Thus, the systems with a catchment area of 200 m
2 could supply, on average, 90.5% of the rainwater consumption simulated in this research among the rainfall regimes studied. Complete financial feasibility results can be found in
Tables S1–S16 in the Supplementary Materials.
3.4. Sensitivity Analysis
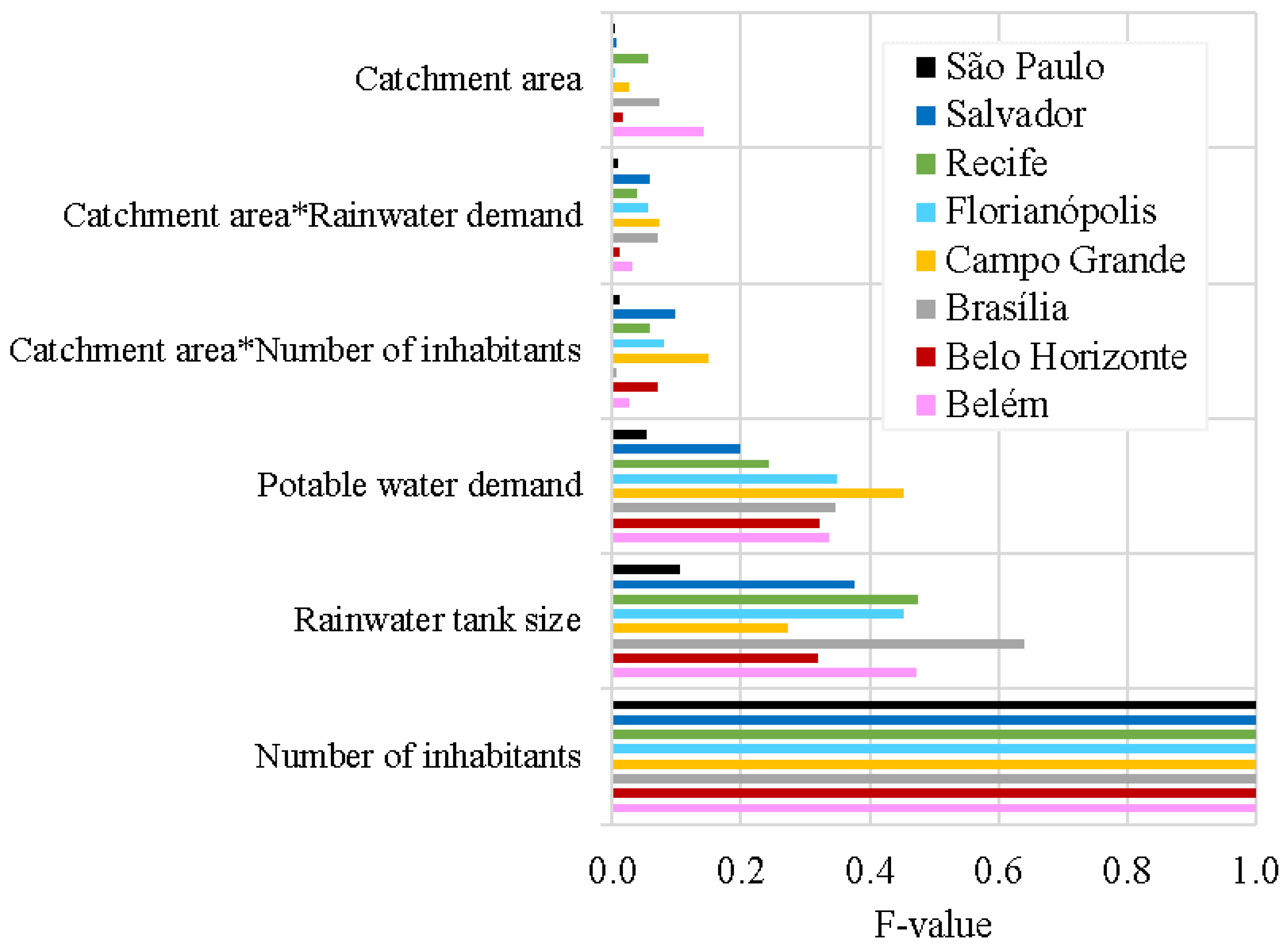
Figure 8 shows the influence of design variables on the net present value of the RWH systems in each of the cities evaluated in this study.
In
Figure 8, F = 1 represents the design variable with the most influence on the net present value, whereas F = 0 represents the least influence. The number of inhabitants was the most influential design variable on the net present value. This variable directly impacts the rainwater consumption in the house and directly influences rainwater savings. This result is in agreement with other studies that, by employing other methods, established a direct relationship between rainwater demand and the financial feasibility of the RWH systems [
9,
12,
17,
18].
Despite being related to rainwater supply, the catchment area was the design variable that exerted the least influence on the net present value of residential RWH systems. This is because the catchment area is not directly linked to the generation of financial benefit throughout the RWH system’s lifespan.
In Brasília, the rainwater tank size significantly influenced the net present value more than observed in the other cities. This is related to the presence of long periods without precipitation in the rainfall regime of this location (maximum duration of 128 days and seasonality equal to 0.74), which requires the installation of larger rainwater tanks and results in a lower potential for potable water savings.
As shown in
Section 3.3, RWH systems in São Paulo are more susceptible to design variables because they present a significant difference between the best and worst feasibility results. In São Paulo, the number of inhabitants resulted in F-values much greater than that observed for other variables. Therefore, potable water demand is of great importance in establishing financially feasible systems in this location.
3.5. Correlation Analysis
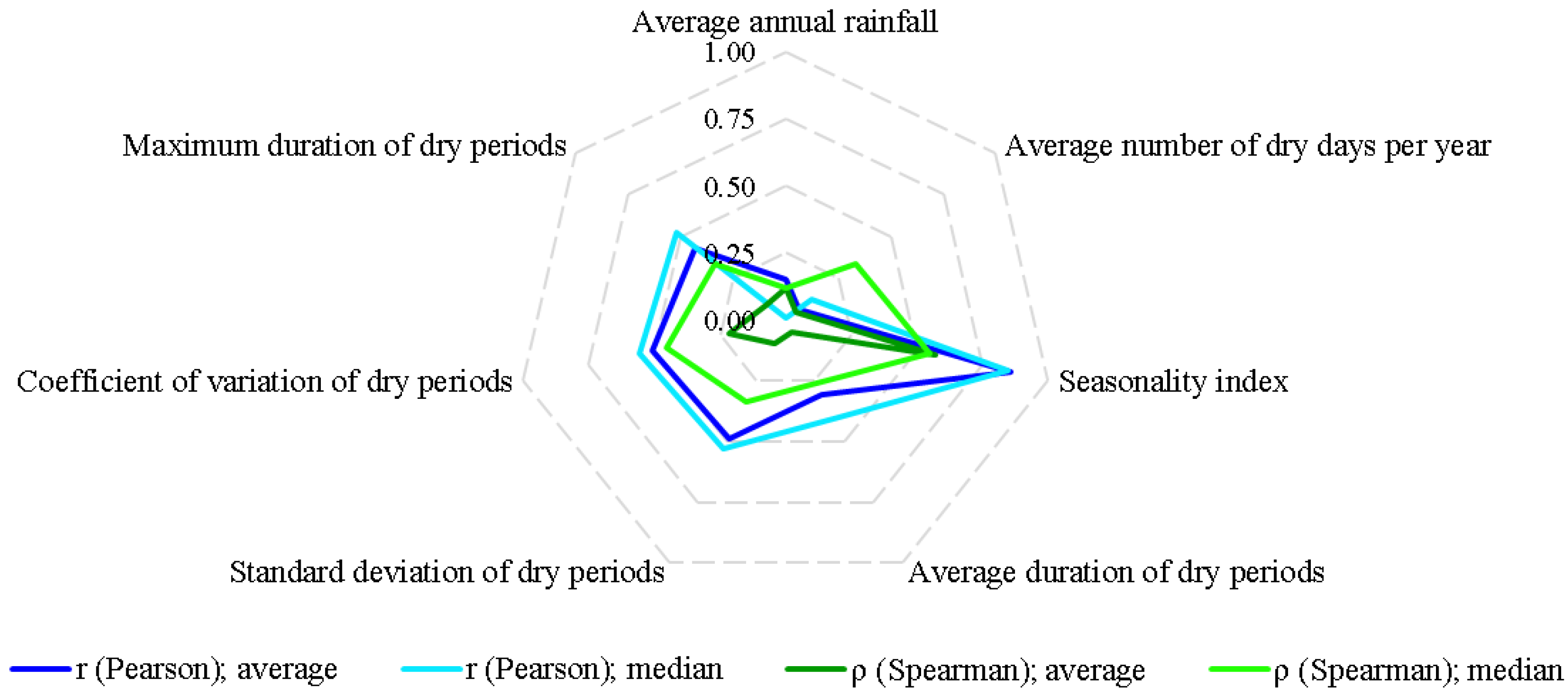
Figure 9 shows the coefficients of correlation between the rainfall indicators and the net present values obtained for residential RWH systems in eight Brazilian cities. All coefficients of correlation can be found in
Table S17 in the Supplementary Materials.
The seasonality index was the rainfall indicator that presented the highest correlation with the net present value of RWH systems, thus linking the financial feasibility of these systems with the uniformity of rainwater distribution throughout the year. Geraldi and Ghisi [
40] also pointed out that the rainfall distribution within the year should be incorporated in future works about RWH design, given its important influence in simulation outcomes.
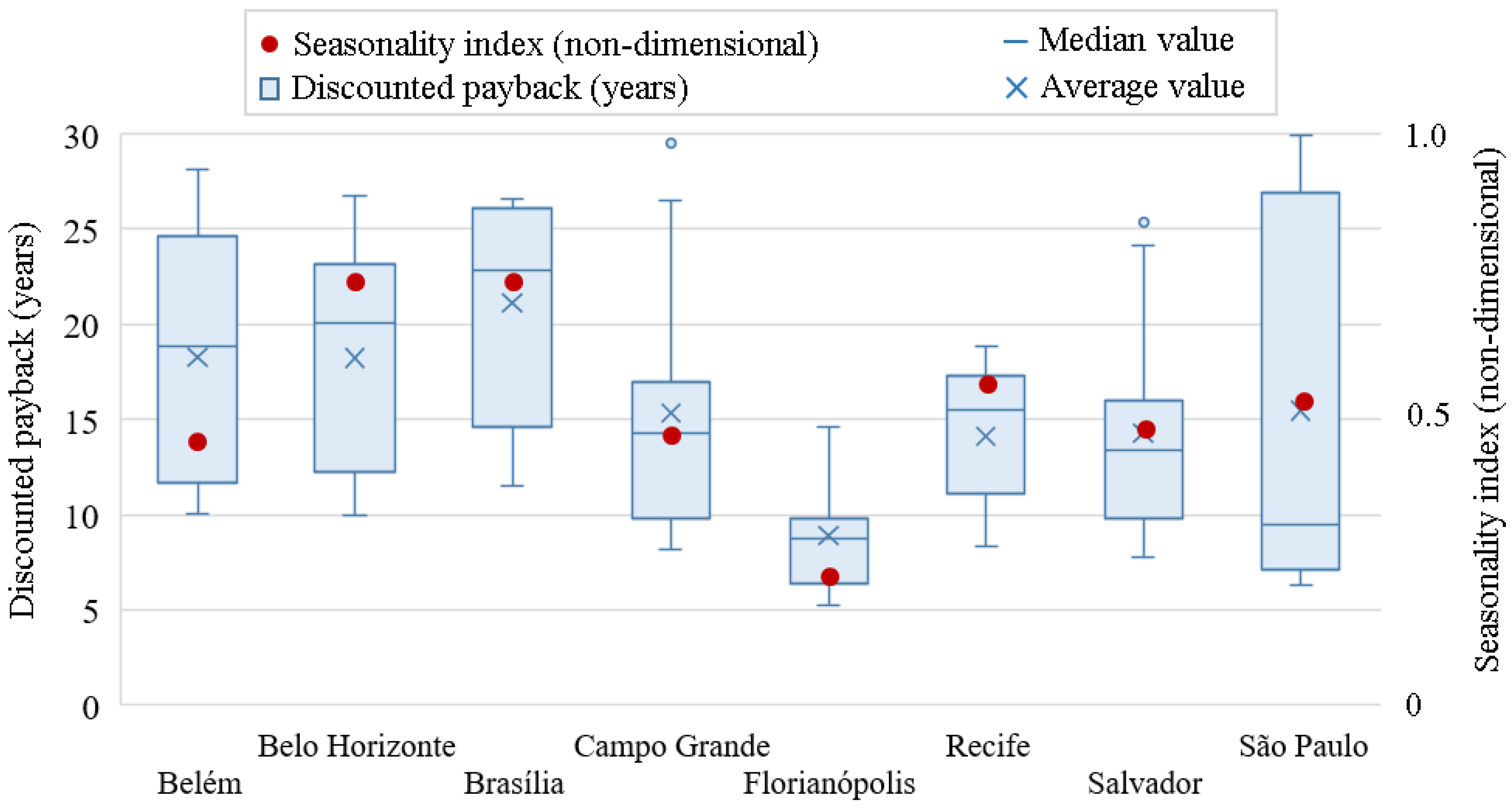
Figure 10 shows the correlation between the seasonality index and the net present value.
Considering that the initial outlays and operational costs of the systems presented coefficients of variation of 24% and 40%, variations extrinsic to the interactions between rainfall and financial feasibility are present in this analysis. In this sense, more direct correlations between rainfall indicators and financial feasibility could be obtained if the financial analysis used the same costs in all cities.
The analysis performed by Geraldi and Ghisi [
28] showed that the average number of dry days per year had major relevance for short-term instead of long-term time series representativeness for RWH systems design. In this sense, the maximum duration, variation coefficient, and standard deviation of the periods without precipitation correlated better with the net present value than those observed for the average annual rainfall. Results corresponding to other rainfall indicators can be found in
Figures S2–S7 in the Supplementary Materials.
4. Conclusions
This study investigated the conditions and compared the financial feasibility of residential RWH systems in eight Brazilian cities. For this, a comprehensible outlay procedure was performed using local-specific costs and tariffs. The study was based on an equivalent RWH system design among all scenarios with two design configurations (direct and indirect rainwater distribution). Rainfall time series indicators were correlated with the financial feasibility of the systems, and sensitivity analysis was used to point the most significant design variables.
The selected cities presented financial feasibility indexes between 30% and 70% of the simulated scenarios, thus presenting a diverse panorama for Brazilian RWH systems. In Florianópolis, the systems presented the best financial feasibility, thus pointing at this city as one of the most favourable cities for financially feasible RWH systems. Recife, Salvador, São Paulo and Campo Grande presented intermediate feasibility results. Correspondingly, the seasonality index was the rainfall indicator that presented the highest correlation with the net present value of the RWH systems, which are clearly benefitted from more uniform rainwater distributions throughout the year.
Despite being drier than most other locations studied, Campo Grande obtained better financial feasibility due to the water tariff scheme adopted by the local water utility. Belém, on the other hand, was negatively influenced by potable water pricing policy. RWH systems in Belém, Brasília, Belo Horizonte yielded the lowest financial feasibility rates. Despite a significant influence of potable water tariff schemes on the financial feasibility of RWH systems was identified, this was not evaluated quantitatively. In this sense, obtaining this correlation would allow comparing this influence with other design variables and rainfall characteristics.
Considering all rainfall patterns studied, RWH systems with a catchment area of 200 m2 were able to supply, on average, 90.5% of the rainwater consumption. In this sense, it can be said that catchment areas above 200 m2 tend to be unnecessary for dwellings of up to six inhabitants in Brazil.
On average, systems with direct rainwater distribution presented initial outlays 1.4% lower than systems with indirect rainwater distribution. In such cases, the higher cost of the pressurising equipment is equivalent to the savings obtained by not using the upper rainwater tank and the necessary complements for its operation. In this sense, it would be interesting to consider solutions that result in initial investment costs that are more different from each other to assess the impact of this difference on the financial feasibility of the systems more comprehensively. In this study, the direct rainwater distribution scheme positively influenced the financial feasibility indexes in four of the eight cities.
The average initial costs of indirect RWH systems varied between BRL 10,999.18 and BRL 18,061.37, depending on the catchment area and tank size. The greater the tank capacity used in the system, the greater its cost relative to the total investment. Among the eight cities, the average operating costs for systems with indirect rainwater distribution varied between BRL 4.31/month and BRL 5.32/month. On average, systems with direct rainwater distribution presented operating costs 3.08% lower than systems with indirect rainwater distribution.
A low correlation was observed between the rainfall indicators and the net present value of the systems. This result is also related to the presence of extrinsic factors in the interactions between rainfall and the financial feasibility of RWH systems. Initial investment costs of RWH systems resulted in a coefficient of variation of 24% among all cities and simulated scenarios. Similarly, operational costs presented a coefficient of variation of 40%. This variation is due to differences in the initial outlays of the systems and the different water and energy pricing schemes practised locally. In this sense, a new financial analysis is suggested by considering a common cost base among the cities evaluated. Thus, more relevant correlations can be obtained between rainfall characteristics and the financial feasibility of generic RWH systems.
Sensitivity analysis pointed to the number of inhabitants as the most influential variable on the financial feasibility of RWH systems. This variable is directly related to the rainwater consumption in the building, often associated to the feasibility of RWH systems in the literature.
The results obtained in this study provide reliable information regarding the costs of installing and operating RWH systems in Brazil. Moreover, the selection of eight representative cities allows direct comparisons, thus covering an important knowledge gap in the field. Considering the relevance of financial feasibility to promote the adoption of RWH systems at a broader scale, the information generated herein can contribute to the elaboration of more assertive public policies and incentive schemes. Finally, the novel approach of evaluating the influence of rainfall indicators over the financial feasibility of RWH systems produced additional insight on which conditions should be verified in the design stage when aiming towards more efficient RWH.