Structure Integrity Analysis Using Fluid–Structure Interaction at Hydropower Bottom Outlet Discharge
Abstract
:1. Introduction
2. Methodology
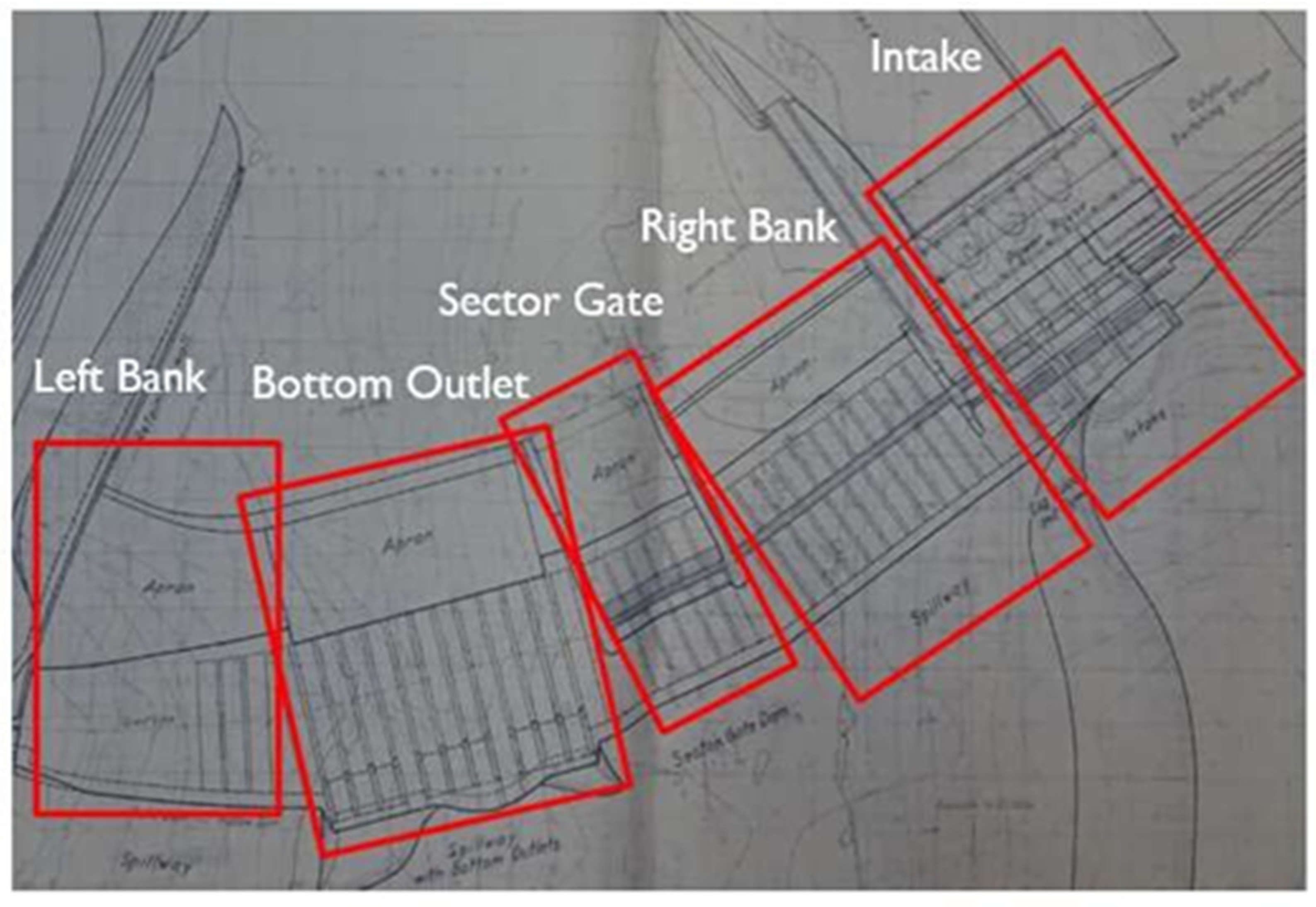
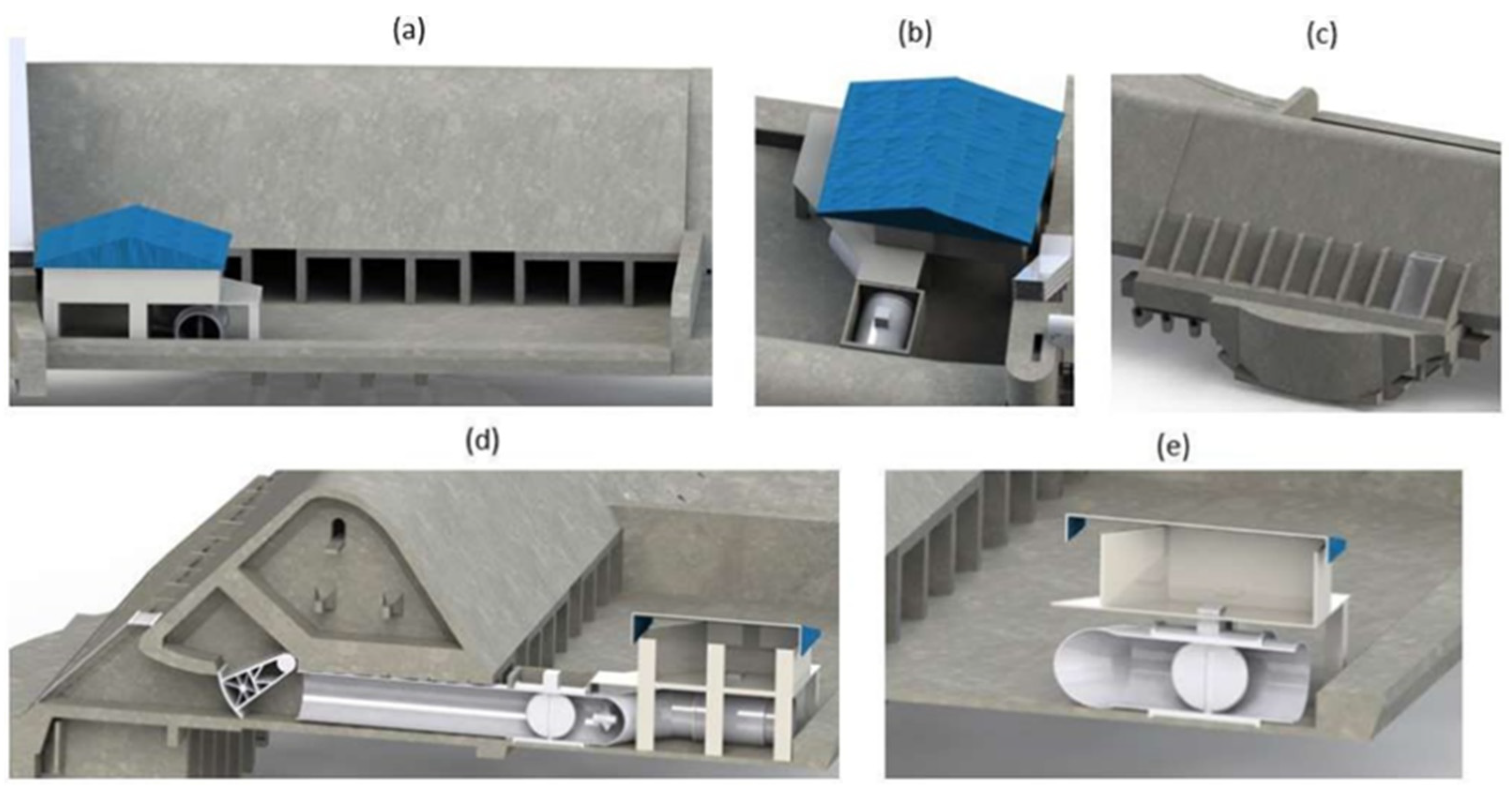
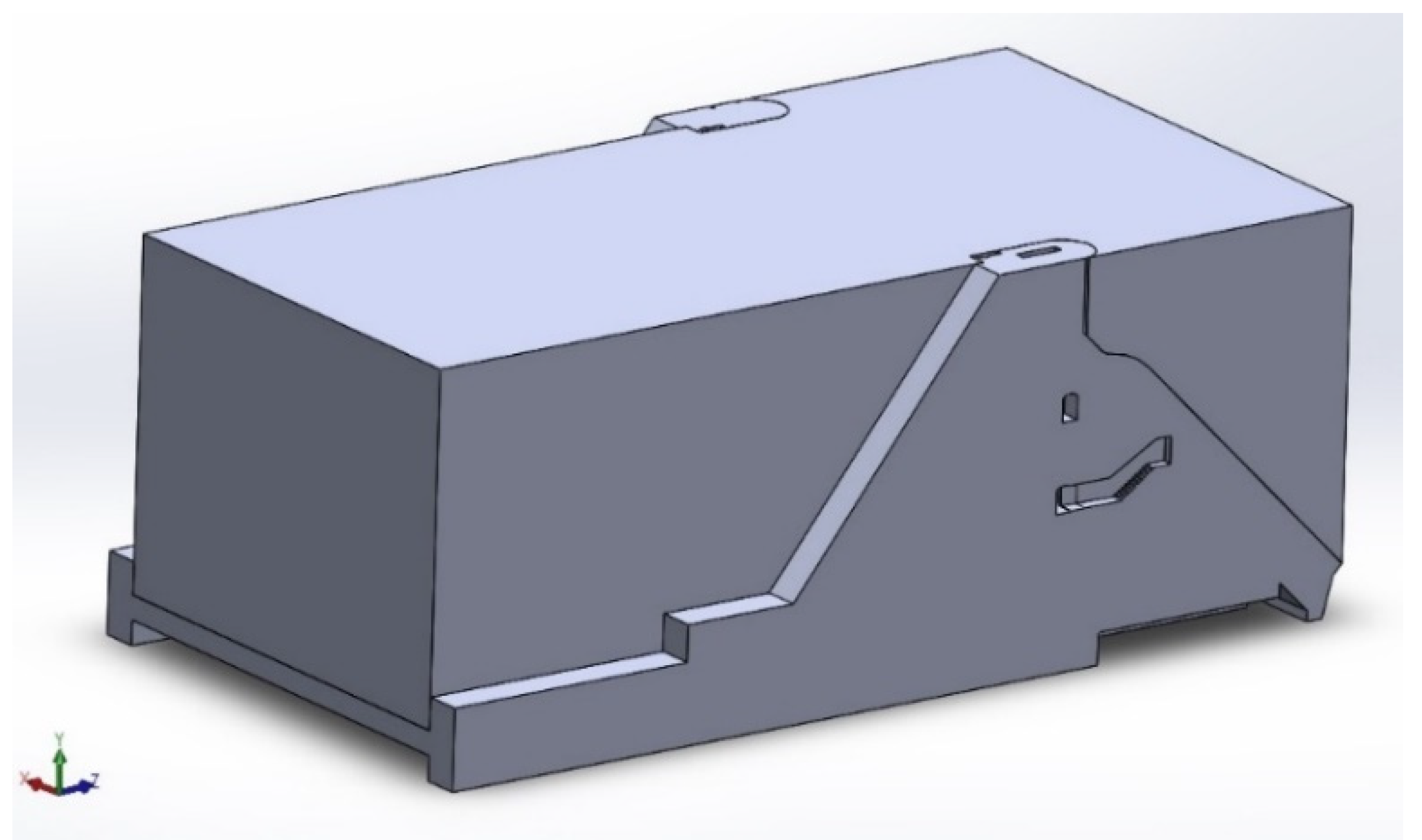
2.1. Three-Dimensional Computer-Aided Drawings of Chenderoh Dam
2.2. Fluid–Structure Interaction Numerical Simulation
2.2.1. Governing Equations
2.2.2. Boundary Conditions
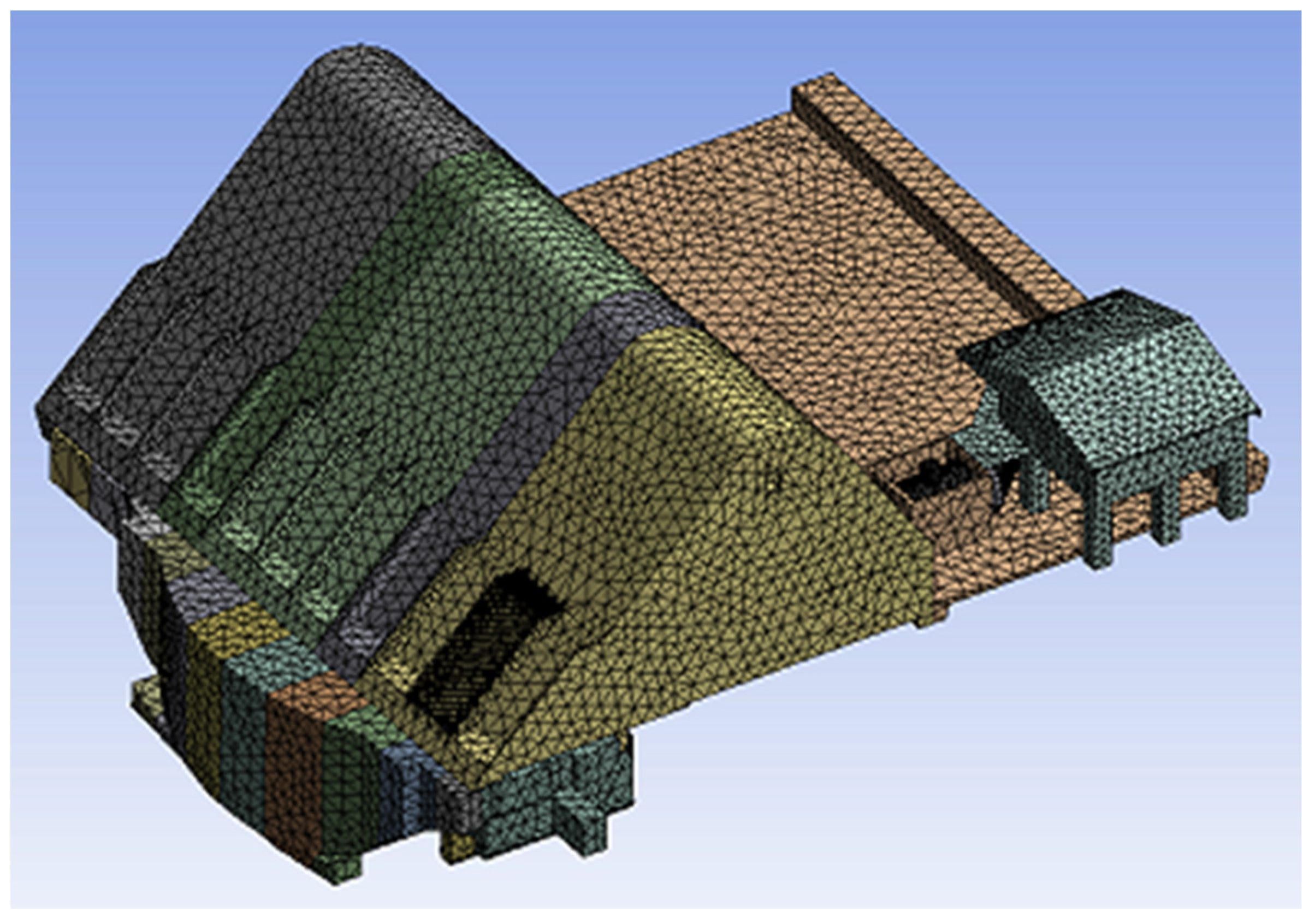
2.2.3. Mesh
2.2.4. Ansys Transient Structural
2.2.5. Ansys System Coupling
3. Results and Discussion
3.1. Fluid–Structure Interaction Numerical Simulation on Bottom Outlet Structures
3.2. Structural Analysis on Bottom Outlet Structures
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chin, D.A.; Mazumdar, A.; Roy, P.K. Water-Resources Engineering; Prentice Hall: Englewood Cliffs, NJ, USA, 2000; Volume 12. [Google Scholar]
- Balmer, M.; Spreng, D. Hydroelectric Power. In Future Energy; Elsevier: Amsterdam, The Netherlands, 2008; pp. 193–209. [Google Scholar]
- Chen, S.-H. Rock Slopes in Hydraulic Projects. In Hydraulic Structures; Springer: Berlin/Heidelberg, Germany, 2015; pp. 813–868. [Google Scholar]
- Michael, C. Environmental Management and Concept During Construction of Dam: A Study Case of Murum Dam, Belaga District, Kapit Division, Sarawak; Universiti Malaysia Sarawak: Sarawak, Malaysia, 2013. [Google Scholar]
- Cook, C.B.; Richmond, M.C.; Serkowski, J.A. The Dalles Dam, Columbia River: Spillway Improvement CFD Study; Pacific Northwest National Lab.(PNNL): Richland, WA, USA, 2006. [Google Scholar]
- Fu, C.; Hafliðason, B. Progressive Failure Analyses of Concrete Buttress Dams: Influence of Crack Propagation on the Structural Dam Safety. In Concrete Structures; Stockholm University: Stockholm, Sweden, 2015. [Google Scholar]
- Zawawi, M.H.; Hassan, N.H.; Ramli, M.Z.; Zahari, N.M.; Radzi, M.R.M.; Saleha, A.; Salwa, A.; Sidek, L.M.; Muda, Z.C.; Kamaruddin, M.A. Fluid-Structure Interactions Study on Hydraulic Structures: A Review. AIP Conf. Proc. 2018, 2030, 20244. [Google Scholar]
- Manikandan, R.; Jayashiri, R.; Indumathi, R.; Archana, J. Fluid Structure Interaction of Arch Dam on Full Reservoir Level under Seismic Loading. In Proceedings of the 2016 COMSOL Conference in Bangalore, Bangalore, India, 20–21 October 2016; Volume 39. [Google Scholar]
- Richter, T. Goal-Oriented Error Estimation for Fluid–Structure Interaction Problems. Comput. Methods Appl. Mech. Eng. 2012, 223, 28–42. [Google Scholar] [CrossRef] [Green Version]
- Bø, A.T. Fluid Structure Interaction in a Pipe. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2018. [Google Scholar]
- Soucek, O. A Brief Introduction to Fluid- Structure Interactions Fluid-Structure Interactions Teaching Slides. 2012. Available online: https://geo.mff.cuni.cz/jednooci_slepym/os-FSI-intro.pdf (accessed on 1 February 2023).
- Hellgren, R. Influence of Fluid Structure Interaction on a Concrete Dam during Seismic Excitation:-Parametric Analyses of an Arch Dam-Reservoir-Foundation System. In Proceedings of the Seconde International Dam World Conference, Lisbon, Portugal, 21–24 April 2015. [Google Scholar]
- Hartmann, S.; Meister, A.; Schäfer, M.; Turek, S. International Workshop on Fluid-Structure Interaction. Theory, Numerics and Applications; Kassel University Press GmbH: Kassel, Germany, 2009; ISBN 3899586670. [Google Scholar]
- International Atomic Energy Agency. Iaea Integration of Tracing with Computational Fluid Dynamics for Industrial Process Investigation; International Atomic Energy Agency: Vienna, Austria, 2004; p. 221. [Google Scholar]
- Frisch, J. Numerical Modelling—Introductory Approach Ppt. In Proceedings of the 9th SimLab Course on Parallel Numerical Simulation, Belgrade, Serbia, 4–8 October 2010. [Google Scholar]
- Fu, S.; Biwole, P.H.; Mathis, C. Numerical and Experimental Comparison of 3D Particle Tracking Velocimetry (PTV) and Particle Image Velocimetry (PIV) Accuracy for Indoor Airflow Study. Build. Environ. 2016, 100, 40–49. [Google Scholar] [CrossRef]
- Parameshwaran, R.; Dhulipalla, S.J.; Yendluri, D.R. Fluid-Structure Interactions and Flow Induced Vibrations: A Review. Procedia Eng. 2016, 144, 1286–1293. [Google Scholar] [CrossRef] [Green Version]
- Arias, I.; Knap, J.; Chalivendra, V.B.; Hong, S.; Ortiz, M.; Rosakis, A.J. Numerical Modelling and Experimental Validation of Dynamic Fracture Events along Weak Planes. Comput. Methods Appl. Mech. Eng. 2007, 196, 3833–3840. [Google Scholar] [CrossRef] [Green Version]
- Hou, G.; Wang, J.; Layton, A. Numerical Methods for Fluid-Structure Interaction—A Review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Zawawi, M.H.; Saleha, A.; Salwa, A.; Hassan, N.H.; Zahari, N.M.; Ramli, M.Z.; Muda, Z.C. A Review: Fundamentals of Computational Fluid Dynamics (CFD). AIP Conf. Proc. 2018, 2030, 20252. [Google Scholar]
- Singarella, P.N.; Adams, E.E. Physical and Numerical Modeling of the External Fluid Mechanics of OTEC Pilot Plants; Massachusetts Institute of Technology, Energy Laboratory: Cambridge, MA, USA, 1982. [Google Scholar]
- Ng, F.C.; Abas, A.; Abustan, I.; Rozainy, Z.M.R.; Abdullah, M.Z.; Kon, S.M. Fluid/Structure Interaction Study on the Variation of Radial Gate’s Gap Height in Dam. IOP Conf. Ser. Mater. Sci. Eng. 2018, 370, 12063. [Google Scholar] [CrossRef]
- Fluent, I. Modeling Turbulent Flows Manual; University of Southampton: Southampton, UK, 2006; Volume 6-2, pp. 6–49. [Google Scholar]
- Delafosse, A.; Line, A.; Morchain, J.; Guiraud, P. LES and URANS Simulations of Hydrodynamics in Mixing Tank: Comparison to PIV Experiments. Chem. Eng. Res. Des. 2008, 86, 1322–1330. [Google Scholar] [CrossRef]
- Rock, A.; Zhang, R.; Wilkinson, D. Velocity Variations in Cross-Hole Sonic Logging Surveys Causes and Impacts in Drilled Shafts; United States Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2008. [Google Scholar]
- Jamshed, S. Using HPC for Computational Fluid Dynamics: A Guide to High Performance Computing for CFD Engineers; Academic Press: Cambridge, MA, USA, 2015; ISBN 0128017511. [Google Scholar]
- Clayton, M.J.; Johnson, R.E.; Song, Y.; Al-Qawasmi, J. Information Content of As-Built Drawings; Texas A&M University: College Station, TX, USA, 1998. [Google Scholar]
- Mohd Nasir, S.R.; Zahari, Z.; Isa, M.; Che Ibrahim, C.K. Delay of as-built drawings submission for malaysian toll highway. J. Teknol. 2016, 78. [Google Scholar]
- Clayton, M.; Johnson, R.; Song, Y.; Al-Qawasmi, J. A Study of Information Content of As-Built Drawings for USAA, the Caudill Rowlett and Scott (CRS) Center. USAA Proj. Coll. Stn. TX 1998. [Google Scholar]
- Azman, A.; Zawawi, M.H.; Hassan, N.H.; Abas, A.; Razak, N.A.; Mazlan, A.Z.A.; Rozainy, M.A.Z.M.R. Effect of Step Height on The Aeration Efficiency of Cascade Aerator System Using Particle Image Velocimetry; EDP Sciences; MATEC Web of Conferences: Les Ulis Cedex A, France, 2018; Volume 217, p. 4005. [Google Scholar]
- Zawawi, M.H.; Aziz, N.A.; Radzi, M.R.M.; Hassan, N.H.; Ramli, M.Z.; Zahari, N.M.; Abbas, M.A.; Saleha, A.; Salwa, A.; Muda, Z.C. Computational Fluid Dynamic Analysis at Dam Spillway Due to Different Gate Openings. AIP Conf. Proc. 2018, 2030, 20245. [Google Scholar]
- Kiricci, V.; Celik, A.O. Modeling Hydraulic Structures With Computational Fluid Dynamics. In Proceedings of the International Scientific Conference People, Buildings and Environment 2014 (PBE2014), Kroměříž, Czech Republic, 15–17 October 2014. [Google Scholar]
- Haga, K.; Terada, A.; Kaminaga, M.; Hino, R. Water Flow Experiment Using the PIV Technique and the Thermal Hydraulic Analysis on the Cross-Flow Type Mercury Target Model. ETDEWEB 2001, 2, 1293–1303. [Google Scholar]
- Thanh, N.C.; Ling-Ling, W. Physical and Numerical Model of Flow through the Spillways with a Breast Wall. KSCE J. Civ. Eng. 2015, 19, 2317–2324. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of Open Channel Flow; Elsevier: Amsterdam, The Netherlands, 2004; ISBN 0080472974. [Google Scholar]
- Duró, G.; de Dios, M.; López, A.; Liscia, S.O. Physical Modeling and CFD Comparison: Case Study of a Hydro-Combined Power Station in Spillway Mode; Utah State University: Logan, UT, USA, 2012. [Google Scholar]
- El-Zayat, A. Physical Modeling For Complex Hydraulic Structures. 2016. Available online: https://www.semanticscholar.org/paper/PHYSICAL-MODELING-FOR-COMPLEX-HYDRAULIC-STRUCTURES-el-Zayat/fb9a73a267077740ade24cce36f18aad116c815b (accessed on 1 February 2023).
- Tafarojnoruz, A.; Lauria, A. Large Eddy Simulation of the Turbulent Flow Field around a Submerged Pile within a Scour Hole under Current Condition. Coast. Eng. J. 2020, 62, 489–503. [Google Scholar] [CrossRef]
- Calomino, F.; Alfonsi, G.; Gaudio, R.; D’Ippolito, A.; Lauria, A.; Tafarojnoruz, A.; Artese, S. Experimental and numerical study of free-surface flows in a corrugated pipe. Water 2018, 10, 638. [Google Scholar] [CrossRef] [Green Version]
- Lauria, A.; Alfonsi, G.; Tafarojnoruz, A. Flow pressure behavior downstream of ski jumps. Fluids 2020, 5, 168. [Google Scholar] [CrossRef]
- Ryan, E.M.; DeCroix, D.; Breault, R.; Xu, W.; Huckaby, E.D.; Saha, K.; Dartevelle, S.; Sun, X. Multi-Phase CFD Modeling of Solid Sorbent Carbon Capture System. Powder Technol. 2013, 242, 117–134. [Google Scholar] [CrossRef]
- Georgoulas, A.; Angelidis, P.; Kopasakis, K.; Kotsovinos, N. 3D Multiphase Numerical Modelling for Turbidity Current Flows. In Numerical Modelling; IntechOpen: London, UK, 2012. [Google Scholar]
- Björkmon, M. Evaluation of Finite Element Tools for Transient Structural Dynamic Simulations of Firing Systems. Master’s Thesis, Chalmers University Of Technolog, Göteborg, Sweden, 2010. [Google Scholar]
- Manafpour, M.; Rovesht, T.J. Numerical Investigation of the Flow Characteristics in the Vicinity of Pressure Conduit’s Gates. In Proceedings of the Long-Term Behaviour and Environmentally Friendly Rehabilitation Technologies of Dams, Iran, Tehran, 17–19 October 2017. [Google Scholar]





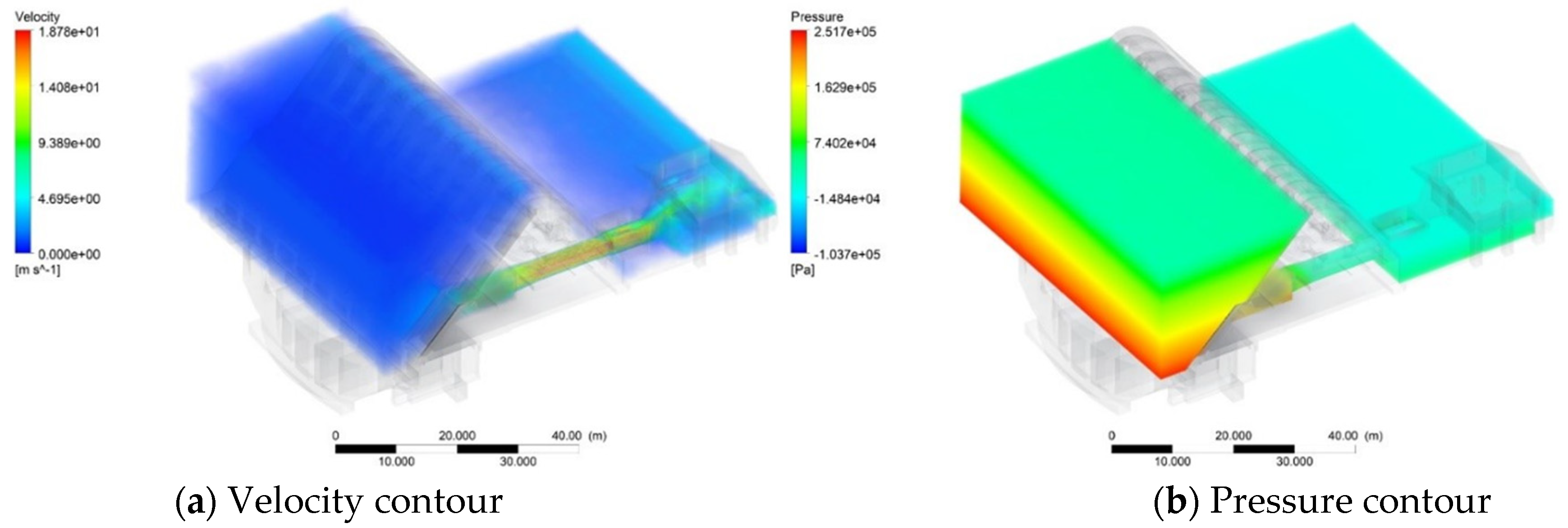
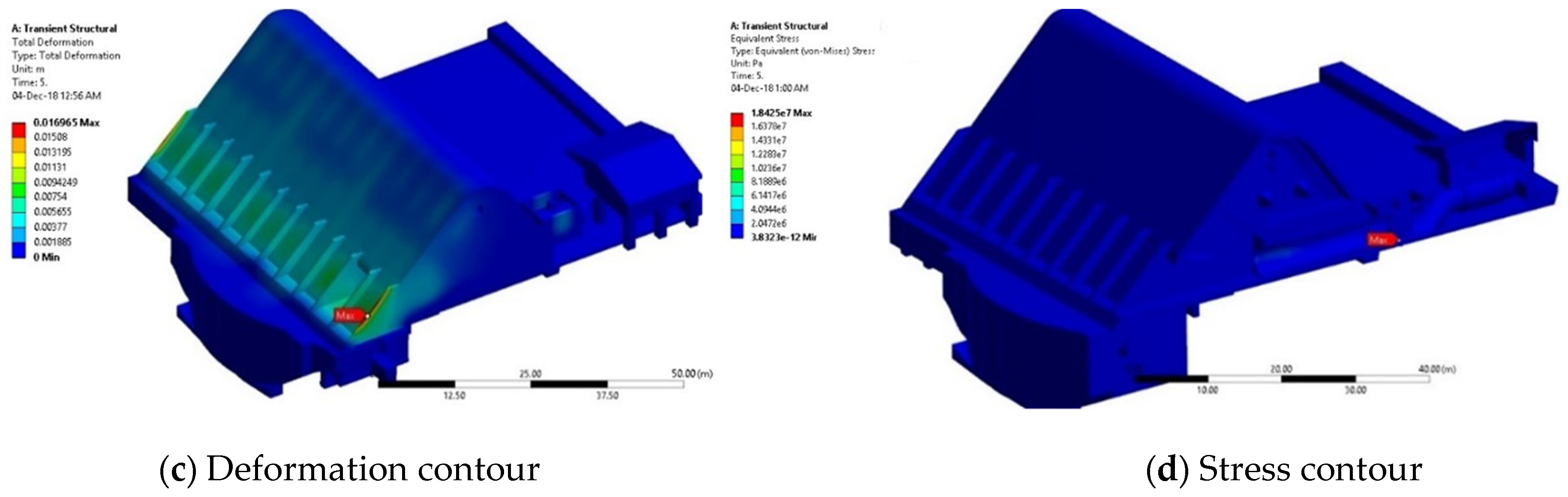

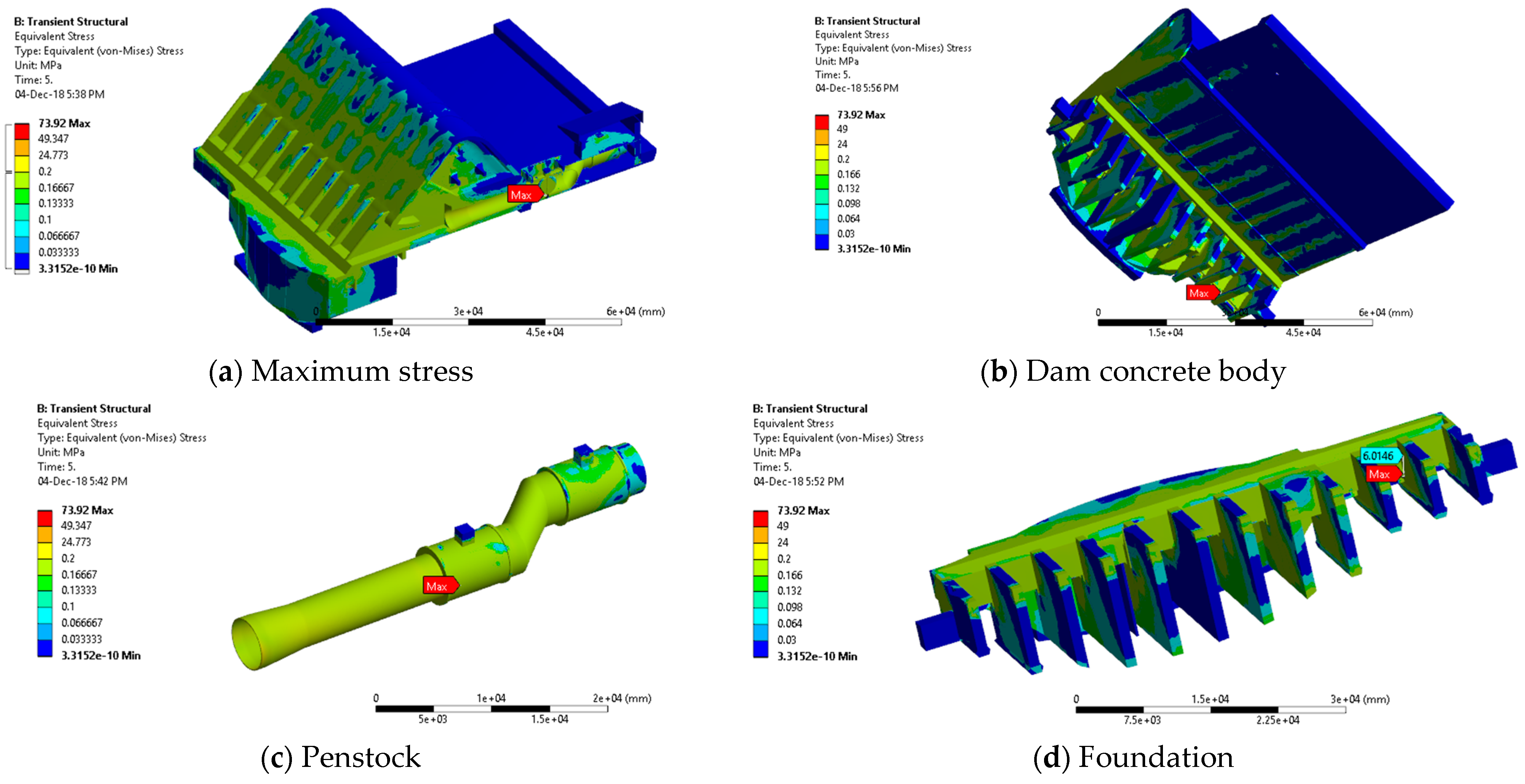

| Mesh Size (m) | Element Number | Maximum Velocity (m/s) |
|---|---|---|
| 0.55 | 386,358 | 124.1 |
| 0.5 | 452,317 | 122.467 |
| 0.45 | 534,276 | 122.367 |
| 0.35 | 797,630 | 122.332 |
| 0.3 | 1,027,179 | 122.3 |
| Case | Chenderoh Dam–Bottom | Case | Seymareh Dam [44] |
|---|---|---|---|
| Butterfly valve is fully closed | 14.1 | Gate opening–10% | 2.0 |
| Butterfly valve is fully opened | 19.97 | Gate opening–30% | 4.0 |
| - | - | Gate opening–70% | 8.0 |
| - | - | Gate opening–100% | 18.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohd Radzi, M.R.; Zawawi, M.H.; Abas, M.A.; Ahmad Mazlan, A.Z.; Mohd Arif Zainol, M.R.R.; Hassan, N.H.; Che Wan Zanial, W.N.; Dullah, H.; Kamaruddin, M.A. Structure Integrity Analysis Using Fluid–Structure Interaction at Hydropower Bottom Outlet Discharge. Water 2023, 15, 1039. https://doi.org/10.3390/w15061039
Mohd Radzi MR, Zawawi MH, Abas MA, Ahmad Mazlan AZ, Mohd Arif Zainol MRR, Hassan NH, Che Wan Zanial WN, Dullah H, Kamaruddin MA. Structure Integrity Analysis Using Fluid–Structure Interaction at Hydropower Bottom Outlet Discharge. Water. 2023; 15(6):1039. https://doi.org/10.3390/w15061039
Chicago/Turabian StyleMohd Radzi, Mohd Rashid, Mohd Hafiz Zawawi, Mohamad Aizat Abas, Ahmad Zhafran Ahmad Mazlan, Mohd Remy Rozainy Mohd Arif Zainol, Nurul Husna Hassan, Wan Norsyuhada Che Wan Zanial, Hayana Dullah, and Mohamad Anuar Kamaruddin. 2023. "Structure Integrity Analysis Using Fluid–Structure Interaction at Hydropower Bottom Outlet Discharge" Water 15, no. 6: 1039. https://doi.org/10.3390/w15061039
APA StyleMohd Radzi, M. R., Zawawi, M. H., Abas, M. A., Ahmad Mazlan, A. Z., Mohd Arif Zainol, M. R. R., Hassan, N. H., Che Wan Zanial, W. N., Dullah, H., & Kamaruddin, M. A. (2023). Structure Integrity Analysis Using Fluid–Structure Interaction at Hydropower Bottom Outlet Discharge. Water, 15(6), 1039. https://doi.org/10.3390/w15061039






