1. Introduction
Time-series estimation of streamflow at the watershed level is the most important information in surface hydrology for the efficient management of water resources [
1]. High-accuracy information on the amount of inflow into the reservoir is needed to ensure continuous and safe water supply and efficient water management of the reservoir in the future [
2]. Currently, the forecasting of inflows in a water resource management system is performed by interpreting the relationship between rainfall and runoff. The effective management of hydrologic resources and hazards often depends on accurate simulations of runoff [
3]. Numerous studies on watershed hydrology and water resource management have used computer models for estimating runoff from rainfall and evaporation data [
4]. Various types of hydrological models have been developed using different programming languages [
5,
6]. Rainfall–runoff modeling is crucial and valuable in hydrological research and for water resource engineers [
7]. Hydrological models that can predict long-term time-series runoff can be divided into metric, physical, conceptual and data-driven models [
8,
9]. Metric models only consider information from existing data without considering the processes of hydrological systems. Conceptual models use a simplified mathematical conceptualization of a system with different components of the hydrological process through recharge and depletion. Physical models represent different hydrological processes through mass, momentum and energy conservation equations. Data-driven models only require creating a relationship between the input and output data without considering the hydrological mechanism [
7,
10,
11].
To improve the accuracy of long-term runoff simulations, it is necessary to minimize the uncertainty in the rainfall–runoff relationship. One way to address this is to calibrate the model frequently [
12]. Each rainfall–runoff model has its own parameters and characteristics and is designed to use various parameters in the hydrological analysis process. The ABCD model [
13,
14] is a simple hydrological model that uses four parameters for simulating streamflow based on precipitation and potential evapotranspiration. The HBV model [
15] analyzes river runoff and was designed using nine parameters with three box layers. The DAWAST model divides the watershed soil into unsaturated and saturated layers using five parameters [
16]. The tank model is a hydrological model that uses sixteen parameters for four tanks and simulates the rainfall–runoff relationship by assuming the watershed to be a linear system of multiple tanks [
17,
18]. GR4J model was designed using four parameters to simulate the daily rainfall-runoff [
19]. Kim [
20] developed the TPHM model, a daily runoff estimation model designed using two parameters with a hyperbolic tangent function to determine the relationship between watershed storage and runoff. The TPHM model was designed using the fewest parameters.
When using a hydrological model, its parameters must be optimized to effectively reproduce the relationship between rainfall and runoff according to the theoretical characteristics of the model. To this end, the parameters must be adjusted and the simulated runoff reproduced for it should be similar to the actual runoff value. In the case of a predictive model, it is essential that the parameters are accurately adjusted [
21,
22]. However, in hydrological modeling, uncertainties may arise when determining parameters owing to the complexity of the model and problems such as parameterization and calibration of the data [
23]. In particular, a model using several parameters can be difficult to use in actual water management situations and, hence, professional skills are needed to correctly adjust the user-specific parameters. Therefore, minimization of the conceptual structure and parameters of a hydrological model is crucial as far as user convenience is considered.
In recent years, artificial intelligence (AI) technology has been widely applied in the field of hydrology [
11]. Artificial neural networks (ANN) have a mathematical structure with complex nonlinear relationships between the input and output data and are an effective alternative to rainfall-runoff for input and output in situations where detailed modeling of the watershed is not required [
24]. ANN have been applied in various studies [
25,
26,
27] to estimate the long-term runoff using daily hydrological data. Other studies [
28,
29,
30,
31] estimated the short-term runoff using time unit information. Van et al. [
32] applied a convolutional neural network (CNN) and long short-term memory (LSTM) models to the Mekong Delta in Vietnam. The CNN and LSTM models demonstrated better performance than existing ANN, genetic algorithm (GA), simulated annealing (SA), autoregressive integrated moving average (ARIMA) and seasonal ARIMA (SARIMA) and were found to be more suitable for rainfall–runoff modeling. Zakizadeh et al. [
33] showed the strong applicability of the LSTM model using meteorological and hydrological data from 671 catchments across the United States. By demonstrating this possibility, its potential for use as a regional hydrology model was emphasized.
Observation of the rainfall and runoff is essential for simulating the rainfall–runoff relationship. Although machine learning techniques have been widely used to perform such simulations, they require large datasets [
34]. The validation of data-driven modeling can be strengthened by increasing the number of available datasets [
35]. When available data are insufficient [
36], AI-based techniques face limitations with regard to their application. Therefore, hydrological modeling of unmeasured watersheds is considered the most suitable for estimating streamflow [
37]. To verify and improve the predictive ability of a rainfall–runoff model, it is necessary to set the parameters of the hydrological model in an appropriate manner. However, if there are insufficient measurement data, such as the streamflow, or there is uncertainty in the data, determining the parameters of the hydrological model becomes difficult [
38,
39]. Additionally, because using a hydrological model designed with several parameters requires user expertise, it is necessary to solve the problem of low usability in the practice of water resources.
The development of a runoff model requires time-series hydrological data recorded over a long period. The most important aspect of runoff analysis is the function of runoff and Korea’s multipurpose dams retain and provide long-term time-series hydrological information, unlike agricultural reservoir, which are not tracked. Therefore, an environment for using hydrological data to develop a new runoff model was prepared to verify the applicability of the developed model. Furthermore, to improve the practical applicability of the rainfall–runoff model and solve the above mentioned problems, it was assumed that the hydrological model uses a single parameter. Therefore, the framework of the hydrological model must be designed using a single parameter. Solving the complex nonlinear problems in natural hydrology for rainfall–runoff modeling is challenging [
31,
40]. To this end, nonlinear methods use an exponential function to predict rainfall-runoff. Therefore, a method was introduced wherein the state of soil water storage in the watershed was tracked and the tracked value was continuously updated depending on the evaporation and runoff in the watershed.
This study aimed to develop a one-parameter new exponential (ONE) model for simulating daily rainfall-runoff using a single parameter to implement a relationship wherein the runoff varies nonlinearly with the soil water storage. This study addresses the current research gap, wherein it is challenging to use a typical hydrological model with several parameters for the quick estimation of the inflow into a water resource system.
2. Materials and Methods
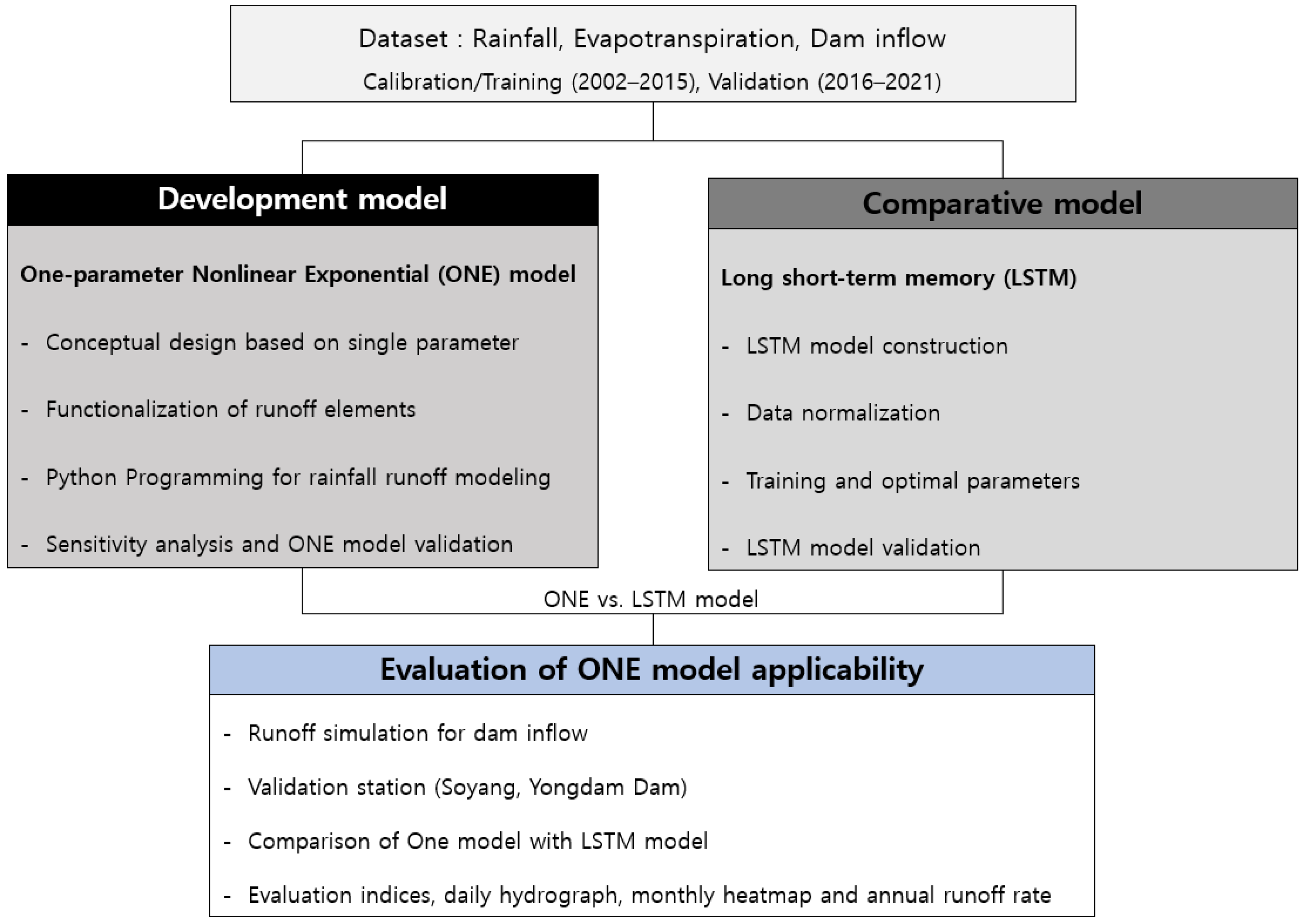
Figure 1 shows the procedure followed in this study. First, we set the input data for the hydrological model; further, we decided on the conceptual design to develop the hydrological model and simplify the hydrological process. By using the observed rainfall and inflow data of the multipurpose dam basin, hydrological elements of the soil water storage based runoff model were functionalized, the code was written and the framework was designed to simulate long-term runoff using only one parameter. To verify the developed model, the inflow data at the outlet of the multipurpose dam basin were used. Additionally, a time-series learning model based on machine learning was constructed to compare the performance of the developed model. Using the same target watershed and rainfall and runoff information, a quantitative evaluation was performed using a performance evaluation index to predict the runoff for each model. Moreover, hydrographs were compared by superimposing the simulated and observed runoff values for each model and the effectiveness of the developed model was validated by comparing the heatmap of the monthly and annual runoff rates. Python, which is open-source, was used as the programming language. The web version of the ONE model was developed using Streamlit’s open-source app framework [
41] and the TensorFlow Ver. 2.1 was used to construct the LSTM model for machine learning.
2.1. Study Area and Hydrological Data
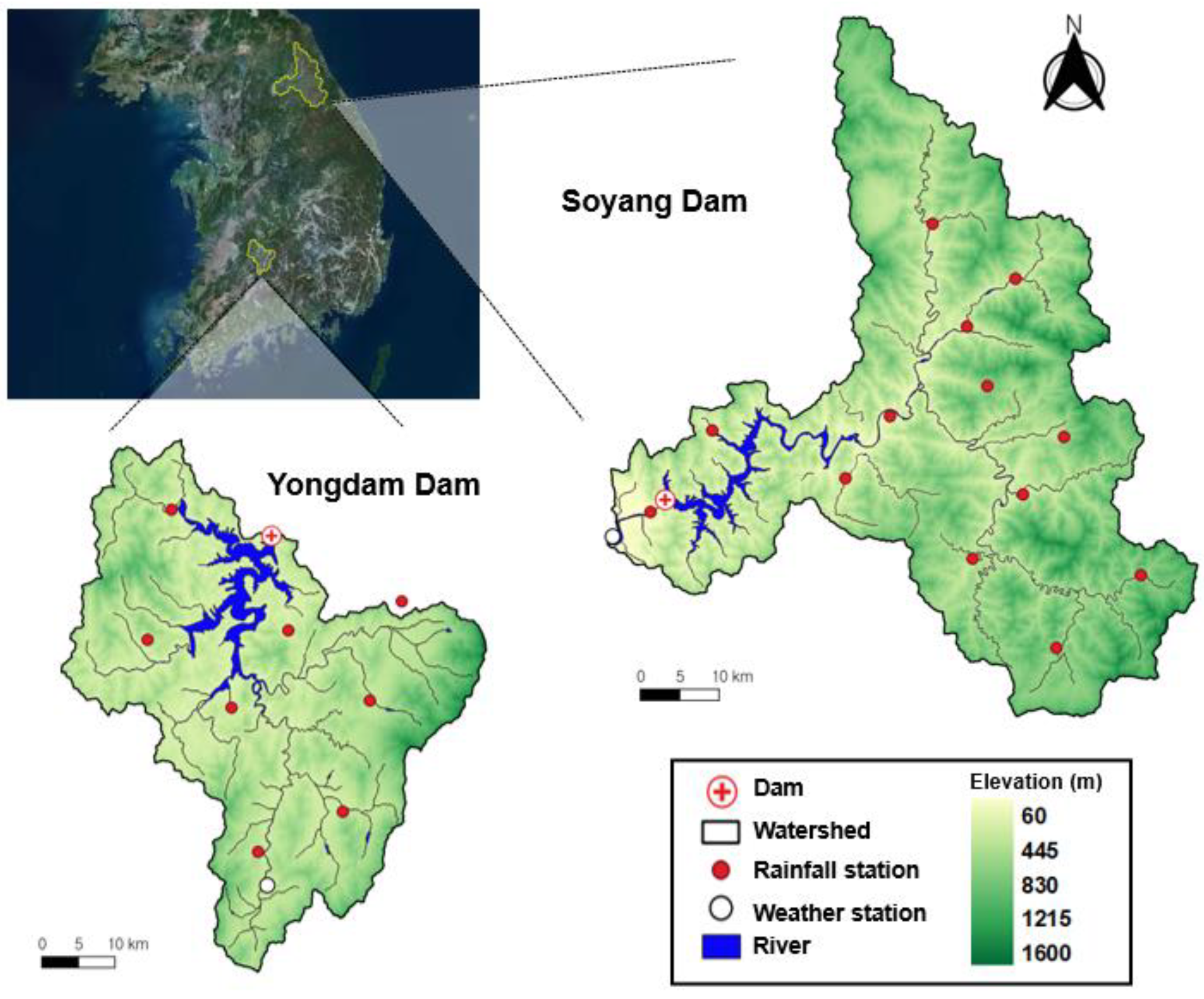
The ONE model developed in this study was applied to two multipurpose dams in Korea to evaluate its applicability. Additionally, dams located upstream were selected as these dams have minimal anthropogenic effects on runoff. The branches of these dams are located upstream of the main rivers, the Han River and the Geum River; this ensures the effective use and management of water resources in Korea.
Figure 2 shows the location map of the study area and the locations of the hydrological and meteorological stations.
Table 1 lists the detailed specifications of multipurpose dams for the target point [
42].
The Soyang (SY) Dam, constructed in 1973, is located upstream of the Han River basin and is the largest multipurpose dam in Korea, supplying water to Seoul and the metropolitan area. It is a concrete-faced rockfill dam with a height and length of 123 m and 530 m, respectively. The watershed area is 2703 km2, the total water storage is 2900 million m3 and the effective water storage capacity is 1900 million m3. The annual water supply is 1213 million m3 with a flood control capacity of 500 million m3. The Yongdam (YD) Dam, constructed in 2001, is a multipurpose dam located upstream of the Geum River Basin that supplies domestic, industrial and agricultural water to six regions in Jeollabuk-do and two regions in the Chungcheong Province. It is a concrete-faced rockfill dam with a height and length of 70 m and 498 m, respectively. The watershed area is 930 km2, the total water storage is 815 million m3 and the effective water storage capacity is 672.5 million m3. The annual water supply is 1143.2 million m3, with a flood control capacity of 137 million m3.
The measurement information was obtained at each dam observation station for the inflow of the target research site. Considering all-natural runoff from the watershed flows into the dam, the inflow can be regarded as the same runoff at the dam point. Therefore, to monitor the data of each dam watershed, the dam operation information provided by the Korea Water Resources Corporation, the management agency of the target facility, was collected from the water information portal [
43]. The water consumption, facility status, inflow and rainfall data have been made publicly accessible. To evaluate the performance of our developed model, we collected the daily rainfall and inflow data for the target watershed. Meteorological and hydrological data were collected for 20 years from 2002 to 2021. The potential evaporation data of the YD Dam were used from the Jangsu weather station and the Chuncheon weather station for the SY Dam. These meteorological data were provided by the open meteorological portal [
44].
2.2. ONE Model Development
In this study, the ONE model was developed to simulate the daily rainfall-runoff using a single parameter that varies according to the soil water storage in the specific watershed. The model uses only one parameter to estimate the daily runoff using an exponential function that models a nonlinear relationship. The hydrological factors of the watershed are divided into three categories: rainfall, evaporation and runoff. The runoff was designed to be affected by the daily soil water storage to minimize the parameters of the hydrological model.
Figure 3 shows a schematic of the ONE model. The boundary of the box represents the watershed and the watershed storage condition increases with the increase in the amount of rainfall in the watershed. This process can also be explained using a simple hydrological structure wherein the watershed storage decreases owing to evaporation and runoff from the watershed. In this case, when the watershed is dry, soil water storage reaches a limit and watershed evaporation does not occur. However, runoff is allowed to occur continuously according to soil water storage even when the watershed is dry. The ONE model uses rainfall and potential evapotranspiration as the input data and is designed to use a single parameter so that the user can easily determine it, considering that a single parameter (
w) is dependent on the local data. The ONE model can determine an optimal parameter so that an excellent evaluation index can be derived by comparing the simulated runoff with the observed runoff.
In the ONE model, various factors such as rainfall, evaporation and runoff affect the soil water storage, and changes in the soil water storage can be estimated using the water balance equation in watershed scale [
45], which is as follows:
where
P is the rainfall,
ET is the evapotranspiration,
Q is the runoff in the watershed outlet and
dS/dt is the change in the soil water storage over time. All units are in mm/day.
Soil water storage in watersheds increases with an increase in rainfall, whereas evaporation and runoff continue to decrease. Accordingly, the daily soil water storage is continuously tracked considering the soil water storage of the previous day and the evaporation and runoff of the present day. This tracked value is updated such that it affects the runoff and evaporation of the following day.
The runoff (
Q) is calculated as the product of the soil water storage
S in the watershed and the runoff coefficient
F and is expressed as
The runoff coefficient
F is designed as a nonlinear exponential function, which is reflected under the influence of the daily updated soil water storage (
S) and a user-specified single parameter (
w); it can be calculated as
where
F is the runoff coefficient,
S is the soil water storage (mm/day),
e is Euler’s number and
w is the single parameter in the ONE model.
The calculated runoff is also reflected in the soil water storage during daily tracking and serves as a circulation value such that it is reduced in the soil water storage the next day to ensure continuous soil water storage tracking. This enables the calculation of the runoff depending on soil water storage as well as the various values of runoff in the watershed even when the rainfall intensity remains the same. The ONE model was designed using only a single parameter (w), which can be determined by the user; this parameter serves as a runoff index that expresses the runoff capacity of the watershed.
Evaporation (
ET) is expressed as the product of the potential evapotranspiration (
ETp) of the watershed and evaporation coefficient (
E), as follows:
The evaporation coefficient
E is designed to reflect a nonlinear exponential function according to the daily updated soil water storage
S. The coefficient value of
E ranges from 0 to 1, making it possible to reflect the characteristics of watershed evaporation according to the potential evaporation and soil water storage conditions of the watershed. The calculated daily evaporation is reflected in the soil water storage during daily tracking, as in the case of runoff calculation. The calculated daily evaporation, similar to the calculated runoff, is designed to serve as a circulation value to ensure continuous soil water storage tracking. This enables the actual evaporation amount to be calculated according to the daily soil water storage and the evaporation coefficient to be reflected in the change in a functional value, even when the amount of potential evaporation remains the same. Therefore, the evaporation coefficient becomes 0 in extremely dry conditions. Although
w of the ONE model is not directly affected by evaporation, it is indirectly affected by the daily update of the soil water storage. To maintain water balance in the watershed, the coefficient of the soil water storage condition can be calculated as
where
E is the evaporation coefficient,
S is the soil water storage (mm/day) and
e is Euler’s number.
2.3. LSTM Model
The use of ANN is becoming increasingly common in the analysis of hydrological and water problems [
46]. This study used the LTSM model, an ANN, to compare its performance with that of the ONE model. The LSTM model is based on a deep-learning-based recurrent neural network that processes inputs and outputs in sequence units and can learn long-term dependencies [
47,
48]; it therefore addresses the shortcomings of the RNN model, which does not remember the data that were learned long ago.
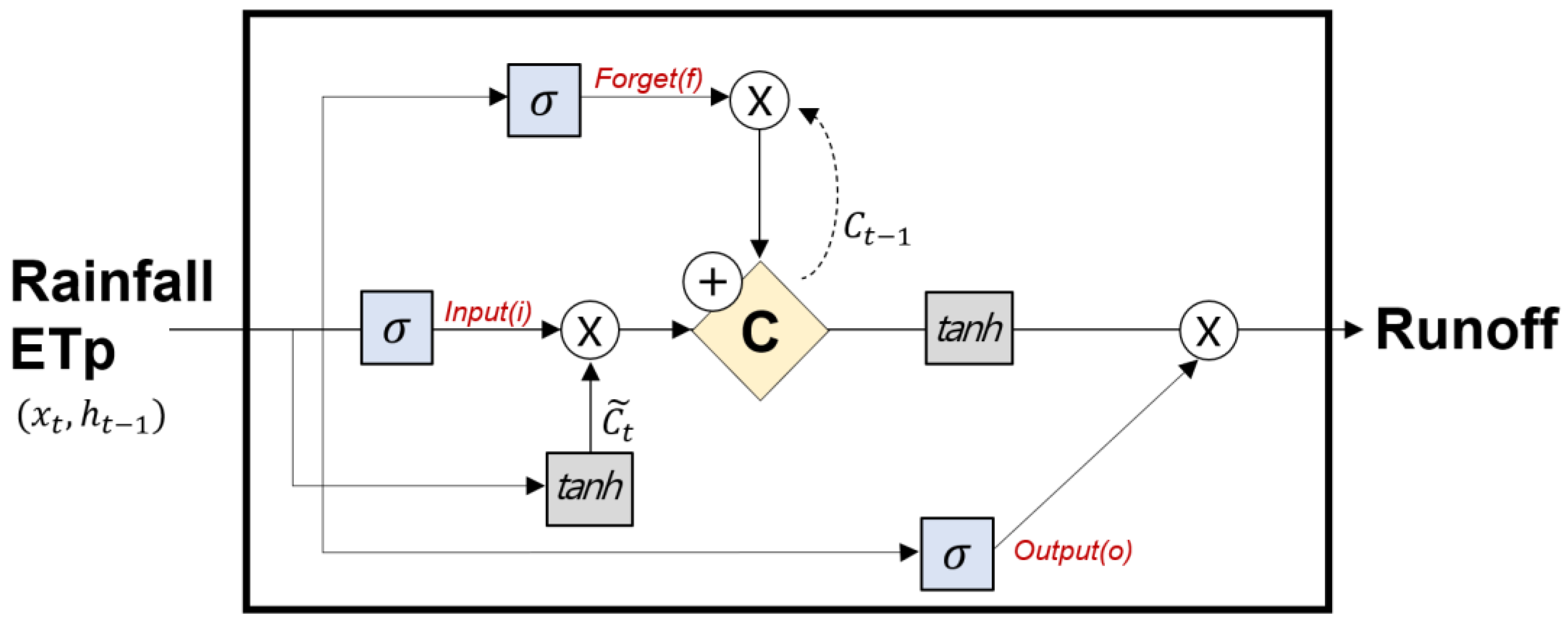
Figure 4 shows a schematic of the LSTM model.
The LSTM model comprises a memory cell (
C) that can maintain the state over time, three nonlinear gates: forget (
f), input (
i) and output (
o), which regulate the flow of data, and a sigmoid (
) function that outputs a value between 0 and 1 as an activation function. First, the forget gate decides whether to remember the past information, which is calculated as
where
f is the forget gate,
i is the input gate,
o is the output gate,
xt is the input value at the present time,
ht−1 is the hidden value of the past time,
W is the weight,
b is the bias,
Ct is the cell state and
is a new candidate value. Second, the input gate (
i) is used for memorizing the current information and is expressed by applying a sigmoid as an activation function. The expression is as follows:
Equation (8) is used as an activation function by applying a hyperbolic tangent function (
tanh) in the range of −1 to 1 to the calculated value for determining how much of the
and
information obtained can be reflected in the cell state value. Previously, as the value of the forget gate (
f) with past information calculated in Equation (6) is multiplied by the value of the current information calculated in Equations (7) and (8), the cell information is updated as
This value can be expressed as a dotted line and is reflected in the calculation at the next point in time. The final step is performed to determine the amount of information to be output to the output gate (
o). The input value passes through the sigmoid function (
) and can be calculated as
This result is expressed as an output value using Equation (11) after the cell information is multiplied by the value passed through the hyperbolic tangent function.
The LSTM model has an input layer, one or more hidden layers and an output layer. To learn the rainfall–runoff relationship using the simple structure of the LSTM model, we composed a single hidden layer. The optimal value was derived using a random function, with the number of units constituting a neuron being less than 210 and the sequence length being less than or equal to 21 days. The learning rate was set to 0.001 and the input data were normalized to minimize the overfitting of the learning model. As training data (2002–2015), we used 70% of the total amount of data and the remaining 30% as validation data (2016–2021). Mean square error (MSE) was used as the loss function to predict the error of the LSTM model for optimization and the Adam optimizer based on gradient descent was applied to update the learning parameters. The epoch was set to 500 and early stopping was used to stop learning if the monitoring metrics did not improve. The usefulness of each model was evaluated using the same performance evaluation index as the ONE model for results determined based on optimally learned information.
2.4. Performance Evaluation of the Runoff Model
Quantitative evaluation was performed using the observed runoff on the results of simulating runoff with the proposed ONE model and a comparative LSTM model. The evaluation indices used were as follows: Nash–Sutcliffe efficiency (NSE), coefficient of determination (R
2), root mean square error (RMSE) and percent bias (PBIAS). NSE and R
2 have a range value and show that the closer their values are to 1, the better the predictive ability of the model is. RMSE is an index that indicates the difference between the simulated and observed values and ranges from 0 to ∞; a value closer to 0 indicates a higher simulation accuracy of the model. It is possible to evaluate the concentration of the simulated values on the best-fitting line. PBIAS represents the average tendency between the observed and simulated values and ranges from 0 to ∞, with values closer to 0 indicating a higher simulation accuracy of the model [
49,
50,
51,
52,
53].
where
O and
S are the observed and simulated values, respectively,
and
are the average observed and simulated values, respectively, and
n is the number of data.
3. Results
3.1. Parameter Sensitivity of the ONE Model
We analyzed the parameter sensitivity based on the results of a runoff simulation obtained using the ONE model.
Figure 5 and
Figure 6 show the changes in the evaluation index according to parameter (
w) at the SY and YD dams. The parameter range was set from 0 to 10 and the NSE, R
2, RMSE and PBIAS values were plotted at 0.1 intervals. The NSE values of the SY and YD dams ranged from 0.1 to 0.9 and the R
2 values ranged from 0.79 to 0.97. Both NSE and R
2 reached their maximum values near parameter 2, starting from a positive value and then appearing as a concave curve. The RMSE index starts from a positive value of 6 mm/day, has a minimum value when the parameter value reaches 2 and assumes a convex curve that increases again with the increase in the value of the parameter. This index shows a continuously increasing trend with only positive values. For the PBIAS index, a positive value of approximately 60% shows a negative value as the parameter increases. Although this index exhibits a continuous tendency to decrease, the slope of the evaluation index decreases as the parameter increases.
Changes were examined in the evaluation index to determine the appropriate parameters of the ONE model. The evaluation indices of NSE and R2 both exhibited concave curves with positive values and the maximum value can be selected as an appropriate parameter. As the slope of the curve for the NSE index is large, the appropriate parameter with the maximum value can be clearly identified. Because the PBIAS evaluation index can continuously decrease from a positive to a negative value, it is appropriate to select an optimal parameter so that the difference between observed and simulated value is 0 with the smallest error. Furthermore, because the RMSE evaluation index increases as the observed simulation error decreases, selecting an appropriate parameter may result in a parameter with a minimum value.
The appropriate parameter was determined as 2.5 and 2.96 for the SY Dam and YD Dam, respectively. When analyzing the parameter sensitivity of the ONE model, all R2 evaluation indices were above 0.7. In addition, the maximum value of NSE where the curve of the evaluation index clearly appears can be confirmed. The range of the minimum value of the RMSE can be referred to and the PBIAS evaluation index can be determined as a parameter with a value close to 0. The ONE model is used for long-term runoff simulation and the PBIAS evaluation index is important owing to the total volume error of runoff over the entire period. Therefore, the user can determine the parameter of the corresponding point by checking the parameter (w) with a PBIAS index close to 0 and comprehensively review the results of the remaining NSE, R2 and RMSE values.
3.2. Comparison of Runoff Simulation Results Obtained by ONE and LSTM
In the ONE model, the parameter (
w) is adjusted using the observed flow for the calibration period and the appropriateness of the simulation results is evaluated for the validation period. The LSTM model trains and verifies the data for the same calibration period. For the quantitative evaluation of the runoff simulation results during the calibration and validation periods, the runoff simulation performances of the two models were compared in terms of NSE, R
2, RMSE and PBIAS.
Table 2 presents the results of the statistical analysis of the daily runoff of the ONE and LSTM models. Each calibration (training) and test period was 2002–2015 and 2016–2021, respectively. The ONE model has one parameter each for the SY Dam and YD Dam, whereas the parameters of the LSTM model are the results calculated using 32,104 and 24,076 parameters for the SY Dam and YD Dam, respectively.
For the SY Dam, the runoff of the ONE model was calculated as 0.87 for NSE, 0.93 for R2, 80.67 m3/s for RMSE and −1.07% for PBIAS during the calibration period. For the validation period, each evaluation index was calculated as 0.86, 0.93, 74.38 m3/s and 0.08% and the simulation results of the ONE model well reflected the observed values. The runoff of the LSTM model was calculated as 0.69 for NSE, 0.83 for R2, 125.72 m3/s for RMSE and 8.86% for PBIAS over the training period. For the validation period, each evaluation index was calculated as 0.58, 0.76, 128.04 m3/s and 8.82%. For the YD Dam, the runoff of the ONE model was calculated as 0.87 for NSE, 0.93 for R2, 27.81 m3/s for RMSE and 2.35% for PBIAS over the calibration period. For the validation period, each evaluation index was calculated as 0.91, 0.95, 25.10 m3/s and 9.95% and the simulation results of the ONE model accurately reflected the observed values. The runoff of the LSTM model was calculated as 0.52 for NSE, 0.72 for R2, 53.37 m3/s for RMSE and −0.37% for PBIAS over the training, respectively. For the validation period, the evaluation indices were calculated as 0.44, 0.67, 62.73 m3/s and 1.58%.
For both dams, the NSE index of the ONE model was 0.8 or higher, which is evaluated as “very good” depending on the criteria presented in the study [
54,
55]. In the LSTM model, the SY Dam was evaluated as “very good” at 0.67 and the YD Dam as “unsatisfactory” at 0.49. In terms of the R
2 index, the ONE model exhibited a value of 0.9 or higher, which is evaluated as “very good” depending on the criteria presented in the study [
56]. In the LSTM model, the SY Dam and YD Dam were evaluated as “very good” and “good” at 0.82 and 0.70, respectively. In terms of the RMSE index, the ONE model was 47.59 m
3/s and 29.30 m
3/s lower than that of the LSTM model for the SY Dam and YD Dam, respectively, which decreases the error. In terms of the PBIAS index, both the ONE and LSTM models had an absolute error of less than 10% and were evaluated as “very good” according to the standard suggested by Van Liew et al. [
57]. Among all four evaluation indices, the ONE model showed a better runoff simulation performance.
Figure 7 and
Figure 8 show the results of the runoff calculated from the ONE and LSTM models by superimposing them with the observed values. The simulation results of the ONE and LSTM models are indicated in red and black, respectively, and the observed values are indicated in gray. The
x-axis represents the year of analysis. The ONE model is divided into calibration and validation periods and the LSTM model is divided into training and validation periods. To evaluate the dry season simulation ability in long-term runoff simulation, the
y-axis is expressed as a logarithmic value.
In general, the ONE and LSTM models predicted values similar to those of the observed values. However, the LSTM model predicted the runoff value with high accuracy during the dry season. In the case of the SY Dam, the LSTM and ONE models in 2005 predicted a similar trend; however, the predicted runoff values were higher than the observed value. In 2014, the value predicted by the LSTM was more similar to the observed value; however, in 2019, the ONE model could predict more accurately than the LSTM model. In the case of the YD Dam, particularly in 2005, the ONE model predicted values more similar to the observed values compared to the LSTM model. In 2017, the LSTM model predicted values similar to the observed values; however, the ONE model predicted lower values. The ONE model showed that the runoff further decreased as soil water storage decreased, owing to the low rainfall in the corresponding year. Overall, the statistical evaluation index and visual results of the ONE model were analyzed to simulate more similar observations compared to those of the LSTM model.
3.3. Comparison of Monthly and Annual Runoff Rate Calculation Results
The relationship between the monthly heatmap and the annual runoff rate was compared using the daily runoff calculation results of the ONE and LSTM models.
Figure 9 and
Figure 10 show a heatmap of the monthly runoff by year. Overall, the runoff was significant in July–September each year and low otherwise. On comparing the monthly observed runoff values from the SY Dam by model, it was found that the ONE model predicted more similar values to the observed values than the LSTM model in July 2006, 2009 and 2013. For the YD Dam, the values predicted by the ONE model in July 2005, 2006 and 2020 and August 2010, 2020 were more similar to the observed values compared to the LSTM model.
Table 3 presents the comparison results of the runoff predicted using each model during the validation period (2016–2021). The runoff rate is expressed as the ratio (%) of runoff to rainfall. In the case of the SY Dam, the annual average values of rainfall, runoff and runoff rate predicted using ONE were 1221.3 mm, 723.1 mm and 59.2%, respectively, and the runoff and runoff rate predicted using LSTM were 780.3 mm and 63.9%, respectively. The average annual observed runoff rate of the SY Dam was 59.2% and the error of both the models was within 5%. In the case of the YD Dam, the annual average values of runoff and the runoff rate predicted by the ONE model were 879.9 mm and 61.5%, respectively, whereas in the case of the LSTM model, these values were 811.6 mm and 56.8%, respectively. The average annual runoff rate of the YD Dam was 56.0%, demonstrating a difference of 5.5% and 0.8% from the observed values predicted by the ONE and LSTM models, respectively. On evaluating the runoff rate calculation results, it was found that both the ONE and LSTM models were appropriately simulated.
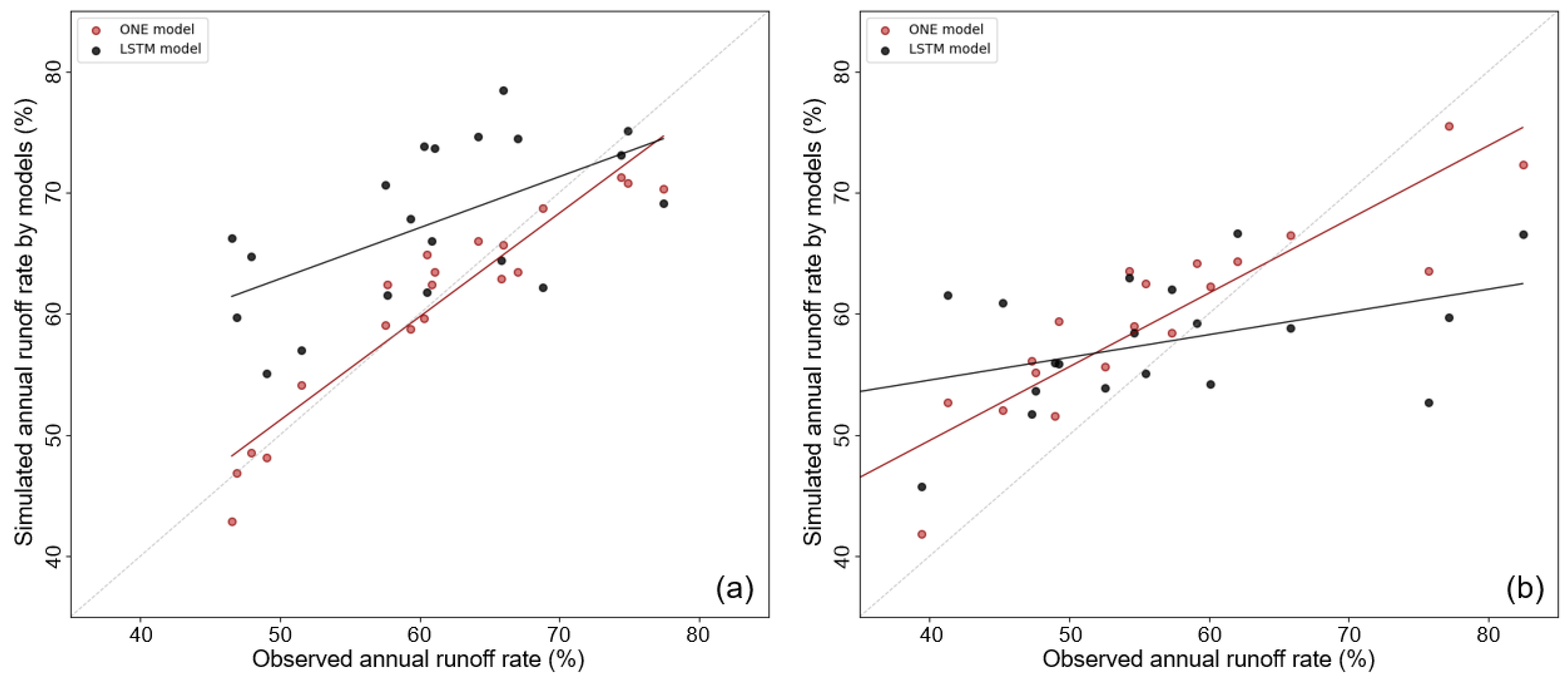
Figure 11 shows a scatter plot of the annual observed and simulated runoff rates predicted by the ONE and LSTM models. In the case of the SY Dam, the R
2 values of the ONE and LSTM models were 0.89 and 0.48, respectively. In the case of the YD Dam, the R
2 values of the ONE and LSTM models were 0.79 and 0.66, respectively. The annual runoff rates predicted by the ONE and LSTM models were evaluated as “very good” (0.75 < R
2 < 1.00) and “good” (0.6 < R
2 < 0.75) or “bad” (0.25 < R
2 < 0.50), respectively, according to the evaluation classification used by Fernandez et al. [
56]. When plotting the scatter plot of the runoff rate, the original model was concentrated on a 1:1 line compared to that of the LSTM, thereby confirming that the distribution of the YD Dam was wider than that of the SY Dam.
4. Discussion
This study developed the ONE model with the aim of maximizing practical utility by using a single parameter that can be set by the user. Although the ONE model has a simple hydrological structure, it uses a nonlinear exponential function and watershed water balance equation to estimate runoff. In particular, we focus on reducing the number of parameters. When the architecture of the ONE and LSTM models were compared, a difference in the number of parameters used was noted. In the LSTM model, weight and deviation are used when the input values are forwarded via the hidden layer to the output [
58]. For example, when building a model, the number of parameters may increase depending on the length of the input sequence and the number of hidden layers [
59,
60]. In other words, the number of parameters may vary depending on the number of hidden layers set by the user as well as the length of the time-series data. Ayzel et al.’s study [
61] demonstrated that if learning lengths of 365 and 256 cells are used, 266,497 parameters can be generated. In our study, the LSTM model considered the same learning lengths for the SY and YD dams, i.e., 21; however, for the unit number, 87 and 75 units of the SY and YD Dams generated 32,104 and 24,076 parameters, respectively. Further, in this LSTM model, the number of parameters varied depending on the units and the learning length and the parameters could be determined via learning. In comparison, the ONE model was developed to simulate runoff according to soil water storage (
S) and focuses on improving user convenience by utilizing a watershed coefficient (
w), a parameter that influences runoff. Therefore, the ONE model is different from the LSTM model in that the latter uses several parameters.
Unlike the LSTM model, which optimizes several parameters via data-based learning, the ONE model uses a single parameter in a simple exponential function. Runoff analysis using a single parameter is feasible because the runoff calculated using this parameter continuously tracks the change in the soil water storage over time. Furthermore, the structure of the LSTM model may exhibit similar characteristics to the ONE model; that is, it continuously learns the runoff using a structure wherein the cell memory reflects the past information. By evaluating the results of the runoff calculation obtained by ONE and LSTM, for the same rainfall and potential evaporation data, we found that runoff can be effectively calculated using the ONE model. By comparing the quantitative evaluation indices, we further verified that the runoff simulation of the ONE model was superior to that of the LSTM model in terms of the number of parameters. The rainfall–runoff model for estimating the inflow of agricultural water supply systems in Korea is based on the TANK model [
62,
63]. For estimating runoff using this model, the rainfall–runoff relationship is calculated on a nonlinear basis based on the number of tanks. The parameters of the model change according to the number of tanks and the user must decide on up to 18 parameters for the four tanks [
7]. To apply and use a model with several parameters to an unmeasured watershed, DIROM was developed based on three tanks and the parameters of the tank model were derived using four watershed factors [
64]. To utilize a model with numerous parameters, a model optimization technique must be employed [
65,
66,
67]. However, such a model is difficult to use, even when the observed streamflow data are available. The ONE model addresses these problems while providing reliable runoff predictions, although designed to use a single parameter. Chiew and McMahon [
68] reported the possibility of sufficiently reproducing the monthly hydrological phenomenon with a hydrological model with three to five parameters in a humid area. However, the model developed in the current study uses even fewer parameters while reproducing the runoff phenomenon accurately, based on daily hydrological information.
The ONE model can therefore be used to predict the inflow of agricultural reservoirs located in the watershed of multipurpose dams. However, the inflow of agricultural reservoirs has not yet been measured. Moreover, if the method of transferring the determined parameters of a multipurpose dam (measurement basin) is used, the utility of water management practices of agricultural reservoirs can be further increased. As a result, it will be possible to quickly simulate runoff at the target point, even when using a simple trial and error method to increase or decrease the parameter value in the ONE model rather than using complex optimization techniques. A hydrological model using a single parameter could match the ratio of rainfall to runoff by referring to the sensitivity analysis results. If it is used as an auxiliary index, i.e., as another evaluation index, its practical utility can be further improved for long-term runoff simulation analyses.
This study developed a framework for a hydrological model using only one parameter and verified its effectiveness in simulating runoff. However, the developed model has limitations in verifying hydrological factors other than runoff based on the results of runoff calculations using the daily soil water storage tracking values. Similar to a data-driven model, the ONE model cannot distinguish between different runoff components (surface, subsurface and groundwater runoffs) due to its simple structure as a conceptual runoff model. The ONE model was developed and implemented in Korea’s monsoon climate region, which experiences heavy summer rainfall and cold, dry winters. However, in Latif et al.’s study [
69], a runoff model that considers snow and glaciers was applied to simulate runoff in a mountainous region. The hydrological characteristics of a specific region must be considered when selecting the most appropriate model. Therefore, to evaluate the applicability of the ONE model, it will be expanded to various regions.
5. Conclusions
Runoff in watersheds is used as important information to establish effective water management plans for water resource facilities. However, a hydrological model with several complex parameters is challenging to use for the quick estimation of flow into a water resource system. This study, therefore, developed the ONE model to simulate rainfall-runoff using a single parameter. The proposed model uses an exponential function to express a relationship wherein the runoff analysis changes nonlinearly according to the amount of soil water storage in the watershed. One parameter was reflected in the runoff calculation coefficient and used to track the daily soil water storage conditions continuously based on the watershed water balance. To evaluate the performance of the developed model using the rainfall and potential evaporation data of a specific area as input data, it was applied to the SY and YD dams in Korea, where the runoff information was secured. Using the same data, the results obtained by the proposed model were compared with those obtained by the learning-based LSTM model. The ONE model outperformed the LSTM model in terms of the following parameters: NSE, R2, RMSE and PBIAS. Furthermore, the runoff simulation performance of the ONE model was superior to that of the learning-based LSTM model in terms of the daily simulation values, monthly heatmaps and annual runoff rates. This study, therefore, demonstrated the possibility of simulating rainfall-runoff using only one parameter and highlights that the practical utility of a hydrological model can be improved by reducing the number of parameters. The use of a single parameter is expected to maximize user convenience for simulating runoff, which is essential in the operation of water resource facilities. In the future, the ONE model will be reviewed for applicability to multipurpose dams across Korea. In addition, a regression equation using data for the rainfall and runoff rate of multipurpose dams will be derived and used as a referential index to determine one parameter of the ONE model. This will expand the model for use in agricultural reservoirs with no inflow data.