Analysis of Preferential Flow in Artificial Substrates with Sedum Roots for Green Roofs: Experiments and Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plants and Substrates
2.2. Solute Breakthrough Experiments
2.3. Preferential Flow Detection
2.4. Determination of Substrate Hydraulic Parameters
2.4.1. Calculation of Substrate Hydraulic Parameters
2.4.2. Validation of Substrate Hydraulic Parameters
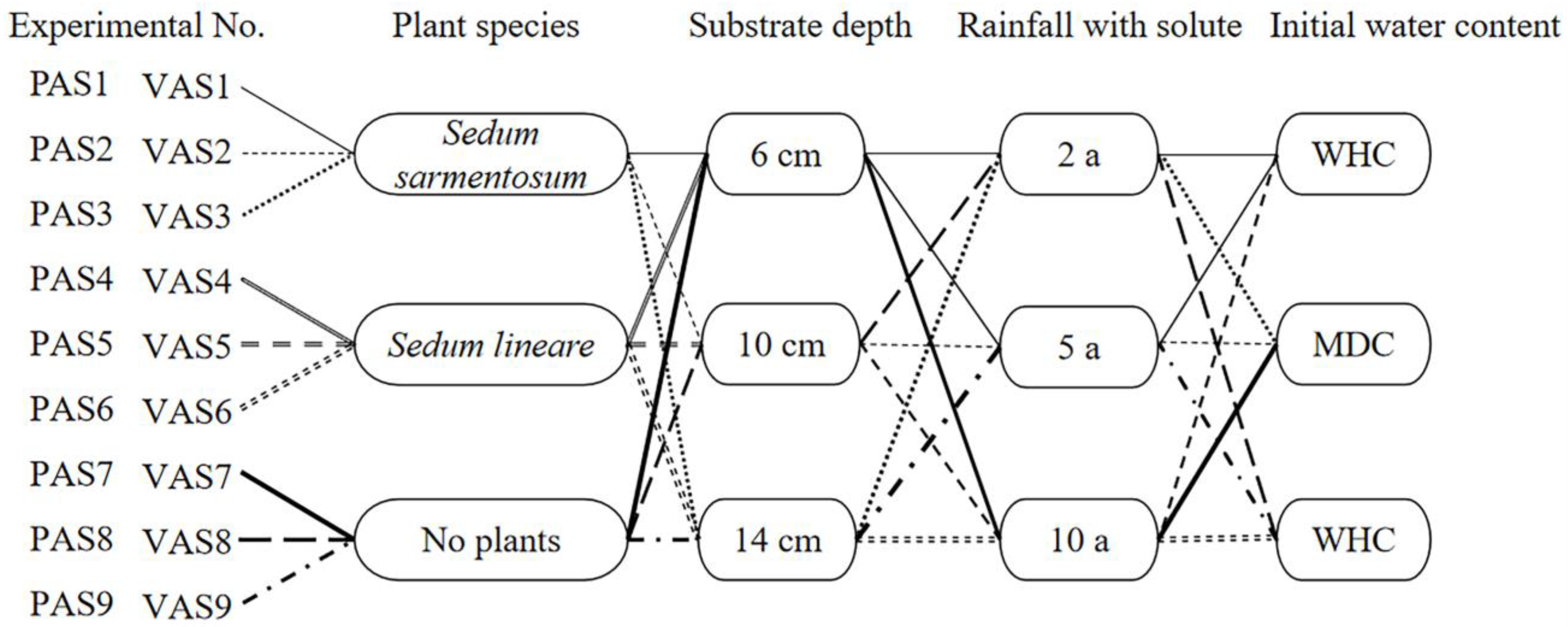
2.5. Preferential Flow and Influential Factors
3. Results and Discussion
3.1. Preferential Flow Detection
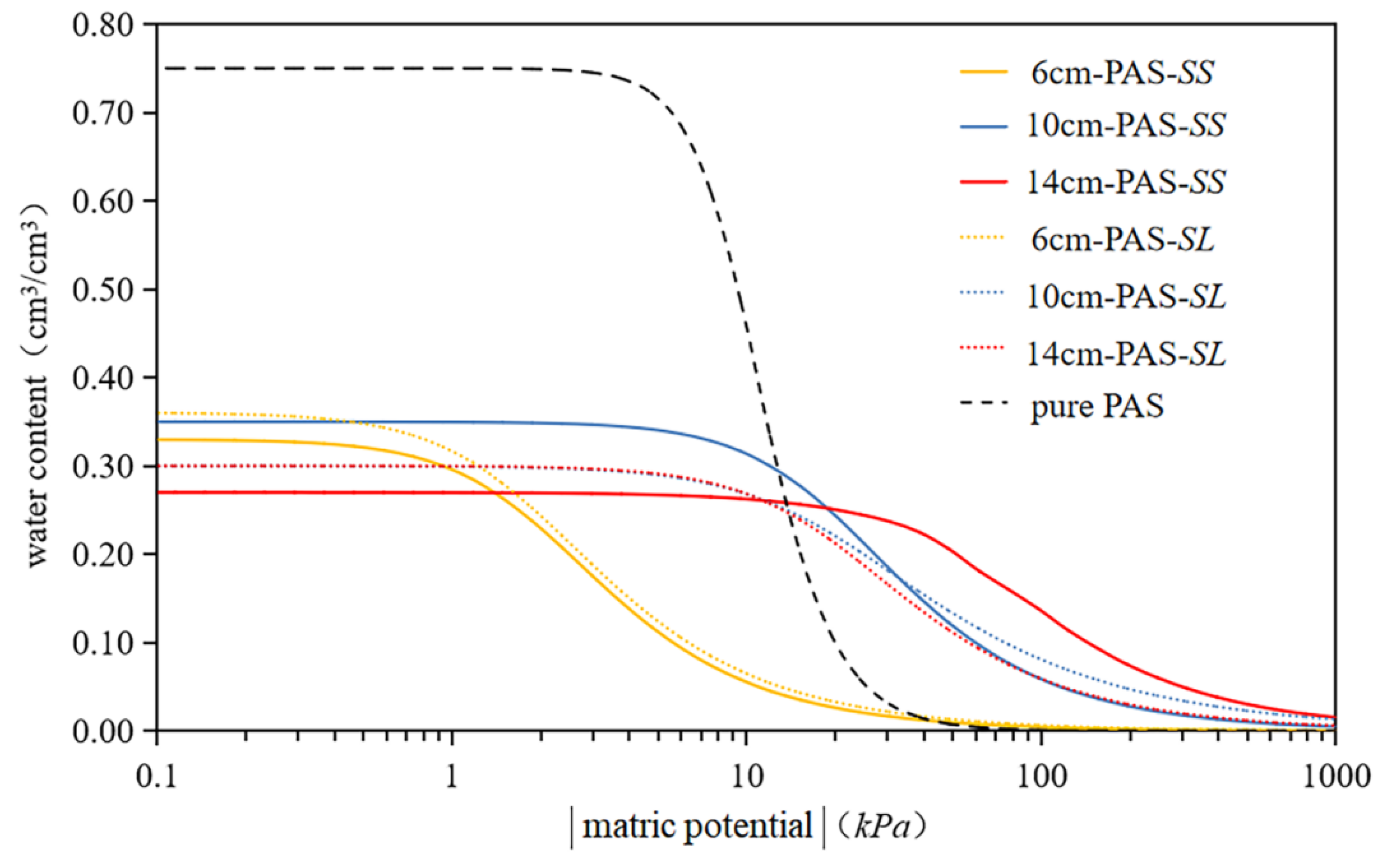
3.2. Substrate Hydraulic Parameters
3.2.1. Results
3.2.2. Implications
3.3. Preferential Flow and Influential Factors
3.3.1. Perlite-Based Substrate (PAS)
3.3.2. Vermiculite-Based Substrate (VAS)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, N.B.; Lu, J.W.; Chui, T.F.M.; Hartshorn, N. Global policy analysis of low impact development for stormwater management in urban regions. Land Use Policy 2018, 70, 368–383. [Google Scholar] [CrossRef]
- Fowdar, H.; Payne, E.; Deletic, A.; Zhang, K.F.; McCarthy, D. Advancing the Sponge City Agenda: Evaluation of 22 plant species across a broad range of life forms for stormwater management. Ecol. Eng. 2022, 175, 106501. [Google Scholar] [CrossRef]
- Liu, R.F.; Stanford, R.L.; Deng, Y.; Liu, D.F.; Liu, Y.; Yu, S.L. The influence of extensive green roofs on rainwater runoff quality: A field-scale study in southwest China. Environ. Sci. Pollut. Res. 2019, 27, 12932–12941. [Google Scholar] [CrossRef]
- MoHURD. Technical Guidelines of the Sponge City Development—Low Impact Development Systems for Storm Water; Ministry of Housing and Urban Rural Development: Beijing, China, 2014.
- Chen, Y.; Chen, H. The collective strategies of key stakeholders in Sponge City Construction: A tripartite game analysis of governments, developers, and consumers. Water 2020, 12, 1087. [Google Scholar] [CrossRef] [Green Version]
- Vijayaraghavan, K. Green roofs: A critical review on the role of components, benefits, limitations and trends. Renew. Sustain. Energy Rev. 2016, 57, 740–752. [Google Scholar] [CrossRef]
- FLL. Guidelines for the Planning, Construction and Execution of Green-Roof Sites; Forschungsgesellschaft Landschaftsentwicklung Landschaftsbau e.V.: Bonn, Germany, 2008. [Google Scholar]
- She, N.; Pang, J. Physically based green roof model. J. Hydrol. Eng. 2010, 15, 458–464. [Google Scholar] [CrossRef]
- Peng, Z.; Smith, C.; Stovin, V. The importance of unsaturated hydraulic conductivity measurements for green roof detention modelling. J. Hydrol. 2020, 590, 125273. [Google Scholar] [CrossRef]
- Farrell, C.; Mitchell, R.E.; Szota, C.; Rayner, J.P.; Williams, N.S.G. Green roofs for hot and dry climates: Interacting effects of plant water use, succulence and substrate. Ecol. Eng. 2012, 49, 270–276. [Google Scholar] [CrossRef]
- Yang, H. Studies on Plants and Substrates Selection for Extensive Green Roofs in Beijing. Master’s Thesis, Beijing Forestry University, Beijing, China, 2012. [Google Scholar]
- Zhang, F.F. A Study on Technology of Producing Sedum spp. Mat for Light Roof-Greening. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2009. [Google Scholar]
- Zhou, Y.; Xu, D.Y.; Dong, Y.F.; Chen, F.Z.; Tong, J.; Xie, Y.F.; Chen, Y.X.; Guo, C.X. Study on drought resistance of 9 Sedums for light roof greening. Chin. Agric. Sci. Bull. 2012, 28, 294–301. [Google Scholar] [CrossRef]
- Xiao, M.; Lin, Y.; Han, J.; Zhang, G. A review of green roof research and development in China. Renew. Sustain. Energy Rev. 2014, 40, 633–648. [Google Scholar] [CrossRef]
- Sang, M.; Zhang, W.; Zhong, X.; Che, W. Influence from conventional substrate on rainwater retention and outflow water quality characteristics of extensive green roof facility. Water Resour. Hydropower Eng. 2018, 49, 163–170. [Google Scholar] [CrossRef]
- Li, X.X.; Cao, J.J.; Xu, P.X.; Fei, L.; Dong, Q.; Wang, Z.L. Green roofs: Effects of plant species used on runoff. Land Degrad. Dev. 2018, 29, 3628–3638. [Google Scholar] [CrossRef]
- Nagase, A.; Dunnett, N. Amount of water runoff from different vegetation types on extensive green roofs: Effects of plant species, diversity and plant structure. Landsc. Urban Plan. 2012, 104, 356–363. [Google Scholar] [CrossRef]
- Zhang, S.X.; Zhang, S.H.; Zhang, Y.; Wu, S.T. Impacts of vegetation on quantity and quality of runoff from green roofs. Environ. Sci. 2019, 40, 3618–3625. [Google Scholar] [CrossRef]
- MacIvor, J.S.; Lundholm, J. Performance evaluation of native plants suited to extensive green roof conditions in a maritime climate. Ecol. Eng. 2011, 37, 407–417. [Google Scholar] [CrossRef]
- Hu, Y.C.; Qin, H.P.; Lin, Z.X. Variation and influencing factors of rainwater retention of green roofs in Shenzhen. J. Shenzhen Univ. Sci. Eng. 2020, 37, 347–354. [Google Scholar] [CrossRef]
- Stovin, V.; Poë, S.; De-Ville, S.; Berretta, C. The influence of substrate and vegetation configuration on green roof hydrological performance. Ecol. Eng. 2015, 85, 159–172. [Google Scholar] [CrossRef] [Green Version]
- Ge, D.; Zhang, S.H. Impacts of vegetation on hydrological performances of green roofs under different rainfall conditions. Environ. Sci. 2018, 39, 5015–5023. [Google Scholar] [CrossRef]
- Skorobogatov, A.; He, J.X.; Chu, A.; Valeo, C.; van Duin, B. The impact of media, plants and their interactions on bioretention performance: A review. Sci. Total Environ. 2020, 715, 136918. [Google Scholar] [CrossRef]
- Zhang, W.J.; Yuan, S.S. Characterizing preferential flow in landfilled municipal solid waste. Waste Manag. 2019, 84, 20–28. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.H.; Zhang, Z.M.; Ma, Z.W.; Chen, J.X.; Akbar, J.; Zhang, S.Y.; Che, C.G.; Zhang, M.X.; Cerdà, A. A review of preferential water flow in soil science. Can. J. Soil Sci. 2018, 98, 604–618. [Google Scholar] [CrossRef]
- Locatelli, L.; Mark, O.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K.; Jensen, M.B.; Binning, P.J. Modelling of green roof hydrological performance for urban drainage applications. J. Hydrol. 2014, 519, 3237–3248. [Google Scholar] [CrossRef]
- Niu, J.Z. Study on Preferential Flow in Forest Ecosystems; Science Publishing House: Beijing, China, 2013. [Google Scholar]
- Wang, J.B.; Zhao, J.S.; Shen, Z.Y.; Wang, H.; Lei, X.H. Discussion about the two rainfall control approaches in Sponge City Construction. J. Hydraul. Eng. 2017, 48, 1490–1498. [Google Scholar] [CrossRef]
- Hashemi, S.S.G.; Mahmud, H.B.; Ashraf, M.A. Performance of green roofs with respect to water quality and reduction of energy consumption in tropics: A review. Renew. Sustain. Energy Rev. 2015, 52, 669–679. [Google Scholar] [CrossRef]
- Sandoval, V.; Bonilla, C.A.; Gironás, J.; Vera, S.; Victorero, F.; Bustamante, W.; Rojas, V.; Leiva, E.; Pastén, P.; Suárez, F. Porous media characterization to simulate water and heat transport through green roof substrates. Vadose Zone J. 2017, 16, 1–14. [Google Scholar] [CrossRef]
- She, N.; Liu, J. Using Preferential Flow to Model Green Roofs. In Proceedings of the World Environmental and Water Resources Congress, Cincinnati, OH, USA, 19–23 May 2013. [Google Scholar]
- Alaoui, A.; Caduff, U.; Gerke, H.H.; Weingartner, R. Preferential flow effects on infiltration and runoff in grassland and forest soils. Vadose Zone J. 2011, 10, 367–377. [Google Scholar] [CrossRef]
- Wu, Q.H.; Zhu, G.S.; Cui, H.D.; Zhang, J.F.; Zhang, F.W. Effect of precipitation intensities on preferential flow and its numerical modeling. Trans. Chin. Soc. Agric. Eng. 2014, 30, 118–127. [Google Scholar] [CrossRef]
- Lu, J.R.; Zhang, Q.; Werner, A.D.; Li, Y.L.; Jiang, S.L.; Tan, Z.Q. Root-induced changes of soil hydraulic properties—A review. J. Hydrol. 2020, 589, 125203. [Google Scholar] [CrossRef]
- Liu, R.F.; Fassman-Beck, E. Hydrologic response of engineered media in living roofs and bioretention to large rainfalls: Experiments and modeling. Hydrol. Process. 2017, 31, 556–572. [Google Scholar] [CrossRef]
- Quinn, R.; Dussaillant, A. The impact of macropores on heavy metal retention in sustainable drainage systems. Hydrol. Research. 2018, 49, 517–527. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.X.; Xu, X.X.; Zhao, J.N.; Zhao, C.P.; Zhang, S.N. Review on macropore flow in soil. Sheng Tai Xue Bao 2014, 34, 2801–2811. [Google Scholar] [CrossRef]
- Zhang, Z.; Szota, C.; Fletcher, T.D.; Williams, N.S.G.; Werdin, J.; Farrell, C. Influence of plant composition and water use strategies on green roof stormwater retention. Sci. Total Environ. 2018, 625, 775–781. [Google Scholar] [CrossRef] [PubMed]
- Chen, X. Effect of Sedum Roots on Preferential Flow Transport of Artificial Substrates on Green Roofs. Master’s Thesis, Hubei University of Technology, Wuhan, China, 2022. [Google Scholar]
- Zhou, M.L. Study on Combination Screening and Application Effect of Plant-Artificial Matrix based on Heavy Rainfall Control. Master’s Thesis, Hubei University of Technology, Wuhan, China, 2021. [Google Scholar]
- Kamra, S.K.; Lennartz, B. Quantitative indices to characterize the extent of preferential flow in soils. Environ. Model. Softw. 2005, 20, 903–915. [Google Scholar] [CrossRef]
- Young, D.F.; Ball, W.P. Column experimental design requirements for estimating model parameters from temporal moments under nonequilibrium conditions. Adv. Water Resour. 2000, 23, 449–460. [Google Scholar] [CrossRef]
- André, L.; Durante, M.; Pauss, A.; Lespinard, O.; Ribeiro, T.; Lamy, E. Quantifying physical structure changes and non-uniform water flow in cattle manure during dry anaerobic digestion process at lab scale: Implication for biogas production. Bioresour. Technol. 2015, 192, 660–669. [Google Scholar] [CrossRef] [PubMed]
- Lamy, E.; Lassabatere, L.; Bechet, B.; Andrieu, H. Modeling the influence of an artificial macropore in sandy columns on flow and solute transfer. J. Hydrol. 2009, 376, 392–402. [Google Scholar] [CrossRef]
- Schwinger, J.; van Genuchten, M.T. Modeling nonequilibrium flow and transport processes using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef] [Green Version]
- Rassam, D.; Šimůnek, J.; Mallants, D.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media: Tutorial; CSIRO Land and Water: Adelaide, Australia, 2018. [Google Scholar]
- Gerke, H.H.; van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 2010, 29, 305–319. [Google Scholar] [CrossRef]
- Arora, B.; Mohanty, B.P.; McGuire, J.T. Inverse estimation of parameters for multidomain flow models in soil columns with different macropore densities. Water Resour. Res. 2011, 47, W04512. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Wang, H.Y.; Zhao, H.Y. Hydrological regulation simulation of rainwater runoff of bioretention based on HYDRUS-1D. Water Resour. Prot. 2022, 38, 102–108. [Google Scholar] [CrossRef]
- Li, F.; Jiao, X.Y.; Li, P.P.; Zhai, D. Parametric inversion of soil water characteristic curves of farmland. J. Hohai Univ. (Nat. Sci.) 2009, 37, 373–377. [Google Scholar] [CrossRef]
- Li, Y.B. Study on Inverse Method of Soil Hydraulic Parameters under Two-dimensional Negative and Positive Pressure Infiltration. Ph.D. Thesis, Northwest A&F University, Xianyang, China, 2018. [Google Scholar]
- Ren, D.Y.; Xu, X.; Hao, Y.Y.; Huang, G.H. Modeling and assessing field irrigation water use in a canal system of Hetao, upper Yellow River basin: Application to maize, sunflower and watermelon. J. Hydrol. 2016, 532, 122–139. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Jia, J.P. Statistics, 5th ed.; China Renmin University Press: Beijing, China, 2012. [Google Scholar]
- Chen, X.B.; Zhang, H.J.; Cheng, J.H.; Zhang, F.; Zhang, X.; Ruan, X.Z. Quantitative evaluation of preferential flow development degree based on dyed image variability analysis. Trans. Chin. Soc. Agric. Mach. 2015, 46, 93–100. [Google Scholar] [CrossRef]
- Nielsen, D.R.; Bouma, J. Soil Spatial Variability. In Proceedings of the A Workshop of the ISSS and the SSSA, Las Vegas, NV, USA, 30 November–1 December 1984. [Google Scholar]
- Zhang, Y.; Niu, J.Z.; Zhang, M.X.; Xiao, Z.X.; Zhu, W.L. Interaction between plant roots and soil water flow in response to preferential flow paths in Northern China. Land Degrad. Dev. 2017, 28, 648–663. [Google Scholar] [CrossRef]
- Lin, H. Linking principles of soil formation and flow regimes. J. Hydrol. 2010, 393, 3–19. [Google Scholar] [CrossRef]
- Shao, W.; Bogaard, T.A.; Bakker, M.; Greco, R. Quantification of the influence of preferential flow on slope stability using a numerical modelling approach. Hydrol. Earth Syst. Sci. 2015, 19, 2197–2212. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Liu, R.F.; Ma, J. The Interaction between Sedum Root Traits and Engineered Media in Green Roofs. In Proceedings of the 7th International Conference on Green Materials and Environmental Engineering, Changsha, China, 16–17 January 2022. [Google Scholar]
- Lei, Z.D. Soil Hydro-Dynamics; Tsinghua University Press: Beijing, China, 1988. [Google Scholar]
- Hu, C.W.; Wang, H.; Liu, C.; Yuan, H.; Li, Y.Y. Difference analysis of hydraulic characteristics of typical soils in South China. J. Soil Water Conserv. 2017, 31, 97–102. [Google Scholar] [CrossRef]
- Jiang, W.J.; Wang, S.J.; Li, X.; Li, D. Soil moisture characteristic curve and model analysis of purple soil with residual plastic film. J. Drain. Irrig. Machinery Eng. 2021, 39, 844–850. [Google Scholar] [CrossRef]
- Ge, D.; Zhang, S.H. Influence of types and depths of substrates on hydrological performances of green roofs. Sci. Soil Water Conserv. 2019, 17, 31–38. [Google Scholar] [CrossRef]




| Characteristics | Substrate Type | |
|---|---|---|
| PAS | VAS | |
| Components (% by volume) | 90% perlite (<6 mm) 10% chicken manure | 90% vermiculite (<5 mm) 10% chicken manure |
| Bulk density (g/cm3) | 0.21 (0.01) | 0.34 (0.01) |
| Total porosity (%) | 91.40 (0.01) | 78.80 (0.02) |
| WHC (%) | 36.65 (1.33) | 64.05 (1.55) |
| Organic matter content (g/kg) | 31.15 (2.72) | 38.64 (2.60) |
| Ks (cm/min) | 54.45 (0.19) | 18.48 (1.39) |
| Substrate Depth-Substrate Type-Plant Species | Root Volume Density /(mm3/cm3) | Root Volume Density of 0.2–0.4 mm Roots/(mm3/cm3) | Ks /(cm/min) |
|---|---|---|---|
| 6 cm-PAS-SS | 0.63 (0.00) | 0.33 (0.00) | 2.12 (0.17) |
| 10 cm-PAS-SS | 0.42 (0.01) | 0.33 (0.01) | 1.97 (0.19) |
| 14 cm-PAS-SS | 1.37 (0.02) | 0.20 (0.01) | 0.56 (0.00) |
| 6 cm-PAS-SL | 0.71 (0.03) | 0.31 (0.01) | 2.64 (0.09) |
| 10 cm-PAS-SL | 0.02 (0.00) | 0.01 (0.00) | 0.68 (0.06) |
| 14 cm-PAS-SL | 1.13 (0.02) | 0.15 (0.00) | 0.74 (0.05) |
| 6 cm-VAS-SS | 2.46 (0.04) | 0.37 (0.02) | 19.19 (0.54) |
| 10 cm-VAS-SS | 0.16 (0.00) | 0.09 (0.00) | 14.14 (1.31) |
| 14 cm-VAS-SS | 5.66 (0.06) | 0.14 (0.01) | 12.77 (0.57) |
| 6 cm-VAS-SL | 1.59 (0.02) | 0.59 (0.01) | 16.94 (1.28) |
| 10 cm-VAS-SL | 1.31 (0.02) | 0.44 (0.01) | 15.44 (0.67) |
| 14 cm-VAS-SL | 8.98 (0.24) | 0.15 (0.01) | 13.60 (0.67) |
| Experimental No. | M0 | M1 | S | Experimental No. | M0 | M1 | S | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAS1 | 2.34 | 0.53 | 0.23 | 1.61 | −0.12 | −0.06 | VAS1 | 1.28 | 0.58 | 0.5 | 0.41 | 0.01 | 0.05 |
| PAS2 | 1.18 | 0.48 | 0.41 | 0.47 | 0.09 | 0.27 | VAS2 | 0.79 | 0.49 | 0.62 | 0.22 | 0.01 | 0.06 |
| PAS3 | 0.81 | 0.35 | 0.43 | 0.29 | 0.05 | 0.34 | VAS3 | 0.45 | 0.47 | 1.05 | 0.07 | 0.01 | 0.30 |
| PAS4 | 1.13 | 0.42 | 0.37 | 0.57 | 0.16 | 0.37 | VAS4 | 0.87 | 0.51 | 0.58 | 0.24 | 0.01 | 0.05 |
| PAS5 | 1.26 | 0.48 | 0.38 | 0.57 | 0.16 | 0.37 | VAS5 | 0.94 | 0.52 | 0.55 | 0.26 | 0.03 | 0.23 |
| PAS6 | 1.25 | 0.50 | 0.40 | 0.49 | 0.07 | 0.22 | VAS6 | 0.87 | 0.50 | 0.58 | 0.25 | 0.00 | 0.01 |
| PAS7 | 3.39 | 0.62 | 0.18 | 2.46 | 0.44 | 0.11 | VAS7 | 1.90 | 0.48 | 0.25 | 1.37 | 0.98 | 0.61 |
| PAS8 | 0.77 | 0.40 | 0.52 | 0.31 | 0.00 | 0.01 | VAS8 | 0.62 | 0.39 | 0.63 | 0.18 | 0.01 | 0.17 |
| PAS9 | 0.76 | 0.37 | 0.49 | 0.26 | 0.03 | 0.21 | VAS9 | 0.57 | 0.37 | 0.64 | 0.17 | 0.02 | 0.26 |
| Name | Matrix Domain | Preferential Flow Domain | / (cm·min−1) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| / (cm3·cm−3) |
/ (cm−1) |
/ (cm·min−1) |
/ (cm3·cm−3) |
/ (cm−1) |
/ (cm·min−1) | |||||
| 6 cm-PAS-SS | 0.150 | 0.008 | 2.50 | 0.100 | 0.33 | 0.050 | 2.1 | 2.0 | 0.12 | 0.75 × 10–6 |
| 10 cm-PAS-SS | 0.35 | 0.050 | 2.1 | 1.8 | 0.11 | |||||
| 14 cm-PAS-SS | 0.27 | 0.002 | 1.5 | 0.4 | 0.05 | |||||
| 6 cm-PAS-SL | 0.36 | 0.054 | 2.0 | 2.5 | 0.14 | |||||
| 10 cm-PAS-SL | 0.30 | 0.005 | 1.8 | 0.5 | 0.07 | |||||
| 14 cm-PAS-SL | 0.30 | 0.005 | 1.8 | 0.6 | 0.07 | |||||
| pure PAS | 0.75 | 0.009 | 3.8 | 54.4 | 0.60 | 0.16 × 10–6 | ||||
| 6 cm-VAS-SS | 0.131 | 0.011 | 2.41 | 0.105 | 0.60 | 0.008 | 2.618 | 19.1 | 0.026 | 0.75 × 10–6 |
| 10 cm-VAS-SS | 14.1 | |||||||||
| 14 cm-VAS-SS | 12.7 | |||||||||
| 6 cm-VAS-SL | 16.9 | |||||||||
| 10 cm-VAS-SL | 15.4 | |||||||||
| 14 cm-VAS-SL | 13.6 | |||||||||
| pure VAS | 18.8 | |||||||||
| Name | Range of Equivalent Pore Sizes (Corresponding Matric Potentials) | ||
|---|---|---|---|
| >0.03 mm (0–−10 kPa) | 0.003–0.03 mm (−10–−100 kPa) | 0.0003–0.003 mm (−100–−1000 kPa) | |
| 6 cm-PAS-SS | 28.48% | 5.34% | 0.42% |
| 10 cm-PAS-SS | 30.60% | 6.34% | 0.61% |
| 14 cm-PAS-SS | 0.99% | 12.47% | 12.30% |
| 6 cm-PAS-SL | 30.63% | 6.12% | 0.60% |
| 10 cm-PAS-SL | 4.18% | 18.80% | 6.92% |
| 14 cm-PAS-SL | 4.30% | 21.05% | 5.42% |
| pure PAS | 41.63% | 48.41% | 0.11% |
| Simulation No. | Plant Species | Substrate Depth/(cm) | Rainfall Intensity/(a) | Initial Water Content/(%) | S | Preferential Outflow/(cm) | PFI/(%) |
|---|---|---|---|---|---|---|---|
| 1 | Sedum sarmentosum | 6 | 2 | WHC | −0.35 | 6.38 | 84.29 |
| 2 | MDC | −0.35 | 6.38 | 84.29 | |||
| 3 | 5 | WHC | −0.06 | 9.01 | 83.43 | ||
| 4 | MDC | −0.06 | 9.01 | 83.43 | |||
| 5 | 10 | WHC | −0.31 | 11.05 | 83.65 | ||
| 6 | MDC | −0.31 | 11.05 | 83.65 | |||
| 7 | 10 | 2 | WHC | 0.64 | 5.08 | 67.19 | |
| 8 | MDC | 0.64 | 5.08 | 67.19 | |||
| 9 | 5 | WHC | 0.04 | 7.59 | 70.32 | ||
| 10 | MDC | 0.04 | 7.59 | 70.32 | |||
| 11 | 10 | WHC | 0.27 | 9.37 | 70.77 | ||
| 12 | MDC | 0.04 | 9.37 | 70.77 | |||
| 13 | 14 | 2 | WHC | 0.34 | 4.35 | 57.51 | |
| 14 | MDC | 0.34 | 4.35 | 57.51 | |||
| 15 | 5 | WHC | 0.12 | 7.71 | 71.43 | ||
| 16 | MDC | 0.12 | 7.71 | 71.43 | |||
| 17 | 10 | WHC | 0.56 | 10.89 | 82.50 | ||
| 18 | MDC | 0.56 | 10.89 | 82.50 | |||
| 19 | Sedum lineare | 6 | 2 | WHC | 0.37 | 6.73 | 89.00 |
| 20 | MDC | 0.37 | 6.73 | 89.00 | |||
| 21 | 5 | WHC | −0.27 | 9.56 | 88.55 | ||
| 22 | MDC | −0.27 | 9.56 | 88.55 | |||
| 23 | 10 | WHC | −0.39 | 11.58 | 87.73 | ||
| 24 | MDC | 0.39 | 11.58 | 87.73 | |||
| 25 | 10 | 2 | WHC | 0.88 | 2.72 | 36.04 | |
| 26 | MDC | 0.88 | 2.72 | 36.04 | |||
| 27 | 5 | WHC | 0.37 | 4.61 | 42.37 | ||
| 28 | MDC | 0.37 | 4.61 | 42.37 | |||
| 29 | 10 | WHC | −0.52 | 6.74 | 51.06 | ||
| 30 | MDC | −0.52 | 6.74 | 51.06 | |||
| 31 | 14 | 2 | WHC | 0.07 | 2.49 | 33.00 | |
| 32 | MDC | 0.07 | 2.49 | 33.00 | |||
| 33 | 5 | WHC | 0.18 | 4.09 | 38.01 | ||
| 34 | MDC | 0.18 | 4.09 | 38.01 | |||
| 35 | 10 | WHC | 0.22 | 8.66 | 65.68 | ||
| 36 | MDC | 0.22 | 8.66 | 65.68 | |||
| 37 | No-plants | 6 | 2 | WHC | 0.09 | 7.59 | 99.97 |
| 38 | MDC | 0.09 | 7.59 | 99.97 | |||
| 39 | 5 | WHC | 0.10 | 10.85 | 100.0 | ||
| 40 | MDC | 0.10 | 10.85 | 100.0 | |||
| 41 | 10 | WHC | 0.11 | 13.21 | 99.92 | ||
| 42 | MDC | 0.11 | 13.21 | 99.92 | |||
| 43 | 10 | 2 | WHC | 0.01 | 7.56 | 99.89 | |
| 44 | MDC | 0.01 | 7.56 | 99.89 | |||
| 45 | 5 | WHC | 0.59 | 10.73 | 99.91 | ||
| 46 | MDC | 0.59 | 10.73 | 99.91 | |||
| 47 | 10 | WHC | 0.63 | 13.08 | 99.92 | ||
| 48 | MDC | 0.63 | 13.08 | 99.92 | |||
| 49 | 14 | 2 | WHC | 0.18 | 7.59 | 99.87 | |
| 50 | MDC | 0.18 | 7.59 | 99.87 | |||
| 51 | 5 | WHC | 0.21 | 10.76 | 99.91 | ||
| 52 | MDC | 0.21 | 10.76 | 99.91 | |||
| 53 | 10 | WHC | 0.46 | 13.19 | 99.77 | ||
| 54 | MDC | 0.46 | 13.19 | 99.77 |
| Sources of Variance | F Values | |
|---|---|---|
| Preferential Outflow | PFI | |
| Plant species | 118.54 ** | 84.98 ** |
| Substrate depth | 31.66 ** | 23.94 ** |
| Plant species × Substrate depth | 13.96 ** | 10.55 ** |
| Rainfall intensity | 268.98 ** | 8.175 * |
| Initial water content | 0.00 | 0.00 |
| Simulation No. (Rainfall Intensity Varying) | Fixed Variables: Plant Species, Substrate Depth, Initial Water Content | Preferential Outflow | PFI | ||
|---|---|---|---|---|---|
| Mean Values /(cm) | Cv /(%) | Mean Values /(cm) | Cv /(%) | ||
| 2, 4, 6 | SS, 6 cm, MDC | 8.81 | 26.56 | 83.79 | 0.53 |
| 20, 22, 24 | SL, 6 cm, MDC | 9.29 | 26.22 | 88.43 | 0.73 |
| 38, 40, 42 | No-plants, 6 cm, MDC | 10.55 | 26.75 | 99.96 | 0.04 |
| 8, 10, 12 | SS, 10 cm, MDC | 7.35 | 29.30 | 69.36 | 2.97 |
| 26, 28, 30 | SL, 10 cm, MDC | 4.69 | 42.88 | 43.16 | 17.47 |
| 44, 46, 48 | No-plants, 10 cm, MDC | 10.46 | 26.49 | 99.91 | 0.02 |
| 14, 16, 18 | SS, 14 cm, MDC | 7.65 | 42.75 | 70.48 | 17.77 |
| 32, 34, 36 | SL, 14 cm, MDC | 3.20 | 63.03 | 45.56 | 38.63 |
| 50, 52, 54 | No-plants, 14 cm, MDC | 10.51 | 26.71 | 99.85 | 0.07 |
| Simulation No. (Plant Species Varying) | Fixed Variables: Substrate Depth, Rainfall Intensity, Initial Water Content | Preferential Outflow | PFI | ||
|---|---|---|---|---|---|
| Mean Values /(cm) | Cv /(%) | Mean Values /(cm) | Cv /(%) | ||
| 2, 20, 38 | 6 cm, 2 a, MDC | 6.90 | 9.02 | 91.09 | 8.83 |
| 4, 22, 40 | 6 cm, 5 a, MDC | 9.81 | 9.63 | 90.66 | 9.36 |
| 6, 24, 42 | 6 cm, 10 a, MDC | 11.95 | 9.42 | 90.43 | 9.36 |
| 8, 26, 44 | 10 cm, 2 a, MDC | 5.12 | 47.26 | 67.71 | 47.16 |
| 10, 28, 46 | 10 cm, 5 a, MDC | 7.64 | 40.04 | 70.87 | 40.60 |
| 12, 30, 48 | 10 cm, 10 a, MDC | 9.73 | 32.74 | 73.92 | 33.26 |
| 14, 32, 50 | 14 cm, 2 a, MDC | 4.81 | 53.66 | 63.46 | 53.31 |
| 16, 34, 52 | 14 cm, 5 a, MDC | 7.52 | 44.40 | 69.78 | 44.40 |
| 18, 36, 54 | 14 cm, 10 a, MDC | 10.91 | 20.76 | 82.65 | 20.62 |
| Simulation No. (Substrate Depth Varying) | Fixed Variables: Plant Species, Rainfall Intensity, Initial Water Content | Preferential Outflow | PFI | ||
|---|---|---|---|---|---|
| Mean Values /(cm) | Cv /(%) | Mean Values /(cm) | Cv /(%) | ||
| 2, 8, 14 | SS, 2 a, MDC | 5.08 | 20.01 | 67.19 | 19.98 |
| 4, 10, 16 | SS, 5 a, MDC | 8.10 | 9.72 | 75.06 | 9.69 |
| 6, 12, 18 | SS, 10 a, MDC | 10.44 | 8.88 | 78.97 | 9.03 |
| 20, 26, 32 | SL, 2 a, MDC | 3.98 | 59.91 | 52.68 | 59.78 |
| 22, 28, 34 | SL, 5 a, MDC | 6.09 | 49.60 | 56.31 | 49.73 |
| 24, 30, 36 | SL, 10 a, MDC | 8.99 | 27.10 | 68.16 | 27.08 |
| 38, 44, 50 | No-plants, 2 a, MDC | 7.58 | 0.23 | 99.91 | 0.05 |
| 40, 46, 52 | No-plants, 5 a, MDC | 10.78 | 0.58 | 99.94 | 0.05 |
| 42, 48, 54 | No-plants, 10 a, MDC | 13.16 | 0.53 | 99.87 | 0.09 |
| Simulation Conditions | Substrate Depth /(cm) | Rainfall Intensity /(a) | Initial Water Content /(%) | S | Preferential Outflow /(cm) | PFI /(%) |
|---|---|---|---|---|---|---|
| 1 | 6 | 2 | WHC | 0.05 | 7.42 | 98.27 |
| 2 | MDC | 0.05 | 7.42 | 98.27 | ||
| 3 | 5 | WHC | 0.06 | 10.62 | 98.33 | |
| 4 | MDC | 0.06 | 10.62 | 98.33 | ||
| 5 | 10 | WHC | 0.30 | 13.01 | 98.26 | |
| 6 | MDC | 0.30 | 13.01 | 98.26 | ||
| 7 | 10 | 2 | WHC | 0.05 | 7.24 | 95.81 |
| 8 | MDC | 0.05 | 7.24 | 95.81 | ||
| 9 | 5 | WHC | 0.23 | 10.36 | 95.84 | |
| 10 | MDC | 0.23 | 10.36 | 95.84 | ||
| 11 | 10 | WHC | 0.01 | 12.67 | 95.84 | |
| 12 | MDC | 0.01 | 12.67 | 95.84 | ||
| 13 | 14 | 2 | WHC | –0.61 | 7.04 | 93.09 |
| 14 | MDC | –0.61 | 7.04 | 93.09 | ||
| 15 | 5 | WHC | 0.17 | 10.05 | 93.06 | |
| 16 | MDC | 0.17 | 10.05 | 93.06 | ||
| 17 | 10 | WHC | 0.26 | 12.31 | 93.12 | |
| 18 | MDC | 0.26 | 12.31 | 93.12 |
| Sources of Variance | F Values | |
|---|---|---|
| Preferential Outflow | PFI | |
| Substrate depth | 104.095 ** | 50,845.585 ** |
| Rainfall intensity | 10,207.964 ** | 1.098 |
| Initial water content | 0.000 | 0.000 |
| Simulation No. (Rainfall Intensity Varying) | Fixed Variables: Substrate Depth, Plant Species, Initial Water Content | Preferential Outflow | PFI | ||
|---|---|---|---|---|---|
| Mean Values /(cm) | Cv /(%) | Mean Values /(cm) | Cv /(%) | ||
| 2, 4, 6 | 6 cm, no-plants, MDC | 10.35 | 27.09 | 98.29 | 0.04 |
| 8, 10, 12 | 10 cm, no-plants, MDC | 10.09 | 26.98 | 95.83 | 0.02 |
| 14, 16, 18 | 14 cm, no-plants, MDC | 9.80 | 26.97 | 93.09 | 0.03 |
| Simulation No. (Substrate Depth Varying) | Fixed Variables: Rainfall Intensity, Plant Species, Initial Water Content | Preferential Out-flow | PFI | ||
|---|---|---|---|---|---|
| Mean Values /(cm) | Cv /(%) | Mean Values /(cm) | Cv /(%) | ||
| 2, 8, 14 | 2 a, no-plants, MDC | 7.24 | 2.62 | 95.72 | 2.71 |
| 4, 10, 16 | 5 a, no-plants, MDC | 10.34 | 2.76 | 95.74 | 2.75 |
| 6, 12, 18 | 10 a, no-plants, MDC | 12.66 | 2.76 | 95.74 | 2.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liu, R.; Liu, D.; Xin, X. Analysis of Preferential Flow in Artificial Substrates with Sedum Roots for Green Roofs: Experiments and Modeling. Water 2023, 15, 914. https://doi.org/10.3390/w15050914
Chen X, Liu R, Liu D, Xin X. Analysis of Preferential Flow in Artificial Substrates with Sedum Roots for Green Roofs: Experiments and Modeling. Water. 2023; 15(5):914. https://doi.org/10.3390/w15050914
Chicago/Turabian StyleChen, Xuan, Ruifen Liu, Defu Liu, and Xiaokang Xin. 2023. "Analysis of Preferential Flow in Artificial Substrates with Sedum Roots for Green Roofs: Experiments and Modeling" Water 15, no. 5: 914. https://doi.org/10.3390/w15050914





