Forecasting the Ensemble Hydrograph of the Reservoir Inflow based on Post-Processed TIGGE Precipitation Forecasts in a Coupled Atmospheric-Hydrological System
Abstract
:1. Introduction
2. Material and Methods
2.1. Research Methodology
2.2. Case Study and Data
2.3. Post-Processing Ensemble Precipitation Forecasts
2.3.1. Multi-Model Ensemble System by the WA-WLSR Model
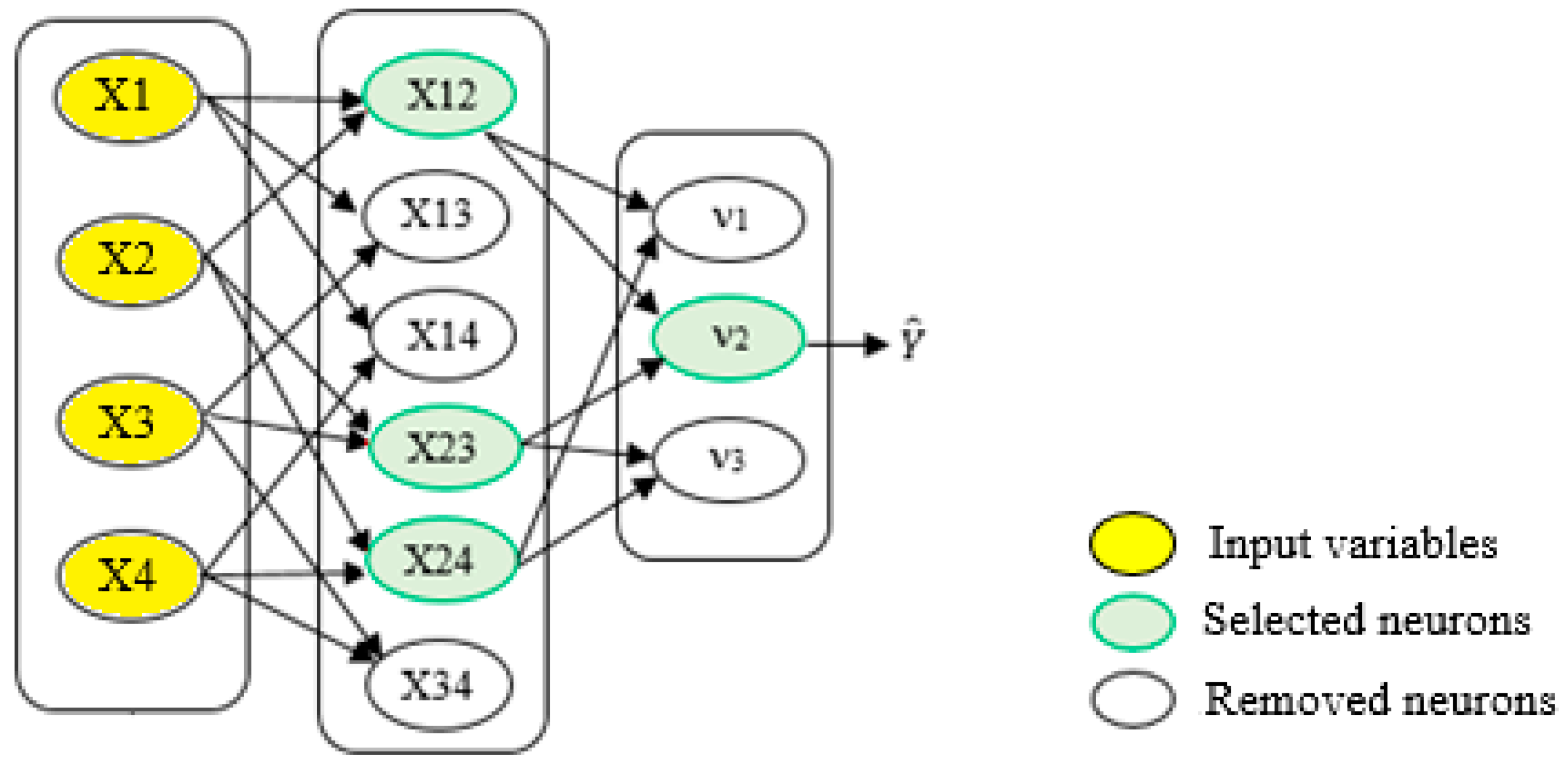
2.3.2. Multi-Model Ensemble System by the GMDH Model
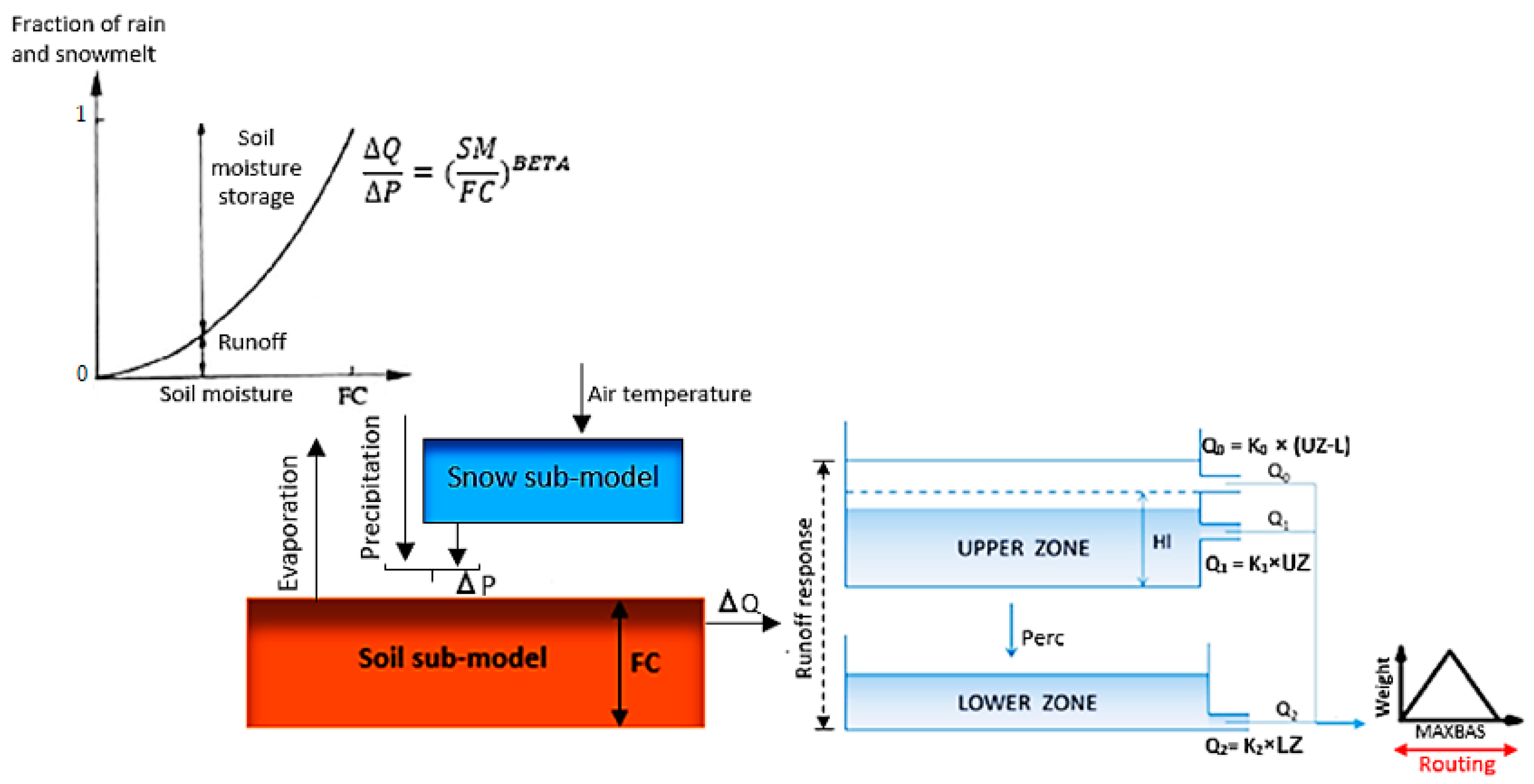
2.4. HBV Hydrological Model
2.5. Goodness-of-Fit Metrics
3. Results and Discussion
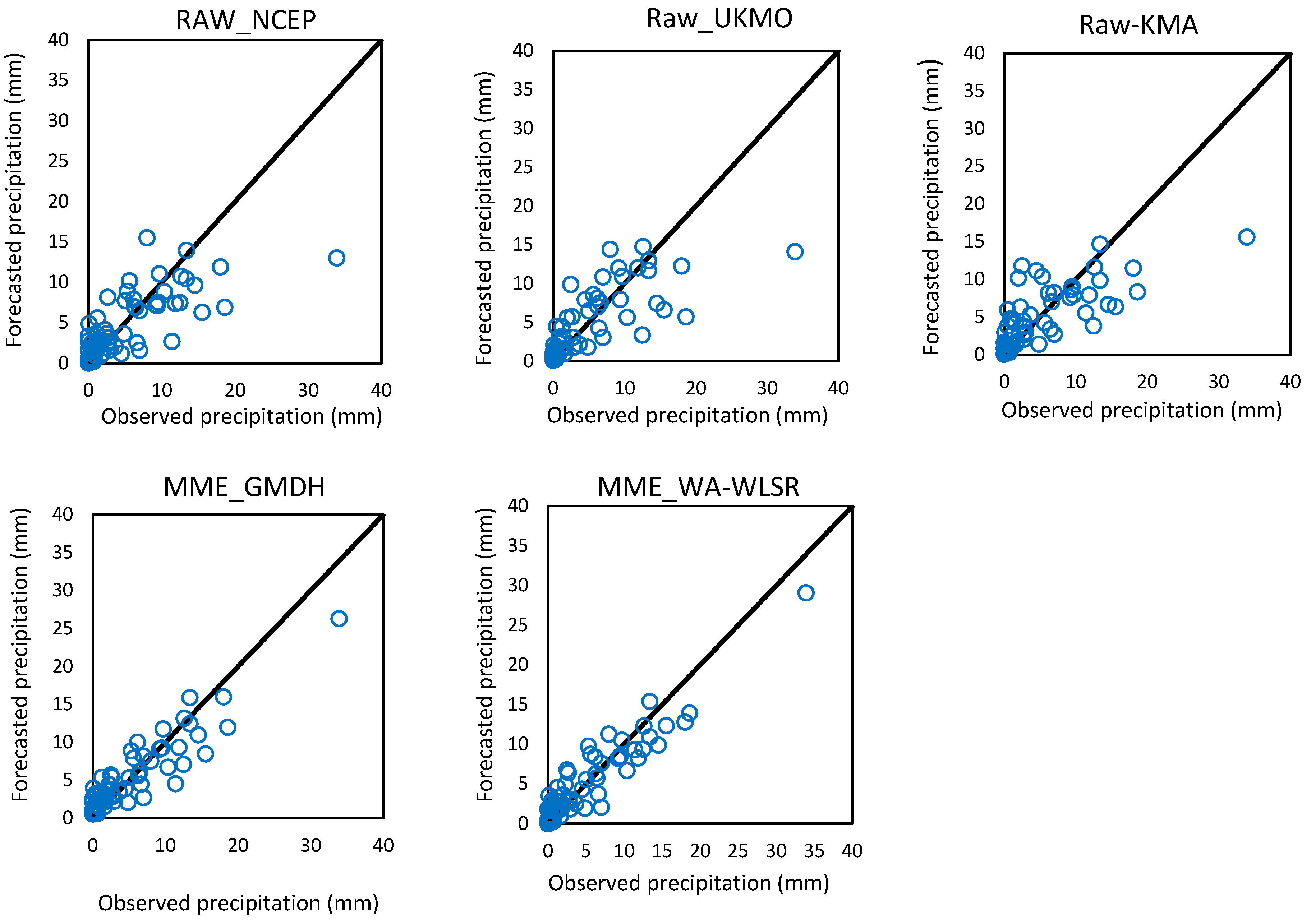
3.1. Correction of Ensemble Precipitation Forecasts
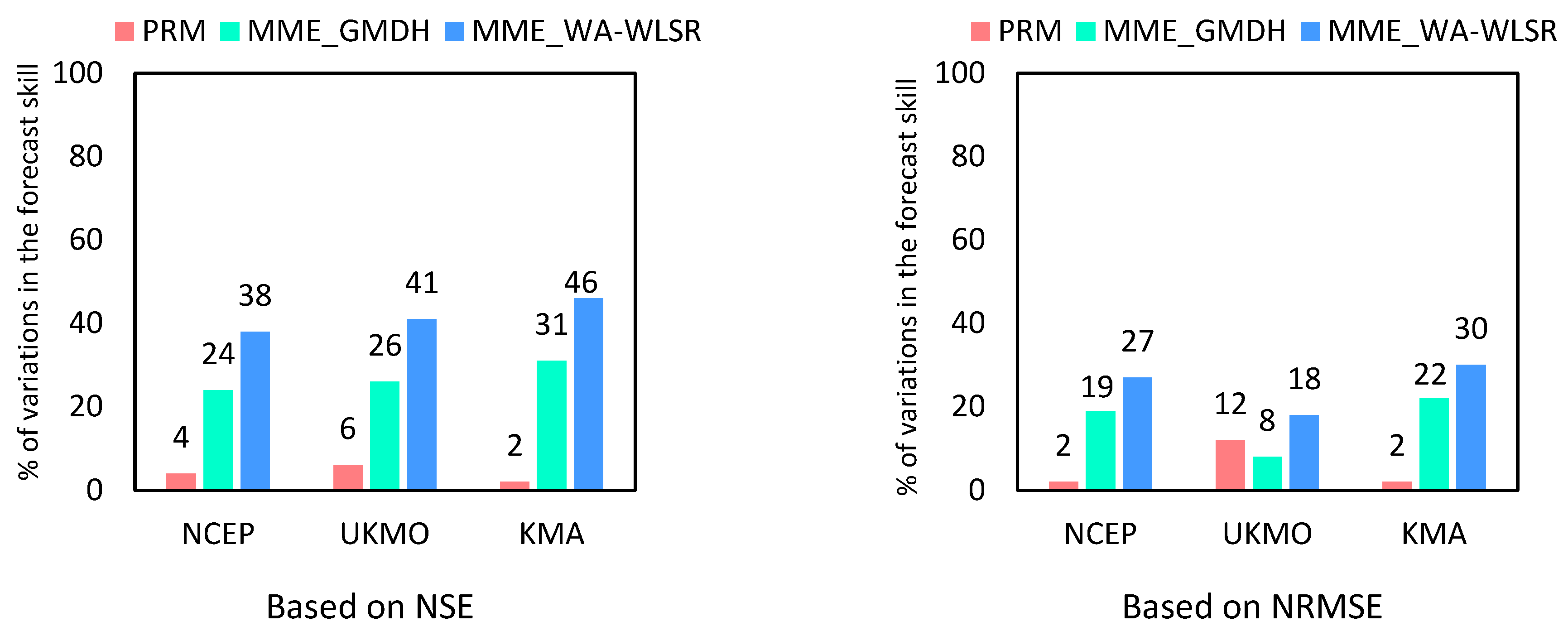
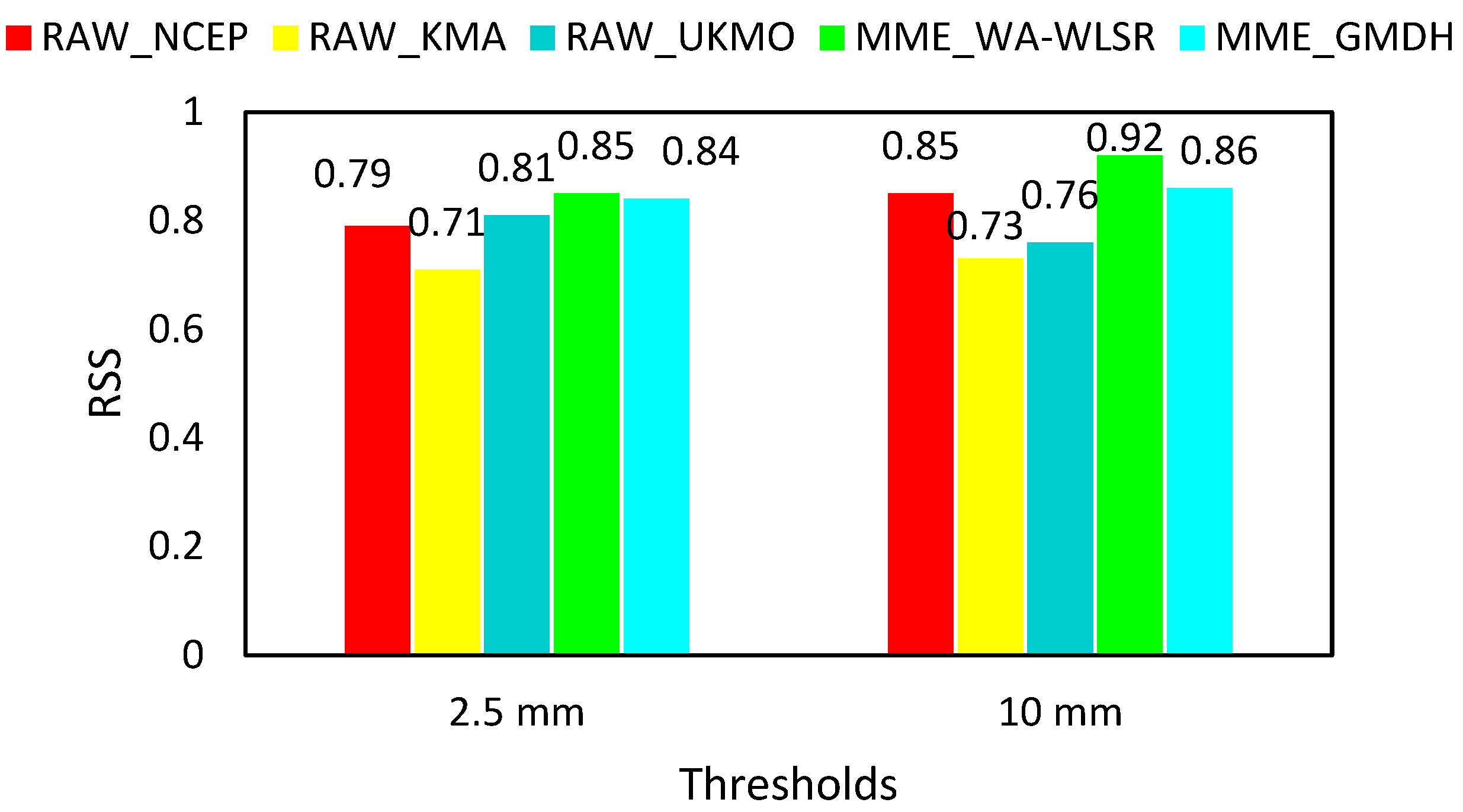
3.2. Multi-Model Ensemble Forecasts
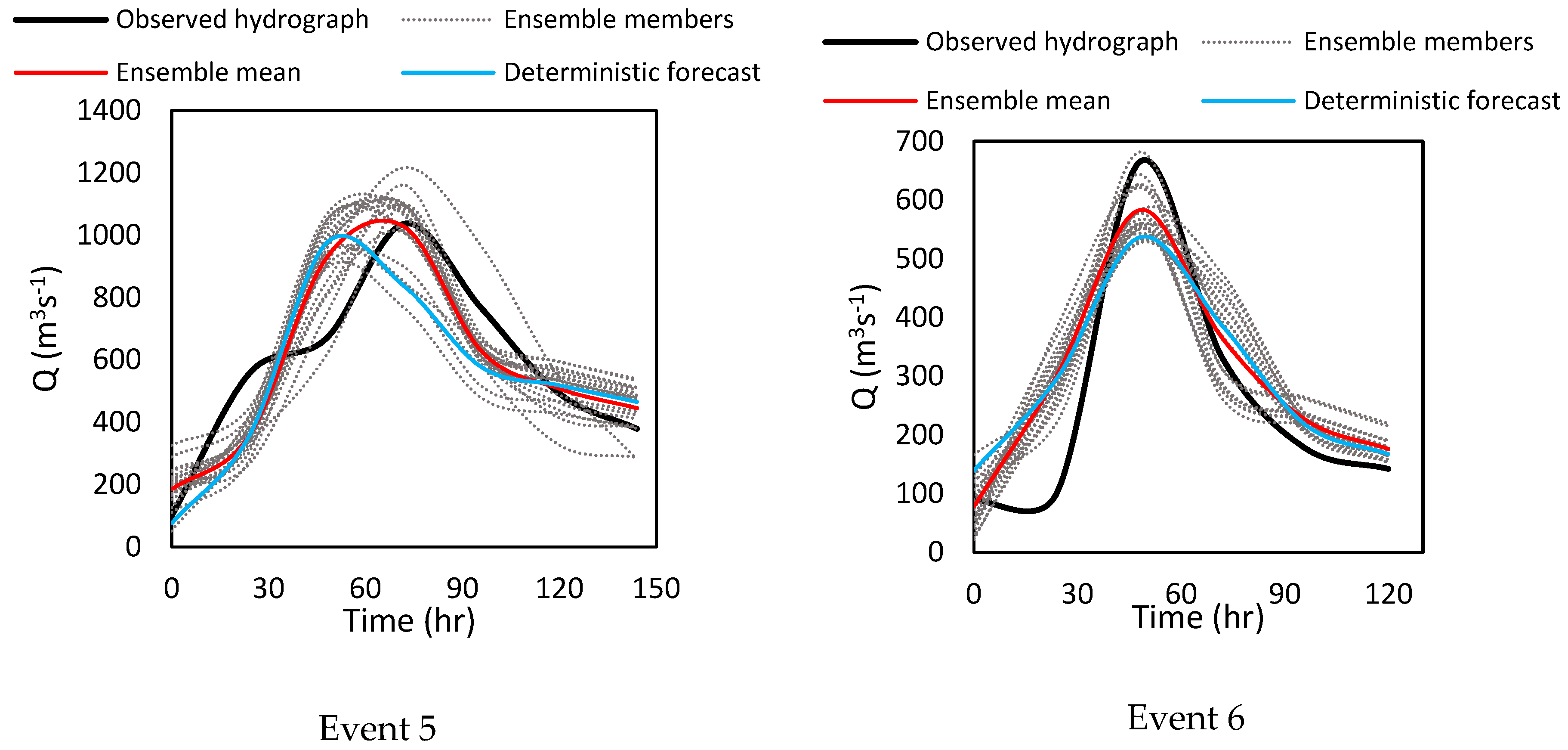
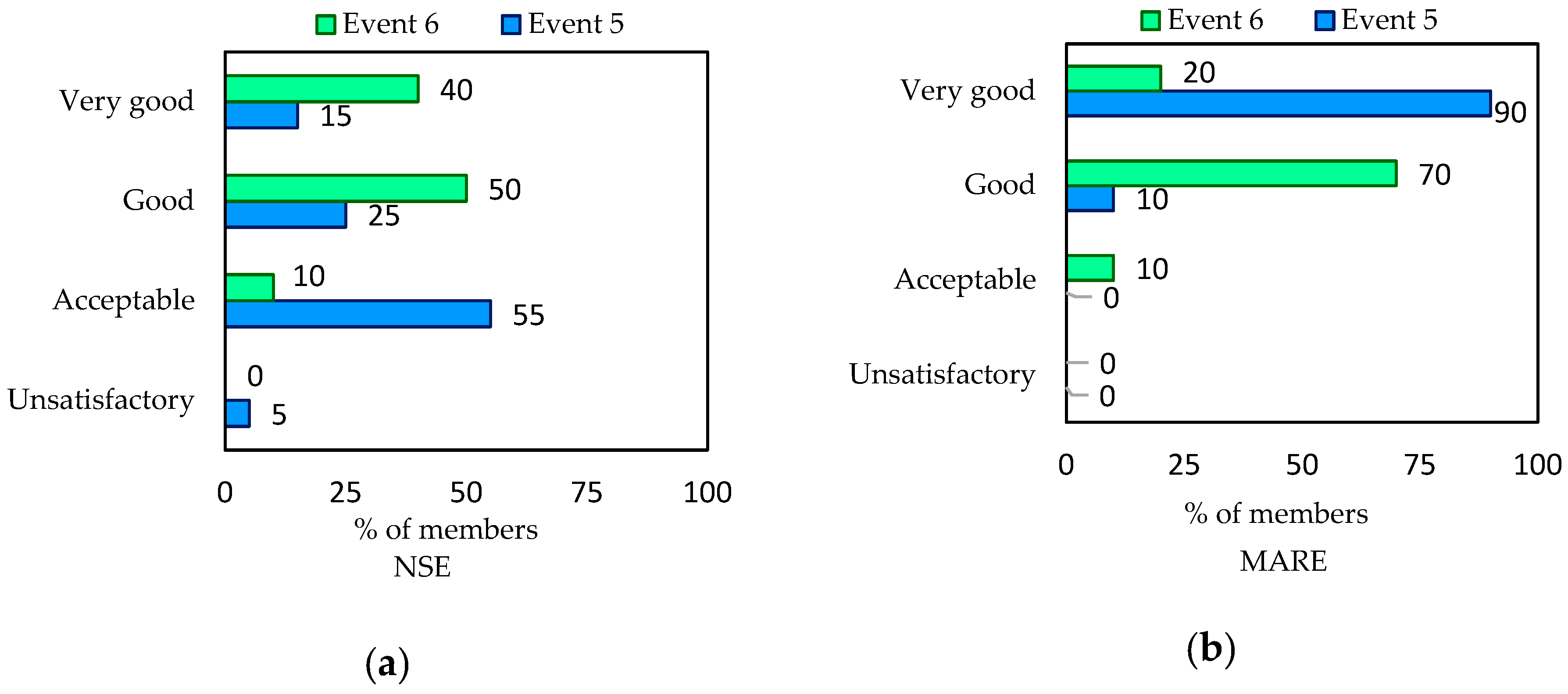
3.3. Ensemble Reservoir Inflow Forecasting
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Xu, B.; Wang, D.; Wang, Q.; Zheng, X.; Xu, J.; Zhou, F.; Huang, H.; Xu, Y. Deterministic and probabilistic evaluation of raw and post-processing monthly precipitation forecasts: A case study of China. J. Hydroinform. 2021, 23, 914–934. [Google Scholar] [CrossRef]
- Wu, L.; Seo, D.-J.; Demargne, J.; Brown, J.D.; Cong, S.; Schaake, J. Generation of ensemble precipitation forecast from single-valued quantitative precipitation forecast for hydrologic ensemble prediction. J. Hydrol. 2011, 399, 281–298. [Google Scholar] [CrossRef]
- Cloke, H.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]
- Wu, J.; Lu, G.; Wu, Z. Flood forecasts based on multi-model ensemble precipitation forecasting using a coupled atmospheric-hydrological modeling system. Nat. Hazards 2014, 74, 325–340. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Arabi, A. The impact of catchment management on emergency management of flash-flood. Int. J. Emerg. Manag. 2016, 12, 185–195. [Google Scholar] [CrossRef]
- Chang, M.-J.; Chang, H.-K.; Chen, Y.-C.; Lin, G.-F.; Chen, P.-A.; Lai, J.-S.; Tan, Y.-C. A support vector machine forecasting model for typhoon flood inundation mapping and early flood warning systems. Water 2018, 10, 1734. [Google Scholar] [CrossRef] [Green Version]
- Maddah, M.A.; Akhoond-Ali, A.M.; Ahmadi, F.; Ghafarian, P.; Rusin, I.N. Forecastability of a heavy precipitation event at different lead-times using WRF model: The case study in Karkheh River basin. Acta Geophys. 2021, 69, 1979–1995. [Google Scholar] [CrossRef]
- Nohara, D.; Nishioka, Y.; Hori, T.; Sato, Y. Real-time reservoir operation for flood management considering ensemble streamflow prediction and its uncertainty. In Advances in Hydroinformatics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 333–347. [Google Scholar]
- Jain, S.K.; Mani, P.; Jain, S.K.; Prakash, P.; Singh, V.P.; Tullos, D.; Kumar, S.; Agarwal, S.; Dimri, A. A Brief review of flood forecasting techniques and their applications. Int. J. River Basin Manag. 2018, 16, 329–344. [Google Scholar] [CrossRef]
- Wu, W.; Emerton, R.; Duan, Q.; Wood, A.W.; Wetterhall, F.; Robertson, D.E. Ensemble flood forecasting: Current status and future opportunities. Wiley Interdiscip. Rev. Water 2020, 7, e1432. [Google Scholar] [CrossRef]
- Ahmad, S.K.; Hossain, F. Maximizing energy production from hydropower dams using short-term weather forecasts. Renew. Energy 2020, 146, 1560–1577. [Google Scholar] [CrossRef]
- Emerton, R.E.; Stephens, E.M.; Pappenberger, F.; Pagano, T.C.; Weerts, A.H.; Wood, A.W.; Salamon, P.; Brown, J.D.; Hjerdt, N.; Donnelly, C. Continental and global scale flood forecasting systems. Wiley Interdiscip. Rev. Water 2016, 3, 391–418. [Google Scholar] [CrossRef] [Green Version]
- Rani, S.I.; Sharma, P.; George, J.P.; Das Gupta, M. Assimilation of individual components of radiosonde winds: An investigation to assess the impact of single-component winds from space-borne measurements on NWP. J. Earth Syst. Sci. 2021, 130, 89. [Google Scholar] [CrossRef]
- Chen, G.; Hou, J.; Zhou, N.; Yang, S.; Tong, Y.; Su, F.; Huang, L.; Bi, X. High-Resolution Urban Flood Forecasting by Using a Coupled Atmospheric and Hydrodynamic Flood Models. Front. Earth Sci. 2020, 8, 545612. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Yan, D.; Ding, L.; Li, C. Ensemble flood forecasting based on a coupled atmospheric-hydrological modeling system with data assimilation. Atmos. Res. 2019, 224, 127–137. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, J.; Lu, G. A one-way coupled atmospheric-hydrological modeling system with combination of high-resolution and ensemble precipitation forecasting. Front. Earth Sci. 2016, 10, 432–443. [Google Scholar] [CrossRef]
- Bourdin, D.R.; Stull, R.B. Bias-corrected short-range Member-to-Member ensemble forecasts of reservoir inflow. J. Hydrol. 2013, 502, 77–88. [Google Scholar] [CrossRef]
- Tao, Y.; Duan, Q.; Ye, A.; Gong, W.; Di, Z.; Xiao, M.; Hsu, K. An evaluation of post-processed TIGGE multimodel ensemble precipitation forecast in the Huai river basin. J. Hydrol. 2014, 519, 2890–2905. [Google Scholar] [CrossRef] [Green Version]
- Daoud, A.B.; Sauquet, E.; Bontron, G.; Obled, C.; Lang, M. Daily quantitative precipitation forecasts based on the analogue method: Improvements and application to a French large river basin. Atmos. Res. 2016, 169, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Amini, S.; Azizian, A.; Daneshkar Arasteh, P. How reliable are TIGGE daily deterministic precipitation forecasts over different climate and topographic conditions of Iran? Meteorol. Appl. 2021, 28, e2013. [Google Scholar] [CrossRef]
- Flowerdew, J. Calibrating ensemble reliability whilst preserving spatial structure. Tellus A Dyn. Meteorol. Oceanogr. 2014, 66, 22662. [Google Scholar] [CrossRef] [Green Version]
- Piani, C.; Haerter, J.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Wang, Q.J.; Wu, W.; Yang, Q. Power transformation of variables for post-processing precipitation forecasts: Regionally versus locally optimized parameter values. J. Hydrol. 2022, 610, 127912. [Google Scholar] [CrossRef]
- Manzanas, R.; Gutiérrez, J.M.; Bhend, J.; Hemri, S.; Doblas-Reyes, F.J.; Torralba, V.; Penabad, E.; Brookshaw, A. Bias adjustment and ensemble recalibration methods for seasonal forecasting: A comprehensive intercomparison using the C3S dataset. Clim. Dyn. 2019, 53, 1287–1305. [Google Scholar] [CrossRef]
- Barnes, C.; Brierley, C.M.; Chandler, R.E. New approaches to postprocessing of multi-model ensemble forecasts. Q. J. R. Meteorol. Soc. 2019, 145, 3479–3498. [Google Scholar] [CrossRef]
- Palmer, T.N.; Alessandri, A.; Andersen, U.; Cantelaube, P.; Davey, M.; Delécluse, P.; Déqué, M.; Diez, E.; Doblas-Reyes, F.J.; Feddersen, H. Development of a European multimodel ensemble system for seasonal-to-interannual prediction (DEMETER). Bull. Am. Meteorol. Soc. 2004, 85, 853–872. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Sun, X.; Sun, J.; Yin, J.; Sun, J.; Liu, C. A Comparative Study of Multi-Model Ensemble Forecasting Accuracy between Equal-and Variant-Weight Techniques. Atmosphere 2022, 13, 526. [Google Scholar] [CrossRef]
- Medina, H.; Tian, D.; Srivastava, P.; Pelosi, A.; Chirico, G.B. Medium-range reference evapotranspiration forecasts for the contiguous United States based on multi-model numerical weather predictions. J. Hydrol. 2018, 562, 502–517. [Google Scholar] [CrossRef]
- Pakdaman, M.; Babaeian, I.; Bouwer, L.M. Improved Monthly and Seasonal Multi-Model Ensemble Precipitation Forecasts in Southwest Asia Using Machine Learning Algorithms. Water 2022, 14, 2632. [Google Scholar] [CrossRef]
- Baran, S. Probabilistic wind speed forecasting using Bayesian model averaging with truncated normal components. Comput. Stat. Data Anal. 2014, 75, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Han, K.; Choi, J.; Kim, C. Comparison of statistical post-processing methods for probabilistic wind speed forecasting. Asia-Pac. J. Atmos. Sci. 2018, 54, 91–101. [Google Scholar] [CrossRef]
- Lee, J.A.; Kolczynski, W.C.; McCandless, T.C.; Haupt, S.E. An objective methodology for configuring and down-selecting an NWP ensemble for low-level wind prediction. Mon. Weather Rev. 2012, 140, 2270–2286. [Google Scholar] [CrossRef]
- Saedi, A.; Saghafian, B.; Moazami, S.; Aminyavari, S. Performance evaluation of sub-daily ensemble precipitation forecasts. Meteorol. Appl. 2020, 27, e1872. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Yang, T.; Li, X.; Shi, P.; Zhou, X. Spatio-temporal changes of precipitation and temperature over the Pearl River basin based on CMIP5 multi-model ensemble. Stoch. Environ. Res. Risk Assess. 2017, 31, 1077–1089. [Google Scholar] [CrossRef]
- Aminyavari, S.; Saghafian, B. Probabilistic streamflow forecast based on spatial post-processing of TIGGE precipitation forecasts. Stoch. Environ. Res. Risk Assess. 2019, 33, 1939–1950. [Google Scholar] [CrossRef]
- Yang, S.-C.; Yang, T.-H. Uncertainty assessment: Reservoir inflow forecasting with ensemble precipitation forecasts and HEC-HMS. Adv. Meteorol. 2014, 2014, 581756. [Google Scholar] [CrossRef] [Green Version]
- Banihabib, M.E.; Bandari, R.; Valipour, M. Improving daily peak flow forecasts using hybrid Fourier-series autoregressive integrated moving average and recurrent artificial neural network models. AI 2020, 1, 17. [Google Scholar] [CrossRef]
- Malekmohammadi, B.; Zahraie, B.; Kerachian, R. A real-time operation optimization model for flood management in river-reservoir systems. Nat. Hazards 2010, 53, 459–482. [Google Scholar] [CrossRef]
- Goodarzi, L.; Banihabib, M.E.; Roozbahani, A. A decision-making model for flood warning system based on ensemble forecasts. J. Hydrol. 2019, 573, 207–219. [Google Scholar] [CrossRef]
- Shope, C.L.; Maharjan, G.R. Modeling spatiotemporal precipitation: Effects of density, interpolation, and land use distribution. Adv. Meteorol. 2015, 2015, 174196. [Google Scholar] [CrossRef] [Green Version]
- Tanhapour, M.; Hlavčová, K.; Soltani, J.; Liová, A.; Malekmohammadi, B. Sensitivity analysis and assessment of the performance of the HBV hydrological model for simulating reservoir inflow hydrograph. In Proceedings of the 16th Annual International Scientific Conference, Science of Youth, Banská Štiavnica, Slovakia, 1–3 June 2022; pp. 115–124. [Google Scholar]
- Mazăre, R.; Borbely, L.; Ghenț, L.; Ienciu, A.; Manea, D. Studies on water requirements in corn crops under the conditions of Arad. Res. J. Agric. Sci. 2018, 50, 413–419. [Google Scholar]
- Theocharides, S.; Makrides, G.; Livera, A.; Theristis, M.; Kaimakis, P.; Georghiou, G.E. Day-ahead photovoltaic power production forecasting methodology based on machine learning and statistical post-processing. Appl. Energy 2020, 268, 115023. [Google Scholar] [CrossRef]
- Liao, W.; Lei, X. Multi-model Combination Techniques for Flood Forecasting from the Distributed Hydrological Model EasyDHM. In Proceedings of the International Symposium on Intelligence Computation and Applications, Wuhan, China, 27–28 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 396–402. [Google Scholar]
- Fathi, M.; Azadi, M.; Kamali, G.; Meshkatee, A.H. Improving precipitation forecasts over Iran using a weighted average ensemble technique. J. Earth Syst. Sci. 2019, 128, 133. [Google Scholar] [CrossRef] [Green Version]
- Hughes, C.E.; Crawford, J. A new precipitation weighted method for determining the meteoric water line for hydrological applications demonstrated using Australian and global GNIP data. J. Hydrol. 2012, 464, 344–351. [Google Scholar] [CrossRef]
- Mutiu, O.S. Application of weighted least squares regression in forecasting. Int. J. Recent. Res. Interdiscip. Sci 2015, 2, 45–54. [Google Scholar]
- Dodangeh, E.; Panahi, M.; Rezaie, F.; Lee, S.; Bui, D.T.; Lee, C.-W.; Pradhan, B. Novel hybrid intelligence models for flood-susceptibility prediction: Meta optimization of the GMDH and SVR models with the genetic algorithm and harmony search. J. Hydrol. 2020, 590, 125423. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Parmar, K.S.; Soni, K.; Kisi, O. Modeling monthly streamflow in mountainous basin by MARS, GMDH-NN and DENFIS using hydroclimatic data. Neural Comput. Appl. 2021, 33, 2853–2871. [Google Scholar] [CrossRef]
- Shaghaghi, S.; Bonakdari, H.; Gholami, A.; Ebtehaj, I.; Zeinolabedini, M. Comparative analysis of GMDH neural network based on genetic algorithm and particle swarm optimization in stable channel design. Appl. Math. Comput. 2017, 313, 271–286. [Google Scholar] [CrossRef]
- Chang, F.J.; Hwang, Y.Y. A self-organization algorithm for real-time flood forecast. Hydrol. Process. 1999, 13, 123–138. [Google Scholar] [CrossRef]
- Parra, V.; Fuentes-Aguilera, P.; Muñoz, E. Identifying advantages and drawbacks of two hydrological models based on a sensitivity analysis: A study in two Chilean watersheds. Hydrol. Sci. J. 2018, 63, 1831–1843. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. Uncertainty and multiple objective calibration in regional water balance modelling: Case study in 320 Austrian catchments. Hydrol. Process. Int. J. 2007, 21, 435–446. [Google Scholar] [CrossRef]
- Valent, P.; Szolgay, J.; Riverso, C. Assessment of the uncertainties of a conceptual hydrologic model by using artificially generated flows. Slovak J. Civ. Eng. 2012, 20, 35. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Hossain, S.; Hewa, G.A.; Wella-Hewage, S. A comparison of continuous and event-based rainfall–runoff (RR) modelling using EPA-SWMM. Water 2019, 11, 611. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.; Wilson, B.; Douglas-Mankin, K.; Arnold, J.; Gowda, P. Hydrologic and water quality models: Use, calibration, and validation. Trans. ASABE 2012, 55, 1241–1247. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- D’onofrio, A.; Boulanger, J.-P.; Segura, E.C. CHAC: A weather pattern classification system for regional climate downscaling of daily precipitation. Clim. Chang. 2010, 98, 405–427. [Google Scholar] [CrossRef]
- Zakeri, Z.; Azadi, M.; Sahraeiyan, F. Verification of WRF forecasts for precipitation over Iran in the period Feb–May 2009. Nivar 2014, 38, 3–10. [Google Scholar]
- Hagedorn, R.; Doblas-Reyes, F.J.; Palmer, T.N. The rationale behind the success of multi-model ensembles in seasonal forecasting—I. Basic concept. Tellus A Dyn. Meteorol. Oceanogr. 2005, 57, 219–233. [Google Scholar]
- Ren, H.-L.; Wu, Y.; Bao, Q.; Ma, J.; Liu, C.; Wan, J.; Li, Q.; Wu, X.; Liu, Y.; Tian, B. The China multi-model ensemble prediction system and its application to flood-season prediction in 2018. J. Meteorol. Res. 2019, 33, 540–552. [Google Scholar] [CrossRef]
- Krishnamurti, T.; Sagadevan, A.; Chakraborty, A.; Mishra, A.; Simon, A. Improving multimodel weather forecast of monsoon rain over China using FSU superensemble. Adv. Atmos. Sci. 2009, 26, 813–839. [Google Scholar] [CrossRef]
- Davolio, S.; Miglietta, M.; Diomede, T.; Marsigli, C.; Morgillo, A.; Moscatello, A. A meteo-hydrological prediction system based on a multi-model approach for precipitation forecasting. Nat. Hazards Earth Syst. Sci. 2008, 8, 143–159. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, Q.; Li, X.; Sun, Y.; Hu, C. Comparison of different ensemble precipitation forecast system evaluation, integration and hydrological applications. Acta Geophys. 2022, 71, 405–421. [Google Scholar] [CrossRef]
- Yin, J.; Hao, Y.; Samawi, H.; Rochani, H. Rank-based kernel estimation of the area under the ROC curve. Stat. Methodol. 2016, 32, 91–106. [Google Scholar] [CrossRef]
- Javanshiri, Z.; Fathi, M.; Mohammadi, S.A. Comparison of the BMA and EMOS statistical methods for probabilistic quantitative precipitation forecasting. Meteorol. Appl. 2021, 28, e1974. [Google Scholar] [CrossRef]
- Ye, J.; Shao, Y.; Li, Z. Flood forecasting based on TIGGE precipitation ensemble forecast. Adv. Meteorol. 2016, 2016, 9129734. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S. Hydrologic Ensemble Predictions Using Ensemble Meteorological Forecasts. Ph.D. thesis, McMaster Univercity, Hamilton, ON, Canada, 2010; p. 91. [Google Scholar]
- Ferretti, R.; Lombardi, A.; Tomassetti, B.; Sangelantoni, L.; Colaiuda, V.; Mazzarella, V.; Maiello, I.; Verdecchia, M.; Redaelli, G. Regional ensemble forecast for early warning system over small Apennine catchments on Central Italy. Hydrol. Earth Syst. Sci. Discuss 2019, 1–25. [Google Scholar] [CrossRef]
- Jie, W.; Wu, T.; Wang, J.; Li, W.; Polivka, T. Using a deterministic time-lagged ensemble forecast with a probabilistic threshold for improving 6–15 day summer precipitation prediction in China. Atmos. Res. 2015, 156, 142–159. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Wang, L.; Zhou, H.; Saavedra Valeriano, O.C.; Koike, T.; Li, W. Ensemble hydrological prediction-based real-time optimization of a multiobjective reservoir during flood season in a semiarid basin with global numerical weather predictions. Water Resour. Res. 2012, 48, 1–21. [Google Scholar] [CrossRef]
- Ran, Q.; Fu, W.; Liu, Y.; Li, T.; Shi, K.; Sivakumar, B. Evaluation of quantitative precipitation predictions by ECMWF, CMA, and UKMO for flood forecasting: Application to two basins in China. Nat. Hazards Rev. 2018, 19, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Yuan, H.; Su, X. Bias correction of ensemble precipitation forecasts in the improvement of summer streamflow prediction skill. J. Hydrol. 2020, 588, 124955. [Google Scholar] [CrossRef]




| Event No | Date of Events | Peak Discharge (m3/s) | Time (h) | Precipitation Depth (mm) |
|---|---|---|---|---|
| 1 | 29.01.2013 | 633 | 48 | 31.33 |
| 2 | 24.03.2017 | 1307 | 72 | 37.93 |
| 3 | 25.02.2018 | 622 | 72 | 19.67 |
| 4 | 01.04.2019 | 5222 | 48 | 104.39 |
| 5 | 28.12.2016 | 1037 | 84 | 101.26 |
| 6 | 18.02.2018 | 665 | 72 | 48.8 |
| Center | Forecast Length (Day) | Model Resolution (lon × lat) | Number of Ensemble Members | Base Time (UTC) |
|---|---|---|---|---|
| NCEP | 16 | 1.00° × 1.00° | 20 | 00/06/12/18 |
| UKMO | 15 | 0.83° × 0.56° | 23 | 00/12 |
| KMA | 10 | 1.00° × 1.00° | 24 | 00/12 |
| Sub-Models | Parameters | Description of the Parameters | Range |
|---|---|---|---|
| Snow | Tr | Temperature threshold above which precipitation is liquid [°C] | 0–2 |
| Ts | Temperature threshold below which precipitation is solid [°C] | −2–0 | |
| Tm | Temperature threshold above which snowmelt starts [°C] | −2–2 | |
| DDF | Degree-day factor determines the speed of the snow melting [mm/°C/day] | 1–5 | |
| SCF | Factor for correcting snow measurements [-] | 1–1.6 | |
| Soil moisture | FC | Field capacity- maximum soil moisture storage [mm] | 100–250 |
| Lp | A limit for potential evapotranspiration [-] | 0.5–1 | |
| BETA | Coefficient influencing the amount of water caused by soil moisture and the upper reservoir [-] | 0.1–2.5 | |
| Runoff response | perc | Constant percolation rate from the upper to the bottom reservoir [mm] | 0.5–4 |
| L | Threshold storage state for initiating very fast surface runoff [mm] | 10–60 | |
| K0 | The recession coefficients associated with the surface (K0), sub-surface (K1), and base flow (K2) [-] | 1–5 | |
| K1 | 5–30 | ||
| K2 | 30–120 | ||
| Maxbas | The parameter for runoff routing [-] | 1–6 |
| Goodness-of-Fit Metrics | Equation | Description | Best Fit/Poorest Fit |
|---|---|---|---|
| Nash-Sutcliffe Efficiency | Measure of the relative magnitude of the residual variance compared with the observed data variance | 1/−∞ | |
| Kling-Gupta Efficiency | A function of correlation, bias, and variability to ensure that the bias and variability ratios are not cross-correlated | 1/−∞ | |
| Pearson coefficient | The capability of a linear relationship between observed and forecasted data | 1/−1 | |
| Normalized Root Mean Square Error | The difference between observed and forecasted data | 0/ | |
| Mean Absolute Error | The difference between observed and forecasted data | 0/ | |
| Mean Absolute Relative Error | The difference between observed and forecasted data | 0/ |
| Model’s Efficiency | The Range of Goodness-of-Fit Criteria | |
|---|---|---|
| Very good | NSE, KGE > 0.75 | MARE < 0.5 |
| Good | 0.65 < NSE, KGE < 0.75 | 0.5 < MARE < 0.6 |
| Acceptable | 0.5 < NSE, KGE < 0.65 | 0.6 < MARE < 0.7 |
| Unsatisfactory | NSE < 0.5 | MARE > 0.7 |
| Observed | Occurrence | Non-Occurrence | Total | |
|---|---|---|---|---|
| Forecasted | ||||
| Alarm | H | FA | A | |
| No-Alarm | MA | CN | A’ | |
| Total | O | O’ | N | |
| NWP Models | Linear Regression Models | Goodness-of-Fit Metrics | |||
|---|---|---|---|---|---|
| Train | Test | ||||
| NSE | MAE | NSE | MAE | ||
| NCEP | 0.531 | 2.838 | 0.651 | 2.108 | |
| KMA | 0.518 | 3.115 | 0.51 | 2.725 | |
| UKMO | 0.473 | 2.704 | 0.462 | 2.671 | |
| NWP Models | Power Regression Models | Goodness-of-Fit Metrics | |||
|---|---|---|---|---|---|
| Train | Test | ||||
| NSE | MAE | NSE | MAE | ||
| NCEP | 0.532 | 2.816 | 0.651 | 2.107 | |
| KMA | 0.53 | 2.972 | 0.5 | 2.658 | |
| UKMO | 0.541 | 2.701 | 0.513 | 2.682 | |
| Goodness-of-Fit Metrics | NCEP | KMA | UKMO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Raw | Corrected-PRM | The Percentage of Variations | Raw | Corrected-PRM | The Percentage of Variations | Raw | Corrected-PRM | The Percentage of Variations | |
| NSE | 0.53 | 0.55 | +4 | 0.51 | 0.52 | +2 | 0.51 | 0.54 | +6 |
| KGE | 0.54 | 0.65 | +20 | 0.53 | 0.65 | +23 | 0.56 | 0.58 | +4 |
| Pearson correlation | 0.74 | 0.74 | 0 | 0.72 | 0.72 | 0 | 0.72 | 0.75 | +4 |
| NRMSE | 0.82 | 0.8 | −2 | 0.85 | 0.83 | −2.3 | 0.81 | 0.71 | −12 |
| MAE | 2.57 | 2.18 | −15 | 2.85 | 2.62 | −8 | 2.78 | 2.21 | −20 |
| Goodness-of-Fit Metrics | GMDH | WA-WLSR | ||
|---|---|---|---|---|
| Train Data | Test Data | All Data | ||
| NSE | 0.68 | 0.65 | 0.68 | 0.76 |
| KGE | 0.75 | 0.68 | 0.73 | 0.73 |
| Pearson correlation | 0.82 | 0.83 | 0.82 | 0.88 |
| NRMSE | 0.63 | 0.64 | 0.65 | 0.58 |
| MAE | 2.15 | 2.18 | 2.11 | 2.02 |
| Goodness-of-Fit Metrics | Modeling Approach | Flood Events | |||
|---|---|---|---|---|---|
| Event 1 | Event 2 | Event 3 | Event 4 | ||
| NSE | Ensemble members | 0.93 | 0.82 | 0.92 | 0.79 |
| Ensemble-mean | 0.97 | 0.88 | 0.97 | 0.81 | |
| Deterministic forecasts | 0.9 | 0.81 | 0.86 | 0.79 | |
| KGE | Ensemble members | 0.92 | 0.83 | 0.88 | 0.7 |
| Ensemble-mean | 0.97 | 0.89 | 0.94 | 0.71 | |
| Deterministic forecasts | 0.89 | 0.7 | 0.83 | 0.68 | |
| MARE | Ensemble members | 0.14 | 0.12 | 0.14 | 0.65 |
| Ensemble-mean | 0.11 | 0.09 | 0.08 | 0.63 | |
| Deterministic forecasts | 0.17 | 0.11 | 0.24 | 0.78 | |
| Goodness-of-Fit Metrics | Modeling Approach | Flood Events | |
|---|---|---|---|
| Event 5 | Event 6 | ||
| NSE | Ensemble members | 0.65 | 0.74 |
| Ensemble-mean | 0.74 | 0.79 | |
| Deterministic forecasts | 0.6 | 0.73 | |
| KGE | Ensemble members | 0.78 | 0.71 |
| Ensemble-mean | 0.87 | 0.73 | |
| Deterministic forecasts | 0.75 | 0.63 | |
| MARE | Ensemble members | 0.35 | 0.53 |
| Ensemble-mean | 0.3 | 0.47 | |
| Deterministic forecasts | 0.34 | 0.54 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanhapour, M.; Soltani, J.; Malekmohammadi, B.; Hlavcova, K.; Kohnova, S.; Petrakova, Z.; Lotfi, S. Forecasting the Ensemble Hydrograph of the Reservoir Inflow based on Post-Processed TIGGE Precipitation Forecasts in a Coupled Atmospheric-Hydrological System. Water 2023, 15, 887. https://doi.org/10.3390/w15050887
Tanhapour M, Soltani J, Malekmohammadi B, Hlavcova K, Kohnova S, Petrakova Z, Lotfi S. Forecasting the Ensemble Hydrograph of the Reservoir Inflow based on Post-Processed TIGGE Precipitation Forecasts in a Coupled Atmospheric-Hydrological System. Water. 2023; 15(5):887. https://doi.org/10.3390/w15050887
Chicago/Turabian StyleTanhapour, Mitra, Jaber Soltani, Bahram Malekmohammadi, Kamila Hlavcova, Silvia Kohnova, Zora Petrakova, and Saeed Lotfi. 2023. "Forecasting the Ensemble Hydrograph of the Reservoir Inflow based on Post-Processed TIGGE Precipitation Forecasts in a Coupled Atmospheric-Hydrological System" Water 15, no. 5: 887. https://doi.org/10.3390/w15050887








