1. Introduction
The impact of the dilution of sewage as a result of inflow and infiltration (I&I), also known as extraneous water or parasitic flows, has been the focus of numerous studies [
1,
2,
3,
4,
5,
6,
7]. Large amounts of I&I can adversely affect the performance of urban drainage systems in many ways, such as hydraulic overloading, increased risk of CSO spills, decreased WWTP performance, increased energy consumption, and risk of structural damage [
6,
8,
9,
10]. In order to predict and mitigate these adverse effects, it is important to be able to identify the sources and locations of I&I flows and quantify their contribution to the total sewage flows.
The identification of sources and locations of I&I flows is mostly performed by tracing experiments (isotope analysis, conductivity) [
11,
12,
13,
14,
15,
16] or the systematic analysis of asset inspections [
17,
18]. If one has a well-delineated and restricted survey area, specific detection measurements such as DTS (Distributed Temperature Sensing) [
19,
20,
21], smoke tests, or CCTV [
22] can also be applied. For an overview of the advantages and disadvantages of each one of these methods, see [
23].
The quantification of I&I flows is mostly performed using some type of hydrograph decomposition method, by which measured flows are split into three fractions: a pure wastewater fraction, a direct stormwater runoff fraction, and an I&I fraction. Such methods range from detailed hydrodynamic models [
24] over conceptual hydrologic models [
25] to simple triangulation methods [
26,
27]. The temporal resolution of the output varies from daily to annual average percentages of the different fractions. Depending on the method used, the I&I fraction may be further split into groundwater infiltration, with a typical rainfall response time of several weeks, and surface water inflow, with a typical rainfall response time of several days [
28]. Other inflows such as pumped groundwater drainage from construction sites have no relation to rainfall and therefore cannot be easily identified by rainfall-based models.
In most cases, the decision on which method to use will depend on the availability and resolution of flow and rainfall data [
29]. Unless dedicated medium- to long-term flow measurement campaigns are undertaken, the availability of continuous flow data in most urban drainage areas is limited to one or a few key locations in the downstream part of the system, e.g., at the inlet of the treatment plant [
3,
4,
7,
30]. Especially in catchments with a downstream concentration time of more than about 6 h, and/or in catchments with multiple pumping stations in series, downstream locations have the disadvantage of flows being highly attenuated. This makes it more difficult to clearly distinguish between contributing I&I flows from different parts of the catchment and with different natures and response times. Therefore, most hydrograph decomposition methods are based on daily aggregates of the measured flows [
25,
27,
31].
If no specific detection measures can be undertaken to locate I&I sources, and I&I flows can be quantified at only one location, proposals for mitigation measures will inevitably be based on the assumption of spatial homogeneity of the contribution of I&I flows. Therefore a proper cost–benefit and risk assessment of such measures [
32,
33] will be necessary.
Finding appropriate locations for high-quality permanent flow measurements in sewer systems is not obvious, and maintaining them over a longer period is labour-intensive and hence expensive [
34,
35]. An alternative way to increase the number of locations with suitable flow measurements is to calculate or derive flows from other types of measurements. Pumping stations are the preferred alternative location for this because data are generally already available at low or no additional cost. Furthermore, classic flow monitoring in the vicinity of pumping stations is often difficult or impossible because of their high impact on the hydraulic behaviour of the surrounding system. All these factors contribute to the added value of developing a methodology for alternative flow analysis.
If the pumped flows through the rising mains are measured (e.g., by means of an electromagnetic flow meter), these flows can be aggregated to hourly or daily values to reproduce the incoming flows. If no pumped flows are measured, different methods can be applied to calculate incoming flows from data logged by the pumping station’s SCADA (Supervisory Control And Data Acquisition) system (e.g., pump switch registrations, water levels, power consumption, etc.) [
2,
36,
37].
In this paper, a novel methodology for flow calculation is presented that combines and extends some of the existing methods using both instantaneous recordings of the pumps’ switch-on/-off timestamps and fixed timestep level measurements. By systematically applying this methodology at all pumping stations in an urban drainage area, the knowledge of and insight into the spatial and temporal distribution of I&I flows in that area can be increased.
2. Materials and Methods
The methodology proposed in this paper consists of three phases, as shown in
Figure 1: (1) an inventory of the configuration and the operational modes of the pumping station; (2) a data preprocessing phase; (3) an iterative calculation of average incoming and outgoing flows for all dry weather cycles. In the following paragraphs, the different phases are explained in more detail.
Throughout the methodology, the term “dry weather” should not be seen as a strictly meteorological condition but as a situation during which the water level in the pumping station is not exceeding the lowest switch-on level. Depending on the installed pump capacities, this can include periods of light-intensity rainfall runoff.
2.1. Inventory and Configuration Phase
For a pumping station containing N
p pumps, a total of
potential pump status combinations (SC) can be defined. These are all the theoretical combinations of the different pumps being idle or active. The total number of transitions from one status combination to another, further called pump status combination changes (SCC), equals
. These SCs and SCCs can be grouped in operational regimes and regime changes: e.g., all SCs that contain a single active pump can be grouped into a regime “single pump use”; all SCs that contain two active pumps can be grouped into a regime “double pump use”, etc. Possible regime changes are then, e.g., the switch from “single pump use” to “double pump use” or vice versa.
Appendix A gives an elaborated example of the operational regimes and regime changes for a typical “2 + 1” pump configuration (2 active pumps + 1 spare).
The inventory and configuration phase consists of identifying all actual operational regimes and regime changes for the considered pumping station and the related operational settings for switch-on and switch-off levels. Those associated with dry weather conditions are labelled as “dry weather regime change”. Additional information and an example are given in
Appendix A. Based on available pump curves, the nominal pump capacity for each pump is estimated for the different regimes in which they can be active.
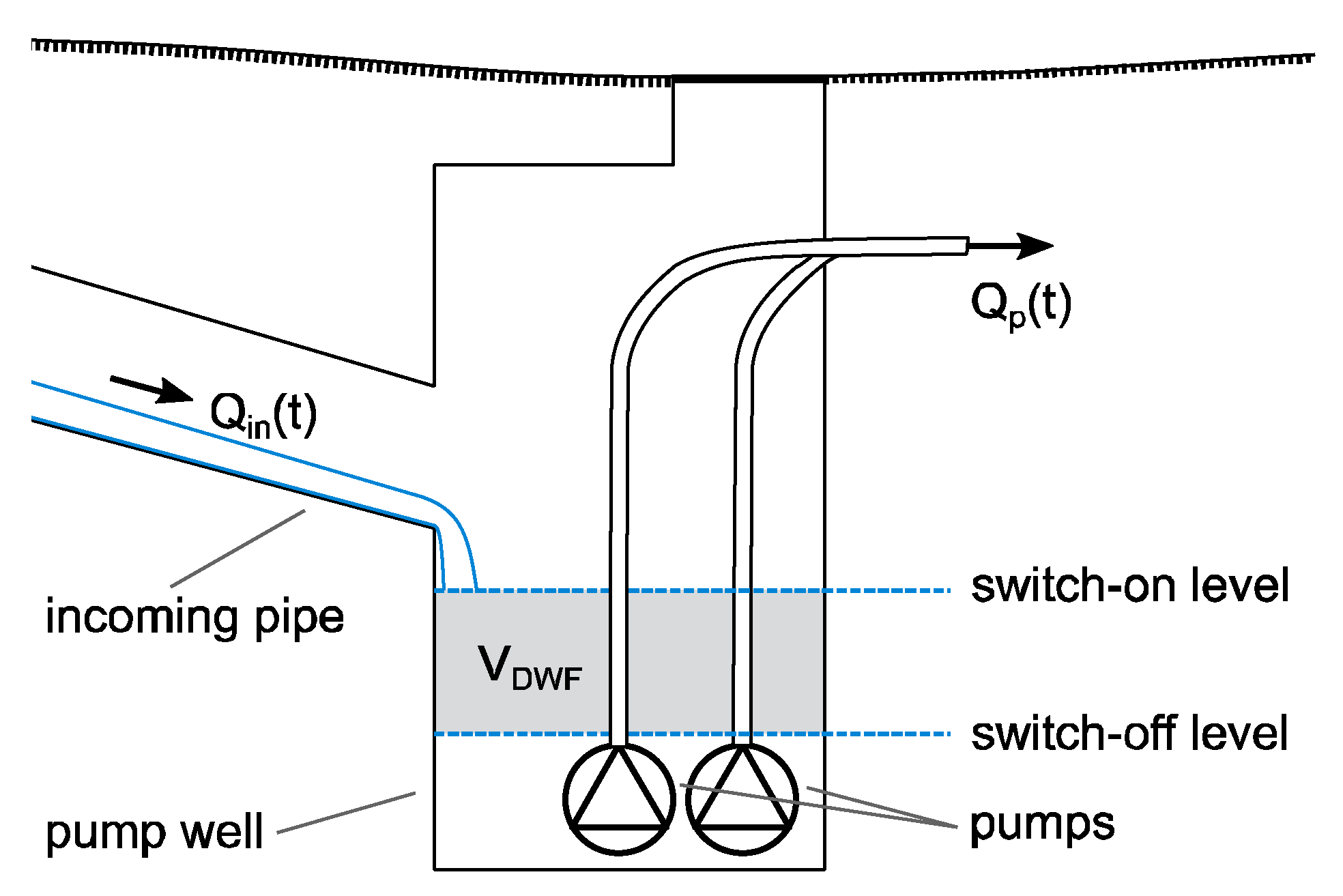
Another aspect of the inventory is the description of the geometry of the pumping well and the incoming pipes. Storage volumes should be described via tables of volume vs. level, rather than as a limited set of fixed volumes between predefined levels. This makes it possible to deal with multiple or time variable switch levels in the most flexible way during the data preprocessing and flow calculation phases (see further). For the pump well, such tables can be produced, e.g., using the most detailed information available (design or construction plans, 3D surveys via Lidar, hydrodynamic models, or other reliable sources). For the incoming pipe storage, volumes can be calculated based on their geometry (diameters, invert levels). Some hydrodynamic modelling packages contain built-in functionalities to generate such storage volume curves.
2.2. Data Preprocessing Phase
In this phase, the raw time series of pump switch-on/-off timestamps and level data are processed in combination with the regime and regime change details resulting from the above-described inventory and configuration phase.
The first purpose of the preprocessing is to identify errors in the raw pump data, i.e., sequences of switch-on and -off registrations that do not yield valid regimes or regime changes (e.g., one pump switch-on followed by a switch-on of the same pump). Such errors can occur when certain switch registrations were lost during the data collection or because manual switch-on/-off operations have taken place during maintenance interventions.
The second purpose of preprocessing is to analyse gaps in the data. Sometimes gaps are clearly too long to represent a real period during which no pump switching took place. They do not necessarily, however, lead to invalid regimes or regime changes because in theory the last and first registration before and after the gap may still yield a valid sequence. Most PLC (Programmable Logic Controller)-controlled pumping stations have a built-in maximum period during which one and the same pump may remain active (leading to regime changes Sx and Dx, as explained in
Appendix A). This maximum time can be used to identify potential gaps in the raw data. Whenever data cannot be assigned a valid regime or regime change or when a gap has been identified, the data set has to be split up into independent subsets to prevent flow calculation errors in further steps of the methodology.
After correcting invalid and missing data, the remaining data subsets consist of a series of pump cycles. These are either filling cycles, which start with a switch-off and end with a switch-on, or emptying cycles, which start with a switch-on and end with a switch-off. Both types of cycle can also contain multiple intermediate timestamps where one pump is replacing another because of the exceedance of the maximum pump time (cfr. the Sx and Dx regime changes, as described in
Appendix A). Pump cycles that start and end with a regime change that is labelled as a “dry weather regime change” are classified as “dry weather cycles”. As explained above, they can be divided further into “dry weather filling cycles” and “dry weather emptying cycles”.
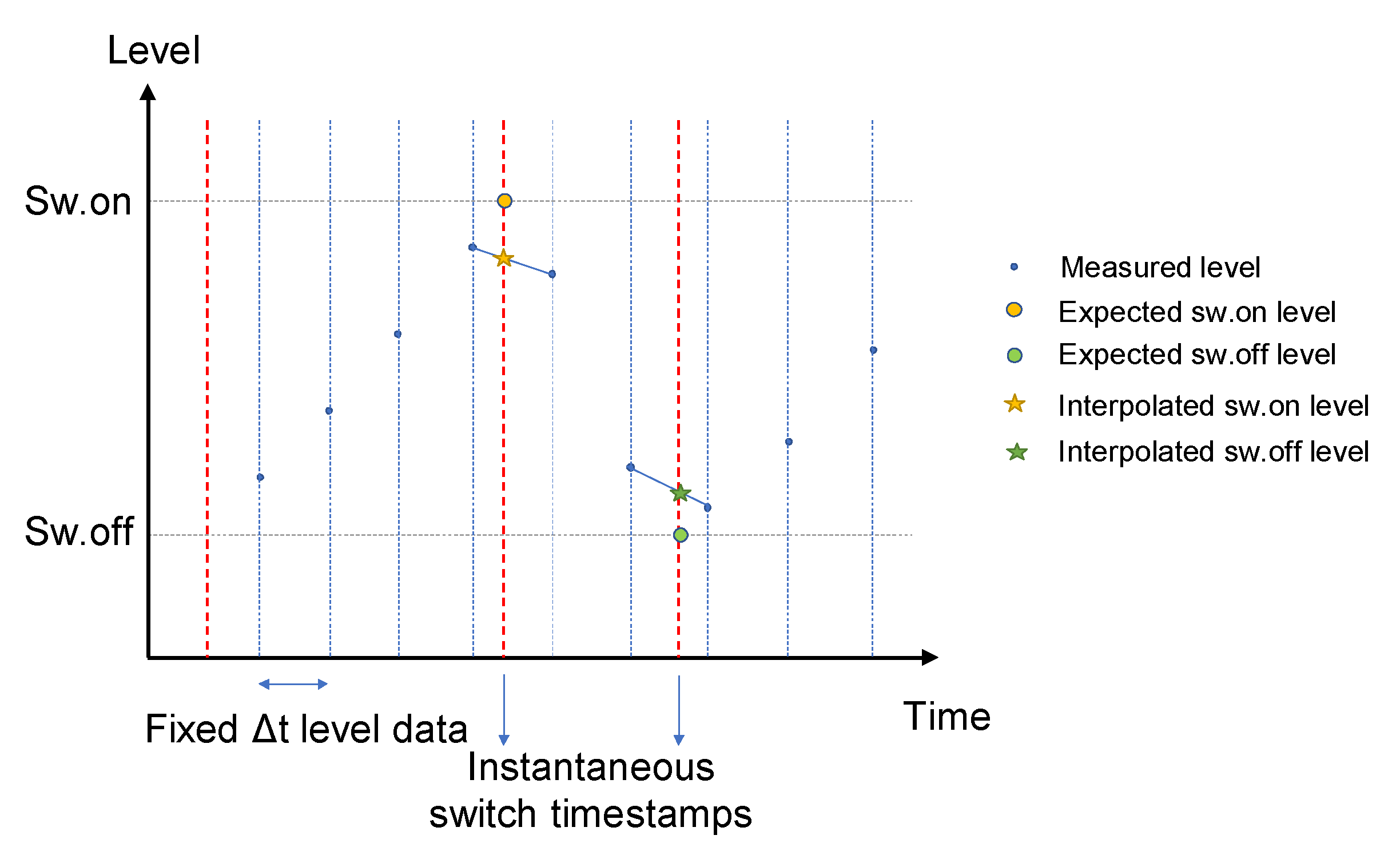
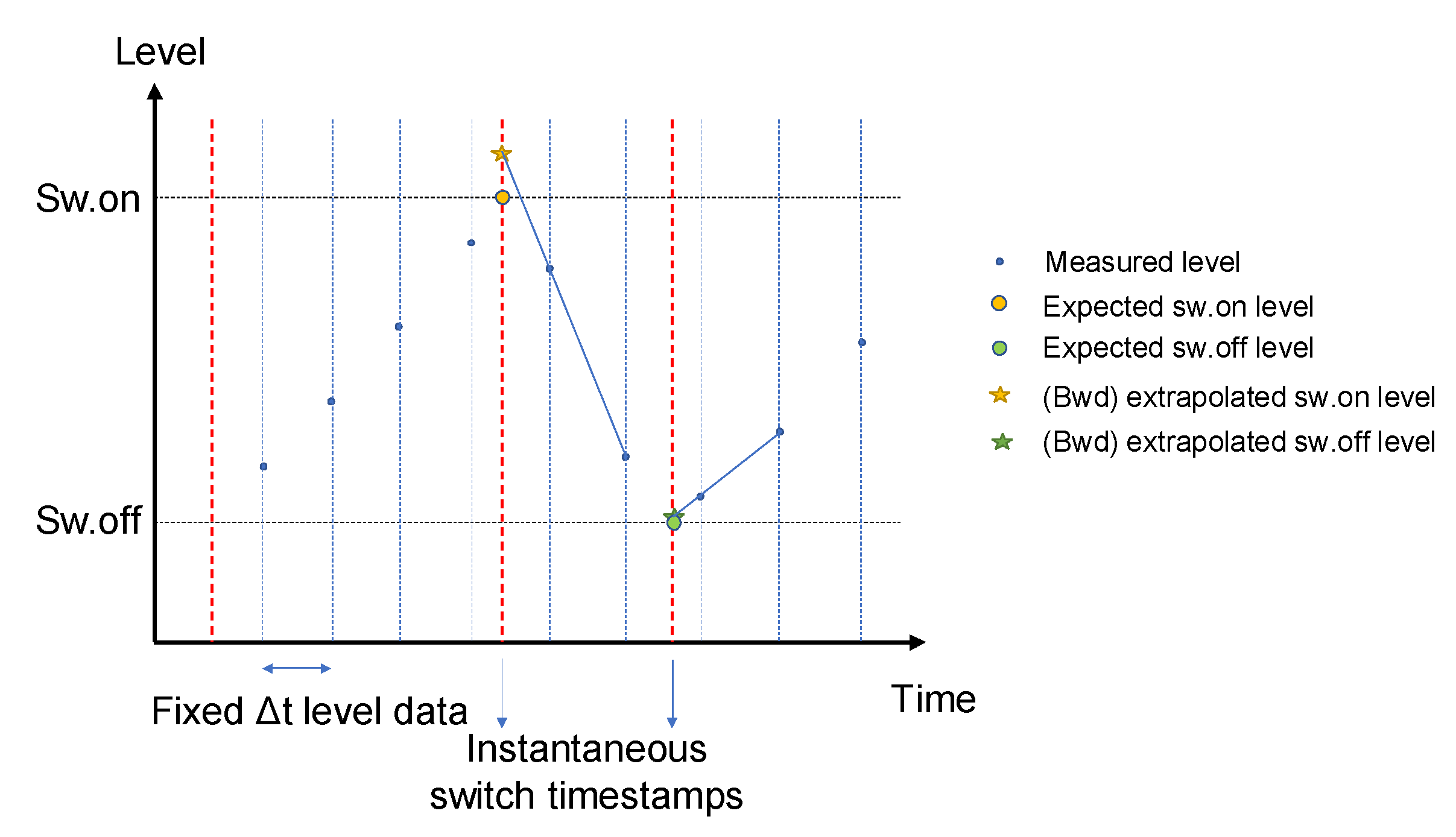
The concept of pump cycles is the key to the flow calculation phase. As will be explained hereafter, an initial cycle-based flow calculation can be performed purely on the basis of pump switch registration data. Water level data are only required in specific cases to improve this initial calculation. However, if level data are available, a useful additional data preprocessing step is the calculation of interpolated levels at the timestamps of switch-on and switch-off. These interpolated values provide a double check of the pre-assumed switch-on and switch-off levels (and the storage volumes corresponding to these levels). Similarly, they can be helpful to identify unknown changes in the level settings when their history is not logged.
Appendix B describes how different interpolation methods can be used to avoid obvious errors in purely linear interpolation.
2.3. Flow Calculation Phase (Cycle Based)
At the end of the preprocessing phase, a list of dry weather filling and emptying cycles is available with their respective start and end times, cycle durations, and switch-on/-off levels. For all these cycles, the cycle-averaged incoming and outgoing flows can now be calculated.
In general, the continuity equation in a pumping station during dry weather flow (Equation (1)) can be formulated as
where
V (t): the instantaneous volume stored in the pumping station (m3);
Qin (t): the flow entering the pumping station (m3/s);
Qout (t): the flow pumped out from the pumping station (m3/s).
When applied over a full pumping cycle this yields
and
for, respectively, a filling cycle (Equation (2)) and an emptying cycle (Equation (3)),
where
V
DWF: the control volume between the dry weather switch-on and switch-off level (m
3) (see
Figure 2);
: the average incoming flow during the filling cycle (m3/s);
: the average incoming flow during the emptying cycle (m3/s);
: the average pumped flow during the emptying cycle (m3/s);
Δtfill: the duration of the filling cycle (s);
Δtempt: the duration of the emptying cycle (s).
This means that cycle-averaged incoming flows can be calculated for all dry weather filling cycles using only the instantaneous timestamp registration of the pump switching on and off and the dry weather control volume. Moreover, assuming that cycle-averaged dry weather flows will not vary significantly between two consecutive filling cycles, of the intermediate emptying cycle can be estimated from the preceding and following values of only (e.g., by linear interpolation). This, in turn, allows one to calculate the average pump flow during the intermediate emptying cycle from Equation (3).
In Equations (2) and (3), VDWF is assumed to be constant. However, in reality, settings of switch levels can change over time, meaning that during the processing of longer data sets, VDWF can vary throughout the data set. This has to be handled during the data preprocessing phase, resulting in a list of VDWF values per cycle.
Sometimes, a pump’s switch-on is not only defined by level but also by the maximum duration of the filling cycle. This can be the case, e.g., for wastewater treatment plants where a maximum idle time of the influent pumps is imposed to ensure the stability of the treatment process and/or to prevent sedimentation build-up in the incoming collector. In such cases, VDWF for the shortened cycles must be calculated by using the interpolated level at the moment of forced switch-on.
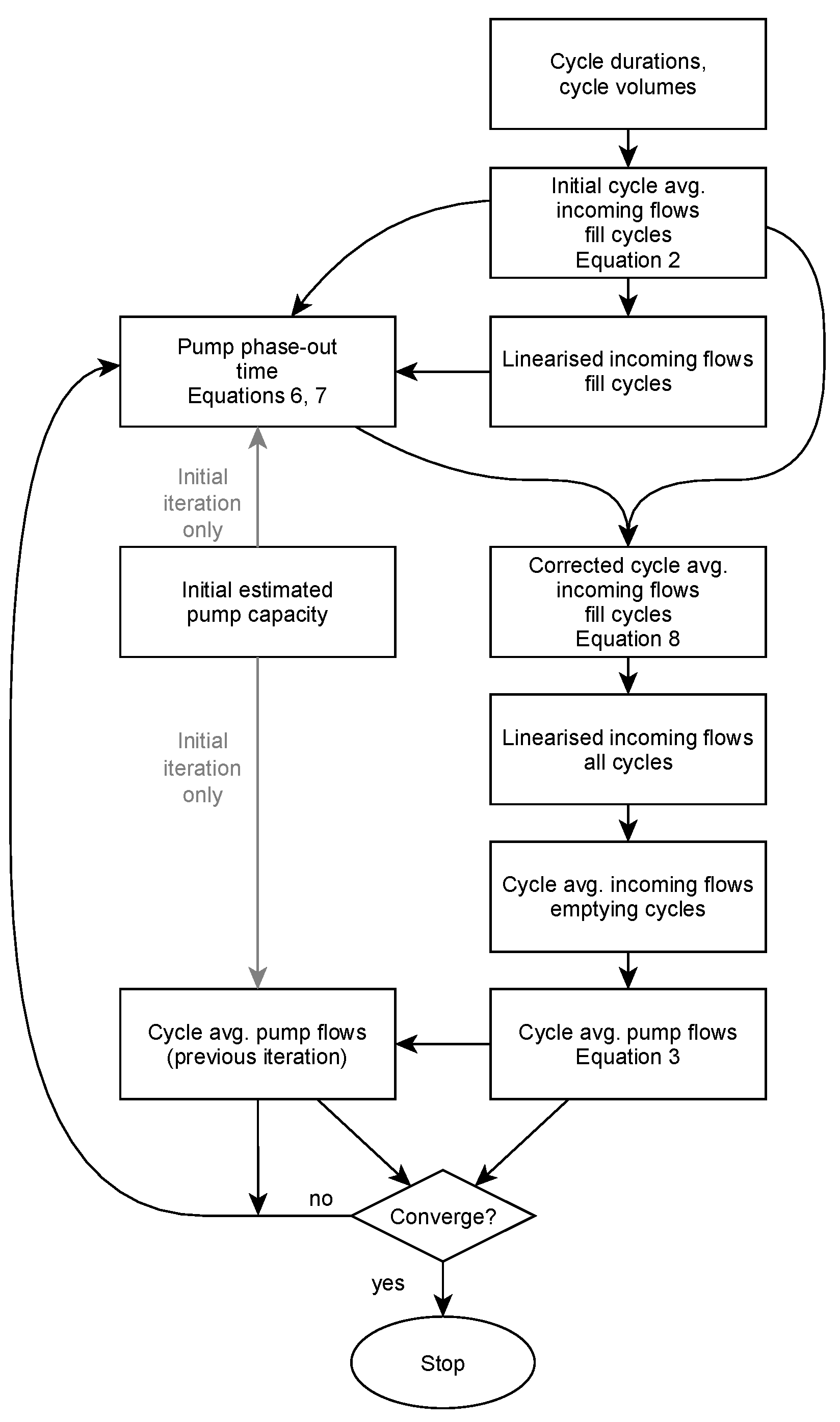
Because the above-described basic flow calculation is still prone to a number of uncertainties and assumptions, an iterative correction procedure is required to yield more accurate results. This is shown in
Figure 3 and described in detail in the following paragraphs.
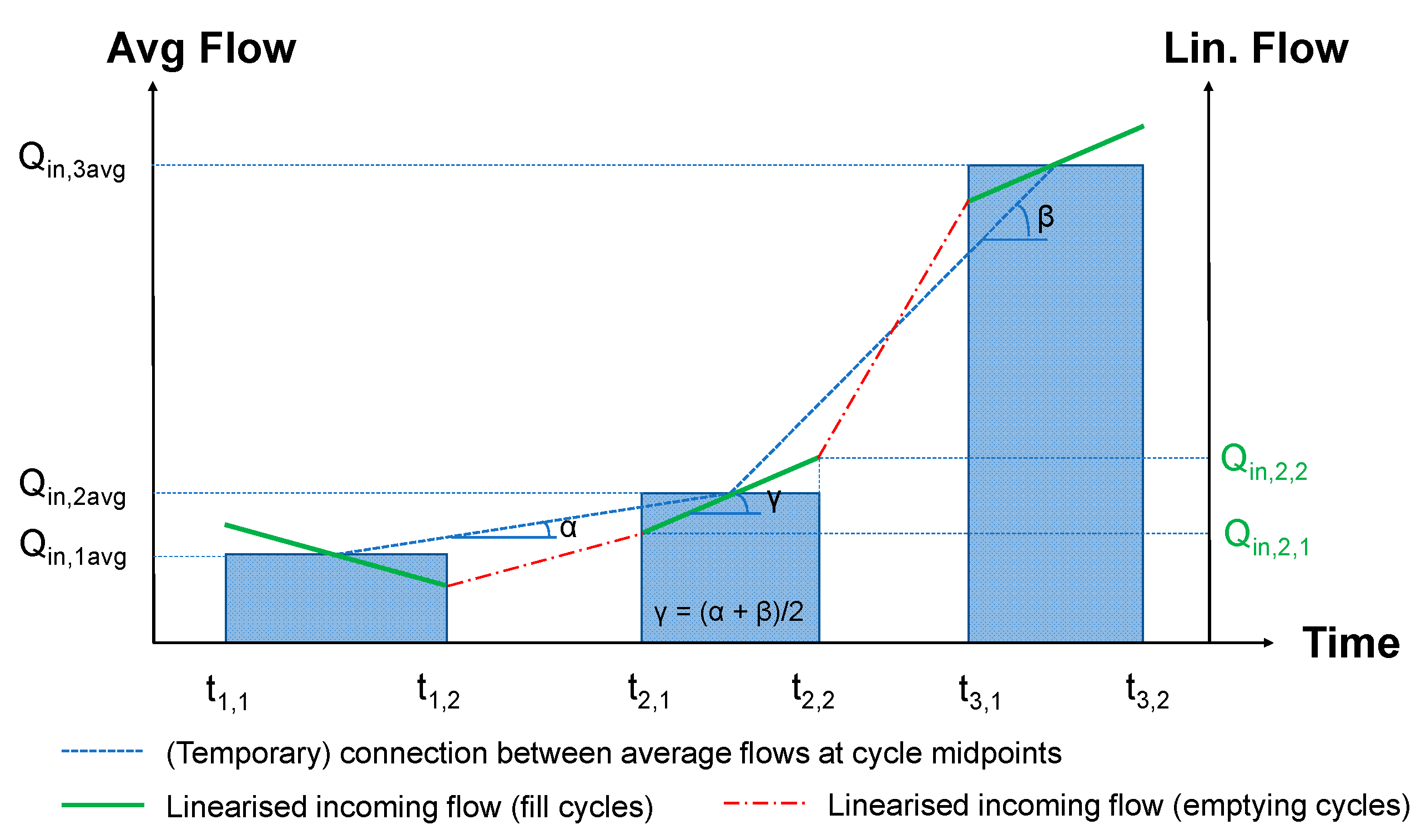
2.4. Linearising the Cycle-Averaged Flows
The incoming flows during filling cycles, as calculated from Equation (2), are average values over the duration of the cycles, whereas, in reality, flows are a continuous function of time. Assuming that dry weather flows will generally not show sudden variations over the relatively short duration of a pumping cycle, a linearisation of the average values is proposed to create a more continuous transition between successive cycles.
This is carried out by averaging gradients between successive filling cycles. During this process, it is important to preserve volumes per cycle, as these are the direct results from Equation (2) and hence should not be smoothened out. This linearisation procedure is illustrated in
Figure 4: the cycle-averaged incoming flow Q
in,2avg for cycle 2 is transformed into a time-dependent flow varying linearly between Q
in,2,1 at time t
2,1, the start of the cycle, and Q
in,2,2 at time t
2,2, the end of the cycle. The gradient of this linear variation during the cycle is found by averaging the gradients of the lines that connect the average flows of the successive filling cycles at their respective midpoints. After this linearisation of the filling flows, the flows during the emptying cycles are calculated as linearly varying flows by connecting the end and start values of the linearised flows of the surrounding filling cycles.
2.5. Correction for Phase-Out Time of Pump Flows
When pumps are switched off, as a result of inertia, they continue to pump some volume for a limited amount of time (the phase-out time Δtph). In some cases, this can cause the water level in the wet well to continue dropping down after the pump has switched off. A similar phenomenon occurs at the switch-on of pumps: because the pump has a delay time to reach its full capacity, the water level can initially continue to rise above the switch level. However, this delayed start does not affect cycle-based calculations and therefore will not be considered further here.
Because Δt
ph is not known, it must be derived from the observed time at which the level reaches the switch-off level again after the initial dropdown. This is further indicated as the zero-level recovery time, or Δt
0 (see
Figure 5). In many cases, it will not be possible to derive Δt
0 from the available level records. Either the time during which the level drops down below the switch-off level can be shorter than the time interval of the available level data series, or the combination of the incoming flow and pump flow can be such that the water level does not initially drop down at all. In such cases, Δt
ph is set to 0.
Assuming (i) a linear decrease in the pump flow between
of the past emptying cycle at switch-off time t
1 and zero flow at the (still unknown) time t
ph (=t
1 + Δt
ph) and (ii) a linear variation of the incoming flow between Q
in,1, at switch-off time t
1, and Q
in,2, at switch-on time t
2, with the cycle duration ∆t
c = t
2 − t
1, Δt
0 can be calculated as:
or
for, respectively, ∆t
0 ≤ ∆t
ph (Equation (4)) and ∆t
0 ≥ ∆t
ph (Equation (5)).
Both equations can now be rewritten to derive ∆t
ph from the observed ∆t
0, which yields Equation (6) for ∆t
0 ≤ ∆t
ph:
and Equation (7) for ∆t
0 ≥ ∆t
ph:
By grouping all fill cycles according to which pump was active in the preceding emptying cycle, all individual cycle values of ∆tph can now be consolidated into a single median value per pump (p = 1…NP). The limitation of this procedure is the assumption that no more than 1 pump is active during dry weather emptying cycles.
Based on this value, Equation (2) can be modified to calculate a corrected value of
for all fill cycles (yielding Equation (8)):
2.6. Further Iterative Calculation of Pump Flows and Incoming Flows
As shown in the detailed flowchart in
Figure 3, the corrected average incoming flows of the different fill cycles, as obtained from Equation (8), can form the start of an iteration loop.
Using again the linearisation procedure on the corrected values of
, corrected linearised incoming flows for the emptying cycles can now also be calculated (as shown in
Figure 4), and from these, corrected values of
and, using Equation (3), corrected values of
for each pump are obtained.
Corrected values of can now be compared to the previously calculated value, which, in the first iteration, is equal to the initially estimated nominal pump capacities. If the difference for each pump is within a preset tolerance, no further iteration is required. If not, the new values of are used as input for a new calculation of the pumps’ phase-out times, which will then again be used in Equation (8) to calculate new corrected incoming flows, until convergence for is achieved.
Even if no pump phase-out times can be calculated, and hence no correction needs to be applied to the fill cycles’ incoming flows, at least one iteration will generally be necessary to validate the initial assumption of the pumps’ nominal capacities.
3. Results
In order to implement the methodology described above, a dedicated tool was built in Matlab [
38].
Four pumping stations (PS Vuntlaan, PS Wijgmaalsesteenweg, PS Zuidstraat—all three in drainage area Leuven—and PS Wauberg—in drainage area Peer) were chosen as pilot sites for testing the methodology. A short overview of their characteristics and the connected catchments is given in
Appendix C, together with an overview of the necessary input data and an example of the result of data preprocessing.
3.1. Results of the Flow Calculation Phase
With the cycle-based approach, incoming flows and pumped flows are calculated for every dry weather cycle. Next, these flows are postprocessed and presented in detailed graphs per day and in overview graphs with daily values. It is important to take into account that for days containing both dry weather and non-dry weather cycles, daily volumes will be an underestimation of the real values, as no flows are being calculated for the non-dry weather cycles.
Figure 6,
Figure 7 and
Figure 8 all show the detailed results of the calculated incoming flows and pumped flows during a dry day.
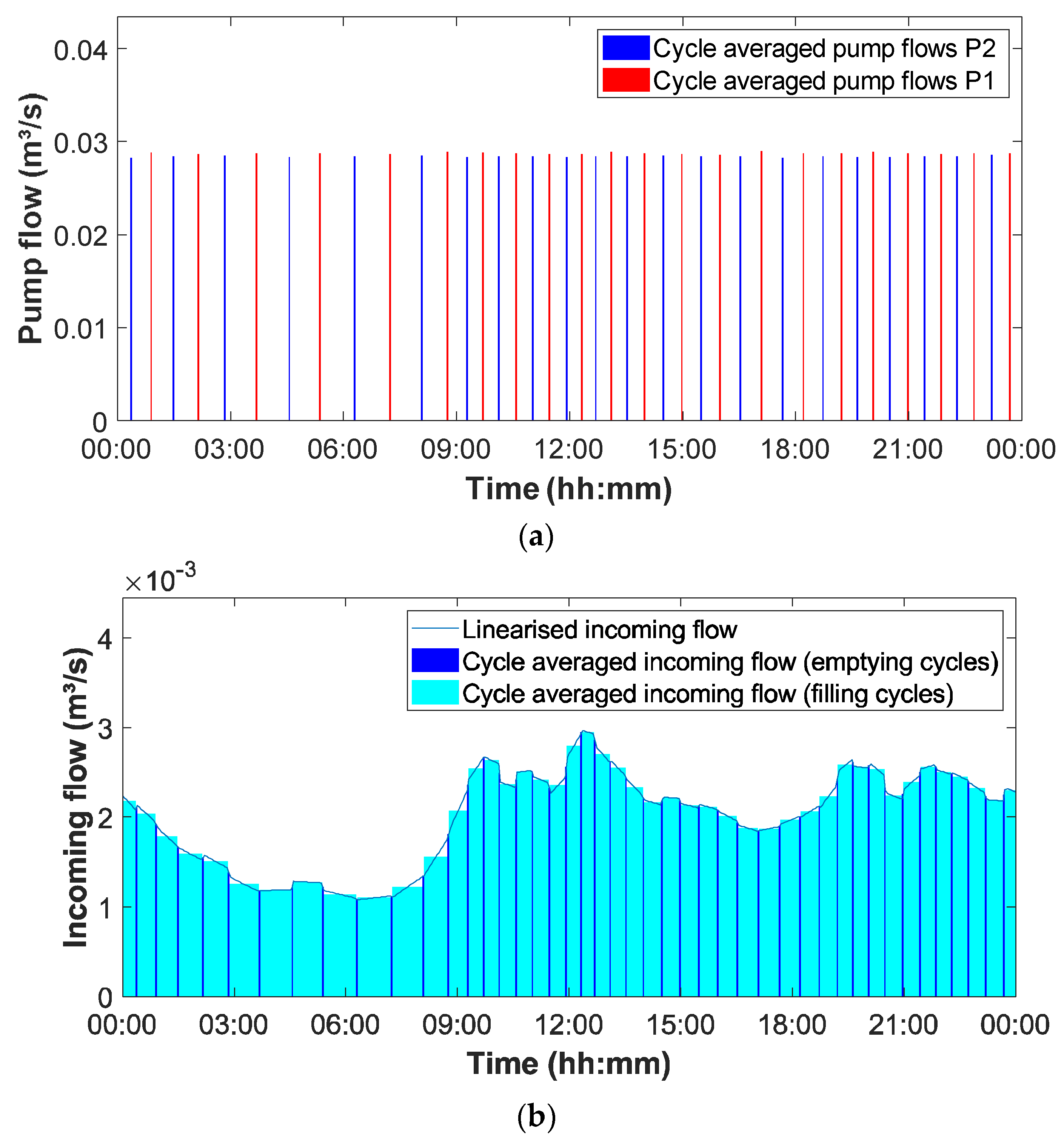
In
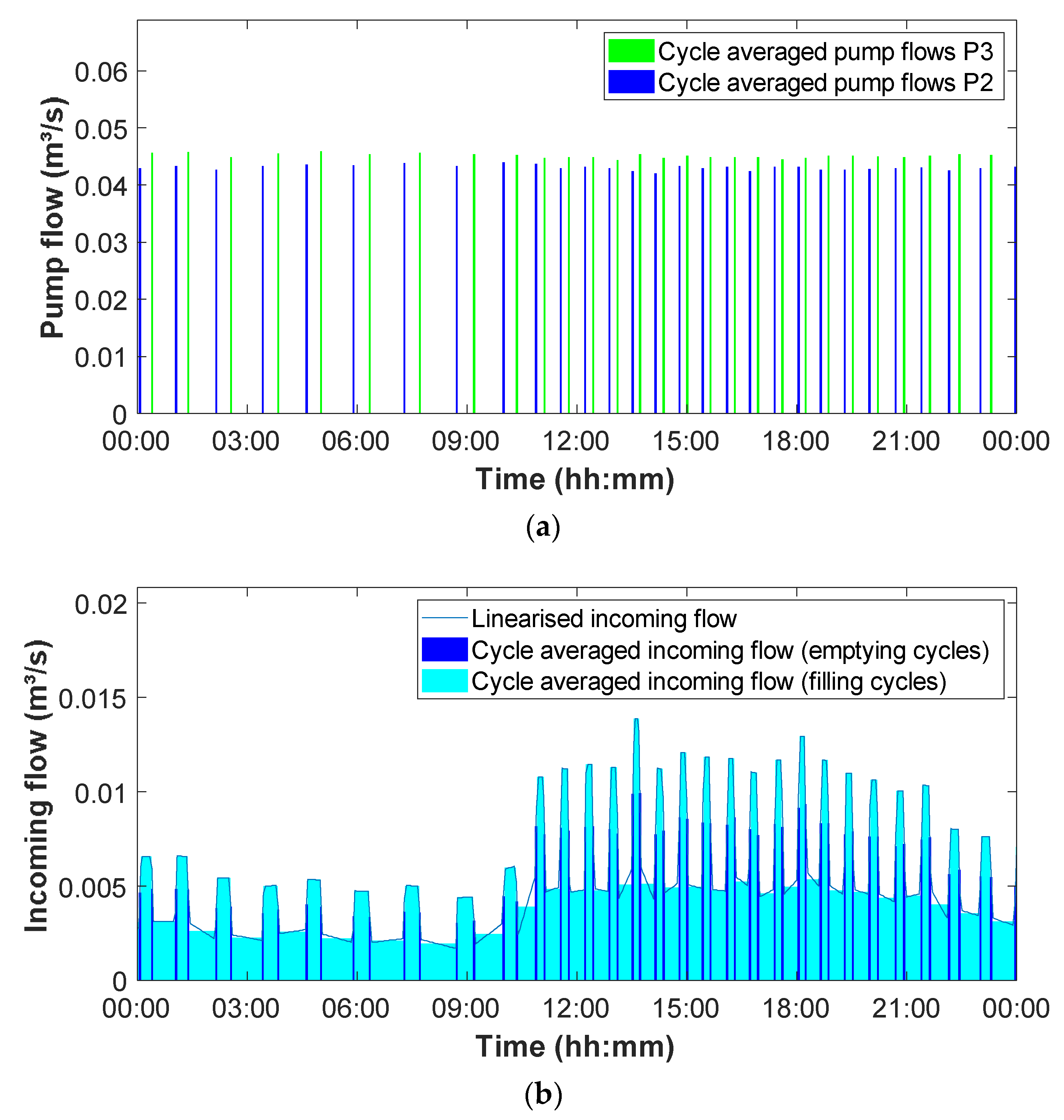
Figure 6, the two pumps have a very similar calculated flow, which is very close to the assumed nominal capacity (31 L/s). In
Figure 7, although the results are about twice as high as the initially assumed nominal capacities (18 L/s for pump1 (P1) and pump2 (P2), and 27 L/s for pump3 (P3)), the ratio between the different pump capacities is preserved. This proves that the methodology is capable of handling such cases without affecting the continuity of the resulting incoming flow curve. The most likely reason for the large deviation of the calculated pump capacities is the overestimation of the control volume V
DWF (see further,
Section 3.2).
In
Figure 8 on the other hand, there is a clear discrepancy between the calculated pump flows and the calculated incoming flows. The pump flows—as expected from the available pump curves—are very similar for both pumps. The incoming flows, however, show significantly different values for the different cycles, depending on which pump was active. In this case, after an investigation on-site, there appeared to be a problem with the wiring of a provisional datalogger. This resulted in one of the pumps failing to log its switches, although it was operating normally. Because of the regular alternation of the three pumps, this did not result in the erroneous identification of regimes and regime changes. However, the calculated cycle duration for the cycles preceding the non-logged ones was not reflecting the real cycle duration and, therefore, yielded lower calculated average cycle flows. Note that in this case, the calculated flows for P2 and P3 are only around two-thirds of the expected value (69 L/s). Additional measurements have to clarify whether this is due to an underestimation of the control volume or if the pumps are not reaching their envisaged capacity.
3.2. Estimation of the Uncertainty of the Results
As can be seen from Equations (2) and (3), the calculated flows are directly proportional to the assumed V
DWF, and the relative error on the calculated flows δQ equals the sum of the relative errors of the control volume and the cycle duration (δV
DWF + δ (Δt
c)). From these two parameters, the control volume is the one with the highest uncertainty. Even if detailed information to calculate this volume is available, it remains very difficult to account for space taken up by objects such as pump bodies, lifting chains, rising mains and valves, ladders, and benchings. Therefore relative errors of >10% on V
DWF are not unusual. If the control volume extends well into the incoming pipes, this error may be even higher, as explained in
Appendix D.
The accuracy of the cycle durations, on the other hand, based on specifications of the SCADA system employed for data communication and logging, is of the order of 1–2 s. With (dry weather) cycle durations rarely being lower than 5 min, the relative error is thus generally well below 1% and hence can be considered negligible in comparison with δVDWF.
The (high) uncertainty of VDWF and hence of the calculated flows can be reduced if independent flow measurements are available. Because the incoming flows and the pump flows are linked by the continuity equation, it takes only one reference flow, either the incoming flow or the pump flows, to correct both calculations.
When reference flows are available, a correction factor K
vol can be determined from the comparison between reference and calculated flows, e.g., based on daily volumes or averages. Because of the linear relationship, as expressed in Equations (2) and (3), the calculated flows simply need to be multiplied by this correction factor. This is illustrated in
Figure 9, where reference pump flows are available from electromagnetic flow meters at the rising mains. The remaining deviations between the calculated and measured pump flows per emptying cycle after correction are due to (i) the differences between the fixed time interval of the measurements (1 min) and the instantaneous registration of the switch times (resolution 1 sec) and (ii) the variability of the pumped flows over the duration of the cycle as a result of the pumps being variable-frequency-driven.
When V
DWF varies over time due to varying switch-on/-off levels or forced switch-on, multiple correction factors have to be determined for different periods. Moreover, when the flow dependency of the in-pipe control volume would have a significant impact on the calculated flows, a simple linear correction may not be sufficient to bring the calculated flows in accordance with reference flows. This is explained in more detail in
Appendix D. More investigation is needed to assess what accuracy can be obtained in such cases.
Even if no reference flows are available (which may often be the case), upper and lower limits of incoming flows and pump flows can generally be estimated based on available pump curves and expert knowledge of the sewer system and the catchment connected to it. This may then already be a useful first step to eliminate large errors in the estimation of the storage geometry.
3.3. Identifying the Presence of Inflow and Infiltration
The objective of this paper is primarily to present a methodology for calculating flows at pumping stations and not to propose algorithms for quantifying I&I contributions to these calculated flows. Nevertheless, some example results show that the high temporal resolution of the calculated flows can contribute to facilitating the quantification of I&I.
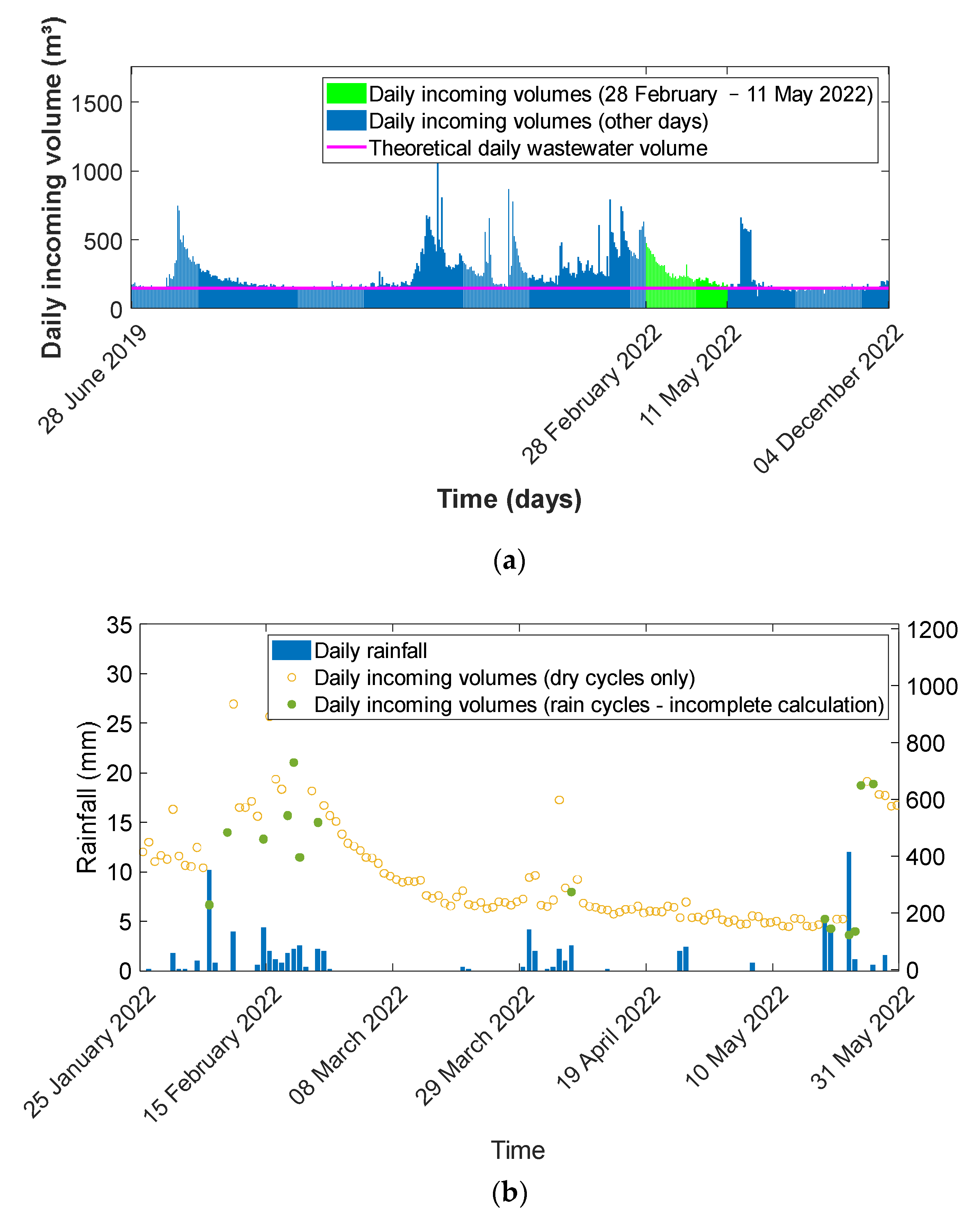
Figure 10a shows the overview of daily volumes for these days that only contain dry weather cycles. The main reason for omitting the other days is that incoming flows (and hence the daily volume) can only be calculated for dry weather cycles. The severity of the underestimation for each day depends on the number and duration of non-dry weather cycles for that day. This variation of underestimations would complicate the interpretation of the graph if all days were shown. This is illustrated in
Figure 10b for a selected period where the daily rainfall is shown against the calculated daily volumes.
The typical exponential decay of infiltration flows during long dry-weather periods can be detected even with only the results of the dry weather days, as can be seen in
Figure 10a. A more detailed analysis of the occurrence of I&I can be made by selecting the relevant days from such periods and comparing the calculated daily flow patterns.
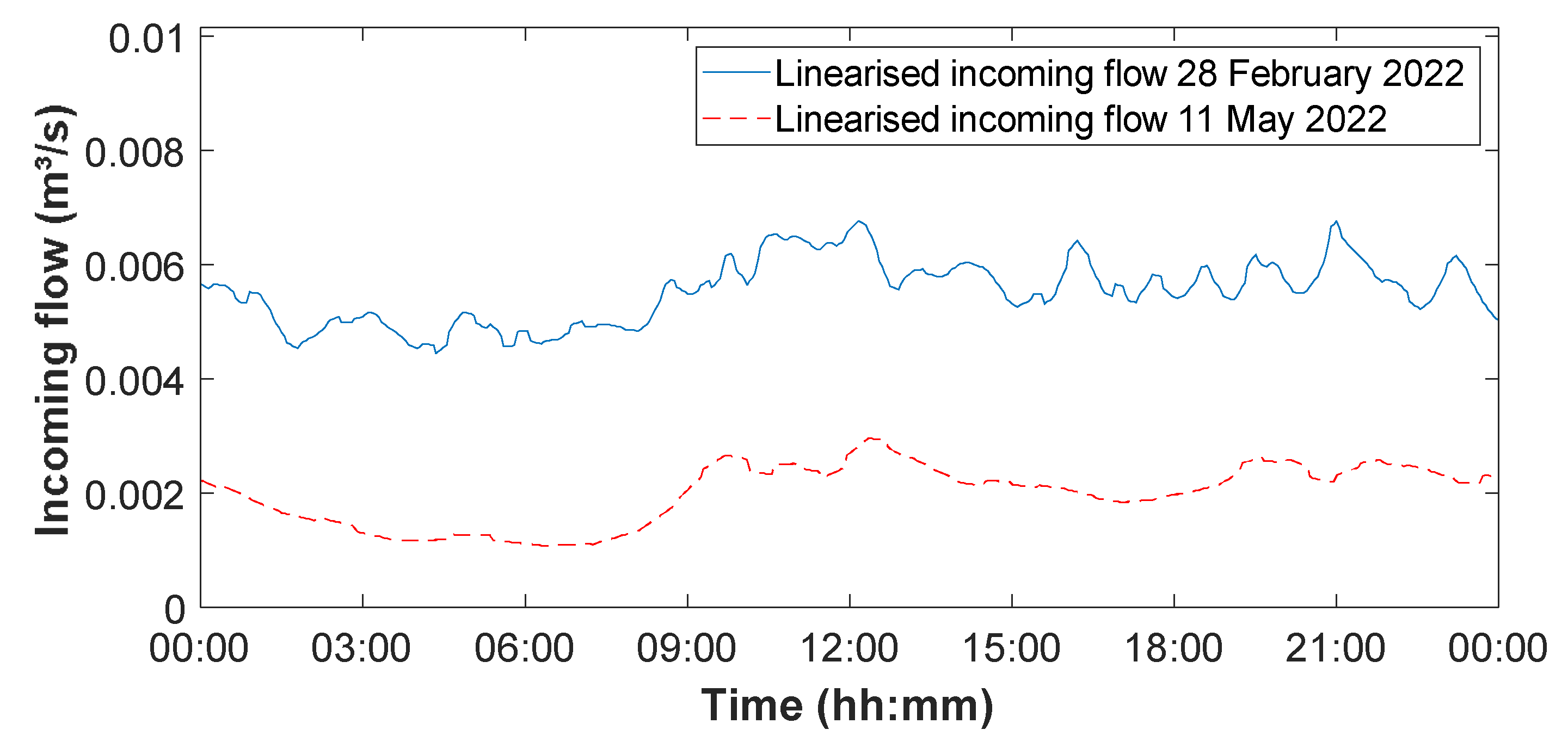
Figure 11 shows the detailed calculated incoming flows for the first and last day of the selected period between 28 February 2022 and 11 May 2022, during which there were only a few days with (insignificant) rain. As can be seen, the high initial infiltration flow offsets the diurnal wastewater profile. Although the two profiles are very similar, the one for 28 February shows less variability. When both patterns are normalised to their respective average value, the one with the higher infiltration flow thus becomes more flattened.
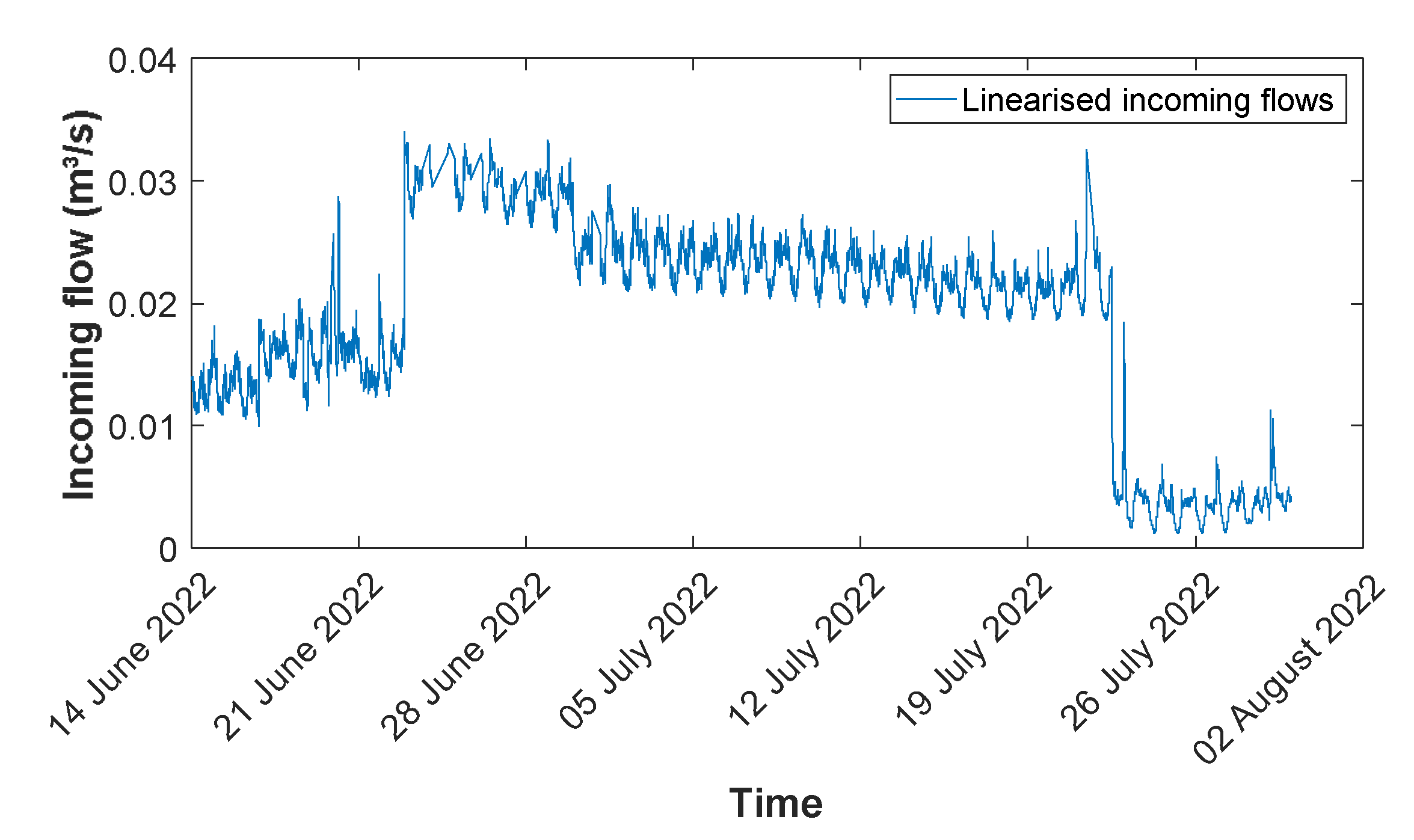
A typical example of high I&I originating from the pumped groundwater drainage of a construction site is shown in
Figure 12. Especially when such I&I contributions coincide with periods of rainfall-dependent infiltration, they can impede the proper calibration of hydrologic models when only daily volumes are available.
Note that the flows in
Figure 12 are still unvalidated. As shown earlier in
Figure 7, the calculated pump flows at this location are about twice as high as the assumed nominal capacities (more precise values may be derived from additional reference measurements). The same correction needs to be applied to the calculated incoming flows. Nevertheless, the pattern showing the impact of the pumped groundwater drainage will remain unaffected by this correction.
4. Discussion
In the above results section, it has been demonstrated that for every pumping station where the necessary data and measurements are available, incoming dry weather flows can be calculated at high temporal resolution. The prerequisites for the methodology to be applicable are (i) the availability of instantaneous pump operation registrations; (ii) preferably, but not mandatorily, the availability of level measurements with sufficient temporal resolution (typically 1 min); (iii) the availability of geometry data for both the pump well and the incoming pipes; (iv) the availability of information about operational regimes and switch levels; (v) under normal dry weather conditions, pumps should not be permanently active; and (vi) the availability of some reference flow measurements for validation purposes (minimum required temporal resolution: daily volumes). These can be either incoming flows or pumped flows and do not need to cover the whole timespan of the analysed data.
The temporal resolution of the results is the pumps’ switch frequency. On average, in dry weather conditions, this frequency can range from once every 1–2 h during low flows to once every 10 min during higher flows. Because the switch frequency is automatically adapted to the magnitude of the incoming flow, this is an intrinsic guarantee that the temporal resolution of the calculated flow is always in line with the expected variation in the flow pattern. Only in very specific circumstances, the switch frequency during dry weather will be too low to identify patterns in the flow. This can be the case, e.g., when a very small amount of PE (population equivalent) is connected, or when the installed pump capacity is much larger than the theoretical wastewater flow, expected on the basis of the connected number of PE. For such cases, a future extension of the methodology based on fixed timesteps (see further) will be necessary to yield useful results.
With the current state of the methodology (cycle-based calculation) it is possible to generate incoming flows, not only for dry periods but equally for periods with light rain where the runoff flows do not exceed the pump capacity (usually, three to six times the designed wastewater flow). This is an added value in comparison with hydrograph decomposition methods based on daily volumes [
31]. Even for days with intense rain in the last hours of the day, incoming dry weather flows will still be reliably calculated for the larger part of the day. Daily volume-based methods, on the contrary, will classify such days as rainy days because of the important contribution of rainfall runoff.
The results also show that non-rainfall-related contributions (e.g., from pumped groundwater drainage at construction sites) can be easily distinguished from the other more slowly varying I&I contributions. The main condition for this is that the pumping station is close enough to the location of such inflows and that the flows are significantly higher than the other dry weather components.
The methodology is equally applicable to systems that are predominantly affected by exfiltration rather than by infiltration. The main difference will be in the shape of the resulting dry weather flow hydrographs (more peaked, and in extreme cases potentially containing periods with zero flows). In general, though, it will be very hard to make a quantitative statement on the mutual ratio of exfiltration and infiltration. In specific cases, a comparison between the results from neighbouring locations might give an indication, but most often, an additional tracing experiment will be required.
The accuracy of the calculated flows depends largely on the estimation of the control volume, compared to which the accuracy of the cycle duration is negligible. When the control volume is not or only marginally extending into the incoming pipes, the relationship between the calculated incoming flows, the calculated pumped flows, and the control volume is linear. This means that, when independent reference measurements are available, the calculated flows can be corrected by applying a simple linear correction factor. Such correction brings the accuracy of the calculated flows to the same level as the accuracy of the reference (direct) flow measurement. This remains valid even if the reference measurements are only available for a limited period of time. The only condition for a single correction factor to be applicable is that switch levels do not vary over the period of flow calculation.
The presented results are from a limited set of pumping stations that were temporarily equipped with a datalogger to capture the required pump switch and water level data. However, during the past three years, more than 1800 pumping stations, managed by Aquafin in Flanders (Belgium), have been equipped with a uniform SCADA system that collects these same and other data. This means that there are sufficient input data available to potentially produce detailed local flow profiles for all these locations by applying the methodology proposed here. In comparison with the effort required to install and maintain a similar number of permanent direct flow measurements, this novel approach makes it possible and affordable to aim at a systematic analysis, resulting in a better understanding and management of I&I flows in the urban drainage systems throughout Flanders, Belgium.
Finally, it must be stressed that the methodology does not only produce incoming flows but also pumped flows for each individual pump. These results have the same temporal resolution and accuracy as the incoming flows and have various additional benefits. On one hand, they will be useful for understanding the hydraulic behaviour of urban drainage systems and for improving hydrodynamic models as an operational tool (e.g., digital twins). On the other hand, they will also be extremely valuable for optimising asset maintenance schemes. Given the constant accuracy at which pump flows are calculated over longer periods of time, these long-term trending results will help to identify decreasing pump performance at an early stage and optimise complex pump control rules.
The current methodology is limited to cycle-based flow calculations. Especially for pumping stations with more complex configurations, this puts a limitation on the degree of accuracy that can be achieved. The envisaged solution for many of these special cases lies in a fixed timestep approach as a fourth phase, following the current cycle-based calculations. Such an approach, where continuity equations are performed at every fixed timestep within the different cycles, will require further iteration of already existing steps in the calculation. More important, however, is that it will mandatorily require level measurements with a sufficiently high measurement interval (as opposed to the cycle-based approach, where level measurements have an added value but are not strictly necessary). Other improvements will focus on cases where there is significant interaction between the pumping well and the incoming pipes, which will require flow-dependent volume corrections rather than a fixed correction factor.
The following is a non-exhaustive list of cases that will benefit from the time-step-based approach
Pumping stations that have at least one pump permanently active during periods of minimum dry weather flow. This means that in such cases, there are no filling cycles without active pumps, for which the incoming flow is only a function of the control volume and the cycle duration.
Pumping stations with only one set of switch levels that make it harder to distinguish between dry weather and non-dry weather cycles, especially for periods of light rain.
Pumping stations with extremely low switch frequencies, where the low number of cycles per day does not allow the reliable linearisation of the calculated average cycle flows.