Estimating the Role of Bank Flow to Stream Discharge Using a Combination of Baseflow Separation and Geochemistry
Abstract
:1. Introduction
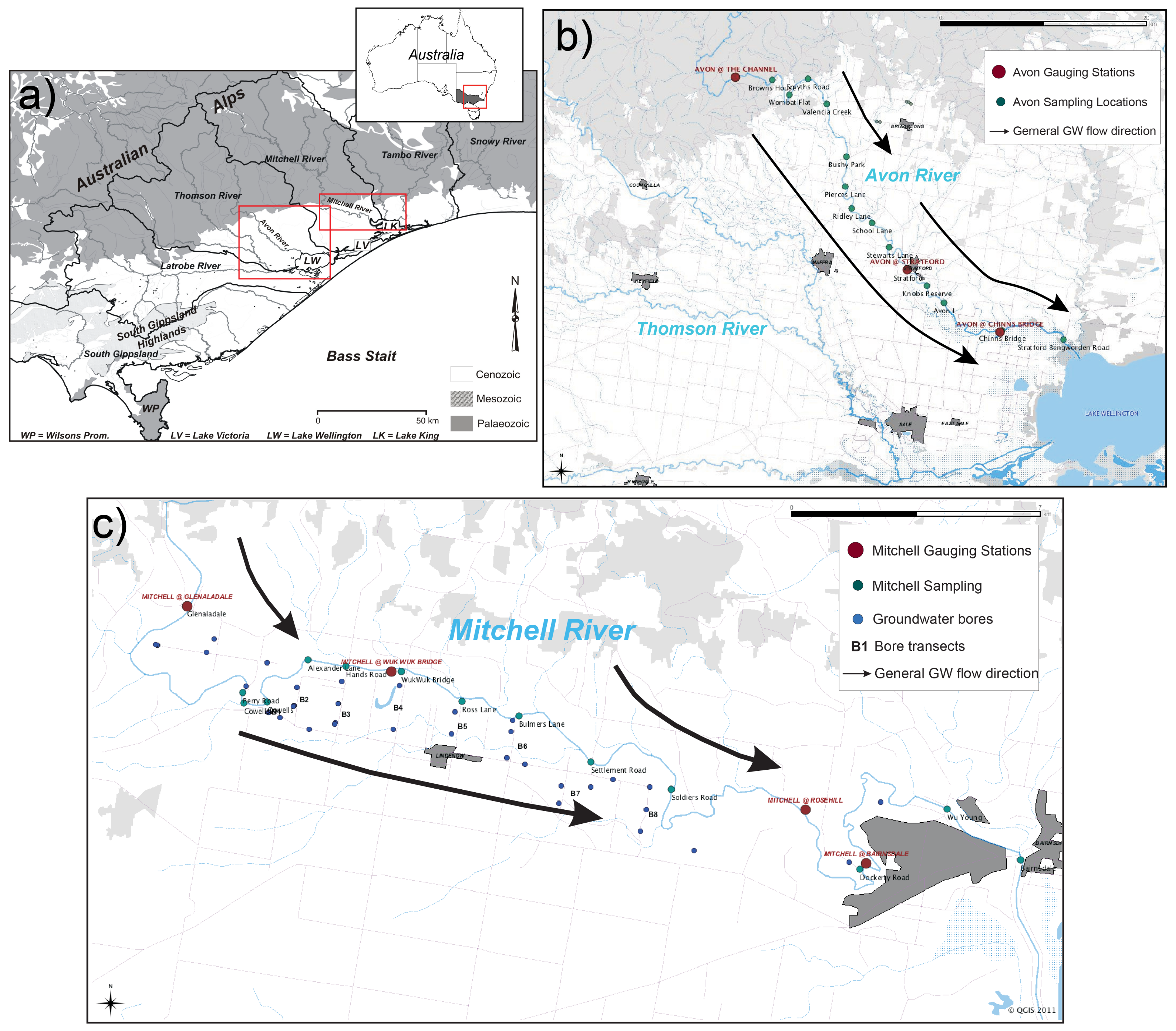
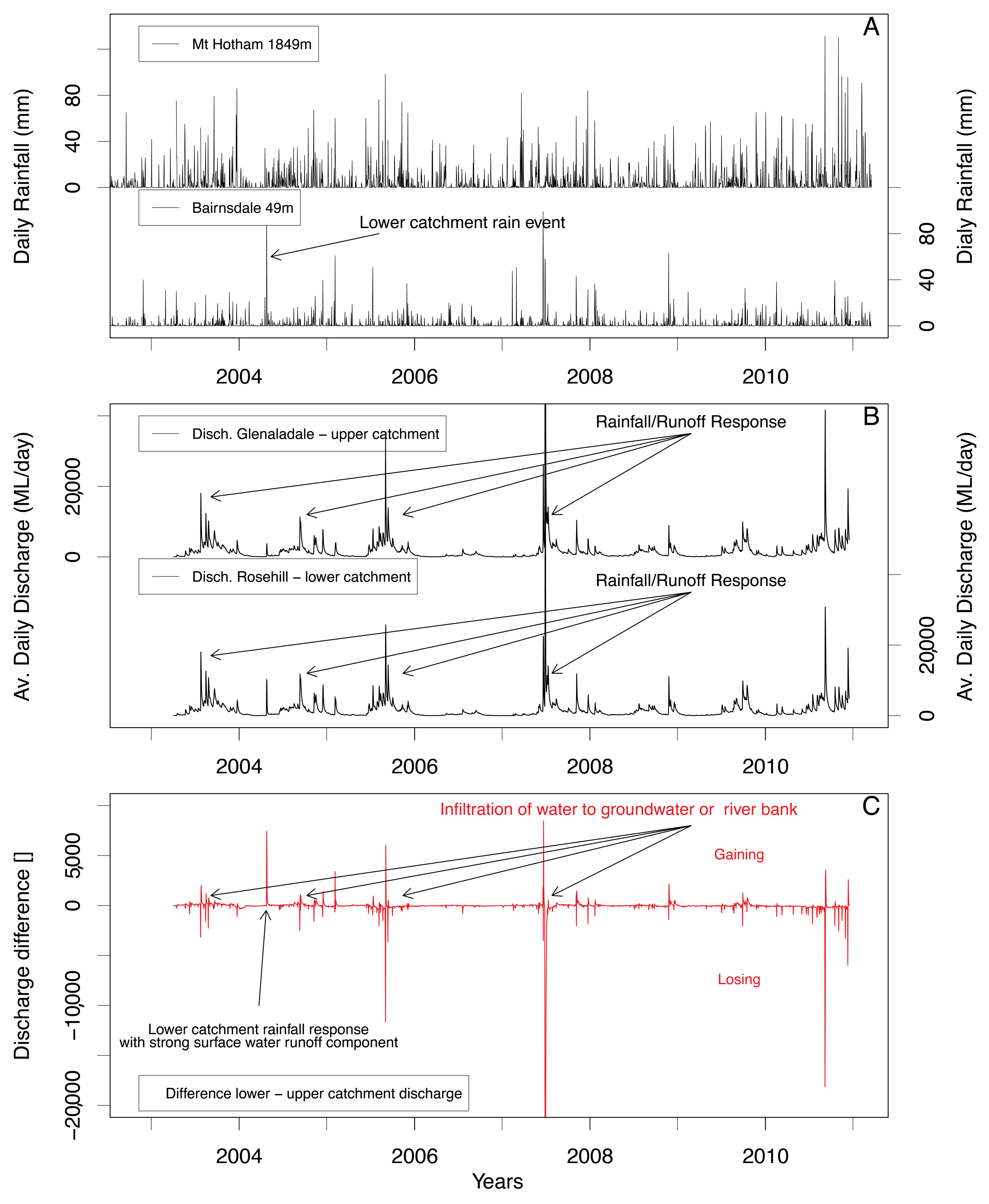
1.1. Geographical and Hydrological Setting
1.2. Theoretical Background
1.2.1. Hydrograph Analysis
1.2.2. Geochemical Baseflow Separation
1.2.3. Radon for Baseflow Estimations
2. Materials and Methods
Data Sources, Sampling and Analytical Techniques
3. Results
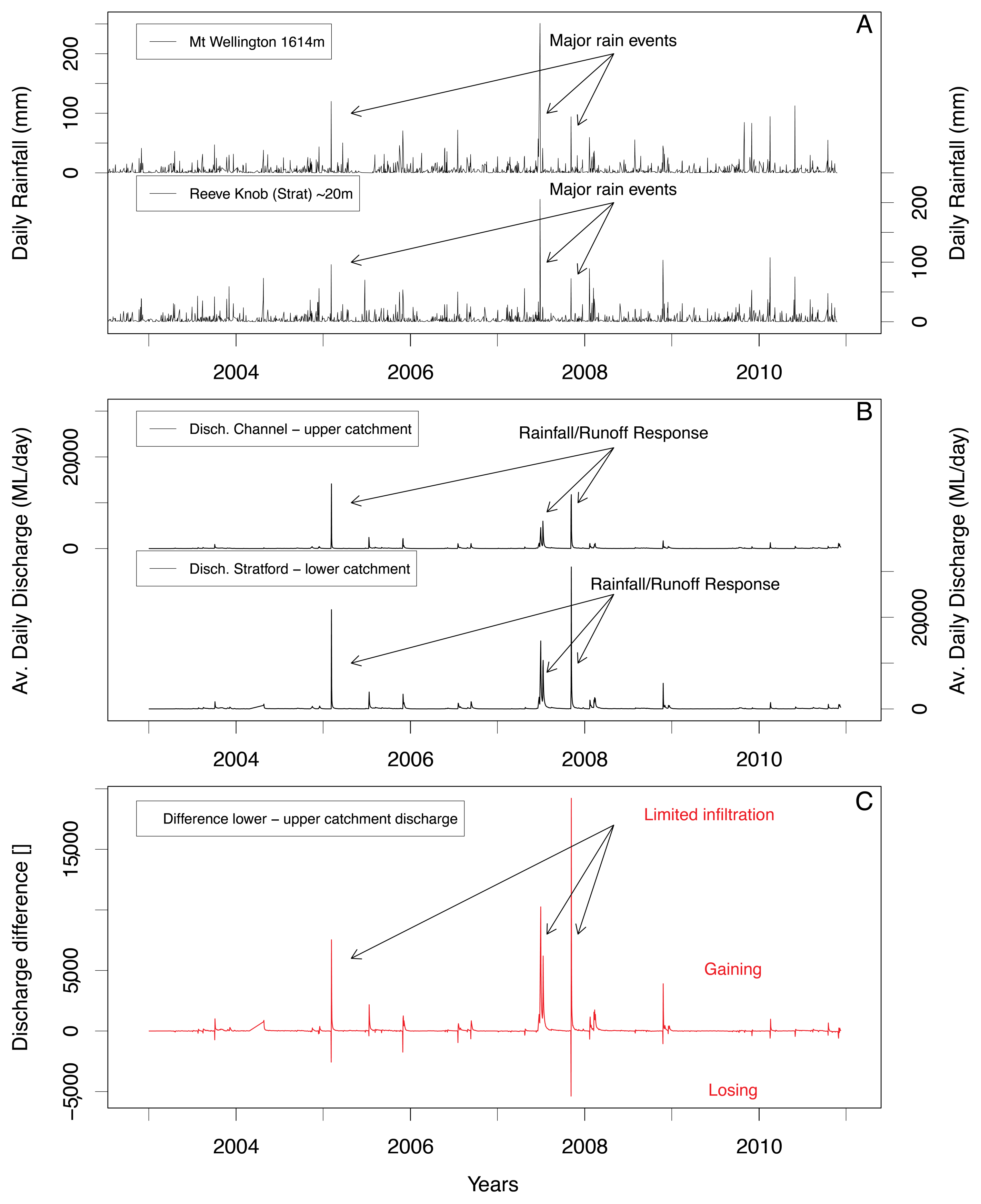
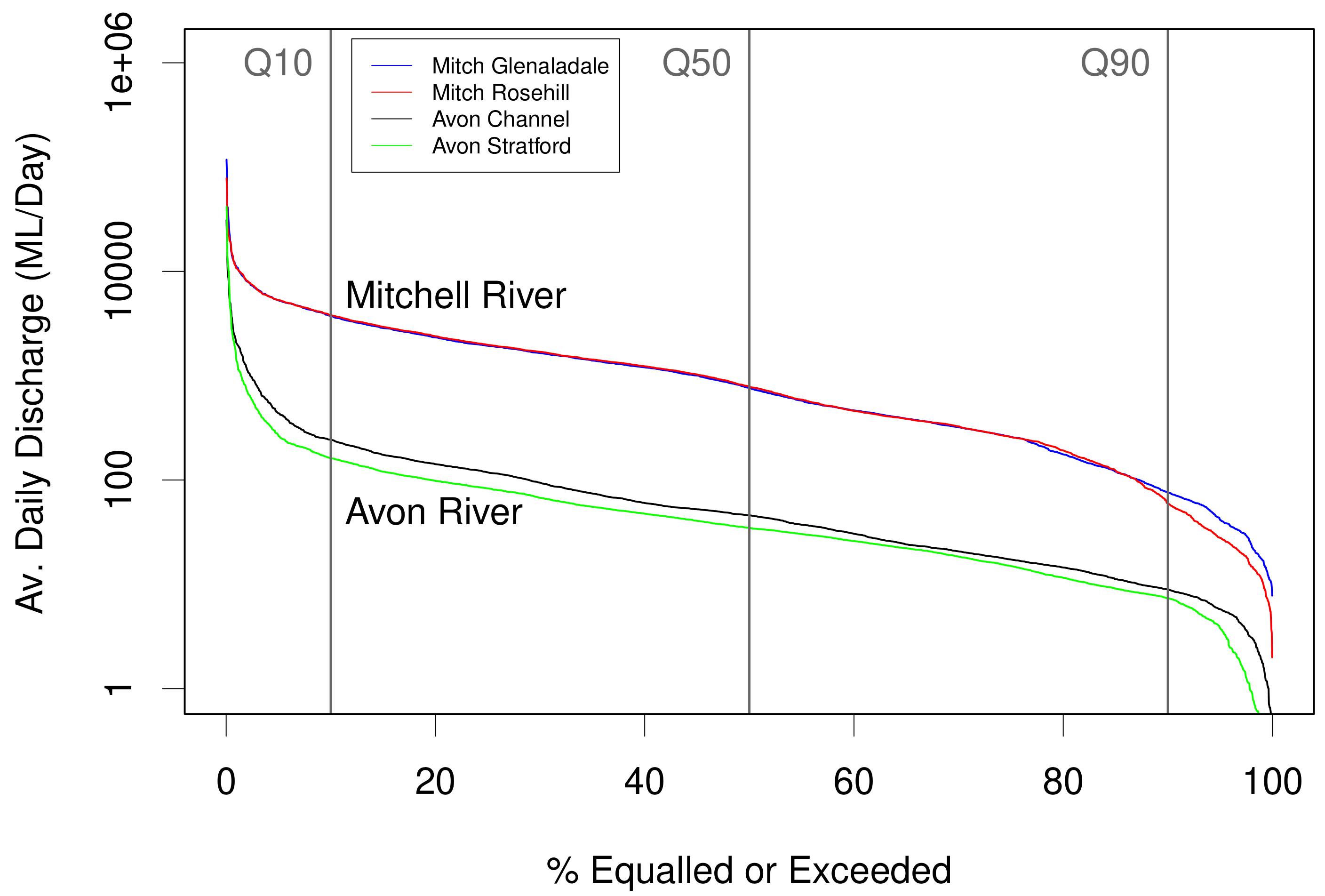
3.1. Water Balance and Hydrograph Analysis
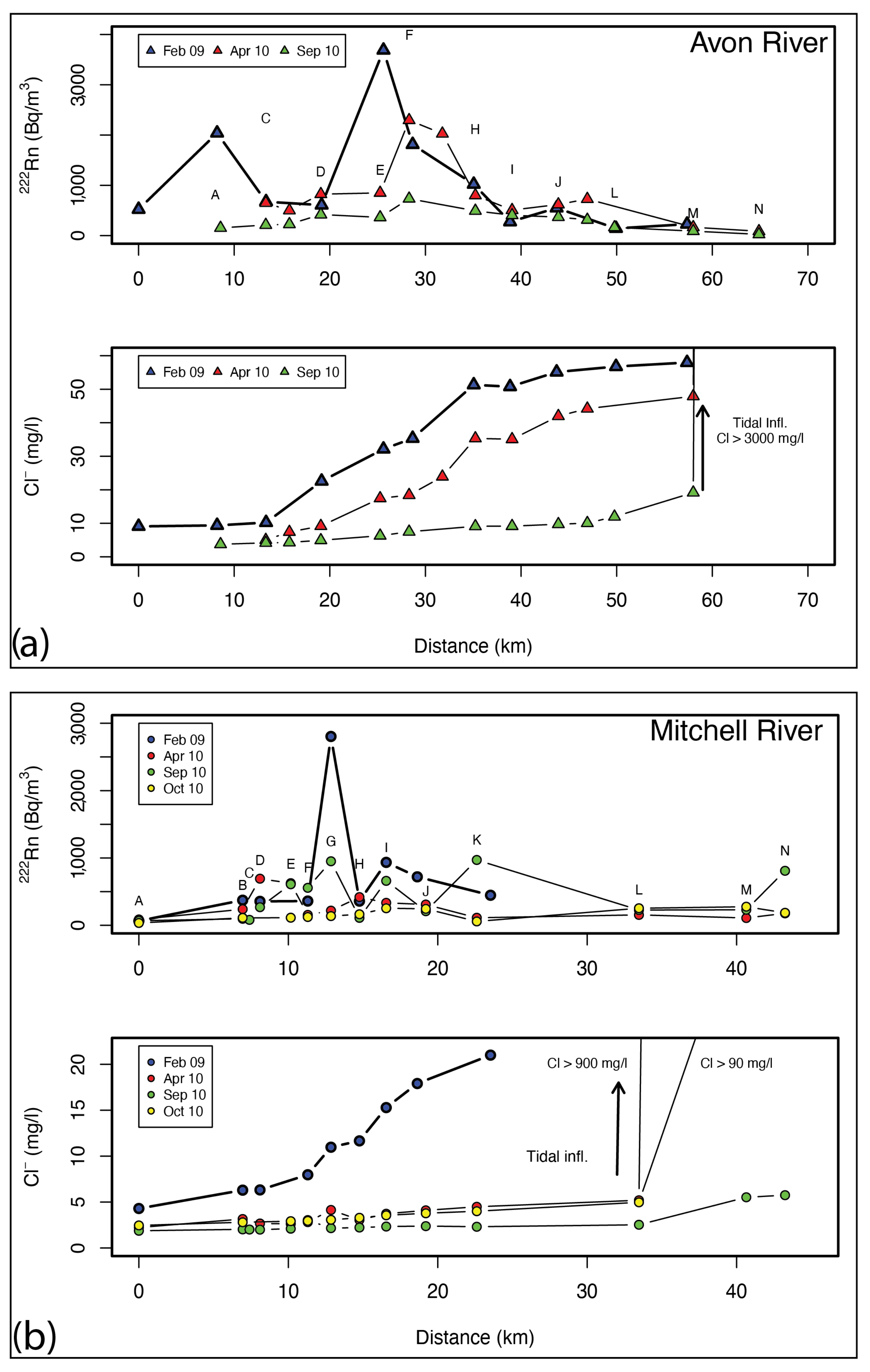
3.2. Major Ion Chemistry
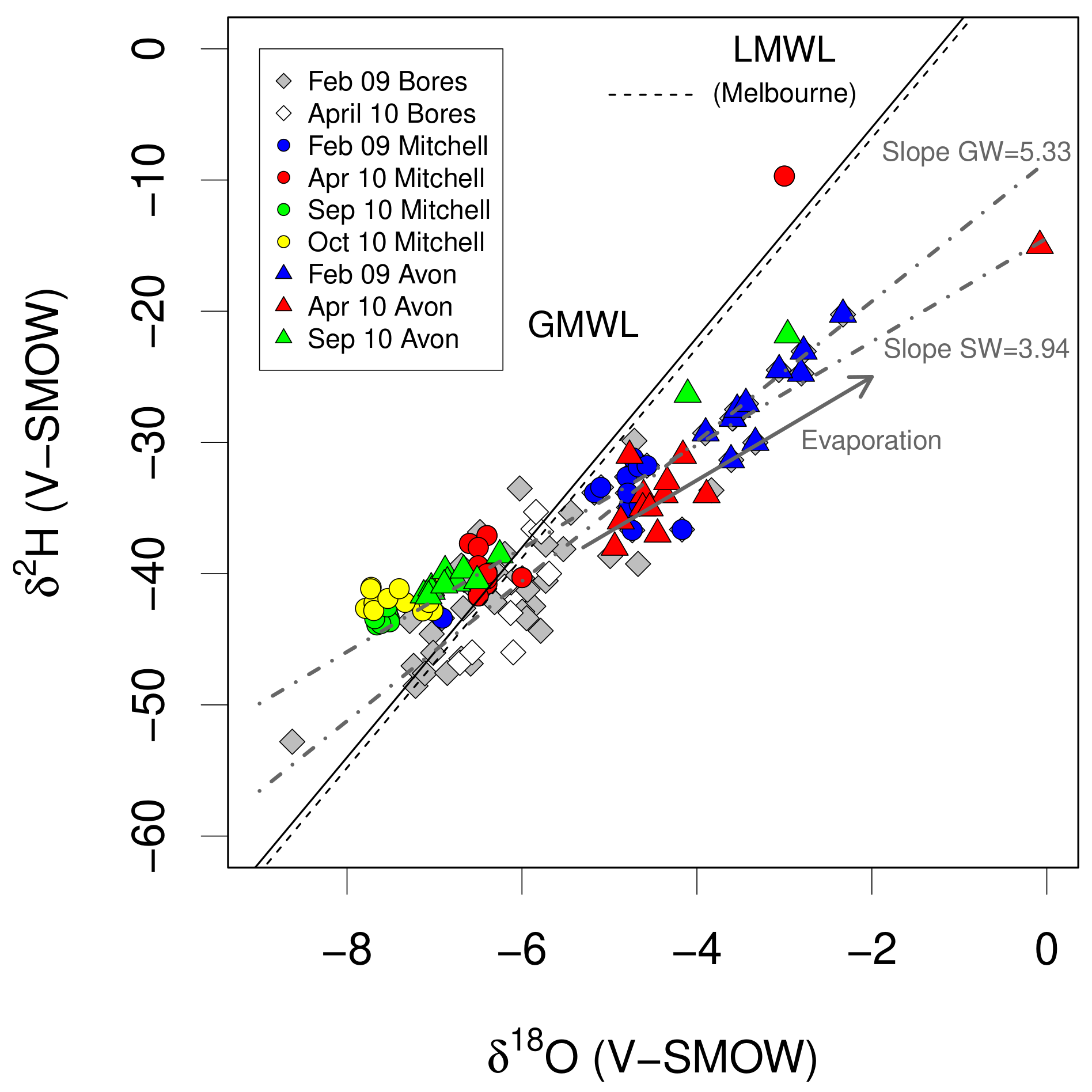
3.3. Stable Isotopes
3.4. Radon
3.5. Hyporheic Zone Exchange
4. Discussion
4.1. Baseflow from Hydrograph Analysis
4.2. Chemical Baseflow Separation
Constraining Baseflow Contributions
5. Conclusions
5.1. Methods Comparison
5.2. Baseflow in the Avon and the Mitchell River and the Implications for Water Resources
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
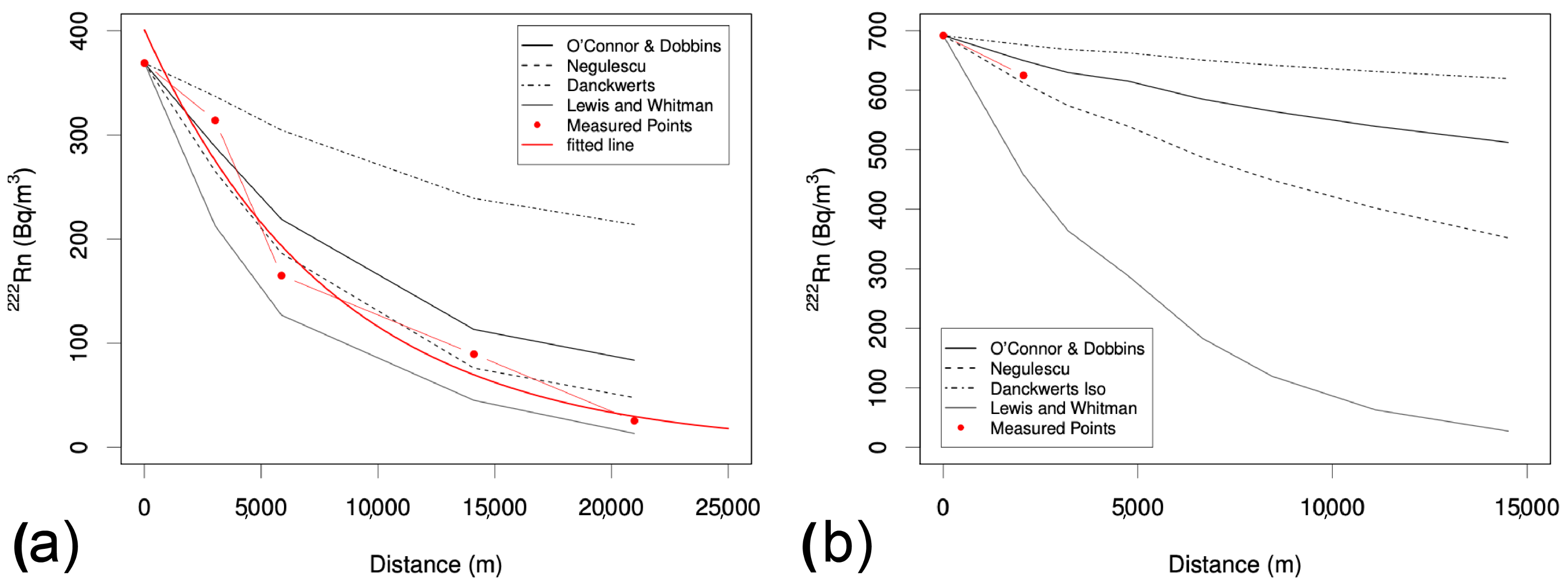
Appendix A. Degassing Models and Parameter Estimation
Appendix A.1. Theoretical Background Radon Degassing
Appendix B. Sensitivity Analysis
Appendix B.1. The Sensitivity of Single Terms in the Mass Balance Equation
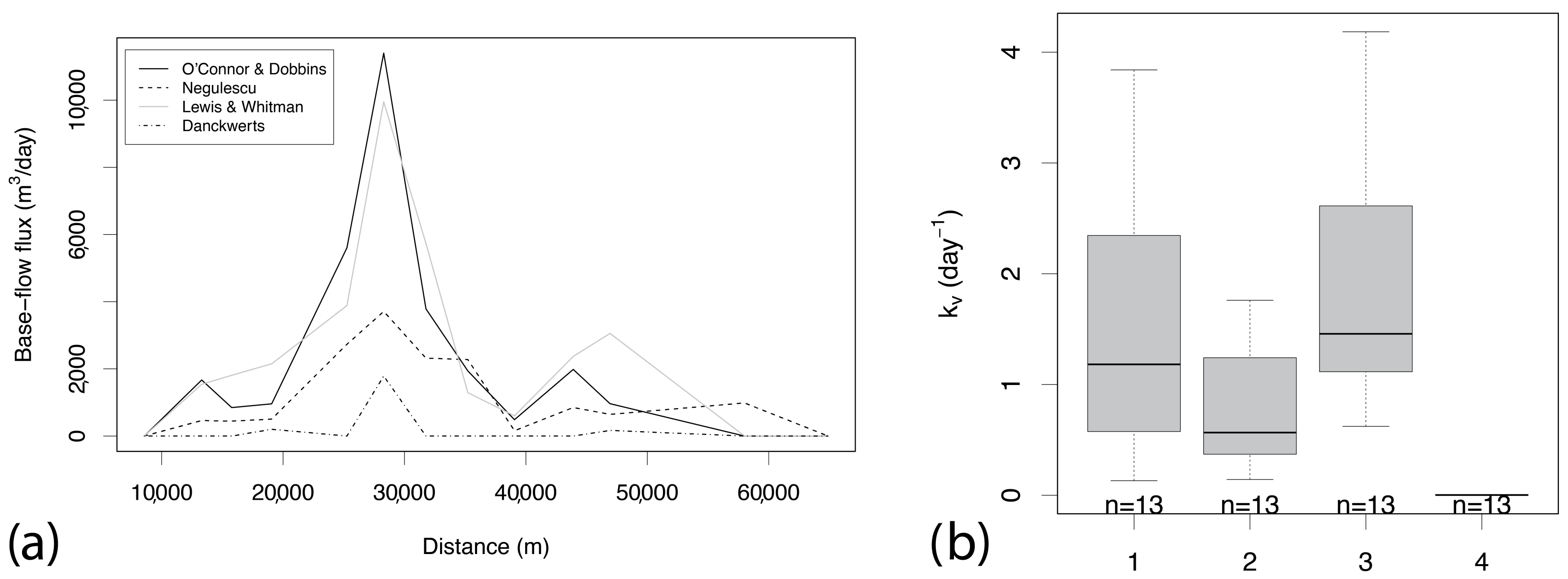
Appendix B.2. Comparison in between 222 Rn and Cl in the Mitchell River and the Mitchell Plains
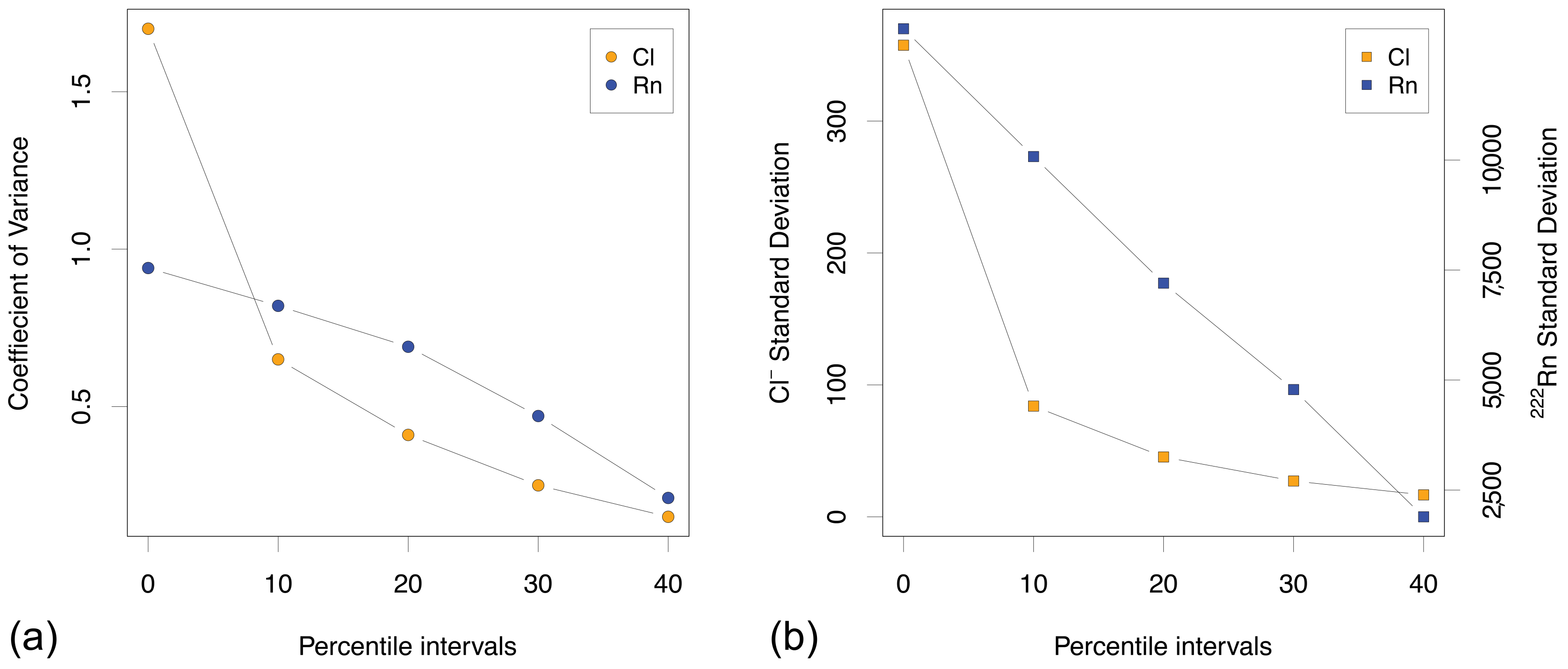
| Radon | Baseflow Flux | Baseflow Flux | Chloride | Baseflow Flux | Baseflow Flux | |
|---|---|---|---|---|---|---|
| mBq m | m d | % | mg L | m d | % | |
| Minimum | 306 | 93,840.00 | 147.69 | 4.9 | 151.62 | 0.24 |
| 1st Qu | 2215 | 219,608.62 | 345.64 | 60 | 42,041.72 | 66.17 |
| Median | 9547 | 22,469.30 | 35.36 | 112 | 11,952.75 | 18.81 |
| Mean | 13,780 | 14,625.74 | 23.02 | 210 | 5284.92 | 8.32 |
| 3rd Qu | 13,700 | 7887.91 | 12.41 | 193 | 5847.10 | 9.20 |
| Maximum | 39,850 | 4383.00 | 6.90 | 2018 | 473.54 | 0.75 |
| Minimum | 607 | 104,801.40 | 164.95 | 8 | 78,954.16 | 124.27 |
| 1st Qu | 2765 | 93,054.47 | 146.46 | 63 | 36,096.86 | 56.81 |
| Median | 10,169 | 20,879.79 | 32.86 | 122 | 105,74.58 | 16.64 |
| Mean | 14,165 | 14,368.82 | 22.62 | 167 | 6986.02 | 11.00 |
| 3rd Qu | 24,105 | 16,206.39 | 25.51 | 187 | 6075.42 | 9.56 |
| Maximum | 33,382 | 5368.63 | 8.45 | 841 | 1161.60 | 1.83 |
| 10 Per. Mean | 12,178.00 | 12,834.55 | 20.20 | 223.70 | 4683.13 | 7.37 |
| 20 Per. Mean | 10,432.00 | 20,273.85 | 31.91 | 266.00 | 4015.68 | 7.37 |
| 30 Per. Mean | 10,151.00 | 20,922.60 | 32.93 | 318.49 | 3278.86 | 5.16 |
| 40 Per. Mean | 9007.00 | 48,167.38 | 75.81 | 347.95 | 2972.94 | 4.68 |
| Bore ID | Zone 55 | Zone 55 | Formation | Total | Min. Screen | Max. Screen | Distance to |
|---|---|---|---|---|---|---|---|
| Easting | Northing | Depth (m) | Depth (m) | Depth (m) | River (m) | ||
| Mitchell R. | |||||||
| B105392 | 533,546.77 | 5,819,040.87 | Haunted Hills | 30.48 | 22.25 | 25.9 | 887 |
| B105476 | 535,250.04 | 5,818,757.04 | Haunted Hills | 15 | 6 | 12 | 370 |
| B105477 | 534,663.30 | 5,818,097.94 | Haunted Hills | 13 | 2.5 | 8.5 | 100 |
| B105478 | 532,174.27 | 5,819,232.81 | Latrobe Valley | 80 | 47.55 | 62.8 | 415 |
| B105479 | 532,177.63 | 5,819,248.46 | Alluvium | 34 | 13 | 28 | 407 |
| B105480 | 544,361.65 | 5,815,254.82 | Haunted Hills | 13 | 3 | 9 | 639 |
| B110165 | 542,495.67 | 5,815,901.64 | Haunted Hills | 13 | 4 | 10 | 1280 |
| B110177 | 533,766.36 | 5,819,424.67 | Latrobe Valley | 64 | 39 | 42 | 1094 |
| B110978 | 532,125.88 | 5,819,256.26 | Latrobe Valley | 74.5 | 51.5 | 56.5 | 378 |
| B110979 | 536,007.00 | 5,817555.00 | Haunted Hills | 14 | 7 | 13 | 776 |
| B111800 | 536,007.12 | 5,817,555.01 | Latrobe Valley | 108.5 | 58 | 73.5 | NA |
| B140279 | 547,251.10 | 5,813,471.72 | Alluvium | 10.5 | 5 | 9 | 963 |
| B140281 | 551,616.33 | 5,813,146.87 | Alluvium | 17 | 11 | 16 | 364 |
| B56528 | 543,527.55 | 5,815,296.52 | Alluvium | 9.14 | 2.43 | 8.53 | 830 |
| B56529 | 543,606.00 | 5,815,859.00 | Alluvium | 12.19 | 7.01 | 10.79 | 260 |
| B56530 | 543,446.96 | 5,814,801.54 | Alluvium | 7.62 | 3.65 | 7.62 | 1330 |
| B56531 | 540,429.49 | 5,816,748.18 | Alluvium | 9.14 | 3.35 | 8.53 | 1020 |
| B56532 | 540,532.95 | 5,817,382.06 | Alluvium | 6.09 | 3.65 | 6.09 | 390 |
| B56533 | 538,790.13 | 5,816,888.64 | Alluvium | 5.48 | 3.04 | 5.18 | 1720 |
| B56534 | 538,900.00 | 5,817,567.00 | Alluvium | 9.14 | 1.52 | 5.18 | 1010 |
| B56535 | 538,983.63 | 5,818,113.26 | Alluvium | 6.09 | 3.35 | 6.09 | 475 |
| B56536 | 537,168.28 | 5,817,065.98 | Alluvium | 6.4 | 3.65 | 5.48 | 1620 |
| B56537 | 537,253.70 | 5,817,597.20 | Alluvium | 8.84 | 4.57 | 8.83 | 1040 |
| B56538 | 537,358.10 | 5,818,228.16 | Alluvium | 8.22 | 4.57 | 8.22 | 440 |
| B56539 | 536,090.28 | 5,818,069.47 | Alluvium | 6.4 | 5.48 | 6.4 | 390 |
| B56540 | 536,004.43 | 5,817,543.67 | Alluvium | 6.26 | 2.74 | 6.09 | 930 |
| B56541 | 535,280.26 | 5,817,366.23 | Alluvium | 8.84 | 260 | ||
| B56546 | 535,307.58 | 5,817,352.47 | Alluvium | 16 | 4.6 | 10.8 | 320 |
| B56547 | 535,617.48 | 5,817,211.60 | Alluvium | 13 | 6 | 12.6 | 605 |
| B56548 | 536,000.03 | 5,817,513.76 | Alluvium | 12.5 | 5.7 | 12.2 | 770 |
| B56549 | 536,431.10 | 5,816,879.87 | Alluvium | 12 | 5.65 | 12 | 1550 |
| B56550 | 537,262.40 | 5,817,625.36 | Alluvium | 13 | 6 | 12.5 | 1040 |
| B56551 | 537,161.16 | 5,817,037.97 | Alluvium | 14 | 6.8 | 13.2 | 1620 |
| B56552 | 541,992.68 | 5,816,076.16 | Alluvium | 10 | 2 | 8.35 | 1130 |
| B56553 | 542,109.82 | 5,816,820.05 | Alluvium | 11 | 2.5 | 9 | 380 |
| B56744 | 542,151.80 | 5,817,128.18 | Haunted Hills | 12 | 3.5 | 9.5 | 60 |
| B80760 | 545,753.20 | 5,814,007.51 | Alluvium | 6.4 | 1.82 | 5.79 | 550 |
| B80761 | 545,917.80 | 5,814,622.14 | Alluvium | 9.14 | 3.96 | 8.22 | 490 |
| B80762 | 546,008.00 | 5,815,253.77 | Alluvium | 6.4 | 2.43 | 3.96 | 595 |
| B80866 | 544,977.66 | 5,815,480.21 | Haunted Hills | 10 | 3 | 7 | 430 |
| Avon R. | |||||||
| B110166 | 506,559.95 | 5,813,840.79 | Alluvium | 16.5 | 5.5 | 11.5 | 7060 |
| B110167 | 506,764.67 | 5,813,738.34 | Alluvium | 14 | 5 | 11 | 7157 |
| B110168 | 506,979.30 | 5,813,603.51 | Alluvium | 14 | 5.5 | 11.5 | 7290 |
| B110171 | 503,950.26 | 5,811,868.86 | Alluvium | 12 | 5.5 | 8.5 | 3760 |
| B110172 | 503,684.46 | 5,811,915.97 | Alluvium | 44 | 2.5 | 6.5 | 3560 |
| Avon R. | |||||||
|---|---|---|---|---|---|---|---|
| Year | Q The Channel | Q Stratford | Q Stratford | Q Valencia | Q Freestone | Difference | Difference |
| (ML y) | (ML y) | (Extr. Corr. 20%) | Cr. (ML y) | Cr. (ML y) | (ML y) | (Extr. Corr.) | |
| 2003 | 16,560.7 | 26,754.3 | 32,105.2 | 3008.0 | 2993.9 | 4191.6 | 9542.5 |
| 2004 | 14,679.6 | 24,608.3 | 29,530.0 | 4079.1 | 6215.1 | −365.5 | 4556.2 |
| 2005 | 53,144.6 | 85,737.0 | 102,884.4 | 149,11.2 | 159,92.7 | 1688.6 | 18,836.0 |
| 2006 | 18,212.0 | 29,517.7 | 35,421.3 | 4551.5 | 3470.0 | 3284.3 | 9187.8 |
| 2007 | 92,915.3 | 183,749.6 | 220,499.6 | 71,291.0 | 108,309.8 | −88,766.4 | −52016.5 |
| 2008 | 37,488.2 | 74,120.0 | 89,027.9 | 14,898.0 | 21,722.4 | 11.4 | 14919.4 |
| 2009 | 12,851.3 | 13,265.2 | 15,918.2 | 2967.2 | 1823.7 | −4377.0 | −1724.0 |
| 2010 | 32,532.1 | 38,215.6 | 45,876.9 | 7501.1 | 9212.8 | −11,030.4 | −3369.1 |
| Mitchell River | |||||
|---|---|---|---|---|---|
| Year | Q Glenaladale | Q Rosehill | Q Rosehill | Difference | Difference |
| (ML y) | (ML y) | (Extraction Corr. 5%) | (Extraction Corr.) | ||
| 2004 | 525,576.0 | 544,578.9 | 571,807.8 | 19,002.9 | 46,231.8 |
| 2005 | 743,244.8 | 707,909.5 | 707,909.5 | −35,335.3 | 60.2 |
| 2006 | 122,620.0 | 112,478.4 | 118,102.3 | −10,141.6 | −4517.7 |
| 2007 | 928,374.2 | 806,524.4 | 846,850.6 | −121,849.9 | −81,523.6 |
| 2008 | 399,924.1 | 400,635.1 | 420,666.9 | 711.0 | 20,742.8 |
| 2009 | 442,722.0 | 437,898.6 | 459,793.5 | −4832.5 | 17,071.5 |
| 2010 | 905,612.3 | 824,233.4 | 865,445.1 | −81,378.9 | −400,167.2 |
| Site Name | Distance | Lon | Lat | EC | T | pH | F | Cl | Br | NO | SO | HCO | Ba | Ca | Fe | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (km) | (S cm) | (C) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | ||||
| February 2009 | ||||||||||||||||
| The Channel | 0 | 146.92629 | −37.80473 | 90.9 | 22 | 7.94 | 0.06 | 9.08 | 0.03 | 0.03 | 1.19 | 5.00 | 0.01 | 6.49 | 0.11 | 1.33 |
| Browns House | 8.21 | 146.94689 | −37.81662 | 98 | 24.7 | 7.64 | 0.07 | 9.38 | 0.87 | 0.02 | 1.22 | 29.00 | 0.01 | 6.09 | 0.17 | 1.35 |
| Wombat Flat | 13.3 | 146.945553 | −37.816774 | 95.5 | 23.1 | 7.74 | 0.06 | 10.23 | 0.69 | 0.04 | 1.25 | 36.00 | 0.01 | 6.03 | 0.19 | 1.40 |
| Valencia Creek | 19.06 | 146.986401 | −37.825054 | 159.4 | 22.3 | 7.51 | 0.07 | 22.57 | 1.37 | 0.11 | 8.75 | 43.00 | 0.02 | 8.31 | 0.21 | 1.55 |
| Bushy Park | 25.26 | 147.008397 | −37.871086 | 184.1 | 22.5 | 7.28 | 0.06 | 32.14 | 1.81 | 0.19 | 10.43 | 34.00 | 0.02 | 8.05 | 0.12 | 1.84 |
| Pierces Lane | 28.29 | 147.007054 | −37.897158 | 212 | 22.3 | 7.65 | 0.06 | 35.34 | 2.47 | 0.96 | 15.04 | 38.00 | 0.03 | 9.42 | 2.06 | |
| School Lane | 35.22 | 147.036527 | −37.929029 | 283 | 24.2 | 7.58 | 0.07 | 51.31 | 3.15 | 0.05 | 14.23 | 41.00 | 0.03 | 9.43 | 2.30 | |
| Stewarts Lane | 39.06 | 147.055492 | −37.950082 | 295 | 24.1 | 7.72 | 0.13 | 50.76 | 3.17 | 0.05 | 22.10 | 46.00 | 0.04 | 10.63 | 3.50 | |
| Stratford | 43.9 | 147.076156 | −37.970044 | 332 | 26 | 7.95 | 0.14 | 55.13 | 3.58 | 0.26 | 24.32 | 53.00 | 0.05 | 11.30 | 4.02 | |
| Redbank Rd | 49.93 | 147.18208 | −38.02224 | 335 | 21.3 | 7.90 | 0.10 | 56.77 | 3.84 | 0.03 | 23.02 | 45.00 | 0.04 | 9.96 | 3.65 | |
| Chinns Bridge | 58.01 | 147.180164 | −38.022914 | 354 | 19.2 | 7.55 | 0.15 | 57.97 | 4.57 | 1.41 | 19.36 | 55.00 | 0.03 | 10.04 | 0.03 | 5.33 |
| April 2010 | ||||||||||||||||
| Wombat Flat | 13.3 | 146.945553 | −37.816774 | 101.7 | 0.05 | 5.02 | 0.02 | 0.07 | 0.94 | 0.01 | 4.90 | 0.07 | 1.13 | |||
| Smyths Road | 15.77 | 146.966165 | −37.803062 | 86.9 | 0.08 | 7.41 | 0.02 | 0.04 | 1.29 | 0.01 | 5.07 | 0.09 | 1.16 | |||
| Valencia Creek Rd | 19.06 | 146.986401 | −37.825054 | 109.8 | 0.08 | 9.18 | 0.03 | 0.08 | 2.82 | 0.02 | 5.92 | 0.11 | 1.26 | |||
| Bushy Park | 25.26 | 147.008397 | −37.871086 | 141.7 | 0.08 | 17.45 | 0.04 | 0.13 | 5.02 | 0.02 | 5.70 | 0.07 | 1.40 | |||
| Pearces Lane | 28.29 | 147.007054 | −37.897158 | 152.6 | 0.07 | 18.42 | 0.07 | 0.42 | 5.93 | 0.02 | 6.32 | 0.04 | 1.50 | |||
| Ridley’s Lane | 31.77 | 147.01 | −37.92 | 184.6 | 0.06 | 23.91 | 0.07 | 0.69 | 7.74 | 0.02 | 6.98 | 0.15 | 1.57 | |||
| School’s Lane | 35.22 | 147.036527 | −37.929029 | 218 | 0.10 | 35.34 | 0.09 | 0.26 | 8.44 | 0.02 | 6.97 | 0.06 | 1.73 | |||
| Stewarts Lane | 39.06 | 147.055492 | −37.950082 | 239 | 0.11 | 35.08 | 0.11 | 0.05 | 14.03 | 0.03 | 7.32 | 0.07 | 2.06 | |||
| Stratford | 43.9 | 147.076156 | −37.970044 | 259 | 0.13 | 41.98 | 0.11 | 0.06 | 14.71 | 0.03 | 7.87 | 0.07 | 2.41 | |||
| Knobs Reserve | 46.93 | 147.097045 | −37.983573 | 372 | 0.14 | 44.20 | 0.12 | 0.17 | 14.73 | 0.04 | 7.93 | 0.06 | 2.47 | |||
| Chinns Bridge | 58.01 | 147.180164 | −38.022914 | 280 | 0.14 | 47.91 | 0.13 | 0.16 | 13.41 | 0.03 | 7.26 | 3.01 | ||||
| Springberg Lane | 64.88 | 147.247886 | −38.030347 | 15,600 | 0.40 | 4833.05 | 23.20 | 1.20 | 926.55 | 142.64 | 0.14 | 168.24 | ||||
| September 2010 | ||||||||||||||||
| Browns House | 8.57 | 146.92663 | −37.804165 | 53.9 | 13 | 0.04 | 3.75 | 0.01 | 0.13 | 0.91 | 0.01 | 3.38 | 0.03 | 0.56 | ||
| Wombat Flat | 13.3 | 146.945553 | −37.816774 | 53 | 11.9 | 0.05 | 4.16 | 0.01 | 0.02 | 1.01 | 0.01 | 3.33 | 0.04 | 0.56 | ||
| Smyths Road | 15.77 | 146.966165 | −37.803062 | 55.3 | 11.8 | 0.05 | 4.29 | 0.00 | 0.01 | 1.04 | 0.00 | 3.38 | 0.04 | 0.57 | ||
| Valencia Creek | 19.06 | 146.986401 | −37.825054 | 63.2 | 13.8 | 0.04 | 4.94 | 0.01 | 0.03 | 1.38 | 0.01 | 3.79 | 0.09 | 0.60 | ||
| Bushy Park | 25.26 | 147.008397 | −37.871086 | 74.2 | 14.5 | 0.05 | 6.30 | 0.02 | 0.03 | 1.95 | 0.01 | 3.63 | 0.08 | 0.73 | ||
| Pierces Lane | 28.29 | 147.007054 | −37.897158 | 77.5 | 14.4 | 0.06 | 7.48 | 0.01 | 0.05 | 2.35 | 0.01 | 3.73 | 0.08 | 0.75 | ||
| School Lane | 35.22 | 147.036527 | −37.929029 | 89.6 | 13.6 | 0.06 | 9.11 | 0.01 | 0.11 | 2.89 | 0.01 | 3.97 | 0.12 | 0.79 | ||
| Stewarts Lane | 39.06 | 147.055492 | −37.950082 | 97.8 | 14.5 | 0.06 | 9.16 | 0.02 | 0.02 | 3.57 | 0.01 | 4.13 | 0.15 | 0.89 | ||
| Stratford | 43.9 | 147.076156 | −37.970044 | 103 | 11.2 | 0.05 | 9.73 | 0.02 | 0.01 | 3.90 | 0.01 | 4.24 | 0.18 | 0.97 | ||
| Knobs Reserve | 46.93 | 147.097045 | −37.983573 | 104.1 | 12.6 | 0.06 | 10.06 | 0.02 | 0.05 | 3.92 | 0.01 | 4.24 | 0.18 | 0.99 | ||
| Redbank Road | 49.77 | 147.115774 | −37.998641 | 106 | 12.4 | 0.06 | 11.97 | 0.03 | 0.02 | 4.40 | 0.01 | 4.24 | 0.16 | 1.00 | ||
| Chinns Bridge | 58.01 | 147.180164 | −38.022914 | 142 | 12.8 | 0.07 | 19.16 | 0.05 | 0.02 | 5.05 | 0.01 | 4.72 | 0.15 | 1.37 | ||
| Springberg | 64.88 | 147.247886 | −38.030347 | 11,500 | 12.2 | 0.39 | 3420.71 | 11.28 | 10.76 | 473.65 | 0.02 | 64.79 | 71.06 | |||
| Stratfieldsaye | 67.97 | 147.286877 | −38.042783 | >30,000 | 0.93 | 4940.82 | 16.94 | 6.79 | 747.70 | 0.03 | 90.62 | 105.45 |
| Site Name | Mg | Na | Si | Sr | Na/Cl | Cl/Br | K/Cl | Ca/Mg | Na/Ca | Ca/Cl | Mg/Cl | O | H | C | Rn | I |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (mg L) | (mg L) | (mg L) | (mg L) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (Bq m) | (g L) | ||||
| February 2009 | ||||||||||||||||
| The Channel | 3.38 | 6.63 | 2.51 | 1.13 | 903.73 | 0.13 | 1.17 | 1.78 | 0.63 | 0.54 | −3.59 | −28.15 | −12.03 | 523.00 | 2.45 | |
| Browns House | 3.62 | 6.76 | 2.40 | 1.11 | 675.05 | 0.13 | 1.02 | 1.93 | 0.57 | 0.56 | −2.81 | −24.74 | −10.42 | 2041.00 | 2.07 | |
| Wombat Flat | 3.80 | 7.19 | 2.33 | 1.08 | 713.21 | 0.12 | 0.96 | 2.09 | 0.52 | 0.54 | −2.33 | −20.25 | −10.96 | 674.38 | 4.18 | |
| Valencia Creek | 5.89 | 14.59 | 2.39 | 1.00 | 801.39 | 0.06 | 0.86 | 3.06 | 0.32 | 0.38 | −3.06 | −24.48 | −11.92 | 607.88 | 2.44 | |
| Bushy Park | 6.86 | 17.81 | 2.05 | 0.85 | 738.74 | 0.05 | 0.71 | 3.86 | 0.22 | 0.31 | −3.61 | −31.34 | −12.88 | 3688.75 | 2.28 | |
| Pierces Lane | 8.68 | 19.90 | 1.83 | 0.87 | 771.63 | 0.05 | 0.66 | 3.69 | 0.24 | 0.36 | −3.90 | −29.29 | −12.66 | 1812.50 | 2.38 | |
| School Lane | 9.96 | 34.51 | 1.91 | 1.04 | 622.20 | 0.04 | 0.57 | 6.39 | 0.16 | 0.28 | −3.33 | −30.01 | −12.11 | 1021.25 | 5.44 | |
| Stewarts Lane | 10.55 | 37.06 | 1.64 | 1.12 | 654.64 | 0.06 | 0.61 | 6.08 | 0.18 | 0.30 | −3.59 | −28.18 | −11.97 | 274.88 | 4.08 | |
| Stratford | 10.76 | 41.74 | 1.82 | 1.17 | 643.64 | 0.07 | 0.64 | 6.44 | 0.18 | 0.28 | −3.54 | −27.49 | −11.90 | 550.00 | 5.42 | |
| Redbank Rd | 10.91 | 43.83 | 1.20 | 1.19 | 652.35 | 0.06 | 0.55 | 7.69 | 0.15 | 0.28 | −3.44 | −27.05 | −12.32 | 143.38 | 9.78 | |
| Chinns Bridge | 11.00 | 47.24 | 0.77 | 1.26 | 557.31 | 0.08 | 0.55 | 8.22 | 0.15 | 0.28 | −2.78 | −23.06 | −11.48 | 228.25 | 12.47 | |
| April 2010 | ||||||||||||||||
| Wombat Flat | 2.94 | 5.41 | 1.72 | 0.02 | 1.69 | 473.33 | 0.21 | 1.02 | 1.97 | 0.26 | 0.85 | −4.94 | −38.00 | 650.00 | ||
| Smyths Road | 3.10 | 6.23 | 1.59 | 0.02 | 1.29 | 696.67 | 0.14 | 0.98 | 2.13 | 0.34 | 0.62 | −4.77 | −31.00 | 502.00 | ||
| Valencia Creek Rd | 3.81 | 9.13 | 1.87 | 0.03 | 1.54 | 647.50 | 0.12 | 0.93 | 2.70 | 0.41 | 0.62 | −4.87 | −36.00 | 825.00 | ||
| Bushy Park | 4.97 | 13.79 | 1.56 | 0.03 | 1.22 | 984.00 | 0.08 | 0.68 | 4.23 | 0.63 | 0.43 | −4.61 | −34.00 | 850.00 | ||
| Pearces Lane | 5.61 | 14.21 | 1.68 | 0.03 | 1.19 | 577.78 | 0.08 | 0.69 | 3.92 | 0.68 | 0.44 | −4.62 | −35.00 | 2296.00 | ||
| Ridley’s Lane | 6.60 | 19.52 | 1.87 | 0.04 | 1.26 | 748.89 | 0.06 | 0.64 | 4.89 | 0.85 | 0.40 | −4.37 | −34.00 | 2028.00 | ||
| School’s Lane | 7.05 | 24.51 | 1.95 | 0.04 | 1.07 | 906.36 | 0.04 | 0.60 | 6.15 | 1.17 | 0.29 | −4.54 | −35.00 | 801.00 | ||
| Stewarts Lane | 7.32 | 26.19 | 1.76 | 0.04 | 1.15 | 706.43 | 0.05 | 0.61 | 6.23 | 1.17 | 0.30 | −4.45 | −37.00 | 508.00 | ||
| Stratford | 7.71 | 30.50 | 1.85 | 0.05 | 1.12 | 845.71 | 0.05 | 0.61 | 6.79 | 1.38 | 0.27 | −4.34 | −33.00 | 620.00 | ||
| Knobs Reserve | 7.86 | 31.85 | 1.71 | 0.05 | 1.11 | 831.33 | 0.05 | 0.62 | 7.02 | 1.45 | 0.26 | −4.16 | −31.00 | 728.00 | ||
| Chinns Bridge | 7.94 | 35.08 | 0.69 | 0.05 | 1.13 | 844.38 | 0.06 | 0.55 | 8.45 | 1.53 | 0.24 | −3.89 | −34.00 | 167.00 | ||
| Springberg Lane | 494.28 | 4062.29 | 4.45 | 2.70 | 1.30 | 469.59 | 0.03 | 0.17 | 49.65 | 0.15 | −0.08 | −15.00 | 87.00 | |||
| September 2010 | ||||||||||||||||
| Browns House | 1.84 | 3.94 | 2.20 | 0.01 | 1.62 | 931.19 | 0.14 | 1.12 | 2.03 | 0.80 | 0.71 | −7.12 | −41.64 | 153.63 | ||
| Wombat Flat | 1.83 | 3.88 | 2.16 | 0.01 | 1.44 | 970.51 | 0.12 | 1.10 | 2.03 | 0.71 | 0.64 | −7.04 | −41.10 | 212.38 | ||
| Smyths Road | 1.87 | 4.02 | 2.17 | 0.01 | 1.44 | 1964.71 | 0.12 | 1.10 | 2.07 | 0.70 | 0.64 | −7.03 | −41.36 | 226.50 | ||
| Valencia Creek | 2.07 | 4.63 | 2.18 | 0.01 | 1.45 | 1946.25 | 0.11 | 1.11 | 2.13 | 0.68 | 0.61 | −7.07 | −41.71 | 419.64 | ||
| Bushy Park | 2.45 | 6.09 | 1.86 | 0.01 | 1.49 | 648.75 | 0.10 | 0.90 | 2.92 | 0.51 | 0.57 | −6.88 | −39.80 | 363.29 | ||
| Pierces Lane | 2.60 | 6.36 | 1.74 | 0.02 | 1.31 | 1270.81 | 0.09 | 0.87 | 2.98 | 0.44 | 0.51 | −6.85 | −40.65 | 734.56 | ||
| School Lane | 3.02 | 8.27 | 1.48 | 0.02 | 1.40 | 1644.43 | 0.08 | 0.80 | 3.63 | 0.39 | 0.48 | −6.74 | −40.74 | 493.38 | ||
| Stewarts Lane | 3.10 | 8.65 | 1.35 | 0.02 | 1.46 | 964.07 | 0.09 | 0.81 | 3.65 | 0.40 | 0.49 | −6.89 | −40.88 | 405.52 | ||
| Stratford | 3.20 | 9.30 | 1.21 | 0.02 | 1.47 | 1245.93 | 0.09 | 0.80 | 3.83 | 0.39 | 0.48 | −41.32 | 368.98 | |||
| Knobs Reserve | 3.26 | 9.65 | 1.13 | 0.02 | 1.48 | 988.06 | 0.09 | 0.79 | 3.97 | 0.37 | 0.47 | −6.67 | −39.74 | 314.02 | ||
| Redbank Road | 3.36 | 10.08 | 1.11 | 0.02 | 1.30 | 951.84 | 0.08 | 0.77 | 4.14 | 0.31 | 0.41 | −6.51 | −40.55 | 164.92 | ||
| Chinns Bridge | 4.06 | 14.85 | 1.06 | 0.03 | 1.20 | 932.94 | 0.06 | 0.70 | 5.49 | 0.22 | 0.31 | −6.25 | −38.59 | 89.48 | ||
| Springberg | 214.49 | 1767.17 | 2.26 | 1.11 | 0.80 | 683.56 | 0.02 | 0.18 | 47.55 | 0.02 | 0.09 | −4.11 | −26.35 | 25.53 | ||
| Stratfieldsaye | 310.09 | 2694.57 | 3.11 | 1.59 | 0.84 | 657.37 | 0.02 | 0.18 | 51.84 | 0.02 | 0.09 | −2.96 | −21.82 |
| Site Name | Distance | Lon | Lat | EC | T | pH | F | Cl | Br | NO | SO | HCO | Ba | Ca | Fe | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (km) | (S cm) | (C) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | ||||
| February 2009 | ||||||||||||||||
| Wentworth River | 147.34671 | −37.59451 | 70.5 | 7.52 | 0.07 | 5.09 | 0.00 | 0.27 | 0.96 | 30.00 | ||||||
| Hortan Rd | 147.37146 | −37.63254 | 71.8 | 7.28 | 0.05 | 3.52 | 0.01 | 0.03 | 0.99 | 38.00 | 0.01 | 4.21 | 0.16 | 1.10 | ||
| Jurgenson Pt | 147.37830 | −37.75795 | 90.5 | 7.45 | 0.05 | 4.13 | 0.01 | 0.01 | 1.02 | 13.00 | 0.01 | 4.28 | 0.13 | 1.57 | ||
| Glenaladale | 0.00 | 147.39366 | −37.78322 | 83.6 | 21.10 | 7.51 | 0.07 | 4.30 | 0.01 | 0.03 | 1.00 | 35.00 | 0.01 | 4.38 | 0.07 | 1.21 |
| Perry Rd | 6.94 | 147.40028 | −37.78764 | 90.7 | 0.06 | 6.30 | 0.02 | 0.24 | 1.93 | 14.00 | 0.01 | 4.62 | 1.18 | |||
| Cowells Rd | 8.10 | 147.42623 | −37.77870 | 97.7 | 24.30 | 7.94 | 0.05 | 6.32 | 0.02 | 0.03 | 1.71 | 40.00 | 0.01 | 4.67 | 0.13 | 1.14 |
| Hands Rd | 11.30 | 147.44339 | −37.78001 | 120.6 | 25.70 | 7.35 | 0.07 | 7.98 | 0.04 | 0.79 | 3.17 | 38.00 | 0.01 | 5.05 | 0.24 | 1.21 |
| Wuk Wuk Bridge | 12.85 | 147.46258 | −37.78642 | 122.4 | 23.10 | 7.68 | 0.07 | 10.98 | 0.04 | 0.49 | 5.12 | 55.00 | 0.01 | 5.71 | 0.05 | 1.28 |
| Ross Ln | 14.76 | 147.48009 | −37.79131 | 148.3 | 23.90 | 7.60 | 0.06 | 11.67 | 0.05 | 1.38 | 6.10 | 25.00 | 0.01 | 6.04 | 0.09 | 1.28 |
| Bulmers Ln | 16.55 | 147.49817 | −37.79791 | 157.2 | 22.80 | 7.56 | 0.08 | 15.29 | 0.06 | 2.42 | 8.26 | 38.00 | 0.02 | 7.68 | 1.32 | |
| Settlement Rd | 18.63 | 147.50438 | −37.80299 | 173.9 | 25.40 | 7.69 | 0.07 | 17.91 | 0.06 | 2.60 | 9.12 | 39.00 | 0.02 | 8.18 | 1.35 | |
| Soldiers Rd | 23.53 | 146.85466 | −37.81140 | 90.9 | 22.00 | 7.94 | 0.08 | 21.00 | 0.08 | 2.14 | 9.77 | 53.00 | 0.02 | 8.68 | 0.11 | 1.40 |
| April 2010 | ||||||||||||||||
| Glenaladale | 0.00 | 147.374558 | −37.763447 | 54.5 | 0.04 | 2.23 | 0.00 | 0.82 | 0.92 | 3.40 | 0.64 | 3.20 | 0.19 | |||
| Perry Rd | 6.94 | 147.391433 | −37.784979 | 58.1 | 0.05 | 3.16 | 0.01 | 0.01 | 1.77 | 4.10 | 0.68 | 3.20 | 0.20 | |||
| Cowells Rd | 8.10 | 147.392372 | −37.788664 | 66.1 | 0.04 | 2.67 | 0.01 | 0.00 | 1.05 | 3.60 | 0.64 | 3.20 | 0.20 | |||
| Alexanders Rd | 10.16 | 147.413379 | −37.777166 | 62.9 | 0.06 | 2.63 | 0.00 | 0.03 | 1.23 | 3.80 | 0.66 | 3.30 | 0.20 | |||
| Hands Rd | 11.30 | 147.425513 | −37.778667 | 62.3 | 0.05 | 2.82 | 0.01 | 1.12 | 1.30 | 3.80 | 0.65 | 3.30 | 0.18 | |||
| WukWuk Bridge | 12.85 | 147.443241 | −37.779986 | 63.7 | 0.05 | 4.14 | 0.01 | 0.00 | 2.83 | 5.20 | 0.69 | 3.50 | 0.19 | |||
| Ross Ln | 14.76 | 147.462571 | −37.787356 | 65.6 | 0.03 | 3.06 | 0.01 | 0.03 | 1.63 | 4.60 | 0.69 | 3.50 | 0.21 | |||
| Bulmers Ln | 16.55 | 147.480801 | −37.791039 | 90.5 | 0.04 | 3.73 | 0.01 | 0.11 | 1.99 | 4.80 | 0.70 | 3.60 | 0.22 | |||
| Settlement Rd | 19.20 | 147.503786 | −37.802592 | 72.2 | 0.04 | 4.10 | 0.01 | 0.30 | 2.20 | 4.90 | 0.68 | 3.70 | 0.19 | |||
| Soldiers Rd | 22.61 | 147.529575 | −37.809491 | 71.8 | 0.05 | 4.49 | 0.02 | 0.21 | 2.75 | 5.20 | 0.70 | 3.80 | 0.19 | |||
| Dockertys Rd | 33.46 | 147.589987 | −37.829372 | 72.8 | 0.05 | 5.20 | 0.02 | 0.25 | 2.33 | 5.40 | 0.71 | 4.00 | 0.19 | |||
| Wy Yung Bridge | 40.65 | 147.617858 | −37.813982 | 2500 | 0.08 | 915.41 | 2.57 | 0.27 | 131.66 | 445.00 | 18.00 | 19.00 | 0.06 | |||
| Bairsdale | 43.24 | 147.641422 | −37.826786 | 1687 | 8.28 | 297.66 | 1.56 | 11.19 | 3360.24 | 4633.00 | 186.00 | 147.00 | 0.00 |
| Site Name | Distance | Lon | Lat | EC | T | pH | F | Cl | Br | NO | SO | HCO | Ba | Ca | Fe | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (km) | (S cm) | (C) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | ||||
| September 2010 | ||||||||||||||||
| D.O. Nargun | 147.286877 | −38.042783 | 39 | 11.90 | 0.03 | 1.93 | 0.00 | 0.46 | 0.80 | 0.01 | 2.05 | 0.05 | 0.65 | |||
| Glenaladale | 0.00 | 147.374558 | −37.763447 | 41 | 15.00 | 7.01 | 0.03 | 1.88 | 0.00 | 0.50 | 0.79 | 0.00 | 1.97 | 0.05 | 0.65 | |
| Perry Road | 6.94 | 147.391433 | −37.784979 | 44.7 | 12.30 | 0.03 | 2.03 | 0.01 | 0.52 | 0.84 | 0.00 | 2.04 | 0.07 | 0.63 | ||
| CowellsB | 7.40 | 147.392372 | −37.788664 | 40.5 | 12.20 | 0.03 | 2.01 | 0.01 | 0.55 | 0.87 | 0.00 | 2.04 | 0.06 | 0.63 | ||
| Cowells | 8.10 | 147.399888 | −37.787553 | 42.3 | 13.50 | 6.22 | 0.03 | 2.00 | 0.00 | 0.52 | 0.86 | 0.00 | 2.03 | 0.06 | 0.64 | |
| Alexander Rd | 10.16 | 147.413379 | −37.777166 | 42.6 | 13.00 | 7.40 | 0.03 | 2.10 | 0.01 | 0.57 | 0.97 | 0.00 | 2.05 | 0.06 | 0.63 | |
| Hands Road | 11.30 | 147.425513 | −37.778667 | 42.5 | 12.50 | 7.37 | 0.03 | 3.03 | 0.01 | 0.57 | 1.13 | 0.00 | 2.00 | 0.06 | 0.63 | |
| WukWuk Bridge | 12.85 | 147.443241 | −37.779986 | 45 | 12.50 | 7.40 | 0.03 | 2.16 | 0.01 | 0.61 | 1.58 | 0.01 | 2.24 | 0.07 | 0.67 | |
| Ross Ln | 14.76 | 147.462571 | −37.787356 | 44 | 12.80 | 0.03 | 2.22 | 0.01 | 0.52 | 1.03 | 0.00 | 2.14 | 0.06 | 0.66 | ||
| Bulmers Ln | 16.55 | 147.480801 | −37.791039 | 42.3 | 12.30 | 7.10 | 0.03 | 2.34 | 0.01 | 0.66 | 1.08 | 0.00 | 2.15 | 0.06 | 0.64 | |
| Settlement Rd | 19.20 | 147.503786 | −37.802592 | 43.3 | 11.80 | 7.40 | 0.03 | 2.39 | 0.02 | 0.61 | 1.10 | 0.00 | 2.17 | 0.06 | 0.66 | |
| Soldiers Rd | 22.61 | 147.529575 | −37.809491 | 44.7 | 11.40 | 7.50 | 0.04 | 2.32 | 0.00 | 0.59 | 1.13 | 0.00 | 2.15 | 0.06 | 0.67 | |
| Dockerty Rd | 33.46 | 147.589987 | −37.829372 | 47.7 | 12.00 | 7.30 | 0.03 | 2.53 | 0.01 | 0.57 | 1.19 | 0.00 | 2.29 | 0.07 | 0.67 | |
| Wu Young | 40.65 | 147.617858 | −37.813982 | 62.4 | 11.40 | 7.11 | 0.03 | 5.52 | 0.02 | 0.59 | 1.57 | 0.00 | 2.42 | 0.07 | 0.77 | |
| Bairnsdale | 43.24 | 147.641422 | −37.826786 | 64.5 | 11.50 | 6.94 | 0.03 | 5.75 | 0.02 | 0.61 | 1.68 | 0.00 | 2.42 | 0.07 | 0.78 | |
| October 2010 | ||||||||||||||||
| Glenaladale | 0.00 | 147.374558 | −37.763447 | 45.6 | 16.20 | 0.04 | 2.46 | 0.00 | 0.00 | 1.09 | 0.00 | 2.50 | 0.13 | 0.60 | ||
| Perry Road | 6.94 | 147.391433 | −37.784979 | 47.3 | 15.90 | 0.04 | 2.81 | 0.01 | 0.00 | 1.23 | 0.00 | 2.57 | 0.14 | 0.60 | ||
| Alexander Rd | 10.16 | 147.413379 | −37.777166 | 48.6 | 16.20 | 0.04 | 2.91 | 0.00 | 0.06 | 1.36 | 0.00 | 2.61 | 0.15 | 0.61 | ||
| Hands Rd | 11.30 | 147.425513 | −37.778667 | 49 | 15.90 | 0.04 | 2.96 | 0.01 | 0.05 | 1.38 | 0.00 | 2.59 | 0.15 | 0.61 | ||
| WukWuk Bridge | 12.85 | 147.443241 | −37.779986 | 50.1 | 16.40 | 0.04 | 3.07 | 0.00 | 0.08 | 1.76 | 0.00 | 2.70 | 0.17 | 0.62 | ||
| Ross Ln | 14.76 | 147.462571 | −37.787356 | 51.4 | 15.90 | 0.04 | 3.29 | 0.01 | 0.07 | 1.68 | 0.00 | 2.71 | 0.16 | 0.62 | ||
| Bulmers Ln | 16.55 | 147.480801 | −37.791039 | 54 | 16.50 | 0.04 | 3.56 | 0.00 | 0.25 | 1.90 | 0.00 | 2.89 | 0.17 | 0.62 | ||
| Settlement Rd | 19.20 | 147.503786 | −37.802592 | 55.1 | 15.70 | 0.04 | 3.78 | 0.01 | 0.20 | 2.01 | 0.01 | 2.97 | 0.18 | 0.63 | ||
| Soldiers Rd | 22.61 | 147.529575 | −37.809491 | 55.5 | 16.00 | 0.03 | 4.01 | 0.01 | 0.16 | 2.06 | 0.00 | 2.91 | 0.20 | 0.63 | ||
| Dockerty Rd | 33.46 | 147.589987 | −37.829372 | 64.9 | 13.90 | 0.04 | 4.98 | 0.01 | 0.21 | 2.13 | 0.01 | 3.28 | 0.23 | 0.64 | ||
| Wu Young | 40.65 | 147.617858 | −37.813982 | 708 | 15.00 | 0.01 | 38.83 | 0.12 | 0.07 | 5.42 | 0.00 | 1.36 | 0.05 | 1.00 | ||
| Bairnsdale | 43.24 | 147.641422 | −37.826786 | 1908 | 15.00 | 0.02 | 98.91 | 0.37 | 0.04 | 14.92 | 0.00 | 2.81 | 0.04 | 2.56 |
| Site Name | Mg | Na | Si | Sr | Na/Cl | Cl/Br | K/Cl | Ca/Mg | Na/Ca | Ca/Cl | Mg/Cl | O | H | C | Rn | I |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (mg L) | (mg L) | (mg L) | (mg L) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (Bq m) | (g L) | ||||
| February 2009 | ||||||||||||||||
| Wentworth River | 2810.06 | −6.91 | −43.39 | −11.22 | 0.00 | 3.97 | ||||||||||
| Hortan Rd | 3.61 | 5.30 | 3.17 | 0.04 | 2.32 | 950.77 | 0.28 | 0.71 | 2.19 | 1.06 | 1.49 | −5.17 | −33.83 | −10.35 | 236.36 | 1.96 |
| Jurgenson Pt | 3.65 | 5.00 | 3.13 | 0.04 | 1.86 | 866.25 | 0.34 | 0.71 | 2.04 | 0.92 | 1.29 | −5.10 | −33.42 | −10.17 | 0.00 | 1.65 |
| Glenaladale | 3.63 | 5.47 | 2.91 | 0.04 | 1.96 | 659.31 | 0.25 | 0.73 | 2.18 | 0.90 | 1.23 | −4.73 | −31.18 | −10.08 | 65.68 | 1.79 |
| Perry Rd | 4.03 | 7.92 | 2.88 | 0.04 | 1.94 | 665.65 | 0.17 | 0.70 | 2.99 | 0.65 | 0.93 | −4.78 | −34.95 | −9.97 | 373.75 | 2.41 |
| Cowells Rd | 3.95 | 6.65 | 2.84 | 0.04 | 1.62 | 604.30 | 0.16 | 0.72 | 2.48 | 0.65 | 0.91 | −4.80 | −32.62 | −10.44 | 355.67 | 1.92 |
| Hands Rd | 4.39 | 8.22 | 2.74 | 0.04 | 1.59 | 437.18 | 0.14 | 0.70 | 2.84 | 0.56 | 0.80 | −4.66 | −34.71 | −9.73 | 360.20 | 3.27 |
| Wuk Wuk Bridge | 4.93 | 9.61 | 2.77 | 0.05 | 1.35 | 566.39 | 0.11 | 0.70 | 2.94 | 0.46 | 0.65 | −4.79 | −33.86 | −10.69 | 2803.99 | 2.55 |
| Ross Street | 5.25 | 10.10 | 2.79 | 0.05 | 1.33 | 554.71 | 0.10 | 0.70 | 2.92 | 0.46 | 0.66 | −4.67 | −31.87 | −10.80 | 359.33 | 2.02 |
| Bulmers Rd | 5.83 | 12.49 | 2.87 | 0.07 | 1.26 | 589.26 | 0.08 | 0.80 | 2.84 | 0.44 | 0.56 | −4.17 | −36.64 | −11.54 | 934.69 | 2.69 |
| Settlement Rd | 6.16 | 13.77 | 2.90 | 0.08 | 1.19 | 623.69 | 0.07 | 0.81 | 2.94 | 0.40 | 0.50 | −4.74 | −36.70 | −12.04 | 720.45 | 2.31 |
| Soldiers Rd | 6.39 | 16.17 | 2.78 | 0.08 | 1.19 | 598.18 | 0.06 | 0.82 | 3.25 | 0.37 | 0.44 | −4.57 | −31.77 | −10.74 | 446.41 | 3.00 |
| April 2010 | ||||||||||||||||
| Glenaladale | 2.70 | 2.00 | 2.35 | 0.26 | 0.72 | 1.85 | 1.27 | 1.76 | −6.50 | −40.00 | 87.00 | |||||
| Perry Rd | 2.90 | 2.10 | 2.00 | 890.00 | 0.20 | 0.67 | 2.23 | 0.90 | 1.34 | −6.40 | −37.10 | 239.00 | ||||
| Cowells Rd | 2.70 | 2.00 | 2.09 | 750.00 | 0.22 | 0.72 | 1.97 | 1.06 | 1.48 | −6.60 | −37.70 | 692.00 | ||||
| Alexanders Rd | 2.80 | 2.00 | 2.23 | 0.23 | 0.72 | 2.00 | 1.11 | 1.55 | −6.40 | −40.80 | 625.00 | |||||
| Hands Rd | 2.80 | 2.00 | 2.06 | 800.00 | 0.21 | 0.72 | 2.00 | 1.03 | 1.44 | −6.40 | −39.90 | 155.00 | ||||
| WukWuk Bridge | 3.10 | 2.10 | 1.93 | 1170.00 | 0.15 | 0.68 | 2.59 | 0.75 | 1.09 | −6.50 | −38.00 | 218.00 | ||||
| Ross Street | 3.10 | 2.00 | 2.33 | 860.00 | 0.20 | 0.68 | 2.29 | 1.02 | 1.49 | −6.50 | −39.40 | 419.00 | ||||
| Bulmers Rd | 3.10 | 2.10 | 1.99 | 1050.00 | 0.17 | 0.70 | 2.33 | 0.86 | 1.22 | −6.40 | −40.10 | 334.00 | ||||
| Settlement Rd | 3.10 | 2.10 | 1.84 | 1160.00 | 0.15 | 0.72 | 2.31 | 0.80 | 1.10 | −6.40 | −40.40 | 309.00 | ||||
| Soldiers Rd | 3.20 | 2.10 | 1.78 | 423.33 | 0.14 | 0.72 | 2.38 | 0.75 | 1.04 | −6.50 | −41.70 | 112.00 | ||||
| Dockertys Rd | 3.20 | 2.10 | 1.60 | 490.00 | 0.12 | 0.76 | 2.35 | 0.68 | 0.90 | −6.40 | −40.00 | 155.00 | ||||
| Wy Yung Bridge | 55.00 | 2.00 | 0.75 | 801.86 | 0.02 | 0.21 | 40.83 | 0.02 | 0.09 | −6.00 | −40.30 | 109.00 | ||||
| Bairsdale | 569.00 | 1.10 | 24.00 | 430.56 | 0.57 | 0.16 | 54.94 | 0.44 | 2.79 | −3.00 | −9.70 | 178.00 |
| Site Name | Mg | Na | Si | Sr | Na/Cl | Cl/Br | K/Cl | Ca/Mg | Na/Ca | Ca/Cl | Mg/Cl | O | H | C | Rn | I |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (mg L) | (mg L) | (mg L) | (mg L) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (Bq m) | (g L) | ||||
| September 2010 | ||||||||||||||||
| D.O. Nargun | 1.87 | 2.86 | 3.87 | 0.02 | 2.28 | 3845.11 | 0.30 | 0.66 | 2.43 | 0.94 | 1.41 | −7.55 | −43.30 | |||
| Glenaladale | 1.82 | 2.78 | 3.83 | 0.02 | 2.28 | 2300.20 | 0.31 | 0.66 | 2.46 | 0.93 | 1.41 | −7.66 | −43.91 | 68.00 | ||
| Perry Road | 1.86 | 2.82 | 3.85 | 0.02 | 2.14 | 865.58 | 0.28 | 0.66 | 2.41 | 0.89 | 1.34 | −7.62 | −43.63 | 97.21 | ||
| CowellsB | 1.86 | 2.84 | 3.86 | 0.02 | 2.18 | 851.48 | 0.28 | 0.66 | 2.43 | 0.90 | 1.35 | −7.60 | −43.43 | 80.59 | ||
| Cowells | 1.86 | 2.88 | 3.86 | 0.02 | 2.22 | 1614.59 | 0.29 | 0.66 | 2.47 | 0.90 | 1.35 | −7.59 | −43.62 | 269.46 | ||
| Alexander Rd | 1.88 | 2.90 | 3.87 | 0.02 | 2.13 | 554.78 | 0.27 | 0.66 | 2.47 | 0.86 | 1.30 | −7.52 | −43.36 | 609.63 | ||
| Hands Road | 1.83 | 2.81 | 3.78 | 0.02 | 1.43 | 518.26 | 0.19 | 0.66 | 2.44 | 0.58 | 0.88 | −7.54 | −42.96 | 556.15 | ||
| WukWuk Bridge | 2.00 | 2.96 | 3.87 | 0.02 | 2.11 | 618.43 | 0.28 | 0.68 | 2.30 | 0.92 | 1.35 | −7.63 | −42.37 | 950.58 | ||
| Ross Ln | 1.93 | 3.00 | 3.91 | 0.02 | 2.08 | 868.99 | 0.27 | 0.67 | 2.45 | 0.85 | 1.26 | −7.51 | −43.68 | 110.16 | ||
| Bulmers Ln | 1.93 | 3.04 | 3.86 | 0.02 | 2.01 | 467.41 | 0.25 | 0.68 | 2.47 | 0.81 | 1.20 | −7.66 | −42.50 | 660.98 | ||
| Settlement Rd | 1.94 | 3.15 | 3.88 | 0.02 | 2.03 | 261.76 | 0.25 | 0.68 | 2.53 | 0.80 | 1.19 | −7.61 | −43.81 | 209.74 | ||
| Soldiers Rd | 1.95 | 3.07 | 3.87 | 0.02 | 2.04 | 1086.00 | 0.26 | 0.67 | 2.48 | 0.82 | 1.23 | −7.68 | −43.43 | 969.82 | ||
| Dockerty Rd | 1.99 | 3.21 | 3.89 | 0.02 | 1.96 | 773.88 | 0.24 | 0.70 | 2.45 | 0.80 | 1.15 | −7.53 | −41.98 | 227.04 | ||
| Wu Young | 2.27 | 5.45 | 3.93 | 0.02 | 1.52 | 747.49 | 0.13 | 0.65 | 3.92 | 0.39 | 0.60 | −7.59 | −42.33 | 230.25 | ||
| Bairnsdale | 2.27 | 5.61 | 3.88 | 0.02 | 1.50 | 532.53 | 0.12 | 0.65 | 4.04 | 0.37 | 0.58 | −7.54 | −42.54 | 810.00 | ||
| October 2010 | ||||||||||||||||
| Glenaladale | 2.18 | 3.25 | 3.56 | 0.02 | 2.04 | −19,718,358.81 | 0.22 | 0.70 | 2.27 | 0.90 | 1.29 | −7.02 | −42.82 | 35.69 | ||
| Perry Road | 2.25 | 3.49 | 3.62 | 0.02 | 1.92 | 1107.32 | 0.20 | 0.69 | 2.37 | 0.81 | 1.17 | −7.02 | −41.06 | 110.13 | ||
| Alexander Rd | 2.29 | 3.57 | 3.63 | 0.02 | 1.89 | 1524.72 | 0.19 | 0.69 | 2.38 | 0.79 | 1.15 | −7.14 | −42.84 | 113.63 | ||
| Hands Rd | 2.27 | 3.59 | 3.57 | 0.02 | 1.87 | 685.96 | 0.19 | 0.69 | 2.42 | 0.77 | 1.12 | −7.34 | −42.19 | 123.35 | ||
| WukWuk Bridge | 2.37 | 3.71 | 3.63 | 0.02 | 1.86 | 1468.02 | 0.18 | 0.69 | 2.40 | 0.78 | 1.12 | −7.79 | −42.65 | 137.50 | ||
| Ross Lane | 2.39 | 3.80 | 3.62 | 0.02 | 1.78 | 904.65 | 0.17 | 0.69 | 2.44 | 0.73 | 1.06 | −7.72 | −41.05 | 163.38 | ||
| Bulmers Ln | 2.46 | 4.03 | 3.64 | 0.03 | 1.75 | 3365.60 | 0.16 | 0.71 | 2.43 | 0.72 | 1.01 | −7.69 | −42.25 | 254.13 | ||
| Settlement Rd | 2.51 | 4.17 | 3.62 | 0.03 | 1.70 | 769.12 | 0.15 | 0.72 | 2.44 | 0.70 | 0.97 | −7.69 | −42.81 | 244.50 | ||
| Soldiers Rd | 2.49 | 4.30 | 3.57 | 0.03 | 1.65 | 1134.79 | 0.14 | 0.71 | 2.58 | 0.64 | 0.91 | −7.73 | −41.16 | 57.88 | ||
| Dockerty Rd | 2.62 | 4.71 | 3.52 | 0.03 | 1.46 | 962.51 | 0.12 | 0.76 | 2.51 | 0.58 | 0.77 | −7.06 | −42.19 | 253.88 | ||
| Wu Young | 2.85 | 20.01 | 0.70 | 0.02 | 0.79 | 707.44 | 0.02 | 0.29 | 25.68 | 0.03 | 0.11 | −7.53 | −41.89 | 275.63 | ||
| Bairnsdale | 7.60 | 59.13 | 0.69 | 0.05 | 0.92 | 600.65 | 0.02 | 0.22 | 36.72 | 0.03 | 0.11 | −7.40 | −41.15 | 185.63 |
| Site Name | Lon | Lat | EC | T | pH | F | Cl | Br | NO | SO | HCO | Ba | Ca | Fe | K | Mn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (S cm) | (C) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | ||||
| February 2009 | ||||||||||||||||
| 97A | 147.04489 | −37.84060 | 249.0 | 19.4 | 6.73 | 0.11 | 63.54 | 0.18 | 6.53 | 9.74 | 0.02 | 2.51 | 2.82 | 0.01 | ||
| 97B | 147.04187 | −37.84018 | 937.0 | 19.3 | 5.27 | 0.06 | 293.98 | 0.88 | 0.05 | 42.61 | 0.10 | 5.81 | 3.95 | 0.05 | ||
| B56529 | 147.49533 | −37.80347 | 913.0 | 18.3 | 7.40 | 1.99 | 95.86 | 0.42 | 52.74 | 3.32 | 353.00 | 0.12 | 52.54 | 0.77 | 7.14 | 0.39 |
| B56530 | 147.49360 | −37.81314 | 795.0 | 18.0 | 7.85 | 0.09 | 187.63 | 0.40 | 4.12 | 1.63 | 123.00 | 0.06 | 49.69 | 4.28 | 0.02 | |
| B56531 | 147.45921 | −37.79574 | 546.0 | 19.2 | 7.55 | 0.20 | 122.43 | 0.36 | 0.30 | 0.53 | 86.00 | 0.31 | 76.31 | 4.24 | 0.34 | |
| B56532 | 147.46035 | −37.79002 | 305.0 | 18.5 | 9.02 | 0.25 | 5.77 | 0.05 | 2.49 | 118.48 | 0.01 | 48.41 | 13.53 | |||
| B56533 | 147.44059 | −37.79454 | 1272.0 | 74.3 | 6.99 | 0.16 | 294.06 | 0.82 | 1.90 | 50.81 | 147.00 | 0.22 | 71.36 | 3.42 | 0.31 | |
| B56535 | 147.44272 | −37.78350 | 1180.0 | 16.0 | 6.44 | 0.15 | 210.61 | 0.72 | 3.19 | 63.45 | 229.00 | 0.16 | 58.47 | 7.21 | 1.73 | |
| B56536 | 147.42215 | −37.79302 | 2000.0 | 7.52 | 0.09 | 124.12 | 0.49 | 0.83 | 117.26 | 314.00 | 0.07 | 36.34 | 36.29 | 0.11 | ||
| B56537 | 147.42310 | −37.78823 | 1017.0 | 15.9 | 8.60 | 0.05 | 74.35 | 0.43 | 22.50 | 353.61 | 153.00 | 0.04 | 29.32 | 3.98 | 0.47 | |
| B56539 | 147.40986 | −37.78402 | 364.0 | 18.6 | 0.13 | 57.14 | 0.30 | 5.76 | 80.74 | 62.00 | 0.11 | 35.28 | 3.11 | |||
| B56540 | 147.40891 | −37.78875 | 997.0 | 18.0 | 7.14 | 0.15 | 61.68 | 0.35 | 57.00 | 44.20 | 343.00 | 0.28 | 73.74 | 27.56 | 0.33 | |
| B56541 | 147.40070 | −37.79039 | 5490.0 | 18.9 | 4.58 | 0.02 | 2017.50 | 5.66 | 0.21 | 147.95 | 12.00 | 0.08 | 46.92 | 1328.69 | 8.53 | 30.95 |
| B56546 | 147.40101 | −37.79051 | 1183.0 | 18.3 | 7.65 | 0.14 | 366.36 | 1.07 | 0.39 | 62.41 | 145.00 | 0.19 | 32.40 | 0.24 | 6.96 | 0.08 |
| B56547 | 147.40453 | −37.79176 | 709.0 | 20.6 | 7.13 | 0.07 | 841.42 | 3.33 | 0.09 | 163.91 | 39.00 | 0.20 | 15.85 | 725.33 | 2.38 | 11.76 |
| B56548 | 147.40887 | −37.78902 | 737.0 | 16.8 | 7.28 | 0.31 | 130.34 | 0.36 | 4.76 | 7.27 | 181.00 | 0.16 | 36.46 | 0.74 | 5.09 | 0.16 |
| B56549 | 147.41379 | −37.79472 | 617.0 | 17.6 | 7.72 | 0.29 | 124.11 | 0.33 | 0.05 | 57.46 | 237.00 | 0.36 | 78.65 | 0.57 | 5.42 | 0.22 |
| B56551 | 147.42208 | −37.79327 | 888.0 | 18.0 | 7.24 | 0.20 | 86.24 | 0.35 | 99.38 | 180.76 | 103.00 | 0.23 | 71.38 | 4.48 | ||
| B56552 | 147.47701 | −37.80173 | 811.0 | 17.5 | 7.31 | 0.51 | 155.12 | 0.42 | 9.75 | 5.28 | 198.00 | 0.25 | 43.99 | 0.08 | 5.42 | 0.42 |
| B56553 | 147.47830 | −37.79502 | 760.0 | 17.4 | 0.06 | 142.47 | 0.45 | 2.73 | 1.23 | 233.00 | 0.17 | 27.49 | 6.98 | 0.17 | ||
| B56744 | 147.47876 | −37.79224 | 1110.0 | 17.2 | 6.87 | 0.33 | 177.21 | 0.53 | 90.01 | 118.47 | 164.00 | 0.20 | 102.52 | 3.00 | ||
| B80760 | 147.51985 | −37.82019 | 0.03 | 70.54 | 0.13 | 0.03 | 0.32 | 8.60 | 30.54 | 5.17 | 0.02 | |||||
| B80761 | 147.52169 | −37.81465 | 14.3 | 18.5 | 7.28 | 0.06 | 65.51 | 0.18 | 4.99 | 26.57 | 10.62 | 5.16 | 0.07 | |||
| B80762 | 147.52267 | −37.80894 | 739.0 | 18.1 | 6.79 | 0.07 | 260.20 | 1.11 | 0.04 | 1.45 | 23.00 | 0.13 | 19.00 | 233.89 | 6.07 | 17.80 |
| B80866 | 147.51096 | −37.80696 | 625.0 | 18.0 | 6.47 | 0.46 | 103.23 | 0.27 | 0.68 | 45.61 | 145.00 | 0.08 | 32.13 | 0.09 | 2.10 | 0.01 |
| B105476 | 147.40029 | −37.77785 | 700.0 | 17.1 | 6.65 | 0.35 | 85.29 | 0.44 | 81.82 | 76.46 | 107.00 | 0.05 | 22.34 | 2.22 | ||
| B105477 | 147.39365 | −37.78381 | 101.0 | 6.53 | 0.07 | 4.99 | 0.03 | 0.08 | 0.95 | 64.00 | 0.06 | 4.53 | 0.99 | 0.02 | ||
| B105479 | 147.36538 | −37.77354 | 440.0 | 16.9 | ||||||||||||
| B110166 | 147.07454 | −37.82282 | 101.7 | 16.5 | 6.64 | 0.07 | 14.35 | 0.04 | 1.62 | 2.97 | 36.00 | 0.01 | 2.76 | 1.60 | ||
| B110167 | 147.07687 | −37.82374 | 116.9 | 18.6 | 6.62 | 0.08 | 17.89 | 0.06 | 0.69 | 2.89 | 33.00 | 0.01 | 3.10 | 1.79 | ||
| B110168 | 147.07930 | −37.82495 | 113.2 | 17.3 | 6.51 | 0.08 | 17.19 | 0.05 | 1.31 | 2.99 | 26.00 | 0.01 | 3.33 | 1.63 | ||
| B110171 | 147.04489 | −37.84060 | 296.0 | 17.8 | 6.26 | 0.07 | 64.91 | 0.13 | 0.74 | 25.65 | 28.00 | 0.13 | 6.89 | 1.43 | 0.07 | |
| B110172 | 147.04187 | −37.84018 | 327.0 | 16.8 | 6.41 | 0.13 | 45.63 | 0.18 | 0.40 | 23.06 | 74.00 | 0.05 | 7.65 | 17.13 | 1.22 | 1.48 |
| B110177 | 147.38340 | −37.77189 | 387.0 | 18.3 | 7.28 | 0.37 | 49.40 | 0.18 | 0.09 | 24.40 | 0.13 | 17.36 | 3.92 | 0.02 | ||
| B110978 | 147.36479 | −37.77347 | 99.1 | 19.0 | 6.55 | 0.12 | 8.09 | 0.03 | 2.07 | 5.93 | 0.01 | 5.20 | 1.96 | 4.14 | 0.05 | |
| B110979 | 147.40894 | −37.78865 | 863.0 | 17.2 | 7.16 | 0.69 | 96.91 | 0.30 | 0.08 | 0.63 | 82.00 | 0.02 | 6.54 | 3.44 | ||
| B111800 | 147.37505 | −37.56747 | 60.2 | 7.47 | 2.78 | 135.14 | 0.44 | 1.06 | 10.47 | 267.00 | 0.23 | 34.04 | 7.65 |
| Site Name | Mg | Na | Si | Sr | Na/Cl | Cl/Br | K/Cl | Ca/Mg | Na/Ca | Ca/Cl | Mg/Cl | H | O | C | Rn | I |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (mg L) | (mg L) | (mg L) | (mg L) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (Bq m) | (g L) | ||||
| February 2009 | ||||||||||||||||
| 97A | 7.85 | 34.91 | 4.26 | 0.02 | 0.85 | 805.21 | 0.04 | 0.19 | 13.93 | 0.04 | 0.12 | −40.00 | −6.29 | −14.46 | 0.61 | 11.33 |
| 97B | 29.67 | 154.81 | 5.66 | 0.05 | 0.81 | 750.18 | 0.01 | 0.12 | 26.64 | 0.02 | 0.10 | −42.90 | −6.00 | −21.00 | 5.45 | 4.28 |
| B56529 | 16.96 | 122.79 | 3.47 | 0.75 | 1.97 | 516.43 | 1.88 | 2.34 | 0.55 | 0.18 | −48.56 | −7.22 | −15.91 | 2.31 | 16.11 | |
| B56530 | 14.77 | 100.40 | 1.09 | 0.58 | 0.82 | 1067.06 | 0.02 | 2.04 | 2.02 | 0.26 | 0.08 | −43.61 | −7.28 | −16.92 | 28.01 | 6.86 |
| B56531 | 13.27 | 63.67 | 8.44 | 0.83 | 0.80 | 763.72 | 0.03 | 3.49 | 0.83 | 0.62 | 0.11 | −40.74 | −6.61 | −14.91 | 0.31 | 13.53 |
| B56532 | 0.98 | 12.30 | 3.90 | 0.18 | 3.29 | 287.63 | 2.13 | 30.11 | 0.25 | 8.40 | 0.17 | −38.13 | −5.53 | −22.69 | 33.38 | 3.64 |
| B56533 | 29.18 | 146.71 | 9.69 | 0.70 | 0.77 | 811.40 | 0.01 | 1.48 | 2.06 | 0.24 | 0.10 | −42.49 | −5.87 | −17.74 | 36.50 | 16.76 |
| B56535 | 43.82 | 125.01 | 6.41 | 0.51 | 0.91 | 657.26 | 0.03 | 0.81 | 2.14 | 0.28 | 0.21 | −33.65 | −3.83 | −16.16 | 19.95 | 43.92 |
| B56536 | 44.13 | 139.15 | 5.27 | 0.53 | 1.73 | 576.57 | 0.26 | 0.50 | 3.83 | 0.29 | 0.36 | −36.83 | −6.48 | −11.36 | 0.70 | 14.34 |
| B56537 | 84.38 | 60.65 | 0.44 | 0.16 | 1.26 | 385.48 | 0.05 | 0.21 | 2.07 | 0.39 | 1.13 | −42.17 | −6.31 | −17.37 | 6.22 | 6.17 |
| B56539 | 36.12 | 54.15 | 9.22 | 0.35 | 1.46 | 430.24 | 0.05 | 0.59 | 1.53 | 0.62 | 0.63 | −35.36 | −5.44 | −14.19 | 10.89 | 6.32 |
| B56540 | 62.42 | 150.85 | 12.56 | 1.06 | 3.77 | 401.35 | 0.40 | 0.72 | 2.05 | 1.20 | 1.01 | −39.39 | −6.69 | −11.91 | 8.10 | 16.23 |
| B56541 | 42.25 | 142.39 | 0.51 | 0.45 | 0.11 | 803.52 | 0.67 | 3.04 | 0.02 | 0.02 | −42.64 | −6.67 | −10.48 | 7.41 | ||
| B56546 | 26.33 | 176.99 | 1.62 | 0.77 | 0.74 | 770.75 | 0.02 | 0.75 | 5.46 | 0.09 | 0.07 | −40.27 | −6.30 | −14.77 | 1.35 | 20.01 |
| B56547 | 4.57 | 180.32 | 8.62 | 0.15 | 0.33 | 569.73 | 2.10 | 11.38 | 0.02 | 0.01 | −33.51 | −6.03 | −14.42 | 19.23 | ||
| B56548 | 15.72 | 102.21 | 8.89 | 0.35 | 1.21 | 821.10 | 0.04 | 1.41 | 2.80 | 0.28 | 0.12 | −47.03 | −7.24 | −12.75 | 12.91 | 12.07 |
| B56549 | 19.26 | 56.98 | 10.84 | 0.82 | 0.71 | 836.60 | 0.04 | 2.48 | 0.72 | 0.63 | 0.16 | −47.60 | −7.11 | −13.41 | 12.38 | 37.92 |
| B56551 | 32.88 | 71.31 | 9.66 | 0.69 | 1.27 | 548.68 | 0.05 | 1.32 | 1.00 | 0.83 | 0.38 | −40.48 | −6.66 | −15.36 | 0.70 | 10.84 |
| B56552 | 15.89 | 104.94 | 3.85 | 1.29 | 1.04 | 824.18 | 0.03 | 1.68 | 2.39 | 0.28 | 0.10 | −46.85 | −6.59 | −12.28 | 11.34 | 15.34 |
| B56553 | 19.32 | 120.34 | 1.39 | 0.54 | 1.30 | 710.11 | 0.04 | 0.86 | 4.38 | 0.19 | 0.14 | −46.48 | −6.69 | −15.00 | 23.30 | 6.86 |
| B56744 | 29.14 | 110.34 | 4.76 | 1.29 | 0.96 | 760.95 | 0.02 | 2.13 | 1.08 | 0.58 | 0.16 | −40.55 | −5.73 | −16.31 | 1.92 | 8.70 |
| B80760 | 1.58 | 7.20 | 0.55 | 0.16 | 1194.92 | 0.07 | 11.71 | 0.24 | 0.43 | 0.02 | −40.35 | −6.00 | −10.20 | 38.53 | 26.24 | |
| B80761 | 4.23 | 23.97 | 0.12 | 0.56 | 812.70 | 0.07 | 1.52 | 2.26 | 0.16 | 0.06 | −44.36 | −5.79 | −15.82 | 5.44 | 3.39 | |
| B80762 | 11.08 | 57.66 | 2.57 | 0.20 | 0.34 | 529.39 | 0.02 | 1.04 | 3.03 | 0.07 | 0.04 | −52.81 | −8.63 | −17.15 | 4.02 | |
| B80866 | 16.18 | 85.94 | 8.97 | 0.43 | 1.28 | 851.76 | 0.02 | 1.20 | 2.68 | 0.31 | 0.16 | −47.57 | −6.85 | −19.21 | 24.92 | 1.94 |
| B105476 | 25.19 | 106.24 | 11.23 | 0.24 | 1.92 | 438.64 | 0.02 | 0.54 | 4.76 | 0.26 | 0.30 | −43.40 | −5.95 | −17.26 | 28.99 | 10.50 |
| B105477 | 4.11 | 6.18 | 4.39 | 0.04 | 1.91 | 439.61 | 0.18 | 0.67 | 1.37 | 0.91 | 0.82 | −38.50 | −6.20 | −19.71 | 8.93 | 3.75 |
| B105479 | 1.14 | |||||||||||||||
| B110166 | 3.97 | 11.05 | 3.14 | 0.02 | 1.19 | 731.31 | 0.10 | 0.42 | 4.00 | 0.19 | 0.28 | −37.80 | −5.73 | −18.33 | 28.84 | 1.59 |
| B110167 | 4.49 | 11.91 | 3.19 | 0.02 | 1.03 | 689.27 | 0.09 | 0.42 | 3.84 | 0.17 | 0.25 | −39.26 | −4.67 | −18.46 | 37.90 | 1.50 |
| B110168 | 4.50 | 11.79 | 3.11 | 0.02 | 1.06 | 710.08 | 0.09 | 0.45 | 3.55 | 0.19 | 0.26 | −38.66 | −4.99 | −19.49 | 39.85 | 1.99 |
| B110171 | 11.35 | 34.72 | 5.82 | 0.04 | 0.82 | 1170.34 | 0.02 | 0.37 | 5.04 | 0.11 | 0.17 | −41.23 | −5.94 | −21.36 | 10.17 | 8.64 |
| B110172 | 9.07 | 36.35 | 7.38 | 0.06 | 1.23 | 563.28 | 0.02 | 0.51 | 4.75 | 0.17 | 0.20 | −40.67 | −6.12 | −19.15 | 19.63 | 2.22 |
| B110177 | 13.72 | 47.84 | 14.64 | 0.21 | 1.49 | 615.26 | 0.07 | 0.77 | 2.76 | 0.35 | 0.28 | −44.60 | −7.03 | −15.91 | 3.22 | 3.76 |
| B110978 | 1.30 | 6.32 | 1.39 | 0.02 | 1.20 | 639.86 | 0.46 | 2.43 | 1.22 | 0.64 | 0.16 | −77.71 | −11.88 | −18.62 | 0.72 | 0.91 |
| B110979 | 7.11 | 77.49 | 0.69 | 0.05 | 1.23 | 722.49 | 0.03 | 0.56 | 11.86 | 0.07 | 0.07 | −41.75 | 18.39 | |||
| B111800 | 21.10 | 126.52 | 6.70 | 0.37 | 1.44 | 690.59 | 0.05 | 0.98 | 3.72 | 0.25 | 0.16 | −46.03 | −7.01 | −12.23 | 0.85 | 16.89 |
| Site Name | Lon | Lat | EC | T | pH | F | Cl | Br | NO | SO | HCO | Ba | Ca | Fe | K | Mg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (S cm) | (C) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | (mg L) | ||||
| April 2010 | ||||||||||||||||
| B56744 | 147.47876 | −37.79224 | 1161.0 | 0.35 | 138.40 | 0.55 | 64.08 | 116.33 | 93.00 | 3.00 | 27.00 | |||||
| B56531 | 147.45921 | −37.79574 | 659.0 | 0.18 | 142.37 | 0.41 | 7.15 | 0.59 | 42.00 | 0.15 | 3.10 | 8.10 | ||||
| B56538 | 147.42425 | −37.78253 | 503.0 | 0.05 | 46.10 | 0.30 | 0.45 | 6.42 | 23.00 | 3.90 | 22.00 | |||||
| B56546 | 147.40101 | −37.79051 | 1269.0 | 0.08 | 352.44 | 0.99 | 0.07 | 11.19 | 49.00 | 6.60 | 29.00 | |||||
| B56547 | 147.40454 | −37.79177 | 1880.0 | 0.05 | 732.86 | 2.20 | 0.12 | 10.38 | 33.00 | 203.00 | 2.60 | 8.00 | ||||
| 91A | 147.04187 | −37.84018 | 881.0 | 0.19 | 205.28 | 0.30 | 0.20 | 19.92 | 5.83 | 10.70 | 14.82 | |||||
| 91B | 147.04489 | −37.8406 | 4410.0 | 0.24 | 1440.53 | 3.91 | 1.54 | 37.16 | 50.21 | 16.05 | 111.73 | |||||
| B110171 | 147.04489 | −37.8406 | 343.0 | 0.08 | 65.48 | 0.16 | 3.86 | 20.29 | 7.25 | 1.64 | 10.69 | |||||
| B110172 | 147.04187 | −37.84018 | 329.0 | 0.12 | 45.78 | 0.24 | 0.25 | 24.70 | 5.53 | 1.73 | 6.57 | |||||
| Site Name | Na | Si | Sr | Na/Cl | Cl/Br | K/Cl | Ca/Mg | Na/Ca | Ca/Cl | Mg/Cl | O | H | C | Rn | I | |
| (mg L) | (mg L) | (mg L) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (molar) | (Bq/m) | (g L) | |||||
| April 2010 | ||||||||||||||||
| B56744 | 120.00 | 9.40 | 1.13 | 1.34 | 566.86 | 0.02 | 2.09 | 2.25 | 0.59 | 0.28 | −5.87 | −36.60 | 23,338.00 | |||
| B56531 | 49.00 | 1.90 | 0.51 | 0.53 | 783.63 | 0.02 | 3.18 | 2.03 | 0.26 | 0.08 | −6.71 | −46.80 | 34,088.00 | |||
| B56538 | 39.00 | 2.20 | 0.23 | 1.31 | 346.67 | 0.08 | 0.63 | 2.98 | 0.44 | 0.70 | −5.78 | −36.80 | 30,450.00 | |||
| B56546 | 166.00 | 2.60 | 0.80 | 0.73 | 802.26 | 0.02 | 1.03 | 5.92 | 0.12 | 0.12 | −6.10 | −46.00 | 12,225.00 | |||
| B56547 | 185.00 | 0.30 | 0.39 | 750.82 | 0.00 | 2.48 | 9.82 | 0.04 | 0.02 | −5.84 | −35.30 | 24,138.00 | ||||
| 91A | 85.56 | 5.03 | 0.08 | 0.64 | 1544.00 | 0.05 | 0.25 | 24.80 | 0.03 | 0.11 | −6.57 | −46.00 | 5750.00 | |||
| 91B | 798.23 | 6.81 | 0.62 | 0.85 | 830.37 | 0.01 | 0.27 | 27.78 | 0.03 | 0.11 | −6.13 | −43.00 | 5301.00 | |||
| B110171 | 34.21 | 5.20 | 0.05 | 0.81 | 925.00 | 0.02 | 0.41 | 8.28 | 0.10 | 0.24 | −5.69 | −40.00 | 5514.00 | |||
| B110172 | 46.09 | 7.26 | 0.05 | 1.55 | 430.00 | 0.03 | 0.52 | 14.29 | 0.11 | 0.21 | −6.20 | −41.00 | 14,625.00 |
References
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Cardenas, B.M. The effect of river bend morphology on floww and timescales of surface water-groundwater exchange across pointbars. J. Hydrol. 2008, 362, 134–141. [Google Scholar] [CrossRef]
- Bakker, M. Hydraulic modeling of riverbank filtration systems with curved boundaries using analytic elements and series solutions. Adv. Water Resour. 2010, 33, 813–819. [Google Scholar] [CrossRef]
- Lautz, L.K.; Siegel, D.I. Modeling surface and ground water mixing in the hyporheic zone using MODFLOW and MT3D. Adv. Water Resour. 2006, 29, 1618–1633. [Google Scholar] [CrossRef]
- Revelli, R.; Boano, F.; Camporeale, C.; Ridolfi, L. Intra-meander hyporheic flow in alluvial aquifers. Water Resour. Res. 2008, 44, 1–10. [Google Scholar] [CrossRef]
- Mucha, I.; Bansky, L.; Hlavaty, Z.; Rodak, D. Impact of Riverbed Clogging—Colmatation-on Groundwater; NATO Science Series; Springer: Berlin/Heidelberg, Germany, 2006; Volume 60, pp. 43–72. [Google Scholar]
- Goldschneider, A.A.; Haralampides, K.A.; MacQuarrie, K.T.B. River sediment and flow characteristics near a bank filtration water supply: Implications for riverbed clogging. J. Hydrol. 2007, 344, 55–69. [Google Scholar] [CrossRef]
- Nowinski, J.D.; Cardenas, M.B.; Lightbody, A.F. Evolution of hydraulic conductivity in the floodplain of a meandering river due to hyporheic transport of fine materials. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Cravotta, C.A., III; Goode, D.J.; Bartles, M.D.; Risser, D.W.; Galeone, D.G. Surface water and groundwater interactions in an extensively mined watershed, upper Schuylkill River, Pennsylvania, USA. Hydrol. Process. 2013, 28, 3574–3601. [Google Scholar] [CrossRef]
- Geris, J.; Comte, J.C.; Franchi, F.; Petros, A.K.; Tirivarombo, S.; Selepeng, A.T.; Villholth, K.G. Surface water-groundwater interactions and local land use control water quality impacts of extreme rainfall and flooding in a vulnerable semi-arid region of Sub-Saharan Africa. J. Hydrol. 2022, 609, 127834. [Google Scholar] [CrossRef]
- Douglas, J.G.; Ferguson, J.A. Geology of Victoria; Geological Society of Australia: Hornsby NSW, Australia, 1988. [Google Scholar]
- Holdgate, G.R.; Cartwright, I.; Blackburn, D.T.; Wallace, M.W.; Gallagher, S.J.; Wagstaff, B.E.; Chung, L. The Middle Miocene Yallourn coal seam—The last coal in Australia. Int. J. Coal Geol. 2007, 70, 95–115. [Google Scholar] [CrossRef]
- Hofmann, H.; Cartwright, I. Using hydrogeochemistry to understand inter-aquifer mixing in the on-shore part of the Gippsland Basin, southeast Australia. Appl. Geochem. 2013, 33, 84–103. [Google Scholar] [CrossRef]
- Thompson, B. The Geology and Hydrogeology of the Mitchell Flats and a Study of Artificial Recharge; Technical Report, Geological Survey Report; Mines Department Victoria: Melbourne, VIC, Australia, 1973.
- Nahm, G.Y. The Hydrogeology of the Gippsland Basin and Its Role in the Genesis and Accumulation of Petroleum. Ph.D. Thesis, School of Earth Sciences, The University of Melbourne, Melbourne, Australia, 2002. [Google Scholar]
- Brodie, R.; Sundarm, B.; Tottenham, R.; Hostetler, S.; Ransley, R. An Overview of Tools for Assessing Groundwater-Surface Water Connectivity; Technical Report; Bureau of Rural Sciences, Canberra: Canberra, Australia, 2007.
- Brodie, R.; Hostetler, S.; Slatter, E. Q-lag: A New Hydrographic Approach to Understanding Stream-Aquifer Connectivity; Technical Report; Australian Department of Agriculture, Fisheries and Forestry: Canberra, Australia, 2007.
- Smakhtin, V.U. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Fetter, C.W. Applied Hydrogeology, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2000. [Google Scholar]
- Nathan, R.J.; McMahon, T.A. Practical aspects of low-flow frequency analysis. Water Resour. Res. 1990, 36, 2135–2141. [Google Scholar]
- Brodie, R.S.; Hostetler, S. A Review of Techniques for Analysing Baseflow from Stream Hydrographs; Technical Report, Managing Connected Water Resources Project, Bureau of Rural Sciences, ABARE, the Australian National University, NSW Department of Infrastructure Planning and Natural Resources and Queensland Department of Natural Resources and Mines; Bureau of Rural Sciences: Canberra, ACT, Australia, 2005.
- Nathan, R.J.; McMahon, T.A. Evaluation of automated techniques for base flow and recession analysis. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Eckhardt, K. How to construct recursive digital filters for baseflow separation. Hydrol. Process. 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Van-Lanen, H.A.J. Hydrological Drought—Processes and Estimation Methods for Streamflow and Groundwater, 1st ed.; Developments in Water Science; Elsevier Science B.V.: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Ellins, K.K.; Roman-Mas, A.; Lee, R. Using 222Rn to examine groundwater/surface discharge interactions in the Rio Grande De Manati, Puerto Rico. J. Hydrol. 1990, 115, 319–341. [Google Scholar] [CrossRef]
- Genereux, D.P.; Hemond, H.F. Naturally occuring Radon-222 as a tracer for streamflow generation: Steady-state methodology and field example. Water Resour. Res. 1990, 26, 3065–3075. [Google Scholar]
- Wels, C.; Cornett, R.J.; Lazerte, B.D. Hydrograph separation: A comparison of geochemical and isotopic tracers. J. Hydrol. 1991, 122, 253–274. [Google Scholar] [CrossRef]
- Rice, K.C.; Hornberger, G.M. Comparison of hydrochemical tracers to estimate source contributions to peak flow in a small, forested, headwater catchment. Water Resour. Res. 1998, 34, 1755–1766. [Google Scholar] [CrossRef]
- Negrel, P.; Lachassgne, P. Geochemistry of the Maoni River (French Guiana) during the low water stage: Implicatoins for water-rock interaction and groundwater characteristics. J. Hydrol. 2000, 376, 58–69. [Google Scholar]
- Tardy, Y.; Bustillo, V.; Boeglin, J.L. Geochemistry applied to the watershed survey: Hydrograph separation, erosion and soil dynamics. A case study: The basin of the niger river, africa. Appl. Geochem. 2004, 19, 469–518. [Google Scholar] [CrossRef]
- Cook, P.G.; Favreau, G.; Dighton, J.C.; Tickell, S. Determining natural groundwater influx to a tropical river using radon, chlorofluorocarbons and ionic environmental tracers. J. Hydrol. 2003, 277, 74–88. [Google Scholar] [CrossRef]
- Cook, P.G.; Lamontagne, S.; Berhane, D.; Clark, J.F. Quantifying groundwater discharge to Cockburn River, South-Eastern Australia, using dissolved gas tracers 222Rn and SF6. Water Resour. Res. 2006, 42, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hooper, R.P.; Christophersen, N.; Peters, N.E. Modelling streamwater chemistry as a mixture of soilwater end-members—An application to the Panola Mountain Catchment, Georgia, USA. J. Hydrol. 1990, 116, 321–343. [Google Scholar] [CrossRef]
- Hooper, R.P. Diagnostic tools for mixing models of stream water chemistry. Water Resour. Res. 2003, 39, 1–13. [Google Scholar] [CrossRef]
- Christophersen, N.; Neal, C.; Hooper, R.P.; Vogt, R.D.; Andersen, S. Modelling streamwater chemistry as a mixture of soilwater end-members—A step towards second-generation acidification models. J. Hydrol. 1990, 116, 307–320. [Google Scholar] [CrossRef]
- Christophersen, N.; Hooper, R.P. Multivariante analysis of stream water chemical data: The use of principle component analysis for the end-member mixing problem. Water Resour. Res. 1992, 28, 99–107. [Google Scholar] [CrossRef]
- Sklash, M.G.; Farvolden, R.N. The role of groundwater in storm runoff. J. Hydrol. 1979, 43, 45–65. [Google Scholar] [CrossRef]
- Buttle, J.M. Isotope hydrogrpah separation and rapid delivery of pre-event water from drainage basins. Cont. Shelf Res. 1994, 18, 16–41. [Google Scholar]
- Hinton, M.J.; Shiff, S.L.; English, M.C. Examining the contribution of glazial till water to storm runoff using two and three component hydrogropah separation. Water Resour. Res. 1994, 30, 983–993. [Google Scholar] [CrossRef]
- Kendall, C.; McDonnell, J.J. Isotope Tracers in Catchment Hydrology, 3rd ed.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Cartwright, I.; Cendón, D.; Currell, M.; Meredith, K. A review of radioactive isotopes and other residence time tracers in understanding groundwater recharge: Possibilities, challenges, and limitations. J. Hydrol. 2017, 555, 797–811. [Google Scholar] [CrossRef]
- Hofmann, H.; Gilfedder, B.S.; Cartwright, I. A Novel Method using a silicone diffusion membrane for continuous 222Rn measurements for the quantification of groundwater discharge to streams and rivers. Environ. Sci. Technol. 2011, 45, 8915–8921. [Google Scholar] [CrossRef]
- Surbeck, H.; Deflorin, O.; Kloos, O. Spatial and temporal variations in the uranium series background in Alpine groundwater. In Uranium in the Environment, Mining Impact and Consequences; Merkel, B.J., Hasche-Berger, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 831–839. [Google Scholar]
- Cartwright, I.; Hofmann, H.; Sirianos, M.A.; Weaver, T.R.; Simmons, C.T. Geochemical and 222Rn constraints on baseflow to the Murry River, Australia, and timescales for the decay of low-salinity. groundwater lenses. J. Hydrol. 2011, 405, 333–343. [Google Scholar] [CrossRef]
- Schubert, M.; Siebert, C.; Knoeller, K.; Roediger, T.; Schmidt, A.; Gilfedder, B. Investigating groundwater discharge into a major river under low flow conditions based on a radon mass balance supported by tritium data. Water 2020, 12, 2838. [Google Scholar] [CrossRef]
- Martindale, H.; Morgenstern, U.; Singh, R.; Stewart, B. Mapping groundwater-surface water interaction using radon-222 in gravel-bed rivers. J. Hydrol. 2016, 55, 121–134. [Google Scholar]
- Martinez, J.L.; Raiber, M.; Cox, M.E. Assessment of groundwater–surface water interaction using long-term hydrochemical data and isotope hydrology: Headwaters of the condamine river, southeast queensland, australia. Sci. Total Environ. 2015, 536, 499–516. [Google Scholar] [CrossRef]
- Genereux, D.P.; Hemond, H.F. Determination of gas exchange rate constant for a small stream on Walker Branch Watershed, Tennessee. Water Resour. Res. 1992, 29, 2365–2374. [Google Scholar] [CrossRef]
- Mullinger, N.J.; Binley, A.M.; Pates, J.M.; Crook, N.P. Radon in Chalk streams: Spatial and temporal variation of groundwater sources in the Pang and Lambourn catchment, UK. J. Hydrol. 2007, 339, 172–182. [Google Scholar] [CrossRef] [Green Version]
- Mullinger, N.J.; Pates, J.M.; Binley, A.M.; Crook, N.P. Controls on the spatial and temporal variability ot 222Rn in riparian groundwater in a Lowland Chalk Catchment. J. Hydrol. 2009, 376, 58–69. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W.; Jirka, G.H. (Eds.) Gas Transfer at Water Surfaces, 1st ed.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1984. [Google Scholar]
- Lamontagne, S.; Cook, P.G. Estimation of hyporheic water residence time in situ using 222Rn disequilibrium. Limnol. Oceanogr. Methods 2007, 5, 407–416. [Google Scholar] [CrossRef]
- Cartwright, I.; Hofmann, H. Using radon to understand parafluvial flows and the changing locations of groundwater inflows in the Avon River, southeast Australia. Hydrol. Earth Syst. Sci. 2016, 20, 3581–3600. [Google Scholar] [CrossRef] [Green Version]
- Cartwright, I.; Hofmann, H.; Gilfedder, B.S.; Smyth, B. Understanding parafluvial exchange and degassing to better quantify groundwater inflows using 222Rn: The King River, southeast Australia. Chem. Geol. 2014, 380, 48–60. [Google Scholar] [CrossRef]
- Unland, N.P.; Cartwright, I.; Andersen, M.S.; Rau, G.C.; Reed, J.; Gilfedder, B.S.; Atkinson, A.P.; Hofmann, H. Investigating the spatio-temporal variability in groundwater and surface water interactions: A multi-technique approach. Hydrol. Earth Sys. Sci. 2013, 17, 3437–3453. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.C.L.; Cartwright, I.; Braden, J.L.; de Bree, S.T. Examining the spatial and temporal variation of groundwater inflows to a valley-to-floodplain river using 222Rn, geochemistry and river discharge: The Ovens River, southeast Australia. Hydrol. Earth Sys. Sci. 2013, 17, 4907–4924. [Google Scholar] [CrossRef] [Green Version]
- Coplen, T.B. Normalization of oxygen and hydrogen isotope data. Chem. Geol. 1988, 72, 293–297. [Google Scholar] [CrossRef]
- Burnett, W.C.; Kim, G.; Lane-Smith, D. A continuous monitor for assessment of 222Rn in the coastal ocean. J. Radioanal. Nucl. Chem. 2001, 249, 167–172. [Google Scholar]
- Burnett, W.C.; Peterson, R.N.; Santos, I.R.; Hicks, R.W. Use of automated radon measurements for rapid assessment of groundwater flow into florida streams. J. Hydrol. 2010, 380, 298–304. [Google Scholar] [CrossRef]
- Burnett, W.C.; Dulaiova, H. Radon as a tracer of submarine groundwater discharge into a boat basin in Donnalucata, Sicily. Cont. Shelf Res. 2006, 26, 862–873. [Google Scholar] [CrossRef]
- Cartwright, I.; Weaver, T.R.; Simmons, C.T.; Fifield, L.K.; Lawrence, C.R.; Chisari, R.; Varley, S. Physical hydrogeology and environmental isotopes to constrain the age, origins, and stability of a low-salinity groundwater lens formed by periodic river recharge: Murray Basin, Australia. J. Hydrol. 2010, 380, 203–221. [Google Scholar] [CrossRef]
- Clark, I.D.; Fritz, P. Environmental Isotopes in Hydrogeology; Lewis Publischers: New York, NY, USA, 1997. [Google Scholar]
- Smetanová, I.; Holý, K.; Müllerová, M.; Polášková, A.; Túnyi, I. Temporal and spatial changes of radon concentration in borehole water (Little Carpathians Mts., Slovakia). Nat. Hazards Earth Syst. Sci. 2010, 10, 1373–1377. [Google Scholar] [CrossRef] [Green Version]
- O’Connor, D.J.; Dobbins, W.E. Mechanisms of reaeration in natural streams. Trans. Am. Soc. Civ. Eng. 1958, 123, 641–684. [Google Scholar] [CrossRef]
- Negulescu, M.; Rojanski, V. Recent research to determine reaeration coefficients. Water Resour. Res. 1969, 3, 189–202. [Google Scholar] [CrossRef]
- Danckwerts, P.V. Significance of Liquid-Film coefficients in gas absorption. Ind Eng. Chem. Res. 1951, 43, 1460–1467. [Google Scholar] [CrossRef]
- Lewis, W.L.; Whitman, W.G. Principles of gas adsorption. Ind Eng. Chem. Res. 1924, 16, 1215. [Google Scholar] [CrossRef]
- McCallum, J.L.; Cook, P.G.; Brunner, P.; Berhane, D. Solute dynamics during bank storage flows and implications for chemical base flow separation. Water Resour. Res. 2010, 46, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Eckhardt, K. A comparison of baseflow indices, which were calculated with seven different baseflow separation methods. J. Hydrol. 2008, 352, 168–173. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Allen, D.J.; Griffiths, K.J. Examining geological controls on Baseflow Index (BFI) using regression analysis: An illustration from the Thames Basin, UK. J. Hydrol. 2009, 373, 164–176. [Google Scholar] [CrossRef] [Green Version]
- Cartwright, I.; Weaver, T.R.; Fifield, L.K. Cl/Br ratios and environmental isotopes as indicators of recharge variability and groundwater flow: An example from the southeast Murray Basin, Australia. Chem. Geol. 2006, 231, 38–56. [Google Scholar] [CrossRef]
- Natermann, E. Der Wasserhaushalt des oberen Emsgebietes nach dem Au-Linien-Verfahren; Technical Report; Ministereium für Ernährung, Landwirtschaft und Forsten NRW: Düsseldorf, Germany, 1958.
- Vogt, T.; Hoehn, E.; Schneider, P.; Freund, A.; Schirmer, M.; Cirpka, O.A. Fluctuations of electrical conductivity as a natural tracer for bank filtration in a losing stream. Adv. Water Resour. 2010, 33, 1296–1308. [Google Scholar] [CrossRef]
- Veličković, B. Colmation as one of the processes in interaction between groundwater and surface water. Facta Univ. 2005, 3, 165–173. [Google Scholar] [CrossRef]
- Tonina, D. Interactions between River Morphology and Intra-Gravel Flow Paths within the Hyporheic Zone. Ph.D. Thesis, Collage of Graduate Studies-University of Idaho, Moscow, ID, USA, September 2005. [Google Scholar]
- Jencso, K.G.; McGlynn, B.L.; Gooseff, M.N.; Bencala, K.E.; Wondzell, S.M. Hillslope hydrologic connectivity controls riparian groundwater turnover: Implications of catchment structure for riparian buffering and stream water sources. Water Resour. Res. 2009, 46, 1–18. [Google Scholar] [CrossRef]
- Stonedahl, S.H.; Harvey, J.W.; Wörman, A.; Salehin, M.; Packman, A.I. A multiscale model for integrating hyporheic exchange from ripples to meanders. Water Resour. Res. 2010, 46, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Kasahara, T.; Hill, A.R. Effects of riffle-step restoration on hyporheic zone chemistry in N-rich lowland streams. Can. J. Fish. Aquat.Sci. 2006, 63, 120–133. [Google Scholar] [CrossRef]
- Bencala, K.E.; Gooseff, M.N.; Kimball, B.A. Rethinking hyporheic flow and transient storage to advance understanding of stream-catchment connections. Water Resour. Res. 2011, 47, 1–9. [Google Scholar] [CrossRef]
- Holley, E.R.; Yotsukura, N. Gas Transfer at Water Surfaces; Chapter Field Techniques for Reaeration Measurements in Rivers; Reidel: Dordrecht, The Netherlands, 1984; pp. 381–401. [Google Scholar]
- Liss, P.S.; Slater, P.G. Flux of gases across the air-sea interface. Nature 1974, 247, 181–184. [Google Scholar] [CrossRef]
- Elsinger, R.J.; Moore, W.S. Gas exchange in the Pee Dee River based on 222Rn evasion. Geophys. Res. Lett. 1983, 10, 443–446. [Google Scholar] [CrossRef]
- Peng, T.H.; Takahashi, T.; Broecker, W.S. Surface radon measurements in the North Pacific Ocean Station Papa. J. Geophys. Res. 1974, 79, 1772–1780. [Google Scholar] [CrossRef]
- Cammann, K. Instrumentelle Analytische Chemie: Verfahren, Anwendugen, Qualitätssicherung; Spektrum: Berlin, Germany, 2010. [Google Scholar]
- Wanninkhof, R.; Mulholl, P.J.; Elwood, J.W. Gas exchange rates for a first-order stream determined with deliberate and natural tracers. Water Resour. Res. 1990, 26, 1621–1630. [Google Scholar]

| Avon River | Mitchell River | ||||||
|---|---|---|---|---|---|---|---|
| Sampling | Q Channel | Q Stratford | Chinns Br. | Loss/Gain (%) | Q Glenaladale | Q Rosehill | Loss/Gain (%) |
| February 2009 | 4.874 | 9.794 | 13.334 | +144.45 | 88.761 | 28.201 | −68.22 |
| April 2010 | 14.248 | 18.063 | 48.646 | +332.67 | 396.820 | 339.688 | −14.39 |
| September 2010 | 97.533 | 135.511 | 140.593 | +40.00 | 4870.742 | 4723.073 | −3.03 |
| October 2010 | 1332.224 | 1204.164 | −9.61 |
| Avon R. | ||||||||
|---|---|---|---|---|---|---|---|---|
| Date | Width | Depth | Discharge | Base-Flow Flux Rn | Base-Flow Flux Cl | |||
| (m) | (m) | (d) | (m d) | (m d) | % | (m d) | % | |
| Feb-09 | 10–20 | 0.3–1.2 | 0.18–1.78 | 15,000 | 9073 | 60.49 | 2392 | 15.95 |
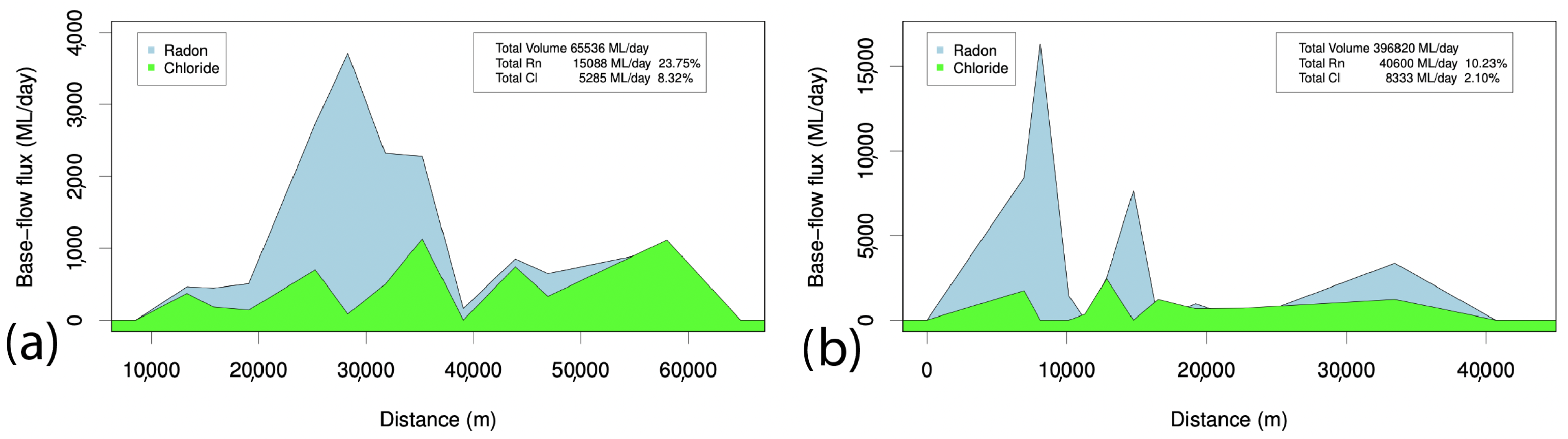
| Apr-10 | 10–20 | 0.3–2 | 0.62–4.18 | 63,536 | 15,088 | 23.75 | 5285 | 8.32 |
| Sep-10 | 10–20 | 0.8–2.5 | 1.12–17.84 | 143,067 | 21,262 | 14.86 | 5126 | 3.58 |
| Mitchell R. | ||||||||
| Date | Width | Depth | Discharge | Base-Flow Flux Rn | Base-Flow Flux Cl | |||
| (m) | (m) | (d) | (m d) | (m d) | % | (m d) | % | |
| Feb-09 | 10–25 | 1–2.5 | 0.04–1.11 | 88,761 | 37,360 | 42.09 | 5341 | 6.02 |
| Apr-10 | 10–25 | 1.5–2.5 | 0.40–1.98 | 396,820 | 40,600 | 10.23 | 8333 | 2.10 |
| Sep-10 | 10–25 | 1.5–2.5 | 0.55–2.88 | 4,870,742 | 201,631 | 4.14 | 112,330 | 2.31 |
| Oct-10 | 10–25 | 1–2.5 | 0.36–1.50 | 1,332,224 | 41,824 | 3.14 | 15,507 | 1.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmann, H. Estimating the Role of Bank Flow to Stream Discharge Using a Combination of Baseflow Separation and Geochemistry. Water 2023, 15, 844. https://doi.org/10.3390/w15050844
Hofmann H. Estimating the Role of Bank Flow to Stream Discharge Using a Combination of Baseflow Separation and Geochemistry. Water. 2023; 15(5):844. https://doi.org/10.3390/w15050844
Chicago/Turabian StyleHofmann, Harald. 2023. "Estimating the Role of Bank Flow to Stream Discharge Using a Combination of Baseflow Separation and Geochemistry" Water 15, no. 5: 844. https://doi.org/10.3390/w15050844





