Transport of Sediment Mixtures in Steady Flow with an Extra Contribution of Their Finest Fractions: Laboratory Tests and Modeling
Abstract
:1. Introduction
2. Materials and Methods
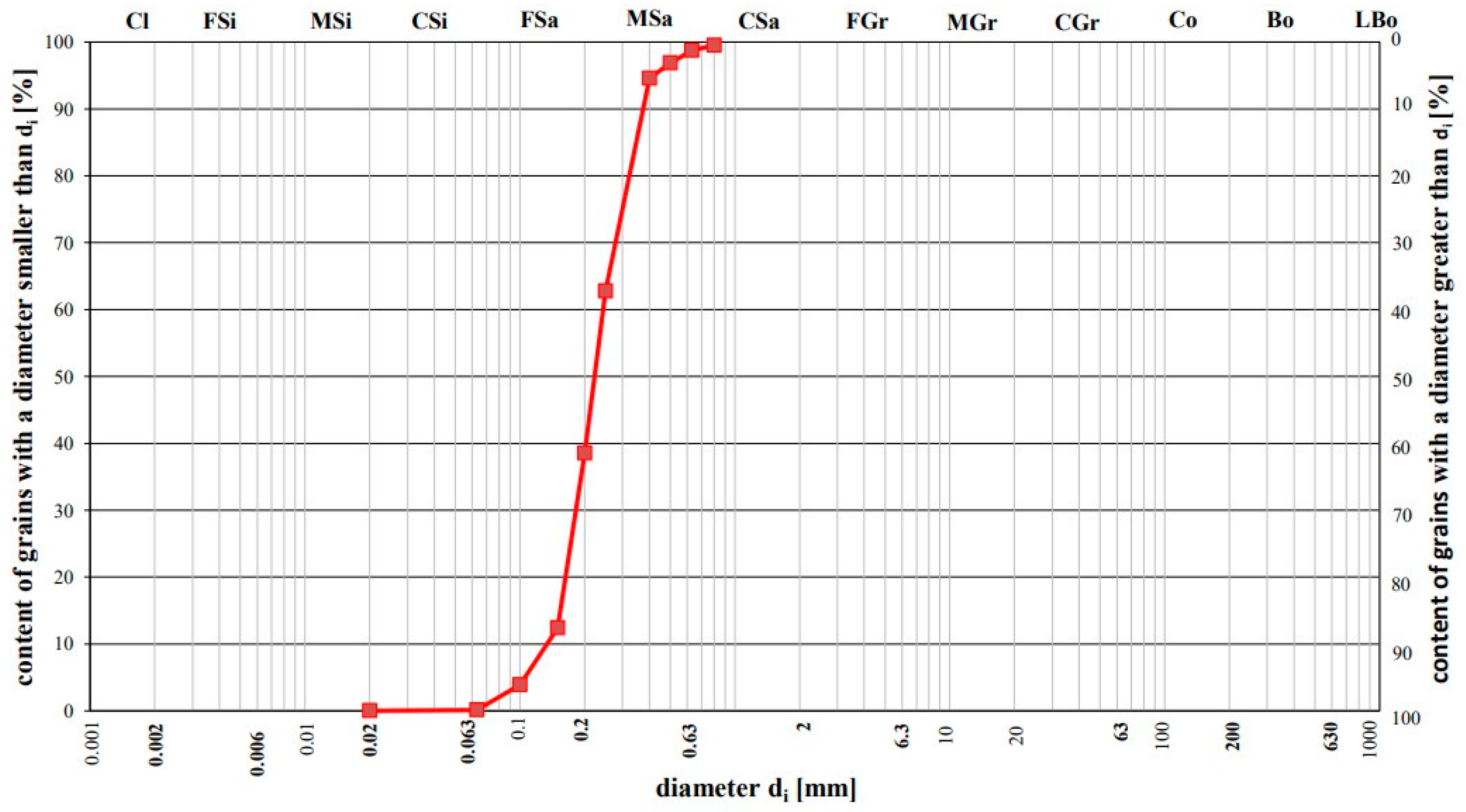
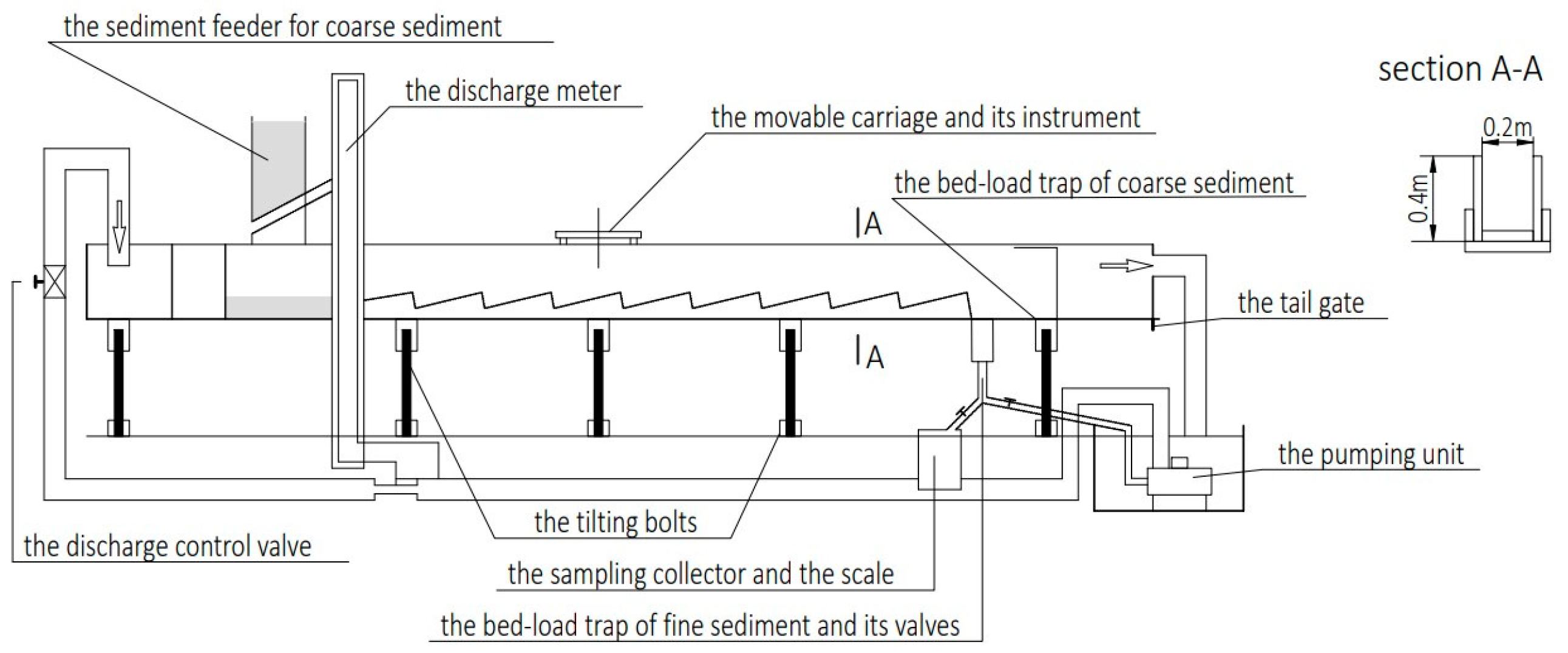
2.1. Experiment Gdańsk, 2021
- a 0.73 m long outflow section, with a bottom inlet supplying the channel with water;
- starting section with a length with a length of 2.5 m;
- a cuvette with the input sediment, i.e., a depression along the entire channel, 1 m long an 0.08 m high;
- the test section 2.5 m long;
- sediment trap, in the form of another cuvette, i.e., a depression channel 0.73 m long and 0.08 m high, with a bottom inlet and outlet.
- Filling the cuvette with the water-saturated sediment. Placing the wet sediment in the cuvette prevented formation of air bubbles in the deposited mixture;
- Taking a sample from the container filled with sediment prepared for testing;
- Leveling the sediment to the edge of the cuvette and removing the remains of sediment from the vicinity of the cuvette;
- Filling the channel up to the water depth H = 0.05 m;
- Performing a test for a given flow (Times for individual tests are given in Table 1;
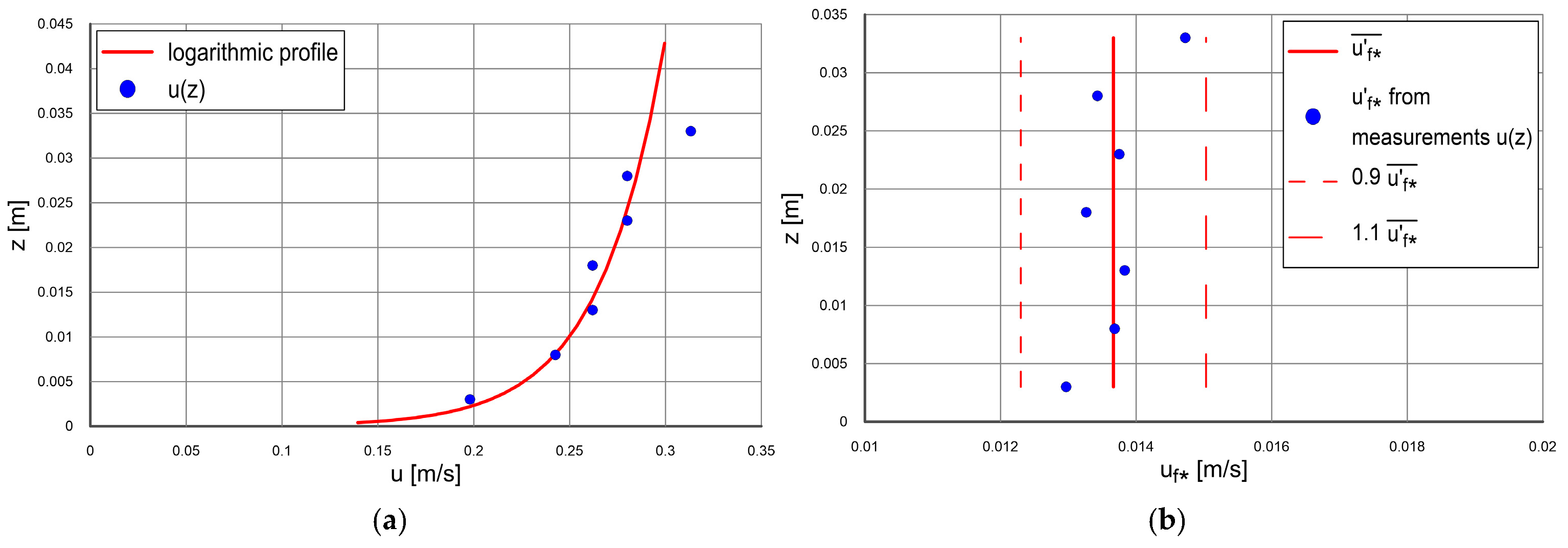
- Measurements of the velocity over the bottom using the Prandtl tube (0.1 m above the lower edge of the cuvette, in the period between the flow stabilization and the development of wrinkles);
- Water removal from the channel after the test is completed;
- Collection of sediment from the trap and control area;
- Measurement of sediment volume captured in the sand trap;
- Documentation of bathymetry in a cuvette by taking photos, performing a bathymetric measurement;
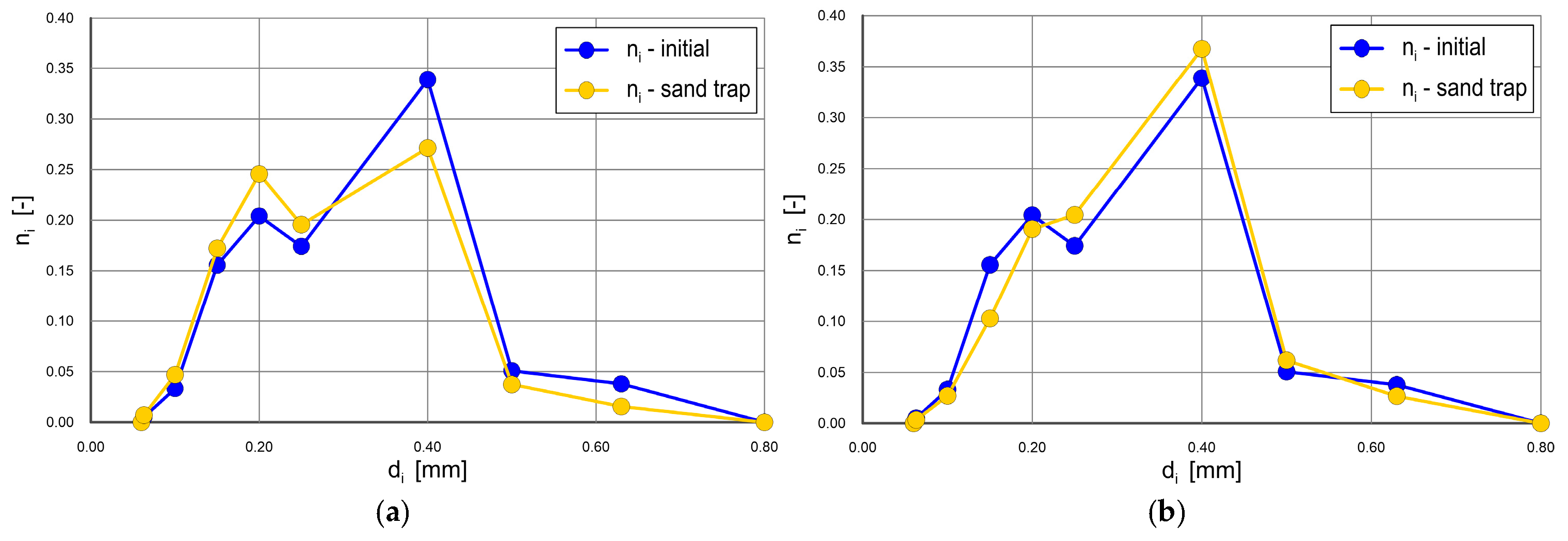
- Collecting sediment samples for sieve analysis;
- Removal of sediment from cuvette and its cleaning.
2.2. Experiment by Elhakeem and Imran (2012) [53]
3. Theoretical Investigations
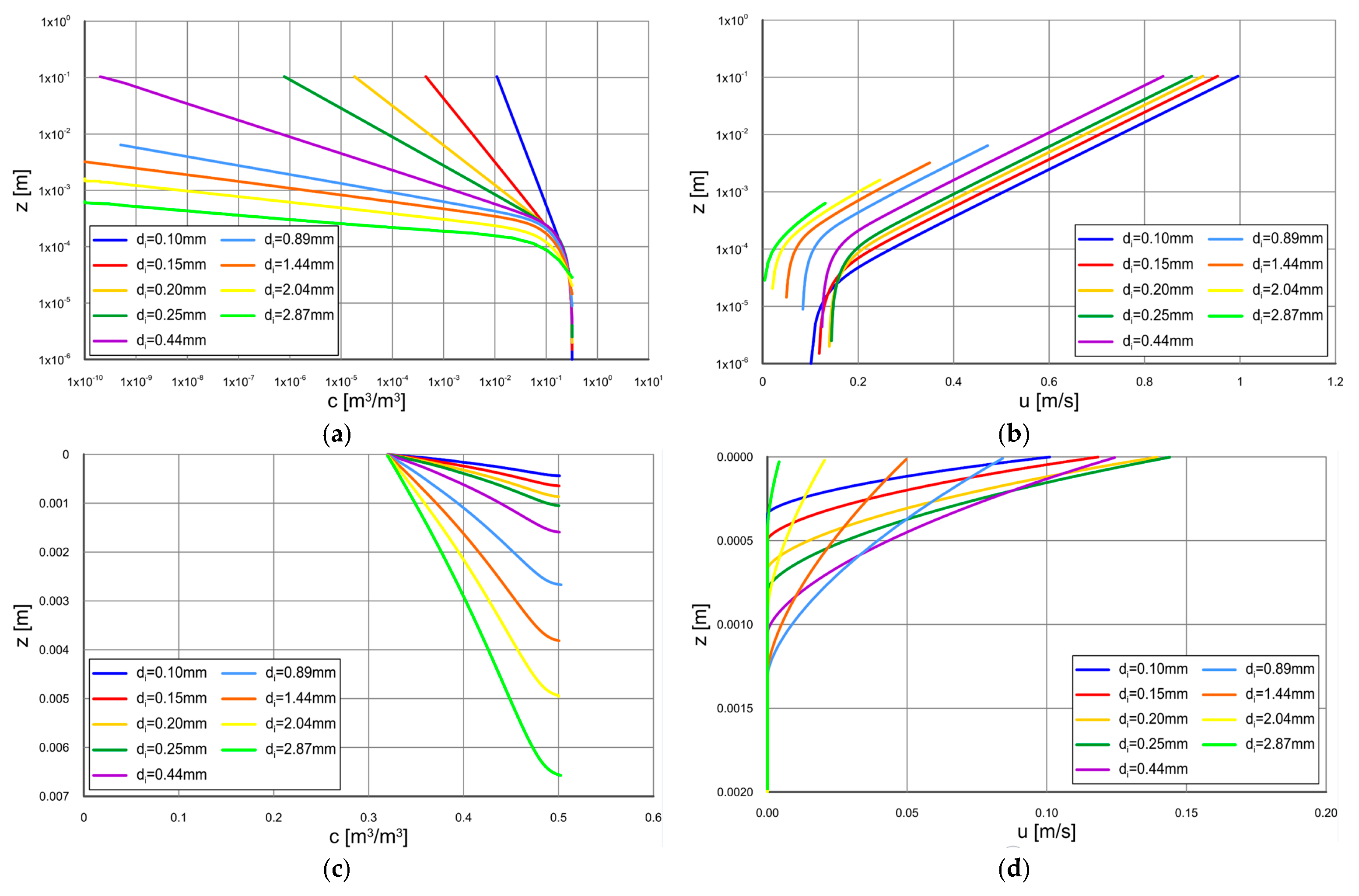
3.1. Transport Model for Non-Uniform Sediment
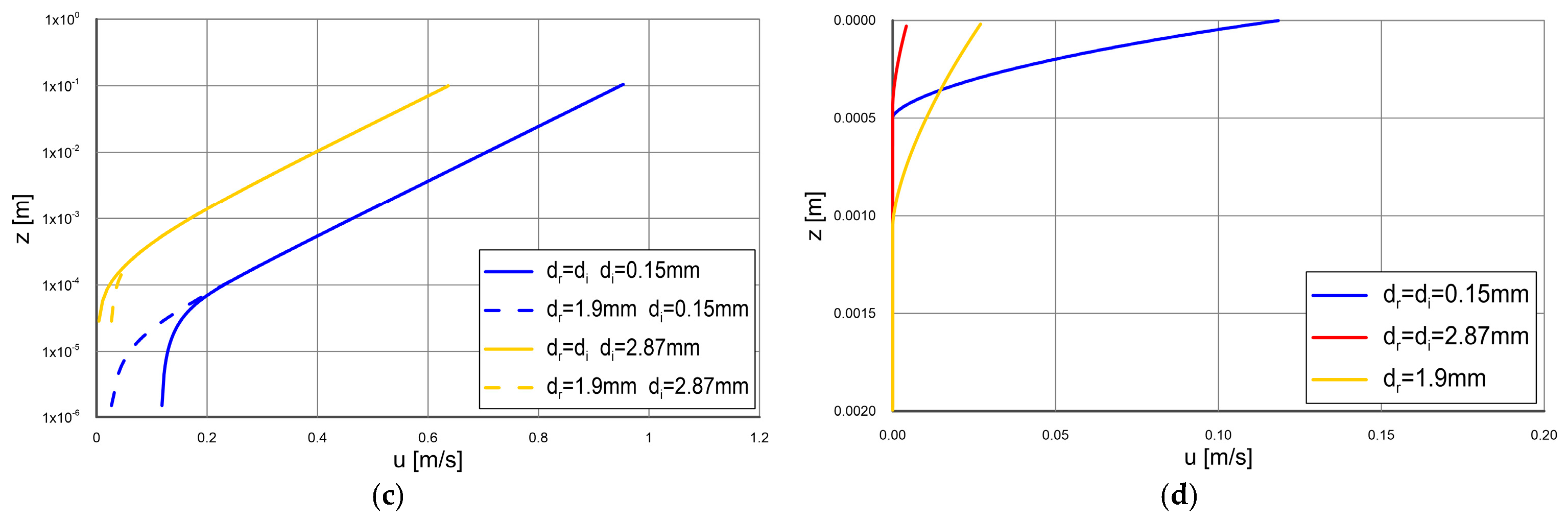
3.2. Model Results for Uniform Sediment
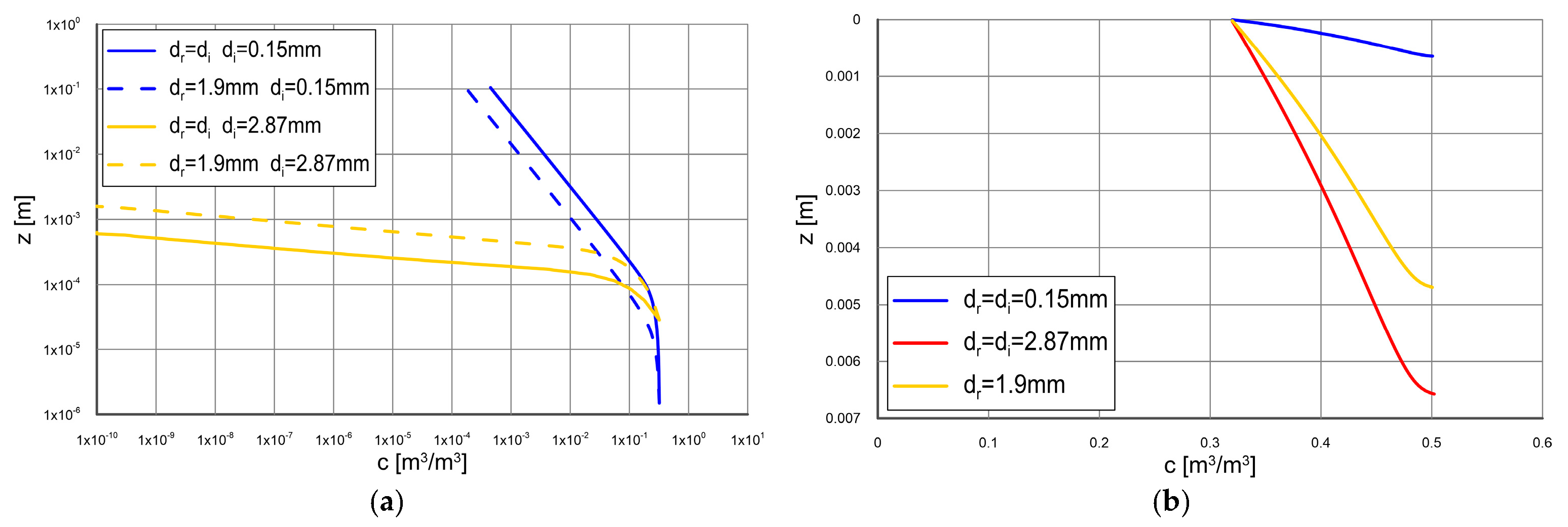
3.3. Model Results for Non-Uniform Sediments
4. Discussion
4.1. Non-Uniform Sediment Transport with Limited Availability of Very Fine Fractions
4.2. Comparison Calculations with Measuremends
4.2.1. Experiment Gdańsk 2021
4.2.2. Experiment by Elhakeem and Imran [53]
5. Conclusions
- Transport calculations conducted by the presented model separately for all sediment fractions in mixture including the mutual interactions between them have shown:
- due to assumed strong interactions between the sediment fractions in the moving layer of densely concentrated sediments all the fractions are characterized by the same velocity and concentration vertical profiles;
- in the contact layer vertical profiles of velocities and concentrations vary for individual fractions due to turbulent water pulsations and chaotic collisions of grains;
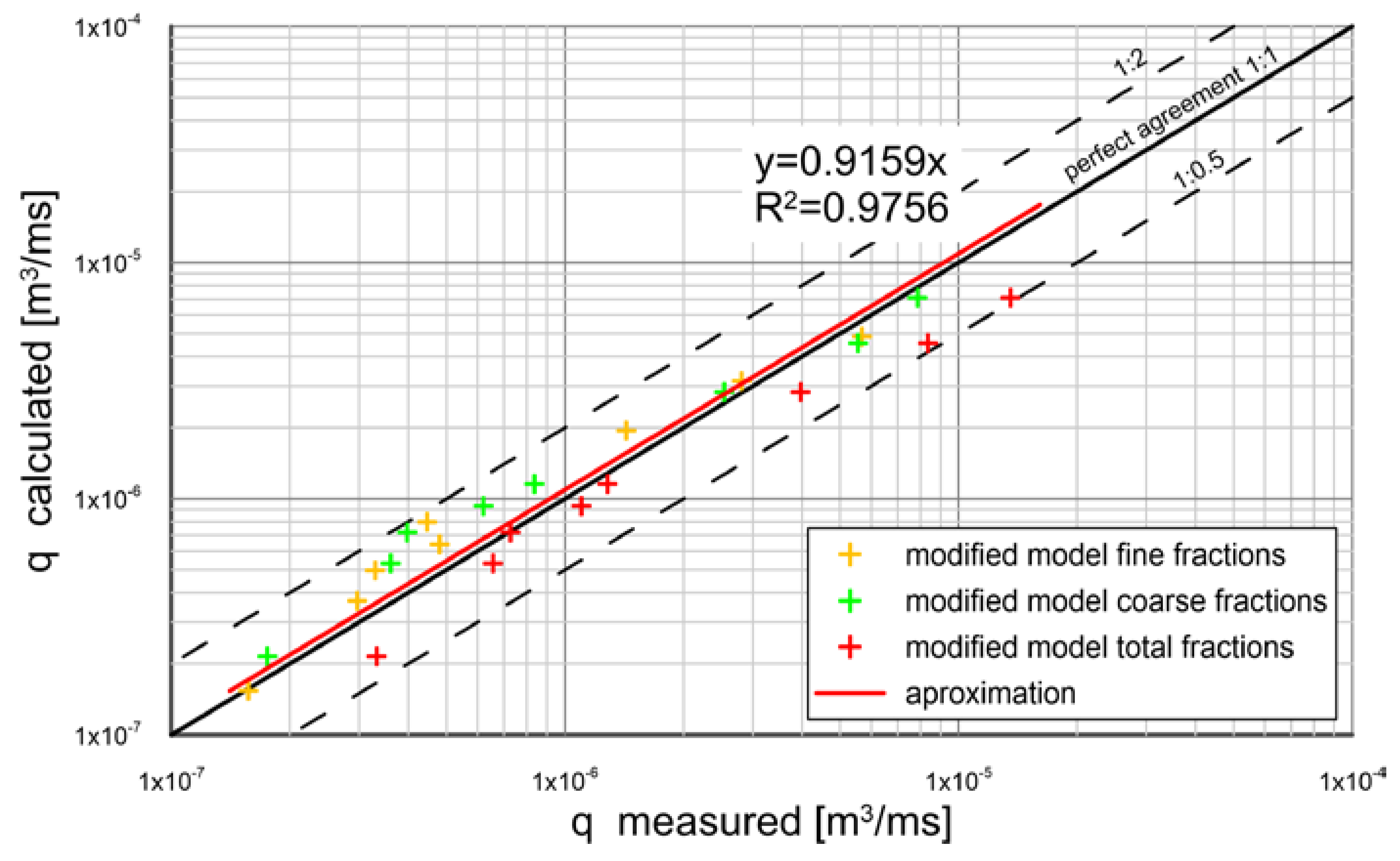
- the agreement between the calculated transport and measurements was achieved within plus/minus a factor of two of the measurements;
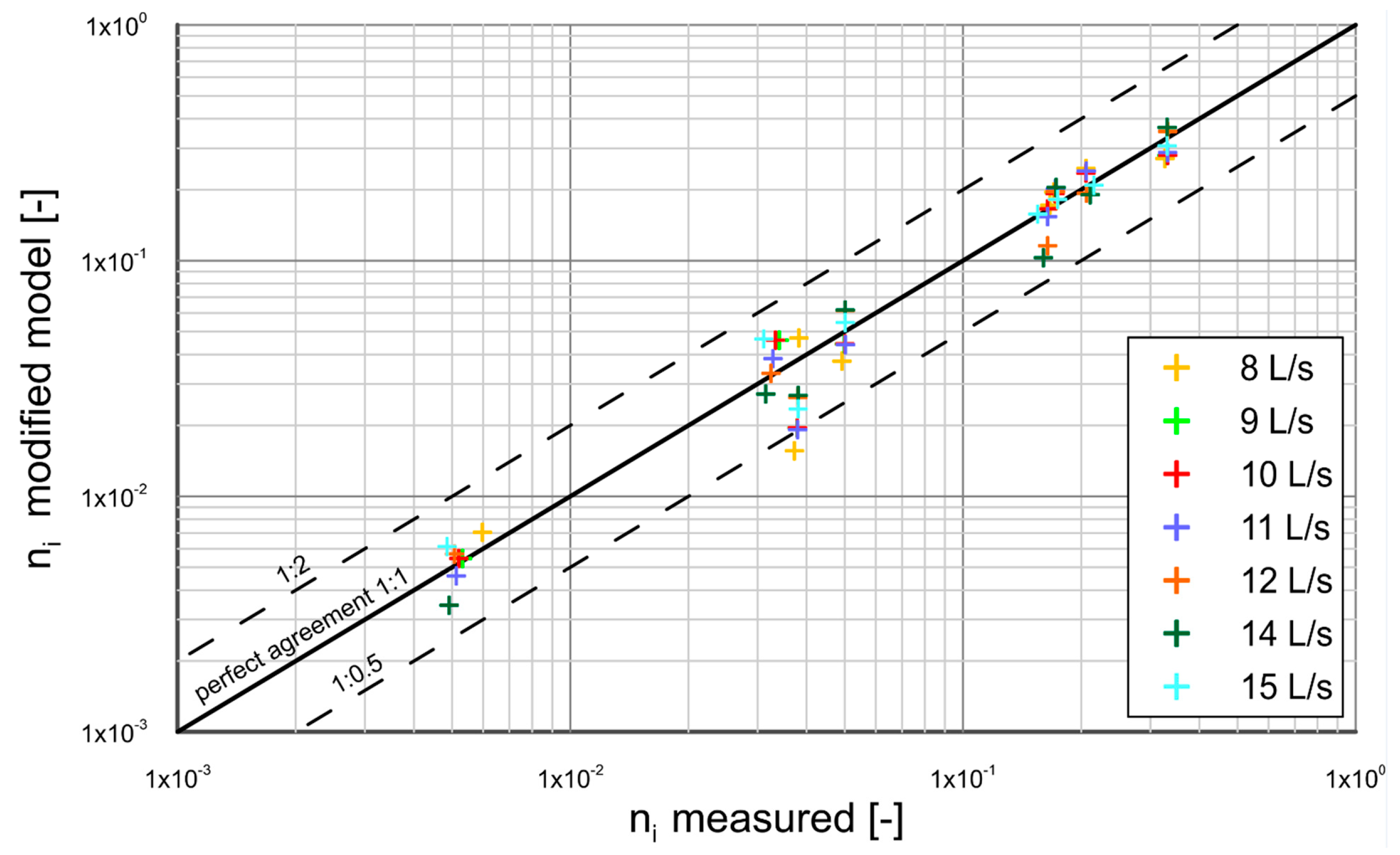
- calculations of the granulometric distributions of sediment from the trap conducted using presented model have shown good agreement with the measurements (plus/minus a factor of two of the measurements);
- results confirm that the mechanism of interactions between fractions, and in particular the influence of finer grains in the mixture on the increase in transport of coarser fractions, is well described by the model.
- The experimental investigations on transport of sediment mixture with large amount of very fine non-cohesive fractions resulted in proposed modification by inclusion of possible deficit of very small fractions in the active layer of the bottom. The compatibility of the transport calculation results for all fractions with measurements Gdańsk 2021 is within plus/minus a factor of two of the measurements. This confirms the lack of full availability of very fine fractions in the bottom and be the reason for a significant reduction in transport of those fractions.
- Comparison of the calculations by presented modified model of grain size distributions with measurements Gdańsk 2021 shows consistency with the experimental results within plus/minus a factor of two of the measurements.
- The presented study provides verified three-layer model which enables the proper description of sediment transport and grain size distributions of transported fractions in steady flow for any bed sediment mixtures, including poorly and well sorted grains with large amount of very fine non-cohesive fractions.
- The present study provides a useful engineering tool for prediction of transport in steady flow of sediment mixtures with various non-cohesive fractions including very fine and fine. Calculations are possible with just a few measurable properties of particles and water. Parameters do not need tuning against experiments.
- The next step of model development will be the extension to transport modeling in steady flow of sand mixtures with cohesive admixtures. The authors look forward to work also on model extension to predict sediment transport under highly transient (e.g., dam-break) flows.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mc Laren, P.; Bowles, D. The Effects of Sediment Transport on Grain-Size Distributions. J. Sediment. Res. 1985, 55, 457–470. [Google Scholar]
- Van Rijn, L.C. Longshore sediment transport, Report Z3054; Delft Hydraulics: Delft, The Netherlands, 2001. [Google Scholar]
- Van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. I: Initiation of Motion, Bed Roughness, and Bed-Load Transport. J. Hydraul. Eng. 2007, 133, 649–667. [Google Scholar] [CrossRef] [Green Version]
- Van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. II: Suspended Transport. J. Hydraul. Eng. 2007, 133, 668–689. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Unified View of Sediment Transport by Currents and Waves. III: Graded Beds. J. Hydraul. Eng. 2007, 133, 761–775. [Google Scholar] [CrossRef] [Green Version]
- Van Rijn, L.C.; Walstra, D.J.R.; van Ormondt, M. Unified view of sediment transport by currents and waves. IV: Application of morpho dynamic model. J. Hydraul. Eng. 2007, 133, 776–793. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Grasmeijer, B.T.; Perk, L. Effect of channel deepening on tidal flow and sediment transport, part 1. Sandy channels. Ocean Dyn. 2018, 68, 1457–1479. [Google Scholar] [CrossRef]
- Egiazaroff, I.V. Calculation of nonuniform sediment concentrations. J. Hydraul. Div. 1965, 91, 225–247. [Google Scholar] [CrossRef]
- Gessler, J. Beginning and ceasing sediment motion. In River Mechanics; Shen, H.W., Ed.; Water Resources: Littleton, CO, USA, 1971; Chapter 7. [Google Scholar]
- Parker, G.; Klingeman, P.C. On why gravel bed streams are paved. Water Resour. Res. 1982, 18, 1409–1423. [Google Scholar] [CrossRef] [Green Version]
- Wilcock, P.R.; Mc Ardell, B.W. Surface-based fractional transport rates: Mobilization thresholds and partial transport of a sand-gravel sediment. Water Resour. Res. 1993, 29, 1297–1312. [Google Scholar] [CrossRef]
- Paola, C.; Seal, R. Grain Size Patchiness as a Cause of Selective Deposition and Downstream Fining. Water Resour. Res. 1995, 31, 1395–1407. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, Delft, The Netherlands, 7 June 1948; International IAHR Congress. International Association for Hydro-Environment Engineering and Research: Stockholm, Sweden, 1948. [Google Scholar]
- Mc Carrona, C.J.; Van Landeghema, K.J.J.; Baasa, J.H.; Amoudryb, L.O.; Malarkey, J. The hiding-exposure effect revisited: A method to calculate the mobility of bimodal sediment mixtures. Mar. Geol. 2019, 410, 22–31. [Google Scholar] [CrossRef]
- Khosravi, K.; Chegini, A.H.N.; Mao, L.; Rodriguez, J.F.; Saco, P.M.; Binns, A.D. Experimental Analysis of Incipient Motion for Uniform and Graded Sediments. Water 2021, 13, 1874. [Google Scholar] [CrossRef]
- Dey, S.; Ravi Kishore, G.; Castro-Orgaz, O.; Ali, S.Z. Hydrodynamics of submerged turbulent plane offset jets. Phys. Fluids 2017, 29, 065112. [Google Scholar] [CrossRef]
- Ancey, C. Stochastic modeling in sediment dynamics: Exner equation for planar bed incipient bed load transport conditions. J. Geo-Phys. Res. 2010, 115, F00A11. [Google Scholar] [CrossRef]
- Furbish, D.J.; Haff, P.K.; Roseberry, J.C.; Schmeeckle, M.W. A probabilistic description of the bed load sediment flux: 1. Theory. J. Geo-Phys. Res. Earth Surf. 2012, 117, F03031. [Google Scholar] [CrossRef] [Green Version]
- Heyman, J.; Ma, H.B.; Mettra, F.; Ancey, C. Spatial correlations in bed load transport: Evidence, importance, and modelling. J. Geo-Phys. Res. Earth Surf. 2014, 119, 1751–1767. [Google Scholar] [CrossRef] [Green Version]
- Bialik, R.J.; Nikora, V.I.; Rowiński, P.M. 3D Lagrangian modeling of saltating particles diffusion in turbulent water flow. Acta Geophys. 2012, 60, 1639–1660. [Google Scholar] [CrossRef]
- Nikora, V.I.; Rowiński, P.M. Rough-bed flows in geophysical, environmental, and engineering systems: Double-Averaging Approach and its applications. Acta Geophys. 2008, 56, 529–533. [Google Scholar] [CrossRef] [Green Version]
- Vowinckel, B.; Nikora, V.; Kempe, T.; Fröhlich, J. Momentum balance in flows over mobile granular beds: Application of double averaging methodology to DNS data. J. Hydraul. Res. 2017, 55, 190–207. [Google Scholar] [CrossRef] [Green Version]
- Vowinckel, B.; Nikora, V.; Kempe, T.; Fröhlich, J. Spatially averaged momentum fluxes and stresses in flows over mobile granular beds: A DNS-based study. J. Hydraul. Res. 2017, 55, 208–223. [Google Scholar] [CrossRef] [Green Version]
- Berzi, D.; Fraccarollo, L. Intense sediment transport: Collisional to turbulent suspension. Phys. Fluids 2016, 28, 023302. [Google Scholar] [CrossRef] [Green Version]
- Jenkins, J.T.; Hanes, D.M. Collisional sheet flows of sediment driven by a turbulent fluid. J. Fluid Mech. 1998, 370, 29–52. [Google Scholar] [CrossRef]
- Pasini, J.M.; Jenkins, J.T. Aeolian transport with collisional suspension. Phil. Trans. R. Soc. A. 2005, 363, 1625–1646. [Google Scholar] [CrossRef] [PubMed]
- Graf, W.H. Hydraulics of Sediment Transport; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Vanoni, V.A. Sedimentation Engineering Practice. American Society of Civil Engineers. In Manuals and Reports on Engineering Practice; American Society of Civil Engineers: Reston, VA, USA, 1975; Volume 54, 745p. [Google Scholar]
- Yalin, M.S. Mechanics of Sediment Transport; Pergamon Press: London, UK, 1977. [Google Scholar]
- Sharma, A.; Kumar, B. Flow structure over uniform and nonuniform sand bed channel E. In Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019. [Google Scholar] [CrossRef]
- Sahoo, A.; Samantaray, S.; Singh, R.B. Analysis of Velocity Profiles in Rectangular Straight Open Channel Flow. Pertanika J. Sci. Technol. 2020, 28, 1–18. [Google Scholar]
- Cheng, C.H.; de Smit, J.C.; Fivash, G.S.; Hulscher, S.J.M.H.; Borsje, B.W.; Soetaert, K. Sediment shell-content diminishes current-driven sand ripple development and migration. Earth Surf. Dynam. 2021, 9, 1335–1346. [Google Scholar] [CrossRef]
- Sleath, J.F.A. Sea Bed Mechanics (Ocean Engineering); John Wiley and Sons Inc.: Chichester, UK, 1984; ISBN 9780471890911. [Google Scholar]
- Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport; Advanced Series on Ocean Engineering; World Scientific: Singapore, 1992; Volume 4. [Google Scholar]
- Fredsøe, J.; Deigaard, R. Mechanics of Coastal Sediment Transport; Advanced Series on Ocean Engineering; World Scientific: Singapore, 1992; Volume 3. [Google Scholar]
- Soulsby, R. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford: London, UK, 1997. [Google Scholar]
- Selim, T.; Hesham, M.; Elkiki, M. Effect of sediment transport on flow characteristics in non-prismatic compound channels. Ain Shams Eng. J. 2022, 13, 101771. [Google Scholar] [CrossRef]
- Miller, M.C.; Mc Cave, I.N.; Komar, P.D. Threshold of sediment motion under unidirectional currents. Sedimentology 1977, 24, 507–527. [Google Scholar] [CrossRef]
- Thorn, M. Coastal and estuarine sediment dynamics by K.R. Dyer. Wiley, Chichester. Geol. J. 1987, 22, 169. [Google Scholar] [CrossRef]
- Voulgaris, G.; Wallbridge, S.; Tomlinson, B.N.; Collins, M.B. Laboratory investigations into wave period effects on sand bed erodibility under the combined action of waves and currents. Coastal Eng. 1995, 26, 117–134. [Google Scholar] [CrossRef]
- Sharma, A.; Kumar, B. Comparison of Flow and Morphological Characteristics in Uniform and Non-uniform Sand Bed Channel. Can. J. Civ. Eng. 2020, 47, 678–690. [Google Scholar] [CrossRef]
- Stone, M.; Krishnappan, B.G.; Silins, U.; Emelko, M.B.; Williams, C.H.S.; Collins, A.L.; Spencer, S.A. A New Framework for Modelling Fine Sediment Transport in Rivers Includes Flocculation to Inform Reservoir Management in Wildfire Impacted Watersheds. Water 2021, 13, 2319. [Google Scholar] [CrossRef]
- Wilcock, P.R.; Kenworthy, S.T.; Crowe, J.C. Experimental study of the transport of mixed sand and gravel. Water Resour. Res. 2001, 37, 3349–3358. [Google Scholar] [CrossRef] [Green Version]
- Radosz, I.; Zawisza, J.; Biegowski, J.; Paprota, M.; Majewski, D.; Kaczmarek, L.M. An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in Wave Motion. Water 2022, 14, 2397. [Google Scholar] [CrossRef]
- Radosz, I.; Zawisza, J.; Biegowski, J.; Paprota, M.; Majewski, D.; Kaczmarek, L.M. An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in the Wave Motion over Sloped Bed. Water 2023, 15, 125. [Google Scholar] [CrossRef]
- Kaczmarek, L.M. Moveable Sea Bed Boundary Layer and Mechanics of Sediment Transport; Institute of Hydroengineering of the Polish Academy of Sciences: Gdańsk, Poland, 1999. [Google Scholar]
- Kaczmarek, L.M.; Biegowski, J.; Ostrowski, R. Modelling cross-shore intensive sand transport and changes of bed grain size distribution versus field data. Coastal Eng. 2004, 51, 501–529. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Sawczyński, S.; Biegowski, J. Hydrodynamic equilibrium for sediment transport and bed response to wave motion. Acta Geophys. 2015, 63, 486–513. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, L.M.; Sawczyński, S.; Biegowski, J. An equilibrium transport formula for modeling sedimentation of dredged channels. Coastal Eng. J. 2017, 59, 1750015-1. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Biegowski, J.; Sobczak, Ł. Modeling of Sediment Transport in Steady Flow over Mobile Granular Bed. J. Hydraul. Eng. 2019, 145, 04019009. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Radosz, I.; Zawisza, J. Numerical Calculations with a Multi -layer Model of Mixed Sand Transport Against Measurements in Wave Motion and Steady Flow. Rocz. Ochr. Sr. 2021, 23, 629–641. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Biegowski, J.; Sobczak, Ł. Modeling of Sediment Transport with a Mobile Mixed-Sand Bed in Wave Motion. J. Hydraul. Eng. 2022, 148, 04021054. [Google Scholar] [CrossRef]
- Elhakeem, M.; Imran, J. Density Functions for Entrainment and Deposition Rates of Nonuniform Sediment. Am. Soc. Civ. Eng. 2012, 138, 591–609. [Google Scholar] [CrossRef]
- Sayed, M.; Savage, S.B. Rapid gravity flow of cohesionless granular materials down inclined chutes. J. Appl. Math. Phys. 1983, 34, 84–100. [Google Scholar] [CrossRef]
- Deigaard, R.A. Note on the three-dimensional shear stress distribution in a surf zone. Coast. Eng. 1993, 20, 157–171. [Google Scholar] [CrossRef]
- Wong, M.; Parker, G. Reanalysis and correction of bed-load relation of Meyer-Peter and Müller using their own database. J. Hydraul. Eng. 2006, 132, 1159–1168. [Google Scholar] [CrossRef] [Green Version]


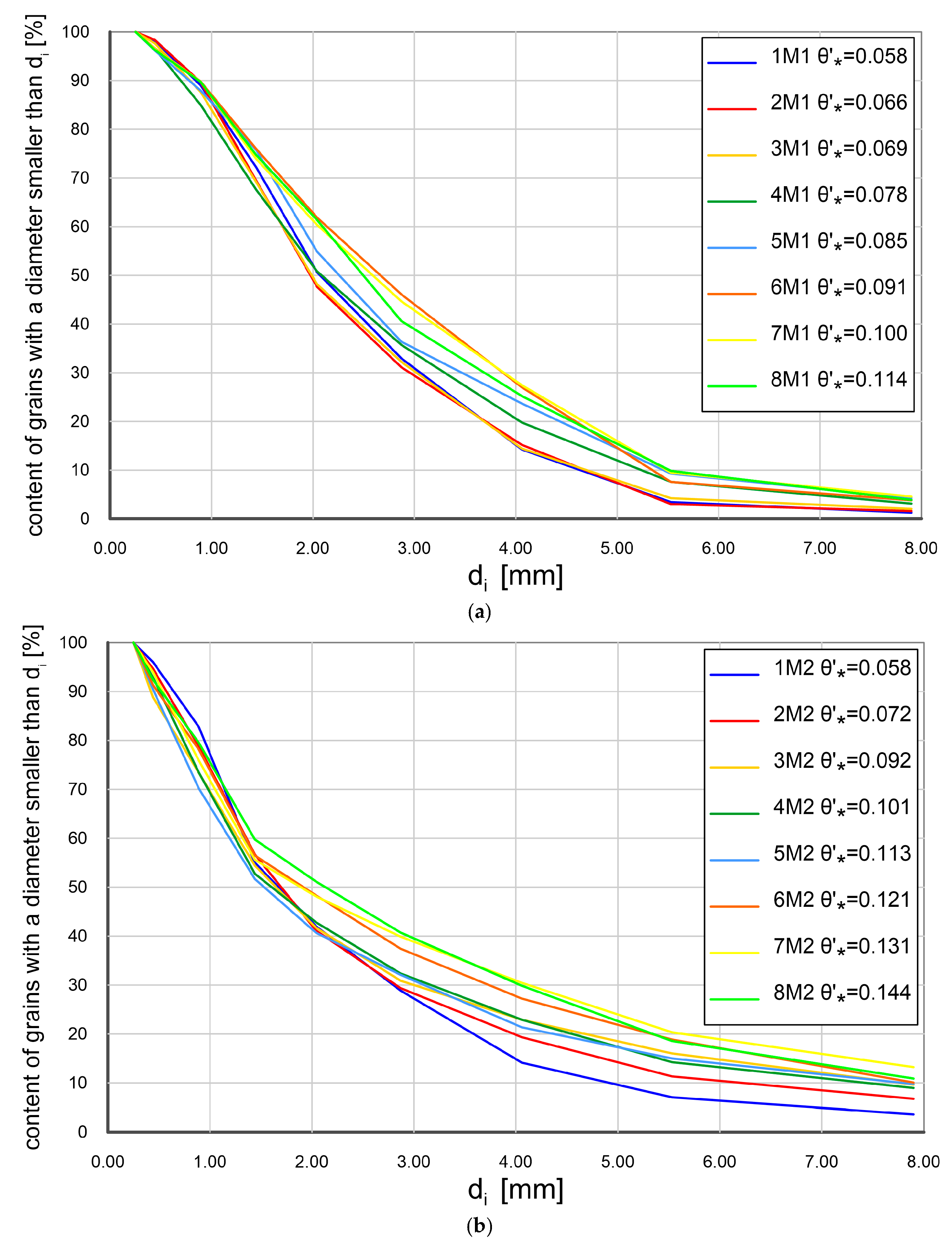
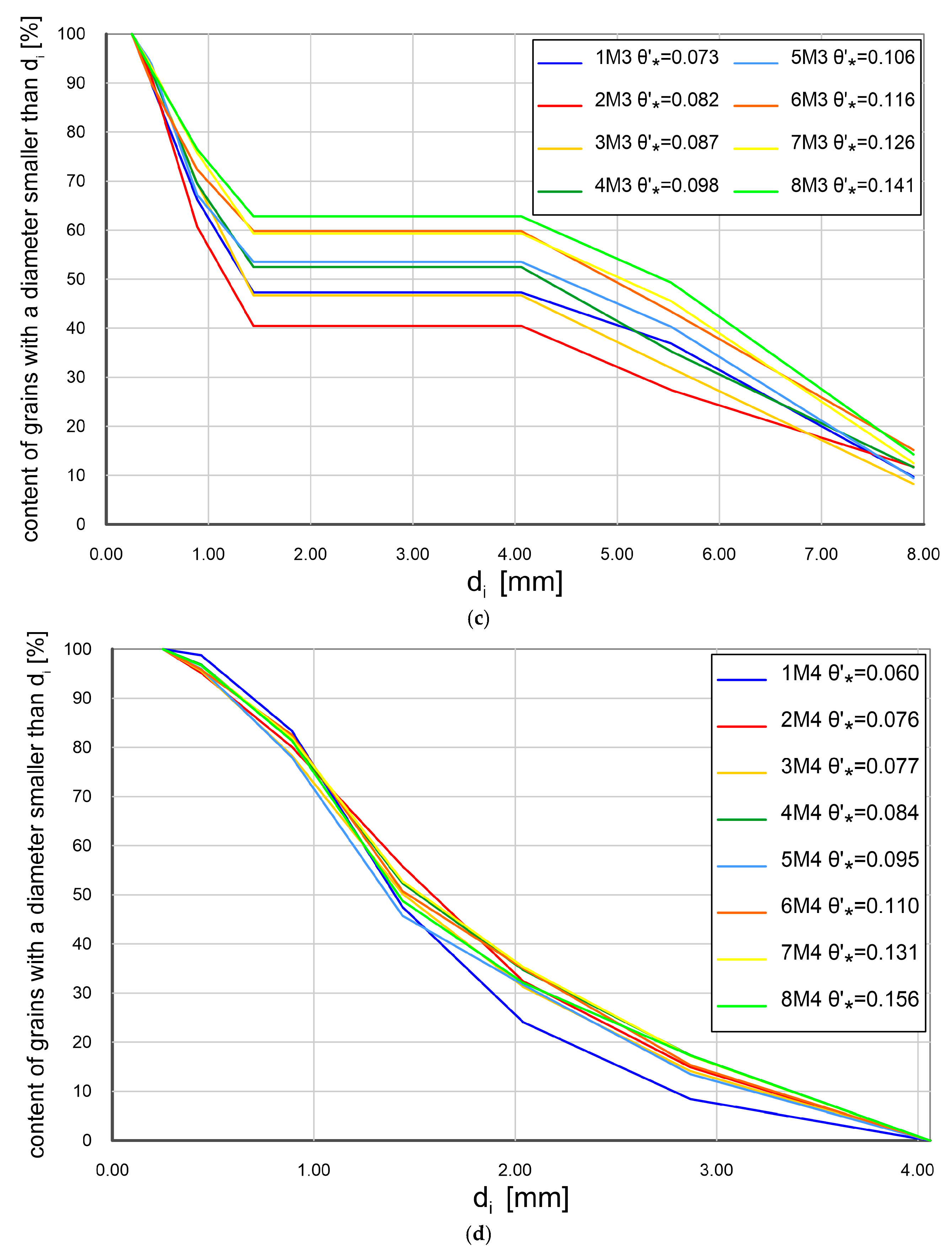






| TR Test | Flow Rate [L/s] | -Depth Averaged [m/s] | Friction | Rep. of Tests [-] | Test Time [s] | Sediment Transport Maximum Mean Minimum [m3/ms] | Fractions d90/d50/d10 [mm] | [-] | |
|---|---|---|---|---|---|---|---|---|---|
| uf* [m/s] | θ* [-] | ||||||||
| Input sand | 0.23/0.22/0.14 | ||||||||
| TR_0_7 | 7.0 | 0.5000 | 0.0097 | 0.2587 | 2 | 3600 | 8.00∙10−9 | 0.23/0.14/0.03 | 13,462 |
| 5.50∙10−9 | |||||||||
| 3.00∙10−9 | |||||||||
| TR_0_8 | 8.0 | 0.5715 | 0.0158 | 0.0690 | 4 | 3600 | 1.90∙10−8 | 0.23/0.21/0.11 | 15,385 |
| 6.60∙10−7 | |||||||||
| 3.43∙10−6 | |||||||||
| TR_0_9 | 9.0 | 0.6429 | 0.0177 | 0.0862 | 3 | 3600 | 7.59∙10−7 | 0.24/0.21/0.12 | 17,308 |
| 6.84∙10−7 | |||||||||
| 5.61∙10−7 | |||||||||
| TR_0_10 | 10.0 | 0.7143 | 0.0185 | 0.0949 | 3 | 3600 | 7.95∙10−7 | 0.24/0.21/0.11 | 19,231 |
| 7.38∙10−7 | |||||||||
| 6.80∙10−7 | |||||||||
| TR_0_11 | 11.0 | 0.7857 | 0.0194 | 0.1035 | 3 | 3600 | 1.16∙10−6 | 0.24/0.22/0.12 | 21,154 |
| 1.08∙10−6 | |||||||||
| 1.00∙10−6 | |||||||||
| TR_0_12 | 12.0 | 0.8571 | 0.0201 | 0.1121 | 3 | 3600 | 1.52∙10−6 | 0.26/0.24/0.13 | 23,077 |
| 1.29∙10−6 | |||||||||
| 1.06∙10−6 | |||||||||
| TR_0_13 | 13.0 | 0.9285 | 0.0244 | 0.1638 | 3 | 1800 | 6.77∙10−6 | 0.24/0.22/0.12 | 25,000 |
| 4.86∙10−6 | |||||||||
| 2.94∙10−6 | |||||||||
| TR_0_14 | 14.0 | 1.0000 | 0.0273 | 0.2070 | 3 | 900 | 1.33∙10−5 | 0.26/0.24/0.14 | 26,923 |
| 9.60∙10−6 | |||||||||
| 5.91∙10−6 | |||||||||
| TR_0_15 | 15.0 | 1.0714 | 0.0306 | 0.2587 | 3 | 900 | 1.80∙10−5 | 0.25/0.22/0.11 | 28,846 |
| 1.44∙10−5 | |||||||||
| 1.07∙10−5 | |||||||||
| 1M1 | 2M1 | 3M1 | 4M1 | 5M1 | 6M1 | 7M1 | 8M1 | |
| [-] | 0.058 | 0.066 | 0.069 | 0.078 | 0.085 | 0.091 | 0.100 | 0.114 |
| 4.24 | 14.37 | 18.98 | 27.05 | 47.89 | 57.81 | 103.63 | 123.23 | |
| [mm] | 2.03 | 1.95 | 1.98 | 2.04 | 2.26 | 2.49 | 2.66 | 2.50 |
| 1M2 | 2M2 | 3M2 | 4M2 | 5M2 | 6M2 | 7M2 | 8M2 | |
| [-] | 0.058 | 0.072 | 0.092 | 0.101 | 0.113 | 0.121 | 0.131 | 0.144 |
| 3.15 | 13.76 | 47.04 | 51.75 | 72.92 | 133.87 | 123.73 | 179.11 | |
| [mm] | 1.67 | 1.70 | 1.65 | 1.65 | 1.53 | 1.92 | 1.89 | 2.13 |
| 1M3 | 2M3 | 3M3 | 4M3 | 5M3 | 6M3 | 7M3 | 8M3 | |
| [-] | 0.073 | 0.082 | 0.087 | 0.098 | 0.106 | 0.116 | 0.126 | 0.141 |
| 8.52 | 22.48 | 26.52 | 34.82 | 60.46 | 69.63 | 137.55 | 151.90 | |
| [mm] | 1.36 | 1.18 | 1.36 | 4.27 | 4.45 | 4.94 | 5.04 | 5.45 |
| 1M4 | 2M4 | 3M4 | 4M4 | 5M4 | 6M4 | 7M4 | 8M4 | |
| [-] | 0.060 | 0.076 | 0.077 | 0.084 | 0.095 | 0.110 | 0.131 | 0.156 |
| 5.93 | 24.42 | 20.20 | 27.36 | 54.77 | 67.70 | 108.36 | 214.55 | |
| [mm] | 1.40 | 1.58 | 1.45 | 1.52 | 1.36 | 1.47 | 1.54 | 1.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawisza, J.; Radosz, I.; Biegowski, J.; Kaczmarek, L.M. Transport of Sediment Mixtures in Steady Flow with an Extra Contribution of Their Finest Fractions: Laboratory Tests and Modeling. Water 2023, 15, 832. https://doi.org/10.3390/w15050832
Zawisza J, Radosz I, Biegowski J, Kaczmarek LM. Transport of Sediment Mixtures in Steady Flow with an Extra Contribution of Their Finest Fractions: Laboratory Tests and Modeling. Water. 2023; 15(5):832. https://doi.org/10.3390/w15050832
Chicago/Turabian StyleZawisza, Jerzy, Iwona Radosz, Jarosław Biegowski, and Leszek M. Kaczmarek. 2023. "Transport of Sediment Mixtures in Steady Flow with an Extra Contribution of Their Finest Fractions: Laboratory Tests and Modeling" Water 15, no. 5: 832. https://doi.org/10.3390/w15050832





