Multi-Objective Lower Irrigation Limit Simulation and Optimization Model for Lycium Barbarum Based on NSGA-III and ANN
Abstract
:1. Introduction
2. Materials and Methods
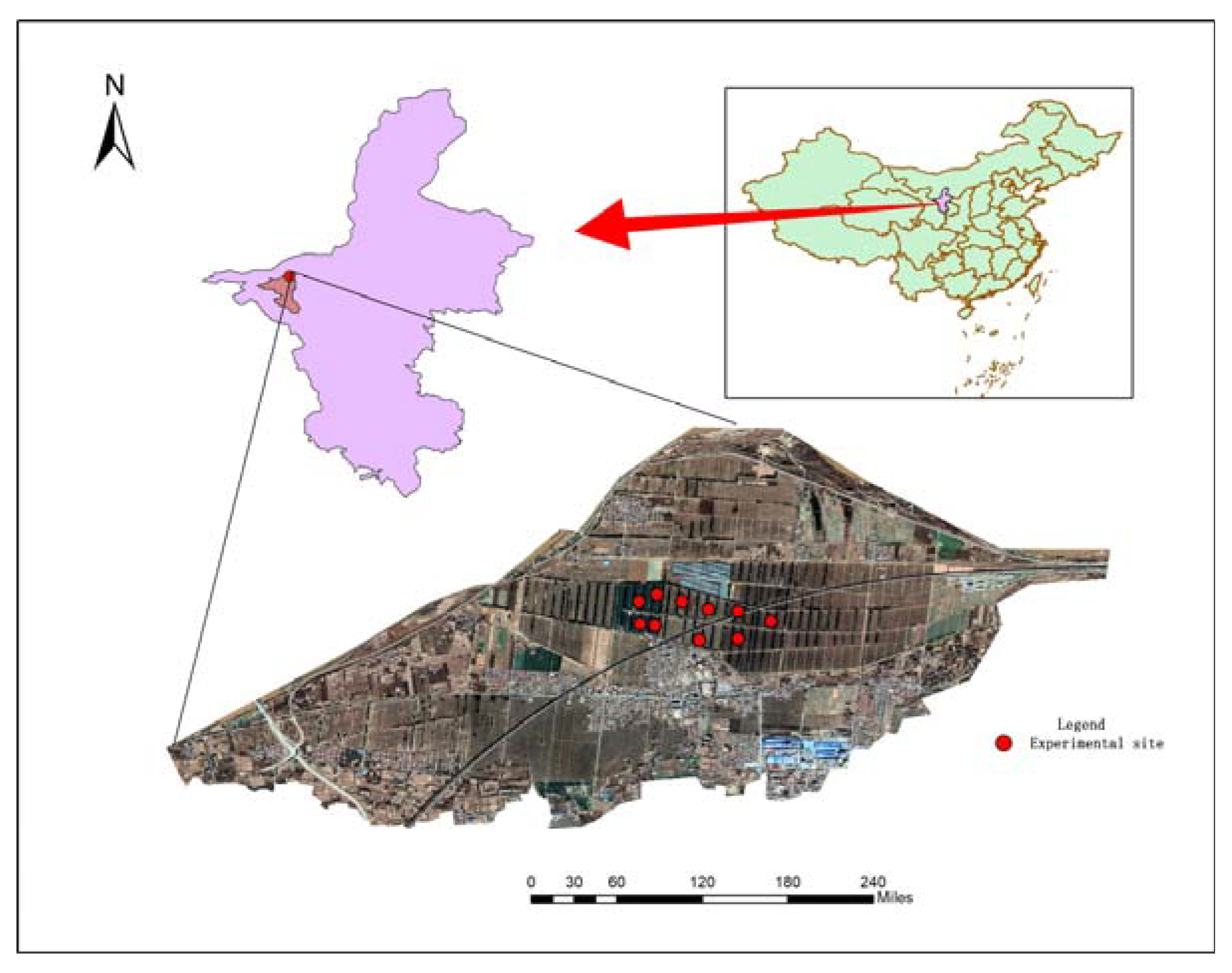
2.1. Overview of the Study Area
2.2. Lycium Barbarum’s Active Root Layer Water Balance Model
2.3. Water Production Function of Lycium barbarum
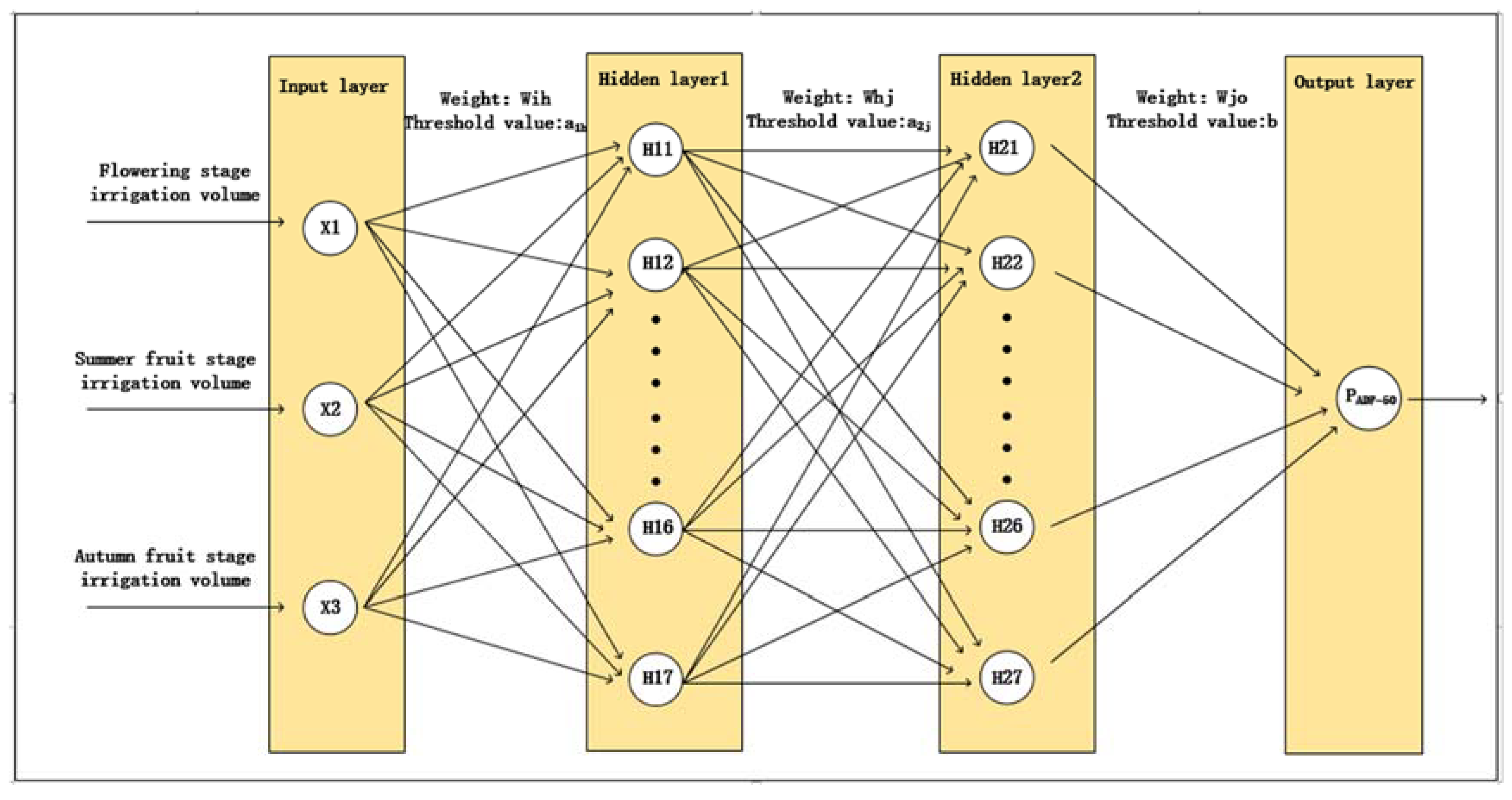
2.4. ADF-50 Artificial Neural Network Model
2.5. Multi-Objective Genetic Algorithm Optimization Model NSGA-III
2.5.1. Decision Variable
2.5.2. Objective Function
2.5.3. Constraint
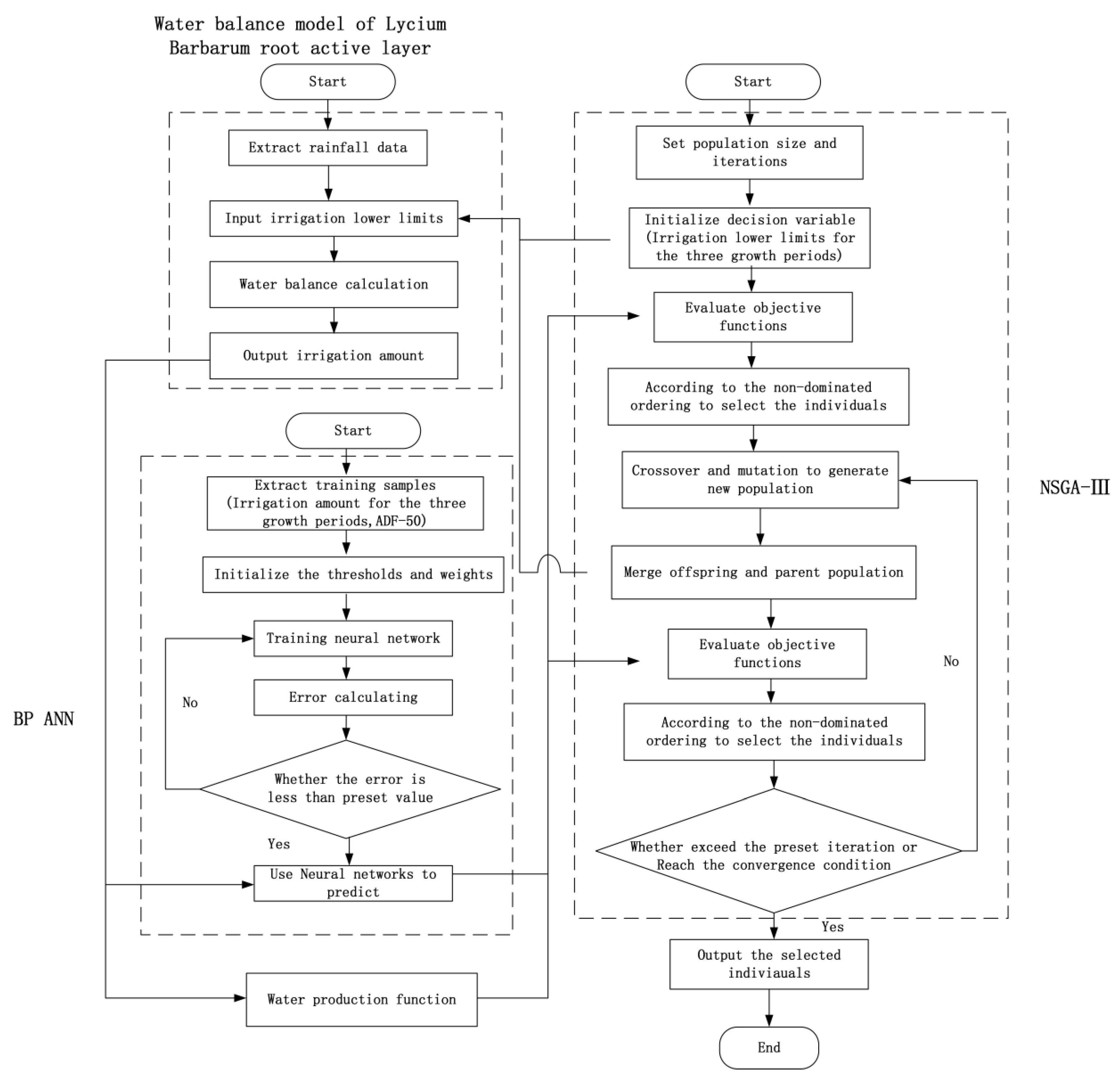
2.6. Construction of the Coupling Model
3. Results
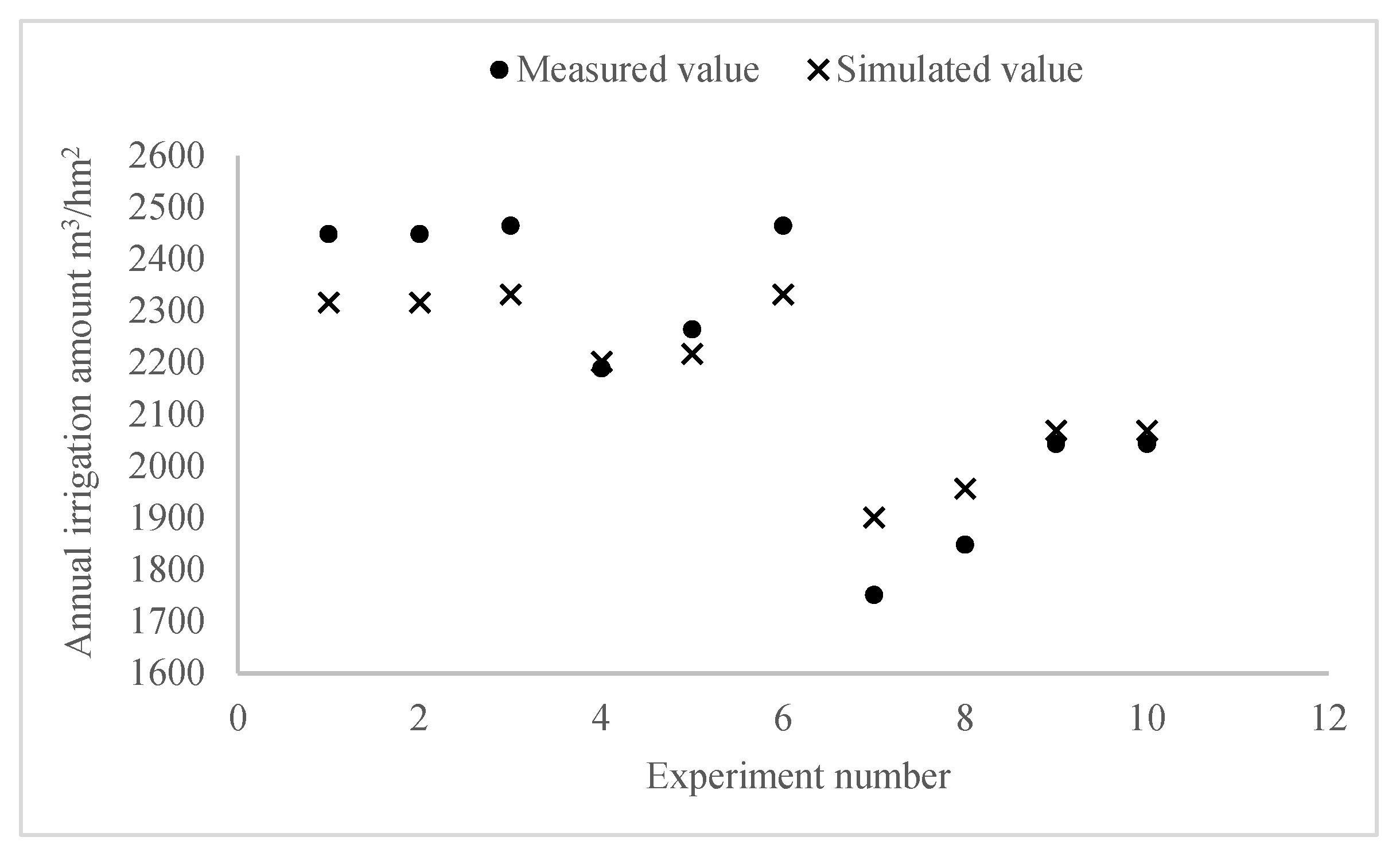
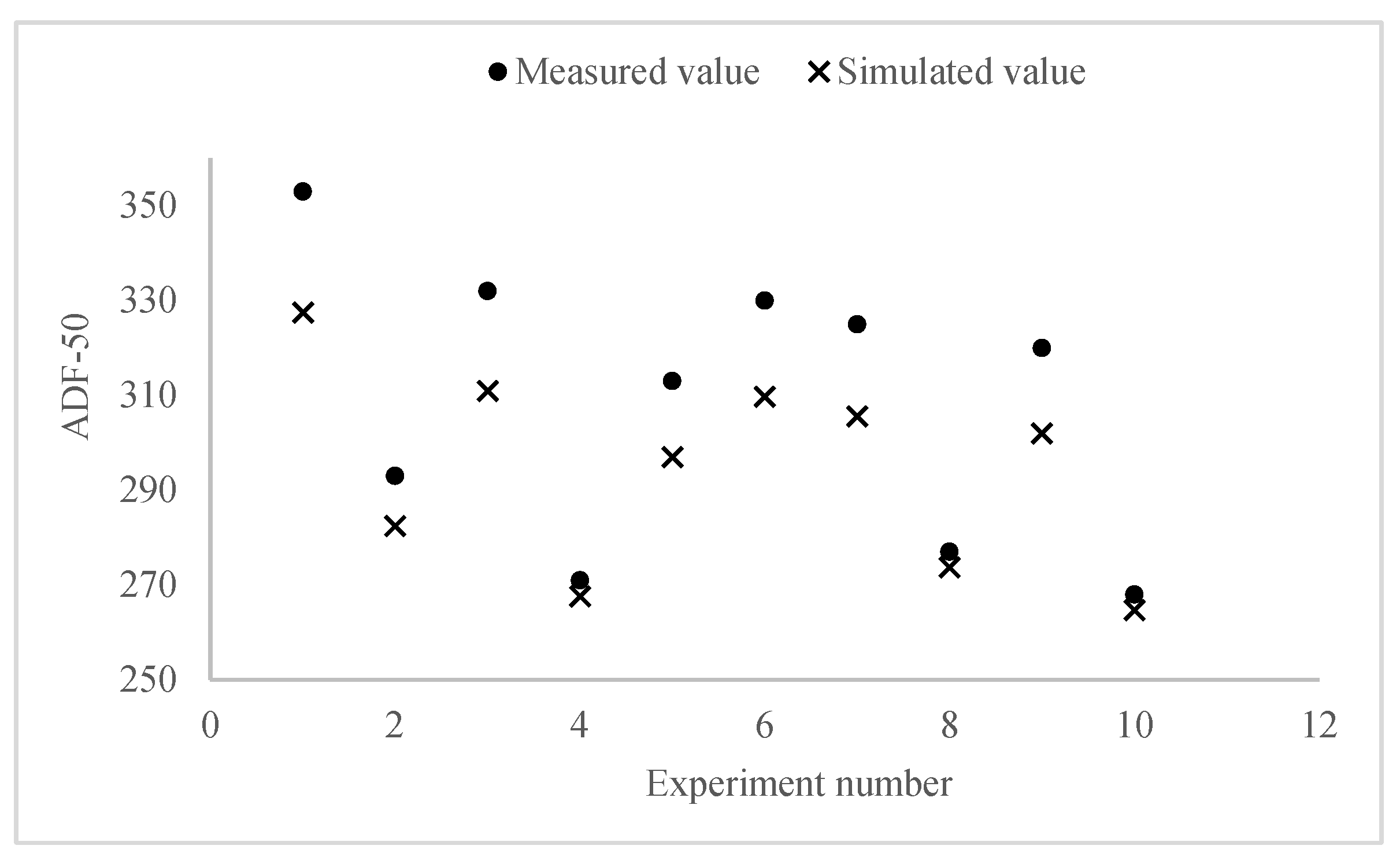
3.1. Simulation Models Validation
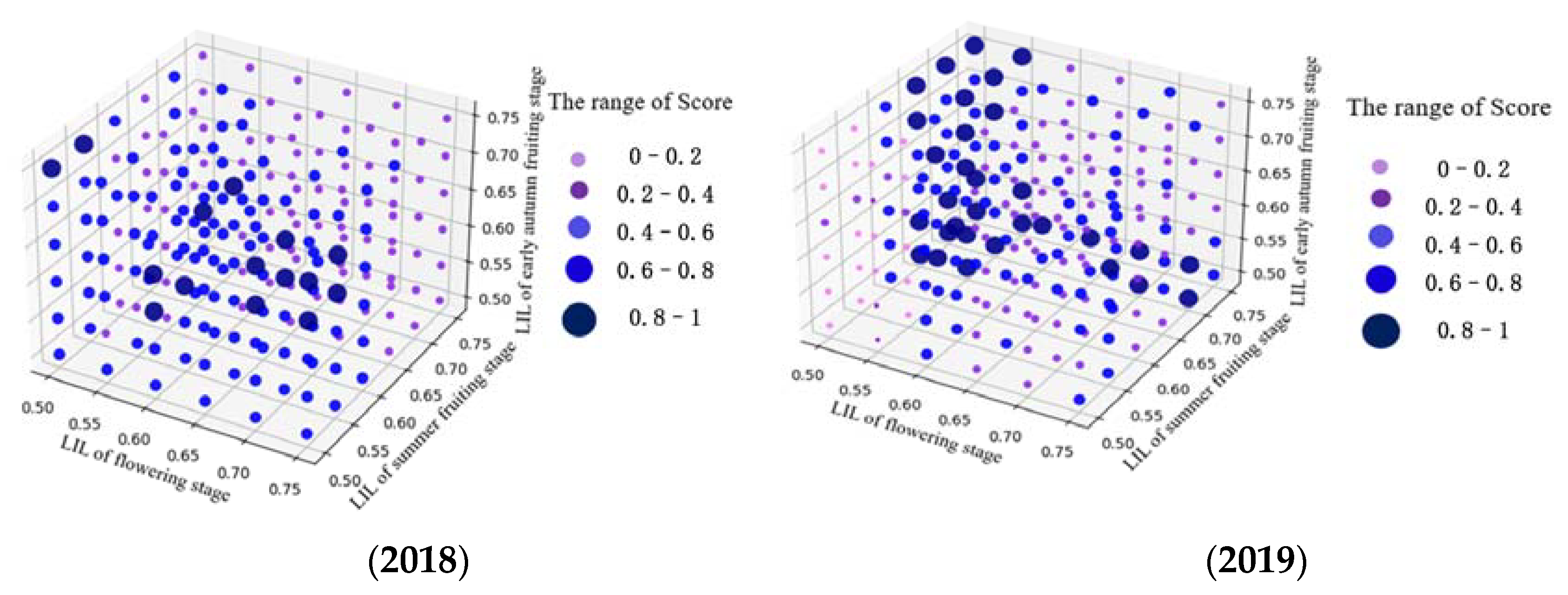
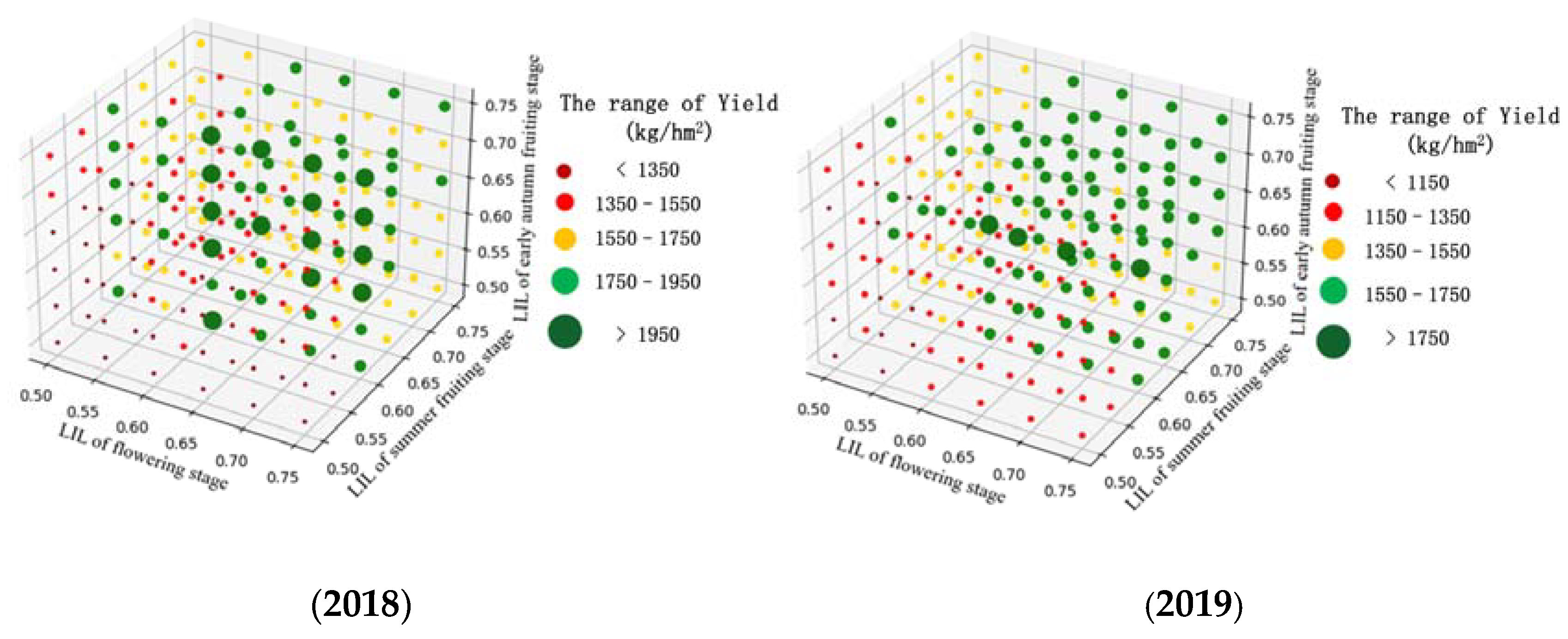
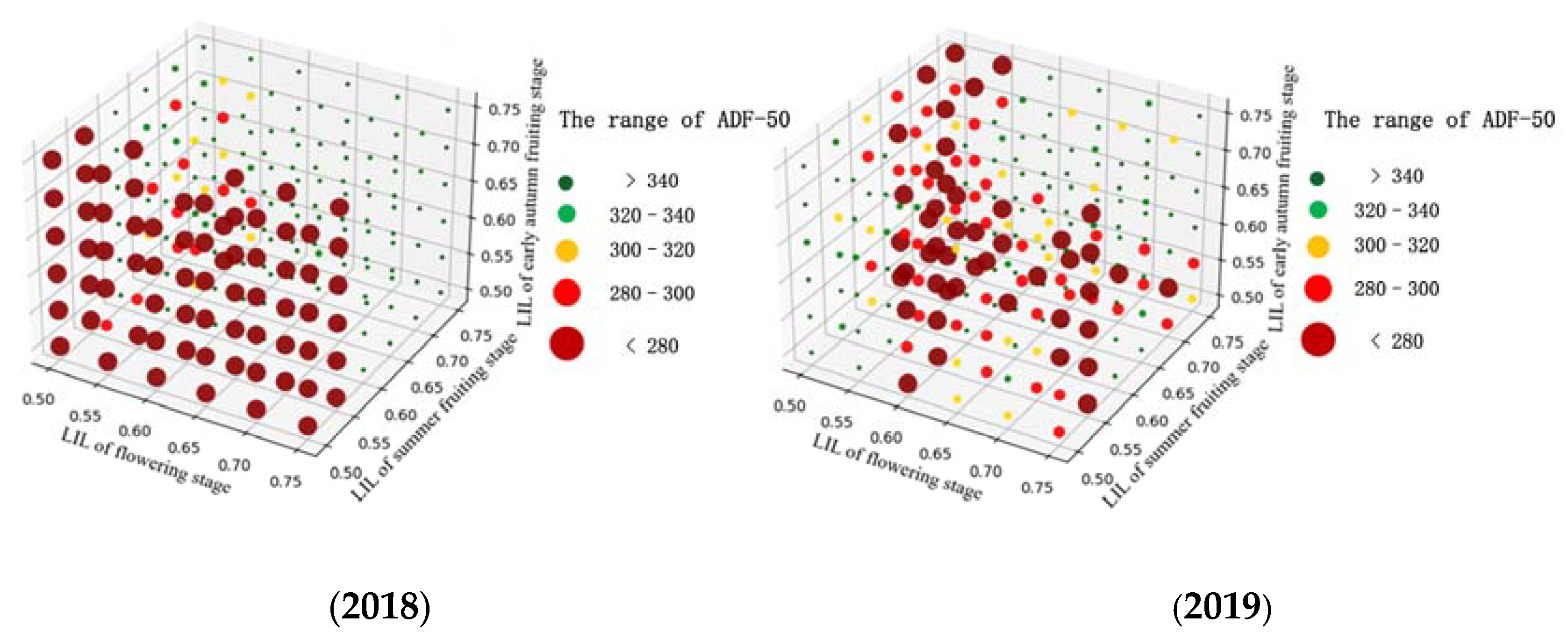
3.2. Optimization Results of Irrigation Drip Lower Irrigation Limit for Lycium barbarum
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, G.Z. Research on Wolfberry Irrigation and Mulching Measures. Master’s Thesis, Gansu Agricultural University, Lanzhou, China, 2009. [Google Scholar]
- Peng, J.; Wang, L.; Wang, M.; Du, R.; Qin, S.; Jin, C.Y.; Wei, Y. Yeast Synthetic Biology for the Production of Lycium barbarum Polysaccharides. Molecules 2021, 26, 1641. [Google Scholar] [CrossRef]
- Cui, F.; Shi, C.L.; Zhou, X.J.; Wen, W.; Gao, X.P.; Wang, L.Y.; He, B.; Yin, M.; Zhao, J.Q. Lycium barbarum Polysaccharide Extracted from Lycium barbarum Leaves Ameliorates Asthma in Mice by Reducing Inflammation and Modulating Gut Microbiota. J. Med. Food 2020, 23, 699–710. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.Q.; Zhang, L.; Zheng, G.B. Effects of irrigation amount on leaf structure photosynthetic physiology and fruit yield of Lycium barbarum in arid area. Chin. J. Appl. Ecol. 2010, 21, 2806–2813. [Google Scholar] [CrossRef]
- Zhou, Q. Effects of Different Water and Nitrogen Coupling and Mulching on the Growth, Yield and Nutrient Uptake of Lycium barbarum. Master’s Thesis, Northwest A&F University, Yangling, China, 2014. [Google Scholar]
- Zhou, Y.Q.; Gao, X.D.; Wang, J.X.; Brett, H.R.; Zhao, X.N. Water-use patterns of Chinese wolfberry (Lycium barbarum L.) on the Tibetan Plateau. Agric. Water Manag. 2021, 255, 107010. [Google Scholar] [CrossRef]
- Zeng, X.C. Irrigation and Overbearing of the Effects of the Growth and Water Utilization Efficiency of Goji Berries. Master’s Thesis, Gansu Agricultural University, Lanzhou, China, 2013. [Google Scholar]
- Zhang, T.B.; Kang, Y.H.; Liu, S.H.; Liu, S.P. Alkaline phosphatase activity and its relationship to soil properties in a saline–sodic soil reclaimed by cropping wolfberry (Lycium barbarum L.) with drip irrigation. Paddy Water Environ. 2014, 12, 309–317. [Google Scholar] [CrossRef]
- Earl, V.; Stevens, W.; Matthew, R.; Zachary, S. Investigating irrigation scheduling for rice using variable rate irrigation. Agric. Water Manag. 2017, 179, 314–323. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, F.W.; Jiang, R.G. Irrigation schedule optimization based on the combination of an economic irrigation quota and the AquaCrop model. Irrig. Drain. 2021, 70, 773–785. [Google Scholar] [CrossRef]
- Albo-Salih, H.; Mays, L. Testing of an Optimization-Simulation Model for Real-Time Flood Operation of River Reservoir Systems. Water 2021, 13, 1207. [Google Scholar] [CrossRef]
- Jamshid Mousavi, S.; Anzab, N.R.; Asl-Rousta, B. Multi-Objective Optimization-Simulation for Reliability-Based Inter-Basin Water Allocation. Water Resour. Manag. 2017, 31, 3445–3464. [Google Scholar] [CrossRef]
- Wang, Y.M.; Yang, J.; Chang, J.X. Development of a coupled quantity-quality-environment water allocation model applying the optimization-simulation method. J. Clean. Prod. 2019, 213, 944–955. [Google Scholar] [CrossRef]
- Kim, Y.G.; Jo, M.B.; Kim, P. Effective Optimization-Simulation Model for Flood Control of Cascade Barrage Network. Water Resour. Manag. 2021, 35, 135–157. [Google Scholar] [CrossRef]
- Aspelund, A.; Gundersen, T.; Myklebust, J.; Nowak, M.P.; Tomasgard, A. An optimization-simulation model for a simple LNG process. Comput. Chem. Eng. 2010, 34, 1606–1617. [Google Scholar] [CrossRef]
- Sedki, A.; Ouazar, D. Simulation-Optimization Modeling for Sustainable Groundwater Development: A Moroccan Coastal Aquifer Case Study. Water Resour. Manag. 2011, 25, 2855–2875. [Google Scholar] [CrossRef]
- Yao, J.; Xu, X.; Huang, Q.Z.; Huo, Z.L.; Huang, G.H. Optimizing regional irrigation water use by integrating a two-level optimization model and an agro-hydrological model. Agric. Water Manag. 2016, 178, 76–88. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Yang, D.W. Irrigation schedule analysis and optimization under the different combination of P and ET0 using a spatially distributed crop model. Agric. Water Manag. 2021, 256, 107084. [Google Scholar] [CrossRef]
- Cobo, M.T.C.; Poyato, E.C.; Montesinos, P.; Díaz, J.A.R. New model for sustainable management of pressurized irrigation networks. Application to Bembézar MD irrigation district (Spain). Sci. Total Environ. 2014, 473, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hu, Y.Q.; Chen, H.R. Conjunctive use of surface water and groundwater in irrigation districts in China. Irrig. Drain. 2020, 69, 135–141. [Google Scholar] [CrossRef]
- Jia, S.; Long, Q.; Wang, R.Y. On the Inapplicability of the Cobb-Douglas Production Function for Estimating the Benefit of Water Use and the Value of Water Resources. Water Resour. Manag. 2016, 30, 3645–3650. [Google Scholar] [CrossRef]
- Li, F.; Zhang, H.; Li, X.; Deng, H.; Chen, X.; Liu, L. Modelling and Evaluation of Potato Water Production Functions in a Cold and Arid Environment. Water 2022, 14, 2044. [Google Scholar] [CrossRef]
- Holzapfel, E.; Merino, R.; Mariño, M. Water production functions in kiwi. Irrig. Sci. 2000, 19, 73–79. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Sudheer, K.P.; Soundharajan, B.S. Implications of uncertainty in inflow forecasting on reservoir operation for irrigation. Paddy Water Environ. 2021, 19, 99–111. [Google Scholar] [CrossRef]
- Kouadri, S.; Pande, C.B.; Panneerselvam, B. Prediction of irrigation groundwater quality parameters using ANN, LSTM, and MLR models. Environ. Sci. Pollut. Res. 2022, 29, 21067–21091. [Google Scholar] [CrossRef] [PubMed]
- Shao, W.Y.; Guan, Q.Y.; Tan, Z.; Luo, H.P.; Li, H.C.; Sun, Y.F.; Ma, Y.R. Application of BP-ANN model in evaluation of soil quality in the arid area, northwest China. Soil Tillage Res. 2021, 208, 104907. [Google Scholar] [CrossRef]
- Deng, Y.; Zhou, X.L.; Shen, J.; Xiao, G.; Hong, H.C.; Lin, H.J.; Wu, F.Y.; Liao, B.Q. New methods based on back propagation (BP) and radial basis function (RBF) artificial neural networks (ANNs) for predicting the occurrence of haloketones in tap water. Sci. Total Environ. 2021, 772, 145534. [Google Scholar] [CrossRef]
- Zhang, J.L. Effects of deficit irrigation on water use efficiency and fruit quality of Lycium barbarum. Res. Agric. Sci. 2015, 36, 29–34. [Google Scholar]
- Zheng, G.B.; Zhang, Y.P.; Zhu, J.X.; Zhou, L.; Kong, D.J.; Wang, Y.P. Study on water effect and water production function of Lycium barbarum in different growth stages. Water Sav. Irrig. 2012, 11, 22–24. (In Chinese). [Google Scholar]
- Bi, S.; Xiong, W. Small sample expansion method based on the data distribution and application. J. Control. Eng. 2019, 26, 1431–1436. [Google Scholar] [CrossRef]
- Fernández Jaramillo, J.M.; Mayerle, R. Sample selection via angular distance in the space of the arguments of an artificial neural network. Comput. Geosci. 2018, 114, 98–106. [Google Scholar] [CrossRef]
- Ai, X.; Sun, B.; Chen, X. Construction of small sample seismic landslide susceptibility evaluation model based on Transfer Learning: A case study of Jiuzhaigou earthquake. Bull. Eng. Geol. Environ. 2022, 81, 116. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Wang, N. Sample extraction and expansion method with feature reconstruction and deformation information. Appl. Intell. 2022, 52, 15916–15928. [Google Scholar] [CrossRef]
- Li, B.; Bao, Z.R.; Yao, M.Z.; Li, C.X.; Sun, X.L. Effects of irrigation lower limit and straw returning amount on yield, quality and water use efficiency of greenhouse tomato. Chin. J. Appl. Ecol. 2020, 31, 493–500. [Google Scholar] [CrossRef]
- Hou, J.; Nan, X.; Kang, C. Effects of drip irrigation frequency and quota on soil water and heat distribution and yield in Lycium barbarum orchard. Econ. For. Res. 2019, 37, 58–66. [Google Scholar]
- Bo, M.A.; Tian, J. Advance in Research on Water and Fertilizer Effect on Yield and Quality of Lycium Barbarum L. Water Sav. Irrig. 2020, 11, 6–11. [Google Scholar]
- Liu, Q.; Liu, X.; Wu, J.; Li, Y. An Improved NSGA-III Algorithm Using Genetic K-Means Clustering Algorithm. IEEE Access 2019, 7, 185239–185249. [Google Scholar] [CrossRef]
- Hou, Y.; Wu, N.Q.; Li, Z.W.; Zhang, Y.X.; Qu, T.; Zhu, Q.H. Many-objective optimization for scheduling of crude oil operations based on NSGA-III with consideration of energy efficiency. Swarm Evol. Comput. 2020, 57, 100714. [Google Scholar] [CrossRef]
- Xu, L.G.; Wang, H.B.; Bao, Z.Y.; Li, J.Z. Experimental study on soil moisture lower limit-based drip irrigation schedule for Lycium barbarum in Ningxia arid area. J. Drain. Irrig. Mach. Eng. 2020, 38, 523–529. [Google Scholar]
- Li, J.; Shang, S.H.; Jiang, H.Z.; Song, J.; Rahman, K.U.; Adeloye, A.J. Simulation-based optimization for spatiotemporal allocation of irrigation water in arid region. Agric. Water Manag. 2021, 254, 106952. [Google Scholar] [CrossRef]
- Kuo, S.F.; Liu, C.W. Simulation and optimization model for irrigation planning and management. Hydrol. Process. 2003, 17, 3141–3159. [Google Scholar] [CrossRef]
- Pan, Y.X.; Yuan, C.F.; Jing, S.Y. Simulation and optimization of irrigation schedule for summer maize based on SWAP model in saline region. Int. J. Agric. Biol. Eng. 2020, 13, 117–122. [Google Scholar] [CrossRef]
- Bedekar, V.; Scantlebury, L.; Panday, S. Axisymmetric Modeling Using MODFLOW-USG. Groundwater 2019, 57, 772–777. [Google Scholar] [CrossRef] [PubMed]
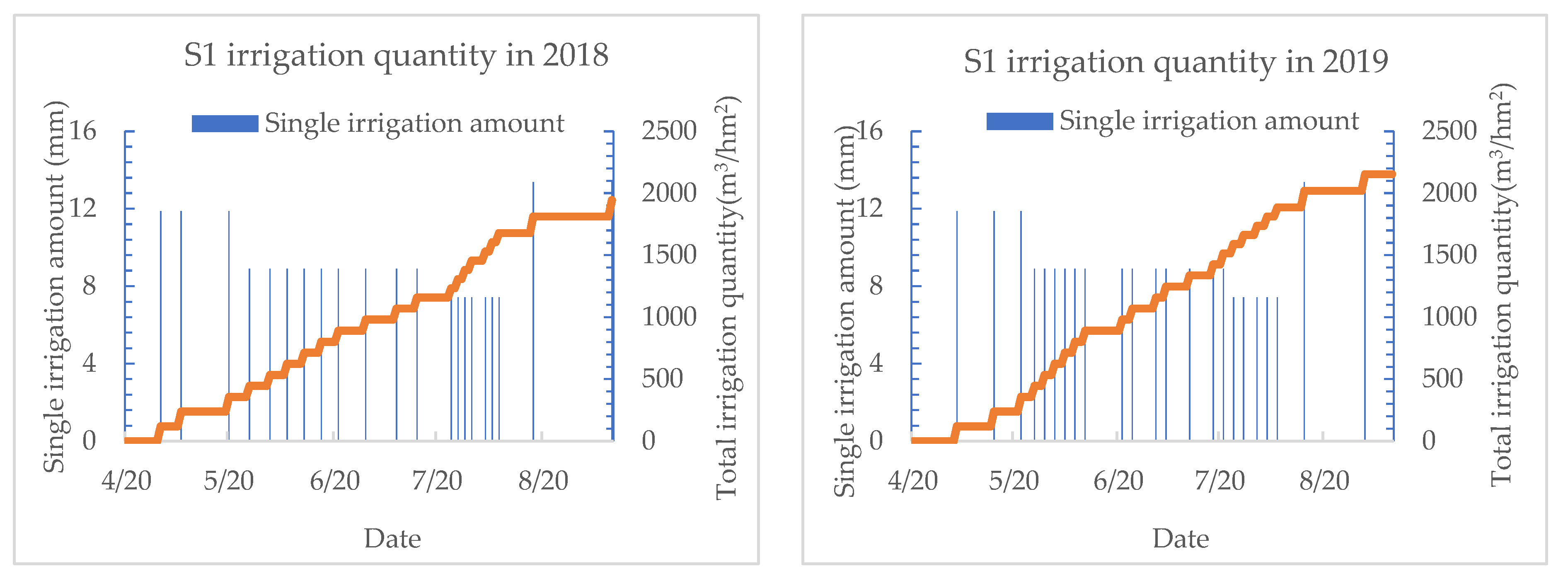
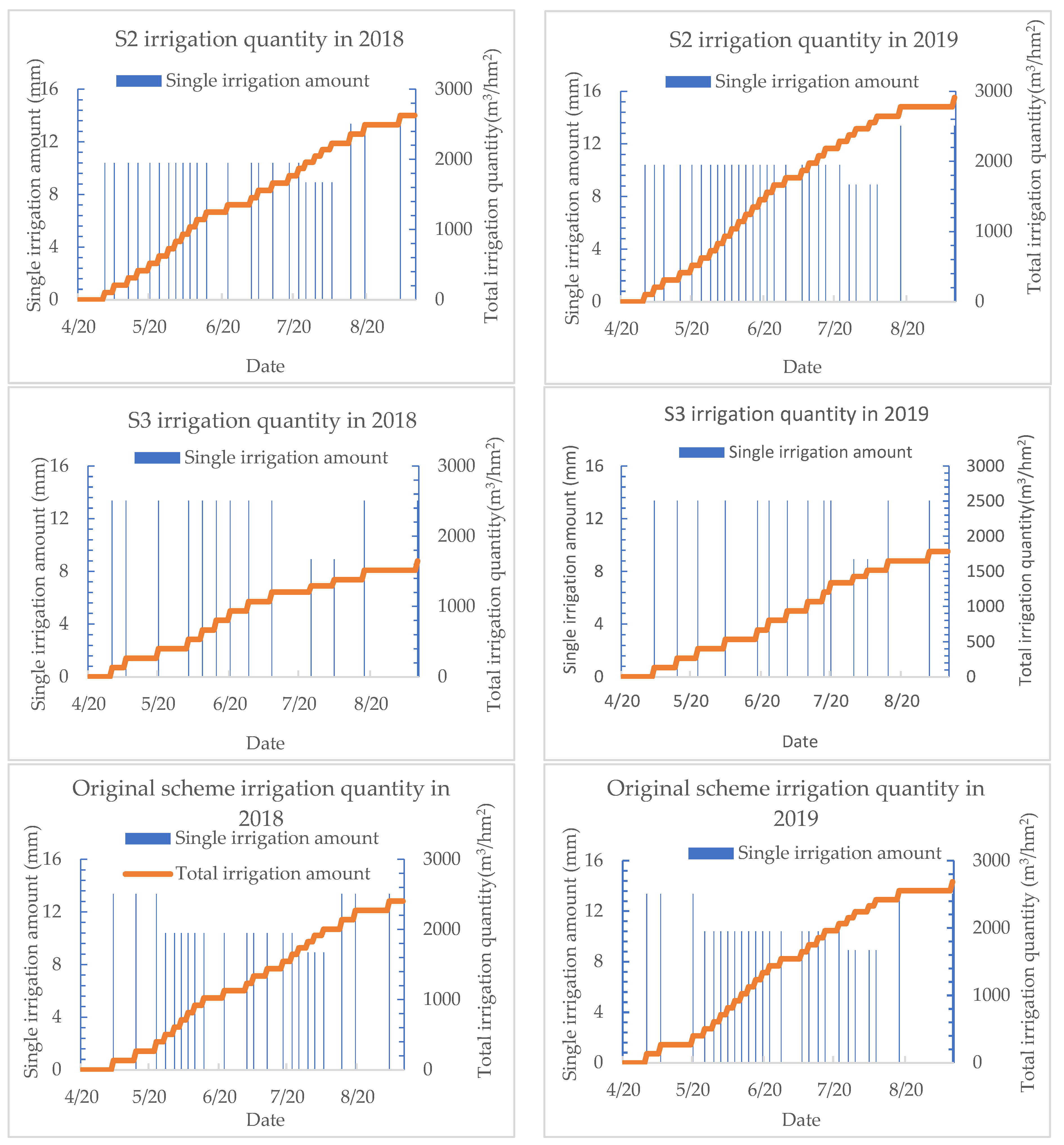
| Scheme | Lower Irrigation Limits (Percentage of Field Capacity) | Yield (kg/hm2) | ADF-50 | ||||
|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | 2018 | 2019 | 2018 | 2019 | |
| S1 | 65% | 50% | 65% | 1655.21 | 1473.34 | 312 | 306 |
| S2 | 70% | 50% | 70% | 1983.69 | 1757.82 | 357 | 352 |
| S3 | 60% | 50% | 65% | 1322.95 | 1271.46 | 247 | 249 |
| Original | 50% | 60% | 65% | 1473.76 | 1348.87 | 342 | 336 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Yu, Y.; Lei, J.; Liu, J. Multi-Objective Lower Irrigation Limit Simulation and Optimization Model for Lycium Barbarum Based on NSGA-III and ANN. Water 2023, 15, 783. https://doi.org/10.3390/w15040783
Zhao J, Yu Y, Lei J, Liu J. Multi-Objective Lower Irrigation Limit Simulation and Optimization Model for Lycium Barbarum Based on NSGA-III and ANN. Water. 2023; 15(4):783. https://doi.org/10.3390/w15040783
Chicago/Turabian StyleZhao, Jinpeng, Yingduo Yu, Jinyang Lei, and Jun Liu. 2023. "Multi-Objective Lower Irrigation Limit Simulation and Optimization Model for Lycium Barbarum Based on NSGA-III and ANN" Water 15, no. 4: 783. https://doi.org/10.3390/w15040783





