1. Introduction
The spillway structures are the most important structures for ensuring the safety of the dam. Their task is to pass the flood discharge downstream of the dams efficiently and safely. These safety structures are designed to operate at a very low risk. Theoretical equations and physical modeling are the two main techniques commonly used to analyze the performance of dam spillways. For a long time, physical scale modeling has been used to design and study hydraulic water structures. Experimental studies for flow over a spillway structure require sensitive measurements and must be appropriately designed to provide reliable information [
1]. However, such studies are time-consuming and may adversely affect the cost of the project. Therefore, researchers have sought different methods.
Due to developments in computer technology, numerical simulations for hydrodynamic processes, including flow over spillways, have become widespread. Computational fluid dynamics (CFD) is a branch of computational modeling developed to solve problems involving fluid motion. The methods developed within the scope of CFD aim to analyze the movements of fluids under different conditions. However, the realism and applicability of the data obtained from CFD models is a topic of debate in current discussion and research. In this respect, there is a need to increase and diversify studies for the verification of numerical findings with experiments.
In the literature, numerous studies make experimental and CFD comparisons for spillway modeling. Olsen and Kjellesvig [
2] numerically modeled the water flow over a two- and three-dimensional spillway by choosing different geometries to estimate the spillway capacity. The k-ε turbulence model was chosen, and the equations of motion were solved accordingly. Numerical results and experimental studies were compared, and close values were obtained. Dargahi [
3] investigated the flow field on a spillway to simulate the flow through a three-dimensional numerical model. The fluid volume (VOF) model was used to calculate the free surface flow over the spillway. The k-epsilon turbulence model was used in the study. The water surface profiles and discharge coefficients were estimated in the range of 1.5–2.9%, depending on the operating height of the spillway. Based on these studies in the literature, the VOF model and the k-epsilon turbulence model were used in the CFD part of this study. Kumcu [
4] hydraulic characteristics of Kavsak Dam and Hydroelectric Power Plant (HEPP), which are under construction and built for producing energy in Turkey, were investigated experimentally by physical model studies. In order to evaluate the capability of computational fluid dynamics for modeling spillway flow, a comparative study was carried out by using results obtained from physical modeling and computational fluid dynamics (CFD) simulation. It was shown that there is reasonably good agreement between the physical and numerical models, in terms of flow characteristics. Demeke [
5] studied the structure of the Tendaho Dam spillway in Ethiopia. In the spillway structure, under the designed capacity, overflows were observed during a flood and, therefore, a 3D CFD study was carried out. As a result of the studies, it was concluded that the spillway structure was not safe. Green [
6] examined three main techniques commonly used to analyze the performance of existing dam spillways. These are theoretical equations, physical modeling, and computational fluid dynamics (CFD). The specified modeling methods were applied for a spillway and comparisons were made. The advantages and disadvantages of each method were discussed. Gadhe [
7], in a study, compared the results obtained by the spillway model of the New Umtru Dam with the CFD model. It was observed from the studies that the original design of the spillway and energy dissipater required revision. Several spillway studies have examined the cavitation problem. Cavitation often creates harmful effects on dam spillways. For this reason, researchers have used various velocity measurement techniques, such as Particle Image Velocimeter (PIV) and Acoustic Doppler Velocimeter (ADV) [
8,
9,
10]. ADV was used in this study. Aydın [
11] analyzed the spillway aerator of a 100 m high roller-compacted concrete dam using a two-phase computational fluid dynamics model to overcome cavitation damage at the spillway surface. Numerical analysis was performed with prototype dimensions for various flow conditions (5223, 3500, 1750, and 1000 m
3/s flow rate) and the obtained results were compared with experimental observations in the literature. Numerical and experimental results have shown that cavitation occurs after a particular downstream point on the surface, based on cavitation indices.
Researchers working on open-channel flow attempt to explain the velocity, one of the most important parameters in open-channel flows. Velocity can be measured with a measuring device and direct methods, or it can be determined by indirect methods such as the float method, or with mathematical models and empirical equations [
12,
13,
14]. The velocity measurement is a task requiring great effort and expense [
15].
In open-channel flows, the velocity varies with depth. It is very important to calculate the mean and maximum velocity values in the velocity distribution depending on the depth. Determining the velocity of the free water surface is much easier than determining the mean and maximum velocities in open channels [
16]. Free water surface velocity can be easily determined with an object that is movable on the water’s surface and not too heavy, such as leaves, twigs, etc. Other methods, such as acoustics, optics, or floats, are used to estimate surface velocity. However, the cheapest and easiest way to determine water surface velocity is to simply float something down the stream and see how fast it travels [
17]. Once the velocity of the floating object is determined, it should be multiplied by the correction coefficients for the mean flow velocity. The correction coefficients vary according to the depth [
18]. Researchers have carried out studies in the past to determine these coefficient values [
19,
20].
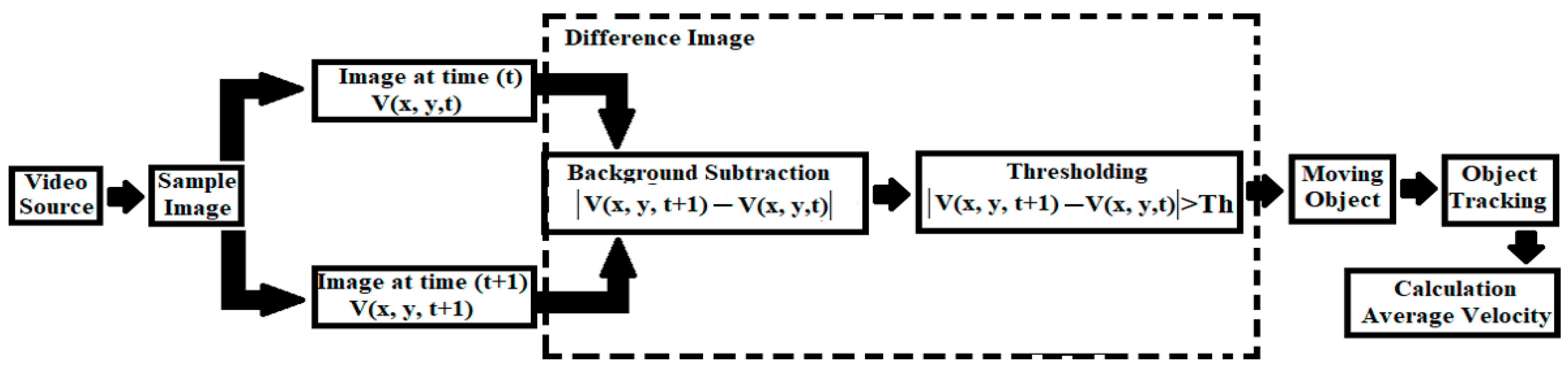
Image processing consists of processing images using digital computers. In recent years, its use has increased exponentially in many areas. One of these is in hydraulic science, where observable flow parameters can be studied with this method. Research has been carried out in the past using image processing techniques to determine velocity and water level in open-channel flows. Since the water level can be observed using these two parameters, it can be measured more easily than the velocity [
21,
22,
23]. Because the water velocity changes depending on the depth and cannot be observed, it is more difficult to measure with this method [
24,
25,
26]. The velocity of a floating object on the water, seen in video images, can be determined by image processing methods. The movement of the floating object on the water can be measured by the object detection and tracking method, one of the image processing methods. This is a method of detecting and locating an object which is in motion with the help of a camera. The detection and tracking method is used in different engineering fields such as vehicle tracking in traffic, object detection, and security [
27,
28]. There are many programming languages and program libraries in which image processing methods can be applied. Recently, Python programming language and OpenCV (Open Source Computer Vision) library are preferred because they are easier to use than others.
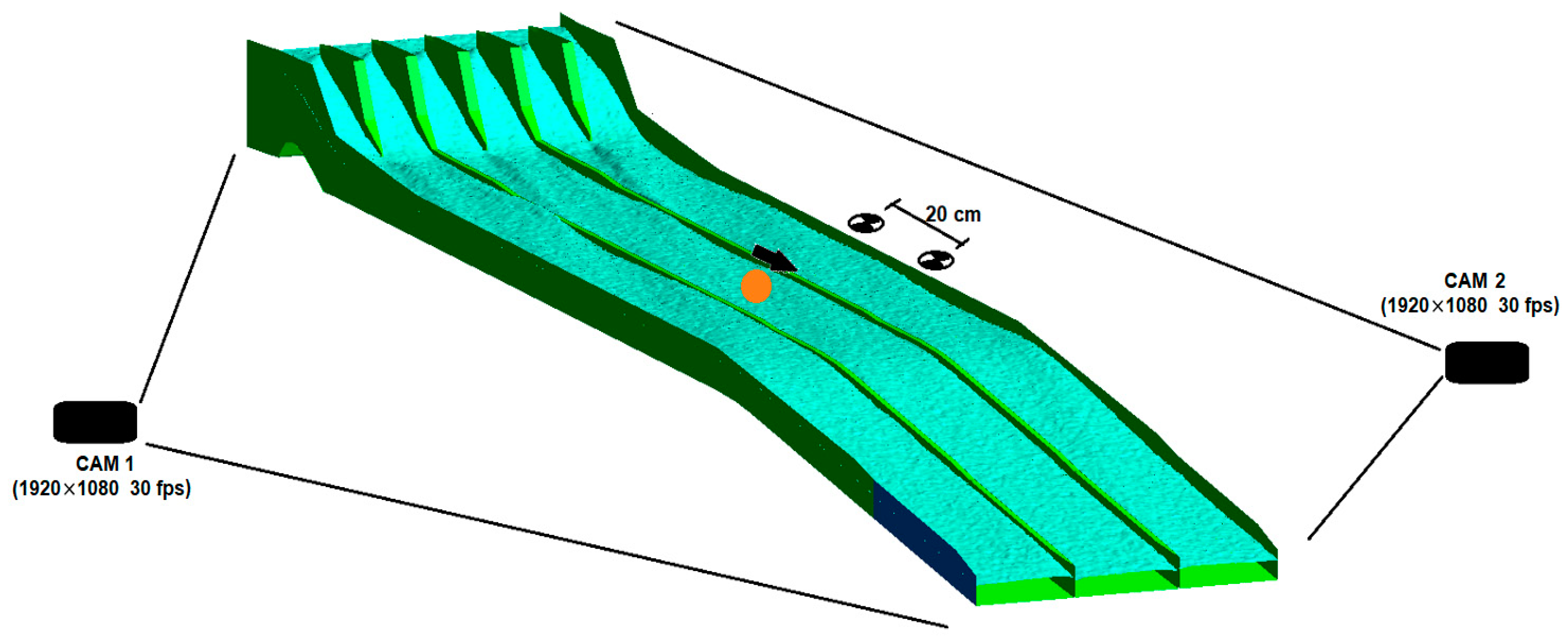
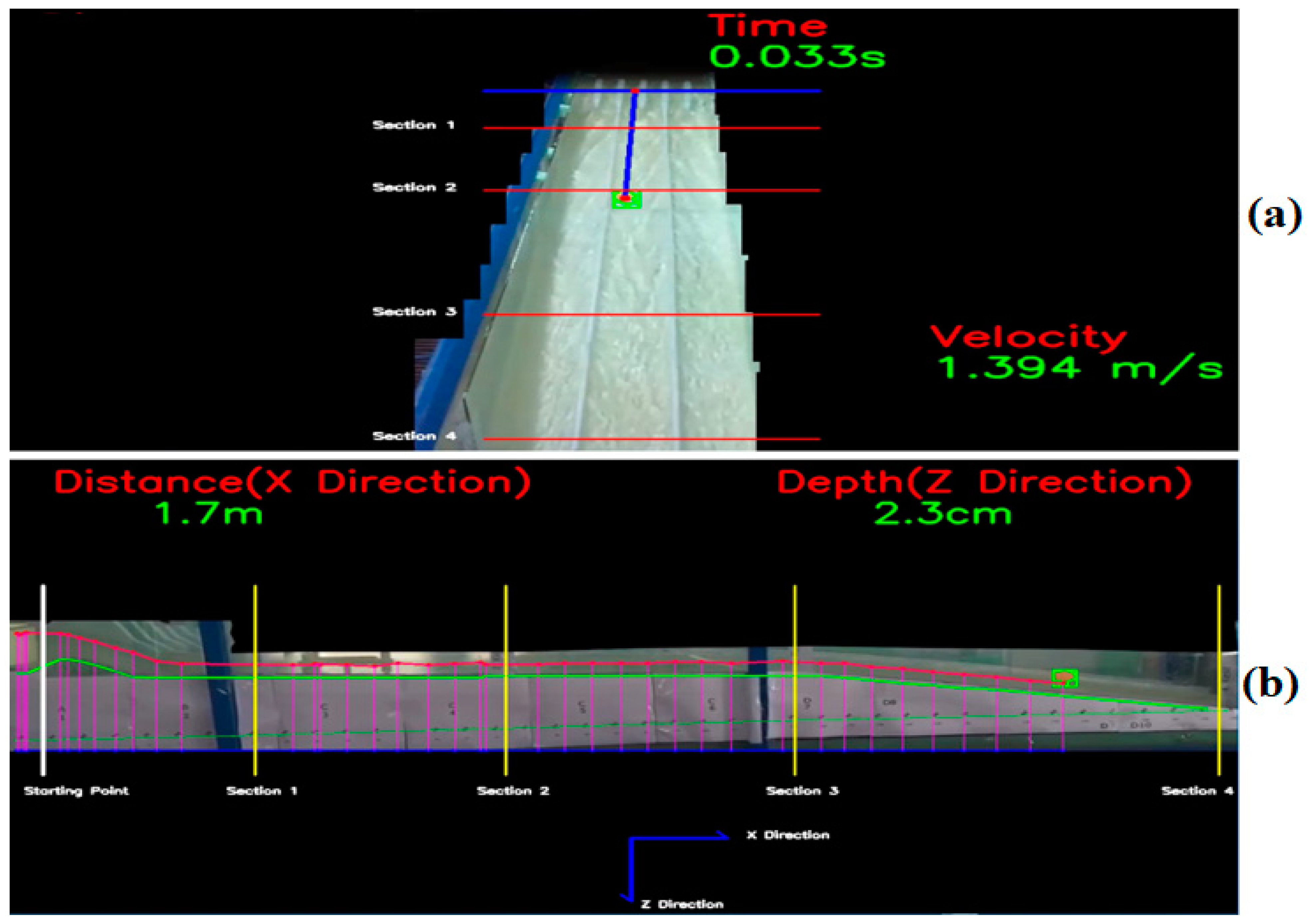
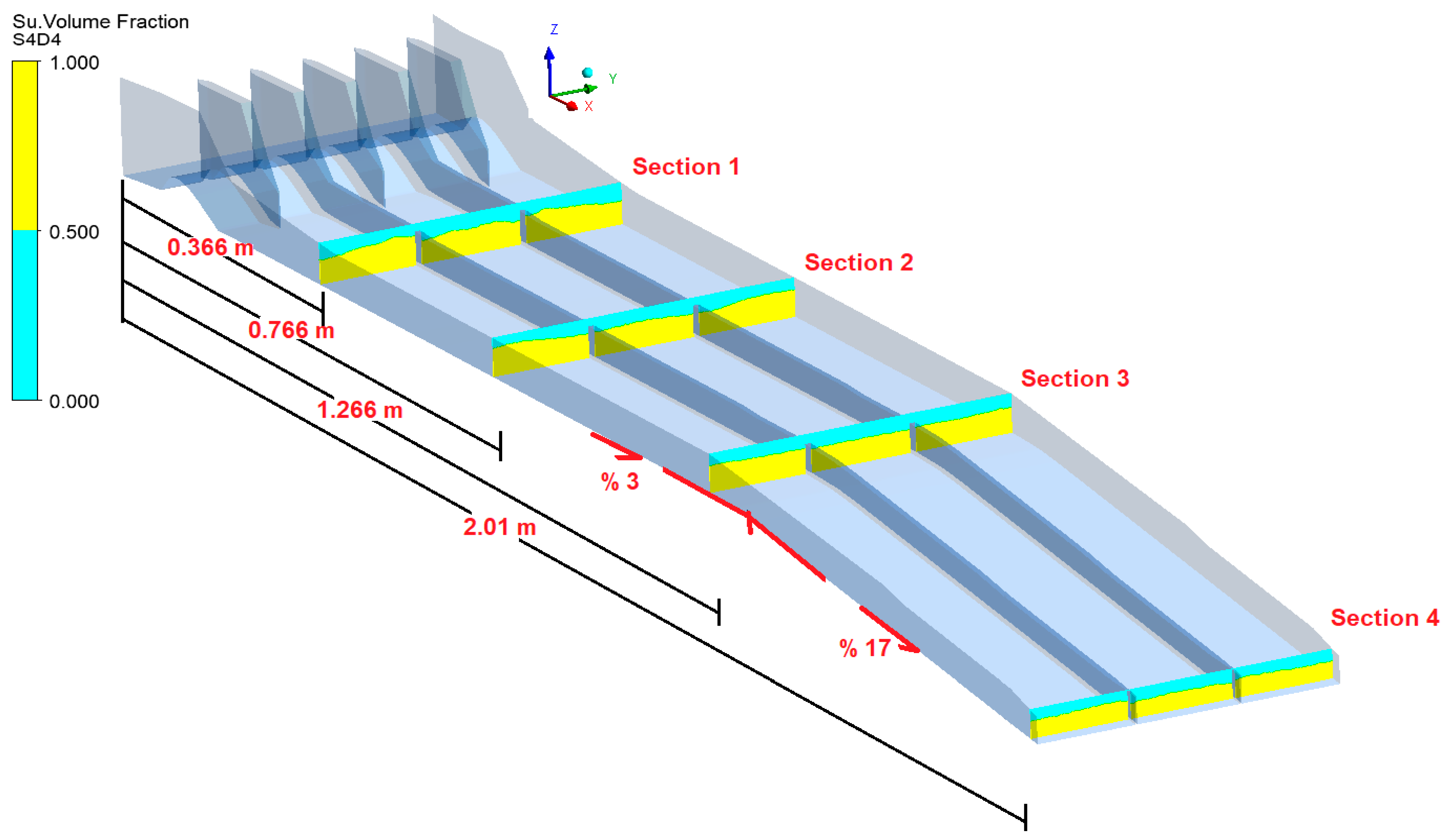
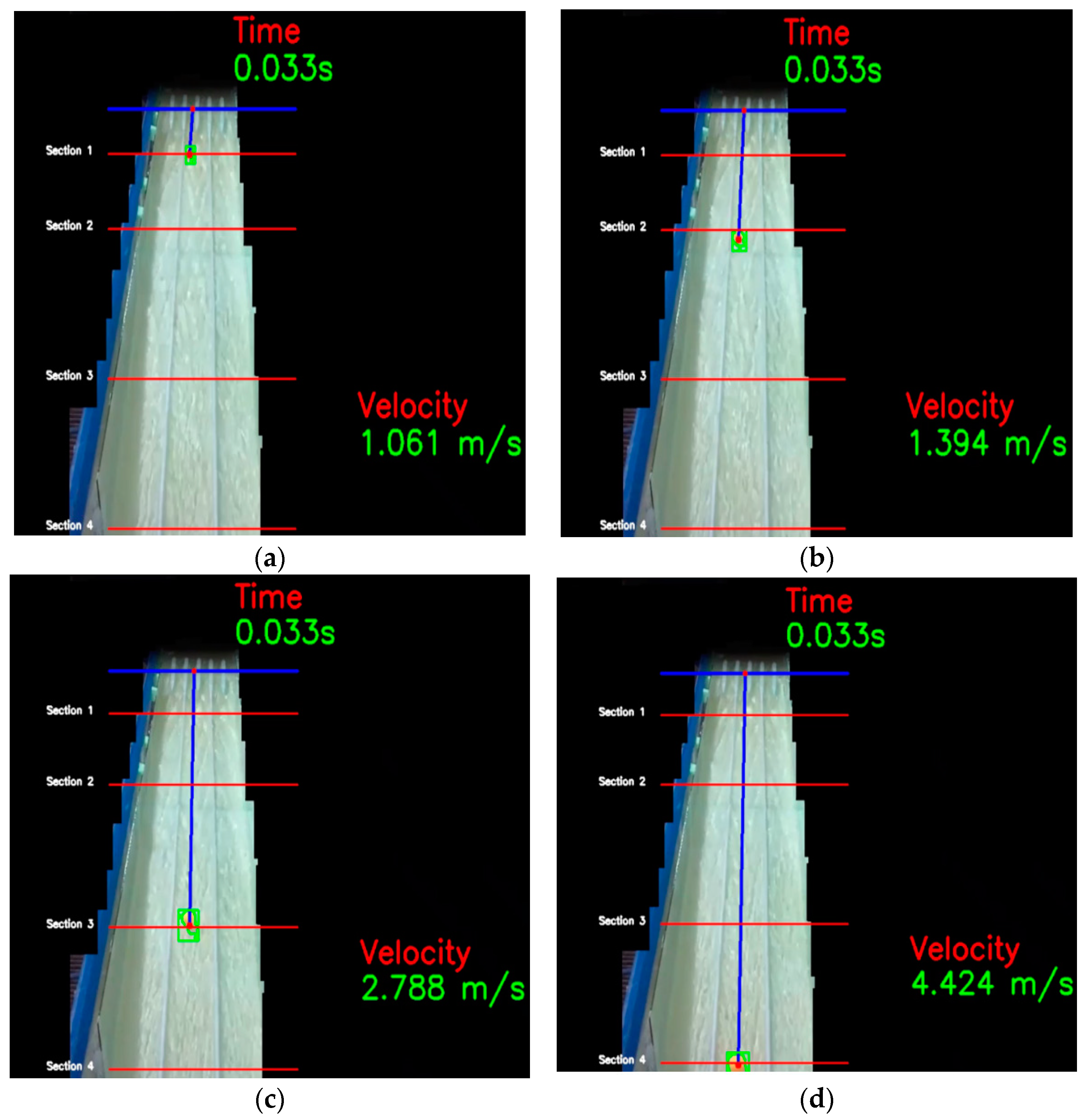
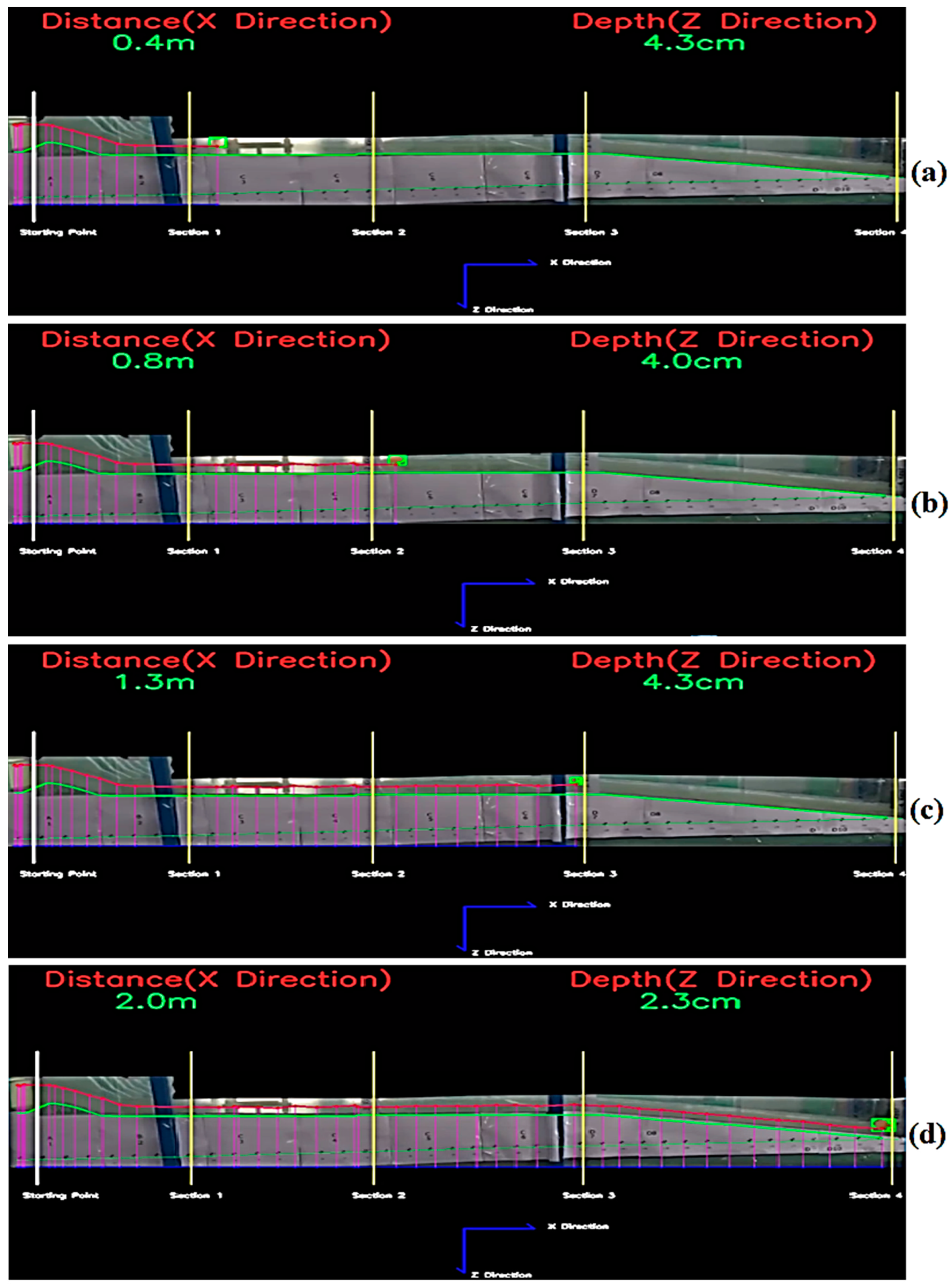
The aim of this research is to develop a three-dimensional CFD model and OpenCV code by comparing the flow over the spillway with the experimental data for use in spillway studies. With the CFD model developed and OpenCV code, the flow parameters, flow characteristics, and changes required for the design of the spillway can be obtained in less time and at a lower cost. The CFD model established and OpenCv code can examine the flow parameters of the existing and future spillway structures. The spillway structure chosen for this purpose is the spillway structure of the Çatalan Dam and Hydroelectric Power Plant in Adana, currently in operation. The spillway discharge channel has 2 slopes, of 3% and 17%. The spillway model was created by reducing the dimensions of the prototype spillway structure to Froude similarity at a 1/200 scale. The flood flow rate and inlet velocities that would occur in the prototype spillway structure were also calculated according to Froude similarity in detail and used in the experimental and numerical model setup. Average flow velocities were measured with an acoustic Doppler velocimeter (ADV) device for four different cross-sections (at five points in each cross-section) along the spillway discharge channel. In addition, water depth was measured in four cross-sections (at nine points in each cross-section). After the experimental studies, a three-dimensional CFD model of the spillway model was created. In CFD studies, the ANSYS Fluent program, which can use the VOF method and k-epsilon turbulence model together, was used. The average flow velocities and water depts obtained along the cross-sections by the experiment are compared with the results of the CFD model and shown in tables, graphs, and figures. In addition, the pressure distributions in four different cross-sections were examined with the CFD model. These pressure values were increased to the model scale according to Froude similarity, and the cavitation index was calculated for four sections of the prototype spillway. In the second part of the experimental studies, a colored floating object was placed in the spillway channel and the movement of the object on the water was recorded with cameras placed at different angles. By using the object tracking method, which is an image processing technique, the position of the floating object was determined in each video frame in the video recordings. Based on this position, the velocity of the floating object and its perpendicular distance from the bottom of the channel was determined. Thus, an OpenCV-Python code has been developed that determines the velocity and water depth of the floating object depending on its position. The floating object velocity values obtained by the algorithm were compared with the velocity values measured during the experiment, and new velocity correction coefficients were obtained for the chute spillways.
3. Experimental Studies
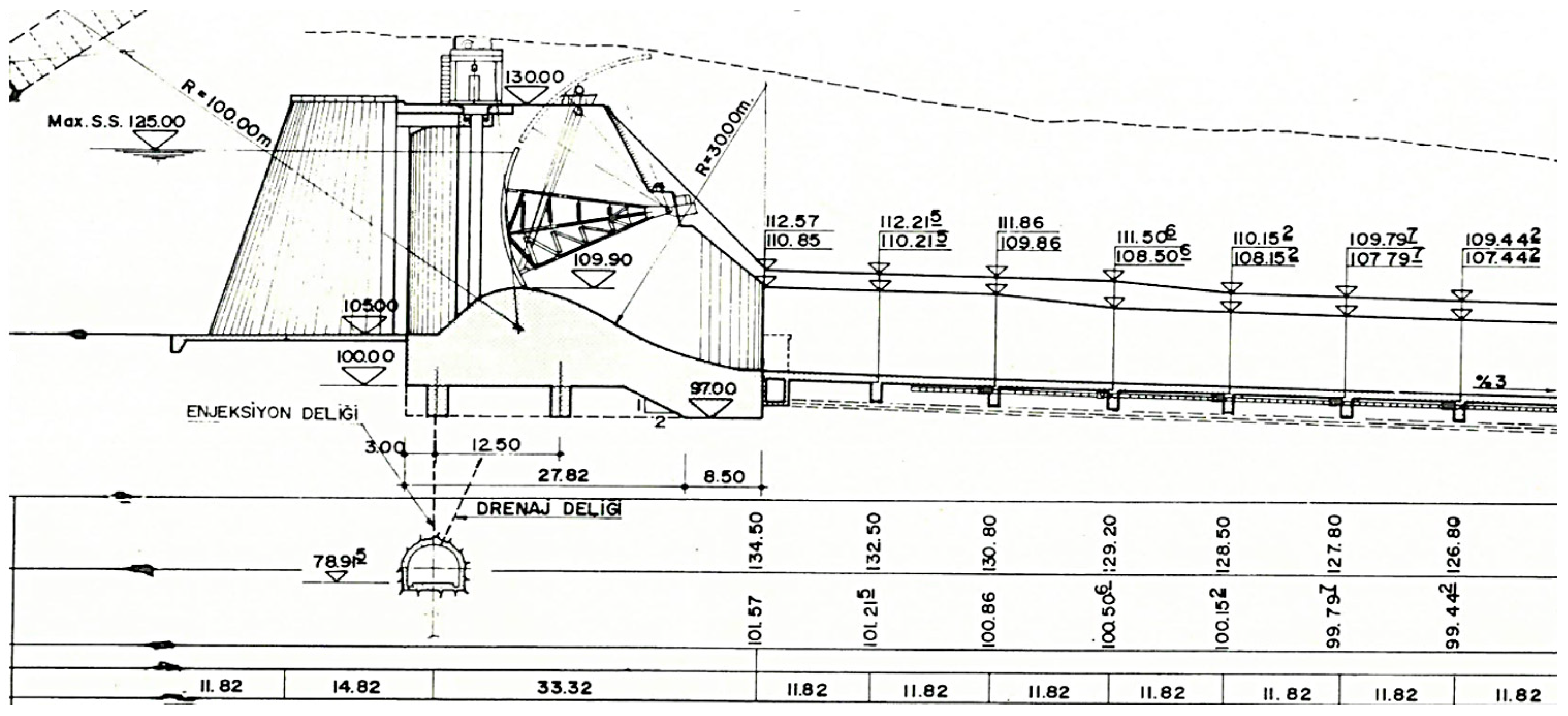
The spillway model was created by reducing the dimensions of the prototype spillway structure with Froude similarity at a 1/200 scale. The flood discharge (supercritical flow) and inlet velocities that would occur in the prototype spillway structure were also calculated according to Froude similarity and are shown in
Table 2.
The model scale was determined to fit the hydraulic channel in which the experiments were carried out. A 1/200 scale model was created in accordance with the 3D geometry of the prototype spillway structure (
Figure 2). The approach channel, weir, and discharge channel of the spillway model were formed. The energy breaker pool at the end of the spillway structure is not included in the model.
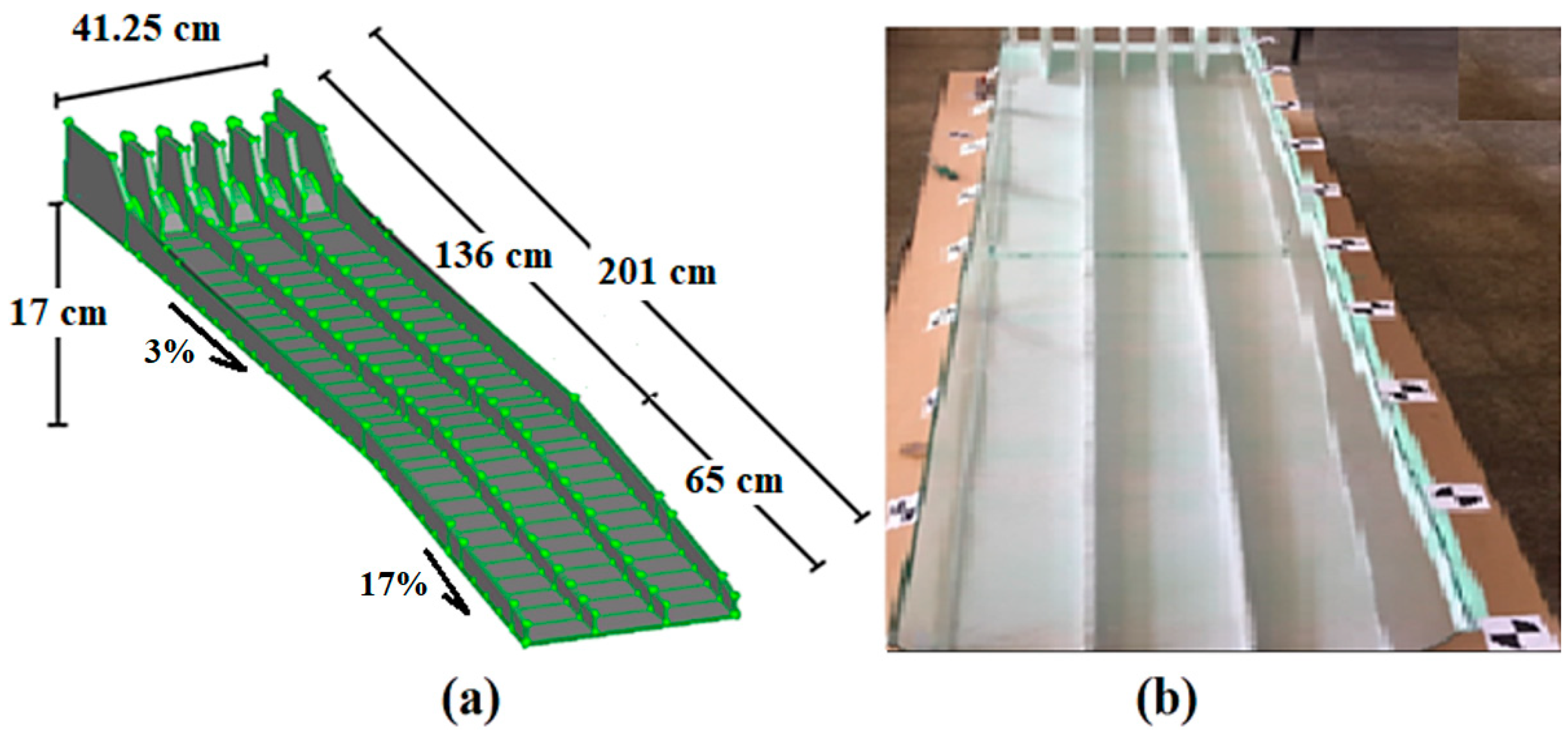
The spillway model was produced in parts, in accordance with the spillway geometry drawn with the AutoCAD 2014 program. The materials used in model making are very light and practical. The parts, made of 5 cm thick Extruded Polystyrene (XPS) styrofoam material, were joined with silicone adhesive. The model, approximately 2 m in length, was formed in 2 parts to be joined later, in the middle, to prevent damage. In order to provide visibility in image processing studies, the edges of the model were covered with glass material.
Figure 3 shows the final version of the spillway model.
In this study, a 1/200 scale model of the Çatalan Dam spillway structure was created and experimental studies were carried out in the hydraulic water channel. Experimental studies were carried out on the open-channel setup in Bartın University, central research, hydromechanics laboratory (
Figure 4).
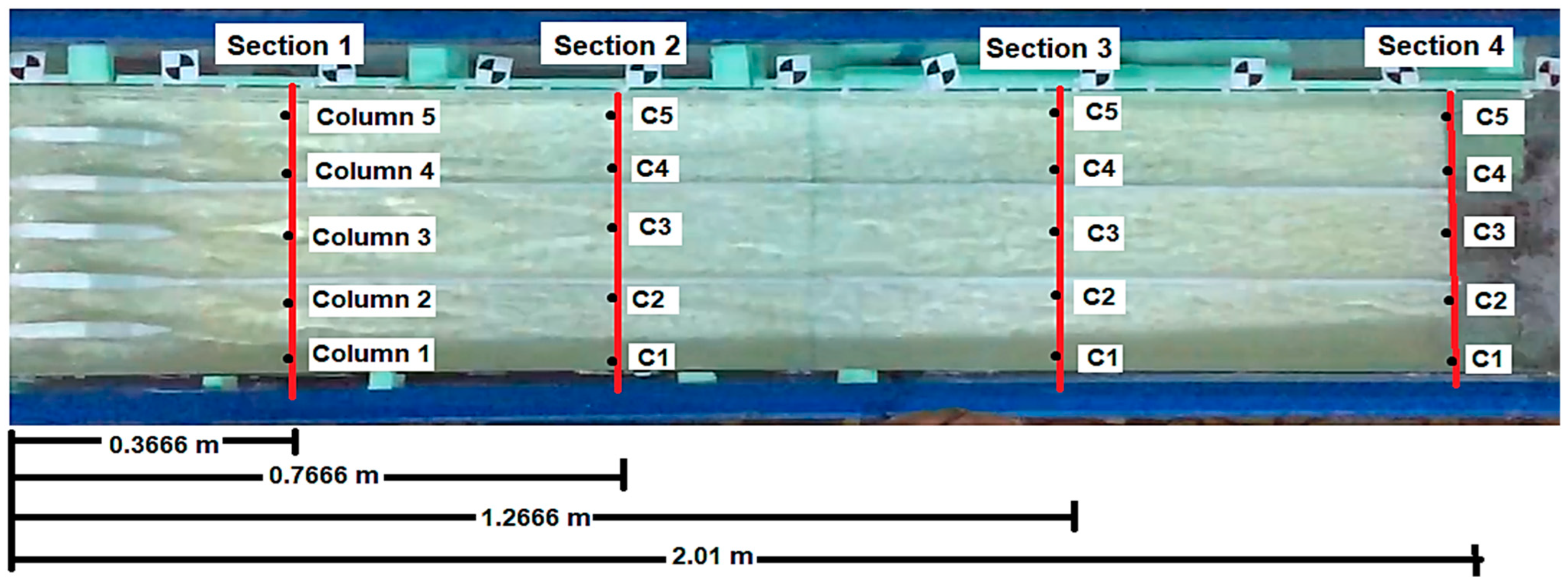
The discharge was adjusted with the help of the valve placed at the pump outlet that provides water circulation to the channels, and the flow entering the system was measured with the help of the ultrasonic flow meter (GE Pnametrics, AT 868 AquaTrans Flowmeter model, Clare, Ireland) placed at the pump inlet. Velocity measurements were made at a total of twenty points in four different cross-sections (five points in each cross-section) in the spillway channel with the ADV device (FlowTracker Handheld model, Hemmant, Australia) (
Figure 5). Due to the low water depths at the measurement points and the turbulence at the tip of the device, the measurements took a long time and erroneous measurements were repeated.
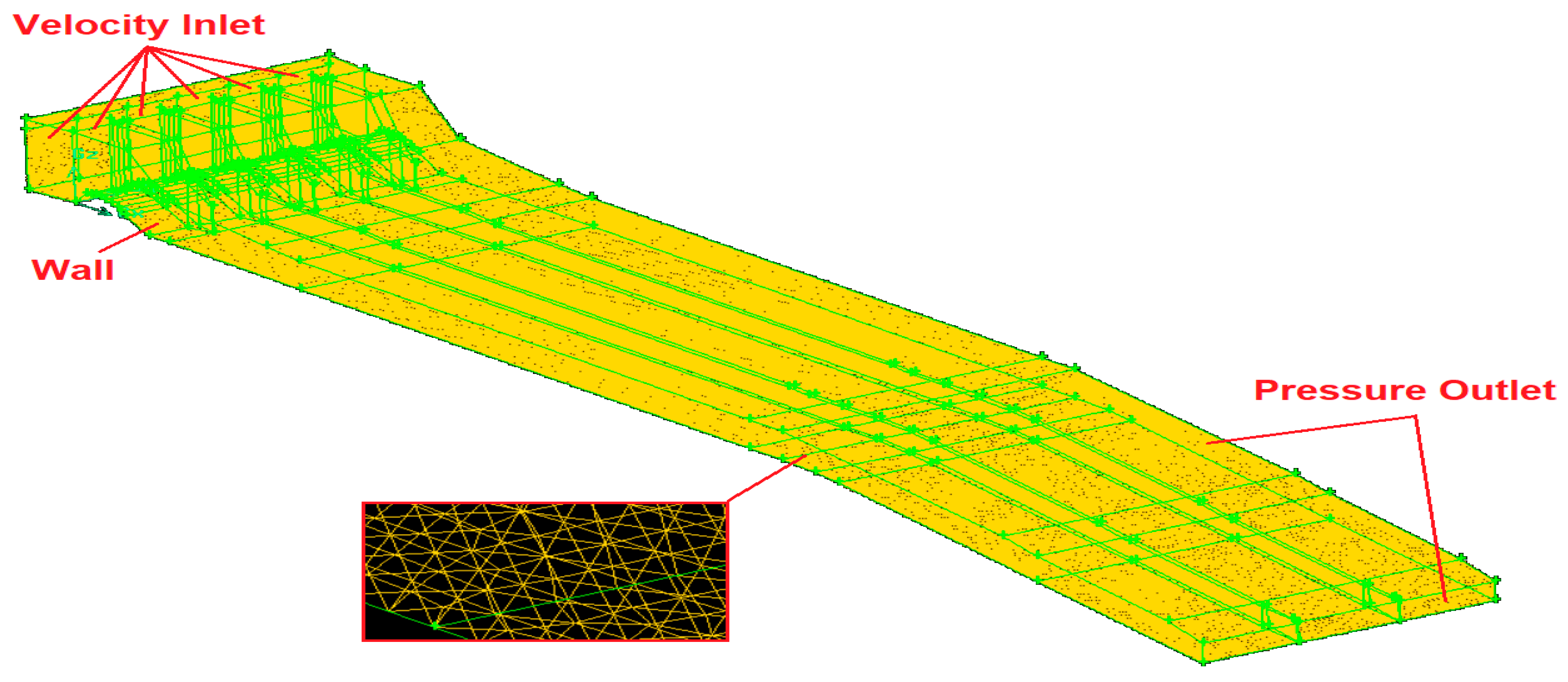
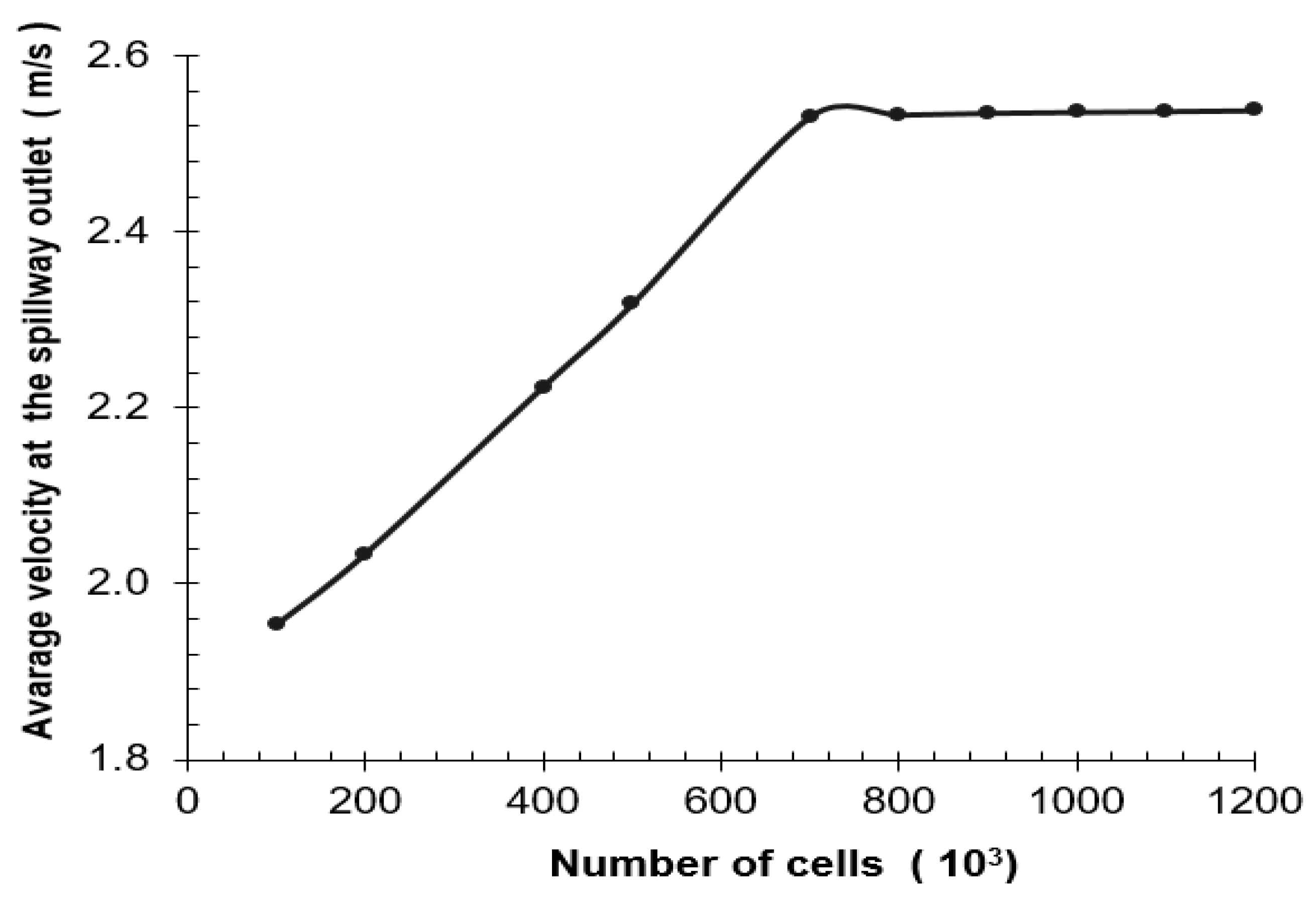
6. CFD Model Results
At the end of the studies, it was observed that both the physical model and the numerical model (10,055 m
3 s
−1) transferred the flood discharge downstream safely.
Figure 13 shows the general view of the flow resulting from the CFD analysis on the spillway model. When
Figure 13 is examined, it is observed that the side walls of the spillway chute channel are sufficient for the flood flow. However, overflows were observed at some points near Cross-section 1 of the separating walls of the chute channel. The velocity and water depth of the physical model and numerical model results are compared in tables, figures, and graphs below. Comparisons, mean absolute error (MAE), root-mean-square error (RMSE), and average percent error (APE) values are calculated and shown in the tables. MAE, RMSE, APE equations provided as:
where “
N” is the number of points measured, “
Yi observed” is the experiment measured, and “
Yi estimate” is the CFD measured.
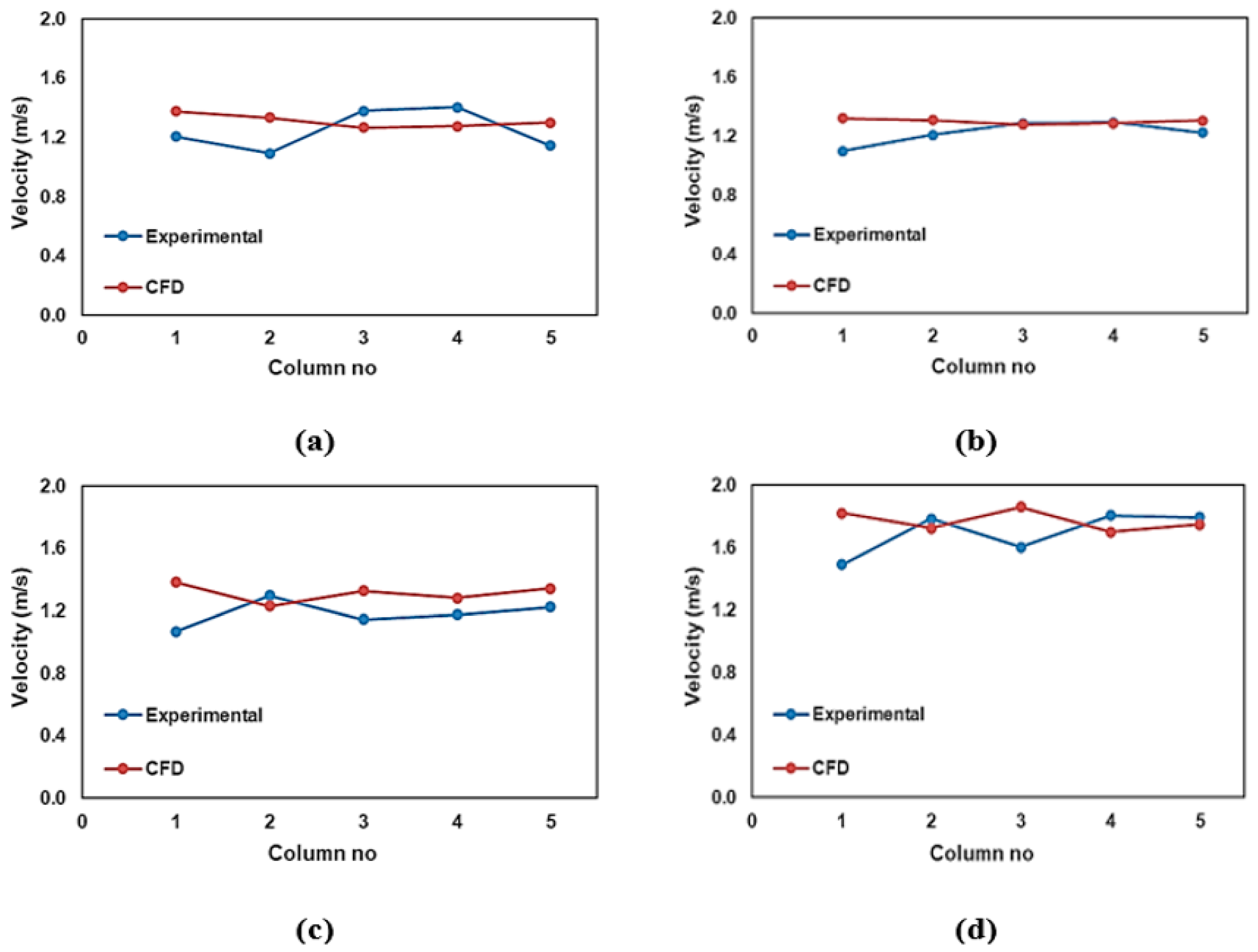
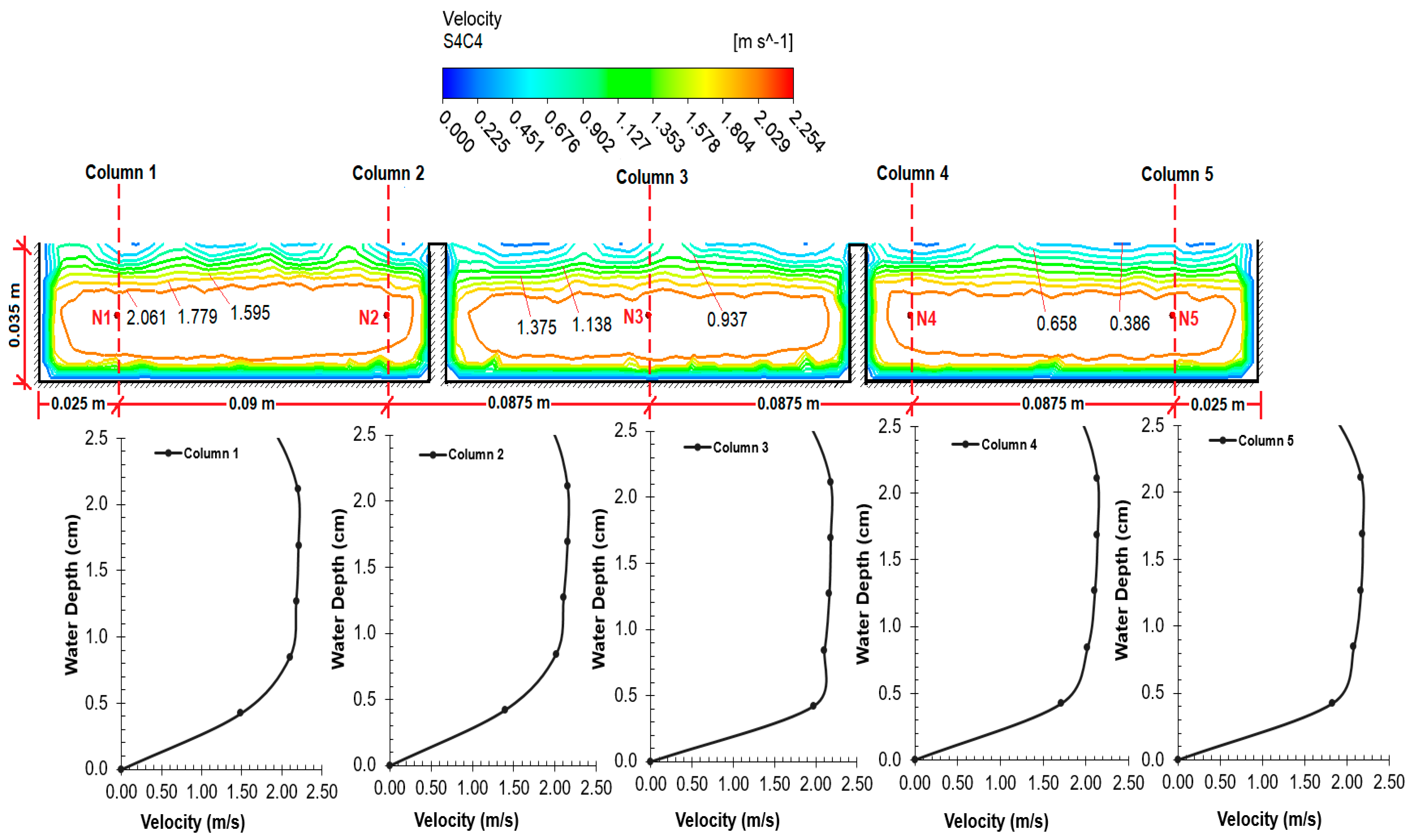
6.1. Comparison of Velocity
Experimental and numerical model velocity values are shown in
Table 4 and, comparatively, in the graphs in
Figure 14.
Table 4 shows the error rates by comparing the experimental and CFD analysis results.
When the table and graph are examined, the percentages of APE error in the sections were found to be 13.4, 7.2, 13.8, and 10.0. It can be seen that the error percentage of the velocities is less at the midpoints than at the edges. The percentage of error (N1 point) in Column 1 was higher than the others in all four cross-sections. Since the N1 point is close to the right side-wall of the chute channel, we believe that the turbulence occurring at this point may have caused errors in the measurements.
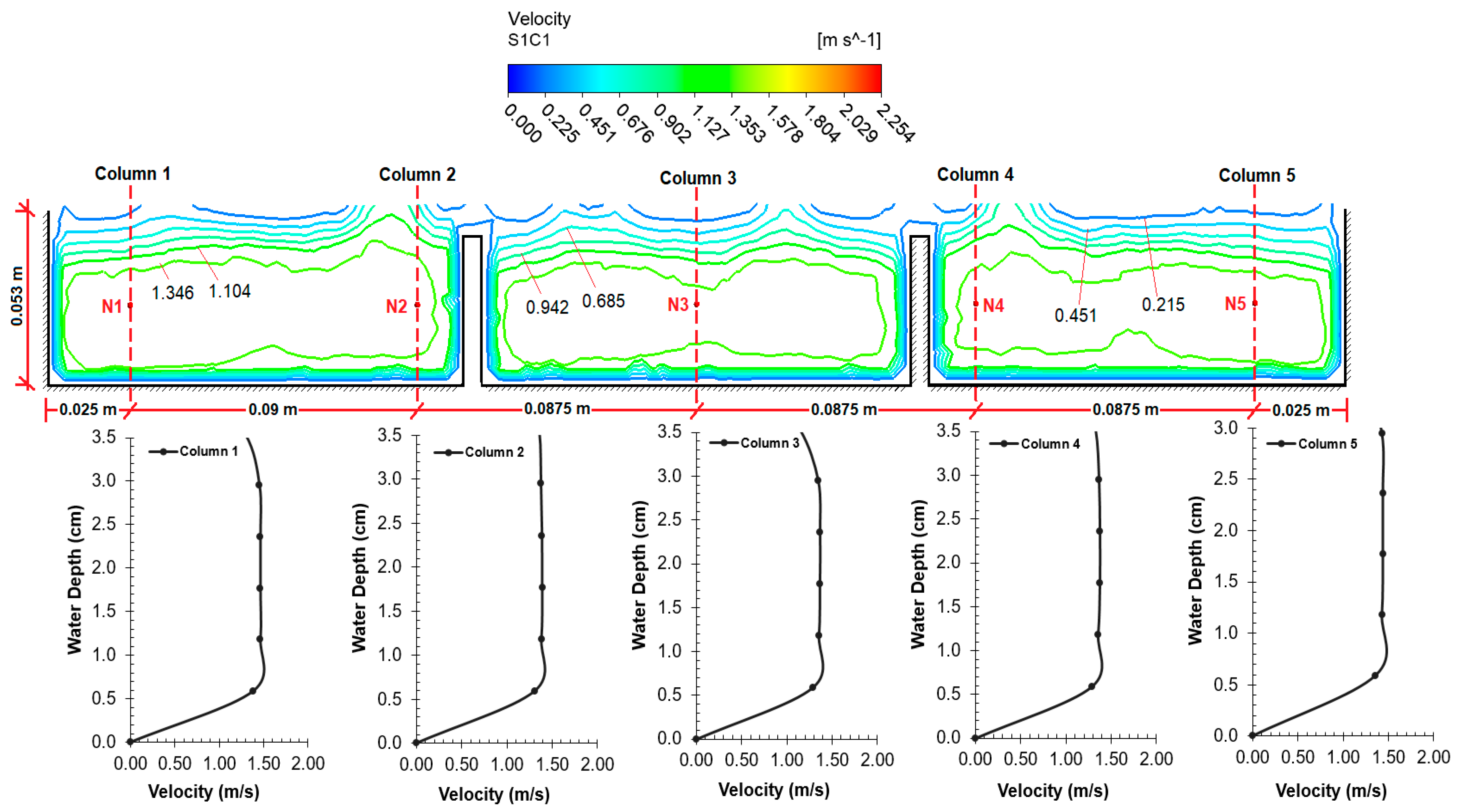
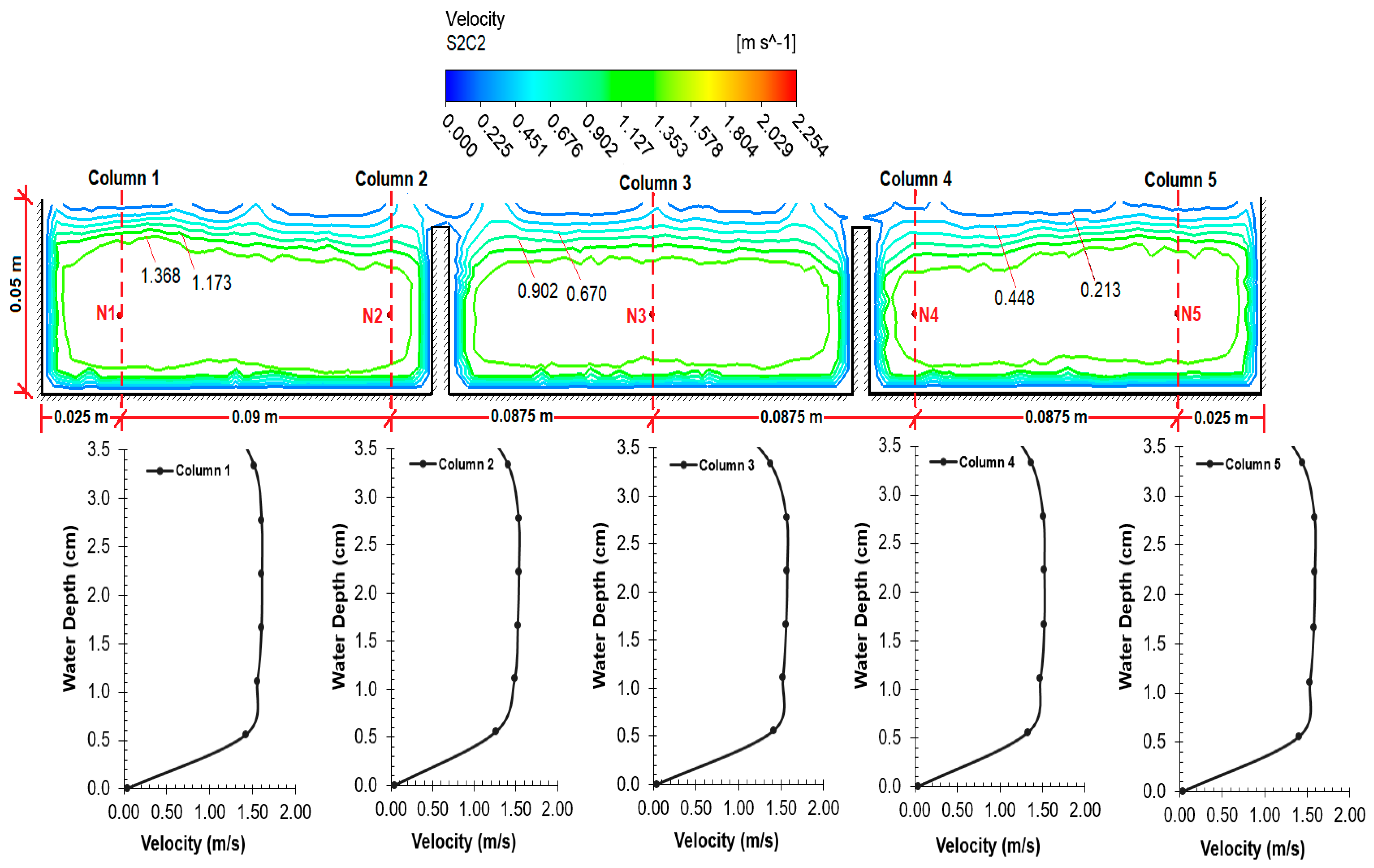
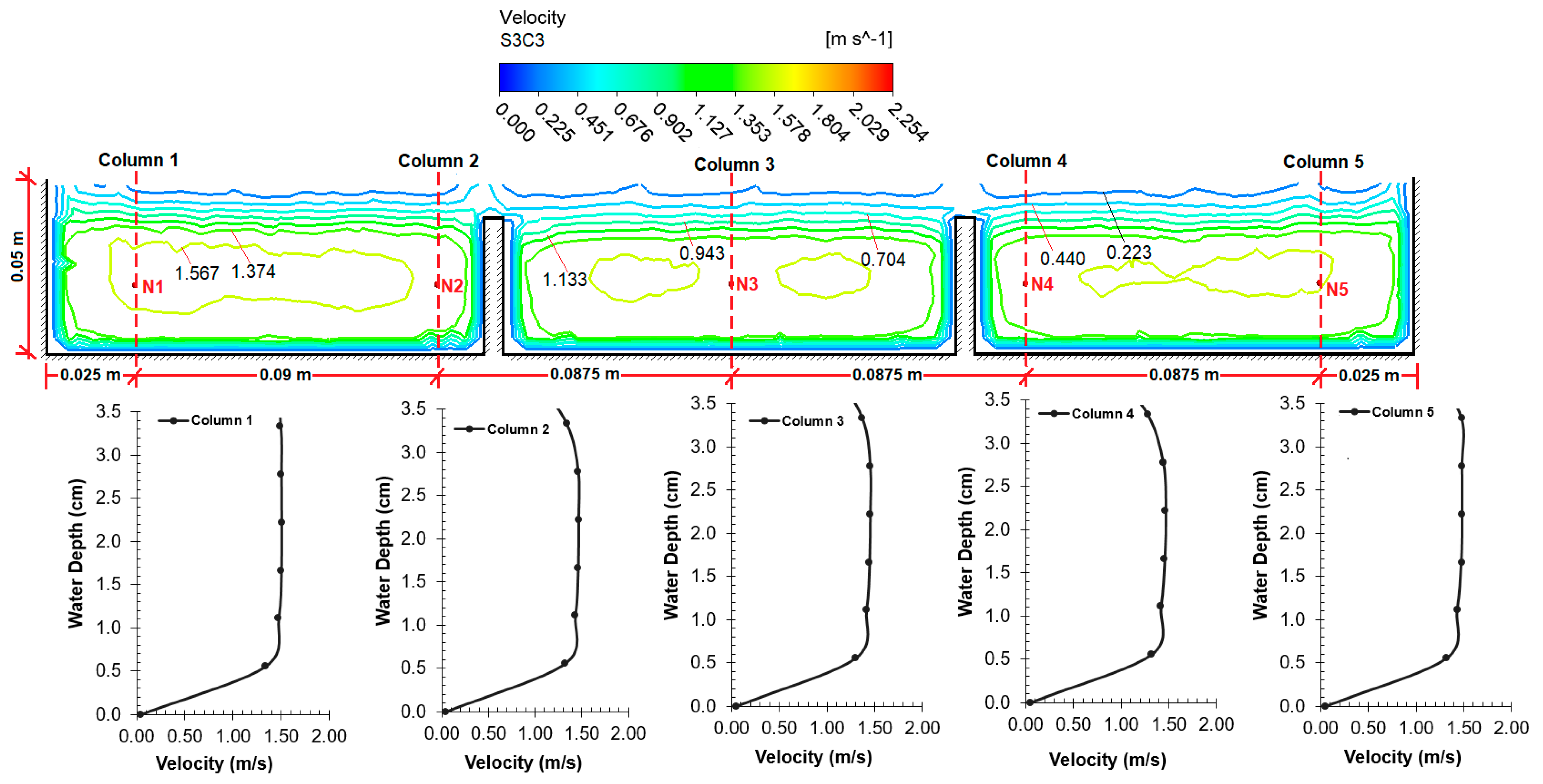
The velocity value contours and depth–velocity profiles obtained as a result of the CFD analysis on the spillway model are provided in
Figure 15,
Figure 16,
Figure 17 and
Figure 18 for four cross-sections. In all figures, it is seen that the velocity values increase from the wall edges to the center. If the velocity values in the cross-sections are examined, it can be observed that the velocity values of the air phase are lower after the water–air separation line. It can be observed that the velocity values were close to each other and the amount of increase was low in Cross-sections 1–3, which had a low slope (3%). However, with the increase of the slope (17%), the velocity value in Cross-section 4, located at the exit of the spillway, is higher than the others, as expected.
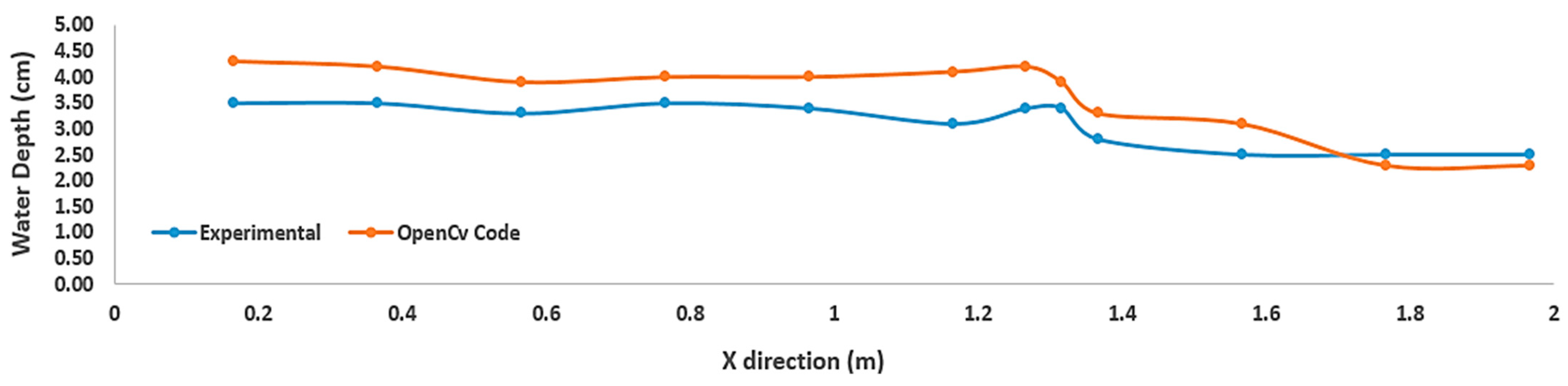
6.2. Comparison of Water Depth
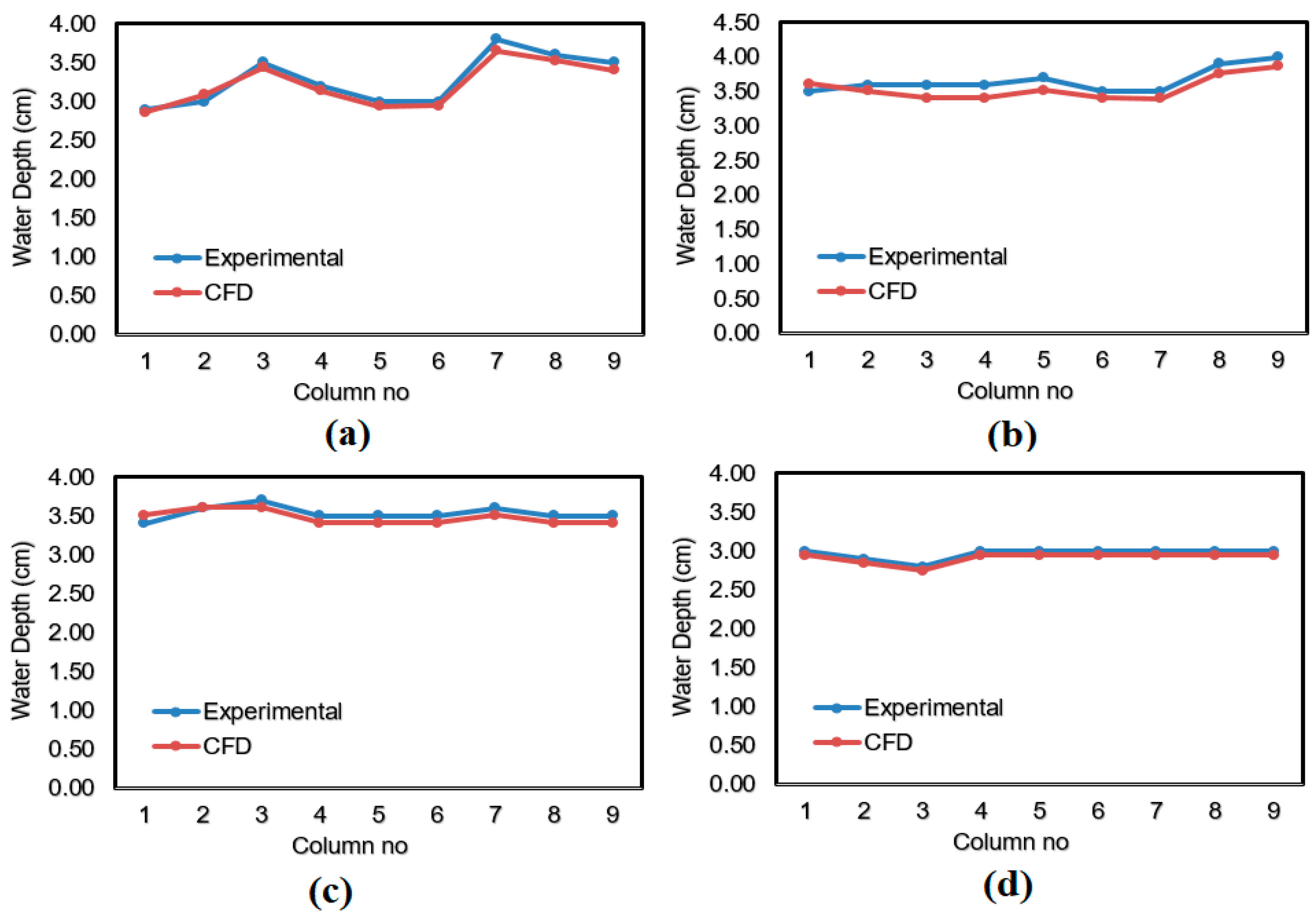
The water depths measured as a result of CFD analysis are shown in
Figure 19 in the general view for four cross-sections. Experimental and numerical model water depths are compared in the graphs in
Figure 20 and in
Table 5.
Table 5 shows the error percentages by comparing the experimental and CFD analysis results.
According to the graphs in
Table 5 and
Figure 20, the experiment and CFD analysis’ water depth measurements appear to be quite compatible with each other. When
Table 5 is examined, the highest APE, 3.8%, is in Cross-section 2. In points other than this, the error percentages vary around 1–2%. The cause of the error is turbulent fluctuations created by the incoming flood flow.
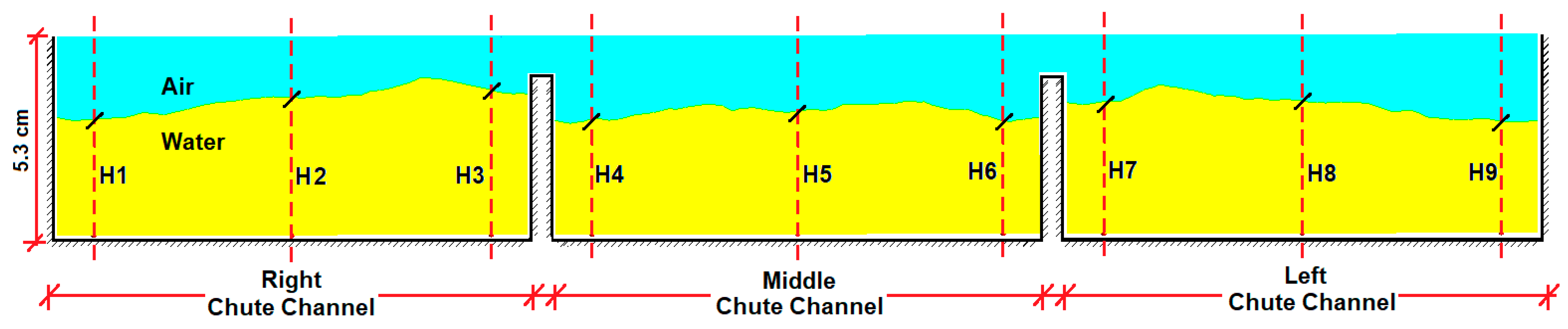
The water depths obtained as a result of the CFD analysis are provided for the four cross-sections in
Figure 21,
Figure 22,
Figure 23 and
Figure 24. It is seen that the water depths in Cross-sections 1–3, which have a 3% slope, were around 3.5 cm; this fell below 3 in Cross-section 4, which had a 17% slope. As expected, the depth decreases as the flow rate increases. When the figures of Cross-sections 1 and 2 are examined, it is observed that the water depths in the right and left chute channels are higher than that in the middle chute channel. On the other hand, in Cross-sections 3 and 4, the water depths in the right, left, and middle chute channels are similar. When the figures are examined, at no point did the water height exceed the side-wall height. However, at some points, it rose above the separation walls in the middle of the chute channels. Depths H3 and H7 in Cross-section 1 can be provided as examples of this; as long as the flood stays in the chute, the situation is not problematic.
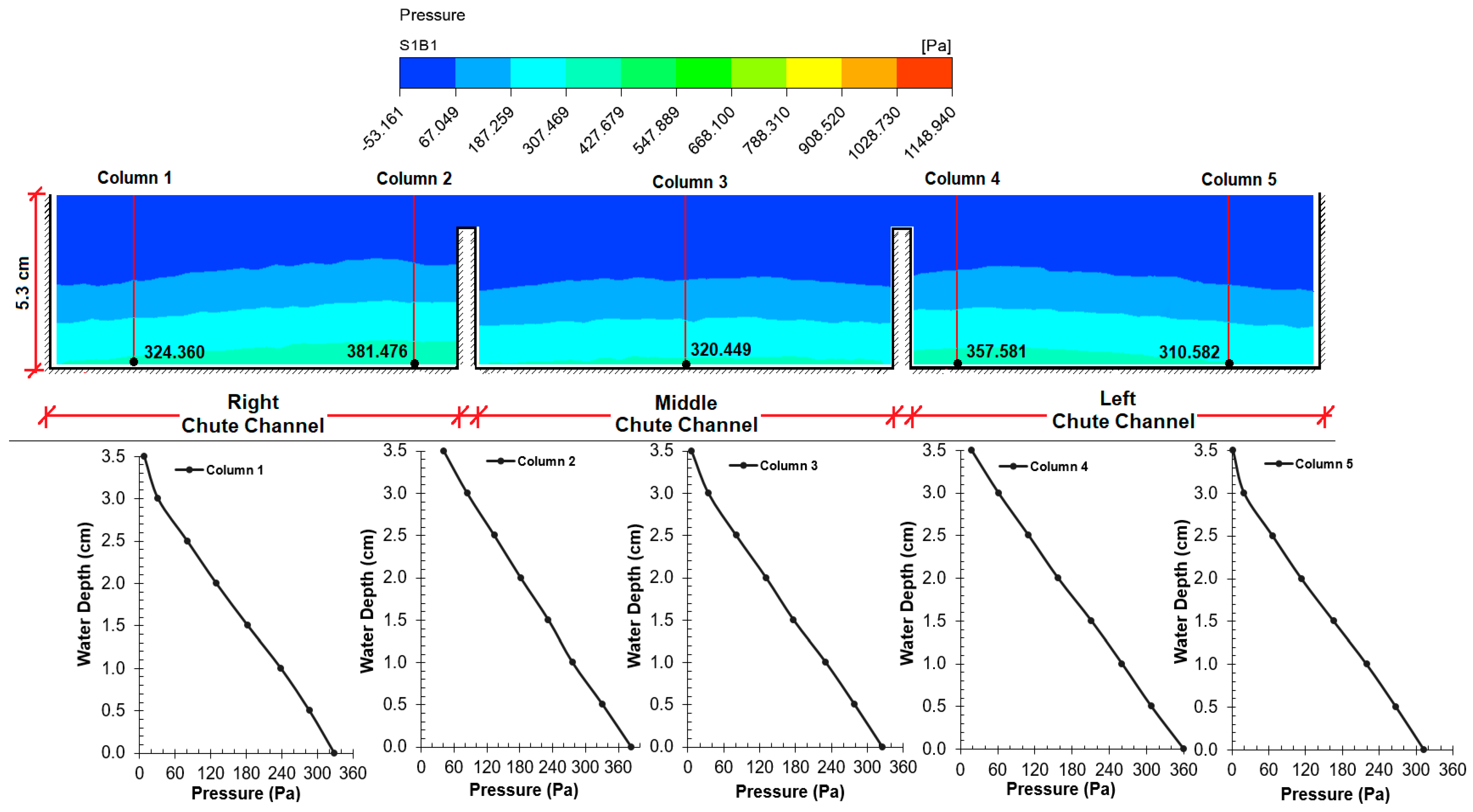
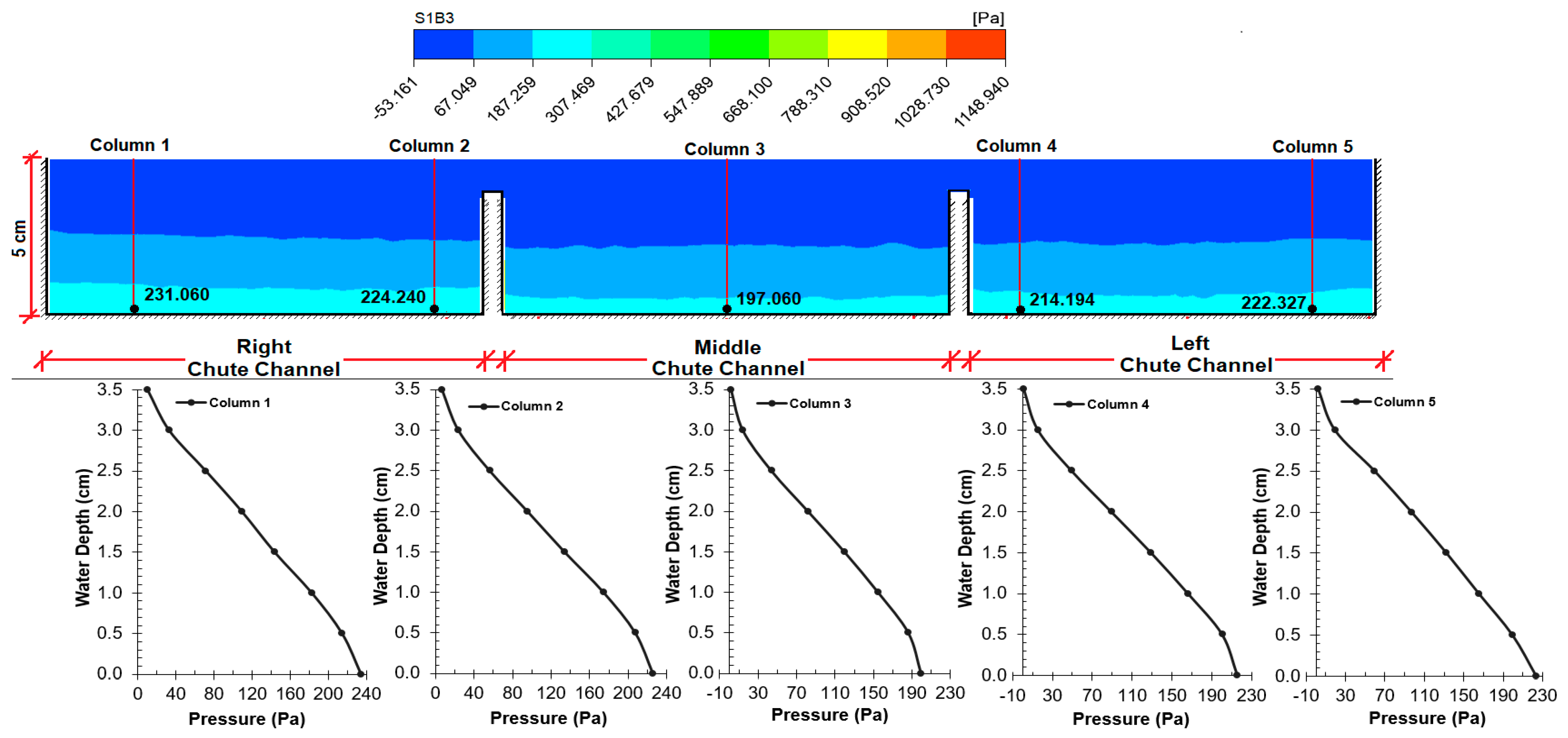
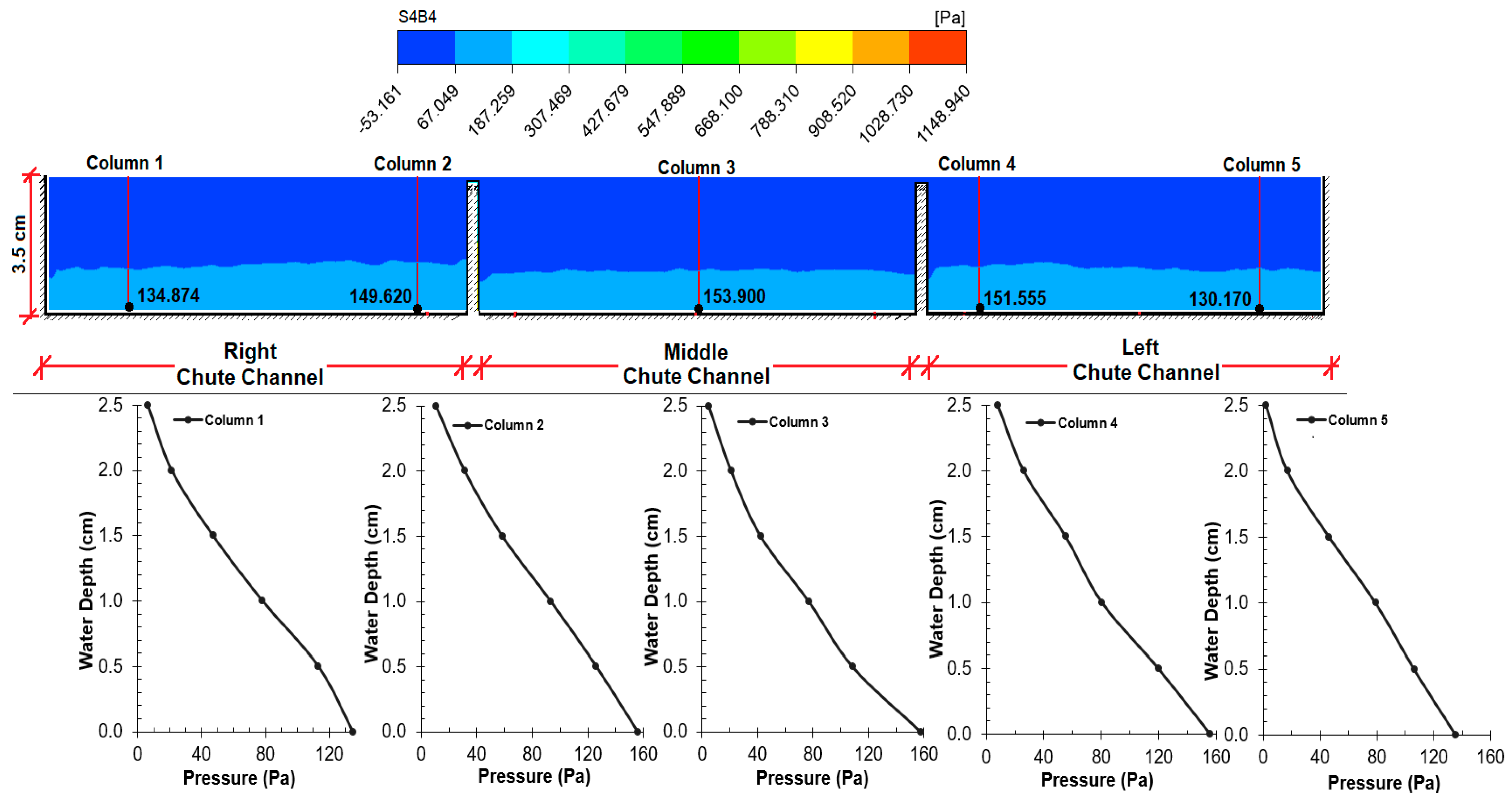
6.3. Investigation of Pressure in CFD Model
The flow of water in the spillway discharge channels in the flood regime causes low pressures. In some regions, cavitation is observed due to negative pressure. Cavitation causes structural deterioration [
6]. For this purpose, pressure controls should be made in the spillway discharge channels. It was observed that the pressure values decreased for each of the four sections (
Figure 25,
Figure 26,
Figure 27 and
Figure 28).
As expected, the pressure decreased with an increase in velocity. Graphs expressing vertical pressure distributions show the dynamic effect and deviation due to channel slope and flow velocity.
6.4. Investigation of Cavitation on Prototype Spillway
In cases where the flow velocity is more than 25–30 m/s, the risk of cavitation can be observed on the spillways [
11,
46]. The reason for this is the formation of steam bubbles in the stream that can damage the concrete as a result of the pressure in the stream decreasing to the value of the vapor pressure. The bubbles which are consequently formed impact the concrete surface at high velocity, condense, and cause wear. This wear damage, which is small in the beginning, increases over time and reaches large sizes. This causes serious risks in the structure. The type of damage that occurs in the structure in this way is called cavitation damage. The damage on the spillway thus caused is calculated with the dimensionless “cavitation index”. In this calculation method, pressure (P) and average velocity (U) values taken from certain points along the channel are used. Falvey [
47] stated that in cases where this calculated dimensionless cavitation index value is lower than 0.20, cavitation damage is highly likely to occur. At a point in the current, the cavitation index is calculated by the following expression:
where
is the cavitation index; P
T is the absolute pressure (P
a), including atmospheric pressure; P
v is the vapor pressure of the water (P
a);
is the density; and U is the velocity of the water. The calculated cavitation indices are presented in
Table 6. While making the calculations, we considered the average temperature as 20 °C, the vapor pressure (P
v) value as 2338 Pa, and the atmospheric pressure (Patm) as 92,801 Pa. The pressure and velocity values obtained with the model were increased in scale ratio according to Froude similarity and the pressure and velocity values were determined for the prototype spillway.
When the table is examined, it can be observed that the cavitation index values gradually decrease along the discharge channel. In the prototype spillway, there is no risk of cavitation, as the index values are above 0.2 at all points in the sections.