Spatial Wave Measurement Based on U-net Convolutional Neural Network in Large Wave Flume
Abstract
:1. Introduction
2. Data and Method
2.1. U-net Basic Principles
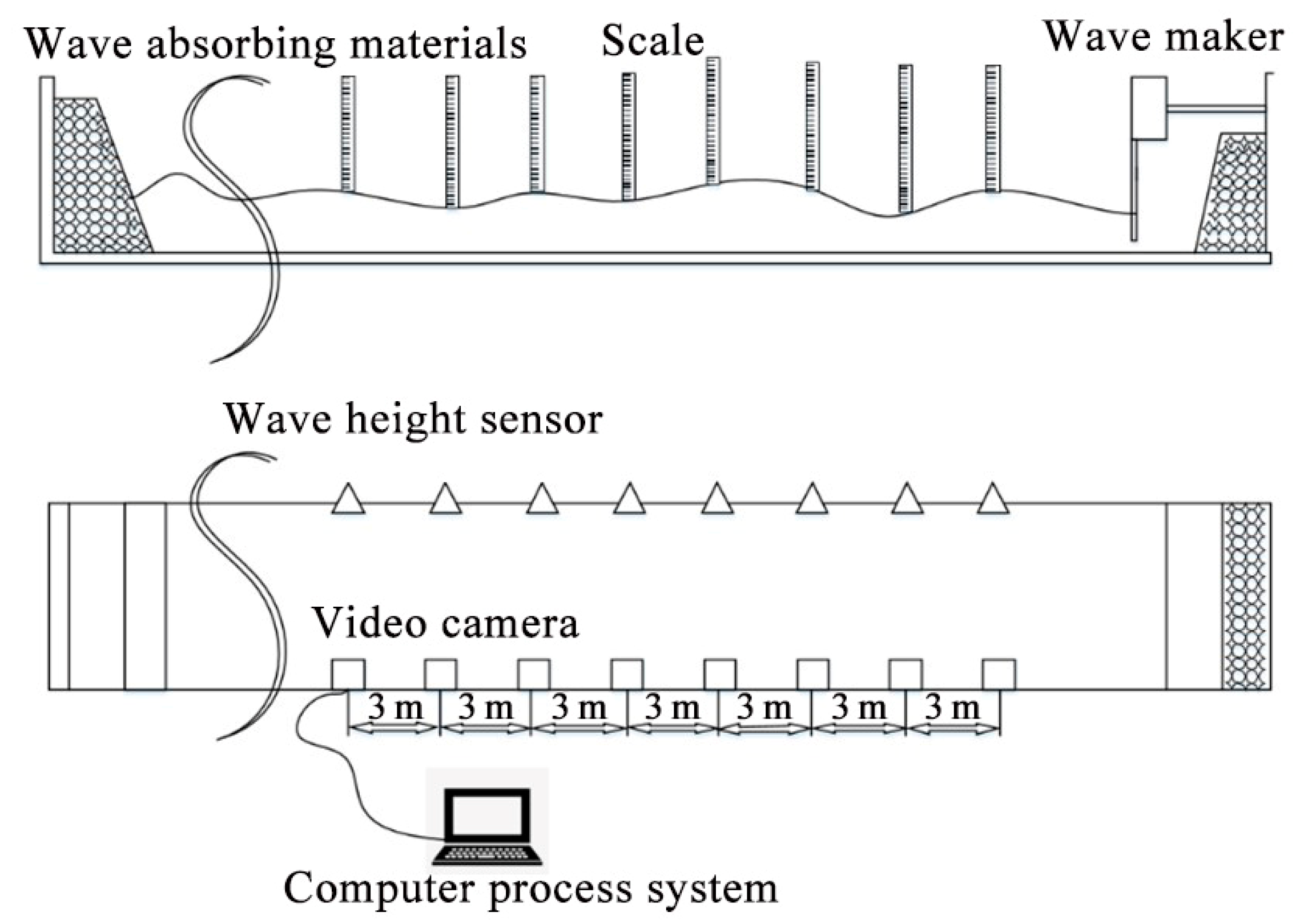
2.2. Data Sources and Data Preprocessing
2.3. Model Training
2.3.1. Training Conditions
2.3.2. Loss Function
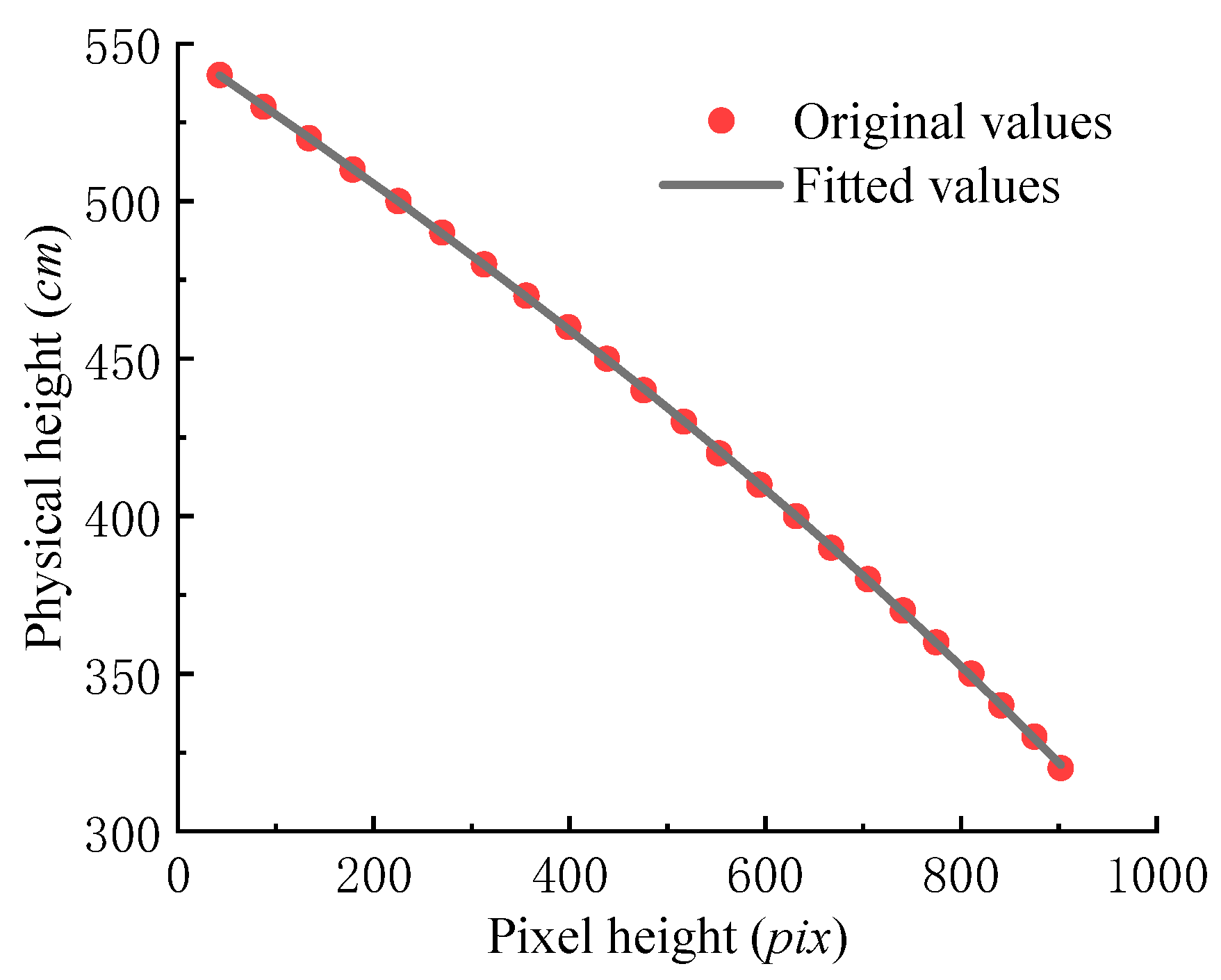
2.4. Scale Calibration
2.5. Evaluation Index
3. Result
3.1. Spatial Wave Measurement Based on U-net Convolutional Neural Network
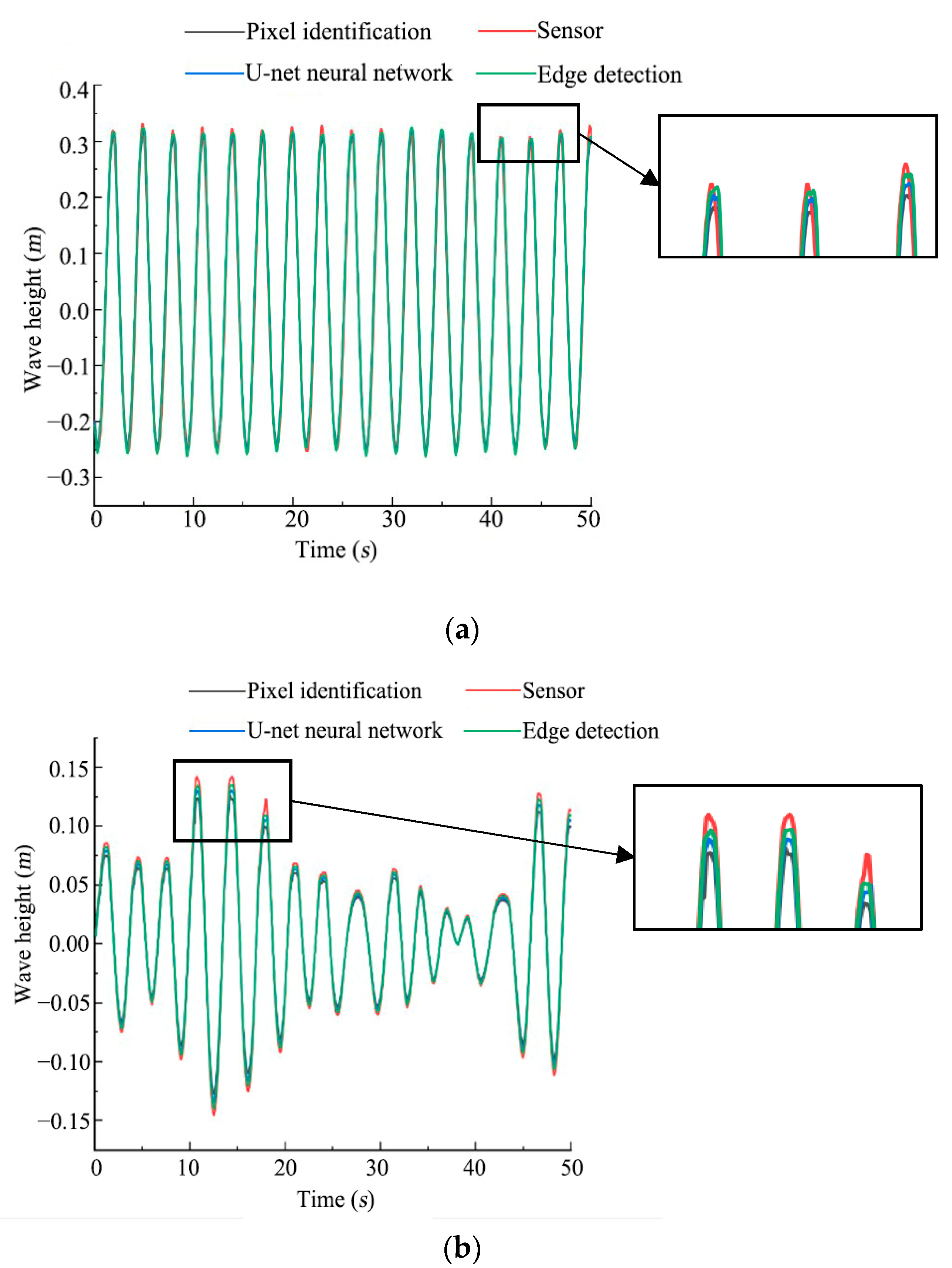
3.2. Comparison of Space Wave Measurement Method Based on U-net and Other Methods
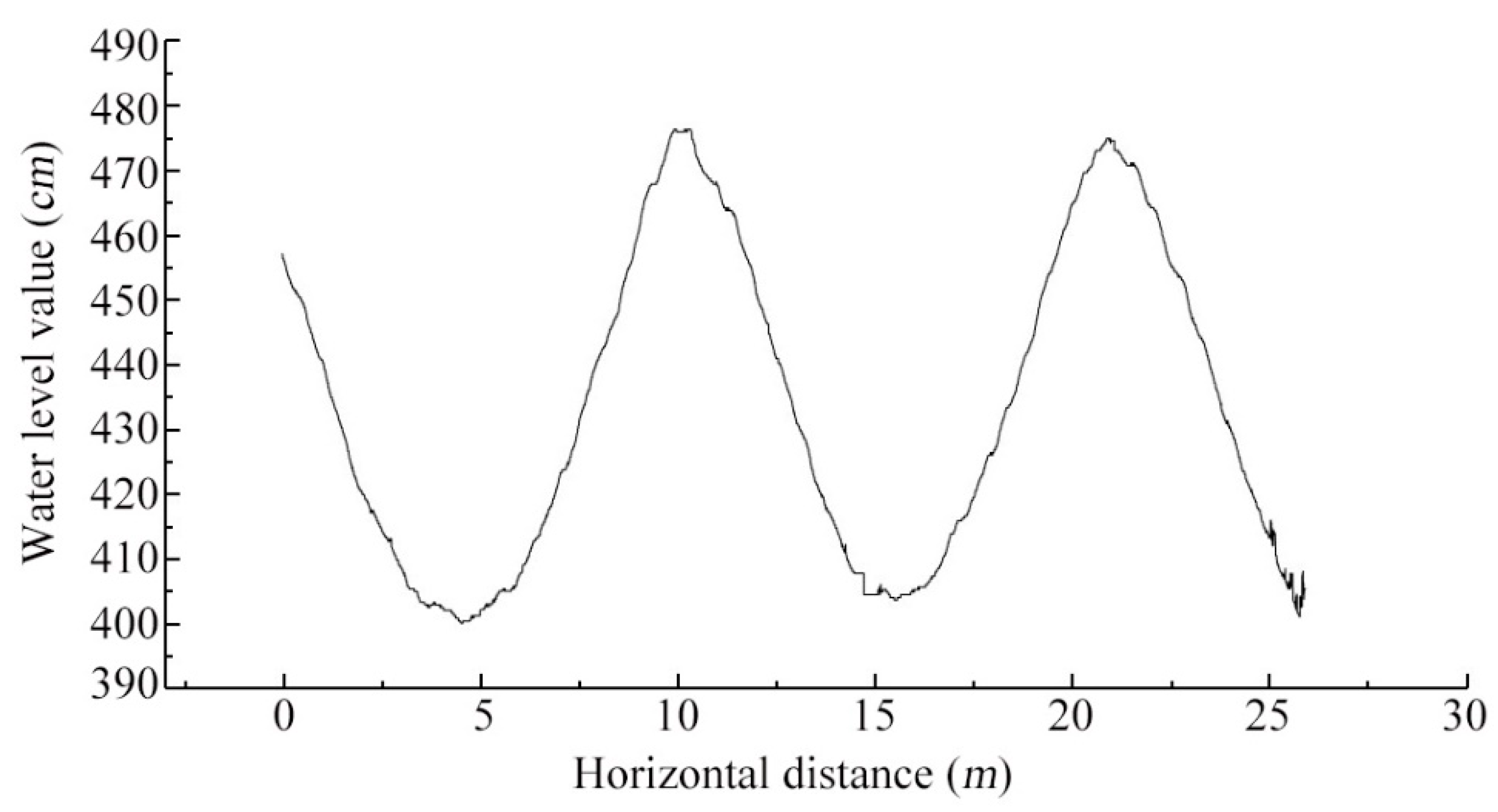
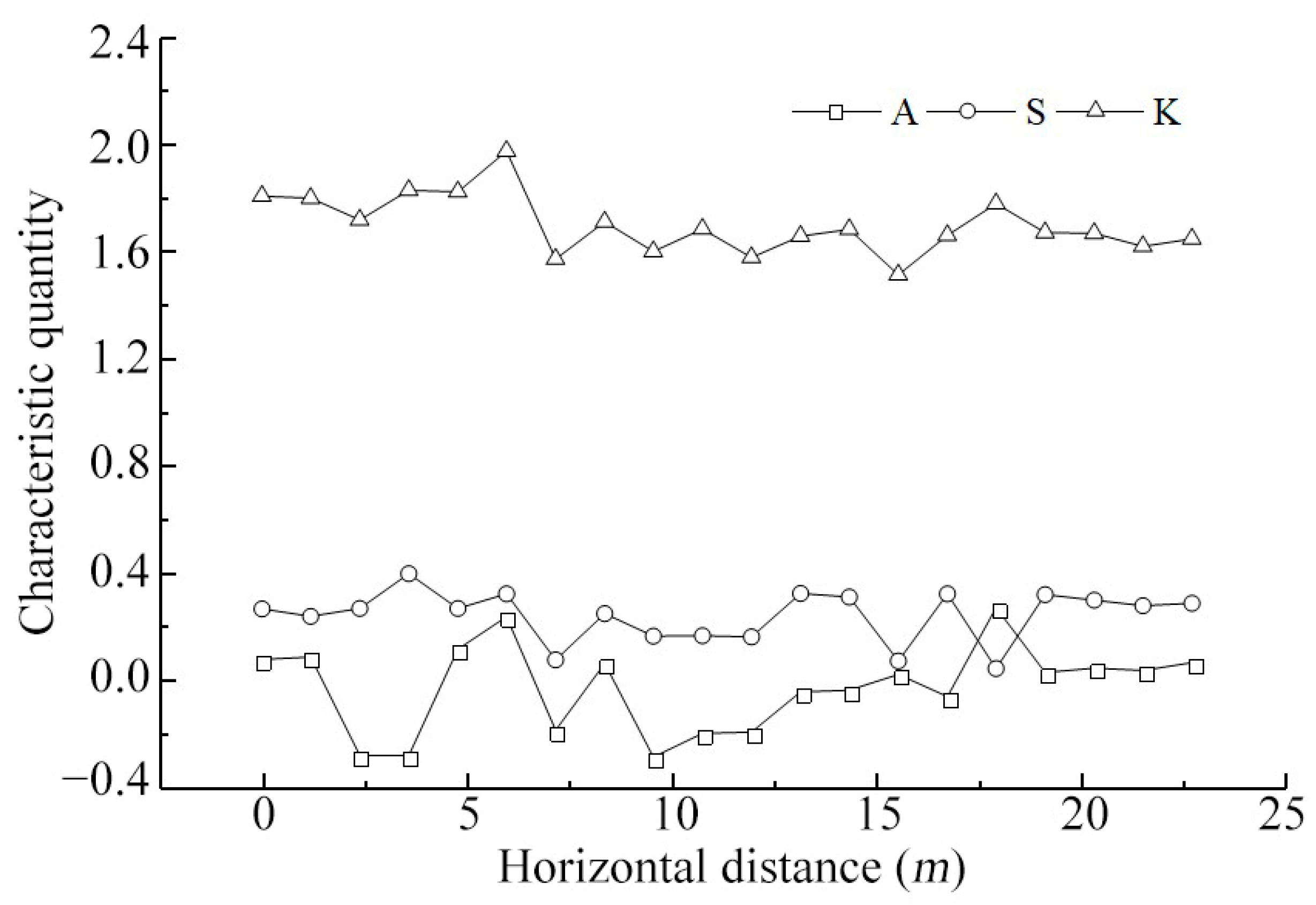
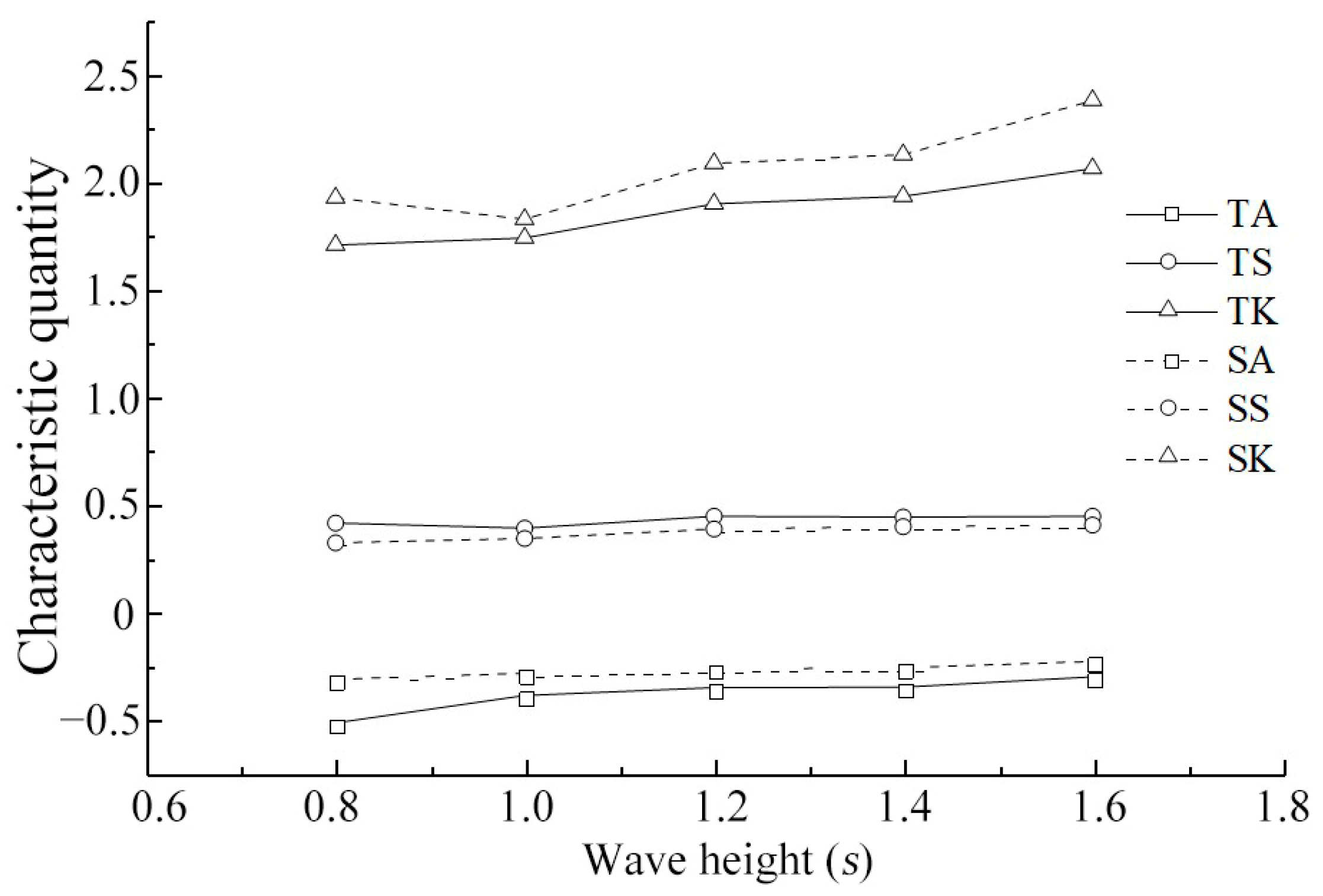
3.3. Study on Nonlinear Characteristic Quantity of Wave
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Genç, R. Catastrophe of environment: The impact of natural disasters on tourism industry. J. Tour. Adventure 2019, 1, 86–94. [Google Scholar] [CrossRef]
- Chen, S.; Xing, J.; Yang, L.; Zhang, H.; Luan, Y.; Chen, H.; Liu, H. Numerical modelling of new flap-gate type breakwater in regular and solitary waves using one-fluid formulation. Ocean Eng. 2021, 240, 109967. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, C.; He, C.; Wang, X.; Huang, J.; Deng, J. A review on applications of capacitive displacement sensing for capacitive proximity sensor. IEEE Access 2020, 8, 45325–45342. [Google Scholar] [CrossRef]
- Jensen, R.E.; Swail, V.; Bouchard, R.H. Quantifying wave measurement differences in historical and present wave buoy systems. Ocean. Dyn. 2021, 71, 731–755. [Google Scholar] [CrossRef]
- Lee, S.C.; Huang, Y.C. Innovative estimation method with measurement likelihood for all-accelerometer type inertial navigation system. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 339–346. [Google Scholar]
- Wang, C.; Wang, S.; Chen, S.; Chen, S. Wave measurement method based on accelerometer and gyroscope. Sci. Technol. Eng. 2019, 19, 44–49. [Google Scholar]
- Ma, T.; Wang, S.; Chen, H.; Huang, M. Application of wave measurement based on optical method in wave shape study. J. Waterw. Harb. 2017, 38, 308–312. [Google Scholar]
- Chang, L.; Xie, J. Prediction of groundwater level by optimized neural network algorithm. Hydro-Sci. Eng. 2005, 4, 66–70. [Google Scholar]
- Huang, P.; Zheng, Q.; Liang, C. Overview of Image Segmentation Methods. J. Wuhan Univ. (Nat. Sci. Ed.) 2020, 6, 519–531. [Google Scholar]
- Hou, H.; Gao, T.; Li, T. Overview of image segmentation methods. Comput. Knowl. Technol. 2019, 15, 176–177. [Google Scholar]
- Xiao, F.; Qin, X. A Survey of Image Segmentation. PLC$FA 2009, 11, 77–79. [Google Scholar]
- Rapp, R.J.; Melville, W.K. Laboratory measurements of deep-water breaking waves. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Sci. 1990, 331, 735–800. [Google Scholar]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Ma, X.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Q.; Chen, S.; Tang, Z. Effects of reef morphology variations on wave processes over fringing reefs. Appl. Ocean. Res. 2019, 82, 52–62. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Wang, R.; Zhang, J.-M. Large wave flume tests on wave-induced response of sandy seabed adjacent a water intake. Ocean. Eng. 2020, 195, 106709. [Google Scholar] [CrossRef]
- Marino, M.; Rabionet, I.C.; Musumeci, R.E. Measuring free surface elevation of shoaling waves with pressure transducers. Cont. Shelf Res. 2022, 245, 104803. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Munich, Germany, 5–9 October 2015. [Google Scholar]
- Wang, T.; Wang, L.; Zhang, W.; Duan, X.; Wang, W. Design of infrared target system with Zhang Zhengyou calibration method. Opt. Precis. Eng. 2019, 27, 1828–1835. [Google Scholar] [CrossRef]
- Russell, B.C.; Torralba, A.; Murphy, K.P.; Freeman, W.T. LabelMe: A Database and Web-Based Tool for Image Annotation. Int. J. Comput. Vis. 2014, 77, 157–173. [Google Scholar] [CrossRef]
- Torralba, A.; Russell, B.C.; Yuen, J. LabelMe: Online Image Annotation and Applications. Proc. IEEE 2010, 98, 1467–1484. [Google Scholar] [CrossRef]
- Tan, J.; Zhong, Y.; Huang, Z. Intelligent segmentation of rectal cancer based on U-net. Comput Era 2020, 8, 18–20+26. [Google Scholar]
- Mutasa, S.; Sun, S.; Ha, R. Understanding artificial intelligence based radiology studies: What is overfitting? Clin. Imaging 2020, 65, 96–99. [Google Scholar] [CrossRef] [PubMed]
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and flexible image augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef]
- Soares, C.G.; Cherneva, Z.; Antão, E.M. Characteristics of abnormal waves in North Sea storm sea states. Appl. Ocean. Res. 2003, 25, 337–344. [Google Scholar] [CrossRef]





| Groups | Water Level (m) | Environment | Wave Type | Wave Height (m) | Period (s) |
|---|---|---|---|---|---|
| 1 | 3.36 | Normal | Regular wave | 0.18 | 3 |
| 2 | 3.36 | Normal | Regular wave | 0.18 | 4.47 |
| 3 | 3.36 | Normal | Regular wave | 0.18 | 5.26 |
| 4 | 3.36 | Wall damage | Regular wave | 0.18 | 5.89 |
| 5 | 3.36 | Normal | Regular wave | 0.27 | 3 |
| 6 | 3.36 | Normal | Regular wave | 0.55 | 3 |
| 7 | 3.36 | Illumination | Regular wave | 0.83 | 3 |
| 8 | 3.36 | Normal | Irregular wave | 0.19 | 3.45 |
| 9 | 3.36 | Normal | Irregular wave | 0.19 | 4 |
| 10 | 3.36 | Normal | Irregular wave | 0.19 | 4.5 |
| 11 | 3.36 | Wall damage | Irregular wave | 0.19 | 5 |
| 12 | 3.36 | Normal | Irregular wave | 0.51 | 3.45 |
| 13 | 3.36 | Normal | Irregular wave | 0.62 | 3.45 |
| 14 | 3.36 | Illumination | Irregular wave | 0.78 | 3.45 |
| Model Measure Index | IOU | Accuracy |
|---|---|---|
| Before data augmentation | 0.954 | 0.963 |
| After data augmentation | 0.985 | 0.984 |
| Groups | Measurement Method | Mean Period (s) | Mean Wave Height (m) | Period Error (%) | Wave Height Error (%) |
|---|---|---|---|---|---|
| 1 | Wave height sensor | 3.01 | 0.184 | 0.33 | 1.6 |
| Canny edge detection | 3 | 0.1835 | 0 | 1.33 | |
| U-net | 3 | 0.183 | 0 | 1.05 | |
| Pixel identification | 3 | 0.1811 | |||
| 2 | Wave height sensor | 4.5 | 0.187 | 0.67 | 3.14 |
| Canny edge detection | 4.48 | 0.1853 | 0.22 | 2.21 | |
| U-net | 4.48 | 0.184 | 0.22 | 1.49 | |
| Pixel identification | 4.47 | 0.1813 | |||
| 3 | Wave height sensor | 5.3 | 0.191 | 0.76 | 4.83 |
| Canny edge detection | 5.24 | 0.179 | 0.38 | 1.76 | |
| U-net | 5.24 | 0.18 | 0.38 | 1.21 | |
| Pixel identification | 5.26 | 0.1822 | |||
| 4 | Wave height sensor | 5.93 | 0.193 | 0.67 | 6.04 |
| U-net | 5.91 | 0.18 | 0.34 | 1.1 | |
| Pixel identification | 5.89 | 0.182 | |||
| 5 | Wave height sensor | 3 | 0.28 | 0 | 2.19 |
| Canny edge detection | 3 | 0.27 | 0 | 1.46 | |
| U-net | 3 | 0.277 | 0 | 1.1 | |
| Pixel identification | 3 | 0.274 | |||
| 6 | Wave height sensor | 3 | 0.585 | 0.33 | 6.17 |
| Canny edge detection | 3 | 0.573 | 0.33 | 3.99 | |
| U-net | 3 | 0.565 | 0.33 | 2.54 | |
| Pixel identification | 2.99 | 0.551 | |||
| 7 | Wave height sensor | 3 | 0.88 | 0 | 6.41 |
| U-net | 3 | 0.851 | 0 | 2.9 | |
| Pixel identification | 3 | 0.827 | |||
| 8 | Wave height sensor | 3.47 | 0.203 | 0.57 | 6.84 |
| Canny edge detection | 3.45 | 0.197 | 0 | 3.68 | |
| U-net | 3.45 | 0.195 | 0 | 2.63 | |
| Pixel identification | 3.45 | 0.19 | |||
| 9 | Wave height sensor | 4 | 0.21 | 0 | 8.8 |
| Canny edge detection | 4 | 0.2 | 0 | 3.63 | |
| U-net | 4 | 0.199 | 0 | 3.11 | |
| Pixel identification | 4 | 0.193 | |||
| 10 | Wave height sensor | 4.53 | 0.217 | 0.66 | 11.8 |
| Canny edge detection | 4.51 | 0.205 | 0.22 | 5.7 | |
| U-net | 4.51 | 0.2 | 0.22 | 3.1 | |
| Pixel identification | 4.5 | 0.194 | |||
| 11 | Wave height sensor | 5.03 | 0.218 | 0.6 | 13.5 |
| U-net | 4.98 | 0.199 | 0.4 | 3.65 | |
| Pixel identification | 5 | 0.192 | |||
| 12 | Wave height sensor | 3.46 | 0.549 | 0.29 | 7.64 |
| Canny edge detection | 3.44 | 0.533 | 0.29 | 4.5 | |
| U-net | 3.44 | 0.53 | 0.29 | 3.92 | |
| Pixel identification | 3.45 | 0.51 | |||
| 13 | Wave height sensor | 3.46 | 0.68 | 0.29 | 9.67 |
| Canny edge detection | 3.44 | 0.657 | 0.29 | 5.97 | |
| U-net | 3.44 | 0.643 | 0.29 | 3.71 | |
| Pixel identification | 3.45 | 0.62 | |||
| 14 | Wave height sensor | 3.47 | 0.88 | 0.57 | 12.53 |
| U-net | 3.44 | 0.812 | 0.29 | 3.84 | |
| Pixel identification | 3.45 | 0.782 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Hu, Y.; Chen, S.; Ren, Z.; Arikawa, T. Spatial Wave Measurement Based on U-net Convolutional Neural Network in Large Wave Flume. Water 2023, 15, 647. https://doi.org/10.3390/w15040647
Chen J, Hu Y, Chen S, Ren Z, Arikawa T. Spatial Wave Measurement Based on U-net Convolutional Neural Network in Large Wave Flume. Water. 2023; 15(4):647. https://doi.org/10.3390/w15040647
Chicago/Turabian StyleChen, Jiangnan, Yuanye Hu, Songgui Chen, Zhiwei Ren, and Taro Arikawa. 2023. "Spatial Wave Measurement Based on U-net Convolutional Neural Network in Large Wave Flume" Water 15, no. 4: 647. https://doi.org/10.3390/w15040647
APA StyleChen, J., Hu, Y., Chen, S., Ren, Z., & Arikawa, T. (2023). Spatial Wave Measurement Based on U-net Convolutional Neural Network in Large Wave Flume. Water, 15(4), 647. https://doi.org/10.3390/w15040647





