Abstract
Under climate warming, the frequency and intensity of extreme rainstorms-induced urban pluvial floods are significantly increasing, leading to severe flooding risks in megacities. An integrated model that incorporates rainfall processing, waterlogging simulation, GIS spatial analysis, risk assessment, and measure evaluation was developed, optimizing both the assessment procedure and the computing efficiency for assessing pluvial flood risk and adaptation measures. The historic “9.13” extreme rainstorm event is simulated, showing excellent consistency of inundation depth and area compared to Shanghai’s “110” alarm validation records. Three extreme rainstorm scenarios, using return periods of 200a, 500a, and 1000a, were generated to evaluate the flooding risk and measures’ performance. The results show that the low-lying areas in the solution district are the most inundated region based on the existing defense measures. The maximum inundation depth of high-extreme rainstorm scenarios is up to 1.5 m, and the low-lying areas would still be above 1 m even in low-extreme scenarios. Increasing the drainage capacity can effectively reduce the total loss by 80% in the low-extreme scenario, yet still suffering a significant loss in both moderate-extreme and high-extreme scenarios. The integrated model can provide technical support for the rapid evaluation of flood control prevention capabilities.
1. Introduction
The sixth assessment report of the Intergovernmental Panel on Climate Change (IPCC) pointed out that the probability of extreme weather events, such as severe urban pluvial flooding, has increased significantly in the 21st century [1]. Flood risk in coastal low-lying cities is very likely to dramatically increase due to the rising sea level induced by climate change [1]. Global warming strengthens the hydrological cycle with increasing global mean precipitation, and the frequency and intensity of extreme rainstorm events are predicted to increase significantly in the future [2,3,4,5,6]. Even though there are variations in the long historic global average precipitation records, the possibilities of extreme precipitation are very likely to increase in cities in the future [7,8,9]. The impacts and threats posed by these extreme flooding events are of great concern to policymakers, scientists, and the public [10,11,12,13].
China’s megacities are facing serious urban pluvial flood problems as frequent rainstorms-induced inundation events have occurred during the past several years. On 24 July 2012, Beijing experienced the largest rainstorm since 1950. The city’s average rainfall was 170 mm, and the maximum rain reached 240.3 mm, causing 79 deaths and direct economic losses of USD 1.66 billion. On 13 September 2013, a severe rainstorm (maximum precipitation reached 130.7 mm in 1 h) hit Shanghai’s central urban region, which broke the historical record (108.8 mm), resulting in serious subway waterlogging and street traffic interruption. On 20 July 2021, Zhengzhou was struck by a devastating rainstorm, with daily rainfall totaling 552.5 mm and three-day rainfall reaching 617.1 mm, which is relatively close to the annual average rainfall of 640.8 mm.
Given the fact that both precipitation and precipitation extremes have increased for decades, the central urban area of Shanghai is experiencing a significant “rain island effect” [14,15]. Regional Climate Models (RCM) predictions show that it is highly likely that the intensity and frequency of short-duration rainstorms in Shanghai will increase significantly in the future [16,17]. If extreme rainstorm events reoccur and strengthen, they will eventually generate an undesirable condition of interior pluvial flooding in low-lying regions [18,19]. Therefore, it is of great significance to simulate future extreme rainstorm scenarios in megacities such as Shanghai and to evaluate flood control measures based on the integrated urban hydrological model to ensure urban safety.
Large bodies of simulations of extreme flood scenarios in Shanghai have been conducted using commercial hydrological models [20,21,22,23,24]. However, two-dimensional (2D) flood simulation at an urban scale requires significant computing resources, leading to a costly simulation time [25], which cannot satisfy the emergency of pluvial flood risk control. Additionally, commercial hydrology software usually does not support the integrated simulation of a whole cascade of procedures, including spatial rainfall datasets, flood simulation, risk assessment, and adaptation measure evaluation. The hydrological model of SCS-CN (Soil Conservation Service Curve Number) has the characteristics of simple parameters and easy access to data, which has been widely applied in Shanghai [26,27,28,29]. This work established the Shanghai Urban Inundation Model (SUIM) based on SCS-CN in order to address the challenges of multi-scenario, multi-model, and large-scale simulation calculations. It aims to establish a rapid and integrated model for minimizing risk and to offer technical support for assessing the capacities of adaptation measures in mitigating urban pluvial flood risk.
2. Model Establishment
2.1. Model Structure
The SUIM encapsulates the sub-modules of the rainfall module, hydrology module, spatial statistics module, risk assessment module, and measure evaluation module to provide technical solution for integrated risk assessment and measure evaluation. The coupled sub-modules can optimize the simulation process and computing efficiency. The model adopts a PostgreSQL database that supports GIS spatial data storage. It supports GIS spatial analysis and calculation, including clipping of features, extraction of layers, coordinate transformation, and spatial interpolation. The model’s underlying data employ a regular grid structure, which has the advantages of speedy calculation, simple logic operation, and automatic processing capability. The integrated model is suitable for various applications, including backtracking of historical events, early warning of inundation forecasting, future scenario evaluation, and pre-planning of hydraulic engineering [30]. The overall architecture process is shown in Figure 1.
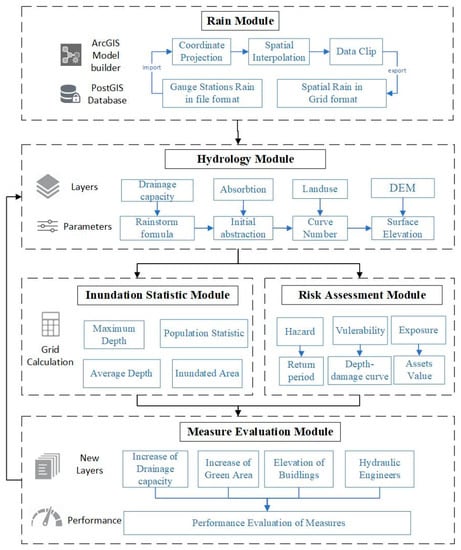
Figure 1.
Conceptual scheme of SUIM model.
2.2. Rainfall Module
The short-duration extreme rainfall often varies greatly in the spatial rainfall distribution at the urban scale. Many studies have used Thiessen polygons to separate sub-catchments using several gauge stations [31]. The precision of spatial rain is limited, either because the geographical distribution of stations is uneven or because the difference in rainfall amounts between sub-catchments is considerable. In this work, the spatial rainfall process is considered at a finer grid level, using multiple gauge stations to interpolate the spatial distribution of the entire catchment. We employed GIS spatial analysis (e.g., Ordinary Kriging or Inverse Distance Weight Interpolation) to interpolate spatial rainfall to smooth rainfall differences across catchments. The raw rainfall station data are usually recorded in the form of a list and cannot be directly run in the SUIM model. First, preprocessing processes such as projection definition, spatial interpolation, raster clipping, and format conversion are implemented in ArcGIS. In order to simplify the process, the automatic processing process of compiling multi-scenario future data based on ArcGIS Model Builder is implemented. The SUIM model can call its output, which is in ASCII binary format. This makes it possible for text data to be quickly turned into an ASCII file that the model can read.
2.3. Hydrology Module
2.3.1. SCS Runoff Model
The SCS-CN model is a widely used formula for calculating surface runoff in agricultural watersheds, forests, and urban areas. It was developed by the Soil and Water Conservation Service of the United States Department of Agriculture in the early 1950s to estimate runoff [32,33]. In recent years, it has also been widely used in the field of urban waterlogging simulation and disaster risk assessment [34]. The SCS-CN method mainly depends on the runoff characteristics of the watershed, soil type, land cover type, and pre-moisture degree. In the process of rainfall runoff, vegetation interception, evapotranspiration during the rainy season, infiltration, mid-soil flow, and underground runoff caused by urban surface unevenness are the main losses. Based on an empirical proportionality relationship, the ratio of cumulative surface runoff and infiltration to their corresponding potentials are equal. The key equations in the SCS-CN model are shown as Equations (1)–(3).
where curve number (CN) is an integrated parameter indicating the properties of underlying surfaces; the theoretical range is 1–100, while the actual application range is 40–98. Data analysis in the SCS-CN literature indicated that Ia = 0.2S in suburban and rural areas but Ia = 0.05S in downtown areas. The detailed parameters are described in Table 1.

Table 1.
SCS parameter.
2.3.2. Runoff Coefficient
CN is a dimensionless parameter that is a function of watershed hydrological characteristics, topography, soil texture, land use, and soil moisture before rainfall (Antecedent Moisture Condition, AMC). In the early stage, the value of CN is related to the three conditions of land use type, soil type, and soil moisture. Its size reflects the influence of the underlying surface conditions on the relationship between rainfall and runoff. A high CN value means small infiltration and large runoff, and vice versa. According to the Antecedent Moisture Condition (AMC) of different soil types, each soil condition can be further divided into three categories in SCS-CN, namely, dry (AMCI), normal (AMCII), and wet (AMCIII). As most land coverage composes of artificial hard ground in central Shanghai, this study uses the value under normal soil wet conditions (AMCII), which also follows the previous research [28,35,36]. The artificial hard surfaces such as cement, asphalt, and other urban land in urban and suburban areas are mainly hardened and impervious surfaces with a CN value of over 92. In contrast, suburban arable land and green space are more porous, with a CN value below 86 [27,28]. The CN values defined in this study are shown in Table 2.

Table 2.
SCS-CN value.
2.3.3. Rainstorm Formula and Drainage
The underground drainage pipeline system is considered as primary flood control infrastructure. The 2D hydrodynamic model based on the pipeline system, which is usually hard to be accessed, requires additional processing resources. In the study, the “Shanghai Master Plan 2017–2035” (Shanghai Master Plan 2017–2035) design standard for drainage capacity was used instead of using accurate pipeline data. Many studies assume that the drainage in the catchment area is smooth during rainfall, in which the drainage capacity is uniform [19,27].
Jia et al. [37] compiled a long-duration comprehensive rainstorm formula based on the rainstorm attenuation characteristics, which is suitable for a return period of 2~100 years and an arbitrary duration of 60~1440 min in Shanghai (DB31/T1121—2018). The Shanghai local standard rainstorm intensity formula and design rain pattern standard (DB31/T1043–2017) is a short-duration rainstorm formula that applies to the return period of 2~100 years with a duration of 5–180 min [38]. The expression is as Equation (4):
where and are both designed rainfall intensity, but in liters per second hectare [L/(s•hm2)] and millimeter per second [mm/s], respectively; T is the design return of years (a); and represent rainfall duration, uniting in minutes (min) and hours (h), respectively.
The SUIM judges the rainfall duration to assign the suitable rainfall formula. The “9.13” rainstorm in Shanghai in 2013 lasted 3 h, and the return period was about 100a [39]. The study applied the long-term formula as the condition of the designed drainage capacity in the SUIM model.
2.3.4. Confluence Process
To simplify the confluence process, the model opts for passive inundation and focuses on runoff generation and drainage processes. The main steps are as follows: (1) each sub-catchment, also known as the drainage unit, is responsible for its own independent calculation of the yield run-off; (2) the drainage capacity of each drainage unit is traversed, in which the drainage volume is calculated according to the short duration rainstorm formula; (3) the flooded depth of each grid is simulated by iteration of the finite volume method to form the waterlogging distribution [19]. The confluence volume can be considered as the difference between the production flow rate and the urban design displacement, which is obtained by multiplying the area of the drainage unit. Therefore, Equation (5) can be used to obtain the volume of waterlogged water.
where W stands for the amount of water accumulated in the interior of the drainage unit; Q_i is the runoff of the i-th drainage unit in the study area; V is the drainage volume (calculated according to the urban rainstorm formula); SS is the area of the drainage unit; n is the number of drainage units.
2.4. Inundation Statistics Module
The “China Technical Code for the Urban Flooding Prevention and Control” (GB51222-2017) stipulates that the depth of waterlogging in the road lane shall not exceed 150 mm, and the area above this depth may cause problems of traffic interruption, residents’ travel difficulties, and water ingression into houses. Therefore, the grid with an inundation area of more than 150 mm shall be studied for the statistical analysis of inundation. The SUIM model adopts three indicators: maximum inundation depth, average inundation depth, and 90th percentile average inundation depth, to calculate inundation statistics under each scenario in the study area.
The affected population can be calculated according to the inundation area and depth under each scenario, combined with the population data. The population is derived from the street-level population derived from statistical data, and the number of affected populations can be calculated as follow (Equation (6).
where Pall refers to the total affected population, P is the population at the grid level, counts the number of grids with inundation depth greater than 150 mm, and is the area of the grid.
2.5. Risk Assessment Module
2.5.1. Process of Risk Assessment
The SUIM risk assessment module assesses inundation risk based on three components: hazard, exposure (elements at risk), and vulnerability. The hazard factor should be first calculated for the return period of future rainstorm events. The exposure estimation of the elements at risk is then established by evaluating the exposed assets’ value. The vulnerability assessment is based on the empirical vulnerability curve. Lastly, the inundation risk is assessed via the three components. According to each grid’s flooding depth and depth–vulnerability curve, the vulnerability distribution of the elements at risk and economic loss in the solution district are calculated.
2.5.2. Exposed Value of Assets
Assets of building values and their indoor properties are evaluated as the exposed value of assets in this work. In highly populated areas, buildings at risk had a fraction of their market value since only a proportion of economic assets are exposed to floods, especially in the high-rise building area. The exposed value of assets therefore should not be the total value of the building. In evaluating the maximum possible loss to the structures, the floor area ratio (FAR) was utilized to evaluate the market worth of the buildings, circumventing the absence of data on the number of stories at each level of urban buildings [40]. The FAR can determine the flood area of the structures; therefore, the buildings’ market worth may be evaluated by multiplying the flood area (m2) by the construction cost ($USD/m2). Assumption based on population density and development intensity is addressed using population data [41]. The distribution of FAR and population density in the central urban area reflect the spatial distribution of asset value [19]. The detailed process is seen in Figure 2. SUIM conducts overlapping analysis on waterlogging scenarios with multiple return periods and the value distribution of elements at risk to calculate exposed assets.
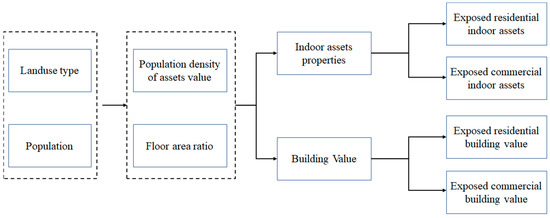
Figure 2.
Exposure of categories of asset value.
2.5.3. Depth–Damage Curve
There are relatively few research contents on correlations between inundation depth and damage rate of flood disasters in Shanghai. Su et al. [42] constructed a land use-based vulnerability classification method and risk discrimination matrix and then analyzed the flood disasters in the Huangpu River Basin. Shi [43] obtained the vulnerability distribution map of street dwellings based on the actual situation of waterlogging distribution in the “Typhoon Matsa” using GIS technology. Researchers have applied the Participatory GIS method to investigate the maximum depth and inundation time of historical waterlogging based on the disaster situation in the community, counted the indoor property loss of each household, and fitted the disaster damage curve of the studied community [44,45]. Ke (2015) [21] constructed the depth–damage rate exposed assets based on the central urban area of Shanghai (including the research area of People’s Square and the Bund). Based on the results of previous studies, this study applied their depth–damage curve to evaluate the vulnerability, as shown in Table 3.

Table 3.
Shanghai depth–damage vulnerability curve.
2.5.4. Loss Evaluation
A comprehensive evaluation of exposure of assets including indoor property, business, and building losses with depth–damage curve.
where
is the total loss in the study region;
is the i-th exposed asset value of the elements at risk; is the j-th loss rate of the elements at risk in different water depth intervals.
2.6. Measure Evaluation Module
SUIM supports parameterization for measure evaluation in applications of engineering scheme implementation and pre-planning of future flood control scenarios. The connection between parameters and various measures needs to be pre-defined before compiling a hydrologic model [46]. For instance, the increase in drainage capacity can be expressed in the drainage layer by modifying the corresponding drainage value at the grid level using Raster Calculator in ArcGIS, and the spatial extent needs to be provided either based on a customization region or default drainage units (sub-catchments). By modifying the values in DEM or CN layers, it is possible to express the changes in buildings’ height or the green space expansion, respectively. Other hydraulic engineers, including a deep tunnel under Suzhou Creek, storage tank and river sluice, etc., can be parameterized in the procedures of runoff and confluence in SCS-CN as well [47]. To evaluate the flood control measures, the inundation statistic is quantified by re-simulation in the baseline scenario in SUIM. For example, the performance of measures of drainage capacity enhancement can be calculated as the loss reduction rate compared to baseline measures under future scenarios.
where
is the flood damage after implementing a flood control measure; accordingly, Performance calculates the reduction rate of loss against its baseline scenario.
3. Study Area and Data
3.1. Study Area
Shanghai has 16 districts with a total area of 6340 km2, including a built-up area of 1237.85 km2, and a permanent population of 24.88 million by the end of 2020. It is one of the most populous estuary cities in the world. It is the largest city in the Yangtze River Delta region, accounting for 3.78% of the country’s gross domestic product (USD 536.1 billion). The average elevation of Shanghai is around 4 m above sea level, with a gently decreasing slope trending from east to west.
Shanghai is easy to be affected by pluvial floods due to the frequent extreme rainstorm events, limited underground drainage capacity, and low-lying elevation. In addition, the amplifying impact of flood risk is significant due to the highly dense population and concentrated assets primarily in the central region. Accordingly, the central urban region of approximately 667 km2 inside Shanghai’s outer ring is chosen as the study area. The “9.13” rainstorm event, which severely influences central Shanghai, is selected as the baseline scenario to evaluate the pluvial flood risk and the performance of adaptation measures. We further constructed future extreme rainstorm scenarios based on return periods and the historic rain gauges’ record in considering spatial distribution. To evaluate the inundation risk and measure’s performance, the increase in drainage capacity is applied in the solution district (70 km2) using SUIM (Figure 3).
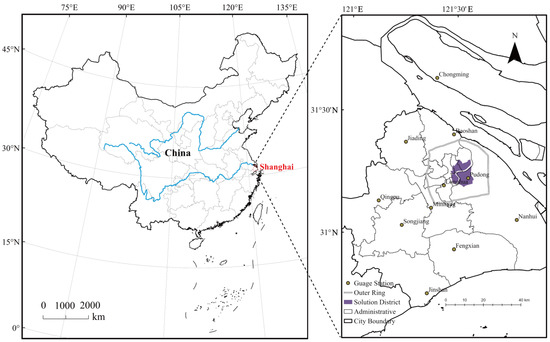
Figure 3.
Study area of central Shanghai and solution district.
3.2. Data
First, we built a geo-database that collected multi-source geographic and social-economic data in PostGIS. The categories of data, which include rainfall, drainage capacity, elevation, socioeconomic statistics, land use, and population, are manipulated into a uniform ASCII-grid format with the same columns and rows using GIS tools.
3.2.1. Rainfall
The hourly rainfall data of 11 meteorological stations in Shanghai, including Xujiahui (representing the central urban area), Minhang, Baoshan, Pudong, Jiading, Nanhui (now part of Pudong New Area), Jinshan, Qingpu, Songjiang, Fengxian, and Chongming, were taken from 16:00 to 19:00 on 13 September 2013. The station observation data are spatially interpolated to the 30 m resolution grid as the precipitation input data of the model. The precipitation data of 11 stations in the central urban area (Longhua Station and Pudong Station) and suburbs districts were collected to study the temporal variation trend and spatial distribution characteristics of each extreme precipitation. As for model simulation verification, this study also used the “110” citizen alarm records showing that of the alarm points’ location and inundated impact.
3.2.2. Drainage Capacity
This study used the 2013 Shanghai drainage capacity data to characterize the design standards of each drainage unit. The study area inside the outer ring was divided into 284 drainage units with an average area of approximately 2.35 km2, in which drainage capacity is designed in three categories. The old-style rainwater and sewage combined pipe network in the main urban area has a design standard of 27 mm/h. Particularly, the low-lying area of the solution district is frequently inundated due to the majority of sewage combined pipelines which are less than the once-a-year designed standard, and the pumping capacity, including separated sewer and storage tank, is urgently being improved [38,48]. Other new drainage units are basically designed in accordance with the standard of once-a-year rainstorm, with a drainage capacity of 36 mm/h. The drainage capacity of the 2010 Shanghai World Expo site is 50 mm/h (Figure 4a). The Urban Rainwater Drainage Plan of Shanghai (2020~2035) stipulates that the area inside the outer ring and the areas outside the outer ring line of Putuo District, Changning District, Xuhui District, and suburban new towns have a design return period of no less than 5 years [49]. Based on this, the study simulates the improvement of Shanghai’s drainage network, selects the low-lying central area as the measured area, improves the drainage capacity to the 5-year return period standard (Figure 4b), and simulates the distribution under the measure scenario.
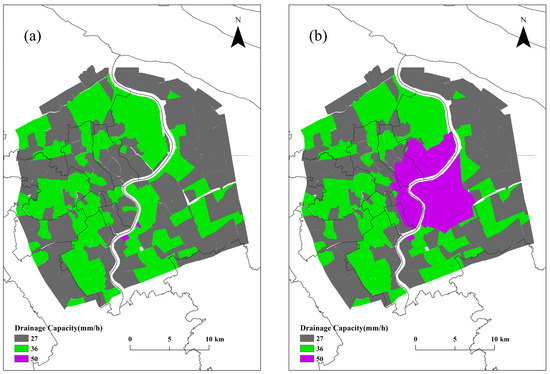
Figure 4.
The drainage capacity of the central urban area of the study area (a) and the capacity of the drainage pipe network enhanced from 27 mm/h to 36 mm/h (b).
3.2.3. Elevation
The digital elevation model (DEM) data in this study have a resolution of 30 m, which is based on detailed observation results of NASA’s earth observation satellite Terra. The relatively lower spatial resolution (30 m) may sacrifice the simulation accuracy at the block level of the micro-scale; however, this compensation is made for the fast-calculation need of the integrated model at the central city level of the meso-scale. On the basis of the source data, the filling of depressions is used to remove some false depressions. The data of residential and commercial types are extracted according to the land use data. Considering that the residential and commercial land generally have a certain step height, we made a correction on the residential and commercial land terrain by adding 150 mm. By doing so, we apply this modification by ArcGIS grid calculator for the land type of residential and commercial.
3.2.4. Land Use
The land use data adopt the remote sensing monitoring data of China’s land use status released in 2015 by the Institute of Geographical Sciences and resources, Chinese Academy of Sciences. The 30 m resolution land use data of Shanghai in the study were selected. They included 9 categories and 32 types of land use. The study re-divided the above categories into 10 types of land use, including industrial and commercial land, new-style residences, and natural villages.
3.2.5. Statistics of Socioeconomic and Population
The data mainly came from the “Shanghai Statistical Yearbook” published by the yearly Shanghai Municipal Bureau of Statistics, including fields of numbers of average household properties and average building construction cost, etc. [47,50]. Population statistics were used to estimate the inundation affection to exposed populations. The population information was gathered from the Sixth National Population Census of China.
3.3. Scenario Setting Up
Taking “9.13” as the baseline scenario, the model simulation and accuracy test were conducted using live rainfall data. We opted for three representative scenarios to enlarge the historic “9.13” extreme event based on the return period of Shanghai’s rainstorm formula, which is composed of low-extreme (200a), medium-extreme (500a), and high-extreme (1000a), taking Pudong Station as examples. Details of scenarios are as follows (Table 4).

Table 4.
Details of extreme rainstorm scenarios in different return periods.
4. Results
4.1. Model Simulation and Validation
SUIM simulation results show that affected by topographic, and drainage capacity, the flooded area caused by rainfall waterlogging during the “9.13” rainstorm mainly occurs in the low-lying areas of central Shanghai. The most inundated depth is above 150 mm, the highest depth of which is over 841 mm. The areas with the maximum inundation depth are near Pudong Century Avenue and Century Park, which is basically consistent with the actual disaster records. As this study filters waterlogging with an inundation depth of less than 150 mm, compared to the “110” alarm data, it demonstrates that even the inundation area of the SUIM model is smaller than the area of alarm data, the spatial distribution of the inundation area is in good agreement with the alarm data (Figure 5a).
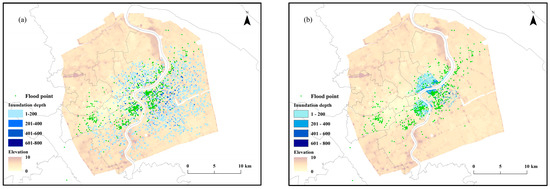
Figure 5.
The validation of ICM InfoWorks (a) and SUIM (b) in simulating historic “9.13” rainstorm events.
To compare the model’s accuracy, this study builds the hydrological model of the study area based on the ICM InfoWorks model to simulate the “9.13” rainstorm inundation. ICM InfoWorks is a hydrodynamic model developed by HR Wallingford Institute, which is a leading professional urban hydrological model. The simulation results show that the spatial distribution is consistent with the alarm data (Figure 5b). By comparing the statistical simulation results of the two models, it is found that the maximum submergence depth is about 800 mm, and the average submergence depth of ICM and SUIM in the study area is 30 mm and 40 mm, respectively. The inundated area of the ICM model is slightly larger than that of the SUIM model because of the removement of the inundated regions lower than 150 mm (Table 5). In all, the average inundation depth of the SUIM model may be slightly higher due to the low waterlogging depth removement, while the maximum waterlogging depth and the inundated area are still reliable under the extreme rainstorm scenario.

Table 5.
Statistics of SUIM and ICM InfoWorks simulation of “9.13” event.
4.2. Risk Assessment
We implemented SUIM to calculate the loss of exposed values based on the “9.13” simulation result of inundation distribution. The simulation process is calculated and counted as both in the study area and solution district, and the result shows that the total loss is 0.82 and 0.49, respectively (Table 6). Given the area of the solution, the district is roughly 0.1 times the study region, and the solution district is obviously more vulnerable due to the high density of assets value and low elevation. Table 6 also shows that indoor property is a major proportion of pluvial flood loss in contrast with loss of building value since the high value in the depth–damage curve.

Table 6.
Statistics of exposed value of elements at risk.
The damage loss estimation is roughly equivalent to the results in related research. For instance, Ke (2015) estimated the flood damage loss of three potential breaching points ranging from 0.11 to 0.56 billion USD within a smaller size of the study area (17.2 km2), which is spatially overlapping with our solution district in central Shanghai [21]. Shan et al. (2021) estimated the flood damage loss under the return periods of 10~1000a in 2010 with a similar simulation size of the area along the Huangpu River in Shanghai, which ranges from 0.15~0.41 to 0.17~0.68 billion USD for the residential land and commercial land, respectively [51].
4.3. Measure Evaluation
In order to evaluate the performance of the improved Shanghai’s drainage network, we evaluate inundation risk by comparing before and after application of the evaluation module. In more detail, the drainage capacity conversion is implemented by modifying the values of grids from 27 mm/h or 36 mm/h to 50 mm/h spatially within the solution district when calling the measure evaluation module (Figure 4). The SUIM initiated the scenarios in the rainfall module and simulated the inundation in two sets of experiments.
The inundation area decreases with a sharp difference between the three pairs of scenarios (Figure 6a–f), showing that the low-extreme scenario (Figure 6b) achieves the best performance of inundation reduction. In contrast, the high-extreme scenario (Figure 6f) still maintains a huge amount of inundated area, and the reduction of inundated area in medium scenario is also not significant (Figure 6d). It also shows that the performance of improved drainage capacity is limited in high-extreme scenario (Figure 6f) since that the inundation area is still at high level which is similar to the performance of baseline drainage capacity in low-extreme scenario (Figure 6a).
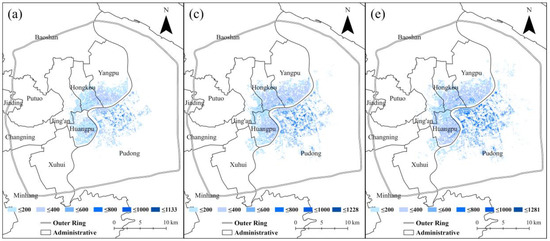
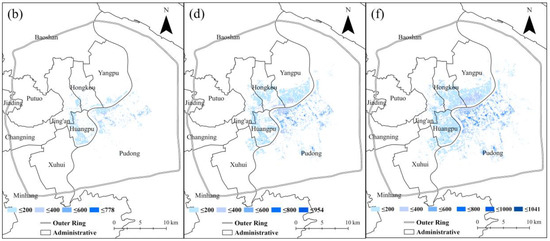
Figure 6.
Comparison of inundation area and depth: (a) low-extreme in test 1, (b) low-extreme in test 2, (c) medium-extreme in test 1, (d) medium-extreme in test 2, (e) high-extreme in test 1, and (f) high-extreme in test 2.
Given that most of the waterlogging was eliminated by the enhanced drainage capacity in the low-extreme scenario, the improvement of drainage capacity played an effective role in alleviating waterlogging. Statistically, the results show that the anomalies of maximum inundation depths are 240 mm, 274 mm, and 355 mm of high-extreme, medium-extreme, and low-extreme in baseline drainage (test 1) compared with the enhanced drainage (test 2), respectively (Table 7). However, for the medium-extreme scenario, the performance of inundation reduction in both average depth (17 mm) and 90-th percentile depth (166 mm) is comparable to high-extreme (17 mm and 148 mm) and low-extreme (14.6 mm and 144 mm).

Table 7.
Statistics under different scenarios by baseline drainage (test 1) and enhanced drainage (test 2) in solution district.
The affected population’s statistical results show a positive correlation between the affected population and the inundation losses under different scenarios. The inundation loss under different scenarios is calculated and counted only in the solution district to compare the performances. The results show that under the current drainage capacity conditions, the loss values under the high-extreme, medium-extreme, and low-extreme scenarios were USD 3.24 billion, 3.08 billion, and 2.46 billion, respectively (test 1). The loss reduction rates under the three scenarios are 30%, 54%, and 80%, respectively, given the enhanced drainage capacity (test 2). It confirms that the enhanced drainage capacity in the low-extreme scenario achieved better risk mitigation capability (30%). In comparison, the mitigation capability was insufficient in the medium-extreme (54%) and high-extreme (80%) scenarios due to the limited reduction of both the inundation depth and area. To this end, the enhancement of drainage capacity performs well in reducing waterlogging in the low-extreme scenario but has a minor effect in medium-extreme and high-extreme scenarios.
5. Discussion and Conclusions
Based on the SCS-CN hydrological model, we developed the SUIM model by integrating rainfall collection treatment, inundation statistics, risk assessment, and measure assessment, which enabled the whole cascade from rainfall scenarios to risk assessment. The model possesses a coherent structure with a simple-logistic yet speedy operation process that can be used for historical rainstorm inundation simulation and retrospective analysis, as well as numerous scenarios involving rapid inundation and risk evaluation of short-term and imminent rainfall forecasts.
Building an integrated urban waterlogging model using SUIM has various benefits. (1) Model data are readily available in cities, particularly in the absence of information on underground pipelines. (2) Two-dimensional simulation is fast and suitable for city-scale simulation, and the model’s accuracy is better than that of the actual situation. (3) The model can optimize the underlying surface conditions, directly reflect the changes in the underlying surface in the relationship between rainfall and runoff, and quantitatively describe the changes in future land use. (4) Model parameters are easy to modify, which can be applied with the expression of adaptive measures to account for the influence of urbanization, land use change, engineering on runoff, etc.
The study simulated the pluvial flood distribution caused by a rainstorm in Shanghai’s outer ring using live rainfall data on 13 September 2013. The result shows that core business and residential districts are the most economically and socially concentrated while also being where the flooding is most likely to occur, resulting in a significant loss of assets and impact on the population. The study assessed the waterlogging risk of low, medium, and high extreme scenarios. It shows that according to the existing defensive measures, there will always be a large inundation risk of waterlogging in low-lying urban areas of the solution district. Although in extreme scenarios, the maximum inundation depth of urban waterlogging was up to 1.5 m, even in low-lying areas in low-extreme scenarios, there will still be more than 1 m of water accumulation. The increased capacity of drainage is proved to be incapable of coping with medium- to high-extreme scenarios due to the huge volume of runoff.
Uncertainties widely exist in future climate change, the social economy, and even decision making, and the complexity of these has not been clearly understood. The influence mechanism of deep uncertainty on complex urban hydrological systems needs to be further discussed. For coastal megacities, the impact of extreme composite flooding disasters caused by rising sea levels and storm surges in combination with astronomically high tides makes it more challenging to maintain urban safety [35]. To mitigate the pluvial and fluvial flooding risk under the rising sea level in the future, non-physical measures, e.g., early warning systems, training of population awareness, and improvement of building codes, are also important options to be quantitatively evaluated in future work. In the future, a lighter WebGIS-based SaaS (software-as-a-Service) online model can be developed to realize massive scenario simulation and visualization, which broadens the application scenarios of the synthesized model and presumably provides technical support for the pluvial floods simulation prediction, assessment of Low Impact Development (LID) measures, and early warning for urban flood mitigation.
Author Contributions
Writing—original draft, visualization, and writing—review and editing, H.H.; software coding—H.Y.; data manipulation—Y.W.; funding acquisition, supervision, and conceptualization—J.W. and M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 42171080, 42171282, and 42001014). The APC was funded by National Natural Science Foundation of China (Grant No. 42171080).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Zhuoran Liang from Hangzhou Meteorological Bureau for his early model coding assistance.
Conflicts of Interest
The authors declare no conflict of interest.
References
- IPCC. Climate Change 2021: The Physical Science Basis, the Working Group I Contribution to the Sixth Assessment Report. Intergovernmental Panel on Climate Change. Available online: https://www.ipcc.ch/report/ar6/wg1/ (accessed on 10 January 2022).
- Hui, P.; Tang, J.; Wang, S.; Niu, X.; Zong, P.; Dong, X. Climate change projections over China using regional climate models forced by two CMIP5 global models. Part II: Projections of future climate. Int. J. Climatol. 2018, 38, e78–e94. [Google Scholar] [CrossRef]
- Westra, S.; Fowler, H.J.; Evans, J.P.; Alexander, L.V.; Berg, P.; Johnson, F.; Kendon, E.J.; Lenderink, G.; Roberts, N. Future changes to the intensity and frequency of short-duration extreme rainfall. Rev. Geophys. 2014, 52, 522–555. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Chen, Y.; Liang, F.; Liu, H. Assessment of future flash flood inundations in coastal regions under climate change scenarios—A case study of Hadahe River basin in northeastern China. Sci. Total Environ. 2019, 693, 133550. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, W.; Hu, C.; Wang, Y.; Wang, Z.; Zhang, X.; Zhu, B.; Cheng, C.; Yin, X.; Liu, B.; et al. Analysis of changes in characteristics of flood and sediment yield in typical basins of the Yellow River under extreme rainfall events. Catena 2019, 177, 31–40. [Google Scholar] [CrossRef]
- Liu, J.; Niyogi, D. Meta-analysis of urbanization impact on rainfall modification. Sci. Rep. 2019, 9, 7301. [Google Scholar] [CrossRef]
- Abadie, L.M.; Jackson, L.P.; de Murieta, E.S.; Jevrejeva, S.; Galarraga, I. Comparing urban coastal flood risk in 136 cities under two alternative sea-level projections: RCP 8.5 and an expert opinion-based high-end scenario. Ocean. Coast. Manag. 2020, 193, 105249. [Google Scholar] [CrossRef]
- Marelle, L.; Myhre, G.; Steensen, B.M.; Hodnebrog, Ø.; Alterskjær, K.; Sillmann, J. Urbanization in megacities increases the frequency of extreme precipitation events far more than their intensity. Environ. Res. Lett. 2020, 15, 124072. [Google Scholar] [CrossRef]
- Schwierz, C.; Köllner-Heck, P.; Zenklusen Mutter, E.; Bresch, D.N.; Vidale, P.L.; Wild, M.; Schär, C. Modelling European winter wind storm losses in current and future climate. Clim. Chang. 2010, 101, 485–514. [Google Scholar] [CrossRef]
- Wu, P.; Christidis, N.; Stott, P. Anthropogenic impact on Earth’s hydrological cycle. Nat. Clim. Chang. 2013, 3, 807–810. [Google Scholar] [CrossRef]
- Aerts, J.C.J.H.; Lin, N.; Botzen, W.J.W.; Emanuel, K.; De Moel, H. Low-probability flood risk modeling for New York City. Risk Anal. 2013, 33, 772–788. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Ghanbari, M.; Arabi, M.; Obeysekera, J.; Sweet, W. A coherent statistical model for coastal flood frequency analysis under nonstationary sea level conditions. Earth’s Future 2019, 7, 162–177. [Google Scholar] [CrossRef]
- Shanghai Climate Center. Shanghai Climate Change Monitoring Bulletin; Shanghai Climate Center: Shanghai, China, 2021. [Google Scholar]
- Liang, P.; Ding, Y. The long-term variation of extreme heavy precipitation and its link to urbanization effects in Shanghai during 1916–2014. Adv. Atmos. Sci. 2017, 34, 321–334. [Google Scholar] [CrossRef]
- Chen, H.-P.; Sun, J.-Q.; Li, H.-X. Future changes in precipitation extremes over China using the NEX-GDDP high-resolution daily downscaled dataset. Atmos. Ocean. Sci. Lett. 2017, 10, 403–410. [Google Scholar] [CrossRef]
- Wu, W.; Liang, Z.; Liu, X. Projection of the daily precipitation using CDF-T method at meteorological observation site scale. Plateau Meteorol. 2018, 37, 796–805. (In Chinese) [Google Scholar]
- He, F.; Hu, H.; Dong, G. Compound Flooding Simulation and Prediction of Future Recurrence in Shanghai Downtown Area. J. Catastrophology 2020, 35, 93–98, 134. (In Chinese) [Google Scholar]
- Hu, H. Robust Decision Making in Mitigating Pluvial Flood Risk under Climate Change Scenarios—A Case Study of Shanghai; Shanghai Normal University: Shanghai, China, 2021. [Google Scholar]
- Li, W.; Wen, J.; Xu, B.; Li, X.; Du, S. Integrated assessment of economic losses in manufacturing industry in Shanghai metropolitan area under an extreme storm flood scenario. Sustainability 2019, 11, 126. [Google Scholar] [CrossRef]
- Ke, Q. Flood Risk Analysis for Metropolitan Areas—A Case Study for Shanghai. Ph.D. Dissertation, Technology of Delft University, Delft, The Netherlands, 2015. [Google Scholar]
- Wang, J.; Yi, S.; Li, M.; Wang, L.; Song, C. Effects of sea level rise, land subsidence, bathymetric change and typhoon tracks on storm flooding in the coastal areas of Shanghai. Sci. Total Environ. 2018, 621, 228–234. [Google Scholar] [CrossRef]
- Zhang, M.; Dai, Z.; Bouma, T.J.; Bricker, J.; Townend, I.; Wen, J.; Zhao, T.; Cai, H. Tidal-flat reclamation aggravates potential risk from storm impacts. Coast. Eng. 2021, 166, 103868. [Google Scholar] [CrossRef]
- Shan, X.M.; Du, S.Q.; Wang, L.Y.; Li, W.J.; Hu, H.Z.; Wen, J.H. Flood risk dynamics and adaptation analyses for coastal cities based on internet big data and hydrology-hydrodynamic models. Chin. Sci. Bull. 2021, 66, 1–13. [Google Scholar] [CrossRef]
- Bulti, D.T.; Abebe, B.G. A review of flood modeling methods for urban pluvial flood application. Model. Earth Syst. Environ. 2020, 6, 1293–1302. [Google Scholar] [CrossRef]
- Fan, F.L.; Deng, Y.B.; Hu, X.F. Estimating Composite Curve Number Using an Improved SCS-CN Method with Remotely Sensed Variables in Guangzhou, China. Remote Sens. 2013, 5, 1425–1438. [Google Scholar] [CrossRef]
- Du, S.; Wang, C.; Shen, J.; Wen, J.; Gao, J.; Wu, J.; Lin, W.; Xu, H. Mapping the capacity of concave green land in mitigating urban pluvial floods and its beneficiaries. Sustain. Cities Soc. 2019, 44, 774–782. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, M.; Wen, J.; Du, S.; Xu, H.; Wang, L.; Yang, Y. A simple GIS-based model for urban rainstorm inundation simulation. Sustainability 2019, 11, 2830. [Google Scholar] [CrossRef]
- Wang, C.; Du, S.; Wen, J.; Zhang, M.; Gu, H.; Shi, Y.; Xu, H. Analyzing explanatory factors of urban pluvial floods in Shanghai using geographically weighted regression. Stoch. Environ. Res. Risk Assess. 2017, 31, 1777–1790. [Google Scholar] [CrossRef]
- Xie, J.; Chen, H.; Liao, Z.; Gu, X.; Zhu, D.; Zhang, J. An integrated assessment of urban flooding mitigation strategies for robust decision making. Environ. Model. Softw. 2017, 95, 143–155. [Google Scholar] [CrossRef]
- Wang, X.; Xia, J.; Dong, B.; Hou, J.; Li, Q. Simulation of urban flood using the SWMM with the hierarchical catchment partition method. Adv. Water Sci. 2022, 33, 196–207. (In Chinese) [Google Scholar]
- USDA SCS. Urban hydrology for small watersheds. Tech. Release 1986, 55, 2–6. [Google Scholar]
- Cronshey, R.G.; McCuen, R.H.; Miller, N. Urban Hydrology for Small Watersheds; USDA, Soil Conservation Service: Washington, DC, USA, 1986; p. 164. [Google Scholar]
- Yin, Z.E.; Yin, J.; Xu, S.; Wen, J. Community-based scenario modelling and disaster risk assessment of urban rainstorm waterlogging. J. Geogr. Sci. 2011, 21, 274–284. (In Chinese) [Google Scholar] [CrossRef]
- Hu, H.; Tian, Z.; Sun, L.; Wen, J.; Liang, Z.; Dong, G.; Liu, J. Synthesized trade-off analysis of flood control solutions under future deep uncertainty: An application to the central business district of Shanghai. Water Res. 2019, 166, 115067. [Google Scholar] [CrossRef]
- Quan, R.; Liu, M.; Hou, L.; Lu, M.; Zhang, J.L.; Ou, D.N. Impact of land use dynamic change on surface runoff: A case study on Shanghai Pudong New District. J Catastr. 2009, 24, 44–49. [Google Scholar]
- Jia, W.; Xu, W.; Li, Q.; Zhou, Z. Study on long duration comprehensive rainstorm formula based on rainstorm attenuation characteristics in Shanghai. Adv. Water Sci. 2021, 32, 211–217. [Google Scholar] [CrossRef]
- DB31/T 1043-2017; Shanghai Local Standard—Rainstorm Intensity Formula and Design Rain Pattern Standard. Shanghai Quality and Technical Supervision Bureau: Shanghai, China, 2017.
- Zhang, Q.; Zhang, J.; Tan, Q. Upgrading plan of the existing drainage system in Shanghai City. Water Wastewater Eng. 2014, 50, 21–25. (In Chinese) [Google Scholar]
- Pan, X.-Z.; Zhao, Q.-G.; Chen, J.; Liang, Y.; Sun, C. Analyzing the variation of building density using high spatial resolution satellite images: The example of Shanghai City. Sensors 2008, 8, 2541–2550. [Google Scholar] [CrossRef]
- Green, C.H. Coastal Cities: Assets at Risk and Depth-Damage Curves; Report Prepared for the OECD; Middlesex University: London, UK, 2010. [Google Scholar]
- Su, F.; Yin, J.; Yin, Z.; Yu, D.; Xu, S. Variation Analysis of Flood Dynamic Risk in Huangpu River Basin. Sci. Geogr. Sin. 2014, 34, 621–626. (In Chinese) [Google Scholar]
- Shi, Y. The vulnerability assessment of residences in rainstorm waterlogging in cities: A case study of shanghai. J. Catastrophol. 2015, 30, 94–98. [Google Scholar]
- Wen, J.H.; Huang, H.; Chen, K.; Ye, X.L.; Hu, H.Z.; Hua, Z.Y. Probabilistic Community-based Typhoon Disaster Risk Assessment: A Case of Fululi Community, Shanghai. Sci. Geogr. Sin. 2012, 32, 348–355. (In Chinese) [Google Scholar]
- Yin, J.; Yin, Z.E.; Yu, D.P.; Xu, S.Y. Hazard analysis of extreme storm flooding in the context of sea level rise: A case study of Huangpu river basin. Geogr. Res. 2013, 32, 2215–2221. (In Chinese) [Google Scholar]
- Rengers, F.K.; McGuire, L.A.; Kean, J.W.; Staley, D.M.; Youberg, A.M. Progress in simplifying hydrologic model parameterization for broad applications to post-wildfire flooding and debris-flow hazards. Earth Surf. Process. Landf. 2019, 44, 3078–3092. [Google Scholar] [CrossRef]
- Shanghai Municipal Water Authority. Shanghai Municipal Rain Drainage Plan (2020~2035). 2020. Available online: http://swj.sh.gov.cn/gsgg/20200915/90c7d3d1ded940bfb397b3525932228c.html (accessed on 20 February 2022).
- Shanghai Urban Planning and Land Resource Administration Bureau, 2018. Shanghai Master Plan 2017–2035. Available online: http://www.shanghai.gov.cn/newshanghai/xxgkfj/2035004.pdf (accessed on 15 February 2022).
- Shanghai Municipal Government, The 13th Five-Year Plan of Shanghai on Water Resource Protection and Utilization and Flooding Control, 2017. (In Chinese). Available online: http://hyj.sh.gov.cn/ghjhua/20211021/b8ab2e3b0072460f8ccb4f2110d34a98.html (accessed on 25 March 2020).
- Statistic Year Book of Shanghai, 2013; Shanghai Statistics Bureau: Shanghai, China, 2013. (In Chinese)
- Shan, X.; Yin, J.; Wang, J. Risk assessment of shanghai extreme flooding under the land use change scenario. Nat. Hazards. 2021, 110, 1039–1060. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).