1. Introduction
The generation and operation of hydropower plants are highly dependent on weather conditions in the particular location of the reservoirs. To efficiently utilize hydropower, it is, therefore, necessary to have an inflow forecast. Prior knowledge about the reservoir inflow would help manage the water resource properly throughout the year. Otherwise, in case of a low inflow year, the water in the reservoirs might be used up before the next rainy season, and the reservoirs will be empty. Consequently, there will be a lot of load shedding until the reservoirs fill up again, which can also affect the start content of the reservoirs for the next planning period. On the other hand, in case of an unexpectedly high inflow year, we may end up spilling much water, and reservoirs could also be flooded.
In Ethiopia and many other countries in East Africa, hydropower is the dominant source of electric power. According to the international hydropower association (IHA) 2022 hydropower status report, Africa’s energy generation by hydropower is 146 TWh in 2021, 21% of this generation being from Eastern African countries, of which 45% is from Ethiopia [
1]. Most of the inflow is during the rainy season, July to September (
Kiremt).
The water in the rainy season is stored in large reservoirs to be distributed over the remaining part of the year until the next rainy season comes again. Therefore, hydropower planners need inflow forecasts for at least one year with a sufficient time resolution. However, the challenge is the limited availability of necessary data. For example, there are no accurate water inflow measurements for each reservoir. Therefore, there is a need to develop a method to randomly generate realistic inflow scenarios from the available data sets, including hydropower generation data and satellite precipitation measurements.
Hydrologists use watershed models to estimate stream flow, surface run-off, water quality, flood management, and water management. The review of different watershed modeling, the use of AI techniques, artificial neural networks (ANNs), fuzzy logic (FL), genetic algorithms (GAs) to improve upon or replace traditional physically-based watershed modeling techniques, and detailed discussions of individual watershed models are presented in [
2]. The precipitation-runoff modeling system (PRMS) is one of the watershed modeling software used to simulate precipitation and snow melt-driven movement of water to produce the daily system response and streamflow for a basin [
3]. PRMS is applied to simulate rainfall runoff in the Zamask–Yingluoxia subbasin of the Heihe River Basin in [
4]. The current and future geographic information systems (GIS) trends and remote sensing technologies in watershed modeling are reviewed in [
5]. It is demonstrated in [
6] that the surface water assessment tool (SWAT) provides a better streamflow estimate with Next Generation Weather Radar (NEXRAD) precipitation input than rain gauge inputs. The accuracy of the model results suggests that NEXRAD is a good alternative to rain gauge data and can be extremely valuable in large watersheds without readily available rain gauge data. In order to utilize the watershed modeling tools, for example, SWAT, we need to have input about soil, land use and management, elevation, and daily rainfall to predict daily stream flow. In addition, we need expert knowledge of hydrology and the use of watershed models, which is beyond the scope of this research work.
There are other methods proposed in the literature that generate random time series, for example, stochastic processes. In [
7], a stochastic process estimation based on the concept of aggregation is presented, and the aggregation of periodic autoregressive (PAR) and periodic autoregressive-moving average (PARMA) models for the seasonal and annual flows of the Niger river are used to illustrate the concept. Inflow is modeled as a stochastic variable by first-order autoregressive model AR(1) in [
8] for a stochastic dual dynamic programming (SDDP) to solve optimal medium-term scheduling in the Norwegian hydropower system. In [
9], a non-parametric simulation model is applied to generate synthetic monthly flows from the Beaver River, Australia. A maximum likelihood procedure for estimating the PARMA model of a monthly average river flows time series is presented in [
10]; the Kalman filtering algorithm is used to estimate the parameters. A non-linear periodic autoregressive model (PAR(p))scenario generation method based on the vine copula model is presented in [
11]; the method incorporates a time dependence more than lag-one, unlike the copula-based models. A monthly stream flow simulation method based on the vine copula model is proposed in [
12] for a catchment of the Yellow River basin upstream of the Tangnaihai hydrological station in the north of China. The ARFIMA model, an extension of the Box–Jenkins family, where the differentiation can take fractional values to capture the long-memory effect present in the time series, is used in [
13] for generating synthetic hydrological scenarios for the Brazilian hydropower system.
However, almost all of the methods described in the literature are based on well-recorded and organized historical data. In the case of the Ethiopian hydropower system, and most African hydropower systems, where there is a significant gap in the availability of organized data, it is necessary to derive a method to generate synthetic historical series.
Therefore, the first contribution of this paper is to derive a method for generating a synthetic historical time series by combining the available data in hand. The second contribution is to generate realistic inflow scenarios by applying existing methods to identify the stochastic process that mimics the synthetic historical time series. The method is applied to the Ethiopian power system. Finally, the paper demonstrates how the generated scenarios can be applied in Ethiopia’s long-term deterministic hydropower planning model.
This paper is organized as follows.
Section 2 presents the materials and methods for deriving the historical time series, the time series analysis, and stochastic model estimation. Then, the study results, synthetic historical time series, scenario generation, and evaluation of the generated inflow scenarios using the deterministic model are presented and discussed in
Section 3. Finally,
Section 4 concludes the work.
3. Result and Discussion
This section discusses the results of the study based on the steps followed in the methodology. The objectives of this study are to derive the synthetic historical inflow time series, perform time series analysis, and estimate the stochastic model that best fits the synthetic series and generate realistic inflow scenarios that can be used in hydropower planning models.
3.1. Synthetic Historical Inflow Time Series
The synthetic historical inflow time series for the past ten years, from 1 July 2010 to 30 June 2020, is derived in a daily time resolution for each reservoir.
Figure 7 shows the aggregate inflow time series of all the reservoirs per year in a daily time resolution.
As can be seen from the figure, there are seasonal variations in the inflows. Most of the reservoirs obtain a considerable inflow during the same season. The reservoirs’ geographical location variations create slightly different precipitation patterns.
In general, all reservoirs obtain considerable rain in the rainy season, July–September, and attain their maximum levels around September and October. When we compare the actual water level, and the synthetic inflows for Gibe 1 and Tekezé reservoirs using historical water levels and synthetic inflows for 2015–2016 and 2018–2019, as shown in
Figure 8, the water levels of Gibe 1 in 2015–2016 and 2018–2019 have almost similar patterns. The maximum level is at the beginning of September for both years, and it starts dropping from October throughout the dry season; the water level reaches its lowest point around April for 2015–2016 and around mid-may for 2018–2019. After that, the level starts rising relatively fast, starting from the end of April on the blue curve and rising relatively slowly from June on the red curve. It can be seen from the same figure that there is a high inflow from July to October in both years, and the inflow starts to lower from November, with very little inflow in the dry seasons in both years. In the dry season, the inflow was better in 2018–2019 than in 2015–2016. However, at the end of the planning year, i.e., from May to June, we saw a higher inflow in 2015–2016 than in 2018–2019, which corresponds to the water level pattern of each year.
The Tekezé reservoir water level for 2015–2016 and 2018–2019 in
Figure 8 have similar patterns but there are big differences in water levels between the two years. When we compare the increase in the water level from July to September and the inflow for the same time, we can see that In 2015–2016 (blue curve), the level increase is only around 6 m.a.s.l, which corresponds to the lower inflow. On the other hand, in 2018–2019 (the red curve), the level increase is around 15 m.a.s.l during the same time, which corresponds to the higher inflow. Therefore, the inflow can justify the variation of the water levels for the two different years; in 2018–2019, the Tekezé reservoir had the highest rainfall in August and September and a small inflow throughout the dry season. On the other hand, in 2015–2016, the year started with a low water level, and it had lower inflow during the wet and dry seasons.
Water levels and inflows varied in a logical pattern in the two reservoirs, which held for the rest of the reservoirs, implying that the generated time series are realistic. Therefore, we can further analyze the developed inflow time series to estimate the stochastic process and generate a random but realistic inflow scenario.
3.2. Scenario Generation
We simulate sample realizations of random scenarios from the estimated SARIMA models, applying the Monte Carlo simulation using the synthetic time series and the inferred residuals as pre-sample data. Fifty different paths for two years of observation were generated for both time resolutions.
3.2.1. Daily Time Resolution
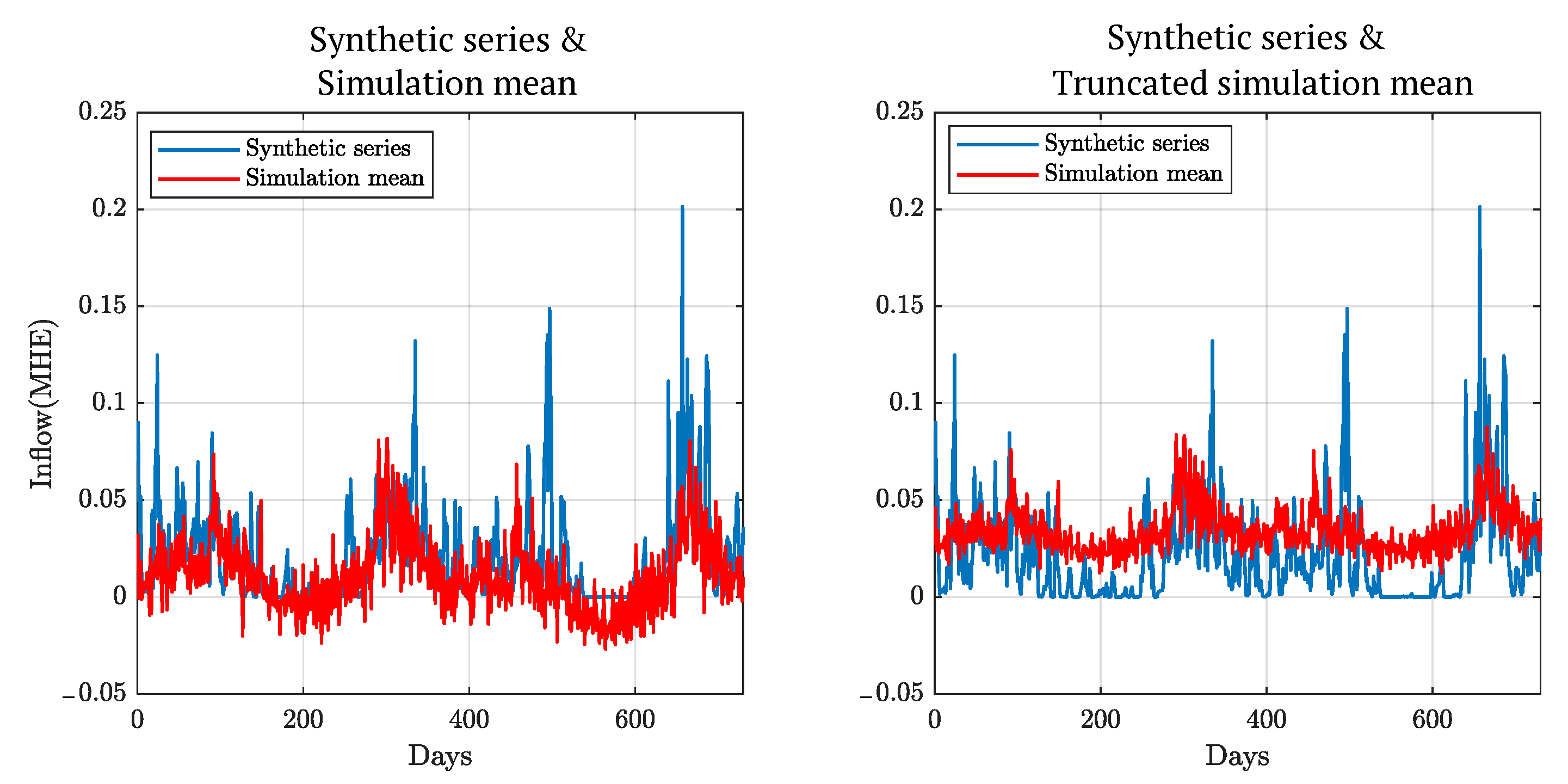
The simulation results in
Figure 6 on the left-hand side show that the model captures the seasonal variation of the inflow series and follows the same pattern as the synthetic time series. It can be noted that the simulation does not have the large peaks seen in the synthetic time series. Moreover, the simulation mean goes down to the negative value when the synthetic inflow is at its minimum; this means there are negative inflows during specific periods, even if there is no negative inflow in the synthetic series. It is not realistic to have negative values for the inflow scenario. These unrealistic results are mainly due to the assumption of a Gaussian distribution in the ARIMA model estimation and the Monte Carlo sample values in the range of (
to
). Therefore, we removed the negative values from the generated scenarios by truncating the negative values to zero. The right-hand side of
Figure 9 shows the synthetic time series and the mean of truncated inflow scenarios; when we compare the two curves, the simulation mean tends to the positive trough out the time of simulation because the truncation process significantly affects the simulation mean.
We can conclude that the sample realizations of the random series generated from the daily time resolution are not realistic scenarios and would not transform the features in the synthetic series to a random, future scenario.
3.2.2. Weekly Time Resolution
The simulation result in
Figure 10 on the left-hand side shows that the simulation mean has an almost similar pattern to the synthetic series. There are two points where the mean becomes negative, indicating the presence of a negative inflow in the generated series. The figure on the right-hand side shows the synthetic series with the mean of the truncated inflow series; the result shows a slight upward shift in the simulation mean. However, the approximation effect is much less for the series in the weekly time resolution.
When we compare the simulation mean of the two data sets, in
Figure 9 and
Figure 10, we can see that the model in the weekly time series best captures the behavior of the synthetic time series; moreover, the effect of the truncation is less visible in the weekly resolution. Therefore we can conclude that the scenarios generated from the weekly resolution time series best capture the features in the synthetic historical series.
3.3. Evaluation of the Generated Inflow Scenarios
Random inflow scenarios could be used for long-term hydropower planning using stochastic models; however, this is beyond the scope of this paper. To verify that the scenarios are useful as inputs for hydropower planning problems, they will be tested in a deterministic model presented in [
14]. The deterministic simulation model is a model used to maximize the value of stored water and minimize load shedding by utilizing the water stored in the rainy season throughout the dry season with optimized water management. The objective here is to simulate the model with the random inflow realizations and see if we can obtain a reasonable generation scheduling, acceptable load shedding, realistic reservoir level patterns, and realistic spillage compared to the actual operation in the Ethiopian power system.
Fifty scenarios have been created using the model with weekly time resolution. In case 1, the inflow is equal to the mean of all these scenarios; case 2 uses the scenario with the highest total inflow, and case 3 uses the scenario with the lowest total inflow. A load demand equal to the actual demand in 2018–2019 is considered for all of the simulations. The simulation results from the three cases are compared to the actual planning of the Ethiopian power system in 2018–2019.
The three cases of inflow scenarios and the synthetic inflow in the 2018–2019 planning year in the weekly time resolution are shown in
Figure 11.
The deterministic hydropower model uses a time resolution of one hour. Therefore the inflows in weekly time resolution shown in
Figure 11 are converted to hourly resolution so that any hour is assumed to be 1/168 of the corresponding weekly inflow.
Figure 12 shows the comparison between the simulation results of generation and load shedding for case 1 and the actual operation in the 2018–2019 planning year, respectively.
The simulation result for the generation and load shedding shows that the model supplies the demanded load with zero load shedding. However, load shedding is observed when there is higher load demand around October and toward the end of the year in the actual operation.
The actual hydropower operation in the Ethiopian power system depends on each reservoir’s historical generation and historical water level trends. In contrast, the model will distribute generation arbitrarily between hydropower plants as long as no reservoir limits are exceeded.
Figure 13 shows the generation scheduling in the actual and simulated operation for ten days in April, when we can see a load shedding in the actual operation and zero load shedding in the simulation.
The figure shows that the actual operation follows the same generation pattern each day, the Gibe 3 reservoir supplies the variation in the load, and the smaller reservoirs have the same generation level; consequently, we see a lot of load shedding during this time of the planning year. However, the model is expected to perform better than the actual operation since it has the perfect information. Therefore, the model schedules the generation arbitrarily between the reservoirs in the simulation to minimize load shedding and maximize stored water.
In
Figure 14, we can see sample reservoirs’ start and final content for actual and simulated operations, which are at the same levels for most reservoirs except the Gibe 3 reservoir. Let us compare the synthetic historical inflow and the inflow scenario. The inflow is slightly higher in the average scenario (12.17 million HE compared to 11.15 million HE in the synthetic scenario for 2018–2019). However, on the other hand, the amount of stored water is around 1.1 million HE higher in the simulated operation of the average scenario compared to the actual operation in 2018–2019. This indicates that the load shedding in 2018–2019 was not because there was insufficient water but because the water was not used efficiently. In practice, water must have been spilled during the earlier rainy seasons. Unfortunately, there are no records of spillage from Ethiopian hydropower plants which can confirm this conclusion.
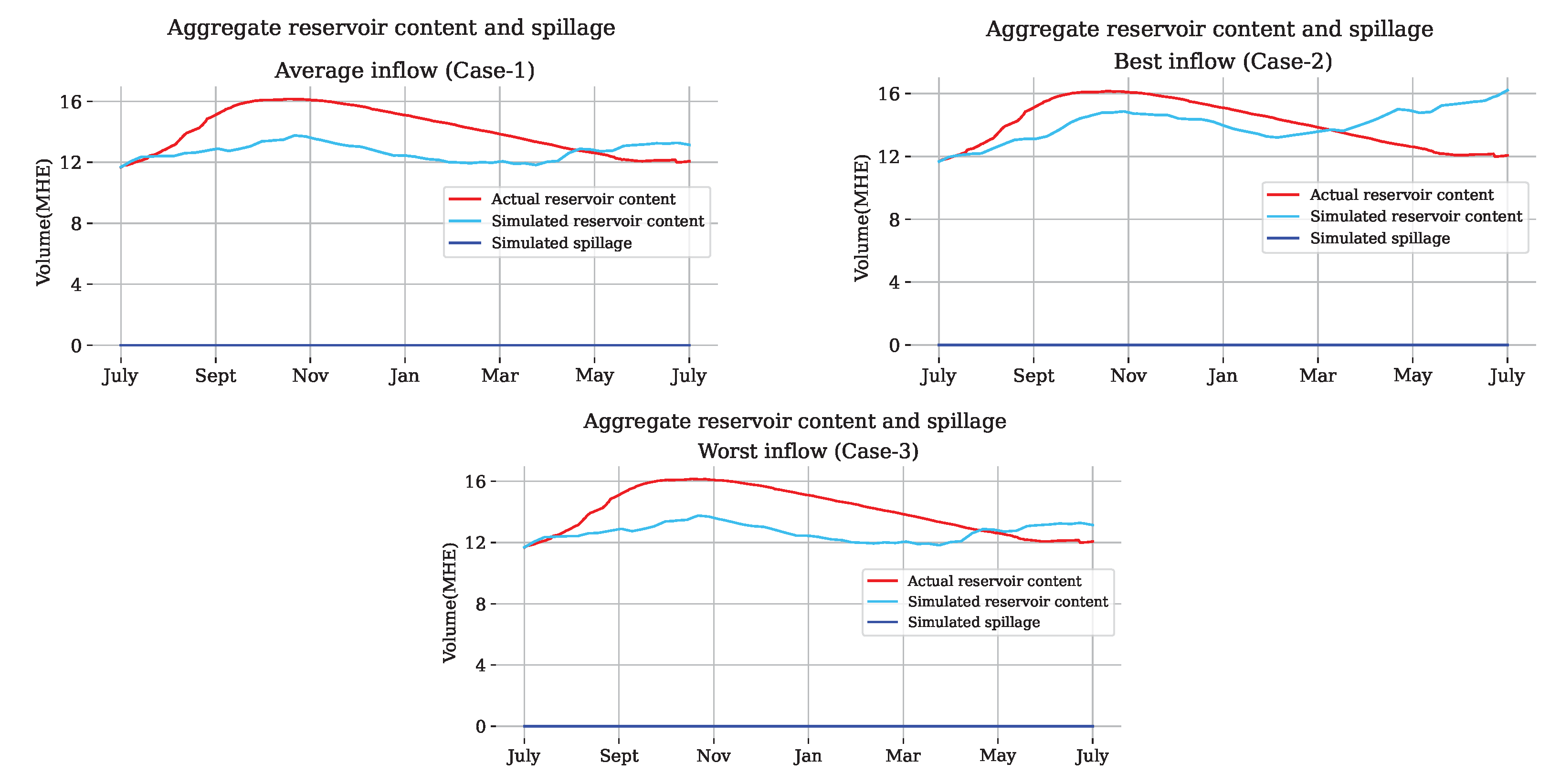
If the inflow scenarios were unrealistic, we could, for example, have periods with full reservoirs (due to inflow peaks) and spillage, or we could have periods with empty reservoirs and plenty of load shedding. However, no such problems are experienced in the simulation of all three cases, as presented in
Figure 15. The figure shows the aggregate reservoir contents in the actual and simulation of the three cases and the corresponding simulated spillage trough out the year. However, we could not compare the actual spillage in reality with the simulation result because there is no data available to compare.
Therefore, we can conclude that the random inflow scenarios generated are good enough to obtain realistic results. From a long-term perspective, it would be more efficient to use planning tools taking into account forecasts rather than the existing rules of thumb or following historical generation trends.
4. Conclusions and Recommendations
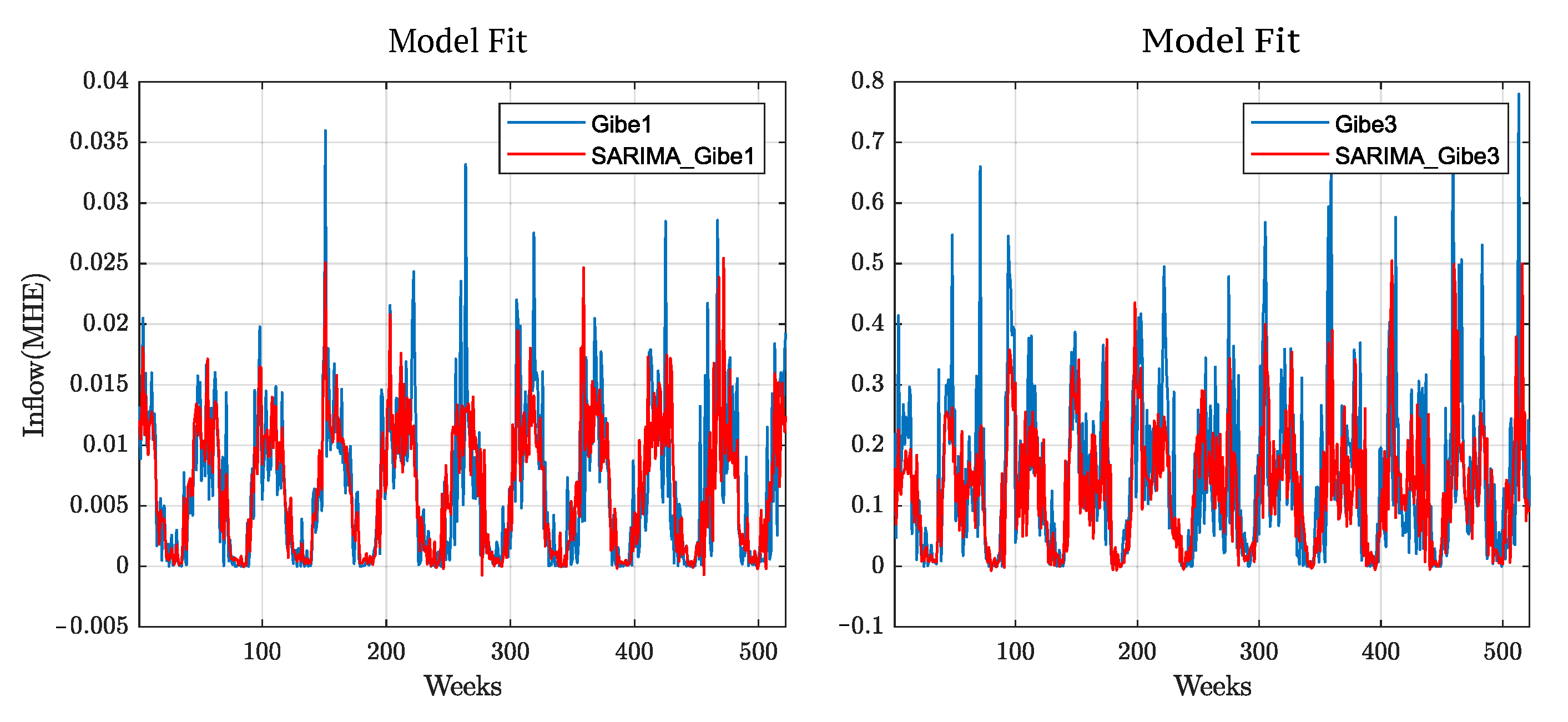
This paper presents a method to develop a synthetic historical inflow time series by combining hydropower generation data and satellite precipitation measurement. The identification of the stochastic process and inflow scenario generation is also presented. With the proposed methods, we can generate two sets of synthetic historical time series with daily and weekly time resolutions from the limited available data. We have shown that existing methods can be applied to identify the stochastic process and generate realistic inflow scenarios for the Ethiopian power system considering the limited data available. We use the Box–Jenkins family of stochastic process estimation models to perform the time series analysis and estimate the stochastic process of each reservoir. In addition, we used the seasonal ARIMA model to estimate the stochastic process and consider the seasonality of 365 for the daily resolution and 52 for the weekly resolution. We observed that, even if these data sets are extracted from the same synthetic historical time series, the time series in the daily time resolution are all non-stationary, seasonal integrated moving average stochastic processes, for example, SARIMA(0,1,2)(0,1,2)[730] for Gibe 1. On the contrary, the time series with weekly time resolutions are all stationary seasonal autoregressive processes of various orders. SARIMA(3,0,0)(3,0,0)[104] for Gibe 1.
The Monte Carlo simulation is used to generate the scenarios from the fitted stochastic models for both data sets. The simulation means from both data sets follow the synthetic historical time series pattern. However, the Gaussian assumption in the ARIMA models and the Monte Carlo sample values in the range ( to ) create a sample with negative inflow values. The problem is mitigated by truncating the negative values to zero. However, this affects the value of the simulation mean, which was significant in the daily time resolution and less significant in the weekly time resolution. Consequently, the time series with daily time resolution overestimates the inflows and misses some peak points from the synthetic series. In contrast, the time series with the weekly resolution best captures the characteristics of the synthetic historical time series and can generate realistic random scenarios. The evaluation of the inflow scenarios indicates that they are good enough to generate reasonable results.
These random inflow scenarios can be used in future works to apply stochastic planning models for hydropower in Ethiopia and other countries. Better planning tools can improve the utilization of hydropower in order to minimize generation costs and load shedding.
If Ethiopia is going to have a modern power system, a detailed hydrological model is necessary; it is not currently in place. A long-term objective to develop such a model is recommended. It could be part of future research work to compare the simplified model with what we could do if we had a detailed hydrological model. We also recommend temporal and spatial correlations in inflows for reservoirs in related locations, considering the correlation between inflow and wind speed, as there might be an expansion of wind power generation in the Ethiopian power system in the future.