The Revised Curve Number Rainfall–Runoff Methodology for an Improved Runoff Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Validity of the Linear Correlation (Ia = 0.2S) and Introduction of Ia = Sλ
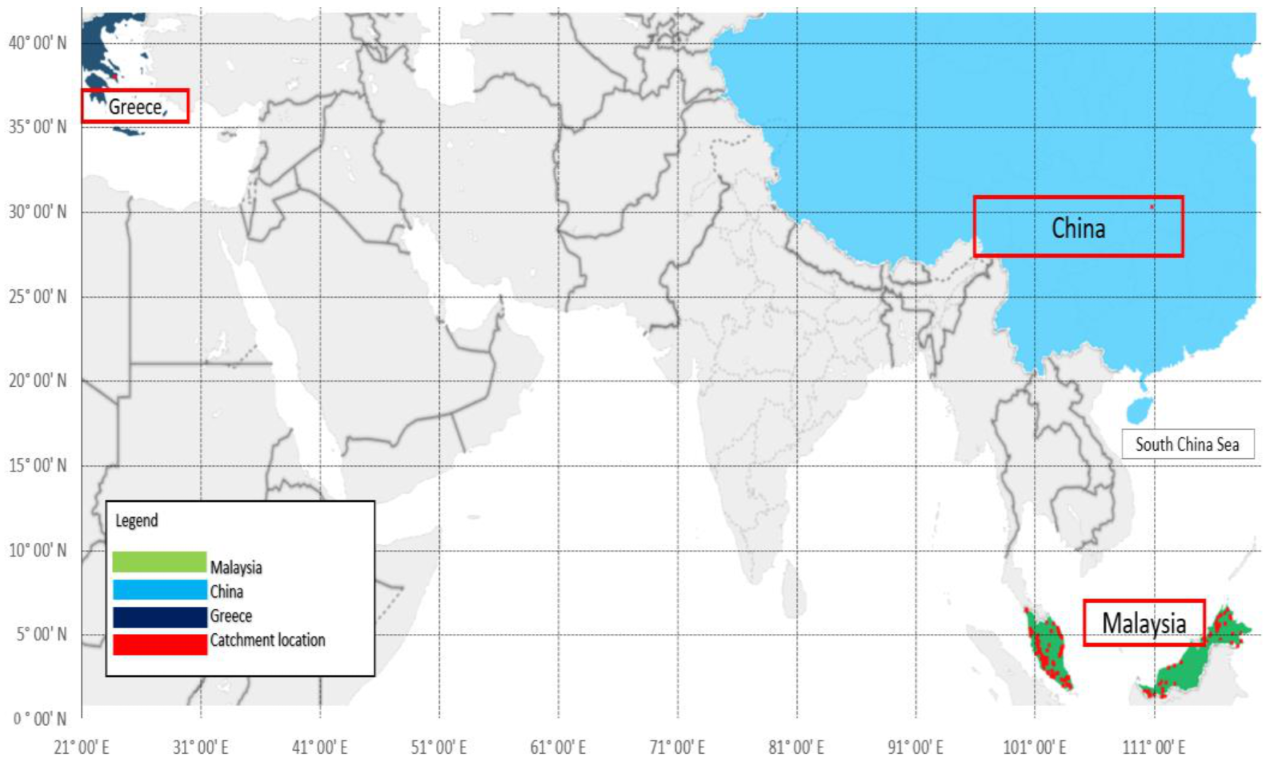
2.2. Study Site and Models’ Performance
3. Results
3.1. Study Site and Models’ Performance
3.2. Derivation of Curve Number and Its Confidence Interval
4. Discussion
4.1. Validity of the Linear Correlation (Ia = 0.2S) and Introduction of Power Regression (Ia = Sλ)
4.2. Application of the Power Regression Model at Different Study Sites
4.3. Application of Machin-Learning Techniques to the Rainfall Runoff Model
5. Conclusions
- The linear correlation hypothesis (Ia = 0.2S) proposed by the SCS was found to be statistically invalid, even in the 1954 original dataset. Therefore, it is important to revise the current conventional SCS runoff prediction model to better prepare for the challenges posed by climate change conditions. The use of Ia = 0.2S to simplify equation (1) into the conventional SCS runoff model (equation 2) may have been an oversight in 1954. The power correlation equation (Ia = S0.111 or Ia = S0.112) should be used to simplify the 1954 SCS runoff model equation (1) and derive the runoff predictive model, as the original SCS dataset was plotted on a log–log graph.
- The newly proposed power regression model (Ia = Sλ) demonstrates good runoff prediction ability at different study sites, including those in Malaysia, Greece, and China. The calibrated SCS rainfall–runoff model based on the proposed power regression model is promising for modelling the rainfall–runoff characteristics of different watersheds in different countries. The ratio of Ia to S for all study sites is mostly 5% or lower, which is in line with past worldwide study results and much lower than the value of 0.2 (20%) as suggested by the SCS.
- There is concern about the use of the original form of the SCS CN model in education, as it may teach students an oversimplified and potentially inaccurate model for predicting runoff, which could have serious consequences for fields such as water resource management, environmental science, and civil engineering. There is also concern about the widespread use of the original form of the model in educational materials, such as textbooks, software, and government agency handbooks and trainings, which may perpetuate the use of an oversimplified and potentially inaccurate model for predicting runoff.
- The proposed methodology has several limitations, including the need for a minimum sample size of at least 20 data pairs to obtain meaningful inferential results and the reliance on the bootstrap BCa method to produce confidence intervals for key variable optimization and the formulation of a new runoff predictive model. The statistical software used must also include the bootstrap BCa method as an option. There are several areas of research that have not been explored in this manuscript due to financial and time constraints. Future studies will examine the potential impacts of the proposed model on flood risk, financial losses caused by flooding, and its potential for downstream development and wider application.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
- Given that the effective rainfall (Pe) = P − Ia and Ia = λS, the SCS runoff model () can be rearranged as follows:where and .
- For each P–Q data pair (Pi, Qi), calculate corresponding λi and Si values via numerical analysis techniques.
- Perform bootstrap BCa procedure, Shapiro–Wilk, and Kolmogorov–Smirnov tests in SPSS (version 18.0 or an equivalent statistics software) for (λi, Si) to check on the normality of both λi and Si.Check the Shapiro–Wilk and Kolmogorov–Smirnov test results of Si and λi to see whether it is normally distributed or not:
- (a)
- If yes, refer to the mean BCa confidence interval for Si and λi optimization.
- (b)
- Otherwise, refer to the median BCa confidence interval for Si and λi optimization.
- Based on the normality of λi and Si, calculate the optimal value for λi and Si, denoted by λoptimum and Soptimum.
- Substitute the λoptimum and Soptimum value into , where Ia = Sλ, to formulate the new SCS CN rainfall–runoff model and calibrate the model according to the given P–Q datasets.
- Given (Pi, Qi) data pairs, compute Si values and λoptimum with (Equation (A1) or (6)) via Excel’s numerical iteration. To date, there is no closed form for the S general equation formula.
- Given (Pi, Qi) data pairs and λ = 0.2, compute S0.2i values with Equation (A3) or (7).
- Correlate S0.2i and Si to obtain a correlation equation between S0.2i and Si via SPSS (or an equivalent statistics software).
- Substitute the S correlation equation from step 9 into the SCS curve number formula to derive CN0.2 value for the watershed of interest.
Appendix D
| Datasets | New SCS (Power) Model | Remark | ||
|---|---|---|---|---|
| E | BIAS | KGE | ||
| DID HP 11, Malaysia | 0.823 | 2.347 | 0.805 | Ia < min rainfall data |
| DID HP 27, Malaysia | 0.919 | 0.647 | 0.956 | Ia < min rainfall data |
| DID HP 11+27, Malaysia | 0.875 | 2.531 | 0.863 | Ia < min rainfall data |
| Kayu Ara, Malaysia | 0.810 | 0 | 0.865 | Ia < min rainfall data |
| Kerayong, Malaysia | 0.888 | 0 | 0.818 | Ia < min rainfall data |
| Attica, Greece | 0.786 | 0 | 0.798 | Ia < min rainfall data |
| Wang Jia Qiao, China | 0.795 | 0 | 0.739 | Ia < min rainfall data |
| Datasets | SCS Model (Equation (2)) | Remark | ||
|---|---|---|---|---|
| E | BIAS | KGE | ||
| DID HP 11, Malaysia | 0.839 | −6.104 | 0.759 | Ia > 60 rainfall data (12.7%) |
| DID HP 27, Malaysia | 0.910 | −4.085 | 0.895 | Ia > 6 rainfall data (2.6%) |
| DID HP 11+27, Malaysia | 0.879 | −4.451 | 0.863 | Ia > 68 rainfall data (9.7%) |
| Kayu Ara, Malaysia | 0.805 | −1.162 | 0.831 | Ia > 6 rainfall data (6.5%) |
| Kerayong, Malaysia | 0.891 | −0.885 | 0.843 | Ia > 2 rainfall data (2.8%) |
| Attica, Greece | 0.780 | −1.846 | 0.784 | Ia > 5 rainfall data (6.6%) |
| Wang Jia Qiao, China | 0.482 | 1.586 | 0.418 | Ia > 4 rainfall data (13.8%) |
Appendix E
| No. | Catchment Locations | Latitude | Longitude |
|---|---|---|---|
| 1 | Attica, Greece | 38° 4′ N | 23° 50′ E |
| 2 | Wangjiaqiao, China | 31° 8′ N | 111° 41′ E |
| Peninsula Malaysian Catchments | |||
| 1 | Kayu Ara, Malaysia | 3° 8′ N | 101° 37′ E |
| 2 | Kerayong, Malaysia | 3° 6′ N | 101° 42′ E |
| 3 | Parit Madirono di Weir | 1° 41′ N | 103° 16′ E |
| 4 | Sg. Johor di Rantau Panjang | 1° 46′ N | 103° 44′ E |
| 5 | Sg. Sayong di Jam. Johor Tenggara | 1° 48′ N | 103° 40′ E |
| 6 | Sg. Kahang di Bt.26 Jln. Kluang | 2° 15′ N | 103° 35′ E |
| 7 | Sg. Lenggor di Bt.42 Kluang/Mersing | 2° 15′ N | 103° 44′ E |
| 8 | Sg. Muar di Buloh Kasap | 2° 33′ N | 102° 45′ E |
| 9 | Sg. Serting di Jam.Padang Gudang | 3° 06′ N | 102° 28′ E |
| 10 | Sg. Triang di Jam. Keretapi | 3° 14′ N | 102° 24′ E |
| 11 | Sg. Bentong di Kuala Marong | 3° 30′ N | 101° 54′ E |
| 12 | Sg. Lepar di Jam. Gelugor | 3° 41′ N | 102° 58′ E |
| 13 | Sg. Kuantan di Bukit Kenau | 3° 55′ N | 103° 03′ E |
| 14 | Sg. Lipis di Benta | 4° 01′ N | 101° 57′ E |
| 15 | Sg. Cherul di Ban Ho | 4° 08′ N | 103° 10′ E |
| 16 | Sg. Kemaman di Rantau Panjang | 4° 16′ N | 103° 15′ E |
| 17 | Sg. Dungun di Jam. Jerangau | 4° 50′ N | 103° 12′ E |
| 18 | Sg. Berang di Menerong | 4° 56′ N | 103° 03′ E |
| 19 | Sg. Telemong di Paya Rapat | 5° 10′ N | 102° 54′ E |
| 20 | Sg. Lebir di Kg. Tualang | 5° 16′ N | 102° 16′ E |
| 21 | Sg. Nerus di Kg. Bukit | 5° 17′ N | 102° 55′ E |
| 22 | Sg. Chalok di Jam. Chalok | 5° 26′ N | 102° 50′ E |
| 23 | Sg. Lanas di Air Lanas | 5° 47′ N | 101° 53′ E |
| 24 | Sg. Besut di Jambatan Jerteh | 5° 44′ N | 102° 29′ E |
| 25 | Sg. Pelarit di Titi Baru | 6° 35′ N | 100° 12′ E |
| 26 | Sg. Buloh di Kg. Batu Tangkup | 6° 33′ N | 100° 17′ E |
| 27 | Sg. Kulim di Ara Kuda | 5° 26′ N | 100° 30′ E |
| 28 | Sg. Kerian di Selama | 5° 13′ N | 100° 41′ E |
| 29 | Sg. Plus di Kg. Lintang | 4° 56′ N | 101° 06′ E |
| 30 | Sg. Raia di Keramat Pulai | 4° 32′ N | 101° 08′ E |
| 31 | Sg. Kampar di Kg. Lanjut | 4° 20′ N | 101° 06′ E |
| 32 | Sg. Bidor di Bidor Malayan Tin Bhd. | 4° 04′ N | 101° 14′ E |
| 33 | Sg. Sungkai di Sungkai | 3° 59′ N | 101° 18′ E |
| 34 | Sg. Slim At Slim River | 3° 49′ N | 101° 24′ E |
| 35 | Sg. Bernam di Tanjung Malim | 3° 40′ N | 101° 31′ E |
| 36 | Sg. Selangor di Rasa | 3° 30′ N | 101° 38′ E |
| 37 | Sg. Gombak di Damsite | 3° 14′ N | 101° 42′ E |
| 38 | Sg. Batu di Kg. Sg. Tua | 3° 16′ N | 101° 41′ E |
| 39 | Sg. Lui di Kg. Lui | 3° 10′ N | 101° 52′ E |
| 40 | Sg. Langat di Dengkil | 2° 59′ N | 101° 47′ E |
| 41 | Sg. Linggi di Sua Betong | 2° 40′ N | 101° 55′ E |
| 42 | Sg. Melaka di Pantai Belimbing | 2° 20′ N | 102° 15′ E |
| 43 | Sg. Kesang di Chin Chin | 2° 17′ N | 102° 29′ E |
| 44 | Sg Sembrong di Bt 2 Air Hitam, Yong Peng | 2° 4′ N | 103° 22′ E |
| 45 | Sg Segamat di Segamat | 2° 31′ N | 102° 51′ E |
| 46 | Sg Sayong di Johor Tenggara | 1° 48′ N | 103° 35′ E |
| 47 | Sg Muar di Bt 57 Jln GemasRompin | 2° 25′ N | 102° 30′ E |
| 48 | Sg Lepar di Jam Gelugor | 3° 43′ N | 102° 56′ E |
| 49 | Sg Lenggor di Bt 42 KluangMersing | 2° 12′ N | 103° 41′ E |
| 50 | Sg Kuantan di Bkt Kenau | 3° 53′ N | 103° 8′ E |
| 51 | Sg Kepis di Jam Kayu Lama | 2° 41′ N | 102° 20′ E |
| 52 | Sg Kemaman di Rantau Panjang | 4° 15′ N | 103° 16′ E |
| 53 | Sg Kecau di Kg Dusun | 4° 22′ N | 102° 6′ E |
| 54 | Sg Kahang di Bt 26 Jln Kluang | 2° 10′ N | 103° 31′ E |
| 55 | Sg Johor di Rantau Panjang | 1° 37′ N | 103° 54′ E |
| 56 | Sg Cherul di Ban Ho | 4° 10′ N | 103° 8′ E |
| 57 | Sg Berang di Menerong | 4° 57′ N | 103° 0′ E |
| 58 | Sg Bentong di Jam K Marong | 3° 31′ N | 101° 55′ E |
| 59 | Sg Bekok di Bt 77 Jln Yong Peng/Labis | 2° 7′ N | 103° 6′ E |
| 60 | Sg Sungkai di Sungkai | 4° 2′ N | 101° 18′ E |
| 61 | Sg Raia di Keramat Pulai | 4° 35′ N | 101° 14′ E |
| 62 | Sg Pari di Jln Silibin, Ipoh | 4° 36′ N | 101° 4′ E |
| 63 | Sg Semenyih di Sg Rinching | 2° 56′ N | 101° 50′ E |
| 64 | Sg Selangor di Rasa | 3° 27′ N | 101° 27′ E |
| 65 | Sg Plus di Kg Lintang | 4° 56′ N | 101° 9′ E |
| 66 | Sg Pelarit di Wang Mu | 6° 34′ N | 100° 13′ E |
| 67 | Sg Melaka di Pantai Belimbing | 2° 20′ N | 102° 14′ E |
| 68 | Sg Lui di Kg Lui | 3° 9′ N | 101° 54′ E |
| 69 | Sg Linggi di Sua Betong | 2° 37′ N | 101° 60′ E |
| 70 | Sg Langat di Dengkil | 2° 58′ N | 101° 38′ E |
| 71 | Sg Kurau di Pondok Tg | 4° 59′ N | 100° 32′ E |
| 72 | Sg Kulim di Ara Kuda | 5° 23′ N | 100° 32′ E |
| 73 | Sg Kerian di Selama | 5° 12′ N | 100° 38′ E |
| 74 | Sg Kinta di Weir G, Tg Tualang | 4° 21′ N | 101° 3′ E |
| 75 | Sg Kesang di Chin Chin | 2° 17′ N | 102° 31′ E |
| 76 | Sg Durian Tunggal di Bt 11 Air Resam | 2° 19′ N | 102° 17′ E |
| 77 | Sg Cenderiang di Bt 32 Jln Tapah | 4° 15′ N | 101° 10′ E |
| 78 | Sg Bidor di Bidor Malayan Tin Bhd | 4° 2′ N | 101° 11′ E |
| 79 | Sg Bernam di Tg Malim | 3° 46′ N | 101° 3′ E |
| 80 | Sg Selangor di Rantau Panjan | 3° 27′ N | 101° 27′ E |
| Sabah State, Malaysian Catchments | |||
| 1 | Sg Tawau di Kuhara | 4° 16′ N | 117° 53′ E |
| 2 | Sg Kalabakan di Kalabakan | 4° 27′ N | 117° 23′ E |
| 3 | Sg Kalumpang di Mostyn Bridge | 4° 38′ N | 118° 9′ E |
| 4 | Sg Talangkai di Lotong | 4° 43′ N | 116° 26′ E |
| 5 | Sg Mengalong di Sindumin | 4° 59′ N | 115° 34′ E |
| 6 | Sg Kuamut di Ulu Kuamut | 5° 4′ N | 117° 26′ E |
| 7 | Sg Lakutan di Mesapol Quarry | 5° 7′ N | 115° 37′ E |
| 8 | Sg Segama di Limkabong | 5° 7′ N | 118° 7′ E |
| 9 | Sg Sook di Biah | 5° 15′ N | 116° 8′ E |
| 10 | Sg Baiayo di Bandukan | 5° 26′ N | 116° 8′ E |
| 11 | Sg Apin-Apin di Waterworks | 5° 29′ N | 116° 15′ E |
| 12 | Sg Kegibangan di Tampias P.H. | 5° 41′ N | 116° 22′ E |
| 13 | Sg Papar di Kaiduan | 5° 46′ N | 116° 5′ E |
| 14 | Sg Papar di Kogopon | 5° 42′ N | 116° 2′ E |
| 15 | Sg Labuk di Tampias | 5° 43′ N | 116° 51′ E |
| 16 | Sg Moyog di Penampang | 5° 54′ N | 116° 6′ E |
| 17 | Sg Tungud di Basai | 6° 3′ N | 117° 18′ E |
| 18 | Sg Tuaran di Pump House 1 | 6° 9′ N | 116° 14′ E |
| 19 | Sg Sugut di Bukit Mondou | 6° 11′ N | 117° 14′ E |
| 20 | Sg Kadamaian di Tamu Darat | 6° 15′ N | 116° 27′ E |
| 21 | Sg Wariu di Bridge No.2 | 6° 19′ N | 116° 29′ E |
| 22 | Sg Bongan di Timbang Batu Sabah | 6° 26′ N | 116° 48′ E |
| 23 | Sg Bengkoka di Kobon | 6° 37′ N | 117° 2′ E |
| Sarawak State, Malaysian Catchments | |||
| 1 | Sg Kayan di Krusen | 1° 4′ N | 110° 29′ E |
| 2 | Sg Kedup di New Meringgu | 1° 3′ N | 110° 33′ E |
| 3 | Sg Entebar di Entebar | 1° 0′ N | 111° 32′ E |
| 4 | Sg Ai di Lubok Antu | 1° 2′ N | 111° 49′ E |
| 5 | Sg Sabal Kruin di Sabal Kruin | 1° 8′ N | 110° 53′ E |
| 6 | Sg Sarawak Kanan di Pk Buan Bidi | 1° 23′ N | 110° 6′ E |
| 7 | Sg Sarawak Kiri di Kg Git | 1° 21′ N | 110° 15′ E |
| 8 | Sg Tuang di Kg Batu Gong | 1° 20′ N | 110° 26′ E |
| 9 | Sg Sekerang di Entaban | 1° 19′ N | 111° 37′ E |
| 10 | Sg Layar di Ng Lubau | 1° 29′ N | 111° 35′ E |
| 11 | Sg Sebatan di Sebatan | 1° 48′ N | 111° 20′ E |
| 12 | Sg Katibas di Ng Mukeh | 1° 50′ N | 112° 37′ E |
| 13 | Sg Sarikei di Ambas | 1° 58′ N | 111° 30′ E |
| 14 | Btg Rajang di Ng Ayam | 1° 56′ N | 111° 53′ E |
| 15 | Sg Oya di Setapang | 3° 1′ N | 112° 35′ E |
| 16 | Btg Mukah di Selangau | 2° 54′ N | 112° 5′ E |
| 17 | Sg Sibiu di Sibiu (Atc) | 3° 13′ N | 113° 9′ E |
| 18 | Sg Limbang di Insungai | 4° 44′ N | 114° 59′ E |
| 19 | Sg Trusan di Long Tengoa D | 4° 35′ N | 115° 20′ E |
References
- Danáčová, M.; Földes, G.; Labat, M.M.; Kohnová, S.; Hlavčová, K. Estimating the Effect of Deforestation on Runoff in Small Mountainous Basins in Slovakia. Water 2020, 12, 3113. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Zhang, D.; Liang, K.; Li, X.; Dong, G. Reduced Runoff due to Anthropogenic Intervention in the Loess Plateau, China. Water 2016, 8, 458. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Xia, J.; Yu, J.; Randall, M.; Zhang, Y.; Zhao, T.; Pan, X.; Zhai, X.; Shao, Q. Simulation and Assessment of Urbanization Impacts on Runoff Metrics: Insights from Landuse Changes. J. Hydrol. 2018, 560, 247–258. [Google Scholar] [CrossRef]
- Zhai, R.; Tao, F. Contributions of Climate Change and Human Activities to Runoff Change in Seven Typical Catchments across China. Sci. Total Environ. 2017, 605–606, 219–229. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Liu, M.; Hu, Y.; Shi, T.; Qu, X.; Walter, M.T. Effects of Urbanization on Direct Runoff Characteristics in Urban Functional Zones. Sci. Total Environ. 2018, 643, 301–311. [Google Scholar] [CrossRef]
- Tedela, N.H.; McCutcheon, S.C.; Rasmussen, T.C.; Hawkins, R.H.; Swank, W.T.; Campbell, J.L.; Adams, M.B.; Jackson, C.R.; Tollner, E.W. Runoff Curve Numbers for 10 Small Forested Watersheds in the Mountains of the Eastern United States. J. Hydrol. Eng. 2012, 17, 1188–1198. [Google Scholar] [CrossRef] [Green Version]
- Ling, L.; Yusop, Z.; Yap, W.-S.; Tan, W.L.; Chow, M.F.; Ling, J.L. A Calibrated, Watershed-Specific SCS-CN Method: Application to Wangjiaqiao Watershed in the Three Gorges Area, China. Water 2019, 12, 60. [Google Scholar] [CrossRef] [Green Version]
- N.E.D.C. Engineering Hydrology Training Series. In Module 205-SCS Runoff Equation; N.E.D.C.: London, UK, 1997; Available online: https://d32ogoqmya1dw8.cloudfront.net/files/geoinformatics/steps/nrcs_module_runoff_estimation.pdf (accessed on 8 July 2022).
- Soil Conservation Service (S.C.S.). National Engineering Handbook; US Soil Conservation Service: Washington, DC, USA, 1964; Chapter 10; Section 4. Available online: https://directives.sc.egov.usda.gov/RollupViewer.aspx?hid=17092 (accessed on 10 July 2022).
- USDA; NRCS. National Engineering Handbook, Part 630 Hydrology; US Soil Conservation Service: Washington, DC, USA, 1964; Chapter 10. [Google Scholar]
- Mishra, S.K.; Babu, P.S.; Singh, V.P. SCS-CN Method Revisited. In Advances in Hydraulics and Hydrology; Water Resources Publications: Littleton, CO, USA, 2007. [Google Scholar]
- Tan, W.J.; Ling, L.; Yusop, Z.; Huang, Y.F. New Derivation Method of Region Specific Curve Number for Urban Runoff Prediction at Melana Watershed in Johor, Malaysia. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 401, p. 012008. [Google Scholar] [CrossRef]
- Yuan, L.; Sinshaw, T.; Forshay, K.J. Review of Watershed-Scale Water Quality and Nonpoint Source Pollution Models. Geosciences 2020, 10, 25. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, R.H.; Yu, B.; Mishra, S.K.; Singh, V.P. Another Look at SCS-CN Method. J. Hydrol. Eng. 2001, 6, 451–452. [Google Scholar] [CrossRef]
- Hawkins, R.; Ward, T.J.; Woodward, E.; van Mullem, J.A. Continuing Evolution of Rainfall-Runoff and the Curve Number Precedent. In Proceedings of the 2nd Joint Federal Interagency Conference, Las Vegas, NV, USA, 27 June–1 July 2010; pp. 1–12. [Google Scholar]
- Tan, W.J.; Ling, L.; Yusop, Z.; Huang, Y.F. Claim Assessment of a Rainfall Runoff Model with Bootstrap. In Proceedings of the Third International Conference on Computing, Mathematics and Statistics (iCMS2017), Langkawi, Malaysia, 7–8 November 2017; Springer Nature: Singapore, 2019. [Google Scholar]
- Hawkins, R.H.; Khojeini, A.V. Initial Abstraction and Loss in the Curve Number Method. Hydrology and Water Resources in Arizona and the Southwest 2000, 30, 29–35. [Google Scholar]
- DID. Hydrological Procedure 27 Design Flood Hydrograph Estimation for Rural Catchments in Malaysia; JPS, DID: Kuala Lumpur, 2010. Available online: https://www.water.gov.my/jps/resources/PDF/Hydrology%20Publication/Hydrological_Procedure_No_27_(HP_27).pdf (accessed on 5 August 2022).
- DID. Hydrological Procedure 11 Design Flood Hydrograph Estimation for Rural Catchments in Malaysia; JPS, DID: Kuala Lumpur, 2018. Available online: http://h2o.water.gov.my/man_hp1/HP11.pdf (accessed on 20 July 2022).
- Abustan, I.; Sulaiman, A.H.; Wahid, N.A.; Baharudin, F. Determination of Rainfall-Runoff Characteristics in An Urban Area: Sungai Kerayong Catchment, Kuala Lumpur. In Proceedings of the 11th International Conference on Urban Drainage, Palermo, Italy, 23–26 September 2018; Springer International Publishing: New York, NY, USA, 2018. [Google Scholar]
- Ling, L.; Chow, M.F.; Tan, W.L.; Tan, W.J.; Tan, C.Y.; Yusop, Z. New Regional-Specific Urban Runoff Prediction Model of Sungai Kayu Ara Catchment in Malaysia. In Lecture Notes in Civil Engineering; Springer Nature: Singapore, 2020; Volume 59, pp. 161–168. [Google Scholar]
- Baltas, E.A.; Dervos, N.A.; Mimikou, M.A. Technical Note: Determination of the SCS Initial Abstraction Ratio in an Experimental Watershed in Greece. Hydrol. Earth Syst. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef] [Green Version]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1993; ISBN 978-0-412-04231-7. [Google Scholar]
- Davison, A.C. Cambridge Series in Statistical and Probabilistic; Cambridge University Press: New York, NY, USA, 2003; ISBN 978-0-511-67299-6. [Google Scholar]
- Efron, B. Large-Scale Inference: Empirical Bayes Methods for Estimation, Testing, and Prediction; Cambridge University Press: New York, NY, USA, 2013; ISBN 978-1-107-61967-8. [Google Scholar]
- Rochowicz, J.A.J. Bootstrapping Analysis, Inferential Statistics and EXCEL. Spredsheets Educ. (Ejsie) 2010, 4, 1–23. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ling, L.; Yusop, Z.; Ling, J.L. Statistical and Type II Error Assessment of a Runoff Predictive Model in Peninsula Malaysia. Mathematics 2021, 9, 812. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical Note: Inherent Benchmark or Not? Comparing Nash—Sutcliffe and Kling—Gupta Efficiency Scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef] [Green Version]
- Miles, J. R Squared, Adjusted R Squared. In Wiley StatsRef: Statistics Reference Online; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Hawkins, R.H.; Theurer, F.D.; Rezaeianzadeh, M. Understanding the Basis of the Curve Number Method for Watershed Models and TMDLs. J. Hydrol. Eng. 2019, 24, 06019003. [Google Scholar] [CrossRef]
- Ling, L.; Yusop, Z. Derivation of Region-Specific Curve Number for an Improved Runoff Prediction. In Improving Flood Management, Prediction and Monitoring: Case Studies in Asia; Community, Environment and Disaster Risk Management; Emerald Publishing Limited: Bingley, UK, 2018; Volume 20, pp. 37–48. ISBN 978-1-78756-552-4. [Google Scholar]
- Ling, L.; Yusop, Z.; Chow, M.F. Urban Flood Depth Estimate with a New Calibrated Curve Number Runoff Prediction Model. IEEE Access 2020, 8, 10915–10923. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Pinos, J.; Quesada-Román, A. Flood Risk-Related Research Trends in Latin America and the Caribbean. Water 2021, 14, 10. [Google Scholar] [CrossRef]
- Fu, M.; Fan, T.; Ding, Z.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Deep Learning Data-Intelligence Model Based on Adjusted Forecasting Window Scale: Application in Daily Streamflow Simulation. IEEE Access 2020, 8, 32632–32651. [Google Scholar] [CrossRef]
- Kaya, C.M.; Tayfur, G.; Gungor, O. Predicting Flood Plain Inundation for Natural Channels Having No Upstream Gauged Stations. J. Water Clim. Change 2019, 10, 360–372. [Google Scholar] [CrossRef] [Green Version]
| Dataset & Location | E | N | Bias (mm) | KGE | Sλ (mm) | Ia = Sλ (mm) | Ia/S |
|---|---|---|---|---|---|---|---|
| DID HP 11, Malaysia | 0.823 | 474 | 2.35 | 0.805 | 139.48 | 3.71 | 0.027 |
| DID HP 27, Malaysia | 0.919 | 227 | 0.65 | 0.956 | 165.94 | 2.33 | 0.014 |
| DID HP 11+27, Malaysia | 0.875 | 701 | 2.535 | 0.863 | 143.99 | 3.19 | 0.022 |
| Kayu Ara, Malaysia | 0.810 | 94 | 0 | 0.865 | 24.79 | 2.20 | 0.089 |
| Kerayong, Malaysia | 0.888 | 73 | 0 | 0.818 | 9.08 | 1.55 | 0.171 |
| Attica, Greece | 0.786 | 77 | 0 | 0.798 | 23.73 | 1.85 | 0.078 |
| Wang Jia Qiao, China | 0.795 | 29 | 0 | 0.739 | 386.57 | 3.57 | 0.009 |
| Dataset & Location | Correlation Equation | R2adj | p-Value |
|---|---|---|---|
| DID HP 11, Malaysia | S0.2 = S0.2650.878 | 0.977 | <0.001 |
| DID HP 27, Malaysia | S0.2 = S0.1660.874 | 0.997 | <0.001 |
| DID HP 11+27, Malaysia | S0.2 = S0.2340.880 | 0.998 | <0.001 |
| Kayu Ara, Malaysia | S0.2 = 4.263 S0.2460.438 | 0.893 | <0.001 |
| Kerayong, Malaysia | S0.2 = 3.223 S0.1990.355 | 0.849 | <0.001 |
| Attica, Greece | S0.2 = 5.057 S0.1940.357 | 0.846 | <0.001 |
| Wang Jia Qiao, China | S0.2 = S0.2140.702 | 0.975 | <0.001 |
| Datasets | BCa 99% Confidence Interval | |||
|---|---|---|---|---|
| S & Curve Numbers | S0.2 (mm) | CN0.2 | ||
| Dataset & Location | Lower | Upper | Lower | Upper |
| DID HP 11, Malaysia | 100.99 | 139.48 | 76.88 | 81.54 |
| DID HP 27, Malaysia | 118.65 | 165.94 | 74.46 | 79.62 |
| DID HP 11+27, Malaysia | 115.01 | 143.98 | 76.21 | 79.60 |
| Kayu Ara, Malaysia | 20.75 | 331.07 | 82.43 | 94.04 |
| Kerayong, Malaysia | 8.77 | 397.55 | 90.40 | 97.33 |
| Attica, Greece | 23.73 | 314.15 | 86.57 | 94.19 |
| Wang Jia Qiao, China | 289.86 | 553.69 | 75.08 | 82.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.K.F.; Ling, L.; Yusop, Z. The Revised Curve Number Rainfall–Runoff Methodology for an Improved Runoff Prediction. Water 2023, 15, 491. https://doi.org/10.3390/w15030491
Lee KKF, Ling L, Yusop Z. The Revised Curve Number Rainfall–Runoff Methodology for an Improved Runoff Prediction. Water. 2023; 15(3):491. https://doi.org/10.3390/w15030491
Chicago/Turabian StyleLee, Kenneth Kai Fong, Lloyd Ling, and Zulkifli Yusop. 2023. "The Revised Curve Number Rainfall–Runoff Methodology for an Improved Runoff Prediction" Water 15, no. 3: 491. https://doi.org/10.3390/w15030491










